One of the basic problems in the field of operator algebras is to develop a functional calculus for either a single operator , or a collection
of operators. These operators could in principle act on any function space, but typically one either considers complex matrices (which act on a complex finite dimensional space), or operators (either bounded or unbounded) on a complex Hilbert space. (One can of course also obtain analogous results for real operators, but we will work throughout with complex operators in this post.)
Roughly speaking, a functional calculus is a way to assign an operator or
to any function
in a suitable function space, which is linear over the complex numbers, preserve the scalars (i.e.
when
), and should be either an exact or approximate homomorphism in the sense that
should hold either exactly or approximately. In the case when the are self-adjoint operators acting on a Hilbert space (or Hermitian matrices), one often also desires the identity
to also hold either exactly or approximately. (Note that one cannot reasonably expect (1) and (2) to hold exactly for all if the
and their adjoints
do not commute with each other, so in those cases one has to be willing to allow some error terms in the above wish list of properties of the calculus.) Ideally, one should also be able to relate the operator norm of
or
with something like the uniform norm on
. In principle, the existence of a good functional calculus allows one to manipulate operators as if they were scalars (or at least approximately as if they were scalars), which is very helpful for a number of applications, such as partial differential equations, spectral theory, noncommutative probability, and semiclassical mechanics. A functional calculus for multiple operators
can be particularly valuable as it allows one to treat
as being exact or approximate scalars simultaneously. For instance, if one is trying to solve a linear differential equation that can (formally at least) be expressed in the form
for some data , unknown function
, some differential operators
, and some nice function
, then if one’s functional calculus is good enough (and
is suitably “elliptic” in the sense that it does not vanish or otherwise degenerate too often), one should be able to solve this equation either exactly or approximately by the formula
which is of course how one would solve this equation if one pretended that the operators were in fact scalars. Formalising this calculus rigorously leads to the theory of pseudodifferential operators, which allows one to (approximately) solve or at least simplify a much wider range of differential equations than one what can achieve with more elementary algebraic transformations (e.g. integrating factors, change of variables, variation of parameters, etc.). In quantum mechanics, a functional calculus that allows one to treat operators as if they were approximately scalar can be used to rigorously justify the correspondence principle in physics, namely that the predictions of quantum mechanics approximate that of classical mechanics in the semiclassical limit
.
There is no universal functional calculus that works in all situations; the strongest functional calculi, which are close to being an exact *-homomorphisms on very large class of functions, tend to only work for under very restrictive hypotheses on or
(in particular, when
, one needs the
to commute either exactly, or very close to exactly), while there are weaker functional calculi which have fewer nice properties and only work for a very small class of functions, but can be applied to quite general operators
or
. In some cases the functional calculus is only formal, in the sense that
or
has to be interpreted as an infinite formal series that does not converge in a traditional sense. Also, when one wishes to select a functional calculus on non-commuting operators
, there is a certain amount of non-uniqueness: one generally has a number of slightly different functional calculi to choose from, which generally have the same properties but differ in some minor technical details (particularly with regards to the behaviour of “lower order” components of the calculus). This is a similar to how one has a variety of slightly different coordinate systems available to parameterise a Riemannian manifold or Lie group. This is on contrast to the
case when the underlying operator
is (essentially) normal (so that
commutes with
); in this special case (which includes the important subcases when
is unitary or (essentially) self-adjoint), spectral theory gives us a canonical and very powerful functional calculus which can be used without further modification in applications.
Despite this lack of uniqueness, there is one standard choice for a functional calculus available for general operators , namely the Weyl functional calculus; it is analogous in some ways to normal coordinates for Riemannian manifolds, or exponential coordinates of the first kind for Lie groups, in that it treats lower order terms in a reasonably nice fashion. (But it is important to keep in mind that, like its analogues in Riemannian geometry or Lie theory, there will be some instances in which the Weyl calculus is not the optimal calculus to use for the application at hand.)
I decided to write some notes on the Weyl functional calculus (also known as Weyl quantisation), and to sketch the applications of this calculus both to the theory of pseudodifferential operators. They are mostly for my own benefit (so that I won’t have to redo these particular calculations again), but perhaps they will also be of interest to some readers here. (Of course, this material is also covered in many other places. e.g. Folland’s “harmonic analysis in phase space“.)
— 1. Weyl quantisation of polynomials —
The simplest class of functions to which one can set up a functional calculus are the polynomials, as this does not require any analytic tools to define. To begin with we will ignore the conjugation structure, thus we will not attempt to implement (2).
In order to be able to freely compose all the operators under consideration, we will assume that there is some dense space of test functions (or perhaps Schwartz functions) which is preserved by all of the
, so that any composition of finitely many of the
will be densely defined. (Alternatively, one could proceed at a purely formal level for this discussion, working in an abstract algebra generated by the
.)
In the case of a single operator
, the polynomial calculus is obvious: given any polynomial
with complex coefficients , one can define
to be the operator
In other words, the functional calculus is the linear map that takes each monomial
to the operator
. This calculus is of course an exact homomorphism, as it is linear and obeys (1) exactly.
Now we consider the situation with multiple operators. For simplicity, let us just consider the case of two operators . We then consider a polynomial
with complex coefficients , and ask how to define the operator
.
The most obvious way to define is by direct substitution, which I will call the Kohn-Nirenberg calculus:
(Depending on the interpretation of the operators , this calculus might also be referred to as the Wick-ordered calculus or normal-ordered calculus.) This is certainly a well-defined calculus, but when
and
do not commute, the calculus has a bias in that it always places
to the left of
; in particular, if one interchanges the roles of
and
then one obtains a different calculus, which one might call the anti-Kohn-Nirenberg calculus:
Intermediate, and more symmetric, between these two calculi, is the Weyl calculus
where the Weyl ordering of the monomial
is defined to be the average of all the
ways to multiply
copies of
and
copies of
together:
where range over all tuples which contain
copies of
and
copies of
, thus for instance
and so forth.
Remark 1 Strictly speaking, the use of the terminology
here is an abuse of notation, because it suggests a functional relationship between
and
which need not be the case. In particular, if the monomials
and
are equal as operators, this does not necessarily imply that the Weyl-ordered monomials
and
are equal. One could fix this notation by working first with formal symbols
generating a free commutative algebra, and writing
in place of
, so that the Weyl map
becomes a not-quite-homomorphism from the commutative algebra generated by
and
to the non-commutative algebra generated by
and
. We have chosen however to not be quite so formal, and allow some abuse of notation to simplify the exposition.
When and
commute, of course, all these calculi coincide with each other; it is only in the non-commuting case that some distinctions between the calculi emerge. The Weyl calculus may seem complicated, but it has somewhat cleaner formulae with regard to products. For instance, the Weyl calculus works perfectly with respect to powers
of affine combinations
of
, where
are scalars:
(By this equation, we mean that if is the polynomial
, then
is the operator
.) Thus for instance
In contrast, the Kohn-Nirenberg calculus (or the anti-Kohn-Nirenberg calculus) distorts this ordering, for instance we have
Indeed, by comparing coefficients in (3) and using linearity we see that the identity (3) (for arbitrary ) in fact uniquely defines the Weyl calculus. One consequence of this is that the Weyl calculus is not only symmetric with respect to interchange of the underlying operators
, but in fact respects all linear changes of variable: if
are scalar affine combinations of
,
is a polynomial of two variables, and
is the polynomial
, then we have that
Indeed, from (3) we see that this identity holds for the mixed monomials , and then by linearity it is true for all polynomials.
One can also extend the Weyl calculus to formal (i.e. not necessarily convergent) infinite series
by declaring to be the formal series of operators
In doing so, the identity (3) can be expressed in a very convenient form
where we view the exponential function here as the formal infinite series
Remark 2 The fact that Weyl calculus preserves the exponential map is the reason why we view this calculus as being analogous to normal coordinates in Riemannian geometry, as well as exponential coordinates (of the first kind) on Lie groups, discussed for instance in this previous blog post. In contrast, the Kohn-Nirenberg quantisation gives
which is analogous to exponential coordinates of the second kind on Lie groups.
Now we study the extent to which the homomorphism property (1) holds in the Weyl calculus, i.e. we study the discrepancy between and
. When
and
commute, it is easy to see that (1) holds exactly. In general, these two expressions can be quite different; but when
and
almost commute, so that the commutator
is non-zero but small, we expect (1) to be approximately true. Motivated by quantum-mechanical examples, we will study a model case when
and
obey the Heisenberg commutator relationship
where is a small positive real number. (In some literature, the sign convention here is reversed.) In this case, we see that any two ways to multiply
copies of
and
copies of
together will differ by polynomials of degree strictly less than
. Among other things, this shows that any polynomial of
and
can be rewritten into a Weyl-ordered form, by first ordering the top degree terms (at the cost of introducing some messy lower degree terms) and then recursively working on the lower order terms. The same procedure also implies that this Weyl-ordered form is unique. For instance,
This already implies that for any two polynomials , there must be a unique “product” polynomial
with the property that
In the classical limit , this operation is simply pointwise product:
Now we work out what the product operation (known as the Moyal product) is for non-zero
. To avoid some rather messy combinatorics, it turns out to be cleanest to proceed using the formal exponential function (5) applied to various combinations
of
and
. (This is an instance of the method of generating functions in action.)
We first observe from (6) that we have the general commutation relationship
where is the anti-symmetric form
This is already the first hint of the correspondence between quantum mechanics (whose dynamics is based on the commutator ) and classical mechanics (whose dynamics is based on the Poisson bracket
). From this and the Baker-Campbell-Hausdorff formula, we conclude (formally, at least) that
One can make this identity rigorous (at the level of formal power series) as follows. We first observe that the Hadamard lemma
holds at the level of formal power series, where is the commutator operation
. This can be seen by first establishing the formal differentiation identity
(which comes from the formal identity and the product rule) and then using this to solve for
as a formal power series to conclude that
and then setting . Using this lemma together with (8), we see in particular that
Now consider the expression
as a formal power series in . Then
is the identity, and the formal derivative
can be expressed as
which after using (10) simplifies to
which on solving the formal series leads to
which gives (9) after setting .
Combining (9), (5) and (7) (as well as the uniqueness of the Weyl ordering), we conclude that
where both sides are viewed as formal power series in indeterminates . Comparing coefficients, we see that
with the convention that vanishes for
, and similarly for
. We write
where is the tensor product of
copies of
. Since
and similarly
where denotes the gradient with respect to the
variables, we conclude that
This formula is valid for all monomials , and so by bilinearity we conclude the explicit formula
for the Moyal product, thus
The expression is also known as the Poisson bracket of
and
, and is denoted
, thus
Note that is symmetric for even
and anti-symmetric for odd
. Subtracting, we conclude that
Thus we see that the normalised commutator of the Moyal product converges in the semiclassical limit
; this is one manifestation of the correspondence principle.
The above discussion was for two operators obeying the Heisenberg commutation relation (6), but one can check that a similar calculus can also be developed for any tuple
of operators, and if they obey a Heisenberg-like commutation law
for some anti-symmetric form , then the Moyal product formula (11) holds; the arguments are basically identical to the two variable case (except for some notational complications) and are left as an exercise to the reader.
Once one has set up a calculus for complex polynomials of some non-self-adjoint operators
, one can then extend it to polynomials
of the original arguments
and their conjugates (or equivalently, to polynomials of the real and imaginary parts of the
) by using the calculus for
. This allows one to define operators
when
is a polynomial of the real and imaginary parts of
, basically by substituting
and
for
and
respectively. One advantage of the Weyl calculus, not shared in general by the Kohn-Nirenberg calculus, is that the identity (2) holds exactly; this is basically a special case of the affine invariance properties of the Weyl calculus mentioned earlier. In a similar vein, the Weyl calculus ensures that
for any complex polynomial , where
is the complex polynomial whose coefficients are the complex conjugates of the coefficients of
. In particular, if
are self-adjoint and
has real coefficients, then
is again self-adjoint.
— 2. Weyl quantisation of smooth symbols —
The above algebraic formalism allowed one to define the Weyl quantisation of any
-tuple of operators (preserving some dense space of test functions) as long as
was a polynomial; one could also handle the case when
was a formal power series, provided that one was willing to make
a formal power series also. But of course we would like to expand the calculus beyond the spaces of polynomials and formal power series.
One obvious way is to work with convergent power series instead of formal power series, but this approach, by definition, only applies for real analytic functions . Also, being real analytic (which, by the root test, can be viewed as an exponential decay hypothesis on the coefficients
) may not be enough in some cases to ensure convergence of the formal power series
; one may need faster decay on the
(e.g. decay like
or something similar) before one can justify convergence in a suitable sense.
To get beyond the analytic category, it turns out that one can use Fourier-analytic methods, using Fourier expansions as a substitute for power series expansions. The key point, of course, is that Fourier analysis works well for spaces of functions that are significantly rougher than real analytic.
To illustrate the method, let us again work with just two operators and
. We will assume that
and
are (essentially) self-adjoint, which by spectral theory suggests that one should be able to define
for (sufficiently nice) real-valued functions
. (The distinction between real and complex functions was not apparent at the polynomial level, since any polynomial on a real vector space can be automatically complexified uniquely to a polynomial on the associated complex vector space.) The starting point is the Fourier inversion formula
where is the Fourier transform, which in our choice of normalisations becomes
From the inversion formula, it is natural to expect that the Weyl quantisation of
should be given by the formula
which in view of (5) leads us to
which we will take as a definition of for general functions
.
Of course, to make this definition rigorous, one has to specify some regularity hypotheses on , and check that the integral actually converges in some suitable sense; also, it would be reassuring to verify that the definition is compatible with the polynomial calculus given earlier. At present,
and
are completely abstract operators, which makes this task quite difficult; so we will now work with a much more concrete situation, namely that of the one-dimensional position operator
and momentum operator
, defined on test functions in
by the formulae
Note that this obeys the Heisenberg relation
and thus by (9) one has (formally, at least)
for any . On the other hand, we have
while from solving the transport equation we see that
for suitable test functions , and thus
Again working formally, we conclude that
which we expand as
Making the change of variables , we rewrite this as
Next, from the distributional Fourier inversion formula
where is the Dirac delta, we can rewrite this as
which on performing the integral simplifies to
or after the change of variables ,
We remark that the Kohn-Nirenberg calculus comes out almost identically, except that the argument
is replaced with
. Similarly for the anti-Kohn-Nirenberg calculus (in which
is replaced by
). The Weyl calculus treats the input variable
and the output variable
on equal footing, whereas the Kohn-Nirenberg calculus prefers one to the other. In particular, we have the convenient formal identity
so that formally self-adjoint when
is real-valued.
We will take the formula (14) as our definition of the Weyl quantisation , at least when
is a Schwarz function and
obeys the weak regularity bounds
for all , all
, some constant
, and some constants
depending on
. (This is weaker than the symbol bounds that usually arise in the theory of pseudodifferential operators, but will suffice for the discussion here.)
Exercise 1 Show that for
and
as above, the integrand
is absolutely integrable in
, and that the integrand
is absolutely integrable in
, making
well-defined. Show in fact that
is a Schwartz function.
Exercise 2 Show that the above definition agrees with the previous definitions of
and
. (One approach is by direct computation; another is to try to make the above formal calculations fully rigorous.)
Exercise 3 (Translation invariance) If
obeys the weak regularity bound (16) and
for some
, show that
where
is the translation operator
and
is the modulation operator
One can in fact obtain similar symmetries for the entire Weil representation of the (affine) metaplectic group, but we will not do so here.
One can get some intuition as to what the operators do by testing them on gaussian wave packets
It turns out that the Taylor series of around
is a good approximation for the action of
on such a packet:
as
, where
denotes a quantity with
norm of
.
Thus we have the asymptotic series
with each term of order being of
norm
. (Note that this does not imply that the series is convergent in
, because we have no control of the dependence on
of the implied constant in the
notation.)
Proof: (Sketch) By using the symmetries in Exercise 3, we may normalise . If
is a polynomial of degree at most
, then the the two sides of (17) agree exactly, with no need for the error term
. By subtracting off the order
Taylor expansion, we thus see that it suffices to show that
whenever vanishes to order at least
at the origin. But this can be verified from (14) and a routine stationary phase computation.
The same computation allows one to replace the norm by any other of the Frechet norms in the Schwartz space, as long as
are assumed to be of polynomial size in
, i.e.
.
From (14), we see that any quantisation is formally an integral operator
with distributional kernel
Applying the Fourier inversion formula, we thus see (formally, at least) that any integral operator (18) is also a quantisation where
is uniquely determined by the formula
In particular, given two quantisations and
, their composition
is formally an integral operator with distributional kernel
and hence is formally a quantisation , where
Thus, for instance,
This integral will, in general, not be absolutely integrable. However, the phase is only stationary at
. By using a suitable smooth dyadic decomposition and many integrations by parts, we can then show that this integral can be given a convergent interpretation if
obey the weak regularity bound (16). Similarly for other evaluations
, as well as higher derivatives of
evaluated at arbitrary points
. Indeed, with a certain amount of technical effort (which we omit here) we see that
is well-defined and obeys (16), and we can rigorously establish the composition law
If and
are polynomials, we see (using the fact that any operator has a unique symbol
) that the product
given here coincides exactly with the Moyal product (11). As a consequence, by testing on gaussian wave packets using Lemma 1, one can show that this composition law
has an asymptotic series given by the Moyal product, thus for any
, one has
where the error obeys the bound (16) (with the constant
independent of
and
, and the constant
depending on
but uniform in
). We will not give full details here, but roughly speaking, bound
to high order at some point
, one can subtract off a Taylor polynomial from both
and
to reduce to the case when at least one of
vanishes to high order at
, at which point Lemma 1 shows that
almost annihilates any gaussian wave packet supported near
in phase space, and thus must have very small symbol at
; a similar (but more complicated) argument also allows one to control derivatives of the symbol of
. In a similar vein, the commutator
of two operators
with symbols
obeying (16) can be described by a symbol with asymptotic series (12); we omit the details. These facts form the basis for the pseudodifferential calculus, which we will not develop further here; see e.g. Taylor’s book or Folland’s book for more details.
We can also relate the Moyal product to the Wigner transform
Comparing this with (19), we see that can also be interpreted as the symbol of the rank one operator
where . Given a quantised operator
, we (formally, at least) have the relatino
and hence (by (15) and (20)) we see (again formally, at least) that
so that the action of pseudodifferential operators such as can be described through the Wigner transform by some applications of the Moyal product.
Continuing this line of thought, suppose that is a time-dependent function obeying Schrödinger’s equation
for some real-valued symbol (representing the Hamiltonian of the system). Passing from the wave function
to the density matrix
, we observe that Schrödinger’s equation implies Heisenberg’s equation
and hence (by formal applicaton of the Moyal product)
Applying (12), we see that the Wigner transform of obeys the perturbed Hamiltonian flow equation
This should be compared with the evolution of a classical density function in phase space with respect to transport along Hamilton’s equation of motion
which is given by the transport equation
Thus we see in the semiclassical limit , the equation of motion for the Wigner transform (21) under the Schrödinger flow converges formally to the equation of motion for a classical density transported under Hamiltonian flow. This is one of the basic manifestations of the correspondence principle relating quantum and classical mechanics, and suggests that the Wigner transform of a wave function is a quantum analogue of a density function in phase space. (But the analogy is not perfect; in particular, the Wigner transform is almost never a non-negative function. See Folland’s book for more discussion.) Making all of these formal calculations and heuristics rigorous is a non-trivial task, requiring the development of the theory of Fourier integral operators, and will not be discussed here.

17 comments
Comments feed for this article
8 October, 2012 at 3:53 am
Fred Lunnon
Section 1 penultimate sentence: F^*(z) definition contradictory?
[Sorry, I don’t see what the problem is here. Note that the use of the asterisk in does not quite denote adjoint or complex conjugation, although it is of course related to those two concepts. -T.]
does not quite denote adjoint or complex conjugation, although it is of course related to those two concepts. -T.]
8 October, 2012 at 5:15 am
David Speyer
I haven’t finished reading to the end yet, but I think the first section would be much easier to read if you started with the observation that Weyl quantization has a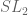 symmetry. Namely, let
symmetry. Namely, let  be the two dimensional vector space generated by
be the two dimensional vector space generated by  and
and  ; let
; let  be the tensor algebra
be the tensor algebra  and let
and let  be the ring generated by the operators
be the ring generated by the operators  and
and  . If
. If  is in
is in  , and
, and  and
and  are operators from
are operators from  , then
, then ![[gu, gv]= [u,v]](https://s0.wp.com/latex.php?latex=%5Bgu%2C+gv%5D%3D+%5Bu%2Cv%5D&bg=ffffff&fg=545454&s=0&c=20201002) . So
. So  acts on
acts on  , and the map
, and the map  commutes with the
commutes with the  action.
action.
The Weyl quantization is to lift an element of to the unique preimage in
to the unique preimage in  which lies in
which lies in  . This choice of lifts manifestly respects the
. This choice of lifts manifestly respects the  symmetry.
symmetry.
Therefore, in section 1, there is no need to carry around the and
and  terms. Just use the
terms. Just use the  symmetry to reduce to the case where one operator is
symmetry to reduce to the case where one operator is  and the other is
and the other is 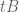 . Moreover, if you want to make life even simpler, you can work with just
. Moreover, if you want to make life even simpler, you can work with just  and
and  and restore the powers of
and restore the powers of  at the end by homogeneity.
at the end by homogeneity.
8 October, 2012 at 11:46 am
Terence Tao
Yes, this would work, although for the purposes of Section 1, one could also proceed without the SL_2 invariance just by writing ,
, 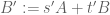 and working with A’ and B’ throughout; this does not significantly affect the length of the presentation in this simple case, but is helpful when working with more than two variables as alluded to at the end of Section 1. To me it is a matter of taste – if one wants to prove some identity about finite-dimensional symplectic vector spaces, for instance, does one work in a coordinate free fashion, or does one apply the linear Darboux theorem first to place the symplectic form in a normal form? Both approaches are useful. (Of course, strictly speaking I did not work in a coordinate free fashion in my notes, since I did write everything in terms of A and B, but as mentioned above it is not too difficult to phrase things in the coordinate free formalism.)
and working with A’ and B’ throughout; this does not significantly affect the length of the presentation in this simple case, but is helpful when working with more than two variables as alluded to at the end of Section 1. To me it is a matter of taste – if one wants to prove some identity about finite-dimensional symplectic vector spaces, for instance, does one work in a coordinate free fashion, or does one apply the linear Darboux theorem first to place the symplectic form in a normal form? Both approaches are useful. (Of course, strictly speaking I did not work in a coordinate free fashion in my notes, since I did write everything in terms of A and B, but as mentioned above it is not too difficult to phrase things in the coordinate free formalism.)
8 October, 2012 at 9:47 am
Anonymous
missing expository tag?
8 October, 2012 at 4:52 pm
Steven Stadnicki
Minor typo: your definition of the position operator is missing the factor of
is missing the factor of  ; presumably it’s meant to be
; presumably it’s meant to be 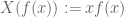 .
.
[Corrected, thanks – T.]
9 October, 2012 at 3:22 am
degosson
Perhaps I missed something, but it seems that you don’t mention a characteristic property of Weyl pseudodifferential operators: they are the only members of the Shubin class that have the property of symplectic/metaplectic covariance (Stein, Wong) . Also, the fact that Weyl operators is the “perfect” quantization procedure in QM is debatable, as has been pointed out by many physicists. In view of Schwartz’s kernel theorem “everything” which is continuous S–>S’ can be written as a Weyl operator, hence any quantum observable could be “dequantized”, but this is physically not true: there are quantum observables which have no classical analogue. A better (i.e. more physical) quantization procedure might very well be the Born-Jordan scheme, which is not always “dequantizable” (see my latest paper “Symplectic covariance properties for Shubin and Born–Jordan pseudo-differential operators” in the Trans. Amer. Math. Soc, online since last Saturday: http://www.ams.org/journals/tran/0000-000-00/).
10 October, 2012 at 5:34 pm
Sam Sachdev
Totally fascinating. Thanks for taking time to make notes on Weyl quantisation.
20 October, 2012 at 3:35 am
����Ԫ
I appreciate it very much that you send every new post of ‘what’s new’, however could you please send me the whole post rather than just a part of it.
Yours sincere,
Han Daoyuan
Sent from my iPad
4 November, 2012 at 6:08 pm
Marcelo de Almeida
Reblogged this on Being simple.
30 November, 2012 at 11:53 am
Lars Hormander « What’s new
[…] to multiplying a phase space distribution by the symbol of that operator, as discussed in this previous blog post. Note that such operators only change the amplitude of the phase space distribution, but not the […]
20 May, 2014 at 11:58 am
Review of wigner nj-Symbols | quantumtetrahedron
[…] Some notes on Weyl quantisation (terrytao.wordpress.com) […]
1 June, 2014 at 8:19 am
Semiclassical Mechanics of the Wigner 6j-Symbol by Aquilanti et al | quantumtetrahedron
[…] Some notes on Weyl quantisation (terrytao.wordpress.com) […]
24 April, 2018 at 1:03 am
João Cortes
Hi professor,
I am trying to understand why the weyl ordering results in an associative product rule for formal series.
I followed your steps up until you combine equations 5,7,9. However, I don’t understand how you “compare coefficients”. In the left hand side of the equation you obtain after that (not numbered), you isolate the term corresponding to the product of the n’th and m’th power of each exponential.
How do you find, in the left hand side, the terms that correspond to this?
Thanks
24 April, 2018 at 7:00 am
Terence Tao
Collect the terms whose total degree is
total degree is  and whose
and whose 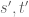 total degree is
total degree is  .
.
27 April, 2018 at 4:21 am
João Cortes
thanks for your reply. It’s weird being able to communicate with you. The wonders of the internet! and m $B’s$) correspond to different polynomials, using the Weyl prescription?
and m $B’s$) correspond to different polynomials, using the Weyl prescription?
I have another question, if you don’t mind.
Do you know any simple argument to show that different orders of a monomial of operators (that is, different ways of multiplying n
27 April, 2018 at 2:23 pm
Terence Tao
Look at what such a monomial does to a monomial .
.
19 May, 2023 at 7:17 am
alwill
Thanks for the derivation, this helps me for doing my homework.