The classical inverse function theorem reads as follows:
Theorem 1 (
inverse function theorem) Let
be an open set, and let
be an continuously differentiable function, such that for every
, the derivative map
is invertible. Then
is a local homeomorphism; thus, for every
, there exists an open neighbourhood
of
and an open neighbourhood
of
such that
is a homeomorphism from
to
.
It is also not difficult to show by inverting the Taylor expansion
that at each , the local inverses
are also differentiable at
with derivative
The textbook proof of the inverse function theorem proceeds by an application of the contraction mapping theorem. Indeed, one may normalise and
to be the identity map; continuity of
then shows that
is close to the identity for small
, which may be used (in conjunction with the fundamental theorem of calculus) to make
a contraction on a small ball around the origin for small
, at which point the contraction mapping theorem readily finishes off the problem.
I recently learned (after I asked this question on Math Overflow) that the hypothesis of continuous differentiability may be relaxed to just everywhere differentiability:
Theorem 2 (Everywhere differentiable inverse function theorem) Let
be an open set, and let
be an everywhere differentiable function, such that for every
, the derivative map
is invertible. Then
is a local homeomorphism; thus, for every
, there exists an open neighbourhood
of
and an open neighbourhood
of
such that
is a homeomorphism from
to
.
As before, one can recover the differentiability of the local inverses, with the derivative of the inverse given by the usual formula (1).
This result implicitly follows from the more general results of Cernavskii about the structure of finite-to-one open and closed maps, however the arguments there are somewhat complicated (and subsequent proofs of those results, such as the one by Vaisala, use some powerful tools from algebraic geometry, such as dimension theory). There is however a more elementary proof of Saint Raymond that was pointed out to me by Julien Melleray. It only uses basic point-set topology (for instance, the concept of a connected component) and the basic topological and geometric structure of Euclidean space (in particular relying primarily on local compactness, local connectedness, and local convexity). I decided to present (an arrangement of) Saint Raymond’s proof here.
To obtain a local homeomorphism near , there are basically two things to show: local surjectivity near
(thus, for
near
, one can solve
for some
near
) and local injectivity near
(thus, for distinct
near
,
is not equal to
). Local surjectivity is relatively easy; basically, the standard proof of the inverse function theorem works here, after replacing the contraction mapping theorem (which is no longer available due to the possibly discontinuous nature of
) with the Brouwer fixed point theorem instead (or one could also use degree theory, which is more or less an equivalent approach). The difficulty is local injectivity – one needs to preclude the existence of nearby points
with
; note that in contrast to the contraction mapping theorem that provides both existence and uniqueness of fixed points, the Brouwer fixed point theorem only gives existence and not uniqueness.
In one dimension one can proceed by using Rolle’s theorem. Indeed, as one traverses the interval from
to
, one must encounter some intermediate point
which maximises the quantity
, and which is thus instantaneously non-increasing both to the left and to the right of
. But, by hypothesis,
is non-zero, and this easily leads to a contradiction.
Saint Raymond’s argument for the higher dimensional case proceeds in a broadly similar way. Starting with two nearby points with
, one finds a point
which “locally extremises”
in the following sense:
is equal to some
, but
is adherent to at least two distinct connected components
of the set
. (This is an oversimplification, as one has to restrict the available points
in
to a suitably small compact set, but let us ignore this technicality for now.) Note from the non-degenerate nature of
that
was already adherent to
; the point is that
“disconnects”
in some sense. Very roughly speaking, the way such a critical point
is found is to look at the sets
as
shrinks from a large initial value down to zero, and one finds the first value of
below which this set disconnects
from
. (Morally, one is performing some sort of Morse theory here on the function
, though this function does not have anywhere near enough regularity for classical Morse theory to apply.)
The point is mapped to a point
on the boundary
of the ball
, while the components
are mapped to the interior of this ball. By using a continuity argument, one can show (again very roughly speaking) that
must contain a “hemispherical” neighbourhood
of
inside
, and similarly for
. But then from differentiability of
at
, one can then show that
and
overlap near
, giving a contradiction.
The rigorous details of the proof are provided below the fold.
— 1. Proof —
Fix . By a translation, we may assume
; by a further linear change of variables, we may also assume
(which by hypothesis is non-singular) to be the identity map. By differentiability, we have
as . In particular, there exists a ball
in
such that
for all ; by rescaling we may take
, thus
Among other things, this gives a uniform lower bound
for all , and a uniform upper bound
for all ; thus
maps
to
.
Proof: Let . From (2), we see that the map
avoids
, and has degree
around
; contracting
to a point, we conclude that
for some
, yielding the claim.
Alternatively, one may proceed by invoking the Brouwer fixed point theorem, noting that the map is continuous and maps the closed ball
to the open ball
by (2), and has a fixed point precisely when
.
A third argument (avoiding the use of degree theory or the Brouwer fixed point theorem, but requiring one to replace with the slightly smaller ball
) is as follows: let
minimise
. From (2) and the hypothesis
we see that
lies in the interior
. If the minimum is zero, then we have found a solution to
as required; if not, then we have a stationary point of
, which implies that
is degenerate, a contradiction. (One can recover the full ball
by tweaking the expression
to be minimised in a suitable fashion; we leave this as an exercise for the interested reader.)
Corollary 4
is an open map: the image of any open set is open.
Proof: It suffices to show that for every , the image of any open neighbourhood of
is an open neighbourhood of
. Proposition 3 handles the case
; the general case follows by renormalising.
Suppose we could show that is injective on
. By Corollary 4, the inverse map
is also continuous. Thus
is a homeomorphism from
to
, which are both neighbourhoods of
by Proposition 3; giving the claim.
It remains to establish injectivity. Suppose for sake of contradiction that this was not the case. Then there exists and
such that
For every radius , the set
is closed and contains both and
. Let
denote the connected component of
that contains
. Since
is non-decreasing in
,
is non-decreasing also.
Now let us study the behaviour of as
ranges from
to
. The two extreme cases are easy to analyse:
Proof: Since is non-singular, we see from differentiability that
for all
sufficiently close to
. Thus
is an isolated point of
, and the claim follows.
Lemma 6 We have
for all
. In particular,
is compact for all
, and contains
for
.
Proof: Since , we see that
; since
is connected and contains
, we conclude that
.
Next, if , then by (3) we have
, and hence
. Thus
is disjoint from the sphere
. Since
lies in the interior of this sphere we thus have
as required.
Next, we show that the increase continuously in
:
Lemma 7 If
and
, then for
sufficiently close to
,
is contained in an
-neighbourhood of
.
Proof: By the finite intersection property, it suffices to show that . Suppose for contradiction that there is a point
outside of
that lies in
for all
. Then
lies in
for all
, and hence lies in
. As
and
lie in different connected components of the compact set
(recall that
is disjoint from
), there must be a partition of
into two disjoint closed sets
that separate
from
(for otherwise the only clopen sets in
that contain
would also contain
, and their intersection would then be a connected subset of
that contains both
and
, contradicting the fact that
lies outside
). By normality, we may find open neighbourhoods
of
that are disjoint. For all
on the boundary
, one has
for all
. As
is compact and
is continuous, we thus have
for all
if
is sufficiently close to
. This makes
clopen in
, and so
cannot lie in
, giving the desired contradiction.
Observe that contains
for
, but does not contain
for
. By the monotonicity of the
and least upper bound principle, there must therefore exist a critical
such that
contains
for all
, but does not contain
for
. From Lemma 7 we see that
must also contain
. In particular, by Lemma 5,
.
We now analyse the critical set . By construction, this set is connected, compact, contains both
and
, contained in
, and one has
for all
.
Proof: The openness is clear from the continuity of (and the local connectedness of
). Now we show disconnectedness. Being an open subset of
, connectedness is equivalent to path connectedness, and
and
both lie in
, so it suffices to show that
and
cannot be joined by a path
in
. But if such a path
existed, then by compactness of
and continuity of
, one would have
for some
. This would imply that
, contradicting the minimal nature of
, and the claim follows.
Proof: Let be a connected component of
; then
is non-empty and contained in
. As
is open,
is also open, and thus by Corollary 4,
is open also.
We claim that is in fact all of
. Suppose this were not the case. As
is connected, this would imply that
is not closed in
; thus there is an element
of
which is adherent to
, but does not lie in
. Thus one may find a sequence
in
with
converging to
. By compactness of
(which contains
), we may pass to a subsequence and assume that
converges to a limit
in
; then
. By continuity, there is thus a ball
centred at
that is mapped to
for some
; this implies that
lies in
and hence in
(since
) and thence in
(since
is strictly less than
). As
is adherent to
and
is connected, we conclude that
lies in
. In particular
lies in
and so
lies in
, a contradiction.
As is equal to
, we thus see that
contains an element of
. However, each element
of
must be isolated since
is non-singular. By compactness of
, the set
(and hence
) thus contains at most finitely many elements of
, and so there are finitely many components as claimed.
Proof: If , then
. If
then
and we are done, so we may assume
. By differentiability, one has
for all sufficiently close to
. If we choose
to lie on a ray emenating from
such that
lies on a ray pointing towards
from
(this is possible as
is non-singular), we conclude that for all
sufficiently close to
on this ray,
. Thus all such points
lie in
; since
lies in
and the ray is locally connected, we see that all such points
in fact lie in
and thence in
. The claim follows.
Corollary 11 There exists a point
with
(i.e.
lies outside
) which is adherent to at least two connected components of
.
Proof: Suppose this were not the case, then the closures of all the connected components of would be disjoint. (Note that an element of one connected component of
cannot lie in the closure of another component.) By Lemma 10, these closures would form a partition of
by closed sets. By Lemma 8, there are at least two such closed sets, each of which is non-empty; by Lemma 9, the number of such closed sets is finite. But this contradicts the connectedness of
.
Next, we prove
Proposition 12 Let
be such that
, and suppose that
is adherent to a connected component
of
. Let
be the vector such that
(this vector exists and is non-zero since
is non-singular). Then
contains an open ray of the form
for some
.
This together with Corollary 11 gives the desired contradiction, since one cannot have two distinct components both contain a ray from
in the direction
.
Proof: As is differentiable at
, we have
for all sufficiently small ; we rearrange this using (5) as
In particular, for all sufficiently small positive
. This shows that all sufficiently small open rays
lie in
, hence in
(since
), and hence in
. In fact, the same argument shows that there is a cone
that will lie in if
is small enough. As this cone is connected, it thus suffices to show that
intersects this cone.
Let be a small radius to be chosen later. As
is non-singular, we see if
is small enough that
whenever
. By continuity, we may thus find
such that
whenever
.
Consider the set
As is adherent to
,
is non-empty. By construction of
, we see that we also have
and so is open. By Corollary 4,
is then also non-empty and open. By construction,
also lies in the set
We claim that is in fact all of
. The proof will be a variant of the proof of Lemma 9. Suppose this were not the case. As
is connected, this implies that there is an element
of
which is adherent to
, but does not lie in
. Thus one may find a sequence
in
with
converging to
. By compactness of
(which contains
), we may pass to a subsequence and assume that
converges to a limit
in
; then
. By continuity, there is thus a ball
centred at
contained in
that is mapped to
for some
; this implies that
lies in
and hence in
(since
) and thence in
(since
is strictly less than
). As
is adherent to
and
is connected, we conclude that
lies in
and thence in
. In particular
lies in
and so
lies in
, a contradiction.
As , we may thus find a sequence
converging to zero, and a sequence
, such that
However, if is small enough, we have
comparable to
(cf. (2)), and so
converges to
. By Taylor expansion, we then have
and thus
for some matrix-valued error . Since
is invertible, this implies that
In particular, lies in the cone (6) for
large enough, and the claim follows.

39 comments
Comments feed for this article
12 September, 2011 at 4:31 pm
Leandro Cioletti
Thanks for sharing this. I read the mathoverflow question and I liked very much this result, but we don’t have in our local library a copy of the papers cited there.
12 September, 2011 at 4:55 pm
Philippe
Small correction: the person that pointed this proof to you is Julien Melleray (not Malleray).
[Corrected, thanks – T.]
12 September, 2011 at 5:54 pm
vineel567
what tools do you use to write such a wonderful technical articles with all the special characters and mathematical style preserved.??? Thanks in advance
15 September, 2011 at 3:17 am
Willie Wong
Take a look at this page: https://terrytao.wordpress.com/about/ especially after the “Some technical remarks” fold.
14 September, 2011 at 7:45 pm
Anonymous
Sorry I mean everywhere invertibility. Is it necessary? If so why is the local invertibility not sufficient?
15 September, 2011 at 3:20 am
Willie Wong
The statement does only require local invertibility, no? It only requires invertibility at every point in the open neighborhood . Or are you asking whether invertibility at a single point is sufficient?
. Or are you asking whether invertibility at a single point is sufficient?
15 September, 2011 at 5:21 am
Anonymous
This result seems counter-intuitive. In the 1D case, if f'(x)<0 for x0 for x>x_0 then it doesn’t seem possible for the function f to be invertible at x_0. Also, the derivative is invertible in a neighborhood of x_0 so it seems to satisfy the conditions of the theorem.
[You will need to use < and > instead of < and > to avoid your comments being mangled by the HTML parser. In any event, in one dimension the result is precisely the contrapositive of Rolle’s theorem. – T.]
15 September, 2011 at 5:30 am
Anonymous
It should be f'(x)0 for x > x0.
17 September, 2011 at 7:30 pm
Josh Swanson
Thank you for typing this up! Reading through it was a nice review of basic real analysis and topology.
The Brouwer fixed point theorem is false with open balls, so the map you mention in the proof of Proposition 3 should be between closed balls. Even so, the fixed point isn’t on the boundary (from (3) scaled by the magnitude of x) so the result still follows easily.
In the same proposition, I wasn’t able to follow the reasoning in your third argument which gives |x| < r (i.e. |x| is not r) without taking |y| < r/3 rather than |y| < r/2. This doesn’t seem to affect anything adversely, though. I really like that argument since it makes the overall proof much more elementary.
I wasn’t able to follow the reasoning in the last few lines–in particular replacing o(||x_n – x_*||) with o(t_n). I was able to show the result anyway, though I had to pass to a further subsequence and use the invertibility of the derivative to do so.
Minor typos/issues:
“point set” -> “point-set”
“A third argument (…) as follows” -> “A third argument (…) is as follows”
“image of any open neighborhood” -> “the image of any open neighborhood”
In the proof of Lemma 6, strictly speaking the B(y, r) should be closed in each case
In Lemma 7, dividing delta by 2 doesn’t seem to serve a purpose
“then f(U_1) is non-empty contained in” -> “then f(U_1) is non-empty and contained in”
“conpactness” -> “compactness”
“This together with Corollary 11 with” -> “This together with Corollary 11”
In defining U’ (and in the restatement right after), there’s a missing vertical bar
[Corrected, thanks – T.]
19 September, 2011 at 12:47 pm
Anonymous
What about the following proof? Is it related to Cernavskii’s or Vaisala’s?
As above, let’s prove that is a local homeomorphism at a point
is a local homeomorphism at a point  . We may assume
. We may assume 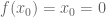 and
and 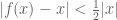 for
for  .
.
Due to Proposition 3 above, for each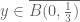 , there is a point in
, there is a point in  such that
such that 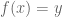 . Moreover,
. Moreover, 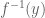 is compact. Take, in
is compact. Take, in 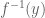 , the point with maximum first coordinate. If there is more than one such point, take the that with maximum second coordinate, and so forth. Let the chosen point equal
, the point with maximum first coordinate. If there is more than one such point, take the that with maximum second coordinate, and so forth. Let the chosen point equal 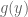 .
.
The function is continuous, since
is continuous, since
i) Because is open, for every point near
is open, for every point near  there is a pre-image near
there is a pre-image near 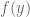 .
.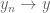 such that, say,
such that, say, 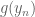 has first coordinate bigger than the first coordinate of
has first coordinate bigger than the first coordinate of 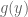 with a non-vanishing difference, we can take a subsequence
with a non-vanishing difference, we can take a subsequence  which converges to a point
which converges to a point  whose first coordinate is bigger than that of
whose first coordinate is bigger than that of  , a contradiction.
, a contradiction.
ii) If there is a sequence
This function is also a left inverse of (that is,
(that is, 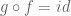 in the image of
in the image of  ). The claim then follows from the fact that injective continuous functions from
). The claim then follows from the fact that injective continuous functions from  -dimensional sets to
-dimensional sets to  -dimensional sets are open.
-dimensional sets are open.
19 September, 2011 at 1:38 pm
Terence Tao
I don’t think the proof of the continuity of g is complete, even in the one-dimensional case. For instance, what prevents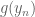 from being significantly below
from being significantly below 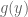 in one dimension?
in one dimension?
Note that there are plenty of continuous proper maps without continuous left-inverses, e.g. in one dimension. (Note in this case that the function g as defined above is discontinuous.)
in one dimension. (Note in this case that the function g as defined above is discontinuous.)
19 September, 2011 at 4:09 pm
Anonymous
Errata: above, the line “which converges to a point whose first coordinate is bigger than that of
whose first coordinate is bigger than that of  , a contradiction” is wrong. Instead of it, define
, a contradiction” is wrong. Instead of it, define 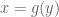 and read “such that
and read “such that 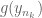 converges to a point
converges to a point 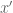 whose first coordinate is bigger than that of
whose first coordinate is bigger than that of  , a contradiction”.
, a contradiction”.
Dear Tao,
indeed that “proof” is wrong. I still think the case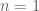 is ok:
is ok:
Take any neighborhood of
of  . If
. If  is sufficiently large,
is sufficiently large, 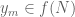 , so we have a candidate
, so we have a candidate  for
for 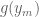 in
in  . We may suppose
. We may suppose  (e.g., by choosing
(e.g., by choosing  as close to
as close to  as possible).
as possible).
In one dimension, by definition, is the biggest element of
is the biggest element of  , so that its lim inf is at least
, so that its lim inf is at least  . Then, as above, if
. Then, as above, if  does not go to
does not go to  , we achieve a contradiction.
, we achieve a contradiction.
However, in more dimensions, I have overlooked something: the coordinates of the ‘s don’t behave in the same way.
‘s don’t behave in the same way.
For the sake of clarity, given any , let’s say
, let’s say  if and only if
if and only if 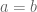 or one of the following conditions holds.
or one of the following conditions holds.
Etc.
The failure of the proof is related to the instability of the relation above: if and
and  are sequences such that
are sequences such that 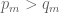 ,
,  and
and  , it is not necessarily true that
, it is not necessarily true that 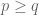 .
.
I will try to fix the argument, even though I think success is not probable.
Question: if were continous, doesn’t the conclusion follow? For it is known that injective continuous maps (in this case,
were continous, doesn’t the conclusion follow? For it is known that injective continuous maps (in this case,  ) are local homeomorphisms. So
) are local homeomorphisms. So  would a homeomorphism between two neighborhoods of
would a homeomorphism between two neighborhoods of  , and
, and  should be its inverse.
should be its inverse.
20 September, 2011 at 11:41 am
Twelth Linkfest
[…] Tao: The inverse function theorem for everywhere differentiable maps, The Brunn-Minkowski inequality for nilpotent […]
21 September, 2011 at 9:50 am
Anonymous
Dear Prof. Tao,
in the proof of lemma 7 you ask the reader to “note that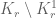 is closed”. Can you give me a hint on how to see this? Components are closed in general (which gives the compactness of
is closed”. Can you give me a hint on how to see this? Components are closed in general (which gives the compactness of 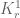 ), but I do not see, why
), but I do not see, why 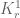 is also open (relative to
is also open (relative to  ).
).
Thanks in advance.
22 September, 2011 at 2:12 am
Terence Tao
Oops, the argument is not quite correct as stated; I’ve rewritten it. The key point is that in a compact set, any two points that don’t lie in the same connected component can be separated from each other by clopen sets (but the connected components themselves need not be clopen).
8 October, 2011 at 10:43 am
Implicit function theorem | Mathitself
[…] deep result is that it’s enough that is everywhere differentiable (see Tao’s post), which remains one an other deep result called invariance of […]
9 March, 2012 at 11:26 pm
francescodifusco
Reblogged this on FRANCESCO DI FUSCO.
19 March, 2012 at 10:01 am
Alan Macdonald
The paper “A Strong Inverse Function Theorem” by William J. Knight
(The American Mathematical Monthly, Vol. 95, No. 7, pp. 648-651) gives an improvement of the standard result in a different direction.
9 September, 2012 at 8:26 am
Olaf Zurth
A Question: Is there in the first line of Lemma 6 a typo?
 should read as
should read as 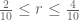 or did I misunderstood something?
or did I misunderstood something?
[Corrected, thanks – T.]
8 November, 2012 at 5:35 am
blindman
Dear Professor Tao,
the local inverses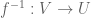 are also differentiable at
are also differentiable at 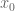
should be replaced by
the local inverses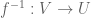 are also differentiable at
are also differentiable at 
[Corrected, thanks – T.]
8 November, 2012 at 6:10 am
blindman
Dear Professor Terence Tao,
In the book “Mathematical Analysis on Manifold” of Michael Spivak, the author gave a counterexample of Theorem 1 (Exercise 2.39, page 52) if the assumption on the continuity of the derivate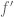 is violated.
is violated. given by
given by
They consider the function
+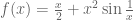 if
if 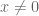 ;
;
+ if
if 
I would to ask your comments about this situation.
Thank your for your helping.
8 November, 2012 at 6:19 am
Terence Tao
This function has non-zero derivative at 0, but has vanishing derivative at many other points (as can be seen for instance from a plot of the function
), and so does not contradict Theorem 1.
8 November, 2012 at 4:02 pm
blindman
Dear Sir. Thank you for your comments and helping.
13 December, 2012 at 3:22 pm
pera
And what would be counterexample?
28 March, 2014 at 12:11 pm
Alexander
Why not just to use the Mean value theorem on a segment $[x_1,x_2]$ to obtain injectivity immidiately instead of all these lemmas?
29 March, 2014 at 3:08 am
Alexander
Ok, I see: because there’s no such a theorem… sorry!
14 December, 2015 at 11:02 am
The inverse function theorem | Negro's notes
[…] differentiable conditions on a mapping which ensure that it is a local diffeomorphism. (But see Terry Tao’s blog for a differentiable, non-smooth inverse function theorem). The main point of such theorems is the […]
24 November, 2016 at 7:11 am
Mladen Đalto
Is there a pseudoinverse version of this theorem for $ f: \mathbb{R}^n \rightarrow \mathbb{R}^m$ where $n$ is not equal $m$ ?
If not, what method of proof/research would you recommend ?
I require it for machine learning research so any pointers would be appreciated.
Thank you.
15 April, 2017 at 2:28 pm
Anonymous
In Spivak’s Calculus on manifolds, there is an exercise that the function defined by
defined by
and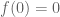 shows that continuity of the derivative cannot be eliminated from the hypothesis of the inverse function theorem. Why does this not contradict Theorem 2?
shows that continuity of the derivative cannot be eliminated from the hypothesis of the inverse function theorem. Why does this not contradict Theorem 2?
16 April, 2017 at 6:45 pm
Terence Tao
This map has an infinite number of critical points near the origin, so the hypotheses of Theorem 2 are not satisfied. (Perhaps the formulation of the inverse function theorem in Spivak is slightly different, in that one only demands invertibility of the derivative at a single point, rather than on an entire domain.)
has an infinite number of critical points near the origin, so the hypotheses of Theorem 2 are not satisfied. (Perhaps the formulation of the inverse function theorem in Spivak is slightly different, in that one only demands invertibility of the derivative at a single point, rather than on an entire domain.)
17 April, 2017 at 10:25 am
Anonymous
I’m very much curious about motivation of considering the map , which is the key step to recover the proof of Theorem 1. Other than just memorizing it, I have never seen in any textbook an explanation for a possible motivation (algebra? geometry? or something else) for this map.
, which is the key step to recover the proof of Theorem 1. Other than just memorizing it, I have never seen in any textbook an explanation for a possible motivation (algebra? geometry? or something else) for this map.
17 April, 2017 at 12:10 pm
Terence Tao
If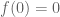 and
and  is the identity, then Taylor expansion suggests the approximation
is the identity, then Taylor expansion suggests the approximation 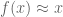 for small
for small  . If this approximation were exact –
. If this approximation were exact –  – then one could easily solve the equation
– then one could easily solve the equation 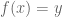 by writing it as
by writing it as 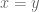 . But the approximation is inexact; the best one can do with regards to transforming
. But the approximation is inexact; the best one can do with regards to transforming 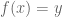 to an equation that looks like
to an equation that looks like 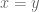 is to add
is to add 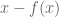 to both sides to obtain
to both sides to obtain  . The error here
. The error here 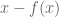 is not zero, but it is “small”, and in particular (for small
is not zero, but it is “small”, and in particular (for small  and continuously differentiable
and continuously differentiable  ) the map
) the map 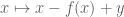 still behaves somewhat like a constant, in that it is a contraction.
still behaves somewhat like a constant, in that it is a contraction.
26 March, 2018 at 9:41 pm
Joe Higgins
Can you give a hint about the statement ‘one can recover the differentiability of the local inverses’ please? Much appreciated.
27 March, 2018 at 5:42 pm
Terence Tao
Let’s say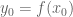 . If
. If 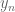 approaches
approaches 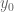 , then by the homeomorphism property we have local inverses
, then by the homeomorphism property we have local inverses  that approach
that approach 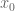 . On the other hand, we have the Newton approximation
. On the other hand, we have the Newton approximation 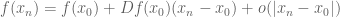 . One can put these facts together to obtain the usual formula for the derivative of
. One can put these facts together to obtain the usual formula for the derivative of 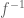 at
at 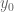 .
.
19 December, 2023 at 9:17 am
Anonymous
I’m a little confused about this, following the hint I obtain $f^{-1}(y) = f^{-1}(y_0) + (Df(x_0))^{-1}(y-y_0) + o(|f^{-1}(y)-f^{-1}(y_0)|$, so I have to prove that $o(|f^{-1}(y)-f^{-1}(y_0)|$ is also $o(|y-y_0|)$, but I can’t find a way without supposing continuity of $Df$ at the point $x_0$. Thank you in advance.
11 July, 2020 at 7:24 pm
Jaikrishnan Janardhanan
There seems to be a new and elementary proof of the inverse function theorem for just everywhere differentiable maps:
https://www.jstor.org/stable/10.14321/realanalexch.43.2.0429
11 January, 2023 at 6:42 pm
Eduardo Ramos
Hello Terence Tao. Are you still interested in such question? I think I solved the infinite dimension case, where I proved the same is true in Bannach Spaces as long as F is “locally proper” in some sense, which includes for instance functions of the form I+K, K being compact. Additionally I think the proof is actually simpler, and generates interesting results in more general spaces. Could you read my proof?
11 January, 2023 at 7:48 pm
Eduardo Ramos
Specifically, I proved that for Banach spaces and
and  , if
, if  is Fréchet differentiable and
is Fréchet differentiable and  invertible for all
invertible for all  , then
, then  will be a local homeomorphism if and only if
will be a local homeomorphism if and only if  is ‘locally proper’.
is ‘locally proper’.
Here being locally proper means that for each
being locally proper means that for each  there exists a closed neighborhood
there exists a closed neighborhood 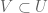 of
of 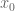 such that if
such that if 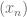 is a sequence in
is a sequence in  with
with  , then
, then 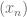 has a convergent subsequence.
has a convergent subsequence.
21 January, 2023 at 3:40 pm
Eduardo Ramos
Well, after checking each detail of my proof I found an error. Actually with the above conditions I can only prove that is an open map. Under the above hypothesis I also found a similar argument for the infinite dimensional case that can follow all steps of your arguments up to Proposition 12, where it sadly fails. Soon I will publish the open mapping result, and will keep working on the local injectivity problem.
is an open map. Under the above hypothesis I also found a similar argument for the infinite dimensional case that can follow all steps of your arguments up to Proposition 12, where it sadly fails. Soon I will publish the open mapping result, and will keep working on the local injectivity problem.