Given two unit vectors in a real inner product space, one can define the correlation between these vectors to be their inner product
, or in more geometric terms, the cosine of the angle
subtended by
and
. By the Cauchy-Schwarz inequality, this is a quantity between
and
, with the extreme positive correlation
occurring when
are identical, the extreme negative correlation
occurring when
are diametrically opposite, and the zero correlation
occurring when
are orthogonal. This notion is closely related to the notion of correlation between two non-constant square-integrable real-valued random variables
, which is the same as the correlation between two unit vectors
lying in the Hilbert space
of square-integrable random variables, with
being the normalisation of
defined by subtracting off the mean
and then dividing by the standard deviation of
, and similarly for
and
.
One can also define correlation for complex (Hermitian) inner product spaces by taking the real part of the complex inner product to recover a real inner product.
While reading the (highly recommended) recent popular maths book “How not to be wrong“, by my friend and co-author Jordan Ellenberg, I came across the (important) point that correlation is not necessarily transitive: if correlates with
, and
correlates with
, then this does not imply that
correlates with
. A simple geometric example is provided by the three unit vectors
in the Euclidean plane :
and
have a positive correlation of
, as does
and
, but
and
are not correlated with each other. Or: for a typical undergraduate course, it is generally true that good exam scores are correlated with a deep understanding of the course material, and memorising from flash cards are correlated with good exam scores, but this does not imply that memorising flash cards is correlated with deep understanding of the course material.
However, there are at least two situations in which some partial version of transitivity of correlation can be recovered. The first is in the “99%” regime in which the correlations are very close to : if
are unit vectors such that
is very highly correlated with
, and
is very highly correlated with
, then this does imply that
is very highly correlated with
. Indeed, from the identity
(and similarly for and
) and the triangle inequality
Thus, for instance, if and
, then
. This is of course closely related to (though slightly weaker than) the triangle inequality for angles:
Remark 1 (Thanks to Andrew Granville for conversations leading to this observation.) The inequality (1) also holds for sub-unit vectors, i.e. vectors
with
. This comes by extending
in directions orthogonal to all three original vectors and to each other in order to make them unit vectors, enlarging the ambient Hilbert space
if necessary. More concretely, one can apply (1) to the unit vectors
in
.
But even in the “” regime in which correlations are very weak, there is still a version of transitivity of correlation, known as the van der Corput lemma, which basically asserts that if a unit vector
is correlated with many unit vectors
, then many of the pairs
will then be correlated with each other. Indeed, from the Cauchy-Schwarz inequality
Thus, for instance, if for at least
values of
, then (after removing those indices
for which
)
must be at least
, which implies that
for at least
pairs
. Or as another example: if a random variable
exhibits at least
positive correlation with
other random variables
, then if
, at least two distinct
must have positive correlation with each other (although this argument does not tell you which pair
are so correlated). Thus one can view this inequality as a sort of `pigeonhole principle” for correlation.
A similar argument (multiplying each by an appropriate sign
) shows the related van der Corput inequality
and this inequality is also true for complex inner product spaces. (Also, the do not need to be unit vectors for this inequality to hold.)
Geometrically, the picture is this: if positively correlates with all of the
, then the
are all squashed into a somewhat narrow cone centred at
. The cone is still wide enough to allow a few pairs
to be orthogonal (or even negatively correlated) with each other, but (when
is large enough) it is not wide enough to allow all of the
to be so widely separated. Remarkably, the bound here does not depend on the dimension of the ambient inner product space; while increasing the number of dimensions should in principle add more “room” to the cone, this effect is counteracted by the fact that in high dimensions, almost all pairs of vectors are close to orthogonal, and the exceptional pairs that are even weakly correlated to each other become exponentially rare. (See this previous blog post for some related discussion; in particular, Lemma 2 from that post is closely related to the van der Corput inequality presented here.)
A particularly common special case of the van der Corput inequality arises when is a unit vector fixed by some unitary operator
, and the
are shifts
of a single unit vector
. In this case, the inner products
are all equal, and we arrive at the useful van der Corput inequality
(In fact, one can even remove the absolute values from the right-hand side, by using (2) instead of (4).) Thus, to show that has negligible correlation with
, it suffices to show that the shifts of
have negligible correlation with each other.
Here is a basic application of the van der Corput inequality:
Proposition 2 (Weyl equidistribution estimate) Let
be a polynomial with at least one non-constant coefficient irrational. Then one has
where
.
Note that this assertion implies the more general assertion
for any non-zero integer (simply by replacing
by
), which by the Weyl equidistribution criterion is equivalent to the sequence
being asymptotically equidistributed in
.
Proof: We induct on the degree of the polynomial
, which must be at least one. If
is equal to one, the claim is easily established from the geometric series formula, so suppose that
and that the claim has already been proven for
. If the top coefficient
of
is rational, say
, then by partitioning the natural numbers into residue classes modulo
, we see that the claim follows from the induction hypothesis; so we may assume that the top coefficient
is irrational.
In order to use the van der Corput inequality as stated above (i.e. in the formalism of inner product spaces) we will need a non-principal ultrafilter (see e.g this previous blog post for basic theory of ultrafilters); we leave it as an exercise to the reader to figure out how to present the argument below without the use of ultrafilters (or similar devices, such as Banach limits). The ultrafilter
defines an inner product
on bounded complex sequences
by setting
Strictly speaking, this inner product is only positive semi-definite rather than positive definite, but one can quotient out by the null vectors to obtain a positive-definite inner product. To establish the claim, it will suffice to show that
for every non-principal ultrafilter .
Note that the space of bounded sequences (modulo null vectors) admits a shift , defined by
This shift becomes unitary once we quotient out by null vectors, and the constant sequence is clearly a unit vector that is invariant with respect to the shift. So by the van der Corput inequality, we have
for any . But we may rewrite
. Then observe that if
,
is a polynomial of degree
whose
coefficient is irrational, so by induction hypothesis we have
for
. For
we of course have
, and so
for any . Letting
, we obtain the claim.

29 comments
Comments feed for this article
5 June, 2014 at 12:14 pm
Fred Lunnon
Single bars in 3 out of 5 displayed formulae preceding (1), perhaps?
5 June, 2014 at 9:42 pm
Emmanuel Kowalski
The non-transitivity of correlation also comes up in representation theory, with characters (or approximate versions such as trace functions) as unit vectors; I’ve taken to interpret “X is correlated with Y” as meaning “X has something in common with Y”, which to me carries the right intuition.
It can be interpreted algebraically rigorously with the “common parts” being common irreducible subrepresentations.
10 June, 2014 at 9:11 am
Emmanuel Kowalski
Ah! And now that I have Jordan’s book, I see that this more or less exactly the interpretation he suggests!
6 June, 2014 at 2:24 am
Basil K
Recently I’ve come across the following property for an element a in some “tolerance space” (A,T) (a set A with a reflexive and symmetric relation T):
for all b, b’ in A, if (b T a) and (a T b’) then (b T b’) .
I was wondering what would make a reasonably “natural” example for such special elements a, which facilitate transitions in an otherwise not necessarily transitive setting, and I’ve been asking everyone I know about it – and even people I don’t know.
I understand that the spirit of this post is analytic rather than algebraic (as my Math Stackexchange question is), but surely the cone intuition seems to be common to both, so I thought I’d share.
7 June, 2014 at 2:16 am
George Shakan
That is quite an elegant proof of Proposition 1!
I think I found a couple typos. Of a single unit vector should be of a single unit vector
should be of a single unit vector  . Also I in Proposition 1, probably the
. Also I in Proposition 1, probably the  should be
should be 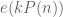 for some positive integer parameter
for some positive integer parameter  .
.
[Corrected, thanks – T.]
7 June, 2014 at 7:59 am
aquazorcarson
Thanks for making Van der Corput so well-motivated. Very enlightening read.
7 June, 2014 at 9:16 am
dzako
I dont get the definition of the ultrafilter product $_p$. This is defined for complex sequences and $e(P)$ is clearly not a complex seq.
7 June, 2014 at 10:24 am
Terence Tao
17 June, 2014 at 10:51 pm
Anonymous
The paragraph after equation 1 seems to have several inaccuracies. First it was not assumed that all the pairs have nonnegative correlations. Then i wasnt able to follow the pigeonhole estimates for both examples. Maybe I am missing something.
18 June, 2014 at 7:50 am
Terence Tao
Both arguments are valid even in the presence of some negative correlations. For instance, once one has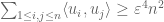 , one must have
, one must have  for at least
for at least 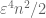 pairs
pairs  , for if this were not the case, one would have
, for if this were not the case, one would have 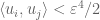 for all but fewer than
for all but fewer than 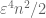 pairs
pairs  , and if one uses the trivial upper bound
, and if one uses the trivial upper bound  for these exceptional pairs, one obtains a contradiction. Note that at no point in this argument is any non-negativity hypothesis on the
for these exceptional pairs, one obtains a contradiction. Note that at no point in this argument is any non-negativity hypothesis on the  required. Similarly for the second argument.
required. Similarly for the second argument.
At a more intuitive level, any negative correlation between one pair of will only cause the other inner products on the RHS of (1) to become even more positive, if (1) is to hold (but the correlation of each pair maxes out at
will only cause the other inner products on the RHS of (1) to become even more positive, if (1) is to hold (but the correlation of each pair maxes out at  , so there has to be a lot of pairs that share in this positive correlation): making a pair of vectors at an obtuse angle will squeeze a lot of other angles to become more acute. So negative correlation is not actually an enemy here, and is in fact helpful in some ways. (For similar reasons, the pigeonhole principle is still mathematically valid – and even “stronger”, in some sense – if some pigeonholes are allowed to have a negative number of pigeons, despite the breakdown of the physical pigeon metaphor in this setting.)
, so there has to be a lot of pairs that share in this positive correlation): making a pair of vectors at an obtuse angle will squeeze a lot of other angles to become more acute. So negative correlation is not actually an enemy here, and is in fact helpful in some ways. (For similar reasons, the pigeonhole principle is still mathematically valid – and even “stronger”, in some sense – if some pigeonholes are allowed to have a negative number of pigeons, despite the breakdown of the physical pigeon metaphor in this setting.)
1 February, 2017 at 3:47 pm
Kodlu
I believe the $\varepsilon^3$s should be $\varepsilon^4$s in the above comment, as in the main text below equation (2).
[Corrected, thanks – T.]
18 June, 2014 at 8:35 pm
Anonymous
Thanks for your enlightening answer. That part is completely clear now. Now I am confused by the paragraph after equation (2). First if the inner product is standard Euclidean, then the set of vectors positively correlated with v is simply a half space, which is not so “narrow”. Also I don’t understand the explanation for why the equation is independent of dimension. Why does it help to know the weakly correlated pairs are exponentially rare as dimension goes up?
18 June, 2014 at 9:13 pm
Terence Tao
Here, one should think of “positively correlated” as meaning “correlation at least epsilon for some fixed epsilon independent of dimension”. Then all the vectors will be squashed into a cone of aperture about
will be squashed into a cone of aperture about  , and the angular measure of this cone decays exponentially with the dimension. This reduces the number of opportunities for pairs of vectors in this cone to be orthogonal or to make obtuse angles with each other.
, and the angular measure of this cone decays exponentially with the dimension. This reduces the number of opportunities for pairs of vectors in this cone to be orthogonal or to make obtuse angles with each other.
22 June, 2014 at 8:52 pm
Anonymous
The triangle inequality seems to give slightly weaker bounds than a determinant based approach (for eg.
http://math.stackexchange.com/questions/147374/correlations-between-3-random-variables) some people have used. For eg. if and are both 0.87, the triangle inequality gives > 0.48, but the determinant based approach gives > 0.5138. Is this alternate approach correct?
22 June, 2014 at 9:01 pm
Anonymous
the second to last line wasnt posted fully by the comment engine. restating that line, given 3 variables 1,2,3 and pairwise correlations x, y, z, triangle inequality gives the minimum bound as 0.48, while determinant > 0 gives a bound around 0.51.
23 June, 2014 at 4:21 pm
Terence Tao
The triangle inequality for angles , which gives the same bound as the determinant approach (as one can verify numerically after using the identity
, which gives the same bound as the determinant approach (as one can verify numerically after using the identity  ), is slightly stronger than the bound coming from the triangle inequality for norms.
), is slightly stronger than the bound coming from the triangle inequality for norms.
25 June, 2014 at 10:46 am
Anonymous
Thanks for clarifying this.
2 July, 2014 at 1:58 am
taking exponentials of stuff | marekgluza
[…] was reding this: https://terrytao.wordpress.com/2014/06/05/when-is-correlation-transitive/ and I got this going for me which is […]
27 October, 2014 at 9:22 pm
The Elliott-Halberstam conjecture implies the Vinogradov least quadratic nonresidue conjecture | What's new
[…] of , this shows that correlates with for various small . By the Cauchy-Schwarz inequality (cf. this previous blog post), this implies that correlates with for some distinct . But this can be ruled out by using Type […]
15 December, 2014 at 1:30 am
hammyhamster
Presumably there are implications for investment porfolios here. It’s well-known that adding a high-volatility (aka variance of return) stock to a portfolio can decrease the portfolio’s overall variance if the high-vol stock is negatively correlated to the others. But lack of transitivity presumably increases the challenge of doing this for large portfolios ?
11 June, 2015 at 4:52 pm
Anonymous
Sorry if I’m being silly, but I don’t understand the explanation below equation (2). For example. let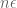 be a positive integer and
be a positive integer and 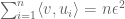 , that is, all the remaining
, that is, all the remaining 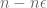 terms be such that there is not correlation between them and
terms be such that there is not correlation between them and  . In this case, what is stated in the paragraph below isn’t true. I think I’m missing something here, please help me out!
. In this case, what is stated in the paragraph below isn’t true. I think I’m missing something here, please help me out!
[Oops, there was a typo – the exponent 3 should have been a 4. Corrected now – T.]
13 July, 2015 at 9:00 am
willis77 comments on “What does it mean for an algorithm to be fair?” | Offer Your
[…] vs causation. In real data, correlation is mostly transitive (there are toy exceptions – https://terrytao.wordpress.com/2014/06/05/when-is-correlatio…, but they are just that). This means that if you want to predict something, and that something is […]
13 July, 2015 at 9:18 am
willis77 comments on “What does it mean for an algorithm to be fair?” | Exploding Ads
[…] vs causation. In real data, correlation is mostly transitive (there are toy exceptions – https://terrytao.wordpress.com/2014/06/05/when-is-correlatio…, but they are just that). This means that if you want to predict something, and that something is […]
1 October, 2015 at 3:37 am
Foucart
See Foucart (1991) Transitivité du produit scalaire. Rev. Stat. Appliquée, XXXIX (3), 57-68 and Foucart (1997) numerical analysis of a correlation matrix, Statistics, 29/4, pp. 347-361.
7 October, 2015 at 6:00 am
War and Picks - datdota.com
[…] note for the mathematically inclined – correlation is not a proper metric and it is not transitive except in the regime of very high correlation. In practice, this means that patch 6.82 can be […]
7 March, 2016 at 2:30 am
Correlation between Probability theory and Vector Algebra – Arindam Ghosh
[…] product/scalar product/projection product” of Vector Algebra while going through this article on “transitiveness of correlation” by Dr. Terrence […]
27 February, 2021 at 12:22 pm
Boosting the van der Corput inequality using the tensor power trick | What's new
[…] this previous blog post I noted the following easy application of […]
1 July, 2021 at 9:46 pm
lotharson
Hi Terence, I wish I could quote your blog post in a paper I am writing! ;-)
[This is fine; see the last paragraph of https://terrytao.wordpress.com/about/ , as well as general guides on how to cite blog posts, e.g., at https://blog.apastyle.org/apastyle/2016/04/how-to-cite-a-blog-post-in-apa-style.html -T.]
7 December, 2021 at 2:32 am
matott
can someone help me with a real world application (not being a mathematician):
I have two logistic regressions (a and b), both being derived of and validated in a database S. Regression a is also tested and validated in a second database T.
Can I now say that my second regression b is also valid in the second database T, since a and b are both valid in S.
Comparing S and T directly, they have the same demographics (plus o moins)
Sorry for intruding with a real life problem. I would really appreciate a helpin hand (brain ;-)