The von Neumann ergodic theorem (the Hilbert space version of the mean ergodic theorem) asserts that if is a unitary operator on a Hilbert space
, and
is a vector in that Hilbert space, then one has
in the strong topology, where is the
-invariant subspace of
, and
is the orthogonal projection to
. (See e.g. these previous lecture notes for a proof.) The same proof extends to more general amenable groups: if
is a countable amenable group acting on a Hilbert space
by unitary transformations
for
, and
is a vector in that Hilbert space, then one has
for any Folner sequence of
, where
is the
-invariant subspace, and
is the average of
on
. Thus one can interpret
as a certain average of elements of the orbit
of
.
In a previous blog post, I noted a variant of this ergodic theorem (due to Alaoglu and Birkhoff) that holds even when the group is not amenable (or not discrete), using a more abstract notion of averaging:
Theorem 1 (Abstract ergodic theorem) Let
be an arbitrary group acting unitarily on a Hilbert space
, and let
be a vector in
. Then
is the element in the closed convex hull of
of minimal norm, and is also the unique element of
in this closed convex hull.
I recently stumbled upon a different way to think about this theorem, in the additive case when
is abelian, which has a closer resemblance to the classical mean ergodic theorem. Given an arbitrary additive group
(not necessarily discrete, or countable), let
denote the collection of finite non-empty multisets in
– that is to say, unordered collections
of elements
of
, not necessarily distinct, for some positive integer
. Given two multisets
,
in
, we can form the sum set
. Note that the sum set
can contain multiplicity even when
do not; for instance,
. Given a multiset
in
, and a function
from
to a vector space
, we define the average
as
Note that the multiplicity function of the set affects the average; for instance, we have
, but
.
We can define a directed set on as follows: given two multisets
, we write
if we have
for some
. Thus for instance we have
. It is easy to verify that this operation is transitive and reflexive, and is directed because any two elements
of
have a common upper bound, namely
. (This is where we need
to be abelian.) The notion of convergence along a net, now allows us to define the notion of convergence along
; given a family
of points in a topological space
indexed by elements
of
, and a point
in
, we say that
converges to
along
if, for every open neighbourhood
of
in
, one has
for sufficiently large
, that is to say there exists
such that
for all
. If the topological space
is Hausdorff, then the limit
is unique (if it exists), and we then write
When takes values in the reals, one can also define the limit superior or limit inferior along such nets in the obvious fashion.
We can then give an alternate formulation of the abstract ergodic theorem in the abelian case:
Theorem 2 (Abelian abstract ergodic theorem) Let
be an arbitrary additive group acting unitarily on a Hilbert space
, and let
be a vector in
. Then we have
in the strong topology of
.
Proof: Suppose that , so that
for some
, then
so by unitarity and the triangle inequality we have
thus is monotone non-increasing in
. Since this quantity is bounded between
and
, we conclude that the limit
exists. Thus, for any
, we have for sufficiently large
that
for all . In particular, for any
, we have
We can write
and so from the parallelogram law and unitarity we have
for all , and hence by the triangle inequality (averaging
over a finite multiset
)
for any . This shows that
is a Cauchy sequence in
(in the strong topology), and hence (by the completeness of
) tends to a limit. Shifting
by a group element
, we have
and hence is invariant under shifts, and thus lies in
. On the other hand, for any
and
, we have
and thus on taking strong limits
and so is orthogonal to
. Combining these two facts we see that
is equal to
as claimed.
To relate this result to the classical ergodic theorem, we observe
Lemma 3 Let
be a countable additive group, with a F{\o}lner sequence
, and let
be a bounded sequence in a normed vector space indexed by
. If
exists, then
exists, and the two limits are equal.
Proof: From the F{\o}lner property, we see that for any and any
, the averages
and
differ by at most
in norm if
is sufficiently large depending on
,
(and the
). On the other hand, by the existence of the limit
, the averages
and
differ by at most
in norm if
is sufficiently large depending on
(regardless of how large
is). The claim follows.
It turns out that this approach can also be used as an alternate way to construct the Gowers–Host-Kra seminorms in ergodic theory, which has the feature that it does not explicitly require any amenability on the group (or separability on the underlying measure space), though, as pointed out to me in comments, even uncountable abelian groups are amenable in the sense of possessing an invariant mean, even if they do not have a F{\o}lner sequence.
Given an arbitrary additive group , define a
-system
to be a probability space
(not necessarily separable or standard Borel), together with a collection
of invertible, measure-preserving maps, such that
is the identity and
(modulo null sets) for all
. This then gives isomorphisms
for
by setting
. From the above abstract ergodic theorem, we see that
in the strong topology of for any
, where
is the collection of measurable sets
that are essentially
-invariant in the sense that
modulo null sets for all
, and
is the conditional expectation of
with respect to
.
In a similar spirit, we have
Theorem 4 (Convergence of Gowers-Host-Kra seminorms) Let
be a
-system for some additive group
. Let
be a natural number, and for every
, let
, which for simplicity we take to be real-valued. Then the expression
converges, where we write
, and we are using the product direct set on
to define the convergence
. In particular, for
, the limit
converges.
We prove this theorem below the fold. It implies a number of other known descriptions of the Gowers-Host-Kra seminorms , for instance that
for , while from the ergodic theorem we have
This definition also manifestly demonstrates the cube symmetries of the Host-Kra measures on
, defined via duality by requiring that
In a subsequent blog post I hope to present a more detailed study of the norm and its relationship with eigenfunctions and the Kronecker factor, without assuming any amenability on
or any separability or topological structure on
.
— 1. Proof of theorem —
If is a tuple of functions
and
, we say that
is
-symmetric if we have
whenever
and
agree in the first
components (that is,
for
). We will prove Theorem 4 by downward induction on
, with the
case establishing the full theorem.
Thus, assume that and that the claim has already been proven for larger values of
(this hypothesis is vacuous for
). Write
We will show that for any , and for sufficiently large
(in the net
), the quantity
can only increase by at most
when one increases any of the
,
, that is to say that
whenever and
. This implies that the limit superior of
exceeds the limit inferior by at most
, and on sending
we will obtain Theorem 4.
There are two cases, depending on whether or
. We begin with the first case
. By relabeling we may take
, so that
. As
is
-symmetric, we can write
where
By the triangle inequality argument used to prove Theorem 2 we thus see that
and so certainly cannot increase by
by increasing
.
Now we turn to the case when . By relabeling we may take
, so that
. We can write
where
On the other hand, the quantity
is the same as , but with
replaced by
. After rearrangement, this is a
-symmetric inner product, and so by induction hypothesis the limit
exists. In particular, for large enough, we have
for all , which by the parallelogram law as in the proof of Theorem 2 shows that
and hence by averaging
whenever . Similarly with
replaced by
. From Cauchy-Schwarz we then have
for some independent of
(depending on the
norms of the
), and the claim follows after redefining
.

12 comments
Comments feed for this article
9 April, 2015 at 10:22 pm
rennydiokno2015
Reblogged this on rennydiokno.com.
9 April, 2015 at 11:27 pm
Anonymous
In the initial definition of sum set, a + is missing (says AB :=… now)
In the proof of Thm 2, there is a lim_{A\to H} (“we conclude that the limit…”)
I’m having some trouble seeing the Cauchy estimate from the parallelogram law in Thm 2. Taking X = ET^a v we have ||X – T^g X||^2 + ||X+ T^g X||^2 = 4||X||^2 and from ||X + T^gX||^2 \geq ||X||^2 – \epsilon we get ||X – T^g X||^2\leq \epsilon + 3||X||^2 instead of 4\epsilon
In the discussion immediately preceding Thm 3, E(f, X^G) has a \mathcal{E} instead of \mathbf
[Corrected, thanks. The lower bound should be on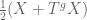 , not
, not 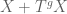 . -T.]
. -T.]
10 April, 2015 at 9:08 am
Anonymous
Ah, yes. There is a 1/2 missing in the RHS of E_{b \in A + {0,g}} = E_a T^a v + T^g E_a T^a v
[Corrected, thanks – T.]
10 April, 2015 at 9:09 am
Craig H
I think you’re still missing the $\frac{1}{2}$.
Specifically, just above the “parallelogram law” link, it should be
$ET^b v = \frac{1}{2} (ET^a v + T^g ET^a v)$,
since the size of the multiset has now doubled.
10 April, 2015 at 12:17 am
Anonymous
In the line below the definition of the average , it seems that “multiplicity of the set
, it seems that “multiplicity of the set  ” should be “multiplicity function of the multiset
” should be “multiplicity function of the multiset  “.
“.
[Corrected, thanks – T.]
10 April, 2015 at 1:09 am
pzorin
Isn’t it the case that all commutative groups are amenable as discrete groups?
10 April, 2015 at 5:25 am
Marcel S.
As far as I am aware all abelian groups are amenable (see e.g. Chapter 10 in “The Banach-Tarski paradox” by Stan Wagon). If I am not mistaken a slight modification of the procedure described in Theorem 2 should provide an invariant mean on bounded functions on the group.
10 April, 2015 at 8:24 am
Terence Tao
Hmm you’re right; uncountable abelian groups don’t have Folner sequences, but they still have invariant means. I guess what I meant to say here is that one can establish the ergodic theorem and construct the Gowers-Host-Kra seminorms without explicit use of Folner sequences, even if the ambient group is still technically amenable.
11 April, 2015 at 8:41 am
Anonymous
I guess in the beginning the link to “previous lecture notes” should be pointing to one lecture earlier (i.e. Lecture 8 not 9.)
[Corrected, thanks – T.]
27 March, 2016 at 5:17 pm
Concatenation theorems for anti-Gowers-uniform functions and Host-Kra characteristic factors; polynomial patterns in primes | What's new
[…] of ways. One is by duality, using the Gowers-Host-Kra uniformity seminorms (defined for instance here) . Namely, is the factor of defined up to equivalence by the requirement […]
10 March, 2023 at 8:59 am
A Host–Kra $latex {bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inve
[…] . Suppose that with an ergodic -system with positive Gowers-Host-Kra seminorm (see for instance this previous post for a definition). Then there exists a measurable polynomial of degree at most such that has a […]
10 March, 2023 at 9:00 am
A Host–Kra ${bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse th
[…] . Suppose that with an ergodic -system with positive Gowers-Host-Kra seminorm (see for instance this previous post for a definition). Then there exists a measurable polynomial of degree at most such that has a […]