The von Neumann ergodic theorem (the Hilbert space version of the mean ergodic theorem) asserts that if is a unitary operator on a Hilbert space
, and
is a vector in that Hilbert space, then one has
in the strong topology, where is the
-invariant subspace of
, and
is the orthogonal projection to
. (See e.g. these previous lecture notes for a proof.) The same proof extends to more general amenable groups: if
is a countable amenable group acting on a Hilbert space
by unitary transformations
, and
is a vector in that Hilbert space, then one has
for any Følner sequence of
, where
is the
-invariant subspace. Thus one can interpret
as a certain average of elements of the orbit
of
.
I recently discovered that there is a simple variant of this ergodic theorem that holds even when the group is not amenable (or not discrete), using a more abstract notion of averaging:
Theorem 1 (Abstract ergodic theorem) Let
be an arbitrary group acting unitarily on a Hilbert space
, and let
be a vector in
. Then
is the element in the closed convex hull of
of minimal norm, and is also the unique element of
in this closed convex hull.
Proof: As the closed convex hull of is closed, convex, and non-empty in a Hilbert space, it is a classical fact (see e.g. Proposition 1 of this previous post) that it has a unique element
of minimal norm. If
for some
, then the midpoint of
and
would be in the closed convex hull and be of smaller norm, a contradiction; thus
is
-invariant. To finish the first claim, it suffices to show that
is orthogonal to every element
of
. But if this were not the case for some such
, we would have
for all
, and thus on taking convex hulls
, a contradiction.
Finally, since is orthogonal to
, the same is true for
for any
in the closed convex hull of
, and this gives the second claim.
This result is due to Alaoglu and Birkhoff. It implies the amenable ergodic theorem (1); indeed, given any , Theorem 1 implies that there is a finite convex combination
of shifts
of
which lies within
(in the
norm) to
. By the triangle inequality, all the averages
also lie within
of
, but by the Følner property this implies that the averages
are eventually within
(say) of
, giving the claim.
It turns out to be possible to use Theorem 1 as a substitute for the mean ergodic theorem in a number of contexts, thus removing the need for an amenability hypothesis. Here is a basic application:
Corollary 2 (Relative orthogonality) Let
be a group acting unitarily on a Hilbert space
, and let
be a
-invariant closed subspace of
. Then
and
are relatively orthogonal over their common subspace
, that is to say the restrictions of
and
to the orthogonal complement of
are orthogonal to each other.
Proof: By Theorem 1, we have for all
, and the claim follows. (Thanks to Gergely Harcos for this short argument.)
Now we give a more advanced application of Theorem 1, to establish some “Mackey theory” over arbitrary groups . Define a
-system
to be a probability space
together with a measure-preserving action
of
on
; this gives an action of
on
, which by abuse of notation we also call
:
(In this post we follow the usual convention of defining the spaces by quotienting out by almost everywhere equivalence.) We say that a
-system is ergodic if
consists only of the constants.
(A technical point: the theory becomes slightly cleaner if we interpret our measure spaces abstractly (or “pointlessly“), removing the underlying space and quotienting
by the
-ideal of null sets, and considering maps such as
only on this quotient
-algebra (or on the associated von Neumann algebra
or Hilbert space
). However, we will stick with the more traditional setting of classical probability spaces here to keep the notation familiar, but with the understanding that many of the statements below should be understood modulo null sets.)
A factor of a
-system
is another
-system together with a factor map
which commutes with the
-action (thus
for all
) and respects the measure in the sense that
for all
. For instance, the
-invariant factor
, formed by restricting
to the invariant algebra
, is a factor of
. (This factor is the first factor in an important hierachy, the next element of which is the Kronecker factor
, but we will not discuss higher elements of this hierarchy further here.) If
is a factor of
, we refer to
as an extension of
.
From Corollary 2 we have
Corollary 3 (Relative independence) Let
be a
-system for a group
, and let
be a factor of
. Then
and
are relatively independent over their common factor
, in the sense that the spaces
and
are relatively orthogonal over
when all these spaces are embedded into
.
This has a simple consequence regarding the product of two
-systems
and
, in the case when the
action is trivial:
Lemma 4 If
are two
-systems, with the action of
on
trivial, then
is isomorphic to
in the obvious fashion.
This lemma is immediate for countable , since for a
-invariant function
, one can ensure that
holds simultaneously for all
outside of a null set, but is a little trickier for uncountable
.
Proof: It is clear that is a factor of
. To obtain the reverse inclusion, suppose that it fails, thus there is a non-zero
which is orthogonal to
. In particular, we have
orthogonal to
for any
. Since
lies in
, we conclude from Corollary 3 (viewing
as a factor of
) that
is also orthogonal to
. Since
is an arbitrary element of
, we conclude that
is orthogonal to
and in particular is orthogonal to itself, a contradiction. (Thanks to Gergely Harcos for this argument.)
Now we discuss the notion of a group extension.
Definition 5 (Group extension) Let
be an arbitrary group, let
be a
-system, and let
be a compact metrisable group. A
-extension of
is an extension
whose underlying space is
(with
the product of
and the Borel
-algebra on
), the factor map is
, and the shift maps
are given by
where for each
,
is a measurable map (known as the cocycle associated to the
-extension
).
An important special case of a -extension arises when the measure
is the product of
with the Haar measure
on
. In this case,
also has a
-action
that commutes with the
-action, making
a
-system. More generally,
could be the product of
with the Haar measure
of some closed subgroup
of
, with
taking values in
; then
is now a
system. In this latter case we will call
-uniform.
If is a
-extension of
and
is a measurable map, we can define the gauge transform
of
to be the
-extension of
whose measure
is the pushforward of
under the map
, and whose cocycles
for
are given by the formula
It is easy to see that is a
-extension that is isomorphic to
as a
-extension of
; we will refer to
and
as equivalent systems, and
as cohomologous to
. We then have the following fundamental result of Mackey and of Zimmer:
Theorem 6 (Mackey-Zimmer theorem) Let
be an arbitrary group, let
be an ergodic
-system, and let
be a compact metrisable group. Then every ergodic
-extension
of
is equivalent to an
-uniform extension of
for some closed subgroup
of
.
This theorem is usually stated for amenable groups , but by using Theorem 1 (or more precisely, Corollary 3) the result is in fact also valid for arbitrary groups; we give the proof below the fold. (In the usual formulations of the theorem,
and
are also required to be Lebesgue spaces, or at least standard Borel, but again with our abstract approach here, such hypotheses will be unnecessary.) Among other things, this theorem plays an important role in the Furstenberg-Zimmer structural theory of measure-preserving systems (as well as subsequent refinements of this theory by Host and Kra); see this previous blog post for some relevant discussion. One can obtain similar descriptions of non-ergodic extensions by working relative to the invariant factor (or via the ergodic decomposition, if one has enough separability hypotheses on the system), but the result becomes more complicated to state, and we will not do so here; see this paper of Austin for details.
— 1. Proof of theorem —
Let be the
-systems in Theorem 6. We can then form the product
-systems
with trivial cocycle (endowing
with the Haar measure
), and also form the skew product
, with the shift
Our argument will hinge on the study of the factor map
defined by
An application of Fubini’s theorem shows that this is indeed a factor map (because the projection from to
was already a factor map, and because multiplication in
is associative). In fact this is a factor map of
-systems, not just
-systems, where
acts on the right factors of
and
by
and
.
Since is a factor of
as a
-system,
is a factor of
as a
-system. But as
is ergodic,
is a point, and so by Lemma 4,
is isomorphic to
. Thus
is a factor of
as a
-system. We now need a baby version of Theorem 6:
Lemma 7 Let
be a compact metrisable group. Then every factor of
(as a
-system acting on the right) is equivalent to
for some closed subgroup
of
(endowing
with the quotiented Haar measure, of course).
Proof: If is a factor of
, then
can be identified with a subspace of
that is invariant with respect to the right
-action. By using the
-action to convolve with continuous approximations to the identity, we see that
is dense in
, where
is the space of continuous functions on
. Let
be the symmetry group of
, that is to say the set of all elements
such that
for all
. Then
is a closed subgroup of
, and
may be identified with a subalgebra of
. By construction,
separates points in
, and is thus (by the Stone-Weierstrass theorem) dense in
in the uniform topology, and hence in
in the
topology. From this it is not difficult to show that
is equivalent to
as claimed.
We conclude that is isomorphic to
as a
-system for some closed subgroup
of
. (This space is known as the Mackey range of the cocycles
.)
Now we need to build the gauge function to conjugate the cocycle
to lie in
. In the usual treatments of Theorem 6, this is achieved by the descriptive set theory device of Borel sections, but in keeping with our “pointless” approach in this post, we will avoid exploiting the point set structure of
or
(although we will rely very much on the point set structure of
and
). We begin with an approximate result:
Proposition 8 Let
be a symmetric neighbourhood of the identity in
. Then there exists a measurable function
such that for each
,
takes values in
(modulo null sets, of course).
Proof: One can view as a positive measure subset of
, which can then be identified with a positive measure
-invariant subset
of
, since
is isomorphic to
. Note that for any
outside of
,
and
are disjoint, and so
and
are also disjoint (recall that
acts on the right on
).
The conditional expectation (that is, the orthogonal projection of
to
) has positive mean and is
-invariant, and is hence equal to a positive constant by the ergodicity of
.
As is compact, we can cover
by a finite number
of left-translates of
. In
, we thus have the inequality
We thus have the pointwise lower bound
Thus, if for each we let
be the first
for which
, and let
, then
is measurable and we have the pointwise lower bound
(indeed, from the pigeonhole principle we could assume a uniform lower bound away from zero if desired). We claim that
Indeed, since and
are disjoint for
, we have
for all ; integrating this in
and taking conditional expectations in
, we obtain the claim thanks to (2).
Meanwhile, applying the action to (2) and using the
-invariance of
, we have
pointwise for any . Comparing this with (3), we conclude that
and in particular that
almost everywhere, which may be rearranged as
and the claim follows.
Now we use compactness to eliminate the neighbourhood :
Proposition 9 There exists a measurable function
such that, for each
,
takes values in
.
Proof: We place a metric on . By the previous proposition, for each natural number
we may find a measurable
such that
lies within
of
pointwise. It thus suffices to find a measurable
such that
is a limit point of the
for every
, so that
is always a limit point of the
. If it were not for the measurability requirement, this would be immediate from the Heine-Borel theorem; so the only issue is to keep
measurable. However, this can be done by an inspection of the proof of the Heine-Borel theorem. Namely, for each natural number
, we cover
by a finite number of balls
of radius
. For each
, one of the
must contain an infinite number of the
; if we recursively select
to be the first such
for which the ball
intersects the previous ball
(with this latter condition being ignored for
), we see that each
is measurable in
. The centres of the balls
converge to a limit
which is then measurable and is a limit point of the
as required.
In view of this proposition, we may assume without loss of generality that the take values in
(replacing
and
with equivalent systems as necessary). The
-systems
and
now split into copies of the
-systems
and
, with the copies indexed by
. As
was isomorphic to
as a factor of
, it is then easy to see that
is trivial. By Corollary 3, this implies that
and
are independent factors of
. In particular, if
and
, so that the function
lies in
, which then embeds into the function
in
, the orthogonal projection of
to
is equal to the orthogonal projection of
onto the trivial factor. Since
is ergodic, we see from Lemma 4 that
, and so we arrive at the identity
for almost all ; as
is continuous, this identity in fact holds for all
, and in particular when
is the identity:
From the monotone convergence theorem, the same claim is then true if is bounded semicontinuous (in particular, the indicator of an open or closed subset of
), and then (as Haar measure is inner and outer regular) the same claim is also true if
is bounded Borel measurable. From this we conclude that
is the product measure of
and Haar measure
, and the claim follows.

15 comments
Comments feed for this article
20 June, 2014 at 9:54 pm
Rex
The abstract ergodic theorem you mention appears as Theorem 5.7, Chapter 1 in Tempelman’s “Ergodic Theorems for Group Actions”, where it is set up in more general language. He attributes the result to Alaoglu and Garrett Birkhoff.
[Reference added, thanks – T.]
20 June, 2014 at 11:47 pm
govwhistleblower
Your proof does not look correct to me. Are you sure?
21 June, 2014 at 1:33 am
alabair
Thank you for what you are doing. However it’s intersting i to see the relationship between the probabilistic version of ergodic theorem in the case of irreductible Markov chain.
21 June, 2014 at 11:04 am
MrCactu5 (@MonsieurCactus)
I am having trouble picturing your main theorem.
Outside of these, what are “interesting” examples of amenable groups? I heard the braid group on 3 strands is amenable, perhaps is this part of something more general.
[The previous blog post https://terrytao.wordpress.com/2009/04/14/some-notes-on-amenability/ has some examples. -T.]
25 June, 2014 at 10:07 am
Lebesgue measure as the invariant factor of Loeb measure | What's new
[…] the abstract ergodic theorem from the previous post, one can also view this conditional expectation as the element in the closed convex hull of the […]
26 June, 2014 at 1:15 am
Gergely Harcos
I think the proof of Corollary 2 can be simplified. Namely, by Theorem 1, , and we are done.
, and we are done.
[Very nice! I’ve replaced my previous argument with yours. – T.]
26 June, 2014 at 8:05 am
Gergely Harcos
Thanks for displaying the new argument. I think there is a typo: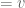 should be deleted, i.e. we only have and only need
should be deleted, i.e. we only have and only need  for
for 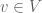 .
.
[Corrected, thanks – T.]
26 June, 2014 at 3:02 pm
Gergely Harcos
Dear Terry, I have trouble following the proof of Lemma 4. We observe first that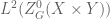 and
and 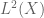 are relatively orthogonal over
are relatively orthogonal over 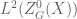 by Corollary 3. This should imply that
by Corollary 3. This should imply that  , but I don’t see how. Similarly, we should have
, but I don’t see how. Similarly, we should have  , so that in the end
, so that in the end  . I don’t see this last step either, but at least I can finish differently:
. I don’t see this last step either, but at least I can finish differently:
We know that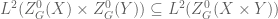 , hence it suffices to show that
, hence it suffices to show that  . Assuming
. Assuming  lies in this space, we can use Corollary 3 to deduce that
lies in this space, we can use Corollary 3 to deduce that  , whence using also
, whence using also  we can conclude
we can conclude  .
.
Can you please clarify or point to a more detailed reference? Thanks in advance.
26 June, 2014 at 5:16 pm
Terence Tao
Oops, that lemma and proof are complete nonsense! I only meant to claim when the action of G on Y is trivial (the claim is false otherwise), and this requires more of an argument than just abstract nonsense, it seems. I’ve rewritten that part completely.
when the action of G on Y is trivial (the claim is false otherwise), and this requires more of an argument than just abstract nonsense, it seems. I’ve rewritten that part completely.
27 June, 2014 at 1:41 am
Gergely Harcos
Thank you! For the restricted situation there is a more direct argument, via Corollary 3. Let and
and  , then we need to prove
, then we need to prove 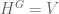 . We have
. We have  , so taking an orthogonal decomposition
, so taking an orthogonal decomposition  it suffices to show that
it suffices to show that  . Let
. Let  , then for any
, then for any  and any
and any  we have
we have 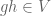 , so
, so  . Here
. Here 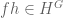 , hence applying Corollary 3 to
, hence applying Corollary 3 to  as a factor of
as a factor of  , we see that the relation
, we see that the relation  extends to any
extends to any  . As a result,
. As a result,  is orthogonal to all of
is orthogonal to all of  , whence
, whence  .
.
[Nice! I’ve replaced my previous argument with this one – T.]
2 July, 2014 at 1:17 am
Markus Haase
Dear Terry,
thank you for this extremely inspiring blog post.
With regard to your “abstract ergodic theorem” I would like to add the following comments:
The result is not bound to unitary groups but holds for all semigroups of contractions on a Hilbert space. Appropriately rephrased it even holds for contraction semigroups on a Banach space E such that E and its dual space E’ are both strictly convex. (In Krengel’s book this is Theorem 2.1.10 and is attributed also to Alaoglu-Birkhoff.) Actually, it is a consequence of a characterization of “mean ergodic semigroups”, due to Nagel (Krengel, Theorem 2.1.11).
According to Nagel (Ann. Inst. Fourier 23 (1973), 75-87) a semigroup of operators on a Banach space is called mean ergodic if its closed convex hull (in the weak=strong operator topology) has a zero element. This zero element, called the mean ergodic projection, is then a projection onto the fixed space of the semigroup. (In the case of a contraction semigroup, the mean ergodic projection is again a contraction, whence orthogonal if the space is a Hilbert space.)
There is a second approach to the result via the Jacobs-deLeeuw-Glicksberg theory. If S is a bounded (weakly=strongly) closed convex group of operators, then it is the trivial group, because according to a theorem of Kakutani the identity operator is an extremal point of the unit ball of operators on a Banach space (Krengel, Lemma 2.1.13). Now if T is a relatively weakly compact semigroup of operators one can form the closed convex hull S, say, of it, which is a compact semitopological semigroup. If S has a unique minimal idempotent Q, then S restricts to a convex compact group of operators on ran(Q), and hence, by the above, leaves ran(Q) fixed. So Q is a zero element in S, whence T is mean ergodic. One can now check for situations when S necessarily has a unique minimal idempotent, and here the standard assumptions are either amenability or the combination of contractivity of the operators with the strict convexity of E and E’.
2 August, 2014 at 11:12 am
Gergely Harcos
Dear Terry, a few typos and a suggestion:
1. In Corollary 3, should be
should be  .
.
2. In Section 1, Line 3, “which the same” should be “which is the same”.
3. In the proof of Proposition 8, in the first paragraph, should be
should be 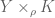 (three occurrences).
(three occurrences).
4. In the proof of Proposition 8, “for all ” should be “for all
” should be “for all 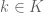 “.
“.
5. In the last line of the post, “Haar measure” should be “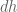 ” for clarity.
” for clarity.
[Corrected, thanks – T.]
9 April, 2015 at 10:16 pm
The ergodic theorem and Gowers-Host-Kra seminorms without separability or amenability | What's new
[…] a previous blog post, I noted a variant of this ergodic theorem (due to Alaoglu and Birkhoff) that holds even when the […]
1 October, 2020 at 8:03 pm
An uncountable Mackey-Zimmer theorem | What's new
[…] this case the theorem in question is the Mackey-Zimmer theorem, previously discussed in this blog post. This theorem gives an important classification of group and homogeneous extensions of […]
1 August, 2022 at 2:13 am
gr.group theory - What does the unique mean on weakly almost periodic functions look like? Answer - Lord Web
[…] can be seen through the Birkhoff-Alaoglu Ergodic Theorem (see Tao’s blog post on this), after looking at the relation between (1) the weak-closed convex hull in […]