In analytic number theory, there is a well known analogy between the prime factorisation of a large integer, and the cycle decomposition of a large permutation; this analogy is central to the topic of “anatomy of the integers”, as discussed for instance in this survey article of Granville. Consider for instance the following two parallel lists of facts (stated somewhat informally). Firstly, some facts about the prime factorisation of large integers:
- Every positive integer
has a prime factorisation
into (not necessarily distinct) primes
, which is unique up to rearrangement. Taking logarithms, we obtain a partition
of
.
- (Prime number theorem) A randomly selected integer
of size
will be prime with probability
when
is large.
- If
is a randomly selected large integer of size
, and
is a randomly selected prime factor of
(with each index
being chosen with probability
), then
is approximately uniformly distributed between
and
. (See Proposition 9 of this previous blog post.)
- The set of real numbers
arising from the prime factorisation
of a large random number
converges (away from the origin, and in a suitable weak sense) to the Poisson-Dirichlet process in the limit
. (See the previously mentioned blog post for a definition of the Poisson-Dirichlet process, and a proof of this claim.)
Now for the facts about the cycle decomposition of large permutations:
- Every permutation
has a cycle decomposition
into disjoint cycles
, which is unique up to rearrangement, and where we count each fixed point of
as a cycle of length
. If
is the length of the cycle
, we obtain a partition
of
.
- (Prime number theorem for permutations) A randomly selected permutation of
will be an
-cycle with probability exactly
. (This was noted in this previous blog post.)
- If
is a random permutation in
, and
is a randomly selected cycle of
(with each
being selected with probability
), then
is exactly uniformly distributed on
. (See Proposition 8 of this blog post.)
- The set of real numbers
arising from the cycle decomposition
of a random permutation
converges (in a suitable sense) to the Poisson-Dirichlet process in the limit
. (Again, see this previous blog post for details.)
See this previous blog post (or the aforementioned article of Granville, or the Notices article of Arratia, Barbour, and Tavaré) for further exploration of the analogy between prime factorisation of integers and cycle decomposition of permutations.
There is however something unsatisfying about the analogy, in that it is not clear why there should be such a kinship between integer prime factorisation and permutation cycle decomposition. It turns out that the situation is clarified if one uses another fundamental analogy in number theory, namely the analogy between integers and polynomials over a finite field
, discussed for instance in this previous post; this is the simplest case of the more general function field analogy between number fields and function fields. Just as we restrict attention to positive integers when talking about prime factorisation, it will be reasonable to restrict attention to monic polynomials
. We then have another analogous list of facts, proven very similarly to the corresponding list of facts for the integers:
- Every monic polynomial
has a factorisation
into irreducible monic polynomials
, which is unique up to rearrangement. Taking degrees, we obtain a partition
of
.
- (Prime number theorem for polynomials) A randomly selected monic polynomial
of degree
will be irreducible with probability
when
is fixed and
is large.
- If
is a random monic polynomial of degree
, and
is a random irreducible factor of
(with each
selected with probability
), then
is approximately uniformly distributed in
when
is fixed and
is large.
- The set of real numbers
arising from the factorisation
of a randomly selected polynomial
of degree
converges (in a suitable sense) to the Poisson-Dirichlet process when
is fixed and
is large.
The above list of facts addressed the large limit of the polynomial ring
, where the order
of the field is held fixed, but the degrees of the polynomials go to infinity. This is the limit that is most closely analogous to the integers
. However, there is another interesting asymptotic limit of polynomial rings to consider, namely the large
limit where it is now the degree
that is held fixed, but the order
of the field goes to infinity. Actually to simplify the exposition we will use the slightly more restrictive limit where the characteristic
of the field goes to infinity (again keeping the degree
fixed), although all of the results proven below for the large
limit turn out to be true as well in the large
limit.
The large (or large
) limit is technically a different limit than the large
limit, but in practice the asymptotic statistics of the two limits often agree quite closely. For instance, here is the prime number theorem in the large
limit:
Theorem 1 (Prime number theorem) The probability that a random monic polynomial
of degree
is irreducible is
in the limit where
is fixed and the characteristic
goes to infinity.
Proof: There are monic polynomials
of degree
. If
is irreducible, then the
zeroes of
are distinct and lie in the finite field
, but do not lie in any proper subfield of that field. Conversely, every element
of
that does not lie in a proper subfield is the root of a unique monic polynomial in
of degree
(the minimal polynomial of
). Since the union of all the proper subfields of
has size
, the total number of irreducible polynomials of degree
is thus
, and the claim follows.
Remark 2 The above argument and inclusion-exclusion in fact gives the well known exact formula
for the number of irreducible monic polynomials of degree
.
Now we can give a precise connection between the cycle distribution of a random permutation, and (the large limit of) the irreducible factorisation of a polynomial, giving a (somewhat indirect, but still connected) link between permutation cycle decomposition and integer factorisation:
Theorem 3 The partition
of a random monic polynomial
of degree
converges in distribution to the partition
of a random permutation
of length
, in the limit where
is fixed and the characteristic
goes to infinity.
We can quickly prove this theorem as follows. We first need a basic fact:
Lemma 4 (Most polynomials square-free in large
limit) A random monic polynomial
of degree
will be square-free with probability
when
is fixed and
(or
) goes to infinity. In a similar spirit, two randomly selected monic polynomials
of degree
will be coprime with probability
if
are fixed and
or
goes to infinity.
Proof: For any polynomial of degree
, the probability that
is divisible by
is at most
. Summing over all polynomials of degree
, and using the union bound, we see that the probability that
is not squarefree is at most
, giving the first claim. For the second, observe from the first claim (and the fact that
has only a bounded number of factors) that
is squarefree with probability
, giving the claim.
Now we can prove the theorem. Elementary combinatorics tells us that the probability of a random permutation consisting of
cycles of length
for
, where
are nonnegative integers with
, is precisely
since there are ways to write a given tuple of cycles
in cycle notation in nondecreasing order of length, and
ways to select the labels for the cycle notation. On the other hand, by Theorem 1 (and using Lemma 4 to isolate the small number of cases involving repeated factors) the number of monic polynomials of degree
that are the product of
irreducible polynomials of degree
is
which simplifies to
and the claim follows.
This was a fairly short calculation, but it still doesn’t quite explain why there is such a link between the cycle decomposition of permutations and the factorisation
of a polynomial. One immediate thought might be to try to link the multiplication structure of permutations in
with the multiplication structure of polynomials; however, these structures are too dissimilar to set up a convincing analogy. For instance, the multiplication law on polynomials is abelian and non-invertible, whilst the multiplication law on
is (extremely) non-abelian but invertible. Also, the multiplication of a degree
and a degree
polynomial is a degree
polynomial, whereas the group multiplication law on permutations does not take a permutation in
and a permutation in
and return a permutation in
.
I recently found (after some discussions with Ben Green) what I feel to be a satisfying conceptual (as opposed to computational) explanation of this link, which I will place below the fold.
To put cycle decomposition of permutations and factorisation of polynomials on an equal footing, we generalise the notion of a permutation to the notion of a partial permutation
on a fixed (but possibly infinite) domain
, which consists of a finite non-empty subset
of the set
, together with a bijection
on
; I’ll call
the support of the partial permutation. We say that a partial permutation
is of size
if the support
is of cardinality
, and denote this size as
. And now we can introduce a multiplication law on partial permutations that is much closer to that of polynomials: if two partial permutations
on the same domain
have disjoint supports
, then we can form their disjoint union
, supported on
, to be the bijection on
that agrees with
on
and with
on
. Note that this is a commutative and associative operation (where it is defined), and is the disjoint union of a partial permutation of size
and a partial permutation of size
is a partial permutation of size
, so this operation is much closer in behaviour to the multiplication law on polynomials than the group law on
. There is the defect that the disjoint union operation is sometimes undefined (when the two partial permutations have overlapping support); but in the asymptotic regime where the size
is fixed and the set
is extremely large, this will be very rare (compare with Lemma 4).
Note that a partial permutation is irreducible with respect to disjoint union if and only if it is a cycle on its support, and every partial permutation has a decomposition
into such partial cycles, unique up to permutations. If one then selects some set
of partial cycles on the domain
to serve as “generalised primes”, then one can define (in the spirit of Beurling integers) the set
of “generalised integers”, defined as those partial permutations that are the disjoint union
of partial cycles in
. If one lets
denote the set of generalised integers of size
, one can (assuming that this set is non-empty and finite) select a partial permutation
uniformly at random from
, and consider the partition
of
arising from the decomposition into generalised primes.
We can now embed both the cycle decomposition for (complete) permutations and the factorisation of polynomials into this common framework. We begin with the cycle decomposition for permutations. Let be a large natural number, and set the domain
to be the set
. We define
to be the set of all partial cycles on
of size
, and let
be the union of the
, that is to say the set of all partial cycles on
(of arbitrary size). Then
is of course the set of all partial permutations on
, and
is the set of all partial permutations on
of size
. To generate an element of
uniformly at random for
, one simply has to randomly select an
-element subset
of
, and then form a random permutation of the
elements of
. From this, it is obvious that the partition
of
coming from a randomly chosen element of
has exactly the same distribution as the partition
of
coming from a randomly chosen element of
, as long as
is at least as large as
of course.
Now we embed the factorisation of polynomials into the same framework. The domain is now taken to be the algebraic closure
of
, or equivalently the direct limit of the finite fields
(with the obvious inclusion maps). This domain has a fundamental bijection on it, the Frobenius map
, which is a field automorphism that has
as its fixed points. We define
to be the set of partial permutations on
formed by restricting the Frobenius map
to a finite Frobenius-invariant set. It is easy to see that the irreducible Frobenius-invariant sets (that is to say, the orbits of
) arise from taking an element
of
together with all of its Galois conjugates, and so if we define
to be the set of restrictions of Frobenius to a single such Galois orbit, then
are the generalised integers to the generalised primes
in the sense above. Next, observe that, when the characteristic
is sufficiently large, every squarefree monic polynomial
of degree
generates a generalised integer of size
, namely the restriction of the Frobenius map to the
roots of
(which will be necessarily distinct when the characteristic is large and
is squarefree). This generalised integer will be a generalised prime precisely when
is irreducible. Conversely, every generalised integer of size
generates a squarefree monic polynomial in
, namely the product of
as
ranges over the support of the integer. This product is clearly monic, squarefree, and Frobenius-invariant, thus it lies in
. Thus we may identify
with the monic squarefree polynomials of
of degree
. With this identification, the (now partially defined) multiplication operation on monic squarefree polynomials coincides exactly with the disjoint union operation on partial permutations. As such, we see that the partition
associated to a randomly chosen squarefree monic polynomial
of degree
has exactly the same distribution as the partition
associated to a randomly chosen generalised integer
of size
. By Lemma 4, one can drop the condition of being squarefree while only distorting the distribution by
.
Now that we have placed cycle decomposition of permutations and factorisation of polynomials into the same framework, we can explain Theorem 3 as a consequence of the following universality result for generalised prime factorisations:
Theorem 5 (Universality) Let
be collections of generalised primes and integers respectively on a domain
, all of which depend on some asymptotic parameter
that goes to infinity. Suppose that for any fixed
and
going to infinity, the sets
are non-empty with cardinalities obeying the asymptotic
Also, suppose that only
of the pairs
have overlapping supports (informally, this means that
is defined with probability
). Then, for fixed
and
going to infinity, the distribution of the partition
of a random generalised integer from
is universal in the limit; that is to say, the limiting distribution does not depend on the precise choice of
.
Note that when consists of all the partial permutations of size
on
we have
while when consists of the monic squarefree polynomials of degree
in
then from Lemma 4 we also have
so in both cases the first hypothesis (1) is satisfied. The second hypothesis is easy to verify in the former case and follows from Lemma 4 in the latter case. Thus, Theorem 5 gives Theorem 3 as a corollary.
Remark 6 An alternate way to interpret Theorem 3 is as an equidistribution theorem: if one randomly labels the
zeroes of a random degree
polynomial as
, then the resulting permutation on
induced by the Frobenius map is asymptotically equidistributed in the large
(or large
) limit. This is the simplest case of a much more general (and deeper) result known as the Deligne equidistribution theorem, discussed for instance in this survey of Kowalski. See also this paper of Church, Ellenberg, and Farb concerning more precise asymptotics for the number of squarefree polynomials with a given cycle decomposition of Frobenius.
It remains to prove Theorem 5. The key is to establish an abstract form of the prime number theorem in this setting.
Theorem 7 (Prime number theorem) Let the hypotheses be as in Theorem 5. Then for fixed
and
, the density of
in
is
. In particular, the asymptotic density
is universal (it does not depend on the choice of
).
Proof: Let (this may only be defined for
sufficiently large depending on
); our task is to show that
for each fixed
.
Consider the set of pairs where
is an element of
and
is an element of the support of
. Clearly, the number of such pairs is
. On the other hand, given such a pair
, there is a unique factorisation
, where
is the generalised prime in the decomposition of
that contains
in its support, and
is formed from the remaining components of
.
has some size
,
has the complementary size
and has disjoint support from
, and
has to be one of the
elements of the support of
. Conversely, if one selects
, then selects a generalised prime
, and a generalised integer
with disjoint support from
, and an element
in the support of
, we recover the pair
. Using the hypotheses of Theorem 5, we thus obtain the double counting identity
and thus for every fixed
, and so
for fixed
as claimed.
Remark 8 One could cast this argument in a language more reminiscent of analytic number theory by forming generating series of
and
and treating these series as analogous to a zeta function and its log-derivative (in close analogy to what is done with Beurling primes), but we will not do so here.
We can now finish the proof of Theorem 5. To show asymptotic universality of the partition of a random generalised integer
, we may assume inductively that asymptotic universality has already been shown for all smaller choices of
. To generate a uniformly random generalised integer
of size
, we can repeat the process used to prove Theorem 7. It of course suffices to generate a uniformly random pair
, where
is a generalised integer of size
and
is an element of the support of
, since on dropping
we would obtain a uniformly drawn
.
To obtain the pair , we first select
uniformly at random, then select a generalised prime
randomly from
and a generalised integer
randomly from
(independently of
once
is fixed). Finally, we select
uniformly at random from the support of
, and set
. The pair
is certainly a pair of the required form, but this random variable is not quite uniformly distributed amongst all such pairs. However, by repeating the calculations in Theorem 5 (and in particular relying on the conclusion
), we see that this distribution is is within
of the uniform distribution in total variation norm. Thus, the distribution of the cycle partition
of a uniformly chosen
lies within
in total variation of the distribution of the cycle partition of a
chosen by the above recipe. However, the cycle partition of
is simply the union (with multiplicity) of
with the cycle partition of
. As the latter was already assumed to be asymptotically universal, we conclude that the former is also, as required.
Remark 9 The above analysis helps explain why one could not easily link permutation cycle decomposition with integer factorisation – to produce permutations here with the right asymptotics we needed both the large
limit and the Frobenius map, both of which are available in the function field setting but not in the number field setting.

10 comments
Comments feed for this article
15 July, 2015 at 8:26 pm
Will
It might be worth pointing out that Deligne’s equidistribution theorem provides another conceptual explanation for why there is a connection between random polynomials and random permutations, which generalizes to cases where the polynomials are constructed by some random process involving the additive structure, like a fixed polynomial plus a random low degree polynomial.
Well, at least some people think it’s conceptual.
[Good point; I added a remark to this effect. -T.]
16 July, 2015 at 2:01 am
MrCactu5 (@MonsieurCactus)
I imagine your generalized primes do not include the primes numbers themselves or your proof of the Prime Number Theorem would not be so short. Are there any objects which interpolate between
or your proof of the Prime Number Theorem would not be so short. Are there any objects which interpolate between 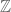 and
and ![\mathbb{F}_q[T]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_q%5BT%5D&bg=ffffff&fg=545454&s=0&c=20201002) ? Perhaps even
? Perhaps even ![\lim_{q \to \infty} \mathbb{F}_q[T] = \mathbb{Z}](https://s0.wp.com/latex.php?latex=%5Clim_%7Bq+%5Cto+%5Cinfty%7D+%5Cmathbb%7BF%7D_q%5BT%5D+%3D+%5Cmathbb%7BZ%7D&bg=ffffff&fg=545454&s=0&c=20201002) which seems ridiculous.
which seems ridiculous.
16 July, 2015 at 5:59 am
Terence Tao
Unfortunately there is no rigorous direct connection currently known between function fields and number fields, which is a pity for many reasons (for instance, the Riemann hypothesis is known for the former but not the latter). Nevertheless the analogies between the two are remarkably strong. I believe part of the motivation of trying to construct a theory of “the field of one element” is to try to create such a connection, but this program has not yet succeeded in this task.
16 July, 2015 at 2:29 am
Anonymous
The partition
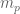 is the multiplicity for each prime
is the multiplicity for each prime  in
in  , is represented (at least formally) by the generating function
, is represented (at least formally) by the generating function
where
Which is equivalent to the fundamental theorem of arithmetic.
It is interesting to observe that the substitution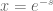 in this partition generating function, gives Euler’s product representation for
in this partition generating function, gives Euler’s product representation for 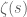 . Is similar connection exists between partition generating functions for permutations and polynomials and corresponding zeta functions?
. Is similar connection exists between partition generating functions for permutations and polynomials and corresponding zeta functions?
16 July, 2015 at 5:53 am
Arul
Nice formula, thank’s for sharing
18 July, 2015 at 11:20 pm
Emmanuel Amiot
I have trouble with the assertion “A randomly selected permutation of {S_n} will be a cycle with probability exactly {1/n}”: in {S_3} I see 5 cycles, barring id; in {S_4} there are 20. Is it a misprint from the average number of {k-}cycles in the decomposition of a random permutation, which is indeed proved to be {1/k} in the cited previous post?
[Corrected, thanks – T.]
20 July, 2015 at 12:50 am
coderodde
Hello, Terry. Did you consider using … in your text? This will align your text in a funky way, and thus, add more awesomeness to already awesome text of yours.
20 July, 2015 at 12:52 am
coderodde
WP did not allow me to post HTML. I was suggesting using “justify” for “align”-attribute in the “p” HTML element.
21 August, 2015 at 7:28 am
JSE
“to produce permutations here with the right asymptotics we needed both the large {q} limit and the Frobenius map, both of which are available in the function field setting but not in the number field setting.” I’ll bet most of what you say here works without the large q limit, though. Your Theorem 5 is fine, and your Theorem 3 just has to be modified: the distribution on irreducible factor degrees of a random polynomial over F_q (with n -> oo) is in a sense a “deformation” of the independent Poissons you get from permutations. (Maybe what I literally mean is that everything is a power series in q^{-1} with those Poissons as leading term.) Of course I am biased by my habit of thinking of these things cohomologically, in which setting the statistics of polynomials are governed by an H^0 (whose contribution agrees exactly with statistics of random permutations) and then a sum over higher H^i; the latter become negligible as q gets big, which gives Theorem 3.
24 November, 2016 at 4:31 pm
onlyearthleft.
sorry you addressed q->infinity and n->infinity but the case of q/n=c a real constant might turn out to be the closest towards any connection to integers. Would there be any nontrivial analogies here?