Klaus Roth, who made fundamental contributions to analytic number theory, died this Tuesday, aged 90.
I never met or communicated with Roth personally, but was certainly influenced by his work; he wrote relatively few papers, but they tended to have outsized impact. For instance, he was one of the key people (together with Bombieri) to work on simplifying and generalising the large sieve, taking it from the technically formidable original formulation of Linnik and Rényi to the clean and general almost orthogonality principle that we have today (discussed for instance in these lecture notes of mine). The paper of Roth that had the most impact on my own personal work was his three-page paper proving what is now known as Roth’s theorem on arithmetic progressions:
Theorem 1 (Roth’s theorem on arithmetic progressions) Let
be a set of natural numbers of positive upper density (thus
). Then
contains infinitely many arithmetic progressions
of length three (with
non-zero of course).
At the heart of Roth’s elegant argument was the following (surprising at the time) dichotomy: if had some moderately large density within some arithmetic progression
, either one could use Fourier-analytic methods to detect the presence of an arithmetic progression of length three inside
, or else one could locate a long subprogression
of
on which
had increased density. Iterating this dichotomy by an argument now known as the density increment argument, one eventually obtains Roth’s theorem, no matter which side of the dichotomy actually holds. This argument (and the many descendants of it), based on various “dichotomies between structure and randomness”, became essential in many other results of this type, most famously perhaps in Szemerédi’s proof of his celebrated theorem on arithmetic progressions that generalised Roth’s theorem to progressions of arbitrary length. More recently, my recent work on the Chowla and Elliott conjectures that was a crucial component of the solution of the Erdös discrepancy problem, relies on an entropy decrement argument which was directly inspired by the density increment argument of Roth.
The Erdös discrepancy problem also is connected with another well known theorem of Roth:
Theorem 2 (Roth’s discrepancy theorem for arithmetic progressions) Let
be a sequence in
. Then there exists an arithmetic progression
in
with
positive such that
for an absolute constant
.
In fact, Roth proved a stronger estimate regarding mean square discrepancy, which I am not writing down here; as with the Roth theorem in arithmetic progressions, his proof was short and Fourier-analytic in nature (although non-Fourier-analytic proofs have since been found, for instance the semidefinite programming proof of Lovasz). The exponent is known to be sharp (a result of Matousek and Spencer).
As a particular corollary of the above theorem, for an infinite sequence of signs, the sums
are unbounded in
. The Erdös discrepancy problem asks whether the same statement holds when
is restricted to be zero. (Roth also established discrepancy theorems for other sets, such as rectangles, which will not be discussed here.)
Finally, one has to mention Roth’s most famous result, cited for instance in his Fields medal citation:
Theorem 3 (Roth’s theorem on Diophantine approximation) Let
be an irrational algebraic number. Then for any
there is a quantity
such that
From the Dirichlet approximation theorem (or from the theory of continued fractions) we know that the exponent in the denominator cannot be reduced to
or below. A classical and easy theorem of Liouville gives the claim with the exponent
replaced by the degree of the algebraic number
; work of Thue and Siegel reduced this exponent, but Roth was the one who obtained the near-optimal result. An important point is that the constant
is ineffective – it is a major open problem in Diophantine approximation to produce any bound significantly stronger than Liouville’s theorem with effective constants. This is because the proof of Roth’s theorem does not exclude any single rational
from being close to
, but instead very ingeniously shows that one cannot have two different rationals
,
that are unusually close to
, even when the denominators
are very different in size. (I refer to this sort of argument as a “dueling conspiracies” argument; they are strangely prevalent throughout analytic number theory.)

14 comments
Comments feed for this article
12 November, 2015 at 9:55 am
Ben Green
I did meet Roth, in Inverness around 7 years ago. I asked him what his favourite proof (among his results was) and he said the lower bound for the L^2 discrepancy of point sets with respect to axis parallel boxes. It is a very elegant argument, nicely described in Bernard Chazelle’s book “Discrepancy Theory”. Later in his career he became quite interested in the “Heilbronn triangle problem”, which came up in conversation the other day: given n points in the unit square, what’s the smallest area of triangle they are guaranteed to span. I believe that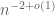 is conjectured, and that Roth was the first to improve on the trivial bound
is conjectured, and that Roth was the first to improve on the trivial bound  . Subsequently bounds of the form
. Subsequently bounds of the form  were obtained.
were obtained.
12 November, 2015 at 1:57 pm
Anonymous
I guess it should be: maximum over n points of the area of the smallest triangle.
5 June, 2018 at 10:41 am
Aritram Dhar
Terence Sir your lecture video on “Discrepancy theory” is
nice.
12 November, 2015 at 2:10 pm
kodlu
RIP. His book “Sequences” with Halberstam is very nice. My knowledge of the overall history of the field is quite limited but could onr say that, besides Erdo”s, he was the major figure who moved what is now called additive combinatorics forward in the middle years of the 20th century?
12 November, 2015 at 4:09 pm
kumaramitdavid
On 8th of this month suddenly Roth’s name came to my brain as I reminded about Gelfond’s proof of Hilbert’s 7th problem – this is where I first heard about Roth, in connection with some extension (or generalisation of Gelfond’s Theorem – I just went to check if he was alive and found him so. So, when I just read this blog, I couldn’t stop saying to myself, “What? he was alive just few days ago!” though soon I realised my mistake.
12 November, 2015 at 4:12 pm
kumaramitdavid
Okay, yes I remembered, it was the theorem that Prof Terry Tao has numbered as 3; it was related to Liouville’s Theorem – my mistake. Nevertheless, I read all that in the same article – Hilbert 7th problem.
12 November, 2015 at 6:58 pm
AG
I just read a very interesting “Conversation with Klaus Roth” in the “Art in the Life of Mathematicians” (AMS 2015) edited by Anna Kepes Szemeredi
13 November, 2015 at 6:23 am
John Cosgrave
I am saddened to hear of the passing of K.F. Roth; he wasn’t just a great mathematician, he was also a kind and gentle soul. I have the happy memory of attending his Imperial College lecture course ‘Landmarks in Number Theory’ in 1969-70 (Roger Baker also attended). I was then a graduate student at another London college (Royal Holloway), was reading the extraordinary papers of Alan Baker, and was in desperate need of someone with whom I could talk about Baker’s work. I wrote to Roth to ask if he would discuss this work with me, and he very generously did so (in so doing I learned more from him in one afternoon than from any other person I ever met) in his office at I.C.
I wrote to thank him, and he replied in a letter dated 4/11/69: “Dear Cosgrave, Thank you for your letter. It is many years since I worked in Diophantine approximations; I am at the moment engaged on problems of quite a different type. But I would be happy to meet you and discuss any specific difficulties you may have encountered. If you phone me at home (352-1363) one evening, we could arrange a time convenient for us both. Yours sincerely. K.F. Roth.”
I have that letter in front of me now (I keep it inside his Sequences book, the one he wrote with Halberstam, autographed by dear Heini himself), and I will send a photo of the letter to anyone who wishes to have it:
jbcosgrave@gmail.com
Incidentally, when I was with him, I asked about the circumstances in which he found the proof of his (remarkable) theorem on rational approximations to algebraic numbers (Theorem 3 of T. Tao’s note on Roth). Many years later I wrote what he replied in the Roth section of the following student aimed lecture (never delivered!) of mine: “An introduction to the history of transcendental numbers”, availabe at
http://staff.spd.dcu.ie/johnbcos/download/Public%20and%20other%20lectures/transcendental%206thMay04/transcendentalTOC.html
25 July, 2017 at 5:51 am
John B. Cosgrave
It has been brought to my attention that the above link is broken (the original web site was taken down by Dublin City University). The CORRECT link is now: http://johnbcosgrave.com/archive/transcendental_numbers.htm
17 November, 2015 at 3:12 am
J.P. McCarthy
Hi,
“(discussed for instance in these lecture notes of mine)”… missing a link.
[Link added, thanks – T.]
17 November, 2015 at 5:33 pm
Bob Vaughan
Hi, With William Chen, Trevor Stuart and David Larman, I am preparing an obituary to send to The (London) Times. Also we will prepare something for the London Math. Soc. and, longer term, will prepare something for the Bibliographical Memoirs of the Royal Society. Any comments and observations would be gratefully received. Bob Vaughan
23 November, 2015 at 6:12 pm
On the vanishing gradient problem | Exploratoria
[…] now recently Roth passed away (a couple of weeks […]
24 November, 2015 at 7:58 pm
The Heilbronn Triangle Problem | Radimentary
[…] was shocked and saddened to discover that Roth passed away that same day. Terry Tao wrote a great post about some of Roth’s most important results in analytic number […]
27 November, 2015 at 3:01 am
John Ashworth
I had the pleasure of attending Roth’s lecture course on Complex Analysis whilst an undergraduate at Imperial in the early 70’s. His lectures were always clear and comprehensive: in particular, though, he communicated his enthusiasm for this particularly beautiful area of mathematics, which made a great impression on, I think, all the young students there. I have never forgotten his wonderful guttural accent stressing the opening “R” as he would say “.. but this is a RRRegular function…” (they are now more commonly referred to as holomorphic or just complex analytic functions). I consider it an honour to have been taught by him.