I’ve just uploaded two related papers to the arXiv:
- The logarithmically averaged Chowla and Elliott conjectures for two-point correlations, submitted to Forum of Mathematics, Pi; and
- The Erdos discrepancy problem, submitted to the new arXiv overlay journal, Discrete Analysis (see this recent announcement on Tim Gowers’ blog).
This pair of papers is an outgrowth of these two recent blog posts and the ensuing discussion. In the first paper, we establish the following logarithmically averaged version of the Chowla conjecture (in the case of two-point correlations (or “pair correlations”)):
Theorem 1 (Logarithmically averaged Chowla conjecture) Let
be natural numbers, and let
be integers such that
. Let
be a quantity depending on
that goes to infinity as
. Let
denote the Liouville function. Then one has
as
.
For comparison, the non-averaged Chowla conjecture would imply that
which is a strictly stronger estimate than (2), and remains open.
The arguments also extend to other completely multiplicative functions than the Liouville function. In particular, one obtains a slightly averaged version of the non-asymptotic Elliott conjecture that was shown in the previous blog post to imply a positive solution to the Erdos discrepancy problem. The averaged version of the conjecture established in this paper is slightly weaker than the one assumed in the previous blog post, but it turns out that the arguments there can be modified without much difficulty to accept this averaged Elliott conjecture as input. In particular, we obtain an unconditional solution to the Erdos discrepancy problem as a consequence; this is detailed in the second paper listed above. In fact we can also handle the vector-valued version of the Erdos discrepancy problem, in which the sequence takes values in the unit sphere of an arbitrary Hilbert space, rather than in
.
Estimates such as (2) or (3) are known to be subject to the “parity problem” (discussed numerous times previously on this blog), which roughly speaking means that they cannot be proven solely using “linear” estimates on functions such as the von Mangoldt function. However, it is known that the parity problem can be circumvented using “bilinear” estimates, and this is basically what is done here.
We now describe in informal terms the proof of Theorem 1, focusing on the model case (2) for simplicity. Suppose for contradiction that the left-hand side of (2) was large and (say) positive. Using the multiplicativity , we conclude that
is also large and positive for all primes that are not too large; note here how the logarithmic averaging allows us to leave the constraint
unchanged. Summing in
, we conclude that
is large and positive for any given set of medium-sized primes. By a standard averaging argument, this implies that
is large for many choices of , where
is a medium-sized parameter at our disposal to choose, and we take
to be some set of primes that are somewhat smaller than
. (A similar approach was taken in this recent paper of Matomaki, Radziwill, and myself to study sign patterns of the Möbius function.) To obtain the required contradiction, one thus wants to demonstrate significant cancellation in the expression (4). As in that paper, we view
as a random variable, in which case (4) is essentially a bilinear sum of the random sequence
along a random graph
on
, in which two vertices
are connected if they differ by a prime
in
that divides
. A key difficulty in controlling this sum is that for randomly chosen
, the sequence
and the graph
need not be independent. To get around this obstacle we introduce a new argument which we call the “entropy decrement argument” (in analogy with the “density increment argument” and “energy increment argument” that appear in the literature surrounding Szemerédi’s theorem on arithmetic progressions, and also reminiscent of the “entropy compression argument” of Moser and Tardos, discussed in this previous post). This argument, which is a simple consequence of the Shannon entropy inequalities, can be viewed as a quantitative version of the standard subadditivity argument that establishes the existence of Kolmogorov-Sinai entropy in topological dynamical systems; it allows one to select a scale parameter
(in some suitable range
) for which the sequence
and the graph
exhibit some weak independence properties (or more precisely, the mutual information between the two random variables is small).
Informally, the entropy decrement argument goes like this: if the sequence has significant mutual information with
, then the entropy of the sequence
for
will grow a little slower than linearly, due to the fact that the graph
has zero entropy (knowledge of
more or less completely determines the shifts
of the graph); this can be formalised using the classical Shannon inequalities for entropy (and specifically, the non-negativity of conditional mutual information). But the entropy cannot drop below zero, so by increasing
as necessary, at some point one must reach a metastable region (cf. the finite convergence principle discussed in this previous blog post), within which very little mutual information can be shared between the sequence
and the graph
. Curiously, for the application it is not enough to have a purely quantitative version of this argument; one needs a quantitative bound (which gains a factor of a bit more than
on the trivial bound for mutual information), and this is surprisingly delicate (it ultimately comes down to the fact that the series
diverges, which is only barely true).
Once one locates a scale with the low mutual information property, one can use standard concentration of measure results such as the Hoeffding inequality to approximate (4) by the significantly simpler expression
The important thing here is that Hoeffding’s inequality gives exponentially strong bounds on the failure probability, which is needed to counteract the logarithms that are inevitably present whenever trying to use entropy inequalities. The expression (5) can then be controlled in turn by an application of the Hardy-Littlewood circle method and a non-trivial estimate
for averaged short sums of a modulated Liouville function established in another recent paper by Matomäki, Radziwill and myself.
When one uses this method to study more general sums such as
one ends up having to consider expressions such as
where is the coefficient
. When attacking this sum with the circle method, one soon finds oneself in the situation of wanting to locate the large Fourier coefficients of the exponential sum
In many cases (such as in the application to the Erdös discrepancy problem), the coefficient is identically
, and one can understand this sum satisfactorily using the classical results of Vinogradov: basically,
is large when
lies in a “major arc” and is small when it lies in a “minor arc”. For more general functions
, the coefficients
are more or less arbitrary; the large values of
are no longer confined to the major arc case. Fortunately, even in this general situation one can use a restriction theorem for the primes established some time ago by Ben Green and myself to show that there are still only a bounded number of possible locations
(up to the uncertainty mandated by the Heisenberg uncertainty principle) where
is large, and we can still conclude by using (6). (Actually, as recently pointed out to me by Ben, one does not need the full strength of our result; one only needs the
restriction theorem for the primes, which can be proven fairly directly using Plancherel’s theorem and some sieve theory.)
It is tempting to also use the method to attack higher order cases of the (logarithmically) averaged Chowla conjecture, for instance one could try to prove the estimate
The above arguments reduce matters to obtaining some non-trivial cancellation for sums of the form
A little bit of “higher order Fourier analysis” (as was done for very similar sums in the ergodic theory context by Frantzikinakis-Host-Kra and Wooley-Ziegler) lets one control this sort of sum if one can establish a bound of the form
where goes to infinity and
is a very slowly growing function of
. This looks very similar to (6), but the fact that the supremum is now inside the integral makes the problem much more difficult. However it looks worth attacking (7) further, as this estimate looks like it should have many nice applications (beyond just the
case of the logarithmically averaged Chowla or Elliott conjectures, which is already interesting).
For higher than
, the same line of analysis requires one to replace the linear phase
by more complicated phases, such as quadratic phases
or even
-step nilsequences. Given that (7) is already beyond the reach of current literature, these even more complicated expressions are also unavailable at present, but one can imagine that they will eventually become tractable, in which case we would obtain an averaged form of the Chowla conjecture for all
, which would have a number of consequences (such as a logarithmically averaged version of Sarnak’s conjecture, as per this blog post).
It would of course be very nice to remove the logarithmic averaging, and be able to establish bounds such as (3). I did attempt to do so, but I do not see a way to use the entropy decrement argument in a manner that does not require some sort of averaging of logarithmic type, as it requires one to pick a scale that one cannot specify in advance, which is not a problem for logarithmic averages (which are quite stable with respect to dilations) but is problematic for ordinary averages. But perhaps the problem can be circumvented by some clever modification of the argument. One possible approach would be to start exploiting multiplicativity at products of primes, and not just individual primes, to try to keep the scale fixed, but this makes the concentration of measure part of the argument much more complicated as one loses some independence properties (coming from the Chinese remainder theorem) which allowed one to conclude just from the Hoeffding inequality.

77 comments
Comments feed for this article
18 September, 2015 at 9:33 pm
Anonymous
In the first paper (page 26) it seems that the integrand in (4.1) is different from the integrand in (7) above (perhaps the arguments of both and
and  in (4.1) should be corrected according to the shift
in (4.1) should be corrected according to the shift  in the summation variables.)
in the summation variables.)
[There is a typo in (4.1) which will be corrected in the next revision – T.]
19 September, 2015 at 7:13 am
Anonymous
Is in (6), (7) over all real
in (6), (7) over all real  ?
?
19 September, 2015 at 10:02 am
Anonymous
Yes.
19 September, 2015 at 7:41 am
John Mangual
@TerryTao It was very hard to program the Möbius function for a large range of N. I could find the primes up to a billion within a reasonable time of 1 minute. Writing the algorithm took several attempts. Indeed, I was able to compute the Mertens function after catching a serious error.
I do not have any specific interest in prime number theory. However, Möbius pseudorandomness is a bottleneck to any asymptotic discussion of integers. Sometimes, when I least expect it.
I am weary of Hardy’s layering of notation and am not sure how to interpret symbols like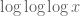 and
and 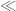 . The computer has been a helpful tool in following along.
. The computer has been a helpful tool in following along.
These subtleties I attribute to the complexity class of the set of primes, which share aspects of random sets. Yet primes are not totally random, e.g. quadratic reciprocity, Fermat’s little Theorem, etc.
19 September, 2015 at 7:59 am
Antonio
offtopic: I love the image of the tree in your blog, Dr Terrence Tao, where can i get it?
19 September, 2015 at 9:56 am
Joseph
I was confused by a little point of the proof in the paper “The Erdös discrepency problem”, where the first inequality p. 11 is used to apply the contrapositive of Theorem 1.8. Indeed, the lower bound given is 1 and the bound needed to apply Theorem 1.8 seems to be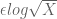 . I think one can instead replace the bound
. I think one can instead replace the bound  by
by  which then allows to apply Theorem 1.8 (with a different value of
which then allows to apply Theorem 1.8 (with a different value of  ).
).
19 September, 2015 at 10:41 am
Gergely Harcos
I agree. I just made a similar comment in the previous blog post, I should have made it here. See https://terrytao.wordpress.com/2015/09/11/the-erdos-discrepancy-problem-via-the-elliott-conjecture/#comment-459463
[Yes, this correction works, and will be implemented in the next revision of the ms, thanks – T.]
19 September, 2015 at 11:21 am
Updates and plans III. | Combinatorics and more
[…] The number theory works by Tao with Matomaki and Radzwill play important role in the proof. See this blog post with links to two new relevant […]
19 September, 2015 at 11:23 am
Polymath5 – Is 2 logarithmic in 1124? | Combinatorics and more
[…] Erdos discrepancy problem and proved that indeed the discrepancy tends to infinity. See also this blog post on Tao’s […]
19 September, 2015 at 5:59 pm
Anonymous
In the paper on Chowla’s conjecture reference [16] is never referenced to in the body of the paper, but listed in the bibliography!
[The estimates we use in [17] are heavily based on those in [16]; I’ll add a mention of this in the next revision of the ms. -T.]
19 September, 2015 at 6:58 pm
Anonymous
Is it possible (with the current methods) to “interpolate” between (2) and (3) by using the multiplicative weight function for some exponent
for some exponent  ?
?
19 September, 2015 at 7:29 pm
Terence Tao
If one uses a quantitative version of the arguments in the paper, one might be able to shave some iterated logarithms off of the weight (e.g. to something like
weight (e.g. to something like  ) but it is unlikely that one can get as far as
) but it is unlikely that one can get as far as 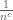 without some dramatic quantitative improvements in the bounds.
without some dramatic quantitative improvements in the bounds.
19 September, 2015 at 7:40 pm
arch1
Congratulations Terry. (Even I can appreciate that any solution to an unsolved conjecture whose statement can be easily explained to a layperson, is pretty significant).
19 September, 2015 at 9:04 pm
Anonymous
What is the probabilistic prediction for the true size of the RHS of (7)?
19 September, 2015 at 9:26 pm
Terence Tao
I would expect this expression to be of size (the usual square root cancellation, with some logarithmic correction to handle the supremum), if X is large enough depending on H.
(the usual square root cancellation, with some logarithmic correction to handle the supremum), if X is large enough depending on H.
20 September, 2015 at 2:49 am
EDP28 — problem solved by Terence Tao! | Gowers's Weblog
[…] posts, a first that shows how to reduce the problem to the Elliott conjecture in number theory, and a second that shows (i) that an averaged form of the conjecture is sufficient and (ii) that he can prove the […]
20 September, 2015 at 10:11 am
Entropy and rare events | What's new
[…] is close to in the sense that , otherwise the bound is worse than the trivial bound of . In my recent paper on the Chowla and Elliott conjectures, I ended up using a variant of (2) which was still non-trivial when the entropy was allowed to be […]
20 September, 2015 at 10:01 pm
Gil Kalai
If I remember correctly, one difficulty in EDP was that it does not generally hold “on average,” namely that for a multiplicative function (say) the average absolute value of partial sums can be bounded. Is it the case that unless g “pretends” to be a modulated Dirichlet character EDP actually does hold on average?
21 September, 2015 at 7:54 am
Terence Tao
Dear Gil,
Offhand I can’t think of an example (pretentious or not) in which the average absolute value of the partial sums are bounded. If does not pretend to be a modulated Dirichlet character then the results in my Elliott conjecture basically say that
does not pretend to be a modulated Dirichlet character then the results in my Elliott conjecture basically say that 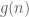 and
and  are uncorrelated for random large n and medium-sized h, which by the second moment method implies that
are uncorrelated for random large n and medium-sized h, which by the second moment method implies that 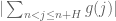 is large on average, which by the triangle inequality in the contrapositive implies that
is large on average, which by the triangle inequality in the contrapositive implies that 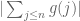 is large on average. In fact it is quite possible that one has a uniform lower bound on
is large on average. In fact it is quite possible that one has a uniform lower bound on  that goes to infinity as
that goes to infinity as  for all completely multiplicative
for all completely multiplicative 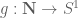 by some refinement of the argument in the paper (this was in fact the original formulation of the "Fourier reduction" of Polymath5).
by some refinement of the argument in the paper (this was in fact the original formulation of the "Fourier reduction" of Polymath5).
22 September, 2015 at 1:59 am
Gil Kalai
(I am not sure either now about the average statement. Quite possibly I was already confused about it at the polymath5 time.)
One idea from early polymath5 was this. Once it was proved that EDP is correct for multiplicative functions that have positive correlation with a Direchlet character, perhaps for functions with vanishing correlation with every Direchlet character something even stronger is correct. (I think the term “pretentious” was not used back then.)
One such potential statement is this:
(*) let f be a multiplicative function from 1,2,…,n with values in [-1,1] or the entire unit disc. Then the discrepancy of f is lower bounded by a function tending to infinity times the ell-2 norm of f. (normalized so that if all values are unir vectors then the l-2 norm is 1.)
(*) is not true in general (which is perhaps one reason why EDP is hard) but maybe it is true (and perhaps follows from the new developments) whenever f has vanishing correlation with every Direchlet character.
22 September, 2015 at 7:48 am
Terence Tao
Nice question! It looks like the van der Corput argument in the Erdos paper does indeed show that for any multiplicative function f taking values in the unit disk, and not pretending to be a modulated Dirichlet character, the discrepancy will be large if the l^2 norm is large (in that one has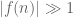 for a positive proportion of the n). I’m not sure if one can hope for a linear relationship between the discrepancy and the l^2 norm, though.
for a positive proportion of the n). I’m not sure if one can hope for a linear relationship between the discrepancy and the l^2 norm, though.
Related to this, it turns out that the Fourier reduction step also works if one assumes rather than
rather than 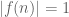 . Thus the EDP can be solved for any sequence avoiding the unit interval (or unit disk), not just +1/-1 sequences (or sequences on the unit circle). This is perhaps not too surprising – larger sequences should intuitively have larger discrepancy. I’ll add these remarks to the next revision of the manuscript.
. Thus the EDP can be solved for any sequence avoiding the unit interval (or unit disk), not just +1/-1 sequences (or sequences on the unit circle). This is perhaps not too surprising – larger sequences should intuitively have larger discrepancy. I’ll add these remarks to the next revision of the manuscript.
24 September, 2015 at 3:48 am
Gil Kalai
That’s interesting! Lets consider finite n’s. It also seems that the weaker version (**) that you indicate (discrepancy bounded by a function of the ell-2 norm of f) holds when f does not correlate just with Direchlet characters that correspond to primes q which are bounded (and not tend to infinity with n).
I.e. if f does not correlate with Direchlet characters corresponding to primes <= q then the discrepancy is bounded below by a function depending on (n,q) of the ell-2 norm of f (perhaps even a function of n and q times the ell-2 norm of f), and this function tends to infinity whenever n and q tends to infinity.
(Maybe its obviously equivalent to what you say though.)
21 September, 2015 at 9:54 am
Anonymous
Since the inner sum in the integrand of (7) (as a trigonometric polynomial) has unit period in (for fixed
(for fixed  ),
),  (as well as the supremum) may be restricted to
(as well as the supremum) may be restricted to  .
. in
in ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) (as a function of x) is fixed as long as the variable x does not cross an integer. Therefore the inner sum (as well as the supremum) is fixed(!) as long as
(as a function of x) is fixed as long as the variable x does not cross an integer. Therefore the inner sum (as well as the supremum) is fixed(!) as long as  is not crossing an integer. So the supremum (as a function of
is not crossing an integer. So the supremum (as a function of  ) is in fact constant between integer values of
) is in fact constant between integer values of  .
. , the integral in (7) is in fact a finite sum!
, the integral in (7) is in fact a finite sum!
Moreover, if H is a fixed integer, the set of integers
Hence for integer
28 September, 2015 at 1:18 pm
Anonymous
In fact, in (7) can be further restricted to
in (7) can be further restricted to ![[0, 1/2]](https://s0.wp.com/latex.php?latex=%5B0%2C+1%2F2%5D&bg=ffffff&fg=545454&s=0&c=20201002) by
by![[-1/2, 1/2]](https://s0.wp.com/latex.php?latex=%5B-1%2F2%2C+1%2F2%5D&bg=ffffff&fg=545454&s=0&c=20201002) (using the unit periodicity in
(using the unit periodicity in  ) and than (ii) using the fact that changing
) and than (ii) using the fact that changing  to
to  is merely equivalent to taking the conjugate value of the sum inside the integrand – without changing its absolute value! (so
is merely equivalent to taking the conjugate value of the sum inside the integrand – without changing its absolute value! (so  can be further restricted to
can be further restricted to ![[0, 1/2]](https://s0.wp.com/latex.php?latex=%5B0%2C+1%2F2%5D&bg=ffffff&fg=545454&s=0&c=20201002) ).
).
(i) restricting it to
22 September, 2015 at 4:41 am
The Erdős discrepancy problem has been solved by Tao | The polymath blog
[…] has now been solved by Terry Tao using important recent developments in analytic number theory. See this blog post from Tao’s blog and this concluding blog post from Gowers’s […]
23 September, 2015 at 5:34 am
Anonymous
In the sum below (6), it seems that the denominator should be (instead of
(instead of  ).
).
[Corrected, thanks – T.]
23 September, 2015 at 10:04 pm
KWRegan
There is a more immediate typo in the first box in the post, Theorem (1): at the bottom “as n \to \infty” should be “as x \to \infty”. It is correctly “x” in the opening lines of the first paper. [Dick Lipton and I are finishing a post on this, our congratulations!]
[Corrected, thanks – T.]
24 September, 2015 at 8:46 am
Frogs and Lily Pads and Discrepancy | Gödel's Lost Letter and P=NP
[…] from discussion of his two earlier posts this month on his blog. They and his 9/18 announcement post re-create much of the content of the […]
24 September, 2015 at 10:50 pm
Anonymous
Can theorem 1 be extended to include the case of bounded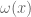 ?
?
25 September, 2015 at 12:15 pm
Terence Tao
I would very much like to extend the theorem in this fashion, as this should recover the original Chowla conjecture in the k=2 case; unfortunately, the arguments I have rely on having a sufficient amount of logarithmic averaging, which forces the assumption that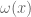 goes to infinity. As discussed in previous posts, it is not completely hopeless to try to remove the log averaging (broadly speaking, it requires one to prove expansion properties of a certain random graph, as opposed to using the entropy decrement argument to finesse the need to establish expansion) but I don’t see how to achieve it right now.
goes to infinity. As discussed in previous posts, it is not completely hopeless to try to remove the log averaging (broadly speaking, it requires one to prove expansion properties of a certain random graph, as opposed to using the entropy decrement argument to finesse the need to establish expansion) but I don’t see how to achieve it right now.
27 September, 2015 at 12:27 am
Anonymous
Is it possible to prove (7) for a sufficiently restricted class of functions under the restriction
under the restriction 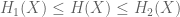 for some (appropriately chosen) functions
for some (appropriately chosen) functions 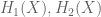 which still enable some applications of (7)?
which still enable some applications of (7)?
27 September, 2015 at 2:03 pm
Terence Tao
Using an estimate of Davenport, one can prove (7) in the range for any fixed
for any fixed  . There ought to be a decent chance of extending this range to
. There ought to be a decent chance of extending this range to  for some absolute constant
for some absolute constant  , and this would be a good warmup problem for proving (7) in full generality, though it seems like there is a significant jump in difficulty past the square root barrier
, and this would be a good warmup problem for proving (7) in full generality, though it seems like there is a significant jump in difficulty past the square root barrier 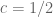 . This may lead to some other applications than Chowla (e.g. asymptotics for counting narrow 3-term progressions or similar patterns in the primes), and indeed I believe some people were already looking at (7) in ranges like this for this sort of applications.
. This may lead to some other applications than Chowla (e.g. asymptotics for counting narrow 3-term progressions or similar patterns in the primes), and indeed I believe some people were already looking at (7) in ranges like this for this sort of applications.
28 September, 2015 at 5:54 am
Cristóbal Camarero
About the sequence in the paper in Remark 1.13 defined by f(jD!+k)=(-1)^jf(k). I think the elements 15 to 18 are wrong and they are -1,1,1,-1 instead. Also, you might add it to the OEIS; it seems pretty and useful.
[Thanks, this will be corrected in the next revision of the ms, and I’ll add the sequence to the OEIS. -T]
29 September, 2015 at 3:28 pm
Terence Tao
This sequence is now at https://oeis.org/A262725 . (Unfortunately I made a data entry for the a(25)-a(48) block, but I have submitted a correction.)
29 September, 2015 at 11:18 am
Anonymous
Straight from “The Book”.
29 September, 2015 at 9:54 pm
275A, Notes 0: Foundations of probability theory | What's new
[…] my research (for instance, the probabilistic concept of Shannon entropy played a crucial role in my recent paper on the Chowla and Elliott conjectures, and random multiplicative functions similarly played a central role in the paper on the Erdos […]
30 September, 2015 at 4:35 am
Epsilon - Ocasapiens - Blog - Repubblica.it
[…] superare la peer-review, ma ha pubblicato tutto sul suo blog (c'è una seconda parte), quindi la peer-review è stata collettiva e […]
1 October, 2015 at 10:57 am
Anonymous
Is there some known generalization of the recent results on short averages of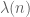 for consecutive integers
for consecutive integers  in
in ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) to the case of arithmetical progressions of
to the case of arithmetical progressions of  in
in ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) ?
? ) on the size of the gaps
) on the size of the gaps  of the arithmetical progressions ?
of the arithmetical progressions ?
Also, is there any restriction (in terms of
1 October, 2015 at 11:57 am
Terence Tao
This is a good question! For bounded values of D (and for H large compared to D) one can derive such results from the existing Matomaki-Radziwill theory by expanding into Dirichlet characters and applying MR to the twisted Liouville functions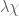 separately (we did this to handle major arcs in our averaged Chowla paper). But this gets inefficient when D is moderately large. Presumably there should be some “q-aspect” version of MR’s work in which one averages both over Archimedean intervals
separately (we did this to handle major arcs in our averaged Chowla paper). But this gets inefficient when D is moderately large. Presumably there should be some “q-aspect” version of MR’s work in which one averages both over Archimedean intervals ![[x,x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2Cx%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) and over characters of a given conductor (or up to a given conductor) that gives better results (particularly if one avoids Siegel zeroes somehow). In principle, many of the ingredients in MR (e.g. mean value theorems) have q-aspect generalisations, but as far as I know nobody has pushed the whole argument through to this setting. (It’s a worthwhile thing to think about though. One could perhaps start with the
and over characters of a given conductor (or up to a given conductor) that gives better results (particularly if one avoids Siegel zeroes somehow). In principle, many of the ingredients in MR (e.g. mean value theorems) have q-aspect generalisations, but as far as I know nobody has pushed the whole argument through to this setting. (It’s a worthwhile thing to think about though. One could perhaps start with the 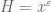 case which is easier, see http://arxiv.org/abs/1502.02374 .)
case which is easier, see http://arxiv.org/abs/1502.02374 .)
1 October, 2015 at 4:42 pm
Anonymous
Thanks for the detailed answer! (i.e. without the outer averaging!) via the following simple approach:
(i.e. without the outer averaging!) via the following simple approach:
My motivation for this question was to check the possibility of proving a slightly stronger version (7′) of (7), namely that the integrand of (7) itself is
1. Denote by the integrand of (6). Clearly
the integrand of (6). Clearly
whenever for any real
for any real 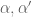 .
.
Therefore, if is approximated by rational
is approximated by rational  with approximation error
with approximation error  , (which is always possible if
, (which is always possible if  has denominator
has denominator 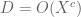 for any fixed
for any fixed  ), one needs only to verify (7′) for a finite(!) set of rational
), one needs only to verify (7′) for a finite(!) set of rational  with denominators
with denominators  with fixed
with fixed  .
.
2. For such rational approximation with denominator
with denominator  , let
, let 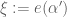 be the corresponding primitive D-th root of unity. The inner sum in (7) is
be the corresponding primitive D-th root of unity. The inner sum in (7) is
Using the fact that the absolute value of the above sum is equal to the absolute value of a polynomial in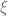 of degree
of degree 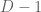 (since
(since 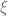 is a primitive root of unity of order
is a primitive root of unity of order  ) whose
) whose  coefficients are the sums of
coefficients are the sums of 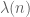 over the
over the  classes mod
classes mod  (i.e.
(i.e.  arithmetic progressions with gap
arithmetic progressions with gap  ) of integers
) of integers  in
in ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) , it follows that if
, it follows that if  then under the generalization of the short averages of
then under the generalization of the short averages of 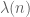 over arithmetic progressions in
over arithmetic progressions in ![[x,x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2Cx%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) , the
, the  coefficients of the above polynomial should be
coefficients of the above polynomial should be  (as being sums of
(as being sums of 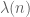 over arithmetic progressions of lengths
over arithmetic progressions of lengths  ) – therefore the integrand of (7) (after dividing the absolute value of the above polynomial in
) – therefore the integrand of (7) (after dividing the absolute value of the above polynomial in 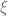 by H) should be
by H) should be  – i.e. (7′).
– i.e. (7′).
2 October, 2015 at 2:36 am
Anonymous
I just realized that in the approximation step (first step in my above comment) the condition
(i.e. it is dependent only on the length of the interval
of the interval ![[x, x+H]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) ).
).
This follows from
Which implies that whenever
whenever
 for all
for all ![n \in [x, x+H]](https://s0.wp.com/latex.php?latex=n+%5Cin+%5Bx%2C+x%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) – which clearly follows from
– which clearly follows from 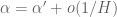
(note that this relaxed condition follows from the need to approximate only(!) the absolute value of the inner sum in (7) – which enable to rotate the sum by multiplying it by before comparing it to the rotated version of the sum corresponding to
before comparing it to the rotated version of the sum corresponding to  ).
).
Therefore, this relaxed approximation for any real by a rational
by a rational  with denominator
with denominator  is possible under the condition
is possible under the condition  (i.e.
(i.e. 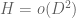 ).
). by rational
by rational  with denominator
with denominator  and
and  is possible whenever
is possible whenever  (relaxing the former condition
(relaxing the former condition  ). One should also add the condition
). One should also add the condition  (needed in the second step of estimating
(needed in the second step of estimating  in the above comment) which gives the relaxed constraints
in the above comment) which gives the relaxed constraints
This shows that the approximation step of
where and
and  for this approach to prove (7').
for this approach to prove (7').
3 October, 2015 at 1:21 pm
Anonymous
In MR paper “Multiplicative functions in short intervals”, the exceptional set of values in
values in ![[X, 2X]](https://s0.wp.com/latex.php?latex=%5BX%2C+2X%5D&bg=ffffff&fg=545454&s=0&c=20201002) in theorem 1 seems (by construction) to be independent (!) of the multiplicative function
in theorem 1 seems (by construction) to be independent (!) of the multiplicative function  (but still may depend on
(but still may depend on  ) – is this true?
) – is this true?
3 October, 2015 at 2:52 pm
Terence Tao
Not quite. They do identify a universal set S of “typical” numbers, independent of f, on which they obtain better estimates (Theorem 3), but within that typical set there can still be an f-dependent set of “bad” x.
1 October, 2015 at 4:55 pm
Miles
I’m curious where one would look to prove this in the specific case of f(x) = sgn(sin(1/x))? (that the discrepancy of this function is infinite)
1 October, 2015 at 6:15 pm
Anonymous
If then
then 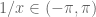 and therefore
and therefore  . In particular,
. In particular, 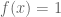 for each positive integer
for each positive integer  .
.
1 October, 2015 at 7:35 pm
Miles
Thanks! Although I must apologize – I meant to define a function with increasingly large, but not infinite, sections of constant sign. I was instead maybe thinking of a function like
8 October, 2015 at 11:15 am
MatjazG
This case of sections of constant sign with unbounded lengths is quite easy. It suffices to take in the discrepancy sum, i.e. to only look at partial sums:
in the discrepancy sum, i.e. to only look at partial sums: 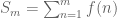 , to show infinite discrepancy.
, to show infinite discrepancy.
Let denote the index of the last element in the section of constant sign
denote the index of the last element in the section of constant sign  , whose length is
, whose length is  . Then:
. Then:  . Thus we have:
. Thus we have:
If the lengths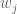 are unbounded (finite or infinite), the
are unbounded (finite or infinite), the  are unbounded as well and the discrepancy is infinite, even with just
are unbounded as well and the discrepancy is infinite, even with just  .
.
(Explicitly, for unbounded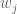 : suppose
: suppose  are bounded, so
are bounded, so 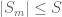 for all
for all  . Choose a
. Choose a  . Then
. Then 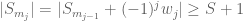 , a contradiction. Hence
, a contradiction. Hence  are unbounded.)
are unbounded.)
If we write for some differentiable function
for some differentiable function 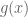 , then
, then 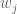 are unbounded (and hence the discrepancy infinite for
are unbounded (and hence the discrepancy infinite for  ) for example if the derivative
) for example if the derivative  as
as  , where
, where 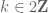 is an even integer.
is an even integer.
(Since then the change in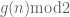 becomes arbitrarily small when
becomes arbitrarily small when  increases by one and the sign of
increases by one and the sign of 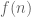 stays constant for an arbitrarily long sequence of consecutive
stays constant for an arbitrarily long sequence of consecutive  .)
.)
In your example: where
where  (at least when
(at least when  is not a multiple of
is not a multiple of 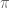 ). As
). As  the derivative
the derivative  , an even integer, and hence the discrepancy of
, an even integer, and hence the discrepancy of 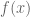 is infinite even with
is infinite even with  . QED
. QED
More generally, if for some differentiable
for some differentiable 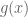 , and
, and 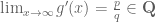 is rational (with
is rational (with  ,
,  ), then the discrepancy of
), then the discrepancy of 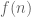 is infinite, where
is infinite, where  suffices.
suffices.
Proof: define , where
, where  . As the derivative
. As the derivative 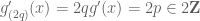 is an even integer, the discrepancy of
is an even integer, the discrepancy of  is infinite with
is infinite with  , and hence the discrepancy of the original
, and hence the discrepancy of the original 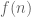 is infinite with
is infinite with  . QED
. QED
Would be nice to complete this discussion with the case of an arbitrary real number, but I’d have to think about that case a bit more (Liouville’s Approximation Theorem comes to mind) …f
an arbitrary real number, but I’d have to think about that case a bit more (Liouville’s Approximation Theorem comes to mind) …f
8 October, 2015 at 11:23 am
MatjazG
P.S. The equidistribution theorem/ergodicity of irrational shifts on a circle come to mind as well … :p
8 October, 2015 at 4:14 pm
MatjazG
Correction: what is stated above about the limits of the derivative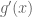 as
as 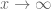 is not entirely true. For example, if
is not entirely true. For example, if  then
then  as
as 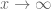 , but the lengths of the intervals
, but the lengths of the intervals 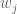 do not diverge. This happens, because the floor function
do not diverge. This happens, because the floor function 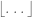 is not continuous.
is not continuous.
All of the analysis where limits of the derivative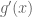 are needed from the previous post is still valid though, if we additionally suppose that:
are needed from the previous post is still valid though, if we additionally suppose that: 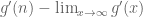 has constant sign or is zero for all natural numbers
has constant sign or is zero for all natural numbers 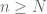 greater than some $N \in {\bf N}$. This is satisfied for example when
greater than some $N \in {\bf N}$. This is satisfied for example when 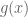 is increasing concave or decreasing convex for large enough
is increasing concave or decreasing convex for large enough  .
.
It is also satisfied in the example: .
.
6 October, 2015 at 9:06 am
Terence Tao magic breakthrough again with EDP, Erdos Discrepancy Problem | Turing Machine
[…] 8. The logarithmically averaged Chowla and Elliott conjectures for two-point correlations; the Erdos di… […]
6 October, 2015 at 10:56 am
vznvzn
:star: :!: :D :cool: congratulations on this amazing breakthrough from, er (as is said in other fields eg hollywood celebrity) “one of your biggest fans”! hope that stanford or someone else does a press release soon, that seems the only reason there is not even more widespread notice so far, suspect it will be a slow-building wave in this case (ie among the public, insiders are now all well aware). some sketch of other possible diverse connections to other math/ CS areas here. am wondering if some more general “theory of pseudorandomness” is lurking and/ or can be devised to attack apparently similar problems and even others now thought apparently dissimilar. also, it would be great if more comment could be made on the efforts underway to independently verify the proof, which is obviously quite/ extremely tricky/ technical. it would also be neat if you remarked somewhere more at length on the Konev/ Lisitsa empirical/ TCS-angle results.
19 October, 2015 at 1:01 am
Il problema della discrepanza: provata una congettura di Erdős? | OggiScienza
[…] dei suggerimenti più utili sia sul blog di Tim Gowers che sul proprio (ha scritto anche una seconda parte) dove la peer-review ha preceduto quella della rivista, tuttora priva di un sito web […]
21 October, 2015 at 10:12 pm
EDP Reflections and Celebrations | Combinatorics and more
[…] posts:) The proof is described in this blog post by Tao. A similar (somewhat simpler) argument proving EDC based on a number-theoretic conjecture (The […]
30 October, 2015 at 2:56 pm
A small remark on the Elliott conjecture | What's new
[…] as for any distinct integers , where is the Liouville function. (The usual formulation of the conjecture also allows one to consider more general linear forms than the shifts , but for sake of discussion let us focus on the shift case.) This conjecture remains open for , though there are now some partial results when one averages either in or in the , as discussed in this recent post. […]
12 November, 2015 at 8:20 am
Klaus Roth | What's new
[…] that generalised Roth’s theorem to progressions of arbitrary length. More recently, my recent work on the Chowla and Elliott conjectures that was a crucial component of the solution of the ErdH{o}s discrepancy problem, relies on an […]
2 December, 2015 at 1:51 pm
A conjectural local Fourier-uniformity of the Liouville function | What's new
[…] to other “non-pretentious” bounded multiplicative functions, was a key ingredient in my recent solution of the Erdös discrepancy problem, as well as in obtaining logarithmically averaged cases of Chowla’s conjecture, such […]
10 December, 2015 at 11:36 pm
White label: the growth of bioRxiv | quantixed
[…] a solution to the Erdos discrepency problem on arXiv (he actually put them on his blog first). This was then “published” in Discrete Analysis, an overlay journal. Read about […]
11 December, 2015 at 9:37 am
Anonymous
In the second arXiv paper (the Erdos discrepancy problem), page 9, line 5, it should be “depending on ” (instead of “depending on
” (instead of “depending on  “).
“).
[Thanks, this will be corrected in the next revision of the ms. -T.]
18 December, 2015 at 9:54 am
Zak
In equation 3.11 (subadditivity of entropy of concatenation of intervals) on the Chowla and Elliot conjectures, it is claimed that this follows from Lemma 2.5, the affine invariance. I don’t think this is the case, since the random variable in consideration is not O(1), and actually can be as large as log(x). Nevertheless, it still should be true, basically because the random variable is as big as log(x) very infrequently.
18 December, 2015 at 11:43 am
Terence Tao
One never has to directly work with random variables of size as large as log x, as one only needs to work with the entropy function (which is uniformly continuous on [0,1]) rather than with
(which is uniformly continuous on [0,1]) rather than with  in isolation.
in isolation.
19 December, 2015 at 11:23 am
Zak
Oh, thanks, probably you are applying Lemma 2.5 times, which I missed.
times, which I missed.
19 December, 2015 at 11:28 am
Zak
In between equations 3.13 and 3.14, it’s stated that . I don’t follow this, since it seems to me that
. I don’t follow this, since it seems to me that  might not be uniformly distributed whilst after conditioning on
might not be uniformly distributed whilst after conditioning on  , it could be.
, it could be.
20 December, 2015 at 9:17 am
Terence Tao
Sorry, the lower bound here should be (from (3.7) and (3.9)). This will be corrected in the next revision of the ms.
(from (3.7) and (3.9)). This will be corrected in the next revision of the ms.
21 December, 2015 at 7:26 pm
Zak
Ah..thanks! is basically uniformly distributed
is basically uniformly distributed
9 January, 2016 at 12:03 pm
Zak
In the blog post, the equation just before equation 7, probably the 2 should be in front of the p instead of the j. Also, would you be able to elaborate a bit on how a bound on correlations of Louisville with nilsequences helps here? I am somewhat familiar with the case when studying k term arithmetic progressions, but here the common differences are restricted to a small subset of primes.
9 January, 2016 at 12:19 pm
Terence Tao
Thanks for the correction. Arithmetic progressions with spacings in the primes (or some affine shift of the primes) can be controlled by Gowers uniformity norms of (say) the von Mangoldt function, which can in turn be controlled (in principle at least) by correlations of the Mobius or Liouville functions with nilsequences. See the papers of Frantzikinakis-Kra and Wooley-Ziegler for some calculations in this direction.
5 April, 2016 at 7:09 pm
Terence Tao
There is a recent paper of Oleksiy Klurman that extends the methods in the above papers to finish off a second question of Erdos closely related to the discrepancy problem. Namely, Klurman completely classifies the functions that are multiplicative (but not necessarily completely multiplicative) and has bounded partial sums. There is an obvious such example, namely the parity function
that are multiplicative (but not necessarily completely multiplicative) and has bounded partial sums. There is an obvious such example, namely the parity function 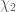 that equals
that equals  on the even numbers and
on the even numbers and  on the odd numbers, and more generally one can multiply
on the odd numbers, and more generally one can multiply 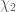 by periodic multiplicative
by periodic multiplicative 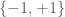 -valued functions of odd period. These turn out to be the only examples; in my paper I was able to eliminate the “non-pretentious” multiplicative functions from consideration, and Klurman performed the complementary analysis of the “pretentious” case to resolve the question completely.
-valued functions of odd period. These turn out to be the only examples; in my paper I was able to eliminate the “non-pretentious” multiplicative functions from consideration, and Klurman performed the complementary analysis of the “pretentious” case to resolve the question completely.
6 April, 2016 at 4:17 am
Anonymous
Is it possible to combine both methods?
16 May, 2016 at 10:29 pm
Equivalence of the logarithmically averaged Chowla and Sarnak conjectures | What's new
[…] distribution and applications” in honour of Robert F. Tichy. This paper is a spinoff of my previous paper establishing a logarithmically averaged version of the Chowla (and Elliott) conjectures in the […]
17 July, 2016 at 8:54 am
Notes on the Bombieri asymptotic sieve | What's new
[…] the Chowla conjecture, for which there has been some recent progress (discussed for instance in these recent posts). Informally, the Bombieri asymptotic sieve lets us (on GEH) view the twin prime […]
1 March, 2017 at 11:59 am
Special cases of Shannon entropy | What's new
[…] able to guess arguments that would work for general random variables. An example of this comes from my paper on the logarithmically averaged Chowla conjecture, in which I showed among other things […]
5 March, 2017 at 10:38 am
Furstenberg limits of the Liouville function | What's new
[…] of Liouville with logarithmic averaging are equivalent to the Bernoulli system. Recently, I was able to prove the two-point […]
9 August, 2017 at 4:34 pm
The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures | What's new
[…] and Elliott conjectures“, submitted to Duke Mathematical Journal. This paper builds upon my previous paper in which I introduced an “entropy decrement method” to prove the two-point […]
20 October, 2017 at 10:44 am
The logarithmically averaged and non-logarithmically averaged Chowla conjectures | What's new
[…] And indeed, significantly more is now known for the logarithmically averaged Chowla conjecture; in this paper of mine I had proven (2) for , and in this recent paper with Joni Teravainen, we proved the conjecture for […]
5 December, 2018 at 3:02 pm
Fourier uniformity of bounded multiplicative functions in short intervals on average | What's new
[…] of this result to arbitrary non-pretentious bounded multiplicative functions) a few years ago to solve the Erdös discrepancy problem, as well as a logarithmically averaged two-point Chowla con…, for instance it implies […]
17 December, 2019 at 8:27 am
254A, Notes 10 – mean values of nonpretentious multiplicative functions | What's new
[…] as if is such that for some fixed . However it is significantly more difficult to understand what happens when grows much slower than this. By using the techniques based on zero density estimates discussed in Notes 6, it was shown by Motohashi that one can also establish (4) as long as (strictly speaking Motohashi discusses the Möbius function only, but one can use a variant of Exercise 1 to then recover the Liouville case). This threshold is still essentially the best one known unconditionally; on the Riemann Hypothesis Maier and Montgomery lowered it to for an absolute constant (the bound is more classical, following from Exercise 33 of Notes 2). On the other hand, the randomness heuristics from Supplement 4 suggest that should be able to be taken as small as , and perhaps even if one is particularly optimistic about the accuracy of these probabilistic models. On the other hand, the Chowla conjecture (mentioned for instance in Supplement 4) predicts that cannot be taken arbitrarily slowly growing in , due to the conjectured existence of arbitrarily long strings of consecutive numbers where the Liouville function does not change sign (and in fact one can already show from the known partial results towards the Chowla conjecture that (4) fails for some sequence and some sufficiently slowly growing , by modifying the arguments in these papers of mine). […]
11 January, 2020 at 8:42 pm
Some recent papers | What's new
[…] to those used in recent progress towards the Chowla conjecture over the integers (e.g., in this previous paper of mine); the starting point is an algebraic observation that in certain function fields, the Mobius […]