Previous set of notes: Notes 4. Next set of notes: 246B Notes 1.
In the previous set of notes we introduced the notion of a complex diffeomorphism between two open subsets
of the complex plane
(or more generally, two Riemann surfaces): an invertible holomorphic map whose inverse was also holomorphic. (Actually, the last part is automatic, thanks to Exercise 41 of Notes 4.) Such maps are also known as biholomorphic maps or conformal maps (although in some literature the notion of “conformal map” is expanded to permit maps such as the complex conjugation map
that are angle-preserving but not orientation-preserving, as well as maps such as the exponential map
from
to
that are only locally injective rather than globally injective). Such complex diffeomorphisms can be used in complex analysis (or in the analysis of harmonic functions) to change the underlying domain
to a domain that may be more convenient for calculations, thanks to the following basic lemma:
Lemma 1 (Holomorphicity and harmonicity are conformal invariants) Let
be a complex diffeomorphism between two Riemann surfaces
.
- (i) If
is a function to another Riemann surface
, then
is holomorphic if and only if
is holomorphic.
- (ii) If
are open subsets of
and
is a function, then
is harmonic if and only if
is harmonic.
Proof: Part (i) is immediate since the composition of two holomorphic functions is holomorphic. For part (ii), observe that if is harmonic then on any ball
in
,
is the real part of some holomorphic function
thanks to Exercise 62 of Notes 3. By part (i),
is also holomorphic. Taking real parts we see that
is harmonic on each ball preimage
in
, and hence harmonic on all of
, giving one direction of (ii); the other direction is proven similarly.
Exercise 2 Establish Lemma 1(ii) by direct calculation, avoiding the use of holomorphic functions. (Hint: the calculations are cleanest if one uses Wirtinger derivatives, as per Exercise 27 of Notes 1.)
Exercise 3 Let
be a complex diffeomorphism between two open subsets
of
, let
be a point in
, let
be a natural number, and let
be holomorphic. Show that
has a zero (resp. a pole) of order
at
if and only if
has a zero (resp. a pole) of order
at
.
From Lemma 1(ii) we can now define the notion of a harmonic function on a Riemann surface
; such a function
is harmonic if, for every coordinate chart
in some atlas, the map
is harmonic. Lemma 1(ii) ensures that this definition of harmonicity does not depend on the choice of atlas. Similarly, using Exercise 3 one can define what it means for a holomorphic map
on a Riemann surface
to have a pole or zero of a given order at a point
, with the definition being independent of the choice of atlas; we can also identify such functions as equivalence classes of meromorphic functions
in complete analogy with the case of meromorphic functions on domains
. Finally, we can define the notion of an essential singularity of a holomorphic function
at some isolated singularity
in a Riemann surface as one that cannot be extended to a holomorphic function
.
In view of Lemma 1, it is thus natural to ask which Riemann surfaces are complex diffeomorphic to each other, and more generally to understand the space of holomorphic maps from one given Riemann surface to another. We will initially focus attention on three important model Riemann surfaces:
- (i) (Elliptic model) The Riemann sphere
;
- (ii) (Parabolic model) The complex plane
; and
- (iii) (Hyperbolic model) The unit disk
.
The designation of these model Riemann surfaces as elliptic, parabolic, and hyperbolic comes from Riemannian geometry, where it is natural to endow each of these surfaces with a constant curvature Riemannian metric which is positive, zero, or negative in the elliptic, parabolic, and hyperbolic cases respectively. However, we will not discuss Riemannian geometry further here.
All three model Riemann surfaces are simply connected, but none of them are complex diffeomorphic to any other; indeed, there are no non-constant holomorphic maps from the Riemann sphere to the plane or the disk, nor are there any non-constant holomorphic maps from the plane to the disk (although there are plenty of holomorphic maps going in the opposite directions). The complex automorphisms (that is, the complex diffeomorphisms from a surface to itself) of each of the three surfaces can be classified explicitly. The automorphisms of the Riemann sphere turn out to be the Möbius transformations with
, also known as fractional linear transformations. The automorphisms of the complex plane are the linear transformations
with
, and the automorphisms of the disk are the fractional linear transformations of the form
for
and
. Holomorphic maps
from the disk
to itself that fix the origin obey a basic but incredibly important estimate known as the Schwarz lemma: they are “dominated” by the identity function
in the sense that
for all
. Among other things, this lemma gives guidance to determine when a given Riemann surface is complex diffeomorphic to a disk; we shall discuss this point further below.
It is a beautiful and fundamental fact in complex analysis that these three model Riemann surfaces are in fact an exhaustive list of the simply connected Riemann surfaces, up to complex diffeomorphism. More precisely, we have the Riemann mapping theorem and the uniformisation theorem:
Theorem 4 (Riemann mapping theorem) Let
be a simply connected open subset of
that is not all of
. Then
is complex diffeomorphic to
.
Theorem 5 (Uniformisation theorem) Let
be a simply connected Riemann surface. Then
is complex diffeomorphic to
,
, or
.
As we shall see, every connected Riemann surface can be viewed as the quotient of its simply connected universal cover by a discrete group of automorphisms known as deck transformations. This in principle gives a complete classification of Riemann surfaces up to complex diffeomorphism, although the situation is still somewhat complicated in the hyperbolic case because of the wide variety of discrete groups of automorphisms available in that case.
We will prove the Riemann mapping theorem in these notes, using the elegant argument of Koebe that is based on the Schwarz lemma and Montel’s theorem (Exercise 58 of Notes 4). The uniformisation theorem is however more difficult to establish; we discuss some components of a proof (based on the Perron method of subharmonic functions) here, but stop short of providing a complete proof.
The above theorems show that it is in principle possible to conformally map various domains into model domains such as the unit disk, but the proofs of these theorems do not readily produce explicit conformal maps for this purpose. For some domains we can just write down a suitable such map. For instance:
Exercise 6 (Cayley transform) Let
be the upper half-plane. Show that the Cayley transform
, defined by
is a complex diffeomorphism from the upper half-plane
to the disk
, with inverse map
given by
Exercise 7 Show that for any real numbers
, the strip
is complex diffeomorphic to the disk
. (Hint: use the complex exponential and a linear transformation to map the strip onto the half-plane
.)
Exercise 8 Show that for any real numbers
, the strip
is complex diffeomorphic to the disk
. (Hint: use a branch of either the complex logarithm, or of a complex power
.)
We will discuss some other explicit conformal maps in this set of notes, such as the Schwarz-Christoffel maps that transform the upper half-plane to polygonal regions. Further examples of conformal mapping can be found in the text of Stein-Shakarchi.
— 1. Maps between the model Riemann surfaces —
In this section we study the various holomorphic maps, and conformal maps, between the three model Riemann surfaces ,
, and
.
From Exercise 20 of Notes 4, we know that the only holomorphic maps from the Riemann sphere to itself (besides the constant function
) take the form of a rational function
away from the zeroes of
(and from
), with these singularities all being removable, and with
not identically zero. We can of course reduce to lowest terms and assume that
and
have no common factors. In particular, if
is to take values in
rather than
, then
can have no roots (since
will have a pole at these roots) and so by the fundamental theorem of algebra
is constant and
is a polynomial; in order for
to have no pole at infinity,
must then be constant. Thus the only holomorphic maps from
to
are the constants; in particular, the only holomorphic maps from
to
are the constants. In particular,
is not complex diffeomorphic to
or
(this is also topologically obvious since the Riemann sphere is compact, and
and
are not).
Exercise 9 More generally, show that if
is a connected compact Riemann surface and
is a connected non-compact Riemann surface, then the only holomorphic maps from
to
are the constants. (Hint: use the open mapping theorem, Theorem 38 of Notes 4.)
Now we consider complex automorphisms of the Riemann sphere to itself. There are some obvious examples of such automorphisms:
- Translation maps
for some
, with the convention that
is mapped to
;
- Dilation maps
for some
, with the convention that
is mapped to
; and
- The inversion map
, with the convention that
is mapped to
.
More generally, given any complex numbers with
, we can define the Möbius transformation (or fractional linear transformation)
for
, with the convention that
is mapped to
and
is mapped to
(where we adopt the further convention that
for non-zero
). For
, this is an affine transformation
, which is clearly a composition of a translation and dilation map; for
, this is a combination
of translations, dilations, and the inversion map. Thus all Möbius transformations are formed from composition of the translations, dilations, and inversions, and in particular are also automorphisms of the Riemann sphere; it is also easy to see that the Möbius transformations are closed under composition, and are thus the group generated by the translations, dilations, and inversions.
One can interpret the Möbius transformations as projective linear transformations as follows. Recall that the general linear group is the group of
matrices
with non-vanishing determinant
. Clearly every such matrix generates a Möbius transformation
. However, two different elements of
can generate the same Möbius transformation if they are scalar multiples of each other. If we define the projective linear group
to be the quotient group of
by the group of scalar invertible matrices, then we may identify the set of Möbius transformations with
. The group
acts on the space
by the usual map
If we let be the complex projective line, that is to say the space of one-dimensional subspaces of
, then
acts on this space also, with the action of the scalars being trivial, so we have an action of
on
. We can identify the Riemann sphere
with the complex projective line by identifying each
with the one-dimensional subspace
of
, and identifying
with
. With this identification, one can check that the action of
on
has become identified with the action of the group of Möbius transformations on
. (In particular, the group of Möbius transformations is isomorphic to
.)
There are enough Möbius transformations available that their action on the Riemann sphere is not merely transitive, but is in fact -transitive:
Lemma 10 (
-transitivity) Let
be distinct elements of the Riemann sphere
, and let
also be three distinct elements of the Riemann sphere. Then there exists a unique Möbius transformation
such that
for
.
Proof: We first show existence. As the Möbius transformations form a group, it suffices to verify the claim for a single choice of , for instance
. If
then the affine transformation
will have the desired properties. If
, we can use translation and inversion to find a Möbius transformation
that maps
to
; applying the previous case with
with
and then applying
, we obtain the claim.
Now we prove uniqueness. By composing on the left and right with Möbius transforms we may assume that . A Möbius transformation
that fixes
must obey the constraints
and so must be the identity, as required.
Möbius transformations are not 4-transitive, thanks to the invariant known as the cross-ratio:
Exercise 11 Define the cross-ratio
between four distinct points
on the Riemann sphere
by the formula
if all of
avoid
, and extended continuously to the case when one of the points equals
(e.g.
).
- (i) Show that an injective map
is a Möbius transform if and only if it preserves the cross-ratio, that is to say that
for all distinct points
. (Hint: for the “only if” part, work with the basic Möbius transforms. For the “if” part, reduce to the case when
fixes three points, such as
.)
- (ii) If
are distinct points in
, show that
lie on a common extended line (i.e., a line in
together with
) or circle in
if and only if the cross-ratio
is real. Conclude that a Möbius transform will map an extended line or circle to an extended line or circle.
As one quick application of Möbius transformations, we have
Proposition 12
is simply connected.
Proof: We have to show that any closed curve in
is contractible to a point in
. By deforming
locally into line segments in either of the two standard coordinate charts of
we may assume that
is the concatenation of finitely many such line segments; in particular,
cannot be a space-filling curve (as one can see from e.g. the Baire category theorem) and thus avoids at least one point in
. If
avoids
then it lies in
and can thus be contracted to a point in
(and hence in
) since
is convex. If
avoids any other point
, then we can apply a Möbius transformation to move
to
, contract the transformed curve to a point, and then invert the Möbius transform to contract
to a point in
.
Exercise 13 (Jordan curve theorem in the Riemann sphere) Let
be a simple closed curve in the Riemann sphere. Show that the complement of
in
is the union of two disjoint simply connected open subsets of
. (Hint: one first has to exclude the possibility that
is space-filling. Do this by verifying that
is homeomorphic to the unit circle.)
It turns out that there are no other automorphisms of the Riemann sphere than the Möbius transformations:
Proposition 14 (Automorphisms of Riemann sphere) Let
be a complex diffeomorphism. Then
is a Möbius transformation.
Proof: By Lemma 10 and composing with a Möbius transformation, we may assume without loss of generality that
fixes
. From Exercise 20 of Notes 4 we know that
is a rational function
(with all singularities removed); we may reduce terms so that
have no common factors. Since
is bijective and fixes
, it has no poles in
, and hence
can have no roots; by the fundamental theorem of algebra, this makes
constant. Similarly,
has no zeroes other than
, and so must be a monomial; as
also fixes
, it must be of the form
for some natural number
. But this is only injective if
, in which case
is clearly a Möbius transformation.
Now we look at holomorphic maps on . There are plenty of holomorphic maps from
to
; indeed, these are nothing more than the entire functions, of which there are many (indeed, an entire function is nothing more than a power series with an infinite radius of convergence). There are even more holomorphic maps from
to
, as these are just the meromorphic functions on
. For instance, any ratio
of two entire functions, with
not identically zero, will be meromorphic on
. On the other hand, from Liouville’s theorem (Theorem 28 of Notes 3) we see that the only holomorphic maps from
to
are the constants. In particular,
and
are not complex diffeomorphic (despite the fact that they are diffeomorphic over the reals, as can be seen for instance by using the projection
).
The affine maps with
and
are clearly complex automorphisms on
. In analogy with Proposition 14, these turn out to be the only automorphisms:
Proposition 15 (Automorphisms of complex plane) Let
be a complex diffeomorphism. Then
is an affine transformation
for some
and
.
Proof: By the open mapping theorem (Theorem 38 of Notes 4), is open, and hence
avoids the non-empty open set
on
. By the Casorati-Weierstrass theorem (Theorem 12 of Notes 4), we conclude that
does not have an essential singularity at infinity. Thus
extends to a holomorphic function from
to
, hence by Exercise 20 of Notes 4 is rational. As the only pole of
is at infinity,
is a polynomial; as
is a diffeomorphism, the derivative has no zeroes and is thus constant by the fundamental theorem of algebra. Thus
must be affine, and the claim follows.
Exercise 16 Let
be an injective holomorphic map. Show that
is a Möbius transformation (restricted to
).
We remark that injective holomorphic maps are often referred to as univalent functions in the literature.
Finally, we consider holomorphic maps on . There are plenty of holomorphic maps from
to
(indeed, these are just the power series with radius of convergence at least
), and even more holomorphic maps from
to
(for instance, one can take the quotient of two holomorphic functions
with
non-zero). There are also many holomorphic maps from
to
, for instance one can take any bounded holomorphic function
and multiply it by a small constant. However, we have the following fundamental estimate concerning such functions, the Schwarz lemma:
Lemma 17 (Schwarz lemma) Let
be a holomorphic map such that
. Then we have
for all
. In particular,
.
Furthermore, iffor some
, or if
, then there exists a real number
such that
for all
.
Proof: By the factor theorem (Corollary 22 of Notes 3), we may write for some holomorphic
. On any circle
with
, we have
and hence
; by the maximum principle we conclude that
for all
. Sending
to zero, we conclude that
for all
, and hence
and
.
Finally, if for some
or
, then
equals
for some
, and hence by a variant of the maximum principle (see Exercise 18 below) we see that
is constant, giving the claim.
Exercise 18 (Variant of maximum principle) Let
be a connected Riemann surface, and let
be a point in
.
- (i) If
is a harmonic function such that
for all
, then
for all
.
- (ii) If
is a holomorphic function such that
for all
, then
for all
.
(Hint: use Exercise 17 of Notes 3 .)
One can think of the Schwarz lemma as follows. Let denote the collection of holomorphic functions
with
. Inside this collection we have the rotations
for
defined by
. The Schwarz lemma asserts that these rotations “dominate” the remaining functions
in
in the sense that
on
, and in particular
; furthermore these inequalities are strict as long as
is not one of the
.
As a first application of the Schwarz lemma, we characterise the automorphisms of the disk . For any
, one can check that the Möbius transformation
preserves the boundary of the disk
(since
when
), and maps the point
to the origin, and thus maps the disk
to itself. More generally, for any
and
, the Möbius transformation
is an automorphism of the disk
. It turns out that these are the only such automorphisms:
Theorem 19 (Automorphisms of disk) Let
be a complex diffeomorphism. Then there exists
and
such that
for all
. If furthermore
, then we can take
, thus
for
.
Proof: First suppose that . By the Schwarz lemma applied to both
and its inverse
, we see that
. But by the inverse function theorem (or the chain rule),
, hence
. Applying the Schwarz lemma again, we conclude that
for some
, as required.
In the general case, there exists such that
. If one then applies the previous analysis to
, where
is the automorphism
, we obtain the claim.
Exercise 20 (Automorphisms of half-plane) Let
be a complex diffeomorphism from the upper half-plane
to itself. Show that there exist real numbers
with
such that
for
. Conclude that the automorphism group of either
or
is isomorphic as a group to the projective special linear group
formed by starting with the special linear group
of
real matrices
of determinant
, and then quotienting out by the central subgroup
.
Remark 21 Collecting the various assertions above about the holomorphic maps between the elliptic, parabolic, and hyperbolic model Riemann surfaces
,
,
, one arrives at the following rule of thumb: there are “many” holomorphic maps from “more hyperbolic” surfaces to “less hyperbolic” surfaces, but “very few” maps going in the other direction (and also relatively few automorphisms from one space to an “equally hyperbolic” surface). This rule of thumb also turns out to be accurate in the context of compact Riemann surfaces, where “higher genus” becomes the analogue of “more hyperbolic” (and similarly for “less hyperbolic” or “equally hyperbolic”). One can formalise this latter version of the rule of thumb using such results as the Riemann-Hurwitz formula and the de Franchis theorem, but these are beyond the scope of this course.
Exercise 22 Let
be a non-constant holomorphic map between Riemann surfaces
. If
is compact connected and
is connected, show that
is surjective and
is compact. Conclude in particular that there are no non-constant bounded holomorphic functions
on a compact connected Riemann surface.
— 2. Quotients of the model Riemann surfaces —
The three model Riemann surfaces ,
,
are all simply connected, and the uniformisation theorem will tell us that up to complex diffeomorphism, these are the only simply connected Riemann surfaces that exist. However, it is possible to form non-simply-connected Riemann surfaces from these model surfaces by the procedure of taking quotients, as follows. Let
be a Riemann surface, and let
be a group of complex automorphisms of
. We assume that the action of
on
is free, which means that the non-identity transformations
in
have no fixed points (thus
for all
). We also assume that the action is proper (viewing
as a discrete group), which means that for any compact subset
of
, there are only finitely many automorphisms
in
for which
intersects
. If the action is both free and proper, then we see that every point
has a small neighbourhood
with the property that the images
are all disjoint; by making
small enough we can also find a holomorphic coordinate chart
to some open subset
of
. We can then form the quotient manifold
of orbits
, using the coordinate charts
for any
defined by setting
for all . One can easily verify that
is a Riemann surface, and that the quotient map
defined by
is a surjective holomorphic covering map. The ability to easily take quotients is one of the key advantages of the Riemann surface formalism; another is the converse ability to construct covers, such as the universal cover of a Riemann surface, defined in Theorem 25 below.
Exercise 23 Let
be a Riemann surface,
a group of complex automorphisms of
acting in a proper and free fashion, and let
be the quotient map. Let
be a holomorphic map to another Riemann surface
. Show that there exists a holomorphic map
such that
if and only if
for all
.
Remark 24 It is also of interest to quotient a Riemann surface
by a group
of complex automorphisms whose action is not free. In that case, the quotient space
might a priori fail to be a manifold, but instead be a more general object known as an orbifold. A typical example is the modular curve
(where
is the group of
matrices with integer coefficients and determinant
); this is of great importance in analytic number theory. However, we will not study orbifolds in this course (and in the case of quotients of Riemann surfaces, it turns out that these quotients still fortunately turn out to be Riemann surfaces).
Since the continuous image of a connected space is always connected, we see that any quotient of a connected Riemann surface is again connected. In the converse direction, one can use this construction to describe a connected Riemann surface as a quotient of a simply connected Riemann surface:
Theorem 25 (Universal cover) Let
be a connected Riemann surface. Then there exists a simply connected Riemann surface
, and a group
of complex automorphisms acting on
in a proper and free fashion, such that
is complex diffeomorphic to
.
Proof: For sake of brevity we omit some of the details of the construction as exercises.
We use the following abstract construction to build the Riemann surface . Fix a base point
in
. For any point
in
, we can form the space of all continuous paths
from
to
for some interval
with
. We let
denote the space of equivalence classes of such paths with respect to the operation of homotopy with fixed endpoints up to reparameterisation; for instance, if
was simply connected, then
would simply be a point. (One could also omit the reparameterisation by restricting the domain of
to be a fixed interval such as
.) As
is connected, all the
are non-empty. We then let
be the (disjoint) union of all the
. This defines a set
together with a projection map
that sends all the homotopy classes in
to
for each
; this is clearly a surjective map.
This defines as a set, but we want to give
the structure of a Riemann surface, and thus must create an atlas of coordinate charts. For every
, let
be a coordinate chart that is a diffeomorphism between some neighbourhood
of
and the unit disk. Given a homotopy class
in
and a point
in
, we can then associate a point
in
by taking a path
from
to
in the homotopy class
, and concatenating it with the path
that connects
to
via a line segment in the disk
using the coordinate chart
; the homotopy class of this concatenated path does not depend on the precise choice of
and will be denoted
. If we let
denote all the points
obtained in this fashion as
varies over
, then it is easy to see (Exercise!) that the
are disjoint and partition the set
. We can then form coordinate charts
for each
and
by setting
for all
. This defines both a topology on
(by declaring a subset
of
to be open if
is open for all
) and a complex structure, as the transition maps are easily verified (Exercise!) to be both continuous and holomorphic (after first shrinking the neighbourhoods
and
if necessary). By construction we now see that
is a covering space of
, with
the covering map.
Let be the homotopy class of the constant curve at
. It is easy to see (Exercise!) that
is connected (indeed, any point
in
determines (more or less tautologically) a family of paths in
from
to
). Next, we make the stronger claim that
is simply connected. It suffices to show that any closed path
from
to
is contractible to a point. Let
denote the projected curve
, thus
is a closed curve from
to itself. From the continuity method (Exercise!) we see that for any
, the restriction
of
to
lies in the homotopy class of
; in particular,
itself lies in the homotopy class of
, and is thus homotopic to a point. Another application of the continuity method (Exercise!) then shows that as one continuously deforms
to a point, each of the curves
obtained in this deformation lifts to a closed curve
in
from
to
, in the sense that
; furthermore,
varies continuously in
, giving the required homotopy from
to a point.
Define a deck transformation to be a holomorphic map such that
(that is to say,
preserves each of the “fibres”
of
). Clearly the composition of two deck transformations is again a deck transformation. From Corollary 51 of Notes 4 we see that for any
and
, there exists a unique deck transformation that maps
to
. Composing that a deck transformations with the deck transformations that maps
to
we see that all deck transformations are invertible and are thus complex automorphisms. If we let
denote the collection of all deck transformations then we see that
is a group that acts freely on
and transitively on each fibre
. For any
, and the neighbourhoods
as before, one can verify (Exercise!) that each deck transformation in
permutes the disjoint open sets
covering
, and given any two of these sets
there is exactly one deck transformation that maps
to
. From this one can check (Exercise!) that
is complex diffeomorphic to
as required.
Exercise 26 Write out the steps marked “Exercise!” in the above argument.
The manifold in the above theorem is called a universal cover of
, and the group
is (a copy of) the fundamental group of
. These objects are basically uniquely determined by
:
Exercise 27 Suppose one has two simply connected Riemann surfaces
and two groups
of automorphisms of
respectively acting in proper and free fashions. Show that the following statements are equivalent:
- (i) The quotients
and
are complex diffeomorphic.
- (ii) There exists a complex diffeomorphism
and a group isomorphism
such that
for all
and
. In particular
and
are complex diffeomorphic, and the groups
and
are isomorphic.
(Hint: use Exercise 23 for one direction of the implication, and Corollary 51 of Notes 4 for the other implication.)
Exercise 28 Let
be a connected Riemann surface, and let
be a point in
. Define the fundamental group
based at
to be the collection of equivalence classes
of closed curves
from
to
, under the relation of homotopy with fixed endpoints up to reparameterisation.
- (i) Show that
is indeed a group, with the equivalence class of the constant curves as the identity element, the inverse of a homotopy class
of a curve
defined as
, and the product
of two homotopy classes of curves
as
.
- (ii) If
are as in Theorem 25, show that
is isomorphic to
.
Exercise 29 Show that the fundamental group of
is isomorphic to the integers
(viewed as an additive group).
Exercise 30 (Universality) Let
be a connected Riemann surface, let
be a universal cover of
with covering map
, and let
be another Riemann surface cover of
with a covering map
. Let
be a point in
, let
be a point in
, and let
be a point in
. Show that there is a unique covering map
with
such that
. This helps justify the terminology “universal cover”.
If we assume for now the uniformisation theorem, we conclude that every connected Riemann surface is the quotient of one of the three model surfaces ,
,
by a group of complex automorphisms that act freely and properly; depending on which surface is used, we call these Riemann surfaces of elliptic type, parabolic type, and hyperbolic type respectively. We can then study each of the three model types in turn:
Elliptic type: By Proposition 14, the automorphisms of are the Möbius transformations. From the quadratic formula (or the fundamental theorem of algebra) we see that every Möbius transformation has at least one fixed point (for instance, the translations
fix
). Thus the only group of complex automorphisms that can act freely on
is the trivial group, so the only Riemann surfaces of elliptic type are those that are complex diffeomorphic to the Riemann sphere.
Parabolic type: By Proposition 14, the automorphisms of are the affine transformations
. These transformations have fixed points in
if
, so in order to obtain a free action we must restrict
to the translations
. Thus we can view
as an additive subgroup of
, with
now being the group quotient; as the action is additive, we can also write
as
. In order for the action to be proper,
must be a discrete subgroup of
(every point isolated). We can classify all such subgroups:
Exercise 31 Let
be a discrete additive subgroup of
. Show that
takes on one of the following three forms:
- (i) (Rank zero case) the trivial group
;
- (ii) (Rank one case) a cyclic group
for some
; or
- (iii) (Rank two case) a group
for some
with
strictly complex (i.e., not real).
We conclude that every Riemann surface of parabolic type is complex diffeomorphic to a plane , a cylinder
for some
, or a torus
for
and
strictly complex.
The case of the plane is self-explanatory. Using dilation maps we see that all cylinders are complex diffeomorphic to each other; for instance, they are all diffeomorphic to . The exponential map
is
-periodic and thus descends to a map from
to
; it is easy to see that this map is a complex diffeomorphism, thus the punctured plane
can be used as a model for all Riemann surface cylinders.
The case of the tori are more interesting. One can use dilations to normalise one of the
to be a specific value such as
, but one cannot normalise both:
Exercise 32 Let
and
be two tori. Show that these two tori are complex diffeomorphic if and only if there exists an element
of the special linear group
(thus
are integers with
) such that
(Hint: lift any such diffeomorphism to a diffeomorphism of
.)
In contrast to the cylinders , which are complex diffeomorphic to a subset
of the complex plane, one cannot model a torus by a subset
of
; indeed, if there were a complex diffeomorphism
, then
would have to be non-empty, compact, and (by the open mapping theorem) open in
, which is impossible since
is non-compact and connected. However, it is an important fact in algebraic geometry, classical analysis and number theory that these tori can be modeled instead by elliptic curves. The theory of elliptic curves is extremely rich, but is beyond the scope of this course and will not be discussed further here (but the Weierstrass elliptic functions used to construct the complex diffeomorphism between tori and elliptic curves may be covered in subsequent quarters).
Exercise 33 Let
be a connected subset of
that omits at least two points of
. Show that
cannot be of elliptic or parabolic type. (Hint: in addition to the open mapping theorem argument given above, one can use either the little Picard theorem, Theorem 56 of Notes 4, or the simpler Casorati-Weierstrass theorem (Theorem 12 of Notes 4).) In particular, assuming the uniformisation theorem, such sets
must be of hyperbolic type. (Note this is compatible with our previous intuition that “more hyperbolic” is analogous to “higher genus” or “has more holes”.)
Hyperbolic type: Here it is convenient to model the hyperbolic Riemann surface using the upper half-plane (the Poincaré half-plane model) rather than the disk
(the Poincaré disk model). By Exercise 20, a Riemann surface of hyperbolic type is then isomorphic to a quotient
of
by some subgroup
of
that acts freely and properly. Properness is easily seen to be equivalent to
being a discrete subgroup of
(using the topology inherited from the embedding of
in
); such groups are known as Fuchsian groups. Freeness can also be described explicitly:
Exercise 34 Show that a subgroup
of
acts freely on
if and only if it avoids all (equivalence classes) of matrices
in
that are elliptic in the sense that they obey the trace condition
.
It turns out that in contrast to the elliptic type and parabolic type situations, there are a very large number of possible subgroups obeying these conditions, and a complete classification of them is basically hopeless. The theory of Fuchsian groups is again very rich, being a foundational topic in hyperbolic geometry, but is again beyond the scope of this course.
Remark 35 The twice-punctured plane
must be of hyperbolic type by the uniformisation theorem and Exercise 33. This gives another proof of the little Picard theorem: an entire function
that omits (say) the points
must then lift (by Corollary 51 of Notes 4) to a holomorphic map from
to
, which must then be constant by Liouville’s theorem. A more complicated argument along these lines also proves the great Picard theorem. It turns out that the covering map from
to
can be described explicitly using the theory of elliptic functions (and specifically the modular lambda function), but this is beyond the scope of this course.
Exercise 36 Show that any annulus
is of hyperbolic type, and is in fact complex diffeomorphic to
for some cyclic group
of dilations. (Hint: first use the complex exponential to cover the annulus by a strip, then use Exercise 7.)
Exercise 37 (Schottky’s theorem on conformal maps between annuli) Let
and
be two annuli with
and
. Show that
and
are complex diffeomorphic (with the conformal map extending continuously to the boundary) if and only if
. (Hint: one can either argue by lifting to the half-plane using the previous exercise, or else using the Schwarz reflection principle (adapted to circles in place of lines) repeatedly to extend a holomorphic map from
to
to a holomorphic map from a punctured disk to a punctured disk; one can also combine the methods by taking logarithms to lift
,
to strips, and then using the original Schwarz reflection principle. This result is due to Schottky, but should not be confused with another theorem of Schottky in complex analysis. The constraint that the conformal map extends continuously to the boundary can be removed, for instance by appealing to a version of Carathéodory’s theorem, but this is beyond the scope of the course.)
Exercise 38
- (i) Show that the punctured disk
is of hyperbolic type, and is complex diffeomorphic to
, where
acts on
by translations.
- (ii) Show that the Jowkowsky transform
is a complex diffeomorphism from
to the slitted extended complex plane
. Conclude that
is also complex diffeomorphic to
.
— 3. The Riemann mapping theorem —
We are now ready to prove the Riemann mapping theorem, Theorem 4, using an argument of Koebe. To motivate the argument, let us rephrase the Schwarz lemma in the following form:
Lemma 39 (Schwarz lemma, again) Let
be a Riemann surface, and let
be a point in
. Let
denote the collection of holomorphic functions
with
. If
contains an element
that is a complex diffeomorphism, then
for all
; if
is a subset of the complex plane
, we also have
. Furthermore, in either of these two inequalities, equality holds if and only if
for some real number
.
Proof: Apply Lemma 17 to the map .
This lemma suggests the following strategy to prove the Riemann mapping theorem: starting with the open subset of the complex plane
, pick a point
in that subset, and form the collection
of holomorphic maps
that map
to
, and locate an element
of this collection for which the magnitude
is maximal. If the Riemann mapping theorem were true, then Lemma 39 would ensure that this
would be a complex diffeomorphism, and we would be done.
It turns out to be convenient to work with the somewhat smaller collection of injective holomorphic maps
(also known as univalent functions from
to
). We first observe that this collection is non-empty for the sets
of interest:
Proposition 40 Let
be a simply connected subset of
that is not all of
. Then there exists an injective holomorphic map
.
Proof: By applying a translation to , we may assume that
avoids the origin
. If
in fact avoided a disk
, then we could use the map
to map
injectively into the disk
. At present,
need not avoid any disk (e.g.
could be the complex plane with the negative axis
removed). However, as
is simply connected and avoids
, we can argue as in Section 4 of Notes 4 to obtain a holomorphic branch
of the square root function, that is to say a holomorphic map
such that
for all
. As
is injective,
must also be injective; it is also clearly non-constant, so from the open mapping theorem
is open and thus contains some disk
. But if
lies in
then
cannot lie in
since this would make the map
non-injective; thus
avoids a disk
, and the claim follows.
If is a point in
, then the map
constructed by the above proposition need not map
to the origin, but this is easily fixed by composing
with a suitable automorphism of
. To prove the Riemann mapping theorem, it will thus suffice to show
Proposition 41 Let
be a simply connected Riemann surface, let
be a point in
, and let
be the collection of injective holomorphic maps
with
. If
is non-empty, then
is complex diffeomorphic to
.
Proof: By identifying with its image under one of the elements of
, we may assume without loss of generality that
is itself an open subset of
, with
.
Define the quantity
As contains the identity map,
is at least
; from the Cauchy inequalities (Corollary 27 of Notes 3) we see that
is finite. Hence there exists a sequence
in
with
converging to
as
. From Montel’s theorem (Exercise 58(i) of Notes 4) we know that
is a normal family, so on passing to a subsequence we may assume that the
converge locally uniformly to some limit
. By Hurwitz’s theorem (Exercise 42 of Notes 4), the limit
is holomorphic and is either injective or constant. But from the higher order Cauchy integral formula (Theorem 25 of Notes 3),
converges to
, hence
and so
cannot be constant, and is thus injective. From the maximum principle (Exercise 18) or the open mapping theorem, we know that
takes values in
, and not just
.
To conclude the proposition, we need to show that is also surjective. Here we use a variant of the argument used to prove Proposition 40. Suppose for contradiction that
avoids some point
in
. Let
be an automorphism of
that sends
to
, then
avoids the origin. As
is simply connected, we can thus find a holomorphic square root
of
, thus
Since and hence
are injective,
is also. Finally, if
is an automorphism of
that sends
to
, then the map
lies in
. The map
is related to
by the formula
where is the squaring map. Observe that the map
is a holomorphic map from
to
that maps
to
, and is not a rotation map (since
is not a Möbius transformation). Thus by the Schwarz lemma (Lemma 17), we have
and hence by the chain rule
But this contradicts the definition of , and we are done.
Exercise 42 Let
be an open connected non-empty subset of
. Show that the following are equivalent:
- (i)
is simply connected.
- (ii) One has
for every holomorphic function
and every closed curve
in
.
- (iii) For every holomorphic function
there exists a holomorphic
with
.
- (iv) For every holomorphic function
there exists a holomorphic
with
.
- (v) The complement
of
in the Riemann sphere is connected.
(Hint: to relate (v) to the other claims, use Exercise 44 from Notes 4.)
— 4. Schwarz-Christoffel mappings —
The Riemann mapping theorem guarantees the existence of complex diffeomorphisms for any simply connected subset
of the complex plane that is not all of
; in particular, such diffeomorphisms exist if
is a polygon, by which we mean the interior region of a simple closed anticlockwise polygonal path
. However, the proof of the Riemann mapping theorem does not supply an easy way to compute what this map
is. Nevertheless, in the case of polygons a reasonably explicit formula for
(or more precisely, for the derivative of the inverse of
) may be found. Our arguments here are based on those in the text of Ahlfors.
To motivate the answer we will arrive at, let us first consider the equivalent problem of finding a complex diffeomorphism from an arbitrary given polygon
to to the standard half-plane
. It turns out that it is easier to think about the inverse problem of finding a complex diffeomorphism
from the standard half-plane
to an arbitrary given polygon
. A good near-example here is the standard branch
of the exponentiation map
for some real number
; this is a complex diffeomorphism from
to the sector
, which one can think of as an infinite version of a polygon with just one vertex and two sides. Note in this example that
actually extends continuously as a map from the closed half-plane
to the closed sector
, and in particular maps the real line
to the polygonal path
. Explicitly, we have
for positive real and
for negative real . Thus as
goes from
to
,
first traverses down the ray
(moving at velocity parallel to
) and then along the ray
(with a velocity parallel to
), with a turning point in the direction of travel as
crosses the origin. The velocity
is given by the formula
so is the standard branch of
, which exhibits the desired “turning point” effect.
By inserting more turning points at different points in the real line, one can make map the real line to more complicated polygonal paths, which should hopefully then lead to mapping the half-plane to the interior of the polygon. Suppose for instance we try to make
the branch of
which is holomorphic on
and positive for
(this is possible because
is simply connected and avoids the branch points
where branches of
cannot be analytically continued to). More precisely, we could take
for , where we implicitly use the branch of
mentioned above. Formally at least,
extends continuously to the real line and we should have
Some thought reveals that should then lie on the lower imaginary axis for
, the positive real axis for
, and the upper imaginary axis for
. Some elementary calculus leads us to then compute that
traverses the polygonal path
and with more effort one can show that is in fact a conformal map from
to the half-strip
These examples leads us to suggest that in general we should look for maps whose derivatives are branches of polynomials raised to various fractional powers if we wish to map the half-plane into polygonal regions. It turns out a similar situation occurs for maps from the unit disk into a polygonal region. To make the discussion rigorous we need to continuously extend the conformal maps required to the boundary, which turns out to be a somewhat non-trivial task; we will also call upon a version of the Schwartz reflection principle to make the maps analytic even at the boundary, except at branch points. But once we do so we will indeed be able to describe the conformal maps between the disk and a polygon in the desired terms, although the precise specification of the polynomials that show up will not be completely determined.
To turn to the details we set up some notation. Let be a simple closed anticlockwise polygonal path (in particular, the
are all distinct), let
be the polygon enclosed by this path, and let
be a complex diffeomorphism, the existence of which is guaranteed by the Riemann mapping theorem. (The map
is only unique up to composition by an automorphism of
, but this will not concern us for the present analysis.) We adopt the convention that
and
, and for
, we let
denote the counterclockwise angle subtended by the polygon at
(normalised by a factor of
), in the sense that
for some real . (Note that
cannot attain the values
or
as this would cause the polygonal path to be non-simple.) It is also convenient to introduce the normalised exterior angle
by
(thus
is positive at a convex angle of the polygon, zero at a reflex angle, and negative at a concave angle), so that
Telescoping this identity, we conclude that must be an even integer. Indeed, from Euclidean geometry we know that the sum of the exterior angles of a polygon add up to
, so that
we will give an analytic proof of this fact presently.
From the local structure of the interior of a closed contour (Exercise 54 of Notes 3) we see that always lies to the left of the polygonal path
. We can formalise this statement as follows. First suppose that
is a non-vertex boundary point of
, thus
for some
and
. Then we can form the affine map
by the formula
and the numbering rule tells us that for small enough, the half-disk
is mapped holomorphically by into
. If
is instead a vertex of
, the situation is a little trickier; we now define the map
by the formula
where we choose the branch of with branch cut at the negative imaginary axis
and to be positive real on the positive real axis. Then again
will map
holomorphically into
for
small enough. (The reader is encouraged to draw a picture to understand these maps.)
Now we perform some local analysis near the boundary. We first need a version of the Schwarz reflection principle (Exercise 37 of Notes 3) for harmonic functions.
Exercise 43 (Dirichlet problem) Let
be a continuous function. Show that there exists a unique function
that is continuous on the closed disk
, harmonic on the open disk
, and equal to
on the boundary
. Furthermore, show that
is given by the formula
for
, where
is the Poisson kernel
(compare with Exercise 17 of Notes 3).
Lemma 44 (Schwarz reflection for harmonic functions) Let
be an open subset of
symmetric around the real axis, and let
be a continuous function on the region
that vanishes on
and is harmonic in
. Let
be the antisymmetric extension of
, defined by setting
and
for
. Then
is harmonic.
Proof: Morally speaking, this lemma follows from the analogous reflection principle for holomorphic functions, but there is a difficulty because we do not have enough regularity on the real axis to easily build a harmonic conjugate that is continuous all the way to the real axis. Instead we shall rely on the maximum principle as follows.
It is clear that is continuous and harmonic away from the real axis, so it suffices to show for any
and any small
that
is harmonic on
.
Using Exercise 43, we can find a continuous function which agrees with
on the boundary and is harmonic on the interior. From the antisymmetry of
and uniqueness (or the Poisson kernel formula) we see that
is also antisymmetric and thus vanishes on the real axis. The difference
is then harmonic on the half-disks
and
and vanishes on the boundary of these half-disks, so by the maximum principle they vanish everywhere in
. Thus
agrees with
on
and is therefore harmonic on this disk as required.
Proposition 45 Let
be a boundary point of
(which may or may not be a vertex). Then for
small enough, the maps
extend holomorphically to a map from
to
which maps the origin to a point on the unit circle. Furthermore, this map is injective for
small enough.
Proof: For any , the preimage
of the closed disk
is a compact subset of
and thus stays a positive distance away from the boundary of
. In particular, for
sufficiently close to the boundary of
,
must exceed
. We conclude that the function
extends continuously to a map from
to
, by declaring the map to equal
on the boundary. In particular, for
small enough, the map
also extends continously to
, and equals
on the real boundary of
. For
small enough,
avoids zero on this region, and so the function
will extend continuously to
, and vanish on the real portion of the boundary. By taking local branches of
we see that this function
is also harmonic. By Lemma 44,
extends harmonically to
, and on taking harmonic conjugates we conclude that
extends holomorphically to
. Taking exponentials, we obtain a holomorphic extension
of
to
, with
. To prove injectivity, it suffices (shrinking
as necessary) to show that the derivative of
at
is non-zero. But if this were not the case, then
would have a zero of order at least two, which by the factor theorem implies that
would not map
to a half-plane bordering the origin, and in particular cannot map to
, a contradiction.
As a corollary, we see that extends to a continuous map
that maps
to
, and around every point
in the boundary of
,
maps a small neighbourhood
of
in
to a small neighbourhood of
in
. As
is injective on
, this implies that
is also injective on the boundary of
. The image
is compact in
and contains
, hence
is in fact a bijective continuous map between compact Hausdorff spaces and is thus a homoeomorphism. Thus we can form an inverse map
, which maps
holomorphically to
. (This latter claim in fact works if one replaces the polygonal path
by a arbitrary simple closed curve; this is a theorem of Carathéodory.)
Consider the function on the line segment from
to
. By Proposition 45,
is smooth on this line segment, has non-zero derivative, and takes values in
; setting
, we see that
must traverse a simple curve from
to
in
. As
is orientation preserving,
lies to the left of the line segment
, and the disk
lies to the left of
traversed anticlockwise, we see that
must traverse the anticlockwise arc from
to
. Following
all around
, we see that
must be arranged anticlockwise in the unit circle in the sense that we have
for all
for some
Inverting, we see that for any ,
smoothly maps the anticlockwise arc
from
to
to the line segment
from
to
, with derivative nonvanishing. Thus on taking arguments
for .
Next, we study near
(and
near
) for some
. From Proposition 45 we see that in a sufficiently small neighbourhood of
in
, one has
for some injective holomorphic map
from a neighbourhood of
in
to a neighbourhood of
in
that maps
to zero. Since
maps the arc from
to
to the line segment from
to
,
must map the portion of the arc from
to
near
to a portion of the positive real axis; in particular, by the chain rule,
is a positive real, call it
. If we factor
noting that the third factor is close to one and the second factor lies in the upper half-plane, we have
and hence from we have the factorisation
for near
in
, for some
that is holomorphic and non-zero in a neighbourhood of
in
. Differentiating using
, we conclude that
for near
in
, for some
that is also holomorphic and non-zero in a neighbourhood of
in
.
The function is holomorphic and non-vanishing; as
is simply connected, we must therefore have
for some holomorphic
(by Exercise 47 of Notes 4). For any
between
and
, we see from the previous discussion that
extends holomorphically to a neighbourhood of
, with
non-vanishing at
, so
extends also. From (3) we see that the argument of
is constant on the interval
, and hence
is also constant on this interval. Meanwhile, from (4) we see that for near
in
, we have
for some holomorphic in a neighbourhood of
in
, where
is a branch of the complex logarithm with branch cut at
. From this we see that the function
has a jump discontinuity with jump
as
crosses
. As this function clearly increases by
when
increases by
, we conclude the geometric identity (2).
Now consider the modified function defined by
Then is holomorphic on
, and by the above analysis it extends continuously to
. We consider the imaginary part at
,
where is a branch of the argument function with branch cut at
. Writing
, we see that
is constant as long as
is not an integer multiple of
. From this, (5), and (2), we see that the function
is constant on each arc
. Thus the function
is harmonic on
, continuous on
, and constant on the boundary
, so by the maximum principle it is constant, which from the Cauchy-Riemann equations makes
constant also. Thus we have
on for some complex constant
, which on exponentiating gives
on for some non-zero complex constant
. Applying the fundamental theorem of calculus, we obtain the Schwarz-Christoffel formula:
Theorem 46 (Schwarz-Christoffel for the disk) Let
be a closed simple anticlockwise polygonal path, and define the exterior angles
as above. Let
be the polygon enclosed by this path, and let
be a complex diffeomorphism. Then there exist phases
,
for some
, a non-zero complex number
, and a complex number
such that
for all
, where the integral is over an arbitrary curve from
to
, and one selects a branch of
with branch cut on the negative imaginary axis
. Furthermore,
converges to
as
approaches
for every
.
Note that one can change the branches of here, and also modify the normalising factors
, by adjusting the constant
in a suitable fashion, as long one does not move the branch cut for
into the disk
; one can similarly change the initial point
of the curve to any other point in
by adjusting
. By taking log-derivatives in (6), we can also express the Schwarz-Christoffel formula equivalently as a partial fractions decomposition of
:
The Schwarz-Christoffel formula does not completely describe the conformal mappings from to the disk, because it does not specify exactly what the phases
and the complex constants
are. As the group of automorphisms
of
has three degrees of freedom (one real parameter
and one complex parameter
), one can for instance fix three of the phases
, but in general there are no simple formulae to then reconstruct the remaining parameters in the Schwarz-Christoffel formula, although numerical algorithms exist to compute them approximately. (In the case when the polygon is a rectangle, though, the Schwarz-Christoffel formula essentially produces an elliptic integral, and the complex diffeomorphisms from the rectangle to the disk or half-space are closely tied to elliptic functions; see Section 4.5 of Stein-Shakarchi for more discussion.)
Exercise 47 (Schwarz-Christoffel in a half-plane) Let
be a closed simple anticlockwise polygonal path, and define the exterior angles
as above. Let
be the polygon enclosed by this path, and let
be a complex diffeomorphism from the upper half-plane
to
.
- (i) Show that
extends to a homeomorphism from the closure
of the upper half-plane in the Riemann sphere to
, and that
all lie on
, where
is the inverse of the extension of
.
- (ii) If all of the
are finite, show that after a cyclic permutation one has
, and that there exists a non-zero complex number
, and a complex number
such that
for all
, where the integral is over any curve from
to
in
.
- (iii) If one of the
are infinite, show after a cyclic permutation that one has
and
, and there exists a non-zero complex number
, and a complex number
such that
for all
.
Remark 48 One could try to apply the Schwarz-Christoffel formula to a closed polygonal path
that is not simple. In such cases (and after choosing the parameters
correctly), what tends to happen is that the map
still maps the circle
to the closed path, but fails to be injective.
Exercise 49 Let
be a complex diffeomorphism from the half-strip
to the upper half-plane
, which extends to a continuous map
to the closures of
,
in the Riemann sphere. Suppose that
maps
to
respectively. Show that
, where we take the branch of the square root that is positive on the real axis and has a branch cut at
. (Hint:
is not quite a polygon, so one cannot directly apply the Schwarz-Christoffel formula; however the proof of that formula will still apply.)
There is a simple description ofin terms of trigonometric functions. What is it?
— 5. The uniformisation theorem (optional) —
Now we discuss a proof of the uniformisation theorem, Theorem 5, following the approach in these notes of Marshall. Unfortunately the argument is rather complicated, and we will only give a portion of the proof here. One of the many difficulties in trying to prove this theorem is the fact that the conclusion is a disjunction of three alternatives, each with a rather different complex geometry; it would be easier if there was only one target geometry that one was trying to impose on the Riemann surface . To begin separating the three geometries from each other, recall from Liouville’s theorem that there are no non-constant bounded holomorphic functions on
or
, but plenty of non-constant bounded holomorphic functions on
. By Lemma 1, the same claims hold for Riemann surfaces that are complex diffeomorphic to
or
or to
respectively. Note that without loss of generality we may normalise “bounded” by replacing it with “mapping into
“. From this we see that the uniformisation theorem can be broken up into two simpler pieces:
Theorem 50 (Uniformisation theorem, hyperbolic case) Let
be a simply connected Riemann surface that admits a non-constant holomorphic map from
to
. Then
is complex diffeomorphic to
.
Theorem 51 (Uniformisation theorem, non-hyperbolic case) Let
be a simply connected Riemann surface that does not admit a non-constant holomorphic map from
to
. Then
is complex diffeomorphic to
or
.
Let us now focus on the hyperbolic case of the uniformisation theorem, Theorem 50. Now we do not have the disjunction problem as there is only one target geometry to impose on ; we will be able to give a complete proof of this theorem here (in contrast to Theorem 51, where we will only give part of the proof). Let
be a point in
, and recall that
denotes the collection of holomorphic maps
that maps
to
. By hypothesis (and applying a suitable automorphism of
),
contains at least one non-constant map. If Theorem 50 were true, then from Lemma 39 we see that
would contain a “maximal” element
which would exhibit the desired complex diffeomorphism between
and
.
It turns out that the converse statement is true: if we can locate “maximal” elements of with certain properties, then we can prove Theorem 50. More precisely, Theorem 50 can be readily deduced from the following claim.
Theorem 52 (Maximal maps into
) Let
be a simply connected Riemann surface, let
be a point in
, and let
be the collection of holomorphic maps from
to
that map
to
. Suppose that
contains a non-constant map. Then
contains a map
with the property that
for all
and
, with equality only if
for some real number
. Furthermore
has a simple zero at
, and no other zeroes.
We have seen how Theorem 50 implies Theorem 52. Let us now demonstrate the converse implication, assuming Theorem 52 for the moment and deriving Theorem 50. Let be a simply connected Riemann surface that admits non-constant holomorphic maps from
to
, and pick a point
in
. By applying a suitable automorphism of
we see that
has a non-constant map, so by Theorem 52 this collection contains an element
with the stated properties. Now let
be two points in
. Since
has a zero only at
, we thus have
. Let
be the automorphism
that maps to
and
to
, then the function
lies in
. From Theorem 52, we thus have
since vanishes, we thus have from the definition of
that
Swapping the roles of and
gives the reverse inequality, thus we in fact have
Applying Theorem 52 again, we conclude that
for some .
Using this identity, we can now show that each of the are injective. Indeed, if
was not injective, then we must have
for some distinct
, neither of which can equal
since
has no other zeroes than
. But then by (8) we see that
, contradicting the fact that
has a zero only at
. Thus
is indeed injective. Applying Proposition 41 we conclude that
and
were complex diffeomorphic. This concludes the derivation of Theorem 50 from Theorem 52.
Remark 53 We only established that
was injective in the above argument, but by inspecting the proof of Proposition 41 and using the maximality properties of
we see that
is also surjective, and thus supplies the required complex diffeomorphism between
and
. In a similar vein, the arguments in the preceding section show that under the hypotheses of Theorem 50, there exists a surjective map from
to
, but one needs something like Theorem 52 to obtain the crucial additional property of injectivity (which was automatic in the preceding section, since one already started with an injection in hand).
To finish off the hyperbolic case of the uniformisation theorem, it remains to prove Theorem 52. It is convenient to work with harmonic functions instead of holomorphic functions. Observe that if were holomorphic with a simple zero at
but no other zeroes, then we have local holomorphic branches of
on small neighbourhoods of any point in
. Taking real parts, we conclude that the function
is harmonic on the punctured surface
; it is also positive since
takes values in
. Furthermore, the function
has a logarithmic singularity at
in the following sense: if
was any coordinate chart on some neighbourhood
of
that mapped
to
, then as
had a simple zero at
, the function
, defined on
, stays bounded as one approaches
.
Conversely, one can reconstruct from
(up to a harmless phase
) by the following lemma.
Lemma 54 (Reconstructing a holomorphic function from its magnitude) Let
be a simply connected Riemann surface, let
be a point in
, and let
be harmonic. Suppose that
has a logarithmic singularity at
in the sense that
is bounded near
for some coordinate chart
on a neighbourhood
of
that maps
to
. Then there exists a holomorphic function
with a simple zero at
and no other zeroes, such that
on
.
Proof: Let be as above. Call a function
on an open subset
of
good if it is holomorphic with
on
(in particular this forces
to be non-zero away from
), and has a simple zero at
if
lies in
. Clearly it will suffice to find a good function on all of
.
We first solve the local problem, showing that for any there exists a neighbourhood
of
that supports a good function
. If
, we can work in a chart
avoiding
which is diffeomorphic to a disk
. If we identify
with
then
restricted to
can be viewed as a harmonic function on
. As this disk is simply connected,
will have a harmonic conjugate and is thus the real part of a holomorphic function
on this disk. Taking
to be
we obtain the required good function. Now suppose instead that
. Using the coordinate chart
to identify
with
, we now have a harmonic function
with
bounded near zero. Applying Exercise 60 of Notes 4, we conclude that
extends to a harmonic function
on
, which is then the real part of a holomorphic function
; taking
then gives a good function on
.
Next, we make the following compatibility observation: if and
are both good functions, then
is constant on every connected component of
(after removing any singularity at
). Indeed, by construction
is holomorphic and of magnitude one, so locally there are holomorphic branches of
that have vanishing real part, hence locally constant imaginary part by the Cauchy-Riemann equations. Hence
is locally constant as claimed.
Now we need to glue together the local good functions into a global good function. This is a “monodromy problem”, which can be solved using analytic continuation and the simply connected nature of by the following “monodromy theorem” argument. Let us pick a good function
on some neighbourhood of
. Given any other point
in
, we can form a path
from
to
. We claim that for any
, we can find a finite sequence
and good functions
for
such that each
contains
, and such that
and
agree on a neighbourhood of
for each
, and
and
also agree on a neighbourhood of
. The set
of such
is easily seen to be an open non-empty subset of
. Now we claim that it is closed. Suppose that
converges to a limit
as
. If any of the
are greater than or equal to
it is easy to see that
, so suppose instead that the
are all less than
. We take a good function
supported on some neighbourhood
of
. By continuity,
will contain
for some sufficiently large
. We would like to append
and
to the sequence of good functions
,
one obtains from the hypothesis
, but there is the issue that
need not agree with
at the endpoint
. However, they only differ by a constant of magnitude one near this endpoint, so after multiplying
by an appropriate constant of magnitude one, we can conclude that
as claimed.
By the continuity method, is all of
, and in particular contains
. Thus we can find
and good functions
for
such that each
contains
, and such that
and
agree on a neighbourhood of
for each
, and
and
also agree on a neighbourhood of
. Consider the final value
obtained by the last good function
at the endpoint
of the curve
. From analytic continuation and a continuity argument we see that if we perform a homotopy of
with fixed endpoints, this final value does not change (even if the number
of good functions may vary). Thus we can define a function
by setting
whenever
is a path from
to
and
is the final good function constructed by the above procedure. From construction we see that
is locally equal to a good function at every point in
, and is thus itself a good function, as required.
Exercise 55 (Monodromy theorem) Let
be a simply connected Riemann surface, let
be another Riemann surface, let
be a point in
, let
be an open neighbourhood of
, and let
be holomorphic. Prove that the following statements are equivalent.
- (i)
has a holomorphic extension to
; that is to say, there is a holomorphic function
whose restriction to
is equal to
.
- (ii) For every curve
starting at
, we can find
and holomorphic functions
for
with
, such that
is an open subset of
containing
, and
and
agree on a neighbourhood of
for each
.
Furthermore, if (i) holds, show that the holomorphic extension
is unique. Give a counterexample that shows that the monodromy theorem fails if
is only assumed to be connected rather than simply connected.
We remark that while the condition (ii) in the monodromy theorem looks somewhat complicated, it becomes more geometrically natural if one adopts the language of sheaves, which we will not do here.
In view of Lemma 54, we may reduce the task of establishing Theorem 52 to that of establishing the existence of a special type of harmonic function on (with one point
removed), namely a Green’s function:
Definition 56 (Green’s function) Let
be a connected Riemann surface, and let
be a point in
. A Green’s function for
at
is a function
with the following properties:
- (i)
is harmonic on
.
- (ii)
is non-negative on
.
- (iii)
has a logarithmic singularity at
in the sense that
is bounded near
for some coordinate chart
that maps
to
.
- (iv)
is minimal with respect to the properties (i)-(iii), in the sense that for any other
obeying (i)-(iii), we have
pointwise in
.
Clearly if a Green’s function for at
exists, it is unique by property (iv), so we can talk about the Green’s function for
at
, if it exists. In the case of the disk
, a Greens’ function may be explicitly computed:
Exercise 57 If
, show that the function
defined by
is a Green’s function for
at
.
Theorem 52 may now be deduced from the following claim.
Proposition 58 (Existence of Green’s function) Let
be a connected Riemann surface, let
be a point in
, and suppose that the collection
of holomorphic maps
that map
to
contains at least one non-constant map. Then the Green’s function
for
at
exists. Furthermore, for any
, one has
for any
.
(Note that in this proposition we no longer need to be simply connected.) Indeed, suppose that Proposition 58 held. Let
be a simply connected Riemann surface, and let
with
containing a non-constant map. By hypothesis, the Green’s function
is non-negative on
. Noting that
remains connected if we remove a small disk around
, and from (iii) that
will be strictly positive on the boundary of that disk, we observe from the maximum principle (Exercise 18) and (ii) that
is in fact strictly positive on
. By Lemma 54 we can find a holomorphic function
with a simple zero at
and no other zeroes, such that
on
. As
is strictly positive,
takes values in
and is thus in
. From Proposition 58 we see that
for all
. If equality occurs anywhere, then the quotient
(after removing the singularity) is a function taking values in the closed unit disk
, which has magnitude
at
; by the maximum principle (or open mapping theorem) we then have
for some real
. Thus
obeys all the properties required for Theorem 52.
It remains to obtain the existence of the Green’s function . To do this, we use a powerful technique for constructing harmonic functions, known as Perron’s method of subharmonic functions. The basic idea is to build a harmonic function by taking a suitable large family of subharmonic functions and then forming their supremum. We first give a definition of subharmonic function.
Definition 59 (Subharmonic function) Let
be a Riemann surface. A subharmonic function on
is an upper semi-continuous function
obeying the following upper maximum principle: for any connected compact set
in
with non-empty boundary and any function
that is continuous on
and harmonic on the interior of
, if
for all
, then
for all
.
A superharmonic function is similarly defined as a lower semi-continuous functionsuch that for any connected compact
with non-empty boundary and any function
continuous on
and harmonic on the interior of
, the bound
for
implies that
for all
.
Clearly subharmonicity and superharmonicity are conformal invariants in the sense that the analogue of Lemma 1 holds for these concepts. We have the following elementary properties of subharmonic functions and superharmonic functions:
Exercise 60 Let
be a Riemann surface.
- (i) Let
be harmonic. Show that a function
is subharmonic if and only if
is superharmonic.
- (ii) Show that a function
is harmonic if and only if it is both subharmonic and superharmonic.
- (iii) If
are subharmonic, show that
is also.
- (iv) Let
be subharmonic, and let
be an open subset of
. Show that the restriction of
to
is subharmonic.
- (v) (Subharmonicity is a local property) Conversely, let
is subharmonic, and suppose that for each
there is a neighbourhood
of
such that the restriction of
to
is subharmonic. Show that
is itself subharmonic. (Hint: If
is continuous on a connected compact set
with non-empty boundary and harmonic on the interior, and
attains a minimum at an interior point of
, show that
is constant in some neighbourhood of that point. Exercise 43 may come in handy, as well as the fact (which you can use without proof) that upper (resp. lower) semi-continuous functions on a compact subset of
can be expressed as the pointwise limit of a decreasing (resp. increasing) sequence of continuous functions.)
- (vi) (Maximum principle) Let
be subharmonic, let
be superharmonic, and let
be a connected compact subset of
with non-empty boundary such that
for all
. Show that
for all
. (This is a similar argument to (v).)
- (vii) Show that the sum of two subharmonic functions is again subharmonic (using the usual conventions on adding
to itself or to another real number).
- (viii) (Harmonic patching) Let
be subharmonic, let
be connected compact with non-empty boundary, and let
be a continuous function on
that is harmonic on the interior of
and agrees with
on the boundary of
. Show that the function
, defined to equal
on
and
on
, is subharmonic.
- (ix) Let
be a holomorphic function. Show that
is subharmonic, with the convention that
. (Hint: first use the maximum principle and harmonic conjugates to show that if
contains a copy of a closed disk
, and
on the boundary of this disk for some continuous
that is harmonic in the interior of the disk, then
in the interior of the disk also.)
For smooth functions on an open subset of , one can express the property of subharmonicity quite explicitly:
Exercise 61 Let
be an open subset of
, and let
be continuously twice (Fréchet) differentiable. Show that the following are equivalent:
- (i)
is subharmonic.
- (ii) For all closed disks
in
, one has
- (iii) One has
for all
.
Show that the equivalence of (i) and (ii) in fact holds even if
is only assumed to be continuous rather than continuously twice differentiable.
However, we will not use the above exercise in our analysis here as it will not be convenient to impose a hypothesis of continuous twice differentiability on our subharmonic functions. For instance, in the unit disk , the function
is an example of a subharmonic function that attains the value
at the origin. A more sophisticated example is
, which is also subharmonic but is now discontinuous at the origin (even if one uses the topology of the extended reals).
The Perron method is based on the observation that under certain conditions, the supremum of a family of subharmonic functions is not just subharmonic (as per Exercise 60(iii)), but is in fact harmonic. A key concept here is that of a Perron family:
Definition 62 Let
be a Riemann surface. A continuous Perron family on
is a family
of continuous subharmonic functions
with the following properties:
- (i) If
, then
.
- (ii) (Harmonic patching) If
,
is a connected compact subset of
with non-empty boundary, and
is a continuous function that is harmonic in the interior of
and equals
on the boundary of
, then the function
defined to equal
on
and
outside of
also lies in
.
One can also consider more general Perron families of subharmonic functions that are merely upper semi-continuous rather than continuous, but for the current application continuous Perron families will suffice.
The fundamental theorem that powers the Perron method is then
Theorem 63 (Perron method) Let
be a non-empty continuous Perron family on a connected Riemann surface
, and set
to be the function
. Then one of the following two statements hold:
- (i)
for all
.
- (ii)
is a harmonic function on
.
Proof: Let us first work locally in some open subset of
that is complex diffeomorphic to a disk
; to simplify the discussion we abuse notation by identifying
with
in the following discussion.
Assume for the moment that is not identically equal to
on
. Let
be an arbitrary point in
(viewed as a subset of
). Then we can find a sequence
such that
as
.
We can use Exercise 43 to find a continuous function that equals
on the boundary of this disk (viewed as a subset of
) and is harmonic and at least as large as
in the interior; if we then let
be the function defined to equal
on
and
outside of this disk, then
is larger than
and also lies in
thanks to axiom (ii). Thus, by replacing
with
, we may assume that
is harmonic on
. Next, by replacing
with
and using axiom (i), we may assume that
pointwise; replacing
with a harmonic function on
as before we may assume that
is harmonic on
. Continuing in this fashion we may assume that
and that
are harmonic on
. Form the function
, then we have
pointwise with
. By the Harnack principle (Exercise 59 of Notes 4), we thus see that
is either harmonic on
, or equal to
on
. The latter cannot occur since we are assuming
not identically equal to
, thus
is harmonic.
Now let be another point in
. We can find another sequence
with
. As before we may assume that the
are increasing and are harmonic on
; we may also assume that
pointwise. Setting
, we conclude that
is harmonic with
on
. In particular
. The harmonic function
is non-negative on
and vanishes at
, hence is identically zero on
by the maximum principle. Since
, we conclude that
and
agree at
. Since
was an arbitrary point on
, we conclude that
is harmonic at
.
Putting all this together, we see that for any point in
there is a neighbourhood
(corresponding to the disk
in the above arguments) with the property that
is either equal to
on
, or is harmonic on
. By a continuity argument we conclude that one of the two options (i), (ii) of the theorem must hold.
Now we can conclude the proof of Proposition 58, and hence the hyperbolic case of the uniformisation theorem, by applying the above theorem to a well-chosen Perron family. Let be a simply connected Riemann surface, and let
be the collection of all continuous subharmonic functions
that vanish outside of a compact subset of
, and which have a logarithmic singularity at
in the sense that
is bounded near
for some coordinate chart
that takes
to
(note that the precise choice of chart here is irrelevant). This collection is non-empty, for it contains the function
that equals (say)
on
, and zero elsewhere (this follows from the observation that
is harmonic away from the origin, and
is harmonic everywhere, as well as the various properties in Exercise 60). From Exercise 60 we see that
is a Perron family; thus, by Theorem 63, the function
is either harmonic on
, or is infinite everywhere. Using the element of
used above we see that
is non-negative.
Let be an arbitrary element of
. By Exercise 60(ix),
is subharmonic, hence
is superharmonic and also non-negative since
takes values in
; as
vanishes at
,
has at least a logarithmic singularity at
in the sense that
is bounded from below near
. If
, then
vanishes outside of a compact set
, hence
outside of
for any
. As
has a logarithmic singularity at
we also have
in a sufficiently small neighbourhood of
. Appying the maximum principle (Exercise 60(vi)) we conclude that
on all of
; sending
to zero and then taking suprema in
we conclude that
or equivalently
pointwise on . In particular, since
contains at least one non-constant map,
cannot be infinite everywhere and must therefore be harmonic.
Similarly, if is a function obeying the properties (i)-(iii) of a Green’s function, and
, then another application of the maximum principle shows that
on
for any
; sending
and taking suprema in
we see that
pointwise.
The only remaining task to show is that has a logarithmic singularity at
. Certainly it has at least this much of a singularity, in that
is bounded from below near
, as can be seen by comparing
to any element of
. To get the upper bound, observe that for any
and
, the function
is subharmonic on
and diverges to
at
, and is hence in fact subharmonic on all of
. In particular, for
in the disk
, we have from the maximum principle that
and hence on taking suprema in and limits in
The right-hand side is finite, and this gives the required upper bound to complete the proof that has a logarithmic singularity at
. This concludes the proof of Proposition 58 and hence Theorem 50.
Before we turn to the non-hyperbolic case of the uniformisation theorem, we record a symmetry property of the Green’s functions that is used to establish that case:
Proposition 64 (Symmetry of Green’s functions) Let
be a connected Riemann surface, and suppose that the Green’s functions
exist for all
. Then for all distinct
, we have
.
When is simply connected, this symmetry can be deduced from (7). For
that are not simply connected, the argument is trickier, requiring one to pass to a universal cover
of
, establish the existence of Green’s functions on
, and find an identity relating the Green’s functions on
with the Green’s functions on
. For details see Marshall’s notes.
Now we can discuss to the non-hyperbolic case of the uniformisation theorem, Theorem 51. Now we do not have any Green’s functions, or any non-constant bounded holomorphic functions. However, note that all three of the model Riemann surfaces ,
and
still have plenty of meromorphic functions: in particular, for any two distinct points
in
, one can find a holomorphic function
that has a simple zero at
, a simple pole at
, and no other zeroes and poles, namely
; one can think of this function with a zero-pole pair as a “dipole“. Similarly if one works on the domain
or
rather than
. From this we see that Theorem 51 would imply the following claim:
Theorem 65 (Existence of dipoles) Let
be a simply connected Riemann surface. Let
be distinct points in
. Then there exists a holomorphic map
that has a simple zero at
, a simple pole at
, and no other zeroes and poles. Furthermore, outside of a compact set
containing
, the function
can be chosen to be bounded away from both
and
(that is, there exists
such that
for all
).
In the converse direction, we can use Theorem 65 to recover Theorem 51 in a manner analogous to how Theorem 52 implies Theorem 50. Indeed, let be a simply connected Riemann surface without non-constant holomorphic maps from
to
. Given any three distinct points
in
, we consider the dipoles
and
. The function
has removable singularities at and at
, no poles, and is also bounded away from a compact set. Thus this function extends to a bounded holomorphic function on
. Since
does not have any non-constant bounded holomorphic functions, the function (9) must be constant, thus
for some complex numbers
; as
is non-constant,
must be non-zero. Since
vanishes only at
, we conclude that
for any
. Since
also has its only zero at
and its only pole at
, we conclude that
is injective. By Exercise 41 of Notes 4,
is thus a complex diffeomorphism from
to an open subset
of
, which of course is simply connected since
is. If
is all of
then we are in the elliptic case and we are done. If
omits at least one point in
then by applying a Möbius transform
is complex diffeomorphic to a simply connected open subset of
; by the Riemann mapping theorem, we conclude that
is either complex diffeomorphic to
or to
. The latter case cannot occur by hypothesis, and we are done.
It remains to prove Theorem 65. As before, we convert the problem to one of finding a specific harmonic function. More precisely, one can derive Theorem 65 from
Theorem 66 (Existence of dipole Green’s functions) Let
be a connected Riemann surface. Let
be distinct points in
, and let
and
be coordinate charts on disjoint neighbourhoods
of
respectively, which map
and
respectively to
. Then there exists a harmonic function
such that
is bounded near
, and
is bounded near
. Furthermore,
is bounded outside of a compact subset
of
.
In the case , one can take the dipole Green’s function
to be the function
for an arbitrary constant
.
Exercise 67 Adapt the proof of Lemma 54 to show that Theorem 66 implies Theorem 65 (and hence Theorem 51).
We still need to prove Theorem 66. If admitted Green’s functions
for every point
, we could simply take
to be the difference
. Unfortunately, as we are in the non-hyperbolic case,
is not expected to have Green’s functions, and it does not appear possible to construct the dipole Green’s functions
directly from Perron’s method due to the indefinite sign of these functions. However, it turns out that if one removes a small disk from
of some small radius
around a third reference point
in a given coordinate chart, then the resulting Riemann surface
will admit Green’s functions
(the basic idea is to apply Perron’s method to non-negative subharmonic functions with a logarithmic singularity at
and which vanish on the boundary of the disk), and by considering limits of the sequence
as
using a version of Montel’s theorem one will be able to obtain the required dipole Green’s function, after first making heavy use of the maximum principle (and an important variant of that principle known as Harnack’s inequality, see Exercise 69 below) to obtain some locally uniform control on the difference
in
. To obtain this locally uniform control, the symmetry property in (64) is key, as it allows one to write
so that the main challenge is to show that the differences and
are bounded uniformly in
, which can be done from the maximum principle and the Harnack inequality. The details are unfortunately a little complicated, and we refer the reader to Marshall’s notes for the complete argument.
To close this section we give a quick corollary to the uniformisation theorem, namely Rado’s theorem on the topology of Riemann surfaces:
Corollary 68 (Rado’s theorem) Every connected Riemann surface is second countable and separable.
Proof: By passing to the universal cover, it suffices to verify this claim for simply connected Riemann surfaces. But the three model surfaces ,
,
are clearly second countable and separable, so the claim follows from the uniformisation theorem.
It is remarkably difficult to prove this theorem directly, without going through the uniformisation theorem. (As just one indication of the difficulty of this theorem, the analogue of Rado’s theorem for complex manifolds in two and higher dimensions is known to be false.)
Exercise 69 (Harnack inequality) Let
be a non-negative continuous function on a closed disk
that is harmonic on the interior of the disk. Show that for every
and
, one has
(Hint: use Exercise 43.)

61 comments
Comments feed for this article
18 October, 2016 at 10:05 pm
maxbaroi
Int he proof of Schwarz’s lemma (Lemma 15), the statement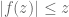 should be replace with
should be replace with 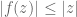
18 October, 2016 at 10:33 pm
maxbaroi
I have a notational question. Why do you write instead of
instead of  when the later seems more commonly used to describe the quotient spaces?
when the later seems more commonly used to describe the quotient spaces?
Sorry for the spam, I have midterms this week and of course trying to do anything but study for them.
[This is an artefact of the fact that my automorphisms area acting on the left. Of course in the case of additive actions, there is no distinction between and
and  ; I’ll adjust the text accordingly. -T.]
; I’ll adjust the text accordingly. -T.]
19 October, 2016 at 8:41 am
Lior Silberman
The adjustment has a typo: to the text above you added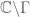 instead of
instead of 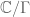 (wrong direction of slash).
(wrong direction of slash).
[Corrected, thanks – T.]
19 October, 2016 at 12:36 am
Anonymous
In the proof of lemma 1(part ii), it should be “By part (i)”.
[Corrected, thanks – T.]
22 October, 2016 at 9:32 am
Anonymous
According to definition 58, if identically, it is (trivially!) subharmonic. Should this trivial example be excluded from the definition?
identically, it is (trivially!) subharmonic. Should this trivial example be excluded from the definition?
[Some authors adopt this convention, but it will not make a difference in the current notes. -T.]
22 October, 2016 at 1:10 pm
Anonymous
In theorem 51 (line 5), should be
should be  .
.
[Corrected, thanks – T.]
22 October, 2016 at 6:08 pm
Anonymous
Mathoverflow: A Generalization of Goldbach’s Conjecture : 2n=p+q,p≡q≡a(mod m)
http://mathoverflow.net/questions/252597/a-generalization-of-goldbach-s-conjecture-2n-pq-p-equiv-q-equiv-a-pmod
23 October, 2016 at 7:32 am
Anonymous
The Schwarz-Christoffel formulas in theorem 45 and exercise 46 are for bounded polygons. Are there similar formulas for unbounded polygons?
24 October, 2016 at 6:42 pm
Anonymous
Few typos “, the expression should be
“, the expression should be  .
.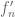 converge locally uniformly” should be
converge locally uniformly” should be 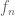 instead.
instead.
1. Second paragraph of section 1, “fundamental theorem of calculus” should be “fundamental theorem of algebra”.
2. Proof of Theorem 25, “concatenating it with the path
3. Proof of Proposition 40, Corollary 27 is from Notes 3, not 2 (the link is actually correct).
4. Same paragraph, “
Thank you!
[Corrected, thanks – T.]
4 November, 2016 at 6:10 am
Anonymous
In proposition 40, is it possible to make the proof more constructive by using the explicit construction of the function from the function
from the function  to give an explicit recursive construction of
to give an explicit recursive construction of  from
from 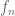 ?
?
4 November, 2016 at 7:34 am
Terence Tao
In principle, yes, but the convergence of this algorithm is incredibly slow. Numerically, there are faster methods, such as the “Zipper” method of Kuhnau and Marshall, discussed for instance here.
4 November, 2016 at 8:11 pm
Joseph
Is it obvious somehow that the group of Moebius-transformations is a simple group? This is an exercise in Conway, preceded by an easy check that the kernel of a homomorphism from GL2(C) to the Moebius transformations under composition is all the multiples of the identity-matrix by the units in C, i.e. GL2(C) is not simple. So, identifying the group of Moebius trans. with GL2(C) seems to contradict this exercise (?)
5 November, 2016 at 6:20 am
Terence Tao
The Mobius transformations are identified with , not
, not  .
.
Saying a group is simple is equivalent to saying that every non-trivial conjugacy class generates the group, so one can establish the simpleness of the Mobius transforms through an understanding of the conjugacy classes. For instance, all parabolic Mobius transforms are conjugate to each other, and it is not difficult to see (e.g. by Gaussian elimination) that all Mobius transforms can be expressed as products of parabolic transforms. If instead one starts with a hyperbolic or elliptic element, one can find a conjugate of it which differs from it by a parabolic element, so from the previous fact we know that these conjugacy classes also generate the group. One can also proceed using the more general structural theory of Lie groups and Lie algebras, but this is probably overkill.
5 November, 2016 at 11:24 am
Joseph
Thanks. Is there a book out there that takes a more algebraic approach to complex analysis?
6 November, 2016 at 2:52 am
Heinrichs Gerhard
There are books about Riemannian Surfaces with more (commutative) algebra e.g. S. Lang Therory of algebraic and abelian Function’s
11 November, 2016 at 5:30 am
Anonymous
Can you add some information on more recent approaches (e.g. the circle packing approach) to conformal mapping ?
27 November, 2016 at 9:36 am
venkyclement
In Proposition 12, why doesn’t the strategy of taking local line segments and passing to a finite subcover of the Riemann sphere not work for an open curve? This proposition suggests that all space filling curves of a unit square must be open.
27 November, 2016 at 3:56 pm
Terence Tao
Both open and closed curves can be space-filling (in the unit square or in the Riemann sphere). What the proof of Proposition 12 shows is that either such curve can be deformed by continuous homotopy to a set which is locally the union of finitely many line segments, and is thus not space filling (but this still permits the original curve to be space-filling).
27 November, 2016 at 5:10 pm
nassoro mtandani
pro. tao i am so interested on how you solve mathematical problems i need to study math please helpme
12 February, 2017 at 7:04 am
Anonymous
One can tell from context though, it might be better to indicate explicitly that the unit disk in the hyperbolic model is an “open” disk?
13 February, 2017 at 11:10 am
Anonymous
This video http://www-users.math.umn.edu/~arnold/moebius/ seems to suggest that Möbius transformations are simplest when viewed on the sphere. But actually, that video only “defines” a Mobius transformation on the sphere and then project the image on the sphere back to the complex plane. Can one show (without using the Cartician coordinates tediously maybe) that it is actually the same as the linear fractional transformation
tediously maybe) that it is actually the same as the linear fractional transformation  on the complex plane?
on the complex plane?
13 February, 2017 at 4:54 pm
Terence Tao
This is perhaps simplest to see for special Mobius transformations such as translation, dilation, rotation, and inversion; general Mobius transformations are compositions of these (see discussion after Exercise 9), so once special Mobius transformations are identified with three-dimensional motions of the sphere, general Mobius transformations are also (because three-dimensional motions of Euclidean space form a group).
13 February, 2017 at 5:49 pm
Anonymous
In this note, what “inversion” really means is “reciprocation” while in geometry, inversion means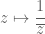 ? (https://en.wikipedia.org/wiki/Inversive_geometry) It might be just a taste of terminology though. Or is there a higher point of view that they are actually the same thing?
? (https://en.wikipedia.org/wiki/Inversive_geometry) It might be just a taste of terminology though. Or is there a higher point of view that they are actually the same thing?
17 February, 2017 at 9:20 am
Anonymous
Is this true that the Schwarz-Christoffel map in Theorem 45 maps the exterior of
in Theorem 45 maps the exterior of 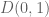 onto the complement of the polygon
onto the complement of the polygon  ?
?
17 February, 2017 at 10:01 pm
Terence Tao
I’m not sure there is any natural way to extend holomorphically to the entire complex plane (basically because of the branch cuts of
holomorphically to the entire complex plane (basically because of the branch cuts of  that one would start encountering). Note that as the only automorphisms of the Riemann sphere are the Mobius transformations, one would only expect to conformally map both the interior and exterior of a domain in a Riemann sphere simultaneously to a disk and its exterior if the domain was already a disk, an exterior of a disk, or a half-plane.
that one would start encountering). Note that as the only automorphisms of the Riemann sphere are the Mobius transformations, one would only expect to conformally map both the interior and exterior of a domain in a Riemann sphere simultaneously to a disk and its exterior if the domain was already a disk, an exterior of a disk, or a half-plane.
18 February, 2017 at 12:59 am
Anonymous
And if we wish to construct a conformal map that maps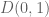 onto the complement of the polygon
onto the complement of the polygon  , can we use the same Schwarz-Christoffel construction (replacing
, can we use the same Schwarz-Christoffel construction (replacing  with the complement angles)?
with the complement angles)?
[Yes – T.]
5 June, 2017 at 10:04 am
Five-Value Theorem of Nevanlinna – Elmar Klausmeier's Weblog
[…] 246A, Notes 5: conformal mapping, covers Picard’s great theorem […]
12 April, 2018 at 9:45 am
246C notes 2: Circle packings, conformal maps, and quasiconformal maps | What's new
[…] theorem was proven in these 246A lecture notes, using an argument of Koebe. At a very high level, one can sketch Koebe’s proof of the […]
8 May, 2018 at 5:40 am
Anonymous
In exercise 9, it seems that M should be connected. From the contradiction, I can just deduce that f is constant on f^{-1}(U’_β)∩U_α(this is defined in notes 4 definition 17) rather than on M. If I wanna expand the domain to M, I find that it’s necessary f^{-1}(U’_β)∩U_α intersects with another f^{-1}(U’_p)∩U_q, but without connectivity I can’t ensure f^{-1}(U’_β)∩U_α intersects with at least one another f^{-1}(U’_p)∩U_q. (if we mark f^{-1}(U’_i)∩U_j as E_ij, we can get M actually equals the union of all the E_ij, and M=E_pq ∪ (the union of the left E_ij), both of the right-hand is open, if M is connected, E_pq ∩ (the union of the left E_ij)!=Φ, E_pq can intersect with at least one another E_ij)
[Corrected, thanks – T.]
9 May, 2018 at 5:44 am
Anonymous
In exercise 22, M should be revised again(2 position in exercise 22, beginning and end).
[Corrected, thanks – T.]
25 April, 2020 at 2:23 pm
Spencer
Some of the latex code in exercise 8 doesn’t render.
[Corrected, thanks – T.]
7 October, 2020 at 10:36 pm
Prateek P Kulkarni
By the definition of the Mobius Transformation, can we also infer that given functions f(z)=Re(z) and g(z)=Im(z) are also Mobius Transformations of z, z∈C ?
8 October, 2020 at 10:50 am
Terence Tao
These are not Mobius transformations (among other things, they are not even meromorphic or conformal).
4 December, 2020 at 4:35 am
Anonymous
In proving that the only holomorphic map from riemann sphere (denote by R) to C are constant can we go as follows :-
Let f : R –> C be a holomorphic function. Since R is compact so, the image of R under f must be compact in particular a bounded subset of C. f is holomorphic on R means f is an entire function and hence by liouville’s theorem f must be constant on C and C is dense in R so, f must be constant on R .
Thanks.
[Yes. See also Exercise 22. -T.]
4 December, 2020 at 2:31 pm
Anonymous
If is holomorphic and has a continuous extension up to the boundary
is holomorphic and has a continuous extension up to the boundary  , can
, can  be extended to a holomorphic function on an open neighborhood
be extended to a holomorphic function on an open neighborhood  of the closed unit disk?
of the closed unit disk?
4 December, 2020 at 2:44 pm
Anonymous
The function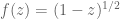 satisfies the above conditions but has a branch point at
satisfies the above conditions but has a branch point at  – hence can’t be holomorphic in any neighborhood of
– hence can’t be holomorphic in any neighborhood of  .
.
4 December, 2020 at 7:52 pm
Anonymous
… in order for to have no pole at infinity,
to have no pole at infinity,  must then be constant.
must then be constant.
I don’t find the notion of “pole at infinity” in notes 4. Do I miss the definition somewhere in the notes?
4 December, 2020 at 7:56 pm
Anonymous
Intuitively, it is understood as zero at . I was wondering if the notion of “poles” was defined for elements in the Riemann sphere in the notes.
. I was wondering if the notion of “poles” was defined for elements in the Riemann sphere in the notes.
[This is briefly discussed after Exercise 3 in the current notes. -T]
5 December, 2020 at 9:45 am
Anonymous
Similarly, “essential singularity at infinity” is mentioned in the proof of Proposition 15; I don’t find where it is defined in the notes.
[Discussion after Exercise 3 expanded to include such a definition. -T]
5 December, 2020 at 10:02 am
Anonymous
In the real case, zero derivatives imply local non-injectivity. How do you show in the proof of Proposition 15 that “as T is a diffeomorphism, the derivative has no zeroes”?
[This is Exercise 40 from Notes 4. -T]
11 December, 2020 at 3:24 pm
Course announcement: 246B, complex analysis | What's new
[…] Schwartz-Christoffel transformations and the uniformisation theorem (using the remainder of the 246A notes); […]
3 January, 2021 at 7:13 pm
Wan-Teh Chang
Prof. Tao: The second part of the proof of Lemma 1 (ii), starting from “By part (i), …”, has an error. The domain of and
and  is
is  , not
, not  , and therefore we can’t apply
, and therefore we can’t apply  or
or  to a ball
to a ball  in
in  .
.
I found a proof by zhw in https://math.stackexchange.com/questions/151827/composition-of-a-harmonic-function-with-a-holomorphic-function-is-still-harmonic.
[Corrected, thanks – T.]
4 January, 2021 at 6:14 pm
Wan-Teh Chang
Prof. Tao: In Section 4. Schwarz-Christoffel mappings, in the equation , the factor
, the factor 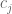 should be changed to
should be changed to  .
.
Also in Section 4, in the sentence “…, thus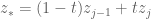 , the subscripts for $z$ on the right hand side should be
, the subscripts for $z$ on the right hand side should be  and
and  , not
, not  and
and  .
.
I have a question about the statement “From the Alexander numbering rule (Exercise 55 of Notes 3) we see that always lies to the left of the polygonal path
always lies to the left of the polygonal path  .” This fact seems intuitively obvious because the simple closed polygonal path is anticlockwise. Why do we need to invoke the Alexander numbering rule to see this fact? To apply the Alexander numbering rule, we need a contour
.” This fact seems intuitively obvious because the simple closed polygonal path is anticlockwise. Why do we need to invoke the Alexander numbering rule to see this fact? To apply the Alexander numbering rule, we need a contour  that intersects the closed contour
that intersects the closed contour  . How should we pick the contour
. How should we pick the contour  ?
?
Thank you!
[Corrected, thanks. Exercise 54 should be used in place of Exercise 55. -T]
10 January, 2021 at 12:55 pm
Anonymous
Do you define the notion of “branch points” somewhere in this series of notes?
Searching around the 246A Notes 4, I don’t see any definition of it.
[Brief definition of branch point added. -T]
20 January, 2021 at 9:27 am
N is a number
In Exercise 60 (iii) we can approach by using the variant of maximum principle for harmonic functions in the case when M is connected. How to deal with the case when M is not connected ?
[Connectedness (or the maximum principle) is not necessary for part (iii) of this exercise. -T]
21 January, 2021 at 4:15 am
N is a number
Yes this just follow tautologically as indicated during yesterday’s class by prof. Tao.
25 January, 2021 at 9:50 am
246B, Notes 1: Zeroes, poles, and factorisation of meromorphic functions | What's new
[…] can be viewed as a more precise assertion of the subharmonicity of (see Exercises 60(ix) and 61 of 246A Notes 5). Here are some quick applications of this […]
27 September, 2021 at 9:13 am
Math 246A, Notes 4: singularities of holomorphic functions | What's new
[…] Previous set of notes: Notes 3. Next set of notes: Notes 5. […]
12 March, 2022 at 2:45 pm
J
The authors of the video below state the following theorem in an AMS Notice article:
A complex mapping is a Möbius transformation if and only if it can be obtained by stereographic projection of the complex plane onto an admissible sphere in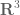 , followed by a rigid motion of the sphere in
, followed by a rigid motion of the sphere in 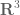 which maps it to another admissible sphere, followed by stereographic projection back to the plane.
which maps it to another admissible sphere, followed by stereographic projection back to the plane.
A sphere in
in 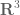 is admissible if its north pole lies in the upper half-space.
is admissible if its north pole lies in the upper half-space.
They say that “We have not been able to ascertain the origin of this simple, elegant result.” (Does anyone know the origin of this result?)
Can the result above be proved by theorems/propositions in this set of notes?
13 March, 2022 at 6:16 am
J
The Notice article actually gives a proof. Denoting by the stereographic projection from the north pole of
the stereographic projection from the north pole of  and
and  a rigid motion of
a rigid motion of 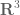 , one can cook up
, one can cook up  (
( ) for a given Mobius transformation
) for a given Mobius transformation  using the composition of translation, inversion, dilation, rotation and then a translation. (This may be a good exercise to put into this set of notes.)
using the composition of translation, inversion, dilation, rotation and then a translation. (This may be a good exercise to put into this set of notes.)
I am wondering if there are any group theory points of view showing that the choice of the sphere and rigid motion
and rigid motion  is not unique.
is not unique.
13 March, 2022 at 10:20 am
Anonymous
The group of Mobius transformations can also be characterized as the largest group of meromorphic transformations on the Riemann sphere.
15 April, 2022 at 7:00 am
A Detailed Proof of the Riemann Mapping Theorem – 爱读书网
[…] This proof is a reproduction of W. Rudin’s Real and Complex Analysis. For a comprehensive further reading, I highly recommend Tao’s blog post. […]
5 May, 2022 at 6:32 am
J
In the proof of Proposition 15:
… we conclude that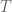 does not have an essential singularity at infinity. Thus
does not have an essential singularity at infinity. Thus 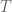 extends to a holomorphic function from
extends to a holomorphic function from  to
to  .
.
Can you elaborate on how exactly Casorati-Weierstrass is used here? When you write “essential singularity at infinity” for the map , do you first consider
, do you first consider 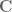 as an open submanifold of the Riemann sphere
as an open submanifold of the Riemann sphere  (and *then* use the discussion after Exercise 3)? (I am probably thinking this in a too complicated way. )
(and *then* use the discussion after Exercise 3)? (I am probably thinking this in a too complicated way. )
Also, why can be extended? Can’t infinity be a non-isolated singularity?
extended? Can’t infinity be a non-isolated singularity?
9 May, 2022 at 1:16 pm
Terence Tao
Here we are applying a coordinate chart to identify a neighborhood of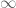 with some portion of the complex plane, for instance by looking at the function
with some portion of the complex plane, for instance by looking at the function  which has an isolated singularity at zero, and for which the image of the unit disk avoids
which has an isolated singularity at zero, and for which the image of the unit disk avoids 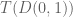 , so that the singularity of
, so that the singularity of 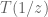 at the origin, which is already isolated, cannot be essential. Which is the statement claimed, expressed in a coordinate chart.
at the origin, which is already isolated, cannot be essential. Which is the statement claimed, expressed in a coordinate chart.
5 May, 2022 at 6:46 am
J
Do you have any heuristic on how one can come up with the key Blaschke factor (moving
(moving  to the origin and maps the disk to itself) in the proof of Theorem 19? (There are so many Mobius transformations, why this one? Any way to see how one can get this naturally?)
to the origin and maps the disk to itself) in the proof of Theorem 19? (There are so many Mobius transformations, why this one? Any way to see how one can get this naturally?)
9 May, 2022 at 1:19 pm
Terence Tao
If the Mobius transformation is to move to the origin then it basically has to have a
to the origin then it basically has to have a 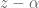 in the numerator (up to constants at least, but the constant can always be transferred to the denominator). If it is to preserve the unit circle, then for
in the numerator (up to constants at least, but the constant can always be transferred to the denominator). If it is to preserve the unit circle, then for  the numerator has to be the same magnitude as the denominator, so in particular must be a unit phase multiple of that numerator (or its complex conjugate). From this and some trial and error one can soon come up with the above choice of transform (up to a unit phase rotation).
the numerator has to be the same magnitude as the denominator, so in particular must be a unit phase multiple of that numerator (or its complex conjugate). From this and some trial and error one can soon come up with the above choice of transform (up to a unit phase rotation).
5 May, 2022 at 4:08 pm
J
In Section 2, given a Riemann surface and a group
and a group 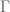 of complex automorphisms of
of complex automorphisms of  , one has the quotient set (orbit space)
, one has the quotient set (orbit space) 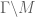 , which has the Riemann surface structure (as the “quotient manifold”). Does one always have such inheritance if
, which has the Riemann surface structure (as the “quotient manifold”). Does one always have such inheritance if  is a set with other structure S (e.g., groups, vectors spaces, topological spaces, etc.) and
is a set with other structure S (e.g., groups, vectors spaces, topological spaces, etc.) and 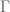 an automorphism group in the corresponding category?
an automorphism group in the corresponding category?
9 May, 2022 at 1:35 pm
Terence Tao
Not automatically. In the Riemann surface category, for instance, it is important that the action be free and proper; in the group category, one needs the orbits to be conjugation invariant (and in particular, if one is acting via a subgroup, the subgroup has to be normal); and so forth. The structure of quotient spaces (or moduli spaces) in general can be quite subtle.
8 May, 2022 at 2:06 pm
J
In the proof of Theorem 52 (Maximal maps into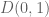 ) implying Theorem 50 (hyperbolic case of the uniformisation theorem), swapping the roles of
) implying Theorem 50 (hyperbolic case of the uniformisation theorem), swapping the roles of 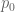 and
and  gives the equality (7), but how does one get the equality
gives the equality (7), but how does one get the equality  above (7)?
above (7)?
9 May, 2022 at 1:37 pm
Terence Tao
Since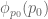 vanishes,
vanishes, 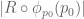 is equal to
is equal to  by definition.
by definition.
12 April, 2023 at 5:04 pm
Complex diffeomorphism and a domain being Polygon – Mathematics – Forum
[…] https://terrytao.wordpress.com/2016/10/18/246a-notes-5-conformal-mapping/#more-9481 […]