Previous set of notes: 246A Notes 5. Next set of notes: Notes 2.
— 1. Jensen’s formula —
Suppose is a non-zero rational function
, then by the fundamental theorem of algebra one can write
Exercise 1 Letbe a complex polynomial of degree
.
- (i) (Gauss-Lucas theorem) Show that the complex roots of
are contained in the closed convex hull of the complex roots of
.
- (ii) (Laguerre separation theorem) If all the complex roots of
are contained in a disk
, and
, then all the complex roots of
are also contained in
. (Hint: apply a suitable Möbius transformation to move
to infinity, and then apply part (i) to a polynomial that emerges after applying this transformation.)
There are a number of useful ways to extend these formulae to more general meromorphic functions than rational functions. Firstly there is a very handy “local” variant of (1) known as Jensen’s formula:
Theorem 2 (Jensen’s formula) Letbe a meromorphic function on an open neighbourhood of a disk
, with all removable singularities removed. Then, if
is neither a zero nor a pole of
, we have
where
and
range over the zeroes and poles of
respectively (counting multiplicity) in the disk
.
One can view (3) as a truncated (or localised) variant of (1). Note also that the summands are always non-positive.
Proof: By perturbing slightly if necessary, we may assume that none of the zeroes or poles of
(which form a discrete set) lie on the boundary circle
. By translating and rescaling, we may then normalise
and
, thus our task is now to show that
by the useful device of Blaschke products. Suppose for instance that
has a zero
inside the disk
. Observe that the function
on the unit circle
, equals
at the origin, has a simple zero at
, but has no other zeroes or poles inside the disk. Thus Jensen’s formula (4) already holds if
is replaced by
. To prove (4) for
, it thus suffices to prove it for
, which effectively deletes a zero
inside the disk
from
(and replaces it instead with its inversion
). Similarly we may remove all the poles inside the disk. As a meromorphic function only has finitely many poles and zeroes inside a compact set, we may thus reduce to the case when
has no poles or zeroes on or inside the disk
, at which point our goal is simply to show that
An important special case of Jensen’s formula arises when is holomorphic in a neighborhood of
, in which case there are no contributions from poles and one simply has
are non-negative; it can be viewed as a more precise assertion of the subharmonicity of
(see Exercises 60(ix) and 61 of 246A Notes 5). Here are some quick applications of this formula:
Exercise 3 Use (6) to give another proof of Liouville’s theorem: a bounded holomorphic functionon the entire complex plane is necessarily constant.
Exercise 4 Use Jensen’s formula to prove the fundamental theorem of algebra: a complex polynomialof degree
has exactly
complex zeroes (counting multiplicity), and can thus be factored as
for some complex numbers
with
. (Note that the fundamental theorem was invoked previously in this section, but only for motivational purposes, so the proof here is non-circular.)
Exercise 5 (Shifted Jensen’s formula) Letbe a meromorphic function on an open neighbourhood of a disk
, with all removable singularities removed. Show that
for all
in the open disk
that are not zeroes or poles of
, where
and
. (The function
appearing in the integrand is sometimes known as the Poisson kernel, particularly if one normalises so that
and
.)
Exercise 6 (Bounded type)
- (i) If
is a holomorphic function on
that is not identically zero, show that
.
- (ii) If
is a meromorphic function on
that is the ratio of two bounded holomorphic functions that are not identically zero, show that
. (Functions
of this form are said to be of bounded type and lie in the Nevanlinna class for the unit disk
.)
Exercise 7 (Smoothed out Jensen formula) Letbe a meromorphic function on an open set
, and let
be a smooth compactly supported function. Show that
where
range over the zeroes and poles of
(respectively) in the support of
. Informally argue why this identity is consistent with Jensen’s formula. (Note: as many of the functions involved here are not holomorphic, complex analysis tools are of limited use. Try using real variable tools such as Stokes theorem, Greens theorem, or integration by parts.)
When applied to entire functions , Jensen’s formula relates the order of growth of
near infinity with the density of zeroes of
. Here is a typical result:
Proposition 8 Letbe an entire function, not identically zero, that obeys a growth bound
for some
and all
. Then there exists a constant
such that
has at most
zeroes (counting multiplicity) for any
.
Entire functions that obey a growth bound of the form for every
and
(where
depends on
) are said to be of order at most
. The above theorem shows that for such functions that are not identically zero, the number of zeroes in a disk of radius
does not grow much faster than
. This is often a useful preliminary upper bound on the zeroes of entire functions, as the order of an entire function tends to be relatively easy to compute in practice.
Proof: First suppose that is non-zero. From (6) applied with
and
one has
Just as (3) and (7) give truncated variants of (1), we can create truncated versions of (2). The following crude truncation is adequate for many applications:
Theorem 9 (Truncated formula for log-derivative) Letbe a holomorphic function on an open neighbourhood of a disk
that is not identically zero on this disk. Suppose that one has a bound of the form
for some
and all
on the circle
. Let
be constants. Then one has the approximate formula
for all
in the disk
other than zeroes of
. Furthermore, the number of zeroes
in the above sum is
.
Proof: To abbreviate notation, we allow all implied constants in this proof to depend on .
We mimic the proof of Jensen’s formula. Firstly, we may translate and rescale so that and
, so we have
when
, and our main task is to show that
. Note that if
then
vanishes on the unit circle and hence (by the maximum principle) vanishes identically on the disk, a contradiction, so we may assume
. From hypothesis we then have
Suppose has a zero
with
. If we factor
, where
is the Blaschke product (5), then
Similarly, given a zero with
, we have
, so using Blaschke products to remove all of these zeroes also only affects the left-hand side of (8) by
(since the number of zeroes here is
), with
also modified by at most
. Thus we may assume in fact that
has no zeroes whatsoever within the unit disk. We may then also normalise
, then
for all
. By Jensen’s formula again, we have
Exercise 10
- (i) (Borel-Carathéodory theorem) If
is analytic on an open neighborhood of a disk
and
, show that
(Hint: one can normalise
,
,
, and
. Now
maps the unit disk to the half-plane
. Use a Möbius transformation to map the half-plane to the unit disk and then use the Schwarz lemma.)
- (ii) Use (i) to give an alternate way to conclude the proof of Theorem 9.
A variant of the above argument allows one to make precise the heuristic that holomorphic functions locally look like polynomials:
Exercise 11 (Local Weierstrass factorisation) Let the notation and hypotheses be as in Theorem 9. Then show thatfor all
in the disk
, where
is a polynomial whose zeroes are precisely the zeroes of
in
(counting multiplicity) and
is a holomorphic function on
of magnitude
and first derivative
on this disk. Furthermore, show that the degree of
is
.
Exercise 12 (Preliminary Beurling factorisation) Letdenote the space of bounded analytic functions
on the unit disk; this is a normed vector space with norm
- (i) If
is not identically zero, and
denote the zeroes of
in
counting multiplicity, show that
and
- (ii) Let the notation be as in (i). If we define the Blaschke product
where
is the order of vanishing of
at zero, show that this product converges absolutely to a holomorphic function on
, and that
for all
. (It may be easier to work with finite Blaschke products first to obtain this bound.)
- (iii) Continuing the notation from (i), establish a factorisation
for some holomorphic function
with
for all
.
- (iv) (Theorem of F. and M. Riesz, special case) If
extends continuously to the boundary
, show that the set
has zero measure.
Remark 13 The factorisation (iii) can be refined further, withbeing the Poisson integral of some finite measure on the unit circle. Using the Lebesgue decomposition of this finite measure into absolutely continuous parts one ends up factorising
functions into “outer functions” and “inner functions”, giving the Beurling factorisation of
. There are also extensions to larger spaces
than
(which are to
as
is to
), known as Hardy spaces. We will not discuss this topic further here, but see for instance this text of Garnett for a treatment.
Exercise 14 (Littlewood’s lemma) Letbe holomorphic on an open neighbourhood of a rectangle
for some
and
, with
non-vanishing on the boundary of the rectangle. Show that
where
ranges over the zeroes of
inside
(counting multiplicity) and one uses a branch of
which is continuous on the upper, lower, and right edges of
. (This lemma is a popular tool to explore the zeroes of Dirichlet series such as the Riemann zeta function.)
— 2. The Weierstrass factorisation theorem —
The fundamental theorem of algebra shows that every polynomial of degree
comes with
complex zeroes
(counting multiplicity). In the converse direction, given any
complex numbers
(again allowing multiplicity), one can form a degree
polynomial
with precisely these zeroes by the formula
is an arbitrary non-zero constant, and by the factor theorem this is the complete set of polynomials with this set of zeroes (counting multiplicity). Thus, except for the freedom to multiply polynomials by non-zero constants, one has a one-to-one correspondence between polynomials (excluding the zero polynomial as a degenerate case) and finite (multi-)sets of complex numbers.
As discussed earlier in this set of notes, one can think of a entire function as a sort of infinite degree analogue of a polynomial. One can then ask what the analogue of the above correspondence is for entire functions are – can one identify entire functions (not identically zero, and up to constants) by their sets of zeroes?
There are two obstructions to this. Firstly there are a number of non-trivial entire functions with no zeroes whatsoever. Most prominently, we have the exponential function which has no zeroes despite being non-constant. More generally, if
is an entire function, then clearly
is an entire function with no zeroes. In particular one can multiply (or divide) any other entire function
by
without affecting the location and order of the zeroes.
Secondly, we know (see Corollary 24 of 246A Notes 3) that the set of zeroes of an entire function (that is not identically zero) must be isolated; in particular, in any compact set there can only be finitely many zeroes. Thus, by covering the complex plane by an increasing sequence of compact sets (e.g., the disks ), one can index the zeroes (counting multiplicity) by a sequence
of complex numbers (possibly with repetition) that is either finite, or goes to infinity.
Now we turn to the Weierstrass factorisation theorem, which asserts that once one accounts for these two obstructions, we recover a correspondence between entire functions and sequences of zeroes.
Theorem 15 (Weierstrass factorization theorem) Letbe a sequence of complex numbers that is either finite or going to infinity. Then there exists an entire function
that has zeroes precisely at
, with the order of zero of
at each
equal to the number of times
appears in the sequence. Furthermore, this entire function is unique up to multiplication by exponentials of entire functions; that is to say, if
are entire functions that are both of the above form, then
for some entire function
.
We now establish this theorem. We begin with the easier uniqueness part of the theorem. If are entire functions with the same locations and orders of zeroes, then the ratio
is a meromorphic function on
which only has removable singularities, and becomes an entire function with no zeroes once the singularities are removed. Since the domain
of an entire function is simply connected, we can then take a branch of the complex logarithm
(see Exercise 46 of 246A Notes 4) to write
for an entire function
(after removing singularities), giving the uniqueness claim.
Now we turn to existence. If the sequence is finite, we can simply use the formula (11) to produce the required entire function
(setting
to equal
, say). So now suppose that the sequence is infinite. Naively, one might try to replicate the formula (11) and set
Lemma 16 (Absolutely convergent products) Letbe a sequence of complex numbers such that
. Then the product
converges. Furthermore, this product vanishes if and only if one of the factors
vanishes.
Products covered by this lemma are known as absolutely convergent products. It is possible for products to converge without being absolutely convergent, but such “conditionally convergent products” are infrequently used in mathematics.
Proof: By the zero test, , thus
converges to
. In particular, all but finitely many of the
lie in the disk
. We can then factor
, where
is such that
for
, and we see that it will suffice to show that the infinite product
converges to a non-zero number. But on using the standard branch
of the complex logarithm on
we can write
. By Taylor expansion we have
, hence the series
is absolutely convergent. From the properties of the complex exponential we then see that the product
converges to
, giving the claim.
It is well known that absolutely convergent series are preserved by rearrangement, and the same is true for absolutely convergent products:
Exercise 17 Ifis an absolutely convergent product of complex numbers
, show that any permutation of the
leads to the same absolutely convergent product, thus
for any permutation
of the positive integers
.
Exercise 18
- (i) Let
be a sequence of real numbers with
for all
. Show that
converges if and only if
converges.
- (ii) Let
be a sequence of complex numbers. Show that
is absolutely convergent if and only if
is convergent.
To try to use Lemma 16, we can divide each factor by the constant
to make it closer to
in the limit
. Since
In order to apply Lemma 16 to make this product converge, we would need to converge for every
, or equivalently that
converge to infinity sufficiently quickly. Not all sequences
covered by Theorem 15 obey this condition, but let us begin with this case for sake of argument. Lemma 16 now tells us that
is well-defined for every
, and vanishes if and only if
is equal to one of the
. However, we need to establish holomorphicity. This can be accomplished by the following product form of the Weierstrass
-test.
Exercise 19 (Product Weierstrass-test) Let
be a set, and for any natural number
, let
be a bounded function. If the sum
for some finite
, show that the products
converge uniformly to
on
. (In particular, if
is a topological space and all the
are continuous, then
is continuous also.)
Using this exercise, we see that (under the assumption (13)) that the partial products converge locally uniformly to the infinite product in (12). Since each of the partial products are entire, and the (locally) uniform limit of holomorphic functions is holomorphic (Theorem 34 of 246A Notes 3), we conclude that the function (12) is entire. Finally, if a certain zero
appears
times in the sequence, then after factoring out
copies of
we see that
is the product of
with an entire function that is non-vanishing at
, and thus
has a zero of order exactly
at
. This establishes the Weierstrass approximation theorem under the additional hypothesis that (13) holds.
What if (13) does not hold? The problem now is that our renormalized factors do not converge fast enough for Lemma 16 or Exercise 19 to apply. So we need to renormalize further, taking advantage of our ability to not just multiply by constants, but also by exponentials of entire functions. Observe that if
is fixed and
is large enough, then
lies in
and we can write
This suggests the way forward to the general case of the Weierstrass factorisation theorem, by using increasingly accurate Taylor expansions of
Exercise 20 Letbe a connected non-empty open subset of
.
- (i) Show that if
is any sequence of points in
, that has no accumulation point inside
, then there exists a holomorphic function
that has zeroes precisely at the
, with the order of each zero
being the number of times
occurs in the sequence.
- (ii) Show that any meromorphic function on
can be expressed as the ratio of two holomorphic functions on
(with the denominator being non-zero). Conclude that the field of meromorphic functions on
is the fraction field of the ring of holomorphic functions on
.
Exercise 21 (Mittag-Leffler theorem, special case) Letbe a sequence of distinct complex numbers going to infinity, and for each
, let
be a polynomial. Show that there exists a meromorphic function
whose singularity at each each
is given by
, in the sense that
has a removable singularity at
. (Hint: consider a sum of the form
, where
is a partial Taylor expansion of
in the disk
, chosen so that the sum becomes locally uniformly absolutely convergent.) This is a special case of the Mittag-Leffler theorem, which is the same statement but in which the domain
is replaced by an arbitrary open set
; however, the proof of this generalisation is more difficult, requiring tools such as Runge’s approximation theorem which are not covered here.
— 3. The Hadamard factorisation theorem —
The Weierstrass factorisation theorem (and its proof) shows that any entire function that is not identically zero can be factorised as
Theorem 22 (Hadamard factorisation theorem) Let, let
, and let
be an entire function of order at most
(not identically zero), with a zero of order
at the origin and the remaining zeroes indexed (with multiplicity) as a finite or infinite sequence
. Then
for some polynomial
of degree at most
. The convergence in the infinite product is locally uniform.
We now prove this theorem. By dividing out by (which does not affect the order of
) and removing the singularity at the origin, we may assume that
. If there are no other zeroes
then we are already done by the previous discussion; similarly if there are only finitely many zeroes
we can divide out by the finite number of elementary factors and remove singularities and again reduce to a case we have already established. Hence we may suppose that the sequence of zeroes
is infinite. As the zeroes of
are isolated, this forces
to go to infinity as
.
Let us first check that the product is absolutely convergent and locally uniform. A modification of the bound (16) shows that
To achieve this convergence we will use the technique of dyadic decomposition (a generalisation of the Cauchy condensation test). Only a finite number of zeroes lie in the disk
, and we have already removed all zeroes at the origin, so by removing those finite zeroes we may assume that
for all
. In particular, each remaining zero
lies in an annulus
for some natural number
. On each such annulus, the expression
is at most
(and is in fact comparable to this quantity up to a constant depending on
, which is why we expect the dyadic decomposition method to be fairly efficient). Grouping the terms in (20) according to the annulus they lie in, it thus suffices to show that
So it remains to establish (21) for in a sufficiently dense set of circles
. We need lower bounds on
. In the regime where the zeroes are distant in the sense that
, Taylor expansion gives
Exercise 23 Establish the upper boundsand
(the latter bound will be useful momentarily).
It thus remains to control the nearby zeroes, in the sense of showing that
Given the set of we are working with, it is natural to introduce the radial variable
. From the triangle inequality one has
, so it will suffice to show that
The point is that this averaging can take advantage of the mild nature of the logarithmic singularity. Indeed a routine computation shows that
Exercise 24 (Converse to Hadamard factorisation) Let, let
be a natural number, and let
be a finite or infinite sequence of non-zero complex numbers such that
for every
. Let
. Show that for every polynomial
of degree at most
, the function
defined by (19) is an entire function of order at most
, with a zero of order
at the origin, zeroes at each
of order equal to the number of times
occurs in the sequence, and no other zeroes. Thus we see that we have a one-to-one correspondence between non-trivial entire functions of order at most
( up to multiplication by
factors for
a polynomial of degree at most
) and zeroes
obeying a certain growth condition.
As an illustration of the Hadamard factorisation theorem, we apply it to the entire function . Since
Hadamard’s theorem also tells us that any other entire function of order at most that has simple zeroes at the integer multiples of
, and no other zeroes, must take the form
for some complex numbers
. Thus the sine function is almost completely determined by its set of zeroes, together with the fact that it is an entire function of order
.
Exercise 25 Show thatfor any complex number
that is not an integer. Use this to give an alternate proof of (24).
— 4. The Gamma function —
As we saw in the previous section (and after applying a simple change of variables), the only entire functions of order that have simple zeroes at the integers (and nowhere else) are of the form
. It is natural to ask what happens if one replaces the integers by the natural numbers
; one could think of such functions as being in some sense “half” of the function
. Actually, it is traditional to normalise the problem a different way, and ask what entire functions of order
have zeroes at the non-positive integers
; it is also traditional to refer to the complex variable in this problem by
instead of
. By the Hadamard factorisation theorem, such functions must take the form
What properties would such functions have? The zero set are nearly invariant with respect to the shift
, so one expects
and
to be related. Indeed we have
Note that as , the function
converges to one, hence
has a residue of
at the origin
; equivalently, by (26) we have
is the unique reciprocal of an entire function of order
with simple poles at the non-positive integers and nowhere else that obeys (26), (27).
From (27), (26) and induction we see that
One can readily establish several more identities and asymptotics for :
Exercise 26 (Euler reflection formula) Show thatwhenever
is not an integer. (Hint: use the Hadamard factorisation theorem.) Conclude in particular that
.
Exercise 27 (Digamma function) Define the digamma function to be the logarithmic derivativeof the Gamma function. Show that the digamma function is a meromorphic function, with simple poles of residue
at the non-positive integers
and no other poles, and that
for
outside of the poles of
, with the sum being absolutely convergent. Establish the reflection formula
or equivalently
for non-integer
.
Exercise 28 (Euler product formula) Show that for any, one has
Exercise 29 Letbe a complex number with
.
- (i) For any positive integer
, show that
- (ii) (Bernoulli definition of Gamma function) Show that
What happens if the hypothesis
is dropped?
- (iii) (Beta function identity) Show that
whenever
are complex numbers with
. (Hint: evaluate
in two different ways.)
We remark that the Bernoulli definition of the function is often the first definition of the Gamma function introduced in texts (see for instance this previous blog post for an arrangement of the material here based on this definition). It is because of the identities (ii), (iii) that the Gamma function often frequently arises when evaluating many other integrals involving polynomials or exponentials, and in particular is a frequent presence in identities involving standard integral transforms, such as the Fourier transform, Laplace transform, or Mellin transform.
Exercise 30
- (i) (Quantitative form of integral test) Show that
for any real
and any continuously differentiable functions
.
- (ii) Using (i) and Exercise 27, obtain the asymptotic
whenever
and
is in the sector
(that is,
makes at least a fixed angle with the negative real axis), where
and
are the standard branches of the argument and logarithm respectively (with branch cut on the negative real axis).
- (iii) (Trapezoid rule) Let
be distinct integers, and let
be a continuously twice differentiable function. Show that
(Hint: first establish the case when
.)
- (iv) Refine the asymptotics in (ii) to
- (v) (Stirling approximation) In the sector used in (ii), (iv), establish the Stirling approximation
- (vi) Establish the size bound
whenever
are real numbers with
and
.
Exercise 31
- (i) (Legendre duplication formula) Show that
whenever
is not a pole of
.
- (ii) (Gauss multiplication theorem) For any natural number
, establish the multiplication theorem
whenever
is not a pole of
.
Exercise 32 Show that.
Exercise 33 (Bohr-Mollerup theorem) Establish the Bohr-Mollerup theorem: the function, which is the Gamma function restricted to the positive reals, is the unique log-convex function
on the positive reals with
and
for all
.
The exercises below will be moved to a more appropriate location after the course has ended.
Exercise 34 Use the argument principle to give an alternate proof of Jensen’s formula, by expressingfor almost every
in terms of zeroes and poles, and then integrating in
and using Fubini’s theorem and the fundamental theorem of calculus.
Exercise 35 Letbe an entire function of order at most
that is not identically zero. Show that there is a constant
such that
for all
outside of the zeroes of
, where
ranges over all the zeroes of
(including those at the origin) counting multiplicity.

73 comments
Comments feed for this article
24 December, 2020 at 4:09 am
Aditya Guha Roy
Wow, thanks for these wonderful notes, sir.
Just some nitpicking: in Exercise 26 it shows \label{bern}. I think you wanted to create a link to that exercise.
[Corrected, thanks – T.]
24 December, 2020 at 6:19 am
Anonymous
In Section 4 of the 246A notes, is reserved as complex logarithm and
is reserved as complex logarithm and  is the real logarithm. (Particularly, the log-derivative of
is the real logarithm. (Particularly, the log-derivative of  seems more related to the complex logarithm.) It may be clearer to either have a comment regarding
seems more related to the complex logarithm.) It may be clearer to either have a comment regarding  in various places of this post or simply use
in various places of this post or simply use  . (The notation
. (The notation  has already been used as
has already been used as  in Exercise 59 of 246A notes 4.)
in Exercise 59 of 246A notes 4.)
It seems that there has never been any consent/standard regarding the use of the logarithm notation in literature and it can only be locally consistent; people would ultimately have to read by context. This seems quite different from the notation issue mentioned in the recent MathOverflow question “How to invoke constants badly”.
24 December, 2020 at 9:50 am
Aditya Guha Roy
I believe that is just the logarithm we use for the reals. (It is easy to see that there exists only one function
is just the logarithm we use for the reals. (It is easy to see that there exists only one function 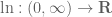 such that
such that 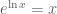 for every real number
for every real number 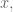 and hence any branch of the complex logarithm which maps the positive real axis to the real axis must agree with
and hence any branch of the complex logarithm which maps the positive real axis to the real axis must agree with  on the positive real axis.
on the positive real axis. and
and 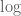 is settled.
is settled.
And as you can see if we choose to work with the principal branch of the complex logarithm (which is usually the case unless specified otherwise), then over the real axis, these two things coincide, and so the confusion between
24 December, 2020 at 3:14 pm
Anonymous
Sorry, I didn’t notice that a short remark has already been in the text:
In this set of notes we use
where the use of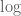 is of course clearly justified.
is of course clearly justified.
24 December, 2020 at 7:24 pm
Aditya Guha Roy
Yes that’s right !
Merry Christmas to prof. Tao and everyone!
24 December, 2020 at 8:33 am
Anonymous
In exercise 11(i), it seems clearer to have the summands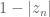 inside parentheses.
inside parentheses.
[Parentheses added – T.]
24 December, 2020 at 9:32 am
Anonymous
Typo: In exercise 6 (i), I believe the inequality should point the other direction
[Actually the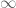 should have been
should have been 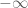 , now corrected – T.]
, now corrected – T.]
24 December, 2020 at 11:08 am
Dan Asimov
I’m looking at equation (23) (and the next one) but not seeing why the number 4 should appear in each factor on the right-hand side.
[Corrected, thanks – T.]
24 December, 2020 at 12:46 pm
Dan Asimov
Also, one side of the Wallis product should be reciprocated.
[Corrected – T.]
24 December, 2020 at 1:19 pm
Anonymous
Similarly, in the two displayed formulas above (22), the factors 2 (in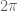 ) and 4 in (
) and 4 in ( ) should be deleted.
) should be deleted. ) the factor 2 in the exponent should be deleted.
) the factor 2 in the exponent should be deleted.
Also, in the third formula above (22) (for
[Corrected – T.]
24 December, 2020 at 3:03 pm
Anonymous
Is it true that the L^infinity norm of a function f is bounded by the L^1 norm of F(f)? Where F(f) denote the Fourier transform of f.
29 December, 2020 at 2:42 pm
Anonymous
Of course.
25 December, 2020 at 8:58 am
Anonymous
It is interesting to observe that the logarithmic convexity of over
over 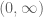 is actually equivalent(!) to Holder’s inequality applied to its Bernoullian integral definition (in exercise 28(i)).
is actually equivalent(!) to Holder’s inequality applied to its Bernoullian integral definition (in exercise 28(i)).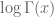 as an infinite sum of convex functions over
as an infinite sum of convex functions over 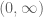 .
.
Another simple derivation of its log-convex property is to use (25) to represent
25 December, 2020 at 9:04 am
Anonymous
Correction: the Bernoullian integral definition of is in exercise 28(ii) (not 28(i)).
is in exercise 28(ii) (not 28(i)).
25 December, 2020 at 2:10 pm
justderiving
Hello Professor Tao, . Thank you! Christina
. Thank you! Christina
This is not a math-related question but how do you write latex on your blog? I have experimented with a number of tex plugins. The best option seems to be, for example,
10 March, 2021 at 10:04 am
David Lowry-Duda
The short answer is “mathjax”. See https://terrytao.wordpress.com/2009/02/10/wordpress-latex-bug-collection-drive/ and https://wordpress.com/support/latex/ to see some of the limitations and official support.
25 December, 2020 at 5:09 pm
Tex Template – DERIVE IT
[…] [2] https://terrytao.wordpress.com/2020/12/23/246b-notes-1-zeroes-poles-and-factorisation-of-meromorphic… […]
27 December, 2020 at 10:15 am
Anonymous
In Exercise 12ii (where you define Blaschke products), the factors need to be normalized (multiply by a suitable unimodular constant) in order to ensure convergence. For example, if the z_n are real (and satisfy the Blaschke condition), then the product as stated diverges at 0.
[Corrected, thanks – T.]
28 December, 2020 at 12:04 pm
Anonymous
Are there positive numbers which are not the order of any entire function?
28 December, 2020 at 1:01 pm
Terence Tao
No; given any positive order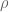 , one can select a sequence of zeroes
, one can select a sequence of zeroes  that go to infinity at the right rate (so that
that go to infinity at the right rate (so that 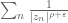 converges for any
converges for any 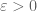 , but
, but  diverges), and then take the entire function appearing in the Hadamard factorisation theorem and apply Exercise 23.
diverges), and then take the entire function appearing in the Hadamard factorisation theorem and apply Exercise 23.
30 December, 2020 at 12:41 pm
Anonymous
It may be added after the product representation (25) that it implies that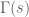 has no zeros.
has no zeros.
[This is mentioned after (26) -T.]
1 January, 2021 at 10:45 am
Anonymous
Let be an entire function.
be an entire function.
Define for each positive integer
Note that the functions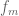 are also entire and satisfy the functional equation
are also entire and satisfy the functional equation
(i.e.
Let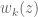 for
for  denote the
denote the  roots of the equation
roots of the equation  .
.
It is not difficult to verify that
If has order
has order 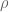 , it follows that each function
, it follows that each function 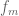 has order
has order  .
.
Examples: Let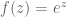 , than
, than
2 January, 2021 at 2:16 am
Anonymous
Correction: The above functional equation is incorrect(!) and should be deleted (along with its rotational invariance interpretation for
is incorrect(!) and should be deleted (along with its rotational invariance interpretation for 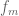 ).
).
2 January, 2021 at 9:25 am
Anonymous
It seems that in (17), the LHS should be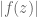 and in the RHS “exp” is missing.
and in the RHS “exp” is missing.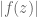 .
.
Similarly, two lines above (17), the LHS of the displayed formula should be
[Corrected, thanks – T.]
3 January, 2021 at 12:52 pm
Anonymous
In the RHS of (17), the “exp” is still missing.
[Corrected, thanks – T.]
4 January, 2021 at 11:29 am
Anonymous
It may be added in theorem 21 that the convergence is locally uniform (which enable certain termwise operations like logarithmic derivative.)
[Suggestion implemented, thanks – T.]
4 January, 2021 at 10:05 pm
Anonymous
In the second part of Exercise 22 the summation should be over |z/zn|>1/2, not <1/2.
[Corrected, thanks – T.]
5 January, 2021 at 5:40 am
Anonymous
Dear Pro Tao,
I have a habit of reading your blog in the early morning before brushing my teeth. It seems tobe my breakfast if I see your breakthrough problems.
So , it’s new year 2021 now. I am always excited about reading what new and more interesting is.
Thank you very much,
23 January, 2021 at 12:56 pm
246B, Notes 2: Some connections with the Fourier transform | What's new
[…] for any positive real number . Explain why this is consistent with Exercise 24 from Notes 1. […]
25 January, 2021 at 11:42 am
Anonymous
Should there be a before the integral in Exercise 6(ii)?
before the integral in Exercise 6(ii)?
[Corrected, thanks – T.]
25 January, 2021 at 9:55 pm
adityaguharoy
In the statement of Theorem 2 (Jensen’s formula), I think you have a very small typo and would like to change the notation to
to 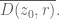
[Corrected, thanks – T.]
26 January, 2021 at 4:57 am
adityaguharoy
During yesterday’s class we developed an impression that the Jensen’s formula is of a similar flavour as the argument principle, and we thought that this similarity may be used somehow to derive one of these results from the other.
Interestingly, I found a related discussion on stack exchange https://math.stackexchange.com/questions/359771/proving-jensens-formula
(While I had a similar approach in mind while asking the question of how these two results are related during yesterday’s class, I did not have the full derivation with me at that time.)
[Nice argument; I have appended it to the notes as an exercise. -T]
26 January, 2021 at 1:39 pm
Anonymous
Is there something similar to Jensen’s formula if f is not meromorphic at Zo? say f has an essential singularity at Zo, but meromorphic at all other points in the complex plane.
26 January, 2021 at 8:02 pm
Terence Tao
Well, the essential singularity is likely to generate an infinite number of zeroes near the singularity (cf. the great Picard theorem), making it difficult to describe the contribution of that singularity in any clean way. On the other hand, one can derive some Jensen type formulas for other domains than the disk, such as an annulus, for instance by applying Green’s theorem to , and this can give some relations between
, and this can give some relations between  and the zeroes and poles near an essential singularity.
and the zeroes and poles near an essential singularity.
28 January, 2021 at 8:20 am
Anonymous
Is there any physical interpretation of Jensen’s formula at least for holomoprphic functions ?
28 January, 2021 at 8:37 am
Anonymous
In the last line of Theorem 2 you have a small typo and would like to change the notation \overline{D(z, r)} to \overline{D(z_0 , r)}.
[Corrected, thanks – T.]
31 January, 2021 at 10:06 am
Anonymous
I think in the Borel-Carathéodory lemma f maps unit disk to {Re f(z)≤1}, but in the hint you have written f maps unit disk to {Re f(z)≥1}. But sup_|z|≤1 Re f(z) =1 so, Re f(z)≤1.
[Corrected, thanks – T.]
31 January, 2021 at 7:16 pm
Wan-Teh Chang
Prof. Tao: I’d like to report some typos in Section 4 (The Gamma function).
1. The equation right above the sentence “It is then natural to normalise to be the real number
to be the real number 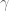 for which …” is missing an equal sign in the second line.
for which …” is missing an equal sign in the second line.
2. In the definition of the Euler-Mascheroni constant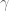 , the summation inside the first limit should read
, the summation inside the first limit should read 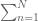 , not
, not 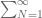 .
.
3. I have a question about the second limit in the definition of the Euler-Mascheroni constant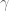 . A direct calculation of
. A direct calculation of  would result in
would result in  . I assume
. I assume 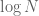 is used in the definition because the limit of
is used in the definition because the limit of 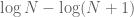 is 0, right?
is 0, right?
4. In the sentence above Equation (27), the function converges to 1, not zero.
converges to 1, not zero.
Thank you!
[Corrected, thanks – T.]
2 February, 2021 at 7:03 pm
246B, Notes 3: Elliptic functions and modular forms | What's new
[…] Somewhat in analogy with the discussion of the Weierstrass and Hadamard factorisation theorems in Notes 1, we then proceed instead by working with the normalised function defined by the formula (6). Let […]
3 February, 2021 at 9:20 am
N is a number
Echoing on a post on the mathoverflow website and keeping in mind the answer posted by you prof. Tao, I wanted to ask whether there is a way in which the zeta function comes as a consequence of the functional equation, in the sense that just like how we see the Gamma function coming as a particular example of a class of functions because it happens to be one of them which satisfies the factorial functional equation, is there some breed of functions such that the zeta function comes as the only one from this class of functions such that the functional equation for the zeta function is satisfied ?
3 February, 2021 at 11:33 am
Terence Tao
There is a classical theorem of Hamburger that asserts that the Riemann zeta function is essentially the only Dirichlet series that obeys the functional equation for the zeta function. However this theorem is somewhat of a curiosity and has not proven to be of much use in practice, nor does it extend well to other L-functions or give more quantitative rigidity statements about zeta. (In particular there are famous examples of Davenport and Heilbronn of Dirichlet series that obey the functional equation for some other Dirichlet L-functions, but which fail to obey the Riemann hypothesis.)
12 February, 2021 at 9:38 am
246B, Notes 4: The Riemann zeta function and the prime number theorem | What's new
[…] for all . (The equivalence between the (5) and (6) is a routine consequence of the Euler reflection formula and the Legendre duplication formula, see Exercises 26 and 31 of Notes 1.) […]
16 February, 2021 at 3:52 pm
Anonymous
In Exercise 3, assume that is a bounded nonconstant entire function. In order to apply (6), one needs a zero of
is a bounded nonconstant entire function. In order to apply (6), one needs a zero of  . How can one get that? Blindly shifting the function seems not useful.
. How can one get that? Blindly shifting the function seems not useful.
[Subtract off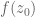 from
from  , where
, where 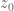 is any point for which
is any point for which  . -T]
. -T]
16 February, 2021 at 3:58 pm
Anonymous
In the first step of the proof of Theorem 2, can you elaborate on how “perturbing ” is done when necessary?
” is done when necessary?
16 February, 2021 at 4:24 pm
Anonymous
Change r to r+/- epsilon.
18 February, 2021 at 4:09 pm
Anonymous
How can you show that the RHS is continuous in ?
?
17 February, 2021 at 6:41 am
Anonymous
In Proposition 8, if one uses instead of
instead of 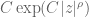 , would one lose anything? Can the constant
, would one lose anything? Can the constant  in the exponent be absorbed somewhere?
in the exponent be absorbed somewhere?
[The former instance of can be absorbed into the latter, but not conversely; if not for the
can be absorbed into the latter, but not conversely; if not for the  in the exponent one could not use this proposition directly to get a good bound for the number of zeroes of, say,
in the exponent one could not use this proposition directly to get a good bound for the number of zeroes of, say,  , unless one rescales as suggested in the comments. -T]
, unless one rescales as suggested in the comments. -T]
17 February, 2021 at 9:41 am
Anonymous
It can be absorbed by rescaling z.
17 February, 2021 at 7:19 am
Anonymous
In the proof of Proposition 8, the symbol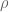 is used as both the order of growth and the dummy variable that represents the zeros of
is used as both the order of growth and the dummy variable that represents the zeros of  .
.
[Corrected, thanks – T.]
20 February, 2021 at 6:51 am
Anonymous
I think typos in (13) and (14): the product should be the sum.
In the Taylor expansions right above (15), the right-hand side should be negative.
[Corrected, thanks – T.]
20 February, 2021 at 7:03 am
Anonymous
There are several big O notations that I don’t quite follow.
1. In theorem 9, does mean
mean  ?
?
and I’m lost in the proof for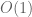 and
and 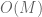 : what is the underlying limiting process?
: what is the underlying limiting process?
2. In the second part of the proof of Theorem 15 (after Exercise 18),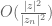 means
means  ?
?
3. What are the first two big O in (16)?
20 February, 2021 at 12:11 pm
Anonymous
21 February, 2021 at 6:33 am
Anonymous
Having read Stein-Shakarchi and your notes more carefully, I think I see what you mean in (16). It is showing that the converge uniformly to $1$ as
converge uniformly to $1$ as 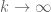 ; so all the big O in (16) implicitly means
; so all the big O in (16) implicitly means 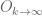 , where
, where  is the asymptotic parameter.
is the asymptotic parameter.
Ultimately it is simply the following estimate that is used

In the writing of (16), would each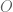 bring a different constant so that the series is not convergent? (I recall that you warn such a situation somewhere in 246a, but I can’t find the exact place.)
bring a different constant so that the series is not convergent? (I recall that you warn such a situation somewhere in 246a, but I can’t find the exact place.)
Also, does one either need to replace the second last equality as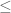 or replace the first O as
or replace the first O as 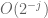 ?
?
22 February, 2021 at 6:23 pm
Terence Tao
In these notes, constants in the big-O notation are uniform among all parameters that are not explicitly subscripted; no asymptotic limit is presumed (in contrast to the little-O notation). For instance, denotes a quantity bounded in absolute value by
denotes a quantity bounded in absolute value by  , where
, where  is uniform in both
is uniform in both  and
and  .
.
A statement with asymptotic notation on the left and right-hand sides is interpreted as saying that every expression of the form of the LHS is also of the form of the RHS, but not necessarily conversely (thus equality is not necessarily symmetric once asymptotic notation is involved). Thus for instance whenever
whenever  .
.
21 February, 2021 at 7:36 am
Anonymous
In the second obstruction mentioned above the Weierstrass factorization theorem, if one considers the constant sequence , then
, then  is the limit of the sequence. But as a set,
is the limit of the sequence. But as a set,  consists of only one point and thus isolated. Why is it still impossible to have this (constant) sequence as zeros of an entire function, i.e., zeros of nonzero entire functions must be of finite order? It seems that Corollary 24 of 246a Notes 3 does not exclude such cases explicitly.
consists of only one point and thus isolated. Why is it still impossible to have this (constant) sequence as zeros of an entire function, i.e., zeros of nonzero entire functions must be of finite order? It seems that Corollary 24 of 246a Notes 3 does not exclude such cases explicitly.
21 February, 2021 at 6:32 pm
Anonymous
If a zero of analytic function has infinite order, all its Taylor coefficients at this zero are vanishing – representing the constant function .
.
22 February, 2021 at 5:21 am
Anonymous
There is no such thing called “infinite order”. It is unclear what one even means when saying a function having the constant sequence
having the constant sequence 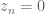 as zeros; but I recall the author said the notion before and hence the question.
as zeros; but I recall the author said the notion before and hence the question.
The “order” of any zero is defined to be a finite number. If one *defines* it as the place where the first nonzero coefficient of its power series around a point, one can of course conclude that it must be constant zero around the point and thus constant.
The question specifically refers to and is meant to ask the statement of Corollary 24 of 246a notes 3, which was summarized as “Non-trivial analytic functions have isolated zeroes”. because this is mentioned explicitly in the note. The constant sequence, as a set, contains only *one* point, which is isolated, does not violate the assumptions of the corollary. And yes, this is question was meant to ask the author of this set of notes.
22 February, 2021 at 2:07 pm
Anonymous
If all Taylor coefficients are zero, the function vanishes identically and it is the only(!) case where the zero order is defined to be infinite (since the zero order of the constant function can’t be finite by any reasonable definition).
can’t be finite by any reasonable definition).
22 February, 2021 at 6:05 am
J.
In the proof of Theorem 2, in the technical case of zeros or poles being on the boundary, if one makes bigger, then more zeros or poles are going into the disk
bigger, then more zeros or poles are going into the disk  so that the two sums may change dramatically, right? (If yes, it seems to be more revealing to write that one is decreasing
so that the two sums may change dramatically, right? (If yes, it seems to be more revealing to write that one is decreasing  . So when perturbing, one can only make it smaller, and the two sums are left continuous in
. So when perturbing, one can only make it smaller, and the two sums are left continuous in  .)
.)
It may be worth adding an exercise or comment for this technical case. It is not immediate that the integral term on the right is (left) continuous in since log is not bounded. One can split the integral as
since log is not bounded. One can split the integral as

and the first term can be done by dominated convergence. How would you deal with the error term?
22 February, 2021 at 6:32 pm
Terence Tao
There is in fact no discontinuity when poles or zeroes enter or exit the disk, this can be seen for instance by rewriting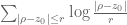 as
as  .
.
The error can bounded by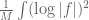 , and the latter integral can be bounded using the fact that
, and the latter integral can be bounded using the fact that  only has a finite number of poles near the circle and the slow divergence of the logarithm function.
only has a finite number of poles near the circle and the slow divergence of the logarithm function.
26 February, 2021 at 1:35 pm
J.
In the argument above (23), is determined by (22). When you say “shifting
is determined by (22). When you say “shifting  by an integer multiple of
by an integer multiple of  ” for the normalization, do you mean changing the branch of
” for the normalization, do you mean changing the branch of  in (22)?
in (22)?
26 February, 2021 at 5:39 pm
Anonymous
No. It means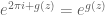 since
since  .
.
27 February, 2021 at 6:50 am
J.
What one concludes from the argument is that for some integer
for some integer  . And thus one has
. And thus one has  . This is already sufficient to conclude (23). Shifting
. This is already sufficient to conclude (23). Shifting  by an integer multiple of
by an integer multiple of  is the same effect as changing the branch of the logarithm in (22).
is the same effect as changing the branch of the logarithm in (22).
27 February, 2021 at 7:40 am
J.
*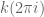 * in the exponent.
* in the exponent.
27 February, 2021 at 9:14 am
Course announcement: 246B, complex analysis | What's new
[…] Jensen’s formula and factorisation theorems (particularly Weierstrass and Hadamard); the Gamma…; […]
24 May, 2021 at 8:59 pm
Convergence of the sum ∑ |f(i)-1| implies convergence of the product ∏ |f(i)| over Mat(m,R) equipped with the operator norm | Aditya Guha Roy's weblog
[…] by professor Terence Tao during one of his lessons from Math 246B in context to the Lemma 16 from Math 246B Notes 1, just as a fun challenging exercise to […]
27 September, 2021 at 9:18 am
246A, Notes 5: conformal mapping | What's new
[…] Previous set of notes: Notes 4. Next set of notes: 246B Notes 1. […]
17 November, 2021 at 1:35 am
Quân Nguyễn
Dear professor Tao, . Does the problem still hold in this case ? Cause I just know the argument for which the sequence
. Does the problem still hold in this case ? Cause I just know the argument for which the sequence  is unbounded.
is unbounded.
I am doing the exercise 20 and wonder what if the sequence has accumulation point on the boundary of
[Yes; the point is to adapt the latter argument to handle the former case also. -T]
17 January, 2022 at 3:22 pm
Anonymous
There’s a small typo in the paragraph immediately before theorem 22. It says “Applying Exercise 29 of 246A Notes 3,” when it should be exercise 31 because Notes 3 was updated recently.
[Corrected, thanks – T.]
22 January, 2022 at 8:24 pm
Anonymous
In exercise 27 should the sum over the integers be replaced with a sum over non-zero integers and a separate term for the zero case (to avoid division by zero)?
[Corrected, thanks – T.]
14 July, 2023 at 11:52 pm
khaledalekasir
In proving Hadamard’s theorem, it’s mentioned that “On the other hand, this logarithmic divergence is rather mild, so one can hope to somehow evade it”.
what do you mean by “mild”?
I can’t see yet intuitively that why Hadamard’s theorem holds.
Thanks.
15 July, 2023 at 5:26 pm
Terence Tao
Functions with a logarithmic singularity, such as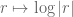 , are still locally absolutely integrable (and in fact lie locally in every
, are still locally absolutely integrable (and in fact lie locally in every 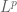 for
for 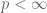 , so they are really close to being bounded (or in
, so they are really close to being bounded (or in 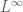 ) despite still being singular.
) despite still being singular.
19 March, 2024 at 2:24 am
khaledalekasir
Dear Terry Tao
I’ve been reflecting on the intuitive underpinnings of Jensen’s formula in complex analysis and found a compelling analogy in physics that I thought might resonate with others here. Imagine, if you will, the complex plane as a vast space where zeros of a holomorphic function act like massive objects generating gravitational fields. These fields influence the path of the function’s growth, much like gravity influences the motion of planets.
keeping in mind that entire functions will to tend to infinity(since a bounded entire function needs to be constant!), every time the function gets zero, it needs to restart trying escape to infinity, so if a functions gets zero several times and is entire this actually shows that the function was able to recover from being zero fast enough, this is analog to the case of gravitational field where an object needs to move with higher velocity in order to escape the gravitational field of a massive object(one can see “failing in escaping the gravitational field” corresponding to entire function being constant!)
Thank you for allowing me to share this perspective. I look forward to any thoughts or corrections you might have.
Thanks.