A basic object of study in multiplicative number theory are the arithmetic functions: functions from the natural numbers to the complex numbers. Some fundamental examples of such functions include
- The constant function
;
- The Kronecker delta function
;
- The natural logarithm function
;
- The divisor function
;
- The von Mangoldt function
, with
defined to equal
when
is a power
of a prime
for some
, and defined to equal zero otherwise; and
- The Möbius function
, with
defined to equal
when
is the product of
distinct primes, and defined to equal zero otherwise.
Given an arithmetic function , we are often interested in statistics such as the summatory function
the logarithmically (or harmonically) weighted summatory function
or the Dirichlet series
In the latter case, one typically has to first restrict to those complex numbers whose real part is large enough in order to ensure the series on the right converges; but in many important cases, one can then extend the Dirichlet series to almost all of the complex plane by analytic continuation. One is also interested in correlations involving additive shifts, such as
, but these are significantly more difficult to study and cannot be easily estimated by the methods of classical multiplicative number theory.
A key operation on arithmetic functions is that of Dirichlet convolution, which when given two arithmetic functions , forms a new arithmetic function
, defined by the formula
Thus for instance ,
,
, and
for any arithmetic function
. Dirichlet convolution and Dirichlet series are related by the fundamental formula
at least when the real part of is large enough that all sums involved become absolutely convergent (but in practice one can use analytic continuation to extend this identity to most of the complex plane). There is also the identity
at least when the real part of is large enough to justify interchange of differentiation and summation. As a consequence, many Dirichlet series can be expressed in terms of the Riemann zeta function
, thus for instance
Much of the difficulty of multiplicative number theory can be traced back to the discrete nature of the natural numbers , which form a rather complicated abelian semigroup with respect to multiplication (in particular the set of generators is the set of prime numbers). One can obtain a simpler analogue of the subject by working instead with the half-infinite interval
, which is a much simpler abelian semigroup under multiplication (being a one-dimensional Lie semigroup). (I will think of this as a sort of “completion” of
at the infinite place
, hence the terminology.) Accordingly, let us define a continuous arithmetic function to be a locally integrable function
. The analogue of the summatory function (1) is then an integral
and similarly the analogue of (2) is
The analogue of the Dirichlet series is the Mellin-type transform
which will be well-defined at least if the real part of is large enough and if the continuous arithmetic function
does not grow too quickly, and hopefully will also be defined elsewhere in the complex plane by analytic continuation.
For instance, the continuous analogue of the discrete constant function would be the constant function
, which maps any
to
, and which we will denote by
in order to keep it distinct from
. The two functions
and
have approximately similar statistics; for instance one has
and
where is the
harmonic number, and we are deliberately vague as to what the symbol
means. Continuing this analogy, we would expect
which reflects the fact that has a simple pole at
with residue
, and no other poles. Note that the identity
is initially only valid in the region
, but clearly the right-hand side can be continued analytically to the entire complex plane except for the pole at
, and so one can define
in this region also.
In a similar vein, the logarithm function is approximately similar to the logarithm function
, giving for instance the crude form
of Stirling’s formula, or the Dirichlet series approximation
The continuous analogue of Dirichlet convolution is multiplicative convolution using the multiplicative Haar measure : given two continuous arithmetic functions
, one can define their convolution
by the formula
Thus for instance . A short computation using Fubini’s theorem shows the analogue
of (3) whenever the real part of is large enough that Fubini’s theorem can be justified; similarly, differentiation under the integral sign shows that
again assuming that the real part of is large enough that differentiation under the integral sign (or some other tool like this, such as the Cauchy integral formula for derivatives) can be justified.
Direct calculation shows that for any complex number , one has
(at least for the real part of large enough), and hence by several applications of (5)
for any natural number . This can lead to the following heuristic: if a Dirichlet series
behaves like a linear combination of poles
, in that
for some set of poles and some coefficients
and natural numbers
(where we again are vague as to what
means, and how to interpret the sum
if the set of poles is infinite), then one should expect the arithmetic function
to behave like the continuous arithmetic function
In particular, if we only have simple poles,
then we expect to have behave like continuous arithmetic function
Integrating this from to
, this heuristically suggests an approximation
for the summatory function, and similarly
with the convention that is
when
, and similarly
is
when
. One can make these sorts of approximations more rigorous by means of Perron’s formula (or one of its variants) combined with the residue theorem, provided that one has good enough control on the relevant Dirichlet series, but we will not pursue these rigorous calculations here. (But see for instance this previous blog post for some examples.)
For instance, using the more refined approximation
to the zeta function near , we have
we would expect that
and thus for instance
which matches what one actually gets from the Dirichlet hyperbola method (see e.g. equation (44) of this previous post).
Or, noting that has a simple pole at
and assuming simple zeroes elsewhere, the log derivative
will have simple poles of residue
at
and
at all the zeroes, leading to the heuristic
suggesting that should behave like the continuous arithmetic function
leading for instance to the summatory approximation
which is a heuristic form of the Riemann-von Mangoldt explicit formula (see Exercise 45 of these notes for a rigorous version of this formula).
Exercise 1 Go through some of the other explicit formulae listed at this Wikipedia page and give heuristic justifications for them (up to some lower order terms) by similar calculations to those given above.
Given the “adelic” perspective on number theory, I wonder if there are also -adic analogues of arithmetic functions to which a similar set of heuristics can be applied, perhaps to study sums such as
. A key problem here is that there does not seem to be any good interpretation of the expression
when
is complex and
is a
-adic number, so it is not clear that one can analyse a Dirichlet series
-adically. For similar reasons, we don’t have a canonical way to define
for a Dirichlet character
(unless its conductor happens to be a power of
), so there doesn’t seem to be much to say in the
-aspect either.

23 comments
Comments feed for this article
9 November, 2017 at 12:09 pm
sylvainjulien
There must be a typo in the equation after the mention of Fubini’s theorem, cause the LHS and RHS are identical. I guess you meant to swap f and g.
9 November, 2017 at 12:24 pm
asahay22
More likely, he wanted to show that the Mellin transform takes the convolution of two functions to products in the frequency space.
[Yes, this is now corrected, thanks – T.]
9 November, 2017 at 12:31 pm
asahay22
Is there a systematic way to convert the heuristic equivalencies to rigorous statements? I know how to individually do some of them, but I’m having a hard time seeing if there’s a more general point of view which let’s one see, for example, the explicit formula for the Chebyshev function and the summatory function asymptotics for the divisor function by Dirichlet’s hyberbola method as the application of the same technique for rigorizing these heuristics.
9 November, 2017 at 2:01 pm
Terence Tao
It’s not a single technique, but rather a choice between “physical space” techniques (such as the hyperbola method) that involve manipulating sums over spatial variables such as , and “frequency space” techniques (such as contour shifting) that involve manipulating integrals over frequency variables such as
, and “frequency space” techniques (such as contour shifting) that involve manipulating integrals over frequency variables such as  (or the imaginary part
(or the imaginary part  of
of  ). In principle, Perron’s formula and its relatives allow one to move back and forth between physical space and frequency space, and so any physical space argument ought to have a frequency space counterpart and vice versa. However, some notions that are easy to understand and use in one space are difficult to use in the other; for instance, positivity of an arithmetic function is easy to see on the physical space side but difficult to discern from looking at the Dirichlet series, and conversely zeroes of a Dirichlet series are hard to see in physical space. Furthermore, there is not a clean equivalence between error term estimates in physical space and error term estimates in frequency space, with the important exception of
). In principle, Perron’s formula and its relatives allow one to move back and forth between physical space and frequency space, and so any physical space argument ought to have a frequency space counterpart and vice versa. However, some notions that are easy to understand and use in one space are difficult to use in the other; for instance, positivity of an arithmetic function is easy to see on the physical space side but difficult to discern from looking at the Dirichlet series, and conversely zeroes of a Dirichlet series are hard to see in physical space. Furthermore, there is not a clean equivalence between error term estimates in physical space and error term estimates in frequency space, with the important exception of 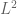 type error estimates in which Parseval’s identity (or Plancherel’s theorem) becomes available. So one often has to make tactical decisions as to what parts of the argument should be conducted in physical space and what parts should be conducted in frequency space. Nevertheless, on a heuristic level, and ignoring the issue of obtaining optimal control on error terms, the two families of approaches are morally equivalent.
type error estimates in which Parseval’s identity (or Plancherel’s theorem) becomes available. So one often has to make tactical decisions as to what parts of the argument should be conducted in physical space and what parts should be conducted in frequency space. Nevertheless, on a heuristic level, and ignoring the issue of obtaining optimal control on error terms, the two families of approaches are morally equivalent.
9 November, 2017 at 2:56 pm
Anonymous
Sort of like we have a simple criterion for a function to have its Fourier transform in L2 but not in L1.
10 November, 2017 at 8:22 am
asahay22
Thanks for the response!
Is there any textbook / course notes / survey that explicitly takes a Fourier viewpoint like this, rather than couching all the theorems in the classical viewpoint (i.e. complex analysis)? I’m not sure if the question is even well-formed, since I understand you can prove the same results with both techniques.
10 November, 2017 at 11:48 am
Lior Silberman
There is a some emphasis on Fourier transforms in my Analytic Number Theory lecture notes. Chapters 1-3 should be ok (bonus points if you report errors); please ignore Chapters 4,5 which are incomplete sketches.
12 November, 2017 at 6:09 pm
asahay22
Thank you!
11 November, 2017 at 9:11 am
Terence Tao
I made some notes on this regarding Fourier perspectives on the prime number theorem at http://www.math.ucla.edu/~tao/preprints/Expository/prime.dvi . I found though it was ultimately more useful (particularly when working with more classically trained analytic number theorists) to try to transfer my Fourier-analytic intuition to the complex variable language, rather than replace complex analytic arguments with their Fourier analogues.
12 November, 2017 at 6:09 pm
asahay22
Thanks!
9 November, 2017 at 11:53 pm
Lior Silberman
There are some -adic analogues. You may want to look at Igusa’s zetafunction for one example.
-adic analogues. You may want to look at Igusa’s zetafunction for one example.
11 November, 2017 at 7:24 am
Aula
On the list of Dirichlet series after (4), the one for the von Mangoldt function is missing the argument s on the LHS.
[Corrected, thanks -T.]
11 November, 2017 at 10:10 am
Lionel
A typo ;-)
;-)
[Corrected, thanks – T.]
14 November, 2017 at 7:46 am
charlie
Hey I finally understand one!
15 November, 2017 at 12:30 am
anon
To get “adelic” analogues, one could try replacing
with
and then define Dirichlet series](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BD%7D%5Bf%5D%28s%2C%5Cchi%29&bg=ffffff&fg=545454&s=0&c=20201002) and Mellin transforms
and Mellin transforms ](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BD%7D_%7B%5Cinfty%7D%5Bf%5D%28s%2C%5Cchi%29&bg=ffffff&fg=545454&s=0&c=20201002) as in the post. One could then take inverse limits (e.g., over powers of
as in the post. One could then take inverse limits (e.g., over powers of  ) and work
) and work  -arithmetically or adelically, but I’m not sure what that would add.
-arithmetically or adelically, but I’m not sure what that would add.
15 November, 2017 at 2:22 am
Kevin
I think that Tate’s thesis ( e.g. equation (22) in https://terrytao.wordpress.com/2008/07/27/tates-proof-of-the-functional-equation/ ) gives some insight here.
Begin by replacing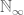 with
with  where
where 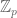 are the usual
are the usual  -adics and
-adics and 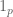 defined to the the characteristic function on this set. Define multiplicative convolution
defined to the the characteristic function on this set. Define multiplicative convolution 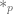 by
by
where denotes the
denotes the  -adic norm with normalization so that
-adic norm with normalization so that 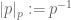 and
and  is the multiplicative Haar measure on
is the multiplicative Haar measure on  normalized so that
normalized so that
with denoting the Haar measure on
denoting the Haar measure on  normalized so that
normalized so that 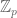 has measure 1.
has measure 1.
Claim: where
where  for
for  .
.
This follows from the computation that
for each such that
such that  .
.
Remark: Initially it seemed to me that the condition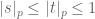 in the definition of convolution is wrong since it reverses the Archimedean one
in the definition of convolution is wrong since it reverses the Archimedean one  . However, it makes sense since on
. However, it makes sense since on 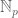 the norm is at most one instead of growing on
the norm is at most one instead of growing on 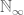 . This also accounts for the minus sign in the definition of
. This also accounts for the minus sign in the definition of  .
.
Carrying on, we define the Mellin type transform as above:
I don’t have the time to follow through at the moment, but this feels like the way forward to me…
16 November, 2017 at 12:12 pm
Terence Tao
The natural analogue of a Dirichlet series of an arithmetic function over a p-adic place would be
over a p-adic place would be  := \sum_n \frac{f(n)}{|n|_p^{s_p}}](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+D%7D_p%5Bf%5D%28s_p%29+%3A%3D+%5Csum_n+%5Cfrac%7Bf%28n%29%7D%7B%7Cn%7C_p%5E%7Bs_p%7D%7D&bg=ffffff&fg=545454&s=0&c=20201002) , but this usually diverges for every
, but this usually diverges for every 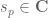 , so one probably has to work with a hybrid of p-adic places and the place at infinity, e.g.
, so one probably has to work with a hybrid of p-adic places and the place at infinity, e.g.
This generalises the usual Dirichlet series which corresponds to the case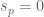 . One could also work with multiple primes
. One could also work with multiple primes  rather than a single prime, but I think this is already illustrative. For instance, the
rather than a single prime, but I think this is already illustrative. For instance, the 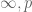 Dirichlet series of
Dirichlet series of  is
is
One still has good behaviour with respect to Dirichlet convolution:
Presumably, continuous counterparts come from functions on using a two-variable Mellin type transform
using a two-variable Mellin type transform
but I haven’t computed this carefully to see what it gives as far as heuristic predictions are concerned (presumably it makes predictions for sums like ).
).
23 November, 2017 at 1:25 am
mallesham kummari
Using the estimates and
and 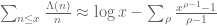 , can one conclude that Riemann zeta function does not vanish on the line
, can one conclude that Riemann zeta function does not vanish on the line 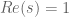 ?
?
26 November, 2017 at 10:38 am
Terence Tao
Not quite: if one only has a single pair of zeroes then the two
then the two  terms in the sum will end up being only
terms in the sum will end up being only 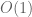 and thus negligible compared to the
and thus negligible compared to the  main term (or the existing
main term (or the existing 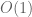 error term).
error term).
However, the Erdos-Selberg proof of the prime number theorem can be interpreted somewhat along these lines, but working with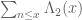 rather than
rather than  . I discuss this at https://mathoverflow.net/questions/259698/ideas-in-the-elementary-proof-of-the-prime-number-theorem-selberg-erd%C5%91s/259719#259719 .
. I discuss this at https://mathoverflow.net/questions/259698/ideas-in-the-elementary-proof-of-the-prime-number-theorem-selberg-erd%C5%91s/259719#259719 .
29 November, 2017 at 5:39 pm
Pedro Caceres
The Harmonic function can be expressed as a function of any z*=1/2+ßi non-trivial zero of Zeta in the critical line. The expression is the following and is valid for all z*:
X(n) = n/(ß^2+(1-α)^2)) for α=1/2
O(n) = ∑(k=1)^n ∑(j≠k)^n (k^(-1/2)*j^(-1/2)*cos(ß*(ln(k/j))
H(n) = ∑(k=1)^n (1/k)
Then:
H(n) = X(n) – O(n) for all z*=1/2+ßi non-trivial zero of zeta
This is easily to see graphically as H(n)+O(n) = X(n) is a straight line as n->infinity, and actually it happens very quickly after n>100. You can see that at:
https://drive.google.com/open?id=1c–u6CJR2Rj4p8YmSteaYbWdNTaztdvS
For values of α 1/2, H(n)+O(n) is always a curve, some examples:
https://drive.google.com/open?id=1zHy-C3UM89IRK5Q4SQiCszx_-VeD3T1M
https://drive.google.com/open?id=1x1OlpuDBzvKGeV_CiDgWIZEyZYm1ARoI
It seems like the “music of the primes shuts down at the non-trivial zeros”, the waves become a straight line.
As a corollary, all non-trivial zeros of zeta can be linked algebraically by the following expression.
if z1=1/2+i*ß1 , z2=1/2+i*ß2 are non-trivial zeros, then:
X(n,z) = n/(ß^2+(1-α)^2)
O(n,z) = ∑(k=1)^n ∑(j≠k)^n (k^(-1/2)*j^(-1/2)*cos(ß*(ln(k/j))
then X(n,z1)+O(n,z1) = X(n,z2)+O(n,z2)
I have developed a Python code to find all non-trivial zeros knowing that z1=1/2+14.13472514173469379*I and it works well.
29 November, 2017 at 8:07 pm
Pedro Caceres
As acontinuation of the previous post,
H(n) = + n/(ß^2+0.25) – sum_(k=1)^n (2*sum_(j=k+1)^n (k^(-1/2)*j^(-1/2)*cos(ß*ln(k/j))))
for those of you that like WolframAlfa, you can try this approximation (for a very low n=20 as WolframAlfa does not want to work for higher values on n):
1) for ß=14.134725, n=20
****** 20/(ß^2+0.25)-H(20) = 20/(ß^2+0.25)-sum_(k-1)^n (1/k) = -3.49776
****** sum_(k=1)^n (2*sum_(j=k+1)^n (k^(-1/2)*j^(-1/2)*cos(ß*ln(k/j)))) = -3.491098
1) for ß=37.586178, n=20
***** 20/(ß^2+0.25)-H(20) = 20/(ß^2+0.25)-sum_(k-1)^n (1/k) = -3.58359
***** sum_(k=1)^n (2*sum_(j=k+1)^n (k^(-1/2)*j^(-1/2)*cos(ß*ln(k/j)))) = -3.57838
with n>500, the error is less than 0.0001.
You can see more results at:
https://drive.google.com/open?id=1t2k690rHr0zes5YrS1dvF7ZWFP1PxEEx
3 December, 2017 at 5:45 am
Occasional corrector
Dear Prof. Tao,
I’d like to thank you for always correcting the mistakes that I may find. I’ve witnessed that occasionally, people react very reluctantly to corrections of all sorts, but I found that those who are the best in their subject will include corrections, because no-one can hurt their scientific reputation.
1 November, 2018 at 3:23 pm
Catalin T.
Dear Prof. Tao,
I have a question on prime zeta function approximations

Have you encountered in the math literature one that resembles the following

Thanks,
Catalin