In this supplemental set of notes we derive some approximations for , when
is large, and in particular Stirling’s formula. This formula (and related formulae for binomial coefficients
will be useful for estimating a number of combinatorial quantities in this course, and also in allowing one to analyse discrete random walks accurately.
From Taylor expansion we have for any
. Specialising this to
we obtain a crude lower bound
In the other direction, we trivially have
so we know already that is within an exponential factor of
. (One can obtain a cruder version of this fact without Taylor expansion, by observing the trivial lower bound
coming from considering the second half of the product
.)
One can do better by starting with the identity
and viewing the right-hand side as a Riemann integral approximation to . Indeed a simple area comparison (cf. the integral test) yields the inequalities
which leads to the inequalities
so the lower bound in (1) was only off by a factor of or so. (This illustrates a general principle, namely that one can often get a non-terrible bound for a series (in this case, the Taylor series for
) by using the largest term in that series (which is
).)
One can do better by using the trapezoid rule. On any interval ,
has a second derivative of
, which by Taylor expansion leads to the approximation
for some error .
The error is absolutely convergent; by the integral test, we have for some absolute constant
. Performing this sum, we conclude that
which after some rearranging leads to the asymptotic
so we see that actually lies roughly at the geometric mean of the two bounds in (3).
This argument does not easily reveal what the constant actually is (though it can in principle be computed numerically to any specified level of accuracy by this method). To find this out, we take a different tack, interpreting the factorial via the Gamma function. Repeated integration by parts reveals the identity
So to estimate , it suffices to estimate the integral in (5). Elementary calculus reveals that the integrand
achieves its maximum at
, so it is natural to make the substitution
, obtaining
which we can simplify a little bit as
pulling out the now-familiar factors of . We combine the integrand into a single exponential,
From Taylor expansion we see that
so we heuristically have
To achieve this approximation rigorously, we first scale by
to remove the
in the denominator. Making the substitution
, we obtain
thus extracting the factor of that we know from (4) has to be there.
Now, Taylor expansion tells us that for fixed , we have the pointwise convergence
as . To be more precise, as the function
equals
with derivative
at the origin, and has second derivative
, we see from two applications of the fundamental theorem of calculus that
This gives a uniform upper bound
for some when
, and
for . This is enough to keep the integrands
dominated by an absolutely integrable function. By (6) and the Lebesgue dominated convergence theorem, we thus have
A classical computation (based for instance on computing in both Cartesian and polar coordinates) shows that
and so we conclude Stirling’s formula
Remark 1 The dominated convergence theorem does not immediately give any effective rate on the decay
(though such a rate can eventually be extracted by a quantitative version of the above argument. But one can combine (7) with (4) to show that the error rate is of the form
. By using fancier versions of the trapezoid rule (e.g. Simpson’s rule) one can obtain an asymptotic expansion of the error term in
, but we will not need such an expansion in this course.
Remark 2 The derivation of (7) demonstrates some general principles concerning the estimation of exponential integrals
when
is large. Firstly, the integral is dominated by the local maxima of
. Then, near these maxima,
usually behaves like a rescaled Gaussian, as can be seen by Taylor expansion (though more complicated behaviour emerges if the second derivative of
degenerates). So one can often understand the asymptotics of such integrals by a change of variables designed to reveal the Gaussian behaviour. A similar set of principles also holds for oscillatory exponential integrals
; these principles are collectively referred to as the method of stationary phase.
One can use Stirling’s formula to estimate binomial coefficients. Here is a crude bound:
Exercise 1 (Entropy formula) Let
be large, let
be fixed, and let
be an integer of the form
. Show that
, where
is the entropy function
For near
, one also has the following more precise bound:
Exercise 2 (Refined entropy formula) Let
be large, and let
be an integer of the form
for some
. Show that
Note the gaussian-type behaviour in . This can be viewed as an illustration of the central limit theorem when summing iid Bernoulli variables
, where each
has a
probability of being either
or
. Indeed, from (8) we see that
when , which suggests that
is distributed roughly like the gaussian
with mean
and variance
.
Update, Jan 4: Rafe Mazzeo pointed me to this short article of Joe Keller that gives a heuristic derivation of the full asymptotic expansion of Stirling’s formula from a Taylor expansion of the Gamma function.

40 comments
Comments feed for this article
3 January, 2010 at 12:57 am
Li Jing
hi, good lecture notes. There is one typo: “so we heuristically have.. ” the formula on right hand side, you miss one negative sign.
[Corrected, thanks – T.]
3 January, 2010 at 1:24 am
Georges Elencwajg
Dear Terry,
this post of yours makes me wonder why the hundreds of books on calculus I have browsed in my life never even came close to your remark at the beginning “so we know already that n! is within an exponential factor of n^n”.
There is obviously something flawed in the realm of pedagogy if it takes a mathematician of your caliber to make such childish remarks.
I am using the word “childish” deliberately, because of the the child in Hans Christian Andersen’s tale who exclaims that the emperor has no clothes.
There is also the well-known Newton quotation
“I was like a boy playing on the sea-shore, and diverting myself now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me”.
And Grothendieck likes to compare himself to a child in his autobiography “Récoltes et Semailles”.
It might seem strange to compare you to Grothendieck, who in a sense is completely antipodal to you ( I’m not sure he knows Sterling’s formula!), but your obvious common love of simplicity and hatred of showing-off might reveal some conceptual similarity, appearances to the contrary notwithstanding.
But enough ot this fuzzy philosophizing: it is high time to thank you heartily for this magnificent note : finally Sterling’s formula is not more mysterious, when explained by you , than the hypercohomology of the De Rham complex on a scheme…
7 January, 2010 at 12:26 am
Manjil P. Saikia
Greatness lies in knowing its boundaries and genius is just that boundary, I guess. It takes the genius and greatness of Prof. Tao to write such nice and illuminating pots.
3 January, 2010 at 10:21 pm
254A, Notes 1: Concentration of measure « What’s new
[…] after using a crude form of Stirling’s formula […]
5 January, 2010 at 4:19 pm
254A, Notes 0: A review of probability theory « What’s new
[…] after using a crude form of Stirling’s formula […]
6 January, 2010 at 11:59 am
254A, Notes 2: The central limit theorem « What’s new
[…] by those with . Now make this intuition precise.) Exercise 2 Use Stirling’s formula from Notes 0a to verify the central limit theorem in the case when is a Bernoulli distribution, taking the […]
9 January, 2010 at 12:02 pm
254A, Notes 3: The operator norm of a random matrix « What’s new
[…] that the median (or mean) of is at least . On the other hand, from Stirling’s formula (Notes 0a) we see that converges to as . Taking to be a slowly growing function of , we conclude […]
10 January, 2010 at 9:54 am
Nathan Cook
I think that in (3) both of the derived bounds are too small by a factor of e. Certainly the upper bound doesn’t hold, for instance if n=2.
[Corrected, thanks – T.]
20 January, 2010 at 7:49 pm
Задача 565. Решение « Le blog de Nicky
[…] P.S. Было вычитано у Теренса Тао. […]
12 March, 2010 at 4:46 pm
Anonymous
Dear Prof. Tao,
How do you get (3) from the inequalities just above it? I could not figure it out
thanks
12 March, 2010 at 4:52 pm
Terence Tao
Compute the antiderivative of , use the fundamental theorem of calculus, then exponentiate all sides of the equation preceding (3).
, use the fundamental theorem of calculus, then exponentiate all sides of the equation preceding (3).
12 March, 2010 at 5:01 pm
Anonymous
I see it now. Thank you. It is really a great post.
14 March, 2010 at 6:06 pm
Weiyu
In the equation before “A classical computation (based for instance on computing”, maybe a “dx” is missing.
[Corrected, thanks. -T]
8 April, 2010 at 2:34 pm
Pablo Lessa
Hi everyone,
I kept wondering about the appearance of entropy in the “entropy formula” (exercise 1), and I found the following probabilistic “almost proof” which I decided to share here (I’m hoping this is considered appropriate, if not I apologize). Does anybody know other interesting explanations as to why entropy occurs in the formula?
Take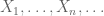 independent random variables with
independent random variables with 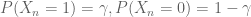 . Define
. Define  and let
and let  for each
for each  .
.
Since takes only
takes only  values it’s entropy is less than
values it’s entropy is less than 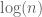 . From this one deduces (exchanging limit with expected value) that almost surely
. From this one deduces (exchanging limit with expected value) that almost surely 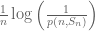 goes to zero. Substituting the expresion for this and using the law of large numbers one obtains that almost surely:
goes to zero. Substituting the expresion for this and using the law of large numbers one obtains that almost surely:
Which is to say that there are a bunch of sequences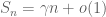 that satisfy the entropy formula (but sadly, it doesn’t show that they all do).
that satisfy the entropy formula (but sadly, it doesn’t show that they all do).
25 April, 2010 at 6:54 pm
t8m8r
In the second paragraph, a formula appears to be missing after “we obtain a crude lower bound”.
[Corrected, thanks – T.]
29 June, 2010 at 6:26 am
Anonymous
Dear Prof.Tao
I am puzzled by Exercise2. Can you give me some hints? Why k=o(n2/3)?
Thanks.
25 August, 2010 at 3:01 am
Anonymous
Dear Prof. Tao
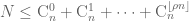
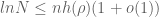
I have a question about Entropy Formula in Exercise 1.
If N is a integer which satisfied
where 0<\rho<1, can we arrive at the conclusion
by Entropy Formula. If it is right, can you tell me how to get it? Some hints will be OK.
25 August, 2010 at 8:15 am
Terence Tao
(Assuming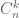 means
means  ) This formula is only valid for
) This formula is only valid for  ; for larger values of
; for larger values of 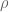 , the partial sum is of size
, the partial sum is of size  .
.
To estimate the order of magnitude of a sum of positive terms, one can often just bound the largest term in the sum, and then multiply by the number of terms, for a crude upper bound. In this case, the largest term will be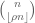 if
if  .
.
26 August, 2010 at 6:40 am
Anonymous
Dear Prof.Tao
 ,
,
 ,
, ,that is,
,that is,
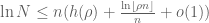 .
. , then
, then
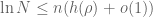 .
. , we have
, we have
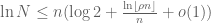 ,
,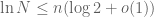 . Am I right? If it is so, there is a typo in the reply.
. Am I right? If it is so, there is a typo in the reply.
Thanks for the quick reply. I see your point. As you said, since
we can get the crude estimate
when
Since
But when
that is,
2 October, 2010 at 10:14 pm
Alon
Dan Romik published a short note with a slick, though perhaps less well-motivated, proof of Stirling’s formula: http://www.stat.berkeley.edu/~romik/paperfiles/stirling.pdf
1 November, 2010 at 11:19 pm
Stirling’s formula « Mathsnail
[…] formula is an approximation for large factorials, that is . A good exposition see Tao’s blog. […]
30 January, 2011 at 2:44 pm
Lower bounds on off-diagonal Ramsey numbers « Annoying Precision
[…] the logarithm of both sides and bounding the corresponding Riemann sum by an integral; see also Terence Tao’s notes on Stirling’s formula) […]
14 March, 2011 at 7:22 am
Pi is still wrong « Annoying Precision
[…] of in the definition of the Gaussian distribution (which is where the factor of comes from in Stirling’s formula) is that the Gaussian distribution is its own Fourier transform. This factor is commonly cited as […]
23 July, 2011 at 7:40 pm
Erdos’ divisor bound « What’s new
[…] with sharper bounds available by using tools such as the Euler-Maclaurin formula (see this blog post). Exponentiating such asymptotics, incidentally, leads to one of the standard proofs of Stirling’s formula (as discussed in this blog post). […]
25 August, 2011 at 2:09 pm
The Collatz conjecture, Littlewood-Offord theory, and powers of 2 and 3 « What’s new
[…] some absolute constant . Meanwhile, Stirling’s formula (as discussed in this previous post) combined with the approximation […]
8 October, 2013 at 5:40 pm
KCd
This proof using the dominated convergence theorem can be found in a 1989 Monthly article: J. M. Patin, A Very Short Proof of Stirling’s Formula, Amer. Math. Monthly 96 (1989), 41–42.
29 December, 2014 at 8:01 pm
Intuition for the definition of the Gamma function? | CL-UAT
[…] these notes by Terence Tao is a proof of Stirling’s formula. I really like most of it, but at a crucial step he uses the […]
2 November, 2015 at 7:06 pm
275A, Notes 4: The central limit theorem | What's new
[…] is a function of that goes to zero as . (A proof of this formula may be found in this previous blog post.) Using this formula, and without using the central limit theorem, show […]
15 April, 2016 at 7:52 pm
Herman Jaramillo
You expanded the argument of the exponential function into a Taylor series. After the term of order $-s^2/2n$ there comes the term $s^3/3n^2$. This terms worries me. Taylor series are local. That is, it should be good for $|s|<<1$. Still the integral is between $-\infty$ to $\infty$. Why does not the error introduce by this next factor $exp(s^3/3n^2)$ count? The integral for that factor alone diverges.
16 April, 2016 at 5:52 am
Herman Jaramillo
I believe I have an answer for my own question above. As $n$ grows the “Gaussian” shape of the integrand t^n exp(-t) narrows around the “center” or peak which is at t=n. Since we are shifting the function to have the origin at t=n. The Taylor approximation makes sense around that location. Yes, the function extendes between -infty and infty, but the gross of the integral is due to the near to the maxima points since in the limit this “Gaussian” shape becomes an spike or some kind of Dirac Delta.
16 April, 2016 at 6:23 am
Anonymous
In the fifth line below (6), it should be “uniform upper bound” (instead of “uniform lower bound”). Also, in the RHS of the second estimate for this bound, “ ” should be replaced by “
” should be replaced by “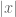 “.
“.
[Corrected, thanks – T.]
17 April, 2016 at 5:03 am
Anonymous
It is not difficult to verify (via maximization over ), that the integrand is dominated by
), that the integrand is dominated by 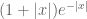 – which is best possible for
– which is best possible for  (as it attained by the integrand for
(as it attained by the integrand for 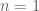 ).
).
18 May, 2016 at 12:13 am
A symmetric formulation of the Croot-Lev-Pach-Ellenberg-Gijswijt capset bound | What's new
[…] tool of Cramer’s theorem, but can also be derived from Stirling’s formula (discussed in this previous post). Indeed, if , , for some summing to , Stirling’s formula […]
22 September, 2016 at 8:45 am
254A, Notes 1: Elementary multiplicative number theory | What's new
[…] any (a weak form of Stirling’s formula, discussed in this previous blog post), and more generally one […]
17 February, 2017 at 9:57 pm
254A, Notes 2: The central limit theorem | What's new
[…] is a function of that goes to zero as . (A proof of this formula may be found in this previous blog post.) Using this formula, and without using the central limit theorem, show […]
13 July, 2017 at 2:50 am
Bruno Bauwens
To go from pointwise convergence to convergence of the integrals below (6), one can use Lebesgue’s monotone convergence theorem: the values \( n log (1+\sqrt(n)) – \sqrt{n} x \) are increasing in n if x is negative, and are decreasing in n if x is positive. This is because for x=0 all values are 0, and the derivative of x evaluates to
\[
\frac{-x}{1+x/\sqrt{n}},
\]
which is decreasing in n both for negative and positive x.
9 November, 2017 at 11:49 am
Continuous approximations to arithmetic functions | What's new
[…] Stirling’s formula, or the Dirichlet series […]
19 January, 2018 at 4:21 am
The De Bruijn-Newman constant is non-negativ | What's new
[…] and using the method of steepest descent (actually it is slightly simpler to rely instead on the Stirling approximation for the Gamma function, which can be proven in turn by steepest descent methods). Fortunately, it […]
6 January, 2019 at 2:35 pm
George Colpitts
See also Gower’s blog article: https://gowers.wordpress.com/2008/02/01/removing-the-magic-from-stirlings-formula/
29 December, 2022 at 9:49 am
Stirling’s formula – On Math
[…] [ 2 ] Terence Tao’s blog article “254A, Notes 0a: Stirling’s formula" : https://terrytao.wordpress.com/2010/01/02/254a-notes-0a-stirlings-formula/ […]