In Notes 1, we approached multiplicative number theory (the study of multiplicative functions and their relatives) via elementary methods, in which attention was primarily focused on obtaining asymptotic control on summatory functions
and logarithmic sums
. Now we turn to the complex approach to multiplicative number theory, in which the focus is instead on obtaining various types of control on the Dirichlet series
, defined (at least for
of sufficiently large real part) by the formula
These series also made an appearance in the elementary approach to the subject, but only for real that were larger than
. But now we will exploit the freedom to extend the variable
to the complex domain; this gives enough freedom (in principle, at least) to recover control of elementary sums such as
or
from control on the Dirichlet series. Crucially, for many key functions
of number-theoretic interest, the Dirichlet series
can be analytically (or at least meromorphically) continued to the left of the line
. The zeroes and poles of the resulting meromorphic continuations of
(and of related functions) then turn out to control the asymptotic behaviour of the elementary sums of
; the more one knows about the former, the more one knows about the latter. In particular, knowledge of where the zeroes of the Riemann zeta function
are located can give very precise information about the distribution of the primes, by means of a fundamental relationship known as the explicit formula. There are many ways of phrasing this explicit formula (both in exact and in approximate forms), but they are all trying to formalise an approximation to the von Mangoldt function
(and hence to the primes) of the form
where the sum is over zeroes (counting multiplicity) of the Riemann zeta function
(with the sum often restricted so that
has large real part and bounded imaginary part), and the approximation is in a suitable weak sense, so that
for suitable “test functions” (which in practice are restricted to be fairly smooth and slowly varying, with the precise amount of restriction dependent on the amount of truncation in the sum over zeroes one wishes to take). Among other things, such approximations can be used to rigorously establish the prime number theorem
as , with the size of the error term
closely tied to the location of the zeroes
of the Riemann zeta function.
The explicit formula (1) (or any of its more rigorous forms) is closely tied to the counterpart approximation
for the Dirichlet series of the von Mangoldt function; note that (4) is formally the special case of (2) when
. Such approximations come from the general theory of local factorisations of meromorphic functions, as discussed in Supplement 2; the passage from (4) to (2) is accomplished by such tools as the residue theorem and the Fourier inversion formula, which were also covered in Supplement 2. The relative ease of uncovering the Fourier-like duality between primes and zeroes (sometimes referred to poetically as the “music of the primes”) is one of the major advantages of the complex-analytic approach to multiplicative number theory; this important duality tends to be rather obscured in the other approaches to the subject, although it can still in principle be discernible with sufficient effort.
More generally, one has an explicit formula
for any (non-principal) Dirichlet character , where
now ranges over the zeroes of the associated Dirichlet
-function
; we view this formula as a “twist” of (1) by the Dirichlet character
. The explicit formula (5), proven similarly (in any of its rigorous forms) to (1), is important in establishing the prime number theorem in arithmetic progressions, which asserts that
as , whenever
is a fixed primitive residue class. Again, the size of the error term
here is closely tied to the location of the zeroes of the Dirichlet
-function, with particular importance given to whether there is a zero very close to
(such a zero is known as an exceptional zero or Siegel zero).
While any information on the behaviour of zeta functions or -functions is in principle welcome for the purposes of analytic number theory, some regions of the complex plane are more important than others in this regard, due to the differing weights assigned to each zero in the explicit formula. Roughly speaking, in descending order of importance, the most crucial regions on which knowledge of these functions is useful are
- The region on or near the point
.
- The region on or near the right edge
of the critical strip
.
- The right half
of the critical strip.
- The region on or near the critical line
that bisects the critical strip.
- Everywhere else.
For instance:
- We will shortly show that the Riemann zeta function
has a simple pole at
with residue
, which is already sufficient to recover much of the classical theorems of Mertens discussed in the previous set of notes, as well as results on mean values of multiplicative functions such as the divisor function
. For Dirichlet
-functions, the behaviour is instead controlled by the quantity
discussed in Notes 1, which is in turn closely tied to the existence and location of a Siegel zero.
- The zeta function is also known to have no zeroes on the right edge
of the critical strip, which is sufficient to prove (and is in fact equivalent to) the prime number theorem. Any enlargement of the zero-free region for
into the critical strip leads to improved error terms in that theorem, with larger zero-free regions leading to stronger error estimates. Similarly for
-functions and the prime number theorem in arithmetic progressions.
- The (as yet unproven) Riemann hypothesis prohibits
from having any zeroes within the right half
of the critical strip, and gives very good control on the number of primes in intervals, even when the intervals are relatively short compared to the size of the entries. Even without assuming the Riemann hypothesis, zero density estimates in this region are available that give some partial control of this form. Similarly for
-functions, primes in short arithmetic progressions, and the generalised Riemann hypothesis.
- Assuming the Riemann hypothesis, further distributional information about the zeroes on the critical line (such as Montgomery’s pair correlation conjecture, or the more general GUE hypothesis) can give finer information about the error terms in the prime number theorem in short intervals, as well as other arithmetic information. Again, one has analogues for
-functions and primes in short arithmetic progressions.
- The functional equation of the zeta function describes the behaviour of
to the left of the critical line, in terms of the behaviour to the right of the critical line. This is useful for building a “global” picture of the structure of the zeta function, and for improving a number of estimates about that function, but (in the absence of unproven conjectures such as the Riemann hypothesis or the pair correlation conjecture) it turns out that many of the basic analytic number theory results using the zeta function can be established without relying on this equation. Similarly for
-functions.
Remark 1 If one takes an “adelic” viewpoint, one can unite the Riemann zeta function
and all of the
-functions
for various Dirichlet characters
into a single object, viewing
as a general multiplicative character on the adeles; thus the imaginary coordinate
and the Dirichlet character
are really the Archimedean and non-Archimedean components respectively of a single adelic frequency parameter. This viewpoint was famously developed in Tate’s thesis, which among other things helps to clarify the nature of the functional equation, as discussed in this previous post. We will not pursue the adelic viewpoint further in these notes, but it does supply a “high-level” explanation for why so much of the theory of the Riemann zeta function extends to the Dirichlet
-functions. (The non-Archimedean character
and the Archimedean character
behave similarly from an algebraic point of view, but not so much from an analytic point of view; as such, the adelic viewpoint is well suited for algebraic tasks (such as establishing the functional equation), but not for analytic tasks (such as establishing a zero-free region).)
Roughly speaking, the elementary multiplicative number theory from Notes 1 corresponds to the information one can extract from the complex-analytic method in region 1 of the above hierarchy, while the more advanced elementary number theory used to prove the prime number theorem (and which we will not cover in full detail in these notes) corresponds to what one can extract from regions 1 and 2.
As a consequence of this hierarchy of importance, information about the function away from the critical strip, such as Euler’s identity
or equivalently
or the infamous identity
which is often presented (slightly misleadingly, if one’s conventions for divergent summation are not made explicit) as
are of relatively little direct importance in analytic prime number theory, although they are still of interest for some other, non-number-theoretic, applications. (The quantity does play a minor role as a normalising factor in some asymptotics, see e.g. Exercise 28 from Notes 1, but its precise value is usually not of major importance.) In contrast, the value
of an
-function at
turns out to be extremely important in analytic number theory, with many results in this subject relying ultimately on a non-trivial lower-bound on this quantity coming from Siegel’s theorem, discussed below the fold.
For a more in-depth treatment of the topics in this set of notes, see Davenport’s “Multiplicative number theory“.
— 1. Dirichlet series to the right of the critical strip —
We begin with the (easy) theory of Dirichlet series to the right of the critical strip , which generalises the theory of Dirichlet series for real
that was used in the previous set of notes.
Given any arithmetic function obeying the crude size bound
is absolutely convergent in the region to the right of the critical strip. Indeed, if
for some
, then we have
for any , and the claim follows by choosing
so that
. Note that this argument also shows that
is bounded in any region of the form
for any
.
The partial sums are clearly holomorphic functions in
on the entire complex plane
, and they converge locally uniformly to
on the region
. Since locally uniform limits of holomorphic functions are holomorphic (Corollary 11 of Supplement 2), we conclude that
is holomorphic on
.
If obey the crude size bound (7), then so does the Dirichlet convolution
(see Exercise 24 of Notes 1). A simple application of Fubini’s theorem then gives the fundamental identity
in the region . Also, by carefully differentiating (8) in
we obtain the additional identity
in the same region, where is the logarithm function
.
From (9), (10) we can express the Dirichlet series of many basic arithmetic functions of number-theoretic interest in terms of the Riemann zeta function, at least in the region :
- By definition,
. Since
, we conclude from (9) that
.
- Clearly
. By (9) and the Möbius inversion formula
, we conclude that
. (In particular,
has no zeroes in the region
.)
- From (10), we have
. By (9) and the basic identity
, we conclude that
.
- From (10), we see that
has a derivative of
. For real
, we already saw (see equation (21) of Notes 1) that this expression was equal to
. Thus we see that
is a branch of the complex logarithm of
to the right of the strip, so we write (by slight abuse of notation)
in this region.
Exercise 3
- (i) Show that
in the region
.
- (ii) Define the Liouville function
by setting
whenever
is the product of
(not necessarily distinct) primes for some
. Show that
in the region
.
Exercise 4 Let
be the higher order von Mangoldt functions (equation (65) from Notes 1). Show that
in the region
, where
is the
-fold derivative of
.
Exercise 5 (Uniqueness for Dirichlet series)
- (i) Let
be two arithmetic functions obeying (7), such that
on the region
. Show that
. (Hint: if
, obtain an asymptotic for
as
along the reals.)
- (ii) Use this uniqueness to give an alternate proof of the identity
for
(equation (66) from Notes 1).
- (iii) Use this uniqueness to give an alternate proof of the Diamond-Steinig identities (Exercise 64 from Notes 1).
Now we establish some crude bounds on Dirichlet series in the region . We will use the following simple application of the triangle inequality: if
and
are arithmetic functions obeying (7) with
for all
, and
for some
and
, then
for all , and hence
In practice, one can use the estimates from Notes 1 to bound . For instance, from Exercise 10 of those notes we have
for all with
and
(the second bound arising from the trivial upper bound
).
We can often obtain matching lower bounds to these upper bounds when is close to
by a number of means. For the Riemann zeta function, one can use the bound
for continuously differentiable (see Exercise 11 from Notes 1), which after a brief calculation gives
for and
. A similar calculation also gives
for and
sufficiently close to
; note that these three estimates were already established in Notes 1 under the additional hypothesis that
was real. One can view (13) as a crude version of the heuristic (4), in which the role of the zeroes
is neglected. When controlling
for a multiplicative function
obeying (7), one can also exploit the Euler product formula
which remains valid in the domain . For instance, under the hypotheses of Theorem 27 of Notes 1, we have
for and
, as can be seen by an inspection of the proof of Theorem 27(i).
Exercise 6 By using the Selberg symmetry formula (equation (67) from Notes 1), show that
whenever
with
and
.
We can obtain better estimates for the zeta function and its relatives once we have some analytic continuation of these functions to the critical strip. However, even before we do so, we can still control various weighted sums of arithmetic functions in terms of integral combinations of the Dirichlet series
. This can be achieved by the following formula:
Proposition 7 (Parseval-type formula) Let
obey (7), and let
be a twice continuously differentiable, compactly supported function. Then for any
, one has
where
is the Fourier transform of
extended to the complex plane, defined by the formula
for
. The integral on the right-hand side of (14) is absolutely integrable.
The formula (14) is similar to the Parseval-type identity
for suitably “nice” functions (see Corollary 32 from Supplement 2). Indeed, one could view
as the Fourier transform of the Radon measure
, which (formally, at least) yields (14) from the Parseval identity. However we will not adopt this measure-theoretic viewpoint explicitly here.
Proof: From Exercise 28 of Supplement 2, we have the bounds
which, together with the boundedness of on
, makes the integral in (14) absolutely integrable as claimed. The same bounds allow one to invoke Fubini’s theorem and rewrite the right-hand side of (14) as
which we rearrange as
By the Fourier inversion formula (Theorem 30 from Supplement 2), this simplifies to
and the claim follows.
Remark 8 The uncertainty principle in Fourier analysis tells us (heuristically, at least) that if we want the function
to exhibit non-trivial oscillation at the scale
, then the Fourier transform
has to spread out over an interval of size
. In particular, if we want to use (14) to investigate fine scale structure of
on intervals such as
, then one expects to need control on the associated Dirichlet series
in which the imaginary part of
can be as large as
in magnitude. Thus, Fourier analysis gives us the insight that the extent to which one can extend control of the Dirichlet series away from the real axis determines the finest scale of
that one can hope to control. For instance, the prime number theorem allows one to counting primes in regions such as
, and so should need control of
on the entire right edge of the critical strip. Conversely, numerical verification of the Riemann hypothesis that establishes zero free regions for
for imaginary parts up to some finite threshold
should yield effective substitutes for the prime number theorem that are able to count primes in intervals such as
.
The most powerful applications of the Parseval-type formula (14) occur when has a meromorphic continuation into the critical strip (or beyond), allowing one to shift
in the right-hand side of (14) to the left of
(picking up various terms from residue calculus along the way). But one can still obtain some useful estimates on various summatory functions involving
even without such meromorphic continuations; in particular, just by using asymptotics near (and to the right of)
such as (13), we can recover estimates of strength comparable to Mertens’ theorems. Here is a basic example, using only the asymptotic (13):
Proposition 9 (Crude Mertens-type theorem) Let
be a continuously twice differentiable compactly supported function. Then for
, one has
This estimate is weaker than the Mertens’ theorems from Notes 1. However, later in these notes we will be able to improve the error term in this proposition if is smoother, by using a more accurate asymptotic expansion than (13). One should also compare (16) to the heuristic (2) (again neglecting the role of the zeroes).
Proof: Since to the right of the critical strip, we can apply Proposition 7 and rewrite the left-hand side of (16) as
where is arbitrary.
A convenient choice of here is
; this is about as far as one can push
to the right (in order to get the best use out of the estimate (11)) before the
shift to
becomes problematic. (Compare with Rankin’s trick, discussed in Notes 1.) In view of (13), it is natural to consider the expression
To compute this expression, we write
and interchange integrals by Fubini’s theorem. From the Fourier inversion formula (Theorem 30 from Supplement 2) and a change of variables one has
so (17) simplifies to the expected main term in (16). It thus suffices to show that
By (13), we can bound in magnitude by
when
is smaller than some absolute constant
. For
, we instead use (11) to bound this quantity by
. Meanwhile, from Exercise 28 of Supplement 2 we have the bounds
Putting these bounds together, we obtain the claim.
Remark 10 In Notes 4 we will use a similar method to that used to prove Theorem 9 to estimate sums such as
where
is the least common multiple of
, and
is a smooth compactly supported function; such expressions will arise naturally when we turn to the topic of sieve theory.
A classical limiting case of Proposition 7 is Perron’s formula:
Exercise 11 (Perron’s formula) Let
obey (7). For any non-integer
and any
, show that
where the integral is a contour integral along the line segment
. What happens when
is an integer?
In practice, the presence of the limit in (18) is inconvenient, and one usually works with smoothed or truncated version of this formula. Proposition 7 can be viewed as a smoothed version of Perron’s formula. Now we establish a truncated version:
Proposition 12 (Truncated Perron’s formula) Let
be such that
for all
, and let
. Then
One can sharpen the factor here slightly, but we will not need such improvements here. The condition
can also be relaxed (at the cost of worsening the error term accordingly); we leave this as an exercise to the reader.
Proof: By perturbing we may assume that
is not an integer. We will assume temporarily that
vanishes at the nearest integer
to
, and remove this hypothesis later. In view of (18), it suffices by dyadic decomposition to show that
for all (not necessarily bounded above by
). By Fubini’s theorem, the left-hand side may be written as
On taking absolute values, we see that
and in particular for
. On the other hand, from integration by parts we have
and thus on taking absolute values
In particular we have
for , and
for . We may thus upper bound (20) using the vanishing of
at
by
Note that as , we can lower bound
by
. The claim now follows from Lemma 2 of Notes 1.
We now have to remove the hypothesis that vanishes by
. By linearity it suffices to address the case where
is supported equal to
at
and vanishes elsewhere (with an error bound of
. But then
, and by the triangle inequality we have
, and the claim follows.
— 2. Meromorphic continuation into the critical strip, and the (truncated) explicit formula —
To get the most use out of Perron-type formulae, we have to extend Dirichlet series such as the Riemann zeta function meromorphically into the critical strip . Not every Dirichlet series with coefficients
obeying (7) has such a meromorphic extension; roughly speaking, the existence of such an extension is morally equivalent to having asymptotic formulae for sums such as
or
whose error term is better than what one can obtain just from (7).
To extend the zeta function into the critical strip, we will use (12), which gives the bound
whenever and
for some
,
with
. (The error term is a bit crude, particularly when
has large imaginary part; we will obtain better estimates in later notes.) From Lemma 5 of Notes 1, this implies that we can find a (unique) complex number
such that
for all and
for some
and
with
. For
, this definition of
agrees with the prior definition of the Riemann zeta function in this range; it also is consistent with the quantity
defined for
in Section 1 of Notes 1.
From (21) we also observe the conjugation symmetry
for any in
. (Indeed, from the unique continuation property for meromorphic functions, this property is automatic for any meromorphic function on a connected domain symmetric around the real axis, which is real on the real axis.)
Observe that the function has a removable singularity at
(it approaches
at that value of
). From (21), we see that on the region
, the function
is the locally uniform limit of the functions
, which are holomorphic on this region once the removable singularity at
is removed. We conclude that
is holomorphic in this region (after removing the singularity at
), and hence
is meromorphic in this region, with a simple pole at
and no other poles. In particular, we have the Laurent expansion
for any natural number and all
sufficiently close to
, where
are complex coefficients. Differentiating, we also see that
for any natural number and all
sufficiently close to
, where
are further complex coefficients. This refines the bound (13).
Exercise 13 Show that
and
, where
is Euler’s constant. (This appearance of
in analytic number theory is largely unrelated to the appearance of
type factors in Notes 1.)
Exercise 14 Prove the following generalisation of Proposition 9: if
is a continuously
-times differentiable compactly supported function for some
, then for
, one has
for some complex coefficients
depending on
. (Hint: repeat the proof of Proposition 9, but use (23) in place of (13).)
Remark 15 Note that the error term in the above exercise improves as
gets smoother, and in fact becomes significantly better than the type of error terms appearing in the elementary approach when
is smooth enough (a special case of the “smoothed sums” philosophy in analysis). Thus we see a contrast between the elementary and complex-analytic methods; the latter approach can provide superior error terms, but also has a preference for smoother sums than the roughly truncated sums that are the main focus of the elementary methods.
From (21) with , we also have the crude bound
in the region . While this is quite a crude bound, it implies a decent upper bound on the log-magnitude of
, namely that
whenever and
. This, combined with Jensen’s formula, gives a useful upper bound on the density of zeroes of
:
Proposition 16 (Crude upper bound on zeta zeroes) For any
and
, there are at most
zeroes of
(counting multiplicity) in the region
.
Proof: We may assume that (say), since for
the claim follows from the discrete nature of the zeroes of a meromorphic function. We may also take
small, say
.
Consider the disk of radius centred at
for some
. By (11), we have
at the centre
of the circle, while from (25) one has
on the boundary of the circle. By Jensen’s formula (Theorem 16 from previous notes), this implies that there are at most
zeroes in the disk of radius
(say) centred at
. Since the region
can be covered by
such disks, the claim follows.
Remark 17 It will be convenient in the following discussion to adopt the convention that all sums over zeroes of
(or of other
-functions) are counted with multiplicity; thus for instance a double zero would contribute twice to such a sum. Indeed, one can think of a zero of order
as being a limiting case of
simple zeroes that are extremely close together (cf. Rouché’s theorem or Hurwitz’s theorem in complex analysis), which helps explain why such zeroes are always counted with multiplicity. It is conjectured that the zeroes of the Riemann zeta function (or of any
-function) are all simple, but this claim looks hopeless to prove using current methods; the problem is that it is nearly impossible for analytic methods to distinguish between a repeated zero, and a pair of simple zeroes that are extremely close together, and we currently do not have good methods to exclude the latter from occurring at least once.
Remark 18 As a corollary of Proposition 16, we see that the number of zeroes of
in the region
is
for any
. Once we establish the functional equation for
, we will be able to match this upper bound with a comparable lower bound, and also set
to zero; see Supplement 3.
This gives an approximate formula for the log-derivative of zeta in terms of the nearby zeroes:
Proposition 19 (Approximate formula for log-derivative of zeta) For any
, we have
whenever
and
.
This proposition should be viewed as a local version of the heuristic (4).
Proof: To eliminate the pole at , it is convenient to work with the modified function
, which is holomorphic in
after removing the singularity at
, and our task is now to show that
whenever and
.
As in the previous proposition, consider the disk of radius centred at
. From (11) we have
in the centre of this disk, and from (25) one has
on the boundary of the disk. The claim now follows from Theorem 21 of Supplement 2 (using Proposition 16 to remove the contribution of zeroes further than
from
).
Among other things, this proposition gives good control on the size of the log-derivative on average, which will be useful in figuring out how to shift a contour without encountering the large values of too often:
Corollary 20 (Local integrability of log-derivative) For any
and
, we have
Proof: We apply Proposition 19. The contribution of the error term is clearly acceptable. Because
is a locally integrable function on the complex plane, we see that the
term contributes a factor of
to the required integral, and every zero within
of
also contributes
. The claim now follows from Proposition 16.
Now we can apply the truncated Perron’s formula with contour shifting to obtain a truncated explicit formula for the von Mangoldt summatory function:
Theorem 21 (Truncated von Mangoldt explicit formula) For any
and
, we have
The error terms here can be improved a little, particularly once one uses the functional equation for ; see Supplement 3. However, the current form of the formula already suffices for many applications. This theorem should be compared with (2).
Proof: From Corollary 20 and the pigeonhole principle, we may find such that
for either choice of sign (note that this implies that the horizontal lines
avoid all the poles of
). (One could use (22) here to eliminate the need to consider a sign
, but it is not necessary to do so here.) On the other hand, from Proposition 12 we have
Observe that on the half-space , the meromorphic function
has a pole at
with residue
, and poles at every zero
of
with residue
(multiplied by the multiplicity of the zero), with no other poles. By the residue theorem (Exercise 13 of Supplement 2) applied to the boundary of the rectangle
for some
to be chosen shortly, with
avoiding the poles of
, and using (26) to bound the upper and lower limits of integration, we thus have
Now, from Corollary 20, and integrating from
to
, we have
where . Thus by the pigeonhole principle we may find
where
where , and so the contour integral in (27) is
. Using Proposition 16, the contribution to
of those zeroes
with
is
, and of those zeroes
with
is
. The claim follows.
Exercise 22 (Smoothed explicit formula) Let
be a smooth, compactly supported function. Then for any
and
, show that
with the sum on the right-hand side being absolutely convergent. (Hint: use Proposition 7 and contour shifting.) This exercise should be compared with (2).
Theorem 21 allows one to use zero-free regions of the Riemann zeta function to improve the error term in the prime number theorem:
Corollary 23 (Zero-free region controls von Mangoldt summatory function) Let
and
, and suppose that there are no zeroes
of
in the rectangle
. Then one has
for all
.
Proof: Apply Theorem 21 with . (As
is bounded away from zero, the implied constant is uniformly bounded in
.)
In fact, we have a fairly tight relationship between zero-free regions and error terms. Here is one example of this:
Proposition 24 Let
. Then the following assertions are equivalent:
- (i) One has
as
.
- (ii) One has
for all
.
- (iii) All the zeroes
of
have real part at most
.
Proof: Clearly (ii) implies (i). If (iii) holds, then by applying Corollary 23 with , we obtain (ii).
Finally, suppose that (i) holds. For , we see from Fubini’s theorem that
and thus
By (i) and Morera’s theorem, the integral on the right-hand side extends holomorphically to the region , and so by unique continuation
cannot have any poles in this region other than at
. This implies (iii).
Remark 25 Proposition 24 illustrates a remarkable “self-improving” property of estimates on the von Mangoldt summatory function: a weak bound of the form
, if true in the asymptotic limit
, automatically implies the stronger bound
for any given
(and in fact the implied constant in the conclusion depends only on
, and not on the decay rate in the hypothesis). This is due to the special structure of this summatory function
, as revealed by the explicit formula, which limits the range of possible asymptotic behaviours of this function, and in particular gives some control on a given value of this function at some choice of
in terms of its values at much larger choices of
. (Compare with the following easy example of a self-improving property: if
is a natural number and
is a polynomial with
as
, then
for all
.)
Exercise 26 Give an alternate proof that (i) implies (iii) in Proposition 24 that uses Theorem 21 (with
set to a large power of
), as well as an inspection of the asymptotics of the expression
as
, where
is a zero of
and
is a smooth compactly supported bump function. (The point is that expression isolates the effect of the single zero
in the von Mangoldt explicit formula.) Give a similar derivation that uses Exercise 22 instead of Theorem 21.
Exercise 27 (Truncated Landau explicit formula) Let
and
, and let
for some
be such that
is not a zero or pole of
. Show that
Unfortunately, none of the statements in Proposition 24 are known to hold for any positive . The infamous Riemann hypothesis asserts that the statements in Proposition 24 hold for
as large as
:
Conjecture 28 (Riemann hypothesis) All the zeroes of
have real part at most
.
Remark 29 This is not quite the traditional formulation of the Riemann hypothesis, which asserts instead that all the zeroes of
on the critical strip lie on the critical line
. However, the two formulations are logically equivalent, once one possesses the functional equation; see Supplement 3.
From the above proposition, we see that the Riemann hypothesis is equivalent to the quite strong estimate
on the von Mangoldt summatory function for all . This already gives a “near miss” to Legendre’s conjecture that there exists a prime between
and
for any
:
Exercise 30 (Conditional near-miss to Legendre’s conjecture) Assume the Riemann hypothesis. Show that there exists a constant
such that there exists a prime between
and
for any
.
We remark that Cramér reduced the term here to a
, however no further improvement is known if one “only” assumes the Riemann hypothesis. (But one can shave the
further to
if one additionally assumes a form of the Montgomery pair correlation conjecture, a result of Goldston and Heath-Brown.) In Notes 6 we will discuss some weaker near-misses to Legendre’s conjecture that are not conditional on unproven statements such as the Riemann hypothesis, by replacing the notion of zero-free region with the weaker, but somewhat comparable in power, notion of a zero-density theorem.
There is a limiting case of Proposition 24, due to Wiener:
Proposition 31 (Equivalent forms of prime number theorem) The following assertions are equivalent:
- (i) One has
as
.
- (ii) All the zeroes
of
have real part strictly less than one.
Proof: First suppose that (ii) fails but (i) holds, so has a zero at
for some non-zero
. Then
has a simple pole at
with residue at most
, and so
as , or in other words
However, from Fubini’s theorem we have
Applying (i), we soon conclude that
as , giving the required contradiction.
Now suppose that (ii) holds. We apply Exercise 22 with (say) to obtain
as , for any smooth compactly supported
independent of
. By (ii), each individual term
is
. Since the zeroes are discrete, we thus have
for any independent of
. To control the remaining portion of the sum, we crudely bound
and
(using Exercise 28 of Supplement 2) and use Proposition 16 to conclude that
and thus on sending to infinity and expanding out
,
Letting be an upper or lower approximant to
, we conclude that
and (i) follows by a telescoping argument.
Some of the above discussion involving the von Mangoldt function has an analogue involving the Möbius function, although it is more difficult to use the residue theorem to obtain a useful explicit formula because the residues of
are significantly less well understood than that of
. Nevertheless, one can still use other complex analytic tools, such as Taylor expansion, to get some weaker statements. We give some examples of this in the exercises below.
Exercise 32 Suppose that the conclusions of Proposition 24 hold for some
.
- (i) For any
, show the bounds
if
with
and
. If
(say), improve this to
- (ii) Show that there is a branch
of the logarithm of
that is holomorphic in the region
, and obeying the bounds
and
for all
,
and
, where
denotes the
-fold derivative of
. (Hint: use the generalised Cauchy integral formulae, see Exercise 9 of Supplement 2. Note that one may have to control the imaginary part of
in addition to the real part.)
- (iii) Show that for any
, we have
if
with
and
sufficiently large depending on
. (Hint: Taylor expand
around
using the bounds from (ii), possibly with a different choice of
.)
Exercise 33 Let
. Show that the conclusions (i)-(iii) of Proposition 24 are equivalent to the assertion
- (iv)
as
.
(Hint: apply the truncated Perron formula to
and shift the contour, using the preceding exercise to control error terms.) In particular, we see that the Riemann hypothesis is equivalent to the assertion that
as
.
Exercise 34 Show that the Riemann hypothesis implies the Lindelöf hypothesis that
as
.
Exercise 35 Let
be a natural number, and let
be a multiplicative function obeying the bounds
for all primes
, and such that
for all primes
and
.
- (i) Show that
has a meromorphic continuation to the half-space
, which has a pole of at most order
at
but no other poles. (Hint: use Euler products to factor
as the product of
and a function holomorphic in this half-space.) Also show that
when
with
and
.
- (ii) Show that
for all
and some
depending only
, where
is a polynomial with leading term
, where the singular series
was defined in Theorem 27 of Notes 1. (Hint: modify Proposition 12 to deal with the fact that
is only bounded by
rather than by
, apply it with
a small power of
, then shift the contour.) Note that this refines Theorem 27(iii) from Notes 1, and also generalises Exercise 32 from those notes.
— 3. The prime number theorem —
We are now finally ready to prove the prime number theorem (3), first established by Hadamard and de la Vallée Poussin. In view of Proposition 31, the task comes down to excluding the possibility that a zero
occurs on the line for some
. Note that
cannot be zero, as
has a pole at
.
The basic point here is that such a zero implies a “conspiracy” between the von Mangoldt function and the multiplicative function
, in that the two functions correlate or “pretend” to be like each other in a certain sense. Indeed, if
has a zero of some positive order
at
, then the log-derivative
has a simple pole with residue
at
, so in particular
for sufficiently close to
. We rewrite this as
On the other hand, from (13) (and (11), when is large) one has
and sending , we already obtain a contradiction if
; thus we have shown that there are no zeroes of multiplicity two or higher on the line
. In the case of a simple zero
, we have not yet obtained a contradiction; but observe that in this case, the triangle inequality (30) is close to being attained with equality. Intuitively, this implies that
on most of the support of
, that is to say that
for “most” primes
. To make this precise, we add (28) to (29) and then take real parts to conclude that
as . In probabilistic terms, if one selects a natural number
at random using the probability density
, divided by the quantity
to normalise the total probability to be one, then the random variable
converges in
to zero. (Note that we are implicitly using the non-negative nature of
in order to access this probabilistic interpretation.)
Following Hadamard, we exploit the following basic observation: if , then
. To use this observation quantitatively, it is convenient (following Mertens, who simplified the original argument of Hadamard) to exploit the trigonometric inequality
for any (which follows from the identity
), which implies that
Inserting this inequality into (31), we conclude that
and hence by (29)
This implies that has a pole at
with residue
, and so
must have a simple pole at
. But the only pole of
is at
, and
is non-zero, giving a contradiction. Thus there are no zeroes of
on the line
, and the prime number theorem follows thanks to Proposition 31.
The key inequality (32) is often written as , or
. In particular, we have
which on multiplying with and summing gives the useful inequality
for any and
. Integrating this in
from
(noting that
as
for any fixed
) gives the variant
(One can also obtain this inequality directly from (34) by multiplying by , summing, then exponentiating; we leave the details to the interested reader.) This variant gives a slightly different way to interpret the above proof of the prime number theorem:
has a simple pole at
, and no pole at
, so from (36) the maximum order of zero it can have at
is
. But the order must be an integer, and so one cannot have a zero of any positive order.
Exercise 36 Use the Selberg symmetry formula (equation (67) from Notes 1) to obtain the asymptotics
and
and
as
, for any fixed
. By using the bound
, conclude that
and use this to give an alternate proof of the prime number theorem. (This argument is related, though not completely identical, to the Erdös-Selberg elementary proof of the prime number theorem, which we will not give here.)
Remark 37 Another heuristic way to see the lack of zeroes on the line
is to return to the explicit formula (1). If there was a zero at
, there would also be a zero at
thanks to the conjugation symmetry (22), and hence
In particular,
should behave like
or less on the average in the region where
(which would imply that other powers
are also comparable to
if
is an integer multiple of
, or else oscillate “orthogonally” to
). But
is non-negative, which heuristically suggests a contradiction. One can interpret the arguments based on (34) above as a rigorous implementation of this heuristic argument.
We have now established that the Riemann zeta function has no zeroes on the line . Since the zeroes of
are discrete, this implies a qualitative zero-free region to the left of this line, in the sense that there is an open neighbourhood of this line that is free of zeroes of
. However, for applications (such as Corollary 23), we need a more quantitative zero-free region. To do this, we return to the bound in Proposition 19 as a quantitative substitute for the bound (28). We specialise to the case where
with
and
, and set
(say). In this case, the
term is
, and we conclude that
Observe that as all the zeroes have real part at most
, the quantity
has non-negative real part. Thus we have
whenever and
. If there is a zero
of
with the same imaginary part as
, with
, then we have the improvement
(note that the term is only of size
and thus negligible if
). This now gives
Proposition 38 (Classical zero-free region) There exists an absolute constant
such that there are no zeroes of
in the region
Proof: Let be a small constant to be chosen later. Suppose for contradiction that one has
for some and
. As
has a simple pole at
, there are no zeroes in a neighbourhood of
, and so one has
if
is small enough. For any
, we conclude from (39) that
while from (38) one has
and from (13) one has
Inserting these bounds into (35), we conclude that
for any . Setting
for a sufficiently large absolute constant
(actually
suffices), we still have
if
is small enough, and the left-hand side is equal to
For large enough,
is negative, we contradict the hypothesis
if
is small enough.
We can insert this zero-free region into Corollary 23, optimising the choice of parameters, to obtain a quantitative form of the prime number theorem, first obtained by de Vallée Poussin:
Corollary 39 (Prime number theorem with classical error term) We have
for all
and some absolute constant
. In particular, one has
for any
and
.
Proof: Apply Corollary 23 with and
for some small absolute constant
; this choice of parameters is designed to roughly balance the size of two error terms in that corollary, which is usually a near-optimal way to choose parameters. The required zero-free region follows from Proposition 38 if
is small enough, and the claim then follows (noting that logarithmic factors
can be absorbed into the decay factors
by shrinking
slightly).
Exercise 40 (Alternate form of prime number theorem) Show that for any
, the number
of primes less than or equal to
obeys the estimate
for some absolute constant
, where the logarithmic integral
is defined by the formula
Conclude in particular that
for all
; in particular, the simple form
of the prime number theorem is not particularly accurate, and one should use the refined version
instead (or better yet, work with the von Mangoldt function).
Exercise 41 (Prime number theorem for Möbius) Show that there is an absolute constant
such that one has the bounds
and
whenever
and
. Conclude the alternate form
of the prime number theorem with classical error term for all
and some
.
Exercise 42 (Landau-Beurling prime number theorem) Let
be a set of real numbers, which we refer to as Beurling primes. Define a Beurling integer to be a real number of the form
for some
and
; note that due to potential collisions between different products of Beurling primes, it is possible for a real number to be a Beurling integer in multiple ways. Let
and
denote the sets of Beurling primes and Beurling integers respectively. If we have the asymptotic bound
for all
and some absolute constant
, establish the Landau-Beurling prime number theorem
for all
and some absolute constant
; this generalises Exercise 40. (Hint: form the Beurling zeta function
and show that it has a meromorphic continuation to the region
, and obeys the bounds
for
,
, and
. Then repeat the proof of the prime number theorem, all the way down to Exercise 40.) This result is essentially due to Landau; Beurling was able to obtain a variant in which the hypothesis (40) and conclusion (41) were both weakened. On the other hand, it was shown by Diamond, Montgomery, and Vorhauer that without any further axioms on Beurling integers beyond (40), it is not possible to improve upon the estimate (41) (other than by sharpening the constant
). Thus, to go beyond the prime number theorem with classical error term, one needs to know more about the natural numbers than just that they are roughly uniformly distributed on the positive real axis in the sense of (40).
In Notes 5, we will obtain better upper bounds on in the critical strip (and particularly near the line
) that improve upon (24). This will allow us to obtain variants of Proposition 19 near the line
in which the error term
is replaced with a smaller quantity. The argument based on (35) will then allow us to enlarge the classical zero-free region in Proposition 38, which in turn leads to an improved error term in the prime number theorem. The asymptotically strongest such result is due to Vinogradov and Korobov, who use new upper bounds on
to obtain a zero-free region of the form
for some , which leads to the prime number theorem
for some and all
; see the exercise below. This still falls short of the claims in Proposition 24 for any fixed
, however it is important for some applications (e.g. finding primes in short intervals) to get some improvement over the classical zero-free region in Proposition 38.
Exercise 43
- (i) Establish the upper bound
whenever
and
for an absolute constant
. (Hint: apply (21) for a suitable choice of
.)
- (ii) Assume that the upper bound (44) in fact holds in the larger region where
and
for some absolute constant
. (This bound, essentially due to Vinogradov and Korobov, will be rigorously established in Notes 5.) Conclude the variant
of (37), whenever
with
and
, and
is an absolute constant.
- (iii) With the assumption in (ii), establish a zero-free region of the form (42).
- (iv) Assuming a zero-free region of the form (42), deduce (43).
- (v) What happens if one starts only with the bound in (i), rather than in (ii)?
— 4. Dirichlet -functions, Siegel’s theorem, and the prime number theorem in arithmetic progressions —
We now extend the above theory of the Riemann zeta function to Dirichlet -functions
, where
is a Dirichlet character of some period
. As already remarked in Remark 1, the theory of such functions is very similar to that of the zeta function, with the character
being like a “non-Archimedean” counterpart of the “Archimedean” character
. However, there is one key new feature, which is that the behaviour near
is not completely understood when
is a real character.
For , the Dirichlet
-functions are defined as
, thus
By the general theory of Dirichlet series, this is an analytic function on the half-space . Since
and
, we then have
and
where the derivative is always understood to be with respect to the variable. In particular, we have the analogue of (11):
whenever with
and
. In particular,
has no zeroes in the region
.
We also have the Euler product
If is a principal character, thus
, then we may compare this Euler product with the corresponding Euler product
of the Riemann zeta function, and conclude that
The product extends analytically to the entire complex plane, and has no zeroes in the region
, so this
-function has a meromorphic extension to
with exactly the same zeroes and poles as
.
The more interesting situation occurs when is non-principal. In particular, it has mean zero on every interval of length
. This gives a bound on slowly varying sums of
(cf. Lemma 71 of Notes 1):
Exercise 44 Let
be a non-principal Dirichlet character of period
, let
, and let
be a continuously differentiable function. Show that
If
is principal, show instead that
Using this exercise, we see that
whenever with
. By Lemma 5 of Notes 1, we conclude that for any such
, there is a unique complex number
such that
for any . In particular, the partial sums
converge locally uniformly to
on the half-space
, and so
is holomorphic on this region. This is similar to
, but with the key difference that there is no longer any pole at
.
Setting in (48), we obtain the crude bound
when with
. Taking logarithms, we have
One can then repeat much of the arguments in Section 2 with few changes (other than replacing logarithmic factors such as with
instead, and removing the effect of a pole at
):
Exercise 45 Let
be a non-principal character of period
.
- (i) (Crude upper bound on
-function zeroes) For any
and
, show there are at most
zeroes of
in the region
. (As with
, zeroes of
are always understood here to be counted with multiplicity.)
- (ii) (Approximate formula for log-derivative of
-function) For any
, show that
whenever
and
. Here and in the rest of this exercise, the sum is over the zeroes
of
.
- (iii) (Local integrability of log-derivative) For any
and
, show that
- (iv) (Truncated twisted von Mangoldt explicit formula) For any
and
, show that
(Compare with (5).)
- (v) (Smoothed twisted explicit formula) Let
be a smooth, compactly supported function. Then for any
and
, show that
with the sum on the right-hand side being absolutely convergent. (Again, compare with (5).)
- (vi) (Zero-free region controls twisted von Mangoldt summatory function) Let
and
, and suppose that there are no zeroes
of
in the rectangle
. Then show that
for all
.
Exercise 46 Let
be a non-principal character of period
, and et
. Show that the following assertions are equivalent:
- (i) One has
as
.
- (ii) One has
for all
.
- (iii) All the zeroes
of
have real part at most
.
Based on this exercise, it is now natural to generalise the Riemann hypothesis:
Conjecture 47 (Generalised Riemann hypothesis) Let
be a Dirichlet character. Then all the zeroes of
have real part at most
.
Given that the Riemann hypothesis (RH) remains unsolved, the stronger assertion of the generalised Riemann hypothesis (GRH) is also unsolved. (But later on we will establish the Bombieri-Vinogradov theorem, of major importance in sieve theory, which can be viewed as a kind of assertion that the generalised Riemann hypothesis holds “on average” in a certain technical sense.
Exercise 48 Assume the Generalised Riemann hypothesis. Show that
for all primitive congruence classes
and all
.
Exercise 49 (Equivalent forms of twisted prime number theorem) Let
be a non-principal Dirichlet character. Show that the following assertions are equivalent:
- (i) One has
as
.
- (ii) All the zeroes
of
have real part strictly less than one.
This exercise should be compared with the derivation of Dirichlet’s theorem (Theorem 70 from Notes 1) from the non-vanishing of
(Theorem 73 from Notes 1).
Now we obtain zero-free regions for for a Dirichlet character
of period
. From the Mertens trigonometric inequality (32) we have
where is the principal character of period
; equivalently, we have
Multiplying by for some
and summing, we obtain a twisted version of (35),
for any and
. Integrating this in
from
gives a twisted version of (36):
We can now strengthen Dirichlet’s theorem (Theorem 65 from Notes 1):
Exercise 50 (Prime number theorem in arithmetic progressions)
- (i) For any Dirichlet character
, show that
has no zeroes on the line
. (You will need Theorem 73 from Notes 1 to deal with the
case.)
- (ii) For any primitive residue class
, show that
as
(keeping
and
fixed). (The decay rate in the
notation may depend on
and
.)
- (iii) For any primitive residue class
, show that the number of primes in
less than
is
as
(keeping
and
fixed).
Next, we obtain the analogue of the classical zero-free region (Proposition 38), though with an important exception due to the lack of control near :
Proposition 51 (Classical zero-free region for
-functions) There exists an absolute constant
such that, for any Dirichlet character
of period
, there are no zeroes of
in the region
with the possible exception of a single real zero
(which we refer to as an exceptional zero or Siegel zero). The exceptional zero can only occur if
is a non-principal real character.
Proof: We may assume that is non-principal, since otherwise the claim follows from Proposition 38. In particular,
.
Let be a small constant to be chosen later, and let
be sufficiently small depending on
.
First suppose that is a complex character, so that
is non-principal. Suppose first that we have
for some
and
. From Exercise 45(ii) and taking real parts, we have
for any . Similarly, because
is non-principal, we have
while from (45) we have
Applying (51), we conclude that
Setting for (say)
, we obtain a contradiction with
small enough. This completes the proof of the proposition when
is complex.
Now suppose that is a real character, so that
. We can adapt the previous argument, but need a new tool to estimate
. By (46) we have
We crudely bound
and then apply Proposition 19 and take real parts to conclude that
Applying (51) as before, we conclude that
As before, we set and conclude that
If , then
(say) if
is small enough, leading again to a contradiction. Thus the only remaining case is when
is real and
.
We now show that there is at most one zero of in the region
. If there are two such zeroes
, then from Exercise 45(ii) and taking real parts we have
comparing this with (45), we conclude that
If we set (say), we obtain a contradiction if
is small enough.
As is real, we have the conjugation symmetry
and so if is a zero of
, then
is one also. Thus there can be no strictly complex zeroes in the region
, and at most one real zero; and the claim follows. (From Theorem 73 from Notes 1,
cannot equal
, and from (45) there are no zeroes to the right of
.)
The exceptional zero in the above theorem is quite a nuisance; if one believes in the generalised Riemann hypothesis, it should not exist, but frustratingly, we have not been able to completely exclude this zero from occurring. However, there is an important repulsion phenomenon (known as the Deuring-Heilbronn repulsion phenomenon), that asserts (roughly speaking) that the existence of one exceptional zero tends to repel away other exceptional zeroes. We already saw one instance of this phenomenon when proving Proposition 51, when we showed that a single character
could not have two or more exceptional zeroes. Another instance appeared in Proposition 76 of Notes 1.
To state the repulsion phenomenon more precisely, we have to exclude a degenerate case, coming from the fact that if one multiplies a Dirichlet character (of some modulus
) by a principal character
(of some modulus
), then the resulting Dirichlet character
(which has modulus
) has essentially the same
-function as
, as
and
differ by a finite number of Euler factors (as in (46)), and so the two
-functions have an identical set of zeroes in the region
. To avoid this problem, let us call a Dirichlet character
of modulus
primitive if it cannot be factored as
, where
is a principal character and
is a character of modulus strictly less than
.
- (i) Show that every Dirichlet character
of modulus
can be factored as
, where
is a primitive character of some modulus
(known as the conductor of
) and
is a principal character whose modulus
is squarefree and coprime to
. Furthermore,
divides
, and
is real if and only if
is real; and even if one drops the requirements that
is squarefree and coprime to
then
is still uniquely determined by
. Thus we see that to understand the zeroes of Dirichlet
-functions
, it suffices to do so for the primitive characters.
- (ii) Let
be primitive Dirichlet characters. Show that
is a principal character if and only if
.
Here is one standard manifestation of the repulsion phenomenon:
Theorem 53 (Landau’s theorem) There is an absolute constant
with the following property: whenever
are two distinct real primitive characters of conductor
respectively, there is at most one real zero
of
or
with
.
Proof: Let be sufficiently small. If the claim failed, then (since each
-function has at most one exceptional zero) we can find
such that
.
In previous arguments, one used the inequality (50). Here, we will instead use the inequality
which we expand as
Multiplying by for some
and summing, we conclude that
(We do not need to take real parts here, as everything in sight is already real.) From (13) we have
and from Exercise 45(ii) we have
and
By Exercise 52(ii), is a non-principal character of modulus at most
, and so from Exercise 45(ii) again we have
Putting all this together, we see that
Setting , we obtain a contradiction if
is small enough.
This gives a variant of Proposition 51, in which the zero-free region is reduced slightly, but there is only one primitive character that has an exceptional zero:
Exercise 54 (Page’s theorem) Let
. Show that for each primitive character
of conductor at most
, the
-function
has a zero-free region of the form
for some absolute constant
, with the possible exception of a single real zero
by a single primitive real character
of modulus at most
.
We will refer to Landau’s theorem and Page’s theorem collectively as the Landau-Page theorem.
Exercise 55 (Prime number theorem in arithmetic progressions with classical error term) Let
be a sufficiently small quantity, and let
be a natural number.
- (i) If
is the principal Dirichlet character modulo
, show that
if
and
.
- (ii) If
is a non-principal Dirichlet character modulo
, show that
if
,
and
has an exceptional zero
(which, for this current exercise, means a zero of
with
). If
has no exceptional zero, then the
term should be deleted; this is for instance the case when
is complex.
- (iii) If
is a primitive residue class modulo
, show that
if
,
, where
is a real non-principal character of modulus
with an exceptional zero
. (Note from Page’s theorem that there is at most one such character for a given
, if
is small enough.) This character
will be called the exceptional character. If there is no exceptional character, the term
should be deleted.
(Note: the constant
may need to be smaller in (iii) than it needs to be for (i) or (ii).)
Remark 56 Informally, the prime number theorem in arithmetic progressions asserts that the primes
are equidistributed in the primitive residue classes modulo
for
, unless there is an exceptional character
with exceptional zero
, in which case the primes
are more or less equidistributed in the primitive residue classes
with
if
, and then become equidistributed in all the primitive residue classes modulo
for
.
The Landau-Page theorem is good at eliminating exceptional zeroes in a power range such as for any fixed
, as it prevents more than a single primitive real character
of conductor
in this range having an exceptional zero
with
for an absolute constant
. However, it loses control of exceptional zeroes in wider ranges than this. For instance, the Landau-Page theorem does not prevent the existence of an infinite sequence of exceptional real primitive characters
whose conductor
grows very rapidly in
(e.g.
), and with each
having an exceptional zero
that converges very quickly to
, e.g.
.
Fortunately we have another way to exploit the repulsion phenomenon even for characters of widely separated modulus. To develop this aspect of the repulsion phenomenon, we first need to establish a link between exceptional zeroes, and exceptionally small values of . We first give one direction of this link:
Lemma 57 (Exceptional zero implies small
) Suppose that
is a real non-principal character of modulus
whose
-function
has a real zero
with
. Then
.
Proof: From (48) with and
we have
for . From the generalised Cauchy integral formula (Exercise 9 of Supplement 2), we thus have
for . Since
, the claim now follows from the fundamental theorem of calculus.
To go in the opposite direction, we will borrow a trick from the proof of the non-vanishing of (Theorem 73 from Notes 1) and exploit the positivity
for various choices of and
. The key estimate is the following (compare with (21) or (48)):
Exercise 58 Let
be a real non-principal character of modulus
, and let
be a real number. Establish the bound
for any
. (Hint: use the Dirichlet hyperbola method and (21), (48), (24).) For an additional challenge, see if you can establish this estimate (possibly with a slightly weaker error term) by using the truncated Perron formula and contour shifting (bearing in mind that
is only bounded by
rather than by
).
Lemma 59 (Small
implies exceptional zero) Suppose that
is a real non-principal character of modulus
such that
for some sufficiently small absolute constant
. Then there is a real zero
of
with
.
Proof: Let for some large absolute constant
, and let
be sufficiently small depending on
, thus
(recall that
is positive), and so
if
is small enough. From (54) we have
for any and so from Exercise 58 we have
(say). Setting (say), we conclude that
if is large enough and
is small enough. By (24),
is negative. Thus,
, and so by the intermediate value theorem there must be a zero
of
between
and
, and the claim follows.
Now suppose we have two distinct real primitive characters of modulus
respectively, so that
is also a real non-principal character of modulus at most
. As in the proof of the Landau-Page theorem, we have the non-negativity
We will instead exploit the multiplicative version of this non-negativity:
The latter bound can be deduced from the former after using the formal identity
that comes from the identity
valid for all characters (cf. (28) from Notes 1); it can also be verified directly. In particular, we have
for any and
. Meanwhile, one has the following variant of Exercise 58:
Exercise 60 Let
be distinct real primitive characters of modulus
,
respectively, and let
for some sufficiently small absolute constant
. Establish the bound
for any
. (Hint: either use a higher-dimensional version of the Dirichlet hyperbola method, or the truncated Perron formula and contour shifting.)
This gives a repulsion phenomenon:
Proposition 61 (Repulsion phenomenon) Let
be a real primitive character of modulus
. Suppose that
for some
, where
is a sufficiently small absolute constant. Then one has
for all real primitive characters
distinct from
, with
denoting the modulus of
.
Proof: From Exercise 60 with and (55) (and shrinking
as needed) one has
for any . If we then set
for a sufficiently large absolute constant
, the error term is less than
, and so
From (53) one has , and from choice of
we have
with implied constants depending on
. The claim follows.
We can now give Siegel’s theorem on exceptional zeroes (or on exceptionally small values of ), which will be the first theorem in this set of notes to feature ineffective implied constants – constants which cannot be explicitly computed in terms of the given data, but are merely known to be finite and positive.
- (i) For any
, one has the bound
for all but at most one real primitive character
of conductor
, and some constant
.
- (ii) For any
, there are no zeroes of
in the interval
for all but at most one real primitive character
of conductor
, and some constant
.
In both (i) and (ii), the constant
is effective: it can be computed explicitly in terms of
. However, if one wishes to replace “all but at most one” with “all” in either (i) or (ii), one can do this at the cost of rendering
ineffective: this constant is still known to be positive, but we no longer know of a way to compute
explicitly in terms of
.
Remark 63 The observation that Siegel’s theorem may be made effective if one exceptional character is removed is due to Tatuzawa. Combined with the class number formula, this can be used to show that with at most one exception, all but an explicitly computable finite list of quadratic fields of negative discriminant do not have unique factorisation. Indeed, using related methods, Heilbronn and Linfott had previously showed that, apart from the nine discriminants
(which all give quadratic fields of unique factorisation), there is at most one further negative discriminant giving a quadratic field of unique factorisation. This elusive “tenth discriminant” was finally ruled out by Heegner by some difficult arguments, which have since been clarified by subsequent work of Stark and many further authors, giving what is now known as the Stark-Heegner theorem.
Proof: From Lemmas 57, 59 we see that (i) and (ii) are equivalent, so we will just prove (i). It suffices to prove the claim with one exceptional character deleted and with effective choices of
, since one can reinstate the exceptional character (at the cost of making
ineffective) just by using the positivity
for the exceptional character.
Let be a small (effective) constant, depending only on
, to be chosen later. We divide into two cases:
- There are no zeroes of
in the interval
for any real primitive character
with a conductor
.
- There exists a real primitive character
of some conductor
with a zero
in
.
In Case 1, Lemma 59 in the contrapositive gives for all real primitive characters
with a conductor
, giving the claim (after adjusting
slightly).
Now suppose we are in Case 2, so for some real primitive character
of conductor
and some
(recall that
is non-vanishing). We may take
to be minimal among all such characters. Note that while
is obviously finite, we do not have any effective bound on
, so we have to proceed a little carefully if one is to avoid the final implied constants from depending on
or
.
Let be a real primitive character of conductor
that is distinct from the exceptional character
. If
then by construction,
has no zeroes in
, and the required bound follows again from Lemma 59 in the contrapositive. Now suppose that
. From Proposition 61, we have
By Lemma 27, we have . Bounding
by
, we conclude that
and using the bound , we obtain the required estimate if
is small enough.
The best known effective lower bounds on for all real primitive characters
(not excluding an exceptional character) go through the class number formula (as briefly discussed in Supplement 1), and take the shape
for some explicit constant ; this corresponds to a zero-free region of
of size
for some effective constants
. The bound (56) is trivial for
since the class number is always at least one; it turns out that one can raise
to be arbitrarily close to
, but this is a difficult result (at least when
is associated to a quadratic field of negative discriminant), due to Goldfeld and Gross-Zagier; see this survey of Goldfeld for further discussion. It is of great interest to improve these effective bounds further, but this has not yet been achieved; despite the conjectural non-existence of Siegel zeroes, they seem to live in a stubbornly self-consistent (though somewhat strange) universe that has defied all efforts to eradicate them to date.
In summary, we can give the following bounds on exceptional zeroes of
-functions of real primitive characters
of conductor
:
- (i) (Class number methods) One has
for some effective
and
.
- (ii) (Siegel) For any
, one has
for some ineffective
.
- (iii) (Tatuzawa) For any
, one has
for some effective
, except possibly for a single exceptional character
.
- (iv) (Page) One has
for some effective
and all real primitive characters
of conductor at most
, except possibly for a single exceptional character
.
One also obtains analogous lower bounds on through Lemma 59, and lower bounds on class numbers (at least in the case of negative discriminant) using the class number formula.
All four of the bounds (i), (ii), (iii), (iv) have their advantages and disadvantages, and are all useful in various applications; the choice of which of (i)-(iv) to use depends on whether one has some argument to deal with a potential exceptional character, whether one can tolerate ineffective values of the implied constant, and whether one has a reasonable bound on the conductor of the characters one wishes to use.
A basic application of Siegel’s theorem is the Siegel-Walfisz theorem.
Exercise 64 (Siegel-Walfisz theorem) For any
, show that there exists an (ineffective) constant
such that
for all primitive residue classes
and all
with
(Hint: use Exercise 55(iii) together with Siegel’s theorem to handle the exceptional zero.) Conclude in particular that
for all primitive residue classes
and all
(without assuming the size restriction (57)), and with an ineffective constant in the
notation.
Of course, the error term in the Siegel-Walfisz theorem can be substantially improved if one assumes the generalised Riemann hypothesis: see Exercise 48. In Notes 3 we will use the Siegel-Walfisz theorem to prove the Bombieri-Vinogradov theorem, which is a theorem of basic importance in sieve theory.
Exercise 65 (Least prime in an arithmetic progression) If
is a primitive residue class, show that
contains a prime
with
, with the implied constants ineffective; by using (56), obtain the alternate bound
with effective constants, and obtain the improvement
with effective constants if there is no exceptional character of modulus
. In Notes 7 we will be able to improve all of these bounds to
with effective constants, a result known as Linnik’s theorem.
Exercise 66 (Siegel-Walfisz for the Möbius function) Show that for any
, one has the bound
for all residue classes
(not necessarily primitive) and all
, with an ineffective constant in the
notation. (Hint: reduce to the case in which
and
is primitive. One can either use a truncated Perron’s formula argument using some lower bounds on
for
slightly to the left of
, or else modify the elementary method from Theorem 58 of Notes 1, using an induction on
.)
Exercise 67 (Elementary lower bound for
) The purpose of this exercise is to give a somewhat reasonable effective lower bound on
by an elementary (but somewhat ad hoc) device. Let
be a real non-principal character of modulus
.
- (i) Establish the identity
for any
, where
is the function
, and the sum is in the conditionally convergent sense.
- (ii) Obtain the bounds
It is possible to use Fourier analysis to improve the upper bound on (58) to
, which almost recovers the bound
coming from the class number formula; but we will not do this here.
Exercise 68 Use (59) and Exercise 58 for a suitable choice of
to give an alternate proof of Lemma 57.

60 comments
Comments feed for this article
9 December, 2014 at 9:34 pm
Nicolas Templier
Dear Terry,
I enjoyed your very nice treatment of the Landau-Siegel zeros. There is an important famous result to be mentioned around the display (55) about the best known effective lower bounds on for all real primitive characters $\chi$:
for all real primitive characters $\chi$:
Briefly the combination of the works of Goldfeld and Gross-Zagier show unconditionally that (55) holds for any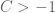 .
. is highly significant since it effectively solves the Gauss class number problem.
is highly significant since it effectively solves the Gauss class number problem.
Being able to pick a
An excellent short account appears in this Bulletin article.
The original article treats both real and imaginary quadratic fields and contains precise bounds with the exact dependence on the order of vanishing at 1/2 of the auxiliary elliptic curve L-function.
[Fair enough; I’ve reworded that portion of the text accordingly. -T.]
10 December, 2014 at 9:30 am
Anonymous
In the line above corollary 39, “la” is missing in “de la Vallee Poussin”.
[Corrected, thanks – T.]
11 December, 2014 at 3:29 am
Anonymous
In the line above (32), “identity” may be replaced by “inequality”.
[Corrected, thanks – T.]
11 December, 2014 at 9:06 am
Eytan Paldi
The derivation of (36) (via integration) from (35) is not sufficiently clear (in particular, the behavior of the LHS of (35) near – because of the essential singularity of
– because of the essential singularity of 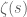 at
at  ).
).
BTW, in the wikipedia article on the PNT, (36) is derived directly (i.e. without integration) from the Euler product and the inequality (32).
[Oops, that should have been an integration in , not
, not  . Corrected and clarified, thanks – T.]
. Corrected and clarified, thanks – T.]
12 December, 2014 at 10:29 am
Kyle Pratt
Very nice set of notes. In parts (I) and (ii) of exercise 46, there should not be a main term, right?
[Corrected, thanks – T.]
13 December, 2014 at 3:20 pm
Anonymous
There may be a problem in the inequality after Exercise 5. As $\sigma$ is complex, the right-hand side $g(n)/n^\sigma$ can be negative ($n^\sigma$ can be real and negative). My apologies if I’m just confused.
That’s a fantastic set of notes.
[ is real (which is the convention in analytic number theory, and also implicitly enforced by the hypothesis
is real (which is the convention in analytic number theory, and also implicitly enforced by the hypothesis 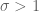 . -T.]
. -T.]
19 December, 2014 at 2:19 pm
Anthony Quas
v. interesting again. Under Exercise 2, I think the Dirichlet series of log should be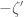 .
.
[Corrected, thanks – T.]
19 December, 2014 at 2:20 pm
Anthony Quas
In the first line of the proof of Proposition 9, the text refers to Equation (7) rather than Proposition 7 (where the hyperlink redirects).
[Corrected, thanks – T.]
19 December, 2014 at 2:21 pm
Anthony Quas
In Remark 10, the brackets failed to appear in the inline text around![[d_1,d_2]](https://s0.wp.com/latex.php?latex=%5Bd_1%2Cd_2%5D&bg=ffffff&fg=545454&s=0&c=20201002) (in my browser at least).
(in my browser at least).
[Corrected, thanks – T.]
19 December, 2014 at 2:26 pm
Anthony Quas
In my browser, the equation number on equation (23) doesn’t show up, which is slightly disconcerting because it is directly referred to.
[Corrected, thanks – T.]
19 December, 2014 at 9:27 pm
Anthony Quas
The first line of the proof of Theorem 21 refers to (20) when I think it should refer to Corollary 20.
21 December, 2014 at 11:36 pm
Anthony Quas
There’s also a reference to Corollary 20 (where the hyperlink points to the wrong place) after equation (27)
[Corrected, thanks – T.]
22 December, 2014 at 7:19 pm
anthonyquas
So I think these corrections have probably been made in the wrong direction! As far as I can tell, both places should refer to Corollary 20, not to equation (20).
[Corrected, thanks – T.]
29 January, 2015 at 11:33 am
254A, Supplement 5: The linear sieve and Chen’s theorem (optional) | What's new
[…] of . If , then , and then by the prime number theorem for the Liouville function (Exercise 41 from Notes 2, combined with Exercise 18 from Supplement 4) we […]
29 January, 2015 at 8:38 pm
Anonymous
I think the horizontals lines mentioned in the “(note…” after (26) should +/- T’ not +/- T
[Corrected, thanks – T.]
7 February, 2015 at 12:07 pm
254A, Notes 5: Bounding exponential sums and the zeta function | What's new
[…] of upper bounding the size of this function within the critical strip; as seen in Exercise 43 of Notes 2, such upper bounds can lead to zero-free regions for , which in turn lead to improved estimates for […]
9 February, 2015 at 8:28 am
Anonymous
In the first proof of the PNT, how does (29) imply the given asymptotic of the sum $latex\sum_{n}\frac{\Lambda(n)}{n^{\sigma}}n^{-2it}$?
[Sorry, there was a real part missing on the LHS, now added. -T.]
13 February, 2015 at 10:16 pm
254A, Notes 6: Large values of Dirichlet polynomials, zero density estimates, and primes in short intervals | What's new
[…] of the Riemann zeta function (counting multiplicity) with and . Recall from Proposition 16 of Notes 2 that there are at most zeroes in any rectangle of the form with . Combining this with the […]
22 February, 2015 at 9:02 am
254A, Notes 7: Linnik’s theorem on primes in arithmetic progressions | What's new
[…] from the Landau-Page theorem (Exercise 54 from Notes 2) that at most one exceptional zero exists (if is small enough). A key point here is that the error […]
24 February, 2015 at 11:28 am
254A, Supplement 6: A cheap version of the theorems of Halasz and Matomaki-Radziwill | What's new
[…] summatory function requires the prime number theorem, which is substantially harder to prove (see Notes 2). (From a complex-analytic or Fourier-analytic viewpoint, the problem is that the logarithmic sums […]
30 March, 2015 at 12:49 pm
254A, Notes 8: The Hardy-Littlewood circle method and Vinogradov’s theorem | What's new
[…] small (of size or so), this estimate will be a consequence of the Siegel-Walfisz theorem ( from Notes 2); it is the application of this theorem that is responsible for the ineffective constants. In the […]
13 April, 2015 at 7:32 am
Karaskas
Proposition 51: missing in the explicit formula for the zero-free region.
in the explicit formula for the zero-free region.
[Corrected, thanks – T.]
19 April, 2015 at 11:02 am
Anonymous
After equation (5), the Dirichlet character had better be no principal. Otherwise you would have the main term x.
[Corrected, thanks – T.]
19 April, 2015 at 11:26 am
Anonymous
Two paragraphs below equation (8), in the second summation in the first line, the n in the upper limit should be N.
[Corrected, thanks – T.]
19 April, 2015 at 2:13 pm
Anonymous
There is an extra period in equation (12).
[Corrected, thanks – T.]
29 April, 2015 at 1:34 pm
Fan
The reference to (13) before equation (29) should perhaps be to (11), as (13) is only valid near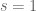 .
.
[Corrected, thanks – T.]
29 April, 2015 at 8:34 pm
Fan
In the proof of Proposition 51, in the paragraph dealing with and t large, in the last display, the inequality should be reversed and the RHS be its negative.
and t large, in the last display, the inequality should be reversed and the RHS be its negative.
[Corrected, thanks – T.]
30 April, 2015 at 12:38 pm
Anonymous
I’m confused about the paragraph after Remark 56: isn’t the sequence of characters still of the form
still of the form 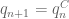 with C=100? Also, isn’t
with C=100? Also, isn’t 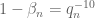 already ruled out by Landau page as
already ruled out by Landau page as  ?
?
[Corrected, thanks – T.]
26 May, 2015 at 9:50 am
254A, Supplement 4: Probabilistic models and heuristics for the primes (optional) | What's new
[…] now move away from the world of multiplicative prime number theory covered in Notes 1 and Notes 2, and enter the wider, and complementary, world of non-multiplicative prime number theory, in which […]
26 August, 2015 at 4:25 pm
Heath-Brown’s theorem on prime twins and Siegel zeroes | What's new
[…] use Siegel’s theorem to obtain the better bound . Standard arguments (see also Lemma 59 of this blog post) then […]
16 May, 2016 at 5:18 am
XiangYu
In the proof of proposition 9, should the second last formula be
![\displaystyle \int_{\mathbf{R}} [\frac{\zeta'(\sigma+it)}{\zeta(\sigma+it)}-\frac{1}{\sigma+it-1}]\hat{f}(t\log x-i)\, dt=O_f(\frac{1}{\log x})](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7B%5Cmathbf%7BR%7D%7D+%5B%5Cfrac%7B%5Czeta%27%28%5Csigma%2Bit%29%7D%7B%5Czeta%28%5Csigma%2Bit%29%7D-%5Cfrac%7B1%7D%7B%5Csigma%2Bit-1%7D%5D%5Chat%7Bf%7D%28t%5Clog+x-i%29%5C%2C+dt%3DO_f%28%5Cfrac%7B1%7D%7B%5Clog+x%7D%29&bg=ffffff&fg=545454&s=0&c=20201002)
[Corrected, thanks – T.]
23 May, 2016 at 10:31 pm
Xiang Yu
Dear Professor Tao
I have just finished reading this fantastic set of notes. There is something I cannot understand. My apologies if I am just confused.
+ Propostion 12: Do we need the assumption that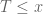 ?
?
+ Corollary 23: If we apply Theorem 21, it should be

 in the big O, is it because that we can make the implied constant uniformly bounded in
in the big O, is it because that we can make the implied constant uniformly bounded in  ?
?
But there is no
+ Propostion 31: In the last part of the proof, I think we should let be an upper or lower approximant to
be an upper or lower approximant to ![1_{[-\log 2,0]}](https://s0.wp.com/latex.php?latex=1_%7B%5B-%5Clog+2%2C0%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
+ In parenthesis after formula (35), it should be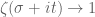 as
as  for any fixed
for any fixed  .
.
+ Theorem 53: There is a typo in the last sentence of proof, we obtain a contradiction if is small enough, not large enough.
is small enough, not large enough.
[Corrected, thanks – T.]
2 July, 2016 at 6:51 am
254A, Supplement 3: The Gamma function and the functional equation (optional) | What's new
[…] Notes 2, the Riemann zeta function (and more generally, the Dirichlet -functions ) were extended […]
28 February, 2017 at 1:17 am
Bernard Victorri
In exercise 42 (Beurling primes) the main term in equation 41 should be x/logx, if I am not mistaken ?
[Corrected, thanks – T.]
7 March, 2017 at 12:35 pm
Lattice Points in High-Dimensional Spheres | a. w. walker
[…] (Truncated Perron, Prop. 12): Suppose that the Dirichlet series given by satisfies for all . Choose . For we […]
8 April, 2017 at 9:57 pm
Claudeh5
Hello professor Tao,
I have a problem with this extract:
“… Thus the only remaining case is when {\chi} is real and {|t| 1 – \frac{c}{\log(q(2+|t|))} \}}. If there are two such zeroes …
The formula is incomplete …
[Corrected, thanks – T.]
9 November, 2017 at 11:49 am
Continuous approximations to arithmetic functions | What's new
[…] Dirichlet series, but we will not pursue these rigorous calculations here. (But see for instance this previous blog post for some […]
14 December, 2018 at 9:42 pm
Math student
Dear Prof. Tao,
the whole page seems to repeat itself (twice!).
[Fixed now – T.]
15 December, 2018 at 4:04 am
Anonymous
Concerning the remark after exercise 30, is there any sufficiently strong “probabilistically reasonable” conjecture on the (asymptotic) correlation of zeta zeros tuples (not only zero pairs) which is sufficiently strong (stronger than Montgomery pair correlation conjecture) to imply the current conjecture that the gap between any two consecutive primes below is
is  ?
?
15 December, 2018 at 11:18 am
Terence Tao
I don’t think there is a clean implication of this type. If one uses the explicit formula to try to work out whether there is a prime in the interval![[x, x + \log^2 x]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x+%2B+%5Clog%5E2+x%5D&bg=ffffff&fg=545454&s=0&c=20201002) , one will find that one needs to understand a highly oscillatory sum that involves all the zeroes up to height about
, one will find that one needs to understand a highly oscillatory sum that involves all the zeroes up to height about  (up to log factors); even assuming the Riemann hypothesis, one would need to understand the cancellation in this sum. One could simply posit that this sum always exhibits the expected amount of cancellation, but this is a rather artificial conjecture which is basically just Cramer’s conjecture expressed in terms of the zeroes, and would be largely orthogonal to the GUE hypothesis which only concerns the local behaviour of zeroes rather than global cancellations.
(up to log factors); even assuming the Riemann hypothesis, one would need to understand the cancellation in this sum. One could simply posit that this sum always exhibits the expected amount of cancellation, but this is a rather artificial conjecture which is basically just Cramer’s conjecture expressed in terms of the zeroes, and would be largely orthogonal to the GUE hypothesis which only concerns the local behaviour of zeroes rather than global cancellations.
4 September, 2019 at 1:46 pm
254A announcement: Analytic prime number theory | What's new
[…] Complex-analytic multiplicative number theory […]
16 October, 2019 at 5:32 am
Kevin Ford
Alternatively, Proposition 9 is valid for any bounded C^1 function on [0,1]. The proof is a couple of lines using partial summation and Mertens.
17 December, 2019 at 8:27 am
254A, Notes 10 – mean values of nonpretentious multiplicative functions | What's new
[…] it to for an absolute constant (the bound is more classical, following from Exercise 33 of Notes 2). On the other hand, the randomness heuristics from Supplement 4 suggest that should be able to be […]
24 January, 2021 at 2:47 pm
246B, Notes 2: Some connections with the Fourier transform | What's new
[…] (The Perron formula and its many variants are of great utility in analytic number theory; see these previous lecture notes for further […]
12 February, 2021 at 9:38 am
246B, Notes 4: The Riemann zeta function and the prime number theorem | What's new
[…] in this course. For some further discussion see this previous set of lecture notes, particularly Notes 2 and Supplement 3 (with much of the material in this post drawn from the […]
15 June, 2021 at 10:42 am
Webspinner
Dear Prof. Tao,
in proposition 24, one may take the term extremely rapidly decreasing, and then the implication (ii) => (i) becomes false. I would be very grateful if this could be corrected.
term extremely rapidly decreasing, and then the implication (ii) => (i) becomes false. I would be very grateful if this could be corrected.
15 June, 2021 at 1:46 pm
Webspinner
Or is this supposed to mean “there exists some ? It could be read either way. Please clarify!
? It could be read either way. Please clarify!
15 June, 2021 at 1:47 pm
Webspinner
Oh, and if you could mention that the can be replaced by “every
can be replaced by “every  “.
“.
16 June, 2021 at 5:24 am
Webspinner
Dear Prof. Tao,
if you refuse to make these changes, I’ll be forced to rely on a different reference.
16 June, 2021 at 11:09 am
Webspinner
There is a German saying that goes “sich keinen Zacken aus der Krone brechen”. You might want to look it up.
16 June, 2021 at 1:00 pm
Anonymous
Spin somewhere else.
16 June, 2021 at 1:10 pm
Webspinner
Dear Anonymous,
if Prof. Tao doesn’t want me to comment on his blog (which thus far, despite him ignoring my suggestions, has not transpired yet), I’ll respect that. However, I have a strong adversion against bullies trying to exclude me from a group or a conversation. Therefore, I have to strongly condemn your comment.
19 September, 2021 at 1:16 pm
James
Why does one assume in Proposition 12, i.e. why “2+” part? I assume it’s because
in Proposition 12, i.e. why “2+” part? I assume it’s because  would be annoying for
would be annoying for  , but wouldn’t that already be solved by
, but wouldn’t that already be solved by 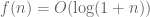 ?
?
27 September, 2021 at 9:23 am
Terence Tao
Yes, that would work also. Sometimes is slightly preferable to
is slightly preferable to  because, when extended to the non-negative real axis
because, when extended to the non-negative real axis  , it stays bounded away from zero all the way up to the endpoint
, it stays bounded away from zero all the way up to the endpoint  , whereas
, whereas  vanishes there, and one doesn’t want to give the impression that this vanishing is in any way relevant.
vanishes there, and one doesn’t want to give the impression that this vanishing is in any way relevant.
4 October, 2021 at 4:12 pm
James
I believe one can easily remove constant in Proposition 19. For example, if
in Proposition 19. For example, if  then
then
i.e.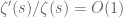 . On the other hand,
. On the other hand, 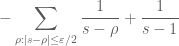 is obviously
is obviously  for
for  .
.
[This seems correct to me, though we rarely need to venture to the right of say in any analytic number theory application anyway, so the dependence on
in any analytic number theory application anyway, so the dependence on  is not terribly important in practice. -T]
is not terribly important in practice. -T]
3 March, 2022 at 9:48 pm
Quân Nguyễn
Dear professor Tao,
In Theorem 21, how can one apply the pigeonhole principle to negate the integral sign and obtain (26) ? The same issue at the end of theorem 21 where there exists \epsilon’ \in \[\epsilon/2 , \epsilon \]. For this approach to work, one condition that I think is that the integrated function should be non-negative. Can one use this approach when one has an improper integral?
4 March, 2022 at 8:27 am
Terence Tao
From Corollary 20, the integral of the left-hand side of (26) (which is non-negative) as ranges from
ranges from  to
to  is
is  , giving the claim from the pigeonhole principle.
, giving the claim from the pigeonhole principle.
4 March, 2022 at 9:14 pm
Quân Nguyễn
Thank you professor. May I have one more question? So in the truncated log-derivative formula (proposition 19, can one modify the factor 1/2 in to a more general domain like
to a more general domain like  with
with  ? I came up an attempt which results that this might be possible.
? I came up an attempt which results that this might be possible.
[Yes – T.]
16 November, 2023 at 5:54 pm
Anonymous
Dear prof. Tao, function based on the truncated log derivative formulation above? Since there can be a root
function based on the truncated log derivative formulation above? Since there can be a root 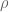 that is closed to
that is closed to  , how can one bound for such roots?
, how can one bound for such roots?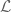 function. Then is
function. Then is  works for every modulus
works for every modulus  or is it dependent on
or is it dependent on  ? In some talks that you gave,
? In some talks that you gave,  is refer to as the “quality” so to speak, and the smaller the value of
is refer to as the “quality” so to speak, and the smaller the value of  the better the exceptional zero gets (in some certain sense). Would you like to give more details on this values and how does it improve certain results?
the better the exceptional zero gets (in some certain sense). Would you like to give more details on this values and how does it improve certain results?
How can one obtain an upper bound of the log derivative of the Dirichlet
Latter on, we obtain a zero free region, except for possible one zero, of the
18 November, 2023 at 2:01 pm
Terence Tao
The in Proposition 51 is an absolute constant. The exceptional zero
in Proposition 51 is an absolute constant. The exceptional zero 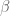 can indeed be very close to
can indeed be very close to  in applications, which does cause a significant problem; one can use Siegel’s theorem (Theorem 62) to get an ineffective amount of separation, which is good enough in some applications, but if one wants effective bounds then one basically has to live with the contribution of the exceptional zero and try to ensure that one has good bounds for the final result even when
in applications, which does cause a significant problem; one can use Siegel’s theorem (Theorem 62) to get an ineffective amount of separation, which is good enough in some applications, but if one wants effective bounds then one basically has to live with the contribution of the exceptional zero and try to ensure that one has good bounds for the final result even when 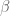 is very close to 1.
is very close to 1.