Just a quick announcement that Dustin Mixon and Aubrey de Grey have just launched the Polymath16 project over at Dustin’s blog. The main goal of this project is to simplify the recent proof by Aubrey de Grey that the chromatic number of the unit distance graph of the plane is at least 5, thus making progress on the Hadwiger-Nelson problem. The current proof is computer assisted (in particular it requires one to control the possible 4-colorings of a certain graph with over a thousand vertices), but one of the aims of the project is to reduce the amount of computer assistance needed to verify the proof; already a number of such reductions have been found. See also this blog post where the polymath project was proposed, as well as the wiki page for the project. Non-technical discussion of the project will continue at the proposal blog post.
Recent Comments
| Anonymous on Erratum for “An inverse… | |
| Anonymous on Pointwise ergodic theorems for… | |
| Anonymous on 275A, Notes 3: The weak and st… | |
| Terence Tao on Pointwise ergodic theorems for… | |
| Terence Tao on Erratum for “An inverse… | |
| Anonymous on Notes on the B+B+t theore… | |
| Anonymous on Pointwise ergodic theorems for… | |
| Anonymous on Erratum for “An inverse… | |
| Erratum for “A… on An inverse theorem for the Gow… | |
| Anonymous on Analysis II | |
| Anonymous on Notes on the B+B+t theore… | |
| Anonymous on Twisted convolution and the se… | |
| Anonymous on A generalized Cauchy-Schwarz i… | |
| Notes on the B+B+t t… on Ultrafilters, nonstandard anal… | |
| Notes on the B+B+t t… on Soft analysis, hard analysis,… |
Articles by others
- Andreas Blass – The mathematical theory T of actual mathematical reasoning
- Gene Weingarten – Pearls before breakfast
- Isaac Asimov – The relativity of wrong
- Jonah Lehrer – Don't! – the secret of self-control
- Julianne Dalcanton – The cult of genius
- Nassim Taleb – The fourth quadrant: a map of the limits of statistics
- Paul Graham – What You'll Wish You'd Known
- Po Bronson – How not to talk to your kids
- Scott Aaronson – Ten signs a claimed mathematical proof is wrong
- Tanya Klowden – articles on astronomy
- Timothy Gowers – Elsevier — my part in its downfall
- Timothy Gowers – The two cultures of mathematics
- William Thurston – On proof and progress in mathematics
Diversions
- Abstruse Goose
- BoxCar2D
- Factcheck.org
- Gapminder
- Literally Unbelievable
- Planarity
- PolitiFact
- Quite Interesting
- snopes
- Strange maps
- Television tropes and idioms
- The Economist
- The Onion
- The Straight Dope
- This American Life on the financial crisis I
- This American Life on the financial crisis II
- What if? (xkcd)
- xkcd
Mathematics
- 0xDE
- A Mind for Madness
- A Portion of the Book
- Absolutely useless
- Alex Sisto
- Algorithm Soup
- Almost Originality
- AMS blogs
- AMS Graduate Student Blog
- Analysis & PDE
- Analysis & PDE Conferences
- Annoying Precision
- Area 777
- Ars Mathematica
- ATLAS of Finite Group Representations
- Automorphic forum
- Avzel's journal
- Blog on Math Blogs
- blogderbeweise
- Bubbles Bad; Ripples Good
- Cédric Villani
- Climbing Mount Bourbaki
- Coloquio Oleis
- Combinatorics and more
- Compressed sensing resources
- Computational Complexity
- Concrete nonsense
- David Mumford's blog
- Delta epsilons
- DispersiveWiki
- Disquisitiones Mathematicae
- Embûches tissues
- Emmanuel Kowalski’s blog
- Equatorial Mathematics
- Erdos problems
- fff
- Floer Homology
- Frank Morgan’s blog
- Gérard Besson's Blog
- Gödel’s Lost Letter and P=NP
- Geometric Group Theory
- Geometry and the imagination
- Geometry Bulletin Board
- George Shakan
- Girl's Angle
- God Plays Dice
- Good Math, Bad Math
- Graduated Understanding
- Hydrobates
- I Can't Believe It's Not Random!
- I Woke Up In A Strange Place
- Igor Pak's blog
- Images des mathématiques
- In theory
- Infinitely more
- James Colliander's Blog
- Jérôme Buzzi’s Mathematical Ramblings
- Joel David Hamkins
- Journal of the American Mathematical Society
- Keith Conrad's expository papers
- Kill Math
- Le Petit Chercheur Illustré
- Lemma Meringue
- Lewko's blog
- Libres pensées d’un mathématicien ordinaire
- LMS blogs page
- Low Dimensional Topology
- M-Phi
- Mark Sapir's blog
- Math Overflow
- Math3ma
- Mathbabe
- Mathblogging
- Mathematical musings
- Mathematics Illuminated
- Mathematics in Australia
- Mathematics Jobs Wiki
- Mathematics Stack Exchange
- Mathematics under the Microscope
- Mathematics without apologies
- Mathlog
- Mathtube
- Matt Baker's Math Blog
- Mixedmath
- Motivic stuff
- Much ado about nothing
- Multiple Choice Quiz Wiki
- MyCQstate
- nLab
- Noncommutative geometry blog
- Nonlocal equations wiki
- Nuit-blanche
- Number theory web
- Online Analysis Research Seminar
- outofprintmath
- Pattern of Ideas
- Pengfei Zhang's blog
- Persiflage
- Peter Cameron's Blog
- Phillipe LeFloch's blog
- ProofWiki
- Quomodocumque
- Ramis Movassagh's blog
- Random Math
- Reasonable Deviations
- Regularize
- Research Seminars
- Rigorous Trivialities
- Roots of unity
- Science Notes by Greg Egan
- Secret Blogging Seminar
- Selected Papers Network
- Sergei Denisov's blog
- Short, Fat Matrices
- Shtetl-Optimized
- Shuanglin's Blog
- Since it is not…
- Sketches of topology
- Snapshots in Mathematics !
- Soft questions
- Some compact thoughts
- Stacks Project Blog
- SymOmega
- Tanya Khovanova's Math Blog
- tcs math
- TeX, LaTeX, and friends
- The accidental mathematician
- The Cost of Knowledge
- The Everything Seminar
- The Geomblog
- The L-function and modular forms database
- The n-Category Café
- The n-geometry cafe
- The On-Line Blog of Integer Sequences
- The polylogblog
- The polymath blog
- The polymath wiki
- The Tricki
- The twofold gaze
- The Unapologetic Mathematician
- The value of the variable
- The World Digital Mathematical Library
- Theoretical Computer Science – StackExchange
- Thuses
- Tim Gowers’ blog
- Tim Gowers’ mathematical discussions
- Todd and Vishal’s blog
- Van Vu's blog
- Vaughn Climenhaga
- Vieux Girondin
- Visual Insight
- Vivatsgasse 7
- Williams College Math/Stat Blog
- Windows on Theory
- Wiskundemeisjes
- XOR’s hammer
- Yufei Zhao's blog
- Zhenghe's Blog
Selected articles
- A cheap version of nonstandard analysis
- A review of probability theory
- American Academy of Arts and Sciences speech
- Amplification, arbitrage, and the tensor power trick
- An airport-inspired puzzle
- Benford's law, Zipf's law, and the Pareto distribution
- Compressed sensing and single-pixel cameras
- Einstein’s derivation of E=mc^2
- On multiple choice questions in mathematics
- Problem solving strategies
- Quantum mechanics and Tomb Raider
- Real analysis problem solving strategies
- Sailing into the wind, or faster than the wind
- Simons lectures on structure and randomness
- Small samples, and the margin of error
- Soft analysis, hard analysis, and the finite convergence principle
- The blue-eyed islanders puzzle
- The cosmic distance ladder
- The federal budget, rescaled
- Ultrafilters, non-standard analysis, and epsilon management
- What is a gauge?
- What is good mathematics?
- Why global regularity for Navier-Stokes is hard
Software
The sciences
Top Posts
- Career advice
- Erratum for "An inverse theorem for the Gowers U^{s+1}[N]-norm"
- Notes on the B+B+t theorem
- On writing
- Books
- Does one have to be a genius to do maths?
- Pointwise ergodic theorems for non-conventional bilinear polynomial averages
- There’s more to mathematics than rigour and proofs
- Learn and relearn your field
- Work hard
Archives
- April 2024 (5)
- March 2024 (1)
- December 2023 (2)
- November 2023 (2)
- October 2023 (1)
- September 2023 (3)
- August 2023 (3)
- June 2023 (8)
- May 2023 (1)
- April 2023 (1)
- March 2023 (2)
- February 2023 (1)
- January 2023 (2)
- December 2022 (3)
- November 2022 (3)
- October 2022 (3)
- September 2022 (1)
- July 2022 (3)
- June 2022 (1)
- May 2022 (2)
- April 2022 (2)
- March 2022 (5)
- February 2022 (3)
- January 2022 (1)
- December 2021 (2)
- November 2021 (2)
- October 2021 (1)
- September 2021 (2)
- August 2021 (1)
- July 2021 (3)
- June 2021 (1)
- May 2021 (2)
- February 2021 (6)
- January 2021 (2)
- December 2020 (4)
- November 2020 (2)
- October 2020 (4)
- September 2020 (5)
- August 2020 (2)
- July 2020 (2)
- June 2020 (1)
- May 2020 (2)
- April 2020 (3)
- March 2020 (9)
- February 2020 (1)
- January 2020 (3)
- December 2019 (4)
- November 2019 (2)
- September 2019 (2)
- August 2019 (3)
- July 2019 (2)
- June 2019 (4)
- May 2019 (6)
- April 2019 (4)
- March 2019 (2)
- February 2019 (5)
- January 2019 (1)
- December 2018 (6)
- November 2018 (2)
- October 2018 (2)
- September 2018 (5)
- August 2018 (3)
- July 2018 (3)
- June 2018 (1)
- May 2018 (4)
- April 2018 (4)
- March 2018 (5)
- February 2018 (4)
- January 2018 (5)
- December 2017 (5)
- November 2017 (3)
- October 2017 (4)
- September 2017 (4)
- August 2017 (5)
- July 2017 (5)
- June 2017 (1)
- May 2017 (3)
- April 2017 (2)
- March 2017 (3)
- February 2017 (1)
- January 2017 (2)
- December 2016 (2)
- November 2016 (2)
- October 2016 (5)
- September 2016 (4)
- August 2016 (4)
- July 2016 (1)
- June 2016 (3)
- May 2016 (5)
- April 2016 (2)
- March 2016 (6)
- February 2016 (2)
- January 2016 (1)
- December 2015 (4)
- November 2015 (6)
- October 2015 (5)
- September 2015 (5)
- August 2015 (4)
- July 2015 (7)
- June 2015 (1)
- May 2015 (5)
- April 2015 (4)
- March 2015 (3)
- February 2015 (4)
- January 2015 (4)
- December 2014 (6)
- November 2014 (5)
- October 2014 (4)
- September 2014 (3)
- August 2014 (4)
- July 2014 (5)
- June 2014 (5)
- May 2014 (5)
- April 2014 (2)
- March 2014 (4)
- February 2014 (5)
- January 2014 (4)
- December 2013 (4)
- November 2013 (5)
- October 2013 (4)
- September 2013 (5)
- August 2013 (1)
- July 2013 (7)
- June 2013 (12)
- May 2013 (4)
- April 2013 (2)
- March 2013 (2)
- February 2013 (6)
- January 2013 (1)
- December 2012 (4)
- November 2012 (7)
- October 2012 (6)
- September 2012 (4)
- August 2012 (3)
- July 2012 (4)
- June 2012 (3)
- May 2012 (3)
- April 2012 (4)
- March 2012 (5)
- February 2012 (5)
- January 2012 (4)
- December 2011 (8)
- November 2011 (8)
- October 2011 (7)
- September 2011 (6)
- August 2011 (8)
- July 2011 (9)
- June 2011 (8)
- May 2011 (11)
- April 2011 (3)
- March 2011 (10)
- February 2011 (3)
- January 2011 (5)
- December 2010 (5)
- November 2010 (6)
- October 2010 (9)
- September 2010 (9)
- August 2010 (3)
- July 2010 (4)
- June 2010 (8)
- May 2010 (8)
- April 2010 (8)
- March 2010 (8)
- February 2010 (10)
- January 2010 (12)
- December 2009 (11)
- November 2009 (8)
- October 2009 (15)
- September 2009 (6)
- August 2009 (13)
- July 2009 (10)
- June 2009 (11)
- May 2009 (9)
- April 2009 (11)
- March 2009 (14)
- February 2009 (13)
- January 2009 (18)
- December 2008 (8)
- November 2008 (9)
- October 2008 (10)
- September 2008 (5)
- August 2008 (6)
- July 2008 (7)
- June 2008 (8)
- May 2008 (11)
- April 2008 (12)
- March 2008 (12)
- February 2008 (13)
- January 2008 (17)
- December 2007 (10)
- November 2007 (9)
- October 2007 (9)
- September 2007 (7)
- August 2007 (9)
- July 2007 (9)
- June 2007 (6)
- May 2007 (10)
- April 2007 (11)
- March 2007 (9)
- February 2007 (4)
Categories
- expository (306)
- tricks (13)
- guest blog (10)
- Mathematics (865)
- math.AC (8)
- math.AG (42)
- math.AP (112)
- math.AT (17)
- math.CA (186)
- math.CO (195)
- math.CT (9)
- math.CV (37)
- math.DG (37)
- math.DS (88)
- math.FA (24)
- math.GM (14)
- math.GN (21)
- math.GR (88)
- math.GT (16)
- math.HO (13)
- math.IT (13)
- math.LO (53)
- math.MG (45)
- math.MP (29)
- math.NA (24)
- math.NT (189)
- math.OA (22)
- math.PR (107)
- math.QA (6)
- math.RA (45)
- math.RT (21)
- math.SG (4)
- math.SP (48)
- math.ST (11)
- non-technical (191)
- admin (46)
- advertising (63)
- diversions (7)
- media (13)
- journals (3)
- obituary (15)
- opinion (34)
- paper (243)
- question (126)
- polymath (85)
- talk (68)
- DLS (20)
- teaching (188)
- 245A – Real analysis (11)
- 245B – Real analysis (21)
- 245C – Real analysis (6)
- 246A – complex analysis (11)
- 246B – complex analysis (5)
- 246C – complex analysis (5)
- 247B – Classical Fourier Analysis (5)
- 254A – analytic prime number theory (19)
- 254A – ergodic theory (18)
- 254A – Hilbert's fifth problem (12)
- 254A – Incompressible fluid equations (5)
- 254A – random matrices (14)
- 254B – expansion in groups (8)
- 254B – Higher order Fourier analysis (9)
- 255B – incompressible Euler equations (2)
- 275A – probability theory (6)
- 285G – poincare conjecture (20)
- Logic reading seminar (8)
- travel (26)
additive combinatorics
approximate groups
arithmetic progressions
Ben Green
Cauchy-Schwarz
Cayley graphs
central limit theorem
Chowla conjecture
compressed sensing
correspondence principle
distributions
divisor function
eigenvalues
Elias Stein
Emmanuel Breuillard
entropy
equidistribution
ergodic theory
Euler equations
exponential sums
finite fields
Fourier transform
Freiman's theorem
Gowers uniformity norm
Gowers uniformity norms
graph theory
Gromov's theorem
GUE
hard analysis
Hilbert's fifth problem
hypergraphs
ICM
incompressible Euler equations
inverse conjecture
Joni Teravainen
Kaisa Matomaki
Kakeya conjecture
Lie algebras
Lie groups
Liouville function
Littlewood-Offord problem
Maksym Radziwill
Mobius function
Navier-Stokes equations
nilpotent groups
nilsequences
nonstandard analysis
politics
polymath1
polymath8
Polymath15
polynomial method
polynomials
prime gaps
prime numbers
prime number theorem
random matrices
randomness
Ratner's theorem
regularity lemma
Ricci flow
Riemann zeta function
Schrodinger equation
Shannon entropy
sieve theory
structure
Szemeredi's theorem
Tamar Ziegler
tiling
UCLA
ultrafilters
universality
Van Vu
wave maps
Yitang Zhang
 The Polymath Blog
The Polymath Blog
- Polymath projects 2021
- A sort of Polymath on a famous MathOverflow problem
- Ten Years of Polymath
- Updates and Pictures
- Polymath proposal: finding simpler unit distance graphs of chromatic number 5
- A new polymath proposal (related to the Riemann Hypothesis) over Tao’s blog
- Spontaneous Polymath 14 – A success!
- Polymath 13 – a success!
- Non-transitive Dice over Gowers’s Blog
- Rota’s Basis Conjecture: Polymath 12, post 3

3 comments
Comments feed for this article
14 April, 2018 at 10:46 pm
Anonymous
Dear Terry,sir
May I ask you a little stupid question that you have any works related to Hadwiger-Nelson problem? Thank for your response.
15 April, 2018 at 8:53 am
Terence Tao
No, I don’t have anything published relating to this problem (I may have written about the tangentially related unit distance problem of Erdos in my book with Van Vu and in some other places, though). I think I played with this problem for a day or so many years ago (hoping to improve upon Falconer’s result in the measurable case) but didn’t get particularly far. I also assigned the problem of proving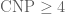 in an undergraduate problem solving class about eighteen years ago; I remember that the majority of students needed quite a few hints to discover the standard Moser spindle solution.
in an undergraduate problem solving class about eighteen years ago; I remember that the majority of students needed quite a few hints to discover the standard Moser spindle solution.
19 April, 2018 at 4:23 pm
Nazgand
Let \(G_0\) be a graph with chromatic number \(c_0\) and vertexes \(v_a,v_b\) such that \(v_a\) and \(v_b\) do not not the same color for any \(c_0\)-coloring of \(G_0\). \(G_0\) can then be used as a `virtual edge’ with distance \(d_0=\left\|{v_a-v_b}\right\|\). Let the chromatic color of a virtual edge be defined as the chromatic color of the graph used to virtualize the edge.
Multiplicative property of virtual edges:
Let \(G_1\) be a graph with chromatic number \(c_0\) which virtualizes an edge length \(d_1\). Then replacing all edges of \(G_0\) with virtual edges of length \(d_1\) produces a virtual edge of chromatic color \(c_0\) with length \(d_0*d_1\).
If a graph, \(G_2\), with chromatic number \(c_2\geq 1+c_0\) is created using virtual edges with chromatic number \(c_0\), then a graph, \(G_3\), of chromatic number \(c_3\) (s.t. \(c_2\geq c_3\geq 1+c_0\)) can be created by replacing the virtual edges with the graphs which virtualize the virtual edges.
More trivially, if a graph, \(G_4\), with chromatic number \(c_4\leq c_0\) is created using virtual edges with chromatic number \(c_0\), then replacing the virtual edges with the graphs which virtualize the virtual edges produces a graph with chromatic number \(c_0\).
If virtual edges with chromatic number 4 are found, then they may be useful to make a graph of chromatic number 5 which uses fewer vertexes than the current smallest graph. In an extreme example, 5 vertices would be enough if each of the distances between pairs of vertices corresponds to a virtual edge with chromatic number 4.