This is the eighth “research” thread of the Polymath15 project to upper bound the de Bruijn-Newman constant , continuing this post. Discussion of the project of a non-research nature can continue for now in the existing proposal thread. Progress will be summarised at this Polymath wiki page.
Significant progress has been made since the last update; by implementing the “barrier” method to establish zero free regions for by leveraging the extensive existing numerical verification of the Riemann hypothesis (which establishes zero free regions for
), we have been able to improve our upper bound on
from 0.48 to 0.28. Furthermore, there appears to be a bit of further room to improve the bounds further by tweaking the parameters
used in the argument (we are currently using
); the most recent idea is to try to use exponential sum estimates to improve the bounds on the derivative of the approximation to
that is used in the barrier method, which currently is the most computationally intensive step of the argument.

114 comments
Comments feed for this article
17 April, 2018 at 3:52 pm
Terence Tao
I have reorganised the writeup a bit to try to put the most interesting results in the introduction. Also I have written down a bound for both the x,y and t derivatives of the quantity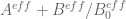 , which in the writeup is now called
, which in the writeup is now called  . These should presumably be useful in the barrier part of the argument. I like KM’s idea of using some exponential sum estimates to do even better; the estimates in the paper of Cheng and Graham aren’t too fearsome, and it may be that all one needs to do is combine them with summation by parts to obtain reasonable estimates. The net savings could potentially be on the order of
. These should presumably be useful in the barrier part of the argument. I like KM’s idea of using some exponential sum estimates to do even better; the estimates in the paper of Cheng and Graham aren’t too fearsome, and it may be that all one needs to do is combine them with summation by parts to obtain reasonable estimates. The net savings could potentially be on the order of 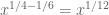 which could be significant at the scales we are considering (in principle we can place our barrier as far out as
which could be significant at the scales we are considering (in principle we can place our barrier as far out as 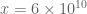 ). I’ll take a look at it.
). I’ll take a look at it.
UPDATE: there is also some followup work to the Cheng-Graham paper by various authors which may also have some useable estimates in this regard.
18 April, 2018 at 8:35 am
Anonymous
citizen scientists don’t have mathscinet
18 April, 2018 at 9:34 am
Anonymous
See e.g. the recent paper by Platt and Trudgian
Click to access 1402.3953.pdf
18 April, 2018 at 8:45 am
KM
It seems the t/4 factor in the ddt bound formula should be 1/4. Also, I was facing a authentication wall with the mathscinet link, so tried Google Scholar instead (link), which provides links to many of the followup papers.
[Corrected, thanks – T.]
21 April, 2018 at 5:47 am
Bill Bauer
There may be sign error in the denominator of definition (16), γ. It currently reads
(16) γ(x+iy) := Mₜ(t,(1-y+i*x)/2)/Mₜ(t,(1+y-i*x)/2)
It should, perhaps, read
(16) γ(x+iy) := Mₜ(t,(1-y+i*x)/2)/Mₜ(t,(1+y+i*x)/2)
The mean value theorem, used in the proof of Proposition 6.6 (estimates) suggests that log|Mₜ(t,(σ+i*x)/2)| should be a function of σ only which it would not be if the signs of ix were different in numerator and denominator.
Apologies if I’m missing something obvious. As far as I’ve checked computationally, the inequality seems to be true in either case.
21 April, 2018 at 7:08 am
Terence Tao
The holomorphic function is real on the real axis and so obeys the reflection equation
is real on the real axis and so obeys the reflection equation 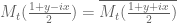 , so if one takes absolute values, the sign of the
, so if one takes absolute values, the sign of the  term becomes irrelevant. I’ll add a line of explanation in the proof of Prop 6.6 to emphasise this.
term becomes irrelevant. I’ll add a line of explanation in the proof of Prop 6.6 to emphasise this.
21 April, 2018 at 10:23 am
William Bauer
Thank you. Wish I’d seen that.
17 April, 2018 at 5:10 pm
anonymous
This is a question which is possibly a bit orthogonal to the main developments of this polymath, but may be able to be answered relatively easily using the insights that the contributors have gained. Is clear how far one can extend to other similar functions the result of Ki, Kim and Lee, that all but finitely many zeros of lie on the real line for any
lie on the real line for any 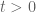 ? I’m thinking of a result along the lines of de Bruijn’s that applies generically to functions with zeros trapped in a certain strip, with the added condition that zeros become more dense away from the origin.
? I’m thinking of a result along the lines of de Bruijn’s that applies generically to functions with zeros trapped in a certain strip, with the added condition that zeros become more dense away from the origin.
For instance is there a pathological example of an entire function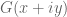 (with rapidly decaying and even Fourier transform) with all zeroes in some strip
(with rapidly decaying and even Fourier transform) with all zeroes in some strip  ,
,  still has infinitely many zeros off the real line? (One could even to make the question more precise suppose
still has infinitely many zeros off the real line? (One could even to make the question more precise suppose  even satisfies a Riemann- von Mangoldt formula with the same sort of error term as the Riemann xi-function.)
even satisfies a Riemann- von Mangoldt formula with the same sort of error term as the Riemann xi-function.)
17 April, 2018 at 7:49 pm
Terence Tao
Well, here is a simple example: the functions , for some constant
, for some constant  , has all zeroes in a strip that become all real at time
, has all zeroes in a strip that become all real at time  , but has infinitely many zeroes off the line before then (the function is
, but has infinitely many zeroes off the line before then (the function is 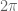 -periodic). But this function doesn’t obey a Riemann von Mangoldt formula.
-periodic). But this function doesn’t obey a Riemann von Mangoldt formula.
For a typical function obeying Riemann von Mangoldt, a complex zero above the real axis of real part would be expected to be attracted to the real axis at a velocity comparable to the
would be expected to be attracted to the real axis at a velocity comparable to the  nearby zeroes, at least half of which will be at or below the real axis. So within time
nearby zeroes, at least half of which will be at or below the real axis. So within time  one would expect such a zero to hit the real axis, suggesting that there are only finitely many non-real zeroes after any finite amount of time. But there could be some exceptional initial configurations of zeroes which somehow “defy gravity” – maybe “pulling each other up by their bootstraps” and stay above the real line for an unusually long period of time. I don’t know how to construct these, but on the other hand I can’t rule such a scenario out either – they seem somewhat inconsistent with physical intuition such as conservation of centre of mass, but I have not been able to make such intuition rigorous.
one would expect such a zero to hit the real axis, suggesting that there are only finitely many non-real zeroes after any finite amount of time. But there could be some exceptional initial configurations of zeroes which somehow “defy gravity” – maybe “pulling each other up by their bootstraps” and stay above the real line for an unusually long period of time. I don’t know how to construct these, but on the other hand I can’t rule such a scenario out either – they seem somewhat inconsistent with physical intuition such as conservation of centre of mass, but I have not been able to make such intuition rigorous.
17 April, 2018 at 11:53 pm
Anonymous
It seems important to classify (e.g. by Cartan’s equivalence method) all the invariants of the zeros ODE dynamics – to get more information and bounds for this dynamics.
18 April, 2018 at 7:49 am
Terence Tao
I’m not sure that there will be many invariants – this is a heat flow (with a very noticeable “arrow of time”) rather than a Hamiltonian flow. Since such flows tend to converge to an equilibrium state at infinity, it’s very hard to have any invariants (as they would have to match the value of the invariant at the equilibrium state). For such flows it is monotone (or approximately monotone) quantities, rather than invariant quantities, that tend to be more useful (such quantities played a key role in my paper with Brad, for instance). But there’s not really a systematic way (a la Cartan) to find monotone quantities (we found the ones we had by reasoning in analogy with quantities that were useful for a similar-looking flow, Dyson Brownian motion).
22 April, 2018 at 6:20 am
Raphael
Sounds a bit like there should be something like an entropy.
22 April, 2018 at 7:12 am
Raphael
I mean for the one the local entropy gain directly follows from the PDE, on the other hand side one could look at particular “subsystems”. I don’t know if the zeros can be interpreted meaningful as subsystems but in any case “phase change”s like what you suggest in your interpretation are nicely traceable with the entropy. Especially there is the interpretation of entropy as the number of degrees of freedom. In that sense if a zero can be complex or exclusively real directly goes into the entropy (like by a factor of two per particle). Just a loose thought.
17 April, 2018 at 8:19 pm
Nazgand
It occurs me that another way to attack the problem is to use a fixed and calculate a mesh barrier over the variables
and calculate a mesh barrier over the variables 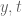 as
as  varies from the verified upper bound of the de Bruijn-Newman constant,
varies from the verified upper bound of the de Bruijn-Newman constant,  to a target upper bound,
to a target upper bound,  and as
and as  varies from 0 to an upper bound of the maximum possible
varies from 0 to an upper bound of the maximum possible  for the current
for the current  . This mesh will take care of any zeroes coming from horizontal infinity.Then one can follow some zero,
. This mesh will take care of any zeroes coming from horizontal infinity.Then one can follow some zero,  greater than
greater than 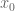 (at both
(at both  through the reverse heat dynamics, and verify that the same number of zeroes exist on the real line up to
through the reverse heat dynamics, and verify that the same number of zeroes exist on the real line up to  . I am assuming that zeroes on the real line are able to join together then exit the real line as
. I am assuming that zeroes on the real line are able to join together then exit the real line as  decreases, but if this is shown to be impossible for some
decreases, but if this is shown to be impossible for some  close enough to
close enough to  , then only the mesh calculation is required, not the counting of real zeroes.
, then only the mesh calculation is required, not the counting of real zeroes.
The current method is working, yet someone may find this idea a useful starting point, as this method nicely recycles previous upper bounds of the constant. This sort of elementary idea is the only thing I see which I can submit that may help, given my shallow understanding of the project.
18 April, 2018 at 7:51 am
Terence Tao
It’s a nice idea to try to move backwards in time from the previous best known bound of rather than move forward in time from
rather than move forward in time from  (which is our current approach that leverages numerical RH). The problem though is that when one moves backwards in time, the real zeroes become very “volatile” – it’s very hard to prevent them from colliding and then moving off the real axis (this basically would require one to somehow exclude “Lehmer pairs” at these values of t. One could potentially do so if one knew that the zeroes were all real at some earlier value of t, but this leads to circular-looking arguments, where one needs to lower the bound on
(which is our current approach that leverages numerical RH). The problem though is that when one moves backwards in time, the real zeroes become very “volatile” – it’s very hard to prevent them from colliding and then moving off the real axis (this basically would require one to somehow exclude “Lehmer pairs” at these values of t. One could potentially do so if one knew that the zeroes were all real at some earlier value of t, but this leads to circular-looking arguments, where one needs to lower the bound on  in order to lower the bound on
in order to lower the bound on  ).
).
18 April, 2018 at 3:25 pm
Nazgand
I do not understand what part of my argument is circular, as it is merely another way of verifying that the rectangular region of possible non-real zeroes of \(H_{t_0}\) has no non-real zeroes. This is the same rectangular region of possible non-real zeroes the current method uses for fixed \(t=t_0\).
If the zeroes are conserved expect for zeroes appearing from horizontal infinity and no zeroes pass through the barrier at \(x=x_0\) then counting the number of real zeroes up to \(z(t)\) for both \(H_{t_0}(z)\) and \(H_{t_0}(z)\) and verifying equality implies the rectangle is free of non-real zeroes. If zeroes collide and exit the real line, then the counts of real zeroes will not match.
Is your concern that multiple real zeroes near each other may be miscounted, and that avoiding such miscounts would be costly computation-wise? Much research has been done on counting real zeroes of \(H_0(z)\), and applying similar methods to \(H_t(z)\) is likely possible.
The idea that the counting of real zeroes might be skip-able is fluffy speculation based on the fact that one world only need to avoid colliding real zeroes for zeroes less than \(z(t)\).
Without such a shortcut, counting real zeroes can be expensive for large \(x_0\), yet the current method likely uses more computation to lower the bound to \(t_0\) because a barrier mesh needs to be calculated which has width \(x_0\), leaving only the cost of the mesh at \(x=x_0\) to consider, which may be cheaper than the current mesh calculation required.
18 April, 2018 at 4:10 pm
Terence Tao
If one is willing to try to count real zeroes of up to some large threshold
up to some large threshold  , then this approach could work in principle, but the time complexity of this is likely to scale like
, then this approach could work in principle, but the time complexity of this is likely to scale like  at best (to scan each unit interval for zeroes takes about
at best (to scan each unit interval for zeroes takes about  time assuming that the Odlyzko-Schonhage algorithm can be adapted for
time assuming that the Odlyzko-Schonhage algorithm can be adapted for  ). We already had a somewhat similar scan in previous arguments using the argument principle for a rectangular region above the real axis, and even with the additional convergence afforded by having
). We already had a somewhat similar scan in previous arguments using the argument principle for a rectangular region above the real axis, and even with the additional convergence afforded by having  equal to 0.4 rather than 0, it took a while to reach
equal to 0.4 rather than 0, it took a while to reach 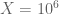 or so. In contrast, the barrier method only has to scan a single unit interval
or so. In contrast, the barrier method only has to scan a single unit interval ![[X,X+1]](https://s0.wp.com/latex.php?latex=%5BX%2CX%2B1%5D&bg=ffffff&fg=545454&s=0&c=20201002) (albeit for multiple values of
(albeit for multiple values of  , which is an issue), and we’ve been able to make it work for
, which is an issue), and we’ve been able to make it work for  up to
up to  so far.
so far.
The circularity I was referring to would arise if one wanted to somehow avoid the computationally intensive process of counting real zeroes up to . In order to do this one would have to somehow exclude the possibility that say
. In order to do this one would have to somehow exclude the possibility that say 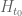 has a Lehmer pair up to this height, as such a pair would make the count of real zeroes very sensitive to the value of
has a Lehmer pair up to this height, as such a pair would make the count of real zeroes very sensitive to the value of  . Given that real zeroes repel each other, the non-existence of Lehmer pairs at
. Given that real zeroes repel each other, the non-existence of Lehmer pairs at  is morally equivalent to
is morally equivalent to  having real zeroes (up to scale
having real zeroes (up to scale  , at least) for some
, at least) for some 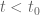 . Actually, now that I write this, I see that this is weaker than requiring one to already possess the bound
. Actually, now that I write this, I see that this is weaker than requiring one to already possess the bound 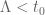 , since one could still have zeroes off the real axis near horizontal infinity. So there need not be a circularity here. Still, I don't see a way to force the absence of Lehmer pairs without either a scan of length
, since one could still have zeroes off the real axis near horizontal infinity. So there need not be a circularity here. Still, I don't see a way to force the absence of Lehmer pairs without either a scan of length  (and time complexity something like
(and time complexity something like  or a barrier method (outsourcing the length
or a barrier method (outsourcing the length  scan to the existing literature on numerical verification of RH).
scan to the existing literature on numerical verification of RH).
17 April, 2018 at 10:19 pm
pisoir
Dear prof. Tao,
I have been watching carefully your (fast) progress on this problem and from my point of view I am confused about several of your comments.
To me it seems that you are aiming for , but from the progress made so far, I have the feeling that this is a rather “artificially” picked bound and if you wanted you could push it even further. Also you mention several times the numerical complexity of the problem, but according to the fast results by KM, Rudolph and others, this also does not seem to be a problem at the moment.
, but from the progress made so far, I have the feeling that this is a rather “artificially” picked bound and if you wanted you could push it even further. Also you mention several times the numerical complexity of the problem, but according to the fast results by KM, Rudolph and others, this also does not seem to be a problem at the moment. and then close the project, because it could then go on forever (pushing the
and then close the project, because it could then go on forever (pushing the  by meaningless 0.01 each month) or you will try to push it as far as you can until you really hit the fundamental border of this method? Is there such border and what could that value be (can it go down to e.g.
by meaningless 0.01 each month) or you will try to push it as far as you can until you really hit the fundamental border of this method? Is there such border and what could that value be (can it go down to e.g.  )?
)?
So my question is, are you aiming at some specific value of
Thanks.
18 April, 2018 at 5:20 am
goingtoinfinity
“by meaningless 0.01 each month” – that would be rather surprising in july 2020.
18 April, 2018 at 7:57 am
Terence Tao
I view the bound on as a nice proxy for progress on understanding the behaviour of the
as a nice proxy for progress on understanding the behaviour of the  , but one should not identify this proxy too strongly with progress itself (cf. Goodhart’s law). Already, the existing efforts to improve the lower bound on
, but one should not identify this proxy too strongly with progress itself (cf. Goodhart’s law). Already, the existing efforts to improve the lower bound on  have revealed a number of useful new results and insights about
have revealed a number of useful new results and insights about  , such as an efficient Riemann-Siegel type approximation to
, such as an efficient Riemann-Siegel type approximation to  for large values of x, an efficient integral representation to
for large values of x, an efficient integral representation to  for small and medium values of x, a “barrier” technique to create large zero free regions for
for small and medium values of x, a “barrier” technique to create large zero free regions for  (assuming a corresponding zero free region for
(assuming a corresponding zero free region for  ), and an essentially complete understanding of the zeroes of
), and an essentially complete understanding of the zeroes of  at very large values of x (
at very large values of x ( ). Hopefully as we keep pushing, more such results and observations will follow. If such results start drying up, and the bound on
). Hopefully as we keep pushing, more such results and observations will follow. If such results start drying up, and the bound on  slowly improves from month to month purely from application of ever increasing amounts of computer time, then that would indicate to me that the project has come close to its natural endpoint and it would be a good time to declare victory and write up the results.
slowly improves from month to month purely from application of ever increasing amounts of computer time, then that would indicate to me that the project has come close to its natural endpoint and it would be a good time to declare victory and write up the results.
18 April, 2018 at 3:54 am
Anonymous
For a given measure of computational complexity (or “effort”), an interesting optimization problem is to find the optimal pair which minimize the bound
which minimize the bound  subject to a given computational complexity constraint.
subject to a given computational complexity constraint.
18 April, 2018 at 8:05 am
Terence Tao
It might be worth resurrecting the toy approximation
for this purpose, where and
and 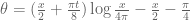 (see this page of wiki). For the purposes of locating the most efficient choice of
(see this page of wiki). For the purposes of locating the most efficient choice of 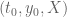 parameters that are still computationally feasible, we can just pretend that
parameters that are still computationally feasible, we can just pretend that  is exactly equal to this toy approximation (thus totally ignoring
is exactly equal to this toy approximation (thus totally ignoring  errors, and also replacing the somewhat messy
errors, and also replacing the somewhat messy  factors by a simplified version). Once we locate the most promising choice, we can then return to the more accurate approximation
factors by a simplified version). Once we locate the most promising choice, we can then return to the more accurate approximation 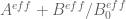 and combine it with upper bounds on
and combine it with upper bounds on 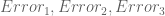 .
.
18 April, 2018 at 8:16 am
Terence Tao
With regards to this toy problem at least, it seems like some version of the Odlyzko–Schönhage algorithm may be computationally efficient in the barrier verification step where we will have to evaluate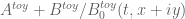 for many mesh points of
for many mesh points of 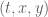 (but with
(but with  in a fixed unit interval
in a fixed unit interval ![[X, X+1]](https://s0.wp.com/latex.php?latex=%5BX%2C+X%2B1%5D&bg=ffffff&fg=545454&s=0&c=20201002) . The first basic idea of this algorithm is to transform this problem by performing an FFT in the x variable, so that one is now evaluating things like
. The first basic idea of this algorithm is to transform this problem by performing an FFT in the x variable, so that one is now evaluating things like
for , where
, where  is a mesh size parameter. The point is that this FFT interacts nicely with the
is a mesh size parameter. The point is that this FFT interacts nicely with the  factors in the toy approximation to give a sum which is substantially less oscillatory, and which can be approximated fairly accurately by dividing up the sum into blocks and using a Taylor expansion on each block, which can allow one to reuse a lot of calculations as
factors in the toy approximation to give a sum which is substantially less oscillatory, and which can be approximated fairly accurately by dividing up the sum into blocks and using a Taylor expansion on each block, which can allow one to reuse a lot of calculations as  varies (basically reducing the time complexity of evaluating (1) for all values of k from the naive cost of
varies (basically reducing the time complexity of evaluating (1) for all values of k from the naive cost of 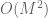 to something much smaller like
to something much smaller like  ; also one should be able to reuse many of these calculations when one varies t and y as well, leading to further time complexity savings). One still has to do a FFT at the end, but this is apparently a very fast step and is definitely not the bottleneck. I’ll have to read up on the algorithm to figure out how to adapt it to this toy problem at least. (In our language, the algorithm is generally formulated to compute the sum
; also one should be able to reuse many of these calculations when one varies t and y as well, leading to further time complexity savings). One still has to do a FFT at the end, but this is apparently a very fast step and is definitely not the bottleneck. I’ll have to read up on the algorithm to figure out how to adapt it to this toy problem at least. (In our language, the algorithm is generally formulated to compute the sum  for many values of
for many values of ![x \in [X,X+1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5BX%2CX%2B1%5D&bg=ffffff&fg=545454&s=0&c=20201002) simultaneously.)
simultaneously.)
18 April, 2018 at 8:01 am
Anonymous
Is it possible to derive (perhaps by using exponential sums estimates) for each given positive an explicit numerical threshold
an explicit numerical threshold  with the property that
with the property that  whenever
whenever  and
and  ?
?
If so, then (clearly) should decrease with increasing
should decrease with increasing 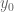 and therefore is preferable over the currently used
and therefore is preferable over the currently used  (i.e. with
(i.e. with  ) in the barrier method.
) in the barrier method.
Since may also be used as a kind of "computational complexity measure", Is it possible that
may also be used as a kind of "computational complexity measure", Is it possible that 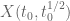 (i.e. with
(i.e. with 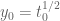 ) grows much slower than
) grows much slower than  as
as  ? (while still giving the bound
? (while still giving the bound  – comparable to the bound
– comparable to the bound  with
with  .)
.)
18 April, 2018 at 8:34 am
Terence Tao
In general it gets harder and harder to keep away from zero as y gets smaller – after all, we expect to have a lot of zeroes
away from zero as y gets smaller – after all, we expect to have a lot of zeroes  with
with 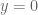 . The two methods that we have been able to use to actually improve the bound on
. The two methods that we have been able to use to actually improve the bound on  only require keeping
only require keeping  away from zero for
away from zero for 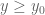 , where
, where 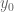 is something moderately large like 0.4. While we do have some capability to probe near
is something moderately large like 0.4. While we do have some capability to probe near 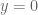 (in particular, in the asymptotics section there are some arguments using Jensen’s formula and the argument principle that make all the zeroes real beyond
(in particular, in the asymptotics section there are some arguments using Jensen’s formula and the argument principle that make all the zeroes real beyond 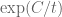 for some large absolute constant
for some large absolute constant  ), I think numerically this sort of control will be much weaker for computationally feasible values of
), I think numerically this sort of control will be much weaker for computationally feasible values of  than the control we can get for large values of
than the control we can get for large values of  . (One can already see this when considering the main term
. (One can already see this when considering the main term 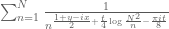 of the toy expansion, in which the role of increasing y in improving the convergence of the sum is quite visible.)
of the toy expansion, in which the role of increasing y in improving the convergence of the sum is quite visible.)
18 April, 2018 at 10:31 am
Anonymous
Correction: in the above required property of , it should be
, it should be 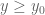 (instead of
(instead of  ).
).
18 April, 2018 at 1:29 pm
Mark
I haven’t been following this project at all, so apologies for the basic question which is perhaps covered in the discussion elsewhere:
But how much of a dictionary relating \Lambda and zero-free regions do we have? The kinds of things that I mean by a “dictionary” might be:
1) If we could prove there is a zero free strip, does that imply anything about \Lambda?
2) If there were only a single pair of off critical line zeros, can we convert this into a value of \Lambda depending on their coordinates?
3) If we knew \lambda < 10^{-1000}, would that give us any usable zero-free region?
More philosophically, I'm curious why in the "de Bruijn-Newman score system" it feels like real progress on the Riemann-Hypothesis is being made while (and I'd love to be wrong here) it doesn't seem that the ideas being applied (numerical verification, etc) are circumventing any of the obstructions to progress in other the other "score systems" (zero-free regions, etc.)
18 April, 2018 at 2:02 pm
Anonymous
wait, are you saying when we reach then we’re *not* really half way to proving rieman hypothesis???
then we’re *not* really half way to proving rieman hypothesis???
18 April, 2018 at 3:57 pm
Terence Tao
The basic theorem here is due to de Bruijn (Theorem 13 of https://pure.tue.nl/ws/files/1769368/597490.pdf ), which in our language says that if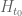 has all zeroes in the strip
has all zeroes in the strip  , then one has the bound
, then one has the bound 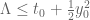 . For instance, the proof of the prime number theorem gives this for
. For instance, the proof of the prime number theorem gives this for 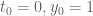 , yielding de Bruijn’s bound
, yielding de Bruijn’s bound  . So zero free regions for zeta or for
. So zero free regions for zeta or for 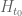 can give bounds on
can give bounds on  . However we don’t seem to have any converse implication, beyond the tautological assertion that
. However we don’t seem to have any converse implication, beyond the tautological assertion that  has all real zeroes for all
has all real zeroes for all 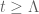 . Having a really good upper bound on
. Having a really good upper bound on  such as
such as 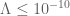 may rule out certain scenarios very far from RH (such as having a single pair of zeroes far from the critical line, and also relatively far from all other zeroes) but it would be tricky to convert it into a clean statement about, say, a zero-free region. So perhaps one reason why we can make progress on bounding
may rule out certain scenarios very far from RH (such as having a single pair of zeroes far from the critical line, and also relatively far from all other zeroes) but it would be tricky to convert it into a clean statement about, say, a zero-free region. So perhaps one reason why we can make progress on bounding  , but not on other approximations to RH, is that the implications only go in one direction.
, but not on other approximations to RH, is that the implications only go in one direction.
If somehow we could show that RH is true with a single exceptional complex pair of zeroes, it should be possible to track that zero numerically with high precision and get a precise value on , assuming that pair was within reach of numerical verification. Otherwise one could use de Bruijn’s theorem to obtain a bound, though it would not be optimal.
, assuming that pair was within reach of numerical verification. Otherwise one could use de Bruijn’s theorem to obtain a bound, though it would not be optimal.
18 April, 2018 at 4:42 pm
Terence Tao
I have a sort of statistical mechanics intuition for the zeroes of which may help clarify the situation. A bit like the three classical states of matter, the zeroes of
which may help clarify the situation. A bit like the three classical states of matter, the zeroes of  seem to take one of three forms: “gaseous”, in which the zeroes are complex, “liquid”, in which the zeroes are real but not evenly spaced, and “solid” in which the zeroes are real and evenly spaced. (This should somehow correspond to the
seem to take one of three forms: “gaseous”, in which the zeroes are complex, “liquid”, in which the zeroes are real but not evenly spaced, and “solid” in which the zeroes are real and evenly spaced. (This should somehow correspond to the  ,
,  , and
, and 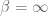 limiting cases of beta ensembles, but I do not know how to make this intuition at all rigorous.) At time zero
limiting cases of beta ensembles, but I do not know how to make this intuition at all rigorous.) At time zero 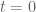 , the zeroes are some mixture of liquid and gaseous, and the RH (as well as supporting hypotheses such as GUE) asserts that it is purely liquid. At positive time, the situation is similar to
, the zeroes are some mixture of liquid and gaseous, and the RH (as well as supporting hypotheses such as GUE) asserts that it is purely liquid. At positive time, the situation is similar to  in a region of the form
in a region of the form 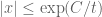 (though perhaps slightly "cooler", with some of the gas becoming liquid), but for
(though perhaps slightly "cooler", with some of the gas becoming liquid), but for  the zeroes have "frozen" into a solid state, so in particular there is only a finite amount of gas or liquid at positive time. As time advances, more of the gas (if any) condenses into liquid, and the liquid freezes into solid; by time
the zeroes have "frozen" into a solid state, so in particular there is only a finite amount of gas or liquid at positive time. As time advances, more of the gas (if any) condenses into liquid, and the liquid freezes into solid; by time  , all the gas is gone, and pretty soon after that it all looks solid. In the reverse direction, we know that at any negative time, there is at least some gas.
, all the gas is gone, and pretty soon after that it all looks solid. In the reverse direction, we know that at any negative time, there is at least some gas.
With this perspective, the reason why it is easier to make progress on than on other metrics towards RH is that we are dealing with an object
than on other metrics towards RH is that we are dealing with an object  which is already almost completely "solidified" into something well understood: the mysterious liquid and gaseous phases that make the Riemann zeta function so hard to understand only have a finite (albeit large) spatial extent, and so can be treated numerically, at least in principle.
which is already almost completely "solidified" into something well understood: the mysterious liquid and gaseous phases that make the Riemann zeta function so hard to understand only have a finite (albeit large) spatial extent, and so can be treated numerically, at least in principle.
19 April, 2018 at 9:48 am
Rudolph01
I really like the analogy and it makes me wonder what then is causing the phase-transitions between solid, liquid and gaseous. Here’s a free-flow of some thoughts, going backwards in time and assuming RH.
From solid to liquid: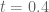 . So, with
. So, with 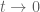 , we could reason that this partial Euler product needs to incrementally grow back towards its well-known infinite version at
, we could reason that this partial Euler product needs to incrementally grow back towards its well-known infinite version at  . When we follow the trajectories of the real zeros going back in (positive) time, they will feel an increasing competitive pressure w.r.t. their neighbouring zeros to occupy the available space to encode all the required information about the primes. This increasingly ‘heated battle’ for available locations when
. When we follow the trajectories of the real zeros going back in (positive) time, they will feel an increasing competitive pressure w.r.t. their neighbouring zeros to occupy the available space to encode all the required information about the primes. This increasingly ‘heated battle’ for available locations when 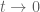 , does ‘bend’ their trajectories and determines the angle and the velocity by which they hit the line
, does ‘bend’ their trajectories and determines the angle and the velocity by which they hit the line  . Statistics will force some angles to become very small and these will then induce a Lehmer-pair. So, it could be the increasing need to encode an infinite amount of information about the primes, that turns up the ‘heat/pressure’ and moves the statistical ensembles of real lines from solid to liquid.
. Statistics will force some angles to become very small and these will then induce a Lehmer-pair. So, it could be the increasing need to encode an infinite amount of information about the primes, that turns up the ‘heat/pressure’ and moves the statistical ensembles of real lines from solid to liquid.
When we were starting to ‘mollify’ the toy-model, I recall the surprise to still see a vestige of a partial Euler product even at
Liquid to gaseous: slowly turns into a gaseous state? I don’t think so, since the ‘heat is already on’ at the line
slowly turns into a gaseous state? I don’t think so, since the ‘heat is already on’ at the line  and all the collision courses for the real zeros have been determined. The real zeros ‘plunge’ as it were into the domain below
and all the collision courses for the real zeros have been determined. The real zeros ‘plunge’ as it were into the domain below 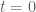 ((like particles flying into a bubble chamber) and their angles and velocities determine at which
((like particles flying into a bubble chamber) and their angles and velocities determine at which  a collision will occur. So, no extra heat source is needed and only the ‘backward heat flow’ logic is required to explain the trajectories below
a collision will occur. So, no extra heat source is needed and only the ‘backward heat flow’ logic is required to explain the trajectories below  .
.
Is there a need for an extra ‘heat/pressure’ source to explain why a perfect liquid at
Of course the key question is why the collisions of real zeros can only occur below . What is it that suddenly allows liquidized real zeros to collide and send off some gaseous complex zeros in
. What is it that suddenly allows liquidized real zeros to collide and send off some gaseous complex zeros in  -steps? What has really changed below
-steps? What has really changed below  ? I looked at potential ‘switches’ in our formulae like the
? I looked at potential ‘switches’ in our formulae like the 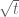 in the 3rd-approach integral, but that doesn’t lead us anywhere. The only thing that I can think of that is really different for
in the 3rd-approach integral, but that doesn’t lead us anywhere. The only thing that I can think of that is really different for  below
below  , is that there is no longer extra ‘heat/pressure’ being added (since the infinite Euler product has been completed at
, is that there is no longer extra ‘heat/pressure’ being added (since the infinite Euler product has been completed at  ). It seems therefore that somehow this incremental ‘heat/pressure’ build-up when
). It seems therefore that somehow this incremental ‘heat/pressure’ build-up when 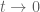 , is at the same time also the prohibiting force for real zeros to collide. And this feels like a circular reasoning and probably brings us back again to the duality between the primes and the non-trivial zeros…
, is at the same time also the prohibiting force for real zeros to collide. And this feels like a circular reasoning and probably brings us back again to the duality between the primes and the non-trivial zeros…
19 April, 2018 at 10:33 am
Rudolph01
Couldn’t resist producing an illustrative visual of the analogy.. The trajectory of the real zeros is based on real data, I manually added fictitious data to reflect the trajectory of the complex zeros.
18 April, 2018 at 6:04 pm
Terence Tao
Consider the model problem of evaluating
for multiple choices of , with
, with  in an interval
in an interval ![[X,X+1]](https://s0.wp.com/latex.php?latex=%5BX%2CX%2B1%5D&bg=ffffff&fg=545454&s=0&c=20201002) . If one does this naively,
. If one does this naively,  different evaluations of this sum would require about
different evaluations of this sum would require about 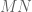 operations. There is a relatively cheap way to cut down this computation (at the cost of a bit of accuracy) without any FFT, simply by performing a Taylor expansion on intervals. Namely, pick some
operations. There is a relatively cheap way to cut down this computation (at the cost of a bit of accuracy) without any FFT, simply by performing a Taylor expansion on intervals. Namely, pick some  between
between  and
and  and split the sum into about
and split the sum into about 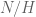 subsums of the form
subsums of the form
(actually it is slightly more advantageous to use summation ranges centred around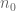 , rather than to the right of
, rather than to the right of 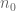 , but let us ignore this for the time being). Writing
, but let us ignore this for the time being). Writing  , and also
, and also  , we can write this expression as
, we can write this expression as
For small compared to
small compared to 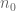 , we can hope to Taylor approximate
, we can hope to Taylor approximate 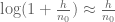 , leading eventually to the first-order approximation
, leading eventually to the first-order approximation
The point of this is that if one wants to evaluate this subsum at different choices of
different choices of  , one only needs
, one only needs 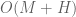 evaluations rather than
evaluations rather than  because one only needs to compute the sums
because one only needs to compute the sums  and
and  once rather than
once rather than  times, as they can be reused across the evaluations. Putting together the
times, as they can be reused across the evaluations. Putting together the 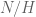 subsums, this cuts down the time complexity from
subsums, this cuts down the time complexity from 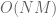 to
to  . One can also Taylor expand to higher order than first-order which allows one to take
. One can also Taylor expand to higher order than first-order which allows one to take  larger at the cost of worsening the implied constant in the
larger at the cost of worsening the implied constant in the 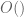 notation. There is some optimisation to be done but this should already lead to some speedup, possibly as much an order of magnitude or so.
notation. There is some optimisation to be done but this should already lead to some speedup, possibly as much an order of magnitude or so.
19 April, 2018 at 3:41 am
Anonymous
The “first sum” can be represented as

 is Hurwitz Zeta function
is Hurwitz Zeta function
where
https://dlmf.nist.gov/25.11
https://en.wikipedia.org/wiki/Hurwitz_zeta_function
The “second sum” is
which has a similar representation in terms of Hurwitz Zeta function.
Efficient algorithms for Hurwitz Zeta and related functions and oscillatory series are given in Vepstas’ paper
Click to access 0702243.pdf
20 April, 2018 at 10:12 pm
KM
With H=10 and near X=6*10^10, I have been able to get a speedup of 3x to 4x (although more should be realizable) which increases gradually as M increases.
To keep H away from n0, the first few terms in the sum are computed exactly (currently I used first 1000 terms for this part), and approximate estimates are used for the remainder sum. Divergence from actual is near the 7th or 8 decimal point.
21 April, 2018 at 7:24 am
Terence Tao
That’s promising! Do you have a rough estimate as to what M (the number of values that need to be evaluated) might be for the barrier computation, based on what happened back at
values that need to be evaluated) might be for the barrier computation, based on what happened back at 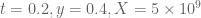 ? The main boost to speed should come in the large M regime. Also, if one uses symmetric sums
? The main boost to speed should come in the large M regime. Also, if one uses symmetric sums  rather than asymmetric sums
rather than asymmetric sums  then the error term should be a bit smaller (by a factor of 4 or so), which should allow one to make H a bit bigger for a given level of accuracy. One could also Taylor expand to second order rather than first to obtain significantly more accuracy, though the formulae get messier when one does so which may counteract the speedup. (Presumably one should start storing quantities such as
then the error term should be a bit smaller (by a factor of 4 or so), which should allow one to make H a bit bigger for a given level of accuracy. One could also Taylor expand to second order rather than first to obtain significantly more accuracy, though the formulae get messier when one does so which may counteract the speedup. (Presumably one should start storing quantities such as 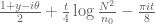 that appear multiple times in such formulae so that one does not compute them multiple times, though this is probably not the bottleneck in the computation.)
that appear multiple times in such formulae so that one does not compute them multiple times, though this is probably not the bottleneck in the computation.)
21 April, 2018 at 10:57 am
KM
I checked the ddx bound at N=69098, y=0.3, t=0 and it comes out to around 1000. If we choose a strip where |(A+B)/B0| seems to stay high (for eg. X = 6*10^10 + 2099 + [0,1] looks good in this respect) and assume it will stay above 1, M too seems to be around 1000. At N=69098, y=0.3, t=0.2, the ddx bound drops significantly to around 5.
The earlier script was refined so that it is now 6x to 7x faster than direct summation. I will check how varying H, number of Taylor terms and optimizing further can result in further speedup.
22 April, 2018 at 1:18 am
KM
Writing the Taylor expansion of the exponential in a more general form, it seems possible to improve the accuracy to as much as desired. Also, retaining and not approximating the two log factors does not incur a noticeable cost (storing the repeatedly occuring quantities kind of offsets it) while improving accuracy a bit. For eg. at H=10 and 4 Taylor terms, accuracy improves to 12 digits, and with 10 terms improves to 28 digits taking only 1.5x more time).
Near X=6*10^10, with H=50 and 4 Taylor terms, I was able to get estimates for 1000 points in around 1.5 minutes with 9 digit accuracy, which was a 20x speedup vs direct estimation.
22 April, 2018 at 7:12 am
Terence Tao
Sounds good! Could you expand a little on which log factors you found it better to not approximate? [EDIT: I guess you mean doing a Taylor expansion in rather than in
rather than in  ? I can see that that would be slightly more efficient.]
? I can see that that would be slightly more efficient.]
For some very minor accuracy improvements, one could work in a range![x \in X + [-1/2,1/2]](https://s0.wp.com/latex.php?latex=x+%5Cin+X+%2B+%5B-1%2F2%2C1%2F2%5D&bg=ffffff&fg=545454&s=0&c=20201002) rather than
rather than ![x \in X + [0,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+X+%2B+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) ; also, since we have some lower bound
; also, since we have some lower bound 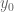 on
on  , we can write
, we can write  (say) and pull out a factor of
(say) and pull out a factor of  rather than
rather than  in order to replace the
in order to replace the  factors with the slightly smaller
factors with the slightly smaller 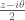 . This should improve the accuracy of the Taylor expansions by a factor of two or so with each term in the expansion, especially in the most important case when t is close to 0 and y close to y_0.
. This should improve the accuracy of the Taylor expansions by a factor of two or so with each term in the expansion, especially in the most important case when t is close to 0 and y close to y_0.
22 April, 2018 at 8:11 am
KM
I will try these out for more improvements. Also, it seems replacing log(N) +- i*Pi/8 with arrays of alpha(s) or alpha(1-s) values to get a close match to the exact (A+B)/B0 estimates also works. I was able to run the script for an entire rectangle (4000 points) in around 6 minutes.
22 April, 2018 at 8:43 am
KM
For the n0 sums, I calculated and stored sums of the form
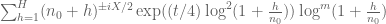
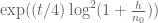 with
with  in the sums did not result in a noticeable speed difference overall, so I kept it in its original form.
in the sums did not result in a noticeable speed difference overall, so I kept it in its original form.
where m ranges from 0 to T-1 and T is the number of desired Taylor terms which can be passed to the function to approximate the larger exponential.
Replacing
22 April, 2018 at 1:09 pm
Terence Tao
Thanks for the clarification. I guess that while we will need to evaluate at thousands of values of (and perhaps hundreds of values of
(and perhaps hundreds of values of  as well), we won’t need as many values of
as well), we won’t need as many values of  to evaluate (and the evaluation becomes much faster as
to evaluate (and the evaluation becomes much faster as  increases), so there is not much advantage to remove the t-dependence in the inner sums, so it makes sense to keep factors such as
increases), so there is not much advantage to remove the t-dependence in the inner sums, so it makes sense to keep factors such as  unexpanded. In that case one can simplify the expressions a bit by writing
unexpanded. In that case one can simplify the expressions a bit by writing
for ,
,  ,
,  as
as
and use Taylor expansion of the exponential to decouple the variable from the
variable from the  variables.
variables.
It seems like we may have a choice of approximations to use: the approximation is our most accurate one (especially if we also insert the
approximation is our most accurate one (especially if we also insert the  correction), but the toy approximation
correction), but the toy approximation  may have acceptable accuracy at the
may have acceptable accuracy at the 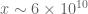 level and will be easier to work with (for instance I’d be likely to make fewer typos with computing d/dt type expressions in the latter : ). Do you have a sense of how complicated it would be to adapt these Taylor expansion techniques to the sums that show up in the
level and will be easier to work with (for instance I’d be likely to make fewer typos with computing d/dt type expressions in the latter : ). Do you have a sense of how complicated it would be to adapt these Taylor expansion techniques to the sums that show up in the  expansion? If it is too messy or slow then it may be worth focusing efforts on establishing a barrier for
expansion? If it is too messy or slow then it may be worth focusing efforts on establishing a barrier for 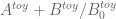 instead and reworking some of the writeup to provide effective estimates for the error of the toy approximation rather than the effective one.
instead and reworking some of the writeup to provide effective estimates for the error of the toy approximation rather than the effective one.
23 April, 2018 at 10:25 am
KM
I have to still try out the y0+z form of the estimate, but in the earlier one it seems instead of calculating



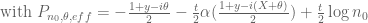
 the sum in the earlier comment, and using an array of
the sum in the earlier comment, and using an array of  instead of
instead of 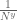 (also with appropriate adjustments for the A sum and when y varies instead of x),
(also with appropriate adjustments for the A sum and when y varies instead of x),
we calculate
and
we can switch from approximations of the toy model to approximations of the effective model, with some additional overhead (however the parigp library atleast does well and keeps the overhead small).
Also, on the discrepancy between the toy and effective estimates, at X=6*10^10, y=0.3, t=0.2 with divergence around the 6th or 7th decimal, but
with divergence around the 6th or 7th decimal, but  are different.
are different.
Some sample values:
theta,[(A+B)/B0]_toy, [(A+B)/B0]_eff, [(A+B)/B0]_toy_with_exact_gamma
0.0, 0.844 + 0.192i, 0.802 + 0.228i, 0.802 + 0.228i
0.5, 0.812 + 0.165i, 0.792 + 0.199i, 0.792 + 0.199i
1.0, 0.787 + 0.128i, 0.782 + 0.150i, 0.782 + 0.150i
the difference being only due to the different gamma factor.
23 April, 2018 at 6:31 pm
Terence Tao
OK, thanks for this. It sounds like the numerics will be able to handle the effective approximation without too much additional difficulty, so this looks to be a better path than trying to fix up the toy approximation to become more accurate (though this could probably be done by using a more careful Taylor expansion of gamma). It will be a bit messier to rigorously control the error in the Taylor expansion for the effective approximation than the toy approximation, but there should be a lot of room in the error bounds (it looks like we could in fact lose several orders of magnitude in the error bounds if we Taylor expand to a reasonably high order) so hopefully we could use relatively crude estimates to handle this.
24 April, 2018 at 10:25 am
KM
After making the three changes (y0+z, [X-1/2,X+1/2], and symmetric n0 sums), accuracy seems to improve by 2-3 digits.
25 April, 2018 at 6:35 am
Terence Tao
Excellent! Hopefully we can trade in surplus accuracy for speed later by increasing the H parameter.
Since we have a fixed value of , and the barrier computation is largely insensitive to the choice of
, and the barrier computation is largely insensitive to the choice of  (in particular, a barrier computation for large t can be re-used as is for any smaller value of t, or for any larger value of
(in particular, a barrier computation for large t can be re-used as is for any smaller value of t, or for any larger value of  ), it seems the next thing to do is to figure out what the smallest value of
), it seems the next thing to do is to figure out what the smallest value of  is for which the barrier computation is feasible. Given that, the main numerical task remaining would be to find the best values of
is for which the barrier computation is feasible. Given that, the main numerical task remaining would be to find the best values of 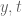 above this
above this  threshold for which the Euler product calculations work at
threshold for which the Euler product calculations work at  and above; combining that with analytic error estimates and some treatment of the case of very large
and above; combining that with analytic error estimates and some treatment of the case of very large  will then presumably yield a bound for
will then presumably yield a bound for  which is close to the limits of our methods.
which is close to the limits of our methods.
25 April, 2018 at 9:10 am
Anonymous
If t0 is small enough and X is carefully chosen, would it be possible to have y0=0 for the barrier computation?
25 April, 2018 at 10:26 am
Rudolph01
Intriguing question, Anonymous!
Just a few thoughts on this, I might be incorrect. If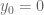 would be in reach of numerical verification to achieve a ‘fully closed’ barrier, isn’t then the issue that at
would be in reach of numerical verification to achieve a ‘fully closed’ barrier, isn’t then the issue that at 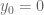 we will find real zeros when
we will find real zeros when  goes from
goes from 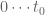 ? Of course, we could carefully pick a
? Of course, we could carefully pick a  and avoid a known real zero at
and avoid a known real zero at  , however we also have to account for all other real zeros that are ‘marching up leftwards’ and could travel through the barrier at
, however we also have to account for all other real zeros that are ‘marching up leftwards’ and could travel through the barrier at 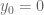 .
.
However, would we actually still require a ‘double’ barrier when the barrier reaches all the way to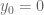 (i.e. no complex zeros can fly from right to left around the
(i.e. no complex zeros can fly from right to left around the 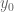 -corner anymore)? If indeed not, then maybe the way out is to just count all real zeros on the line
-corner anymore)? If indeed not, then maybe the way out is to just count all real zeros on the line 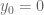 and
and  and subtract them from the total winding number found when scanning the entire barrier ‘rectangle’?
and subtract them from the total winding number found when scanning the entire barrier ‘rectangle’?
25 April, 2018 at 2:05 pm
Terence Tao
Yes, it seems theoretically possible to achieve this, though it may require a stupendous amount of numerical accuracy to actually pull off. It will probably help to have vary a bit in time, moving to the left to stay away from zeroes. If we can find a continuously varying function
vary a bit in time, moving to the left to stay away from zeroes. If we can find a continuously varying function  such that for all
such that for all  , there are no zeroes in the line segment
, there are no zeroes in the line segment  (including at the real endpoint
(including at the real endpoint  ), and all zeroes to the left of
), and all zeroes to the left of  are known to be real at time
are known to be real at time  , then this already implies that all zeroes to the left of
, then this already implies that all zeroes to the left of  are real at times
are real at times  , since no complex zeroes can penetrate the barrier, and no real zeroes can become complex at later times. But this would require a very accurate approximation of
, since no complex zeroes can penetrate the barrier, and no real zeroes can become complex at later times. But this would require a very accurate approximation of  near
near  , since no matter where one places
, since no matter where one places  one is going to be quite close to one of the real zeroes. In particular the
one is going to be quite close to one of the real zeroes. In particular the  type approximations we have been using may be inadequate for this, one may need to use
type approximations we have been using may be inadequate for this, one may need to use 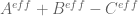 or an even higher order expansion. (My understanding is that similar higher order Riemann-Siegel expansions were what were already used in existing numerical verifications of RH. It may be that this is a task better suited for some experts in numerical RH verification, rather than our current Polymath group.)
or an even higher order expansion. (My understanding is that similar higher order Riemann-Siegel expansions were what were already used in existing numerical verifications of RH. It may be that this is a task better suited for some experts in numerical RH verification, rather than our current Polymath group.)
25 April, 2018 at 5:53 pm
Anonymous
> some experts in numerical RH verification, rather than our current Polymath group
it’s about 20 degrees cooler in this shade
26 April, 2018 at 11:19 am
KM
At N=69098 and t=0.2, we are getting these lower bounds
y, Bound type, Bound value, verification required upto approx N
0.20, Euler 5 Lemma, 0.0699, 1.5 million
0.25, Euler 3 Triangle, 0.0270, 900k
The first one currently looks quite slow to compute and also requires a large verification range. The second one looks feasible.
27 April, 2018 at 2:24 pm
Terence Tao
OK, so I guess we can try to target then (which would give
then (which would give 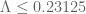 ). It all hinges on whether we can still compute enough of a mesh for the barrier though…
). It all hinges on whether we can still compute enough of a mesh for the barrier though…
26 April, 2018 at 11:39 am
Anonymous
Since the bound is , it seems that it does not make sense for a given
, it seems that it does not make sense for a given  to expand much effort to reduce
to expand much effort to reduce  much below
much below  .
.
28 April, 2018 at 2:25 am
Anonymous
Another possible strategy is to reduce slightly from 0.2 to 0.15 (say), and compensate for the added computational complexity by increasing(!) slightly
from 0.2 to 0.15 (say), and compensate for the added computational complexity by increasing(!) slightly 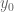 from 0.25 to 0.3 (say), with the resulting bound
from 0.25 to 0.3 (say), with the resulting bound 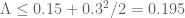 – (better even than the limiting choice
– (better even than the limiting choice  for
for  ).
).
The idea behind this optimization of and
and 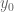 is that if
is that if  is sufficiently smaller than
is sufficiently smaller than  , it seems better to reduce slightly
, it seems better to reduce slightly  and increase(!) slightly
and increase(!) slightly 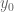 to keep reasonable computational complexity rather than the strategy of reducing both
to keep reasonable computational complexity rather than the strategy of reducing both  and
and 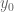 .
.
28 April, 2018 at 6:43 am
KM
I was kind of intrigued by the n0 sums so have been working to optimize it further. Firstly, just like X, after making y0+z symmetric so that the anchor point is (1+y0)/2, it seems the accuracy is more consistent along the rectangle.
Eliminating any head or tail exact partial sums, making H=N, and increasing the number of Taylor terms to something like 30 or 50 (with 50 terms, we seem to get above 25 digit accuracy), the same rectangle (4000 mesh points) can be computed under 10 seconds (from 6 min earlier).
It seems this way the entire barrier strip can be covered within a day. Working now on combining this with the adaptive t mesh.
29 April, 2018 at 1:29 pm
Terence Tao
Wow, that is surprisingly good performance! It actually surprises me that H can be taken as large as N, I would have expected the Taylor series expansion to start becoming very poorly convergent at this scale, but I guess the point is that by taking a huge number of Taylor terms one can compensate for this. An analogy would be computing by Taylor expansion (where for our purposes
by Taylor expansion (where for our purposes  could be something on the order of
could be something on the order of 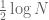 after the various symmetrising tricks). Normally one would only want to perform Taylor expansion for x in a range like [-1,1], but if one is willing to take 50 terms then I guess things are good up to something like [-10,10] (the Taylor series
after the various symmetrising tricks). Normally one would only want to perform Taylor expansion for x in a range like [-1,1], but if one is willing to take 50 terms then I guess things are good up to something like [-10,10] (the Taylor series  for
for  peaks at around
peaks at around 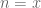 ) and so perhaps one can indeed treat expressions that are of magnitude
) and so perhaps one can indeed treat expressions that are of magnitude  or so for our current choice of
or so for our current choice of  .
.
28 April, 2018 at 8:49 pm
KM
The barrier strip X=6*10^10+2099 + [0,1] (N=69098), y=[0.2,1], t=[0,0.2] was covered (moving forward in t) and the output is kept here and here. The first file gives summary stats for each t in the adaptive t mesh, and the second file gives (A+B)/B0 values for all (x,y,t) mesh points considered. The winding number came out to be zero for each rectangle.
The multieval method with 50 Taylor terms was used to estimate (A+B)/B0 values along each rectangle. The overall computation time for the strip was around 2.5 hours. Since ddt bounds and ddx bounds take time to compute, they were updated only after every 100 rectangles. For each rectangle, the number of mesh points for each side was kept as ceil(ddx bound) (the strip was chosen where minabb = min rectangle mesh |(A+B)/B0| value was expected to be above 1, indicating an allowable step size above 1/(ddx bound)). This overcompensates a bit for the constant x sides since they are a bit shorter. The t jump used was minabb/(2*ddt bound).
29 April, 2018 at 1:51 pm
Terence Tao
That’s great progress! What is the minimum distance of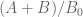 amongst the mesh points? At such large values of
amongst the mesh points? At such large values of 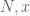 , the error terms
, the error terms  should be essentially negligible in this setting, though now that
should be essentially negligible in this setting, though now that  and
and  are a bit lower than what we have dealt with in the past, one may have to be a bit more careful, particularly when
are a bit lower than what we have dealt with in the past, one may have to be a bit more careful, particularly when  . However, there is a tradeoff between t and y that we could potentially exploit: I think it is possible to replace the condition
. However, there is a tradeoff between t and y that we could potentially exploit: I think it is possible to replace the condition 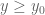 in the barrier with the slightly weaker
in the barrier with the slightly weaker  , thus one can make the barrier higher at small values of t and only reach
, thus one can make the barrier higher at small values of t and only reach 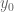 at the final time
at the final time  , basically because even if a zero sneaks underneath the elevated barrier at the earlier time it will still be attracted to its complex conjugate and eventually fall down to height
, basically because even if a zero sneaks underneath the elevated barrier at the earlier time it will still be attracted to its complex conjugate and eventually fall down to height 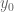 or below at time
or below at time  . I haven’t fully checked this claim and having such a moving barrier would also complicate the derivative analysis (one has to compute a total derivative rather than a partial derivative). But it looks like the numerics on the barrier side are now good enough that it is no longer the bottleneck (if I understand your previous comments correctly, the Euler mollifier component of the argument may now be the dominant remaining computation), so maybe this refinement is not needed at this stage.
. I haven’t fully checked this claim and having such a moving barrier would also complicate the derivative analysis (one has to compute a total derivative rather than a partial derivative). But it looks like the numerics on the barrier side are now good enough that it is no longer the bottleneck (if I understand your previous comments correctly, the Euler mollifier component of the argument may now be the dominant remaining computation), so maybe this refinement is not needed at this stage.
28 April, 2018 at 8:57 pm
KM
Also forgot to mention that y=[0.2,1] was used since the Euler 5 Lemma bound is positive at N=69098,y=0.2,t=0.2 and maybe there will be a faster way to calculate this up to the required N. Although right now I am finding it too slow, so will start with y=0.25, t=0.2 and the Euler 3 and 2 triangle bounds.
29 April, 2018 at 8:46 am
Rudolph01
Using KM’s latest script, a rerun for the same barrier strip![X=6 \cdot 10^{10}+2099 + [0,1], y=[0.2,1], t=[0,0.2]](https://s0.wp.com/latex.php?latex=X%3D6+%5Ccdot+10%5E%7B10%7D%2B2099+%2B+%5B0%2C1%5D%2C+y%3D%5B0.2%2C1%5D%2C+t%3D%5B0%2C0.2%5D&bg=ffffff&fg=545454&s=0&c=20201002) , but now recalculating the ddx and ddt-bounds for each rectangle, completed in 2 hours and 17 minutes. As expected the number of rectangles (or t-steps) to be verified, dropped from
, but now recalculating the ddx and ddt-bounds for each rectangle, completed in 2 hours and 17 minutes. As expected the number of rectangles (or t-steps) to be verified, dropped from  to
to  .
.
Here is the output:
Summary per rectangle
Full detail
30 April, 2018 at 6:50 am
KM
At t=0, y=0.2, N=69098, e_A + e_B + e_C,0 is 0.0012, hence not that small. For the t=0 rectangle, the gap between mesh points was taken as around 1/(ddx bound at t=0) for the sides where x varies and 0.8/ddx bound for the sides where y varies (using the ddx terminology for both ddx and ddy).
In this particular strip, the minimum |(A+B)/B0| for the t=0 mesh point set turned out to be around 2.374, and above 1.3 for the all the mesh points in all the rectangles considered. From this it seems that between the mesh points, |(A+B)/B0| here can’t go below about 1.185 for t=0 or below 0.65 for the other rectangles (or maybe a bit larger since the step size along the rectangles was conservative than what a adaptive ddx based mesh would have allowed).
Since t_next was set as t + min_|(A+B)/B0|_t / ddt_bound, it seems |(A+B)/B0| can’t go below 0.325 between the t points, though not sure whether the |f(z)|/2 concept can be applied in the t dimension.
30 April, 2018 at 8:30 am
Terence Tao
It’s interesting that is now exceeding 1 at t=0. Is this the reason for selecting
is now exceeding 1 at t=0. Is this the reason for selecting ![X = 6 \times 10^{10} + 2099 + [0,1]](https://s0.wp.com/latex.php?latex=X+%3D+6+%5Ctimes+10%5E%7B10%7D+%2B+2099+%2B+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) ? I would have expected this function to have average size comparable to 1, so the minimum would usually be less than 1.
? I would have expected this function to have average size comparable to 1, so the minimum would usually be less than 1.
I think the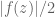 lower bound should work in the t variable as it does in the x or y variables (as long as the quantity
lower bound should work in the t variable as it does in the x or y variables (as long as the quantity  is estimated on the entire contour, and not just on the mesh, so one also needs some control on x and y derivatives). But it does seem that there is plenty of room between
is estimated on the entire contour, and not just on the mesh, so one also needs some control on x and y derivatives). But it does seem that there is plenty of room between 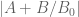 and the error terms
and the error terms 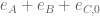 to accommodate any other errors we have to deal with (e.g. the error term in the 50-term Taylor expansion; I’m not sure how best to control that error yet, but given how small it is compared to everything else presumably we will be able to get away with a quite crude estimate here).
to accommodate any other errors we have to deal with (e.g. the error term in the 50-term Taylor expansion; I’m not sure how best to control that error yet, but given how small it is compared to everything else presumably we will be able to get away with a quite crude estimate here).
30 April, 2018 at 11:06 am
KM
Yes, this particular X was chosen after some exploration to get large jumps in t. |(A+B)/B0| does seem to have a tendency to jump sharply occasionally near t=0.
For example, I recently accidentally hit upon X=201062000500 (N=126491), y=0.2, t=0, where the estimate is 15.92 (error bound 0.0009). Changing y to 0.1 gives 23.16, and changing y to 0 gives 38.51. It seems local spikes of H_0 do not die down that quickly.
30 April, 2018 at 11:52 am
KM
To accelerate the mollifier bounds calculations (2-b-a), can we use a strategy like this:
Suppose we know the bound at N and it is positive enough and we are trying to reuse it for the bound at N+1. The DN terms each for the A and B parts) for the bounds at N and N+1 are similar except for the (t/2)Re(alpha) factor. Hence we subtract the the extra D terms from the bound at N to get a conservative estimate for that at N+1. Similarly to get the bound at N+2 from that at N+1. The conservative bound slowly decreases towards a postive predetermined threshold and we then update the base N again with the exact bound. Actually it seems this looks quite similar to a N mesh except there are a few calculations for each N.
30 April, 2018 at 5:23 pm
Terence Tao
This looks like it should work. Another variant, which may be a little simpler, is to take the current approximation, which I will call
approximation, which I will call  to make the dependence on
to make the dependence on  explicit, and approximate it by
explicit, and approximate it by  for
for  in a mesh interval
in a mesh interval 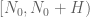 . For
. For  small, say
small, say 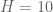 , one can hopefully estimate the error between the two approximations and keep it well under acceptable levels. Then we can apply the Euler mollifier method to
, one can hopefully estimate the error between the two approximations and keep it well under acceptable levels. Then we can apply the Euler mollifier method to  and bound this for all
and bound this for all  in the range with
in the range with 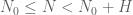 . With this approach, one doesn't have to analyse the more complicated sums arising from the Euler mollifications of
. With this approach, one doesn't have to analyse the more complicated sums arising from the Euler mollifications of 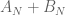 .
.
Also, relating to Euler mollification: the vestige of the Euler product formula suggests, heuristically at least, that
suggests, heuristically at least, that  will be a little larger than usual when the argument of
will be a little larger than usual when the argument of  is close to zero for small primes
is close to zero for small primes  , or equivalently if
, or equivalently if  is close to an integer for (say)
is close to an integer for (say)  . This heuristic seems to be in good agreement with your choice of
. This heuristic seems to be in good agreement with your choice of 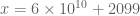 , where
, where 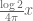 has fractional part
has fractional part  and
and 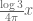 has fractional part
has fractional part  (though things are worse at p=5). It might be that one could use this heuristic to locate some promising further candidate scales x which one could then test numerically to see if they outperform the ones you already found. In particular, a partial Euler product
(though things are worse at p=5). It might be that one could use this heuristic to locate some promising further candidate scales x which one could then test numerically to see if they outperform the ones you already found. In particular, a partial Euler product  for some small value of
for some small value of  (e.g.
(e.g.  ) could perhaps serve as a proxy for how large one might expect
) could perhaps serve as a proxy for how large one might expect  to be. (Not coincidentally, these factors also show up in the Euler mollification method. One might also work with the more complicated variant
to be. (Not coincidentally, these factors also show up in the Euler mollification method. One might also work with the more complicated variant 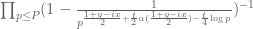 , though this may not make too much difference especially since we are primarily concerned with
, though this may not make too much difference especially since we are primarily concerned with  near zero. )
near zero. )
1 May, 2018 at 4:54 am
Anonymous
Dirichlet’s theorem on simultaneous Diophantine approximation (which follows from the pigeonhole principle) states that for any sequence of real numbers , any sequence of consecutive integers
, any sequence of consecutive integers  contains an integer
contains an integer  such that
such that
Where denotes the distance from
denotes the distance from  to its nearest integer.
to its nearest integer.
Hence (with ) where
) where  denotes the j-th prime, it follows that for a mollifier based on three primes, and
denotes the j-th prime, it follows that for a mollifier based on three primes, and  , it is possible to find
, it is possible to find  such that
such that
1 May, 2018 at 8:37 am
KM
By evaluating sum(||x * alpha_p||) or evaluating the Euler product for a large number of x (for eg. 6*10^10 + n, n the first 100k integers), and sorting to get small sums or large products, we get several candidates where |(A+B)/B0| is greater than 50. It seems this can be turned into a general method to choose a good barrier strip.
Some optimizations which further help are to compute the Euler products for x-0.5,x,x+0.5 and filter for x where all three are high, and to use a larger number of primes. Even with these the whole exercise is quite fast (about 2-3 minutes). Also since min |(A+B)/B0| for a rectangle generally occurs on the y=1 side, it helps to search for candidates using the Euler products at both y=0 and y=1.
Using first 5 primes and the above filters, I could find a candidate X=6*10^10+83952, where the estimate is 72.5 at y=0 and 5.13 at y=1. Running the barrier strip with X+[-0.5,0.5], y=[0.2,1], min |(A+B)/B0| started at 4.32 for the t=0 rectangle (2.374 for the earlier strip), and much fewer t steps were overall needed (280 instead of 440).
2 May, 2018 at 2:36 am
Rudolph01
KM’s idea (outlined a few posts back), for optimizing the ‘mollified’ computations that need to ensure that does not vanish in the range from the Barrier (N=69098) till the point where analytics take over (N=1,500,000), seems to work out very well! Only calculating a small number of incremental terms when moving from N to N+1, dramatically improves speed and indeed results in a slowly declining (hence more conservative) lower bound. We actually found the bound declines so slowly and stayed so far above a full-recomputation-threshold, that we never had to recompute the bound at all throughout the entire range. This implies we only require a full (relatively slow) compute of the first N in the range (i.e. at the Barrier) and this also enables the use of higher mollifiers again (for speed reasons we were considering moving back to
does not vanish in the range from the Barrier (N=69098) till the point where analytics take over (N=1,500,000), seems to work out very well! Only calculating a small number of incremental terms when moving from N to N+1, dramatically improves speed and indeed results in a slowly declining (hence more conservative) lower bound. We actually found the bound declines so slowly and stayed so far above a full-recomputation-threshold, that we never had to recompute the bound at all throughout the entire range. This implies we only require a full (relatively slow) compute of the first N in the range (i.e. at the Barrier) and this also enables the use of higher mollifiers again (for speed reasons we were considering moving back to  with Euler 3, but now could easily use
with Euler 3, but now could easily use  with Euler 5).
with Euler 5).
The run for , step 1, Euler 5 mollifier, completed in just 60 minutes. Output run. Fields: N, bound.
, step 1, Euler 5 mollifier, completed in just 60 minutes. Output run. Fields: N, bound.
Here are also the upper error bounds for in steps of
in steps of 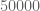 . Fields:
. Fields:  .
.
If all correct, this would bring us close to a :)
:)
2 May, 2018 at 11:23 am
Terence Tao
Great news! It seems like we have all the pieces needed to complete the proof of , I guess one has to check the analytic argument for
, I guess one has to check the analytic argument for  but perhaps you have done this already. It looks like both of the big computations (the barrier computation and the Euler mollification bound computation) are now quite feasible, but I don’t know whether there is much hope to push
but perhaps you have done this already. It looks like both of the big computations (the barrier computation and the Euler mollification bound computation) are now quite feasible, but I don’t know whether there is much hope to push  and
and  much further, at some point I would imagine the Euler mollification bounds will simply fail to prevent zeroes at
much further, at some point I would imagine the Euler mollification bounds will simply fail to prevent zeroes at  at which point we will be stuck (since it is probably not feasible to scan all of this region (as opposed to a narrow barrier) with direct evaluation of
at which point we will be stuck (since it is probably not feasible to scan all of this region (as opposed to a narrow barrier) with direct evaluation of  ).
).
2 May, 2018 at 12:15 pm
KM
While computing the exact mollifier bounds with Euler 7 and higher looks generally infeasible at these heights, is it possible to use an estimate like this to check whether a bound with a high enough mollifier turns positive. Only the first N terms in the B and A mollified bounds are computed exactly, and the remainder is bounded using the approach in the Estimating a Sum wiki.
2 May, 2018 at 3:08 pm
Terence Tao
Yes, this should work, and also combines well with the strategy of grouping the into batches
into batches ![N \in [N_0,N_0+H]](https://s0.wp.com/latex.php?latex=N+%5Cin+%5BN_0%2CN_0%2BH%5D&bg=ffffff&fg=545454&s=0&c=20201002) and trying to prove an Euler bound for an entire batch simultaneously. The tail bound could get rather messy though at Euler7.
and trying to prove an Euler bound for an entire batch simultaneously. The tail bound could get rather messy though at Euler7.
3 May, 2018 at 10:39 am
KM
In practice decoupling n and d as above seems to give bounds which are quite different from the exact ones and the gap increases if a higher mollifier is used. Instead of the tail sum bound I also checked the exact value of which too is relatively large, so a bit stuck here.
which too is relatively large, so a bit stuck here.
The error between (A+B)/B_0 and (A+B)/B_0 truncated to N_0 terms is much smaller compared to |(A+B)/B_0| and seems roughly dependent on N_0. For eg. using N_0=60000, the error is around 10^-4.
4 May, 2018 at 2:47 am
KM
It seems the tail sum bound can be replaced with a sharper quantity
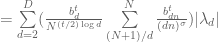

and with similar adjustments for the A tail sum
Also, if we then use a weaker mollifier with only prime terms and no interaction terms (for eg.![[\lambda_1,\lambda_2,\lambda_3,\lambda_5,\lambda_7,..]](https://s0.wp.com/latex.php?latex=%5B%5Clambda_1%2C%5Clambda_2%2C%5Clambda_3%2C%5Clambda_5%2C%5Clambda_7%2C..%5D&bg=ffffff&fg=545454&s=0&c=20201002) ) the gap between the approximate and the actual bound decreases sharply (I think since the terms in the mollified sum all have the same sign), but the bound still becomes more negative as the mollifier is taken higher.
) the gap between the approximate and the actual bound decreases sharply (I think since the terms in the mollified sum all have the same sign), but the bound still becomes more negative as the mollifier is taken higher.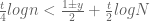 ) we could use
) we could use

If we assume the tail terms take a trapezoid shape with a curved side instead of a convex shape (which should be the case for
instead of the max factor in the tail bound.
With this the bound does improve as we we keep on increasing the mollifier, although atleast with the triangle bound at N=69098 and t=y=0.2, it plateaud at a negative value. Will also now check the behavior for the approximate lemma bound.
4 May, 2018 at 2:49 pm
Terence Tao
Thanks for this. The mollifier calculations seem to be getting quite complicated, we may well be near the limits of what can be done here even if we assume enough computational capacity to evaluate all the mollifier bounds. Do you have a sense of how badly things start breaking down if one tries to decrease t or y any further beyond 0.2? (Maybe one could continue this discussion on the new thread though, this one has become rather full.)
19 April, 2018 at 7:48 am
Sylvain JULIEN
Dear Terry,
Your analogy is interesting and as the physical state of matter is essentially determined by two physical parameters, namely temperature and pressure, it could be useful to define analogues thereof and maybe to show that $ latex \Lambda $ corresponds to the triple point of water, where it can exist under the three states solid liquid and gaseous simultaneously. This would be consistent with the seemingly “critical” nature of this constant.
19 April, 2018 at 7:55 am
Sylvain JULIEN
Perhaps a first step to do so would be to establish theoretically an analogue of the ideal gas relation $ \latex P=nkT $ where $ P $ is the pressure, $ T $ the absolute temperature, k a universal constant and n the number of particles per unit volume. I guess the analogue of the latter would be the number of zeroes in a domain of area 1.
19 April, 2018 at 7:52 pm
Anonymous
How uniform is the ddt bound in lemma 8.2 in the writeup?
20 April, 2018 at 9:24 am
Terence Tao
It holds for all in the region given by (5).
in the region given by (5).
20 April, 2018 at 10:38 pm
Anonymous
Perhaps “uniform” was the wrong word to use, but I don’t understand how a ddt bound for (x, y, t) helps to establish claim (i) unless the ddt bound applies to an interval, preferably an interval like (X <= x <= X+1, y0 <= y <= 1, t_i <= t <= t_j).
21 April, 2018 at 7:36 am
Terence Tao
Each individual term in the bound is either monotone decreasing or increasing in each of the variables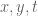 , so in a range such as the one you indicate, you can replace the occurrence of each variable by either its lower or its upper bound as appropriate. (In some cases one may need Lemma 5.1(vi) to establish monotonicity of terms such as
, so in a range such as the one you indicate, you can replace the occurrence of each variable by either its lower or its upper bound as appropriate. (In some cases one may need Lemma 5.1(vi) to establish monotonicity of terms such as  in
in  .)
.)
21 April, 2018 at 12:08 pm
Anonymous
Something strange is going on between gamma and lambda (both lower case) in the writeup. Should the instances of lambda that are not related to mollification be replaced by gamma?
[Yes, this is now fixed – T.]
21 April, 2018 at 2:56 pm
Anonymous
There is a line in the writeup like “log lambda = (t/4)[…]” and later there is a line like “d/dt log gamma = (t/4)[…]”. Should the first line be changed to “log gamma = (t/4)[…]” and the second line be changed to “d/dt log gamma = (1/4)[…]”?
[Yes, this is now fixed – T.]
21 April, 2018 at 3:37 pm
Anonymous
To me it looks like the “log gamma = …” and the “d/dt log gamma = …” lines conflict with each other. In the d/dt log gamma line, should t/4 be replaced by 1/4?
[Ah, I see now. Corrected in latest version – T.]
22 April, 2018 at 7:23 am
Anonymous
In github comments there is still some question about some of the terms in the d/dt bound in lemma 8.2. Specifically the derivation of the (pi/4)*log(n) term in both sums, and why the 2*log(n)/(x-6) term is in the first sum but not the second sum.
22 April, 2018 at 7:56 am
Terence Tao
The second was omitted by mistake, I have restored it. As for the first term, I have added an additional line of explanation: because we have
was omitted by mistake, I have restored it. As for the first term, I have added an additional line of explanation: because we have
we can conjugate to obtain
Incidentally, I do not know how to find the github comments you are referring to, do you have a link?
22 April, 2018 at 9:32 am
Anonymous
If I understand the comments in github, the question is about the expression (1/4) log(n) log(x / 4 pi n) + (pi/4) log(n) in the first and second sums of the |d/dt| bound, and whether (pi/4) log(n) could be changed to (pi/8) log(n).
I think the reasoning was that the expression originally comes from (alpha((1 + y – ix)/2)/2) log(n), and that alpha((1 + y – ix)/2) is approximated by (1/2)log(x / 4 pi) – (pi i)/4 + …, so when this is divided by two and multiplied by log(n) and the triangle inequality is applied, it should end up with a (pi/8) log(n) term instead of a (pi/4) log(n) term.
The comment I was referring to is at https://github.com/km-git-acc/dbn_upper_bound/pull/77#issuecomment-383368402. The github for this project is not organized in a normal way.
22 April, 2018 at 12:49 pm
Terence Tao
Thanks for the clarification and the link. KM was correct, there was a typo and one could replace the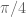 factor here by the
factor here by the  factor.
factor.
Perhaps the best thing to do, as suggested elsewhere by KM, is to replace the approximation by a very slightly less accurate approximation in which the rather messy
approximation by a very slightly less accurate approximation in which the rather messy  factors are replaced by
factors are replaced by 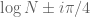 , making the approximation resemble the
, making the approximation resemble the  approximation instead. Actually I am tempted to simply _use_ the toy approximation and derive effective error bounds for that approximation; this toy approximation was not so great at the previous values of
approximation instead. Actually I am tempted to simply _use_ the toy approximation and derive effective error bounds for that approximation; this toy approximation was not so great at the previous values of  we were working with, but with
we were working with, but with  as large as
as large as  it’s actually not that bad. (The error between the two is something of the order of
it’s actually not that bad. (The error between the two is something of the order of  , I think.) I guess it should not be too difficult to do some numerical experimentation to get some idea of the discrepancy between
, I think.) I guess it should not be too difficult to do some numerical experimentation to get some idea of the discrepancy between  and
and 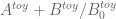 ; if the discrepancy is small enough, we can perhaps just use the toy approximation throughout which will make things like the d/dt calculations and Taylor expansion calculations a lot cleaner.
; if the discrepancy is small enough, we can perhaps just use the toy approximation throughout which will make things like the d/dt calculations and Taylor expansion calculations a lot cleaner.
22 April, 2018 at 7:42 am
Anonymous
In the writeup Lemma 8.2 applies to region (5) which includes 0 < t <= 1/2. Do either of the bounds in that lemma apply to t=0? In particular I would like to use the |d/dt| bound at t=0 as an upper bound of |d/dt| on some interval if possible.
22 April, 2018 at 7:58 am
Terence Tao
Yes, varies smoothly in
varies smoothly in  , so one can extend these bounds to the
, so one can extend these bounds to the  case.
case.
23 April, 2018 at 7:48 am
Anonymous
Is the change of from
from 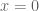 to
to  , being only
, being only 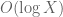 for large
for large  ?
?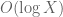 values of
values of  .
.
If so, it seems that tracking the argument changes can be done using only(!)
23 April, 2018 at 6:27 pm
Terence Tao
The ratio converges to 1 as
converges to 1 as 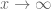 for any fixed
for any fixed 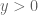 , and should also be quite close to 1 when y is large (e.g.
, and should also be quite close to 1 when y is large (e.g.  and
and  should suffice). So, assuming no zeroes of
should suffice). So, assuming no zeroes of  for
for 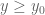 , the total variation of argument of
, the total variation of argument of  should be bounded from
should be bounded from  to
to  . But since we don’t actually know in advance that this is a zero free region, one would presumably have to scan the entire range
. But since we don’t actually know in advance that this is a zero free region, one would presumably have to scan the entire range 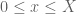 (or use something like the barrier argument we are currently using) in order to actually compute this variation.
(or use something like the barrier argument we are currently using) in order to actually compute this variation.
24 April, 2018 at 2:12 am
Anonymous
It seems that you meant “as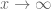 “. [Corrected, thanks – T.]
“. [Corrected, thanks – T.] is positive on an horizontal sub-interval
is positive on an horizontal sub-interval ![[x_k + i y, x_{k+1} + i y]](https://s0.wp.com/latex.php?latex=%5Bx_k+%2B+i+y%2C+x_%7Bk%2B1%7D+%2B+i+y%5D&bg=ffffff&fg=545454&s=0&c=20201002) , the magnitude of its argument increment over this sub-interval should be less than
, the magnitude of its argument increment over this sub-interval should be less than 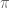 . Is it possible to improve the adaptive mesh used to evaluate the winding number of
. Is it possible to improve the adaptive mesh used to evaluate the winding number of  around a given rectangle ?
around a given rectangle ?
Anyway, if the real part of
24 April, 2018 at 7:03 am
Terence Tao
Some improvement to previous winding number arguments are presumably possible. But the most extensive calculation we were able to accomplish so far was to scan a region at
at 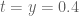 . Currently we are taking
. Currently we are taking  to be significantly smaller, and
to be significantly smaller, and  to be as large as
to be as large as  , so many orders of magnitude improvement over the previous state of the art for the argument principle methods would need to be established for these methods to be competitive.
, so many orders of magnitude improvement over the previous state of the art for the argument principle methods would need to be established for these methods to be competitive.
24 April, 2018 at 6:51 am
Anonymous
In page 4 of the paper, in the estimate (sixth line below (24))
Is the constant of the O-term dependent on (and unbounded as
(and unbounded as 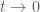 )?
)?
27 April, 2018 at 6:23 am
Rudolph01
Just for fun, here is a visual that (almost exactly) captures the trajectories of both the real and the complex zeros into a single 3D-plot for a certain range of . For the evaluation of
. For the evaluation of 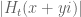 I used the third approach integral (the unbounded version).
I used the third approach integral (the unbounded version).
The real zeros are calculated exactly, however for the complex zeros I used a proxy and stopped scanning when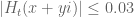 for the first time. I normalised
for the first time. I normalised  by simply multiplying it with
by simply multiplying it with  .
.
I believe the 3D root trajectories look exactly as the theory predicts :)
27 April, 2018 at 6:52 am
Anonymous
This is interesting since one can use this plot by pairing known consecutive real roots of by going backwards in time to see from which double real root of
by going backwards in time to see from which double real root of 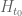 (for some negative “initial time”
(for some negative “initial time”  ) they “emerge” and what is the value of their common “initial time”
) they “emerge” and what is the value of their common “initial time”  .
.
27 April, 2018 at 9:06 am
Rudolph01
Yes, that is indeed the case. You can make pairs of real roots and find common ‘initial time of birth’. There a snag though about the ‘known consecutive real roots at ‘. Just take a look at the attached 2D frame for
‘. Just take a look at the attached 2D frame for 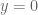 , that outlines a wider view of the trajectories of the real roots over time. It immediately becomes clear that pairs of real zeros are not necessarily consecutive (at
, that outlines a wider view of the trajectories of the real roots over time. It immediately becomes clear that pairs of real zeros are not necessarily consecutive (at  ) and also that they could have been born out of complex pair collision a ‘long time ago’.
) and also that they could have been born out of complex pair collision a ‘long time ago’.
Trajectories of real zeros
27 April, 2018 at 10:34 am
Anonymous
Yes, immediately after their “birth” (from a double zero) they are consecutive, but later a new pair may appear between them.
27 April, 2018 at 1:55 pm
Rudolph01
General theory predicts that all complex zeros of must travel within a ‘hyperbolic tunnel’
must travel within a ‘hyperbolic tunnel’  , until they collide with their conjugates.
, until they collide with their conjugates.
Using the ‘barrier approach’, we have shown that for , the rectangle
, the rectangle 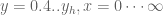 is zero-free, hence
is zero-free, hence 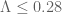 . In this diagram I tried to visualise this situation. The zero-free rectangle is shown as a red ‘ceiling’ at
. In this diagram I tried to visualise this situation. The zero-free rectangle is shown as a red ‘ceiling’ at  , where complex zeros can’t travel through (note that I exchanged
, where complex zeros can’t travel through (note that I exchanged  and
and  to obtain the blue hyperbola
to obtain the blue hyperbola  ). The area directly above the red ceiling (marked in darker green) now also must be free of complex zeros.
). The area directly above the red ceiling (marked in darker green) now also must be free of complex zeros.
I then wondered whether these red ‘ceilings’ also cast down a ‘zero-free shadow’, that further constrains the possible trajectories for the complex zeros below it. My logic would be that $\Lambda \le 0.28$ could be construed from many different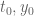 -combinations. E.g.
-combinations. E.g.  or
or 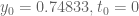 . These combinations are reflected as points on the smaller red-dashed hyperbola, with the greyed areas as the new zero-free regions. Is this reasoning correct?
. These combinations are reflected as points on the smaller red-dashed hyperbola, with the greyed areas as the new zero-free regions. Is this reasoning correct?
If this is correct, then an idea could be to use a previously achieved result to further reduce the -width of a new barrier to be verified (due to a smaller hyperbola). This of course only makes sense when the X-location of the barrier is moved further up in the new calculation, otherwise just lowering
-width of a new barrier to be verified (due to a smaller hyperbola). This of course only makes sense when the X-location of the barrier is moved further up in the new calculation, otherwise just lowering  would allow full reuse of the already verified barrier.
would allow full reuse of the already verified barrier.
28 April, 2018 at 3:39 am
Rudolph01
Oops. I suddenly saw where my logic fails. There are indeed many combinations of that lead to a
that lead to a  , however these combinations are not equivalent. I believe it is still true that a proven zero-free rectangle at
, however these combinations are not equivalent. I believe it is still true that a proven zero-free rectangle at 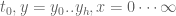 makes all rectangles for combinations
makes all rectangles for combinations  for the same
for the same  that occur ‘later’ (i.e.
that occur ‘later’ (i.e.  ) also zero-free, however the reverse is clearly not true.
) also zero-free, however the reverse is clearly not true.
Take for instance the rectangle that resides way ‘earlier’ than the proven zero-free rectangle
that resides way ‘earlier’ than the proven zero-free rectangle  . Both yield
. Both yield  , but still zeros could fly through the ‘earlier’ rectangle and collide on the real axis way below
, but still zeros could fly through the ‘earlier’ rectangle and collide on the real axis way below  …
…
I still believe that there is some sort of a smaller zero-free ‘shade’ just below the proven rectangles. Is this correct?
29 April, 2018 at 1:37 pm
Terence Tao
Nice visual! Unfortunately, while we have a lower bound on the rate at which the furthest zero falls towards the real axis, we don’t have an upper bound (in addition to the attraction that this zero feels to its complex conjugate, it will also be attracted to the infinitely many other zeroes). So I don’t know how to establish a zero free region of the sort you indicate; it could be that a zero stays close to the original de Bruijn bound until just before time , when it decides for some random reason to fall very rapidly towards the real axis. This is a very unlikely scenario, and possibly one that can be eliminated to some extent with a more delicate analysis (based on some sort of statement asserting that if a zero experiences an unusually strong pull towards the real axis at time
, when it decides for some random reason to fall very rapidly towards the real axis. This is a very unlikely scenario, and possibly one that can be eliminated to some extent with a more delicate analysis (based on some sort of statement asserting that if a zero experiences an unusually strong pull towards the real axis at time  , then it must also experience unusually strong pulls at some earlier times), but I don’t see a “cheap” way to do so.
, then it must also experience unusually strong pulls at some earlier times), but I don’t see a “cheap” way to do so.
3 May, 2018 at 3:54 pm
Anonymous
In the writeup, it seems that in the line below (32), “zero” should be “nonzero at “.
“.
[Corrected, thanks -T.]
4 May, 2018 at 1:18 pm
Rudolph01
Acknowledging that lowering towards
towards 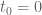 or even below it, would make the verification of a zero-free region for
or even below it, would make the verification of a zero-free region for 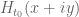 probably exponentially harder, I would like to test a thought that I have outlined in this visual.
probably exponentially harder, I would like to test a thought that I have outlined in this visual.
There are many combinations that would give a
combinations that would give a  , e.g.
, e.g.  . I believe the formula for the width of a particular ‘ceiling’ to be verified then is:
. I believe the formula for the width of a particular ‘ceiling’ to be verified then is: 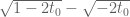 . This would imply that when
. This would imply that when  , the ‘ceiling’ width to be verified becomes infinitely small. Is this indeed correct?
, the ‘ceiling’ width to be verified becomes infinitely small. Is this indeed correct?
Going back in time, there will be a point when the number of complex zeros will stabilise, i.e. the point before which all real zeros have ‘collided’ and no new complex zeros will be ‘generated’ (up to a certain ). After the collision of two real zeros, the complex zeros will ‘take-off’ from the real line at a guaranteed minimum velocity (there is however no limit on the maximum take-off velocity), hence they will all move steadily away from the real line and travel closer and closer towards the edge of the De Bruijn hyperbola (blue curve in the visual). Could these movements imply that the situation at very large negative
). After the collision of two real zeros, the complex zeros will ‘take-off’ from the real line at a guaranteed minimum velocity (there is however no limit on the maximum take-off velocity), hence they will all move steadily away from the real line and travel closer and closer towards the edge of the De Bruijn hyperbola (blue curve in the visual). Could these movements imply that the situation at very large negative  becomes less ‘gaseous’ and sufficiently ‘solid’ again, thereby potentially re-enabling the verification of a zero-free ‘ceiling’?
becomes less ‘gaseous’ and sufficiently ‘solid’ again, thereby potentially re-enabling the verification of a zero-free ‘ceiling’?
4 May, 2018 at 2:38 pm
Terence Tao
Our understanding of the zeroes for negative time is rather poor. De Bruijn’s upper bound is only available at times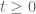 . In my paper with Brad Rodgers, we were not able to get a uniform bound on the imaginary parts of zeroes at negative times; instead we got the weaker bound
. In my paper with Brad Rodgers, we were not able to get a uniform bound on the imaginary parts of zeroes at negative times; instead we got the weaker bound 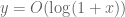 which is undoubtedly not optimal, but is the best we could manage. One can already see the difficulty in the A+B approximation (it has not been rigorously proven yet that the A+B approximation is accurate in the negative t regime, but I could imagine that this could be done with some effort). This approximation contains terms like
which is undoubtedly not optimal, but is the best we could manage. One can already see the difficulty in the A+B approximation (it has not been rigorously proven yet that the A+B approximation is accurate in the negative t regime, but I could imagine that this could be done with some effort). This approximation contains terms like 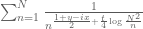 . For positive
. For positive  , the
, the  factor eventually helps with the convergence and makes the
factor eventually helps with the convergence and makes the 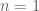 term dominate, which is where the “freezing to solid” behavior is coming from. But for negative
term dominate, which is where the “freezing to solid” behavior is coming from. But for negative  , this term now hurts instead of helps, and makes the sum much wilder, particularly at large values of
, this term now hurts instead of helps, and makes the sum much wilder, particularly at large values of  . So I would expect it should become increasingly “gaseous”, though I don’t have a good intuition on exactly how much so.
. So I would expect it should become increasingly “gaseous”, though I don’t have a good intuition on exactly how much so.
4 May, 2018 at 2:23 pm
Polymath15, ninth thread: going below 0.22? | What's new
[…] thread of the Polymath15 project to upper bound the de Bruijn-Newman constant , continuing this post. Discussion of the project of a non-research nature can continue for now in the existing proposal […]
26 May, 2018 at 11:29 am
El proyecto Polymath15 logra reducir la cota superior de la constante de Bruijn-Newman | Ciencia | La Ciencia de la Mula Francis
[…] el método numérico [Tao, 28 Mar 2018], hasta alcanzar una cota de Λ ≤ 0.28 [Tao, 17 Apr 2018]. El método de la barrera desarrollado para el ataque analítico prometía […]
6 June, 2018 at 8:28 pm
JUN-HAO
Dear Pro. Tao,
I am the high school student, and want to enter the university, but my parents say that major in math, it has disadvantages when I search occupation.Is that ok major in engeeniring or other science area,then, research math? And if you don’t mind,can you tell me what you major in university?
24 August, 2018 at 8:23 pm
a
Is going below $0.28$ and for that matter below $\epsilon>0$ a complexity theoretic problem? Can complexity theory say anything here substantial?
25 August, 2018 at 8:20 am
Terence Tao
Very roughly speaking, getting below
below  is of comparable difficulty to establishing a zero-free region for the zeta function up to height
is of comparable difficulty to establishing a zero-free region for the zeta function up to height  , where
, where 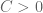 is an absolute constant. The known algorithms for verifying such a zero free region are polynomial in the height, so the verification time for proving
is an absolute constant. The known algorithms for verifying such a zero free region are polynomial in the height, so the verification time for proving  currently is exponential in the reciprocal of
currently is exponential in the reciprocal of  . Of course, if the Riemann hypothesis is ever proved, the verification time becomes
. Of course, if the Riemann hypothesis is ever proved, the verification time becomes 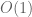 . :-)
. :-)
26 August, 2018 at 5:56 am
a
Still does not clarify if it is in $NP$ and perhaps there are approximations.
26 August, 2018 at 8:47 am
Terence Tao
The situation should again be broadly analogous to that of finding a zero-free region of the zeta function up to height . At present there is no certificate known for verifying such a region that also does not require
. At present there is no certificate known for verifying such a region that also does not require  amount of time to verify (even assuming unlimited space). It’s possible though that there is a probabilistic algorithm that verifies in much smaller time but using an exponential amount of space, in the spirit of the PCP theorem, but I am not an expert on these matters.
amount of time to verify (even assuming unlimited space). It’s possible though that there is a probabilistic algorithm that verifies in much smaller time but using an exponential amount of space, in the spirit of the PCP theorem, but I am not an expert on these matters.
Of course, as before, if one manages to find a proof of RH, all these tasks can then be done in O(1) time and space. :)
UPDATE: After looking up the statement of the PCP theorem, it seems that it can be applied directly to conclude that (assuming a zero free region of height exists) there exists a probabilistically checkable proof of length
exists) there exists a probabilistically checkable proof of length 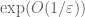 that can be probabilistically verified (with, say, greater than 2/3 probability of accuracy) using only
that can be probabilistically verified (with, say, greater than 2/3 probability of accuracy) using only 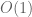 query complexity. Of course, actually constructing this proof should still take exponential time…
query complexity. Of course, actually constructing this proof should still take exponential time…
26 August, 2018 at 11:59 pm
a
Typically ‘proof’s do not change wrt to $\epsilon$ (sort of the situation like P/poly where if something is in P/poly we expect to be in P). We may have to show a certain property for a sequence of 0’s and 1’s whose length depends on epsilon but typically for various epsilon we should expect the proof structure to be same (which can be extrapolated all the way to epsilon=0). This is consistent with the known fact that RH is a Pi_1 statement. May be there is an alternate route to going past 0.22 or so and may be all the way to 0.
27 August, 2018 at 12:24 am
a
‘ something is in P/poly’ should ‘something that is provable, natural and not totally out of the world is in P/poly’.
6 September, 2018 at 7:19 pm
Polymath15, tenth thread: numerics update | What's new
[…] thread of the Polymath15 project to upper bound the de Bruijn-Newman constant , continuing this post. Discussion of the project of a non-research nature can continue for now in the existing proposal […]