This is a sequel to this previous blog post, in which we discussed the effect of the heat flow evolution
on the zeroes of a time-dependent family of polynomials , with a particular focus on the case when the polynomials
had real zeroes. Here (inspired by some discussions I had during a recent conference on the Riemann hypothesis in Bristol) we record the analogous theory in which the polynomials instead have zeroes on a circle
, with the heat flow slightly adjusted to compensate for this. As we shall discuss shortly, a key example of this situation arises when
is the numerator of the zeta function of a curve.
More precisely, let be a natural number. We will say that a polynomial
of degree (so that
) obeys the functional equation if the
are all real and
for all , thus
and
for all non-zero . This means that the
zeroes
of
(counting multiplicity) lie in
and are symmetric with respect to complex conjugation
and inversion
across the circle
. We say that this polynomial obeys the Riemann hypothesis if all of its zeroes actually lie on the circle
. For instance, in the
case, the polynomial
obeys the Riemann hypothesis if and only if
.
Such polynomials arise in number theory as follows: if is a projective curve of genus
over a finite field
, then, as famously proven by Weil, the associated local zeta function
(as defined for instance in this previous blog post) is known to take the form
where is a degree
polynomial obeying both the functional equation and the Riemann hypothesis. In the case that
is an elliptic curve, then
and
takes the form
, where
is the number of
-points of
minus
. The Riemann hypothesis in this case is a famous result of Hasse.
Another key example of such polynomials arise from rescaled characteristic polynomials
of matrices
in the compact symplectic group
. These polynomials obey both the functional equation and the Riemann hypothesis. The Sato-Tate conjecture (in higher genus) asserts, roughly speaking, that “typical” polyomials
arising from the number theoretic situation above are distributed like the rescaled characteristic polynomials (1), where
is drawn uniformly from
with Haar measure.
Given a polynomial of degree
with coefficients
we can evolve it in time by the formula
thus for
. Informally, as one increases
, this evolution accentuates the effect of the extreme monomials, particularly,
and
at the expense of the intermediate monomials such as
, and conversely as one decreases
. This family of polynomials obeys the heat-type equation
In view of the results of Marcus, Spielman, and Srivastava, it is also very likely that one can interpret this flow in terms of expected characteristic polynomials involving conjugation over the compact symplectic group , and should also be tied to some sort of “
” version of Brownian motion on this group, but we have not attempted to work this connection out in detail.
It is clear that if obeys the functional equation, then so does
for any other time
. Now we investigate the evolution of the zeroes. Suppose at some time
that the zeroes
of
are distinct, then
From the inverse function theorem we see that for times sufficiently close to
, the zeroes
of
continue to be distinct (and vary smoothly in
), with
Differentiating this at any not equal to any of the
, we obtain
and
and
Inserting these formulae into (2) (expanding as
) and canceling some terms, we conclude that
for sufficiently close to
, and
not equal to
. Extracting the residue at
, we conclude that
which we can rearrange as
If we make the change of variables (noting that one can make
depend smoothly on
for
sufficiently close to
), this becomes
Intuitively, this equation asserts that the phases repel each other if they are real (and attract each other if their difference is imaginary). If
obeys the Riemann hypothesis, then the
are all real at time
, then the Picard uniqueness theorem (applied to
and its complex conjugate) then shows that the
are also real for
sufficiently close to
. If we then define the entropy functional
then the above equation becomes a gradient flow
which implies in particular that is non-increasing in time. This shows that as one evolves time forward from
, there is a uniform lower bound on the separation between the phases
, and hence the equation can be solved indefinitely; in particular,
obeys the Riemann hypothesis for all
if it does so at time
. Our argument here assumed that the zeroes of
were simple, but this assumption can be removed by the usual limiting argument.
For any polynomial obeying the functional equation, the rescaled polynomials
converge locally uniformly to
as
. By Rouche’s theorem, we conclude that the zeroes of
converge to the equally spaced points
on the circle
. Together with the symmetry properties of the zeroes, this implies in particular that
obeys the Riemann hypothesis for all sufficiently large positive
. In the opposite direction, when
, the polynomials
converge locally uniformly to
, so if
,
of the zeroes converge to the origin and the other
converge to infinity. In particular,
fails the Riemann hypothesis for sufficiently large negative
. Thus (if
), there must exist a real number
, which we call the de Bruijn-Newman constant of the original polynomial
, such that
obeys the Riemann hypothesis for
and fails the Riemann hypothesis for
. The situation is a bit more complicated if
vanishes; if
is the first natural number such that
(or equivalently,
) does not vanish, then by the above arguments one finds in the limit
that
of the zeroes go to the origin,
go to infinity, and the remaining
zeroes converge to the equally spaced points
. In this case the de Bruijn-Newman constant remains finite except in the degenerate case
, in which case
.
For instance, consider the case when and
for some real
with
. Then the quadratic polynomial
has zeroes
and one easily checks that these zeroes lie on the circle when
, and are on the real axis otherwise. Thus in this case we have
(with
if
). Note how as
increases to
, the zeroes repel each other and eventually converge to
, while as
decreases to
, the zeroes collide and then separate on the real axis, with one zero going to the origin and the other to infinity.
The arguments in my paper with Brad Rodgers (discussed in this previous post) indicate that for a “typical” polynomial of degree
that obeys the Riemann hypothesis, the expected time to relaxation to equilibrium (in which the zeroes are equally spaced) should be comparable to
, basically because the average spacing is
and hence by (3) the typical velocity of the zeroes should be comparable to
, and the diameter of the unit circle is comparable to
, thus requiring time comparable to
to reach equilibrium. Taking contrapositives, this suggests that the de Bruijn-Newman constant
should typically take on values comparable to
(since typically one would not expect the initial configuration of zeroes to be close to evenly spaced). I have not attempted to formalise or prove this claim, but presumably one could do some numerics (perhaps using some of the examples of
given previously) to explore this further.

18 comments
Comments feed for this article
7 June, 2018 at 6:10 am
Anonymous
It seems that Riemann zeta function (whose zeros are pseudo-randomly distributed) can’t be interpreted (in any sense) as some “limiting case” of the above local zeta functions (having uniformly distributed zeros.)
8 June, 2018 at 1:56 pm
Joseph
I would have the intuition that maybe the value of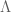 should be closer to zero than
should be closer to zero than  because of the zeros which are close to each other: if the closest pair of zeros has distance
because of the zeros which are close to each other: if the closest pair of zeros has distance  and if we run the flow backwards, then they attract each other with speed about
and if we run the flow backwards, then they attract each other with speed about 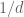 , and then would collide at time about
, and then would collide at time about  if we neglect the other zeros (which are at much larger distance). For characteristic polynomial of
if we neglect the other zeros (which are at much larger distance). For characteristic polynomial of  where
where  has order
has order  , I would expect
, I would expect 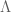 of about
of about  if my intuition is correct.
if my intuition is correct.
9 June, 2018 at 6:54 am
Terence Tao
Hmm, I think you’re right; the time to relaxation to equilibrium gives a lower bound on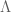 but it is far from optimal.
but it is far from optimal.
In the case of zeroes on the real line, there is a criterion of Csordas, Smith and Varga (see Theorem 1 of https://link.springer.com/article/10.1007/BF01205170 ) that says, roughly speaking, that if one has a pair of zeroes at separation , and the other zeroes are significantly further away from this pair than
, and the other zeroes are significantly further away from this pair than  , then
, then  . It may well be that an analogous result holds on the circle.
. It may well be that an analogous result holds on the circle.
9 June, 2018 at 1:01 pm
Joseph
I think it is equivalent to have points on the circle or all the determinations of their arguments on the real line (which gives a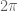 -periodic set), because of the formula
-periodic set), because of the formula  .
.
9 June, 2018 at 8:35 am
Aula
The third display above (3) is too wide.
[Corrected, thanks – T.]
9 June, 2018 at 10:04 am
Will Sawin
It should possible to obtain the “time to relaxation” upper bound using only the middle coefficient. It has variance , so it is presumably typically of size
, so it is presumably typically of size  , meaning at time
, meaning at time  , it is of size
, it is of size  compared to the first and last coefficients, compared to the bound
compared to the first and last coefficients, compared to the bound  for polynomials with all roots on the unit circle.
for polynomials with all roots on the unit circle.
18 June, 2018 at 9:22 am
Anonymous
Dear Terry,
I am not an expert mathematician.But I think the Riemann’s difficult level is 5 times more than Poincare.Because one only needs one way to go to the destination,Riemann must has 5 ways done:straight and then go back,attack the middle point,the first point and then the final point.And not enough, you must go with the first step on the old road many times.I know Terry very well.Someday not so long,the community of maths has amusing news from Terry.
Best wishes,
(Company of Pro.Tao -two decades)
2 July, 2018 at 3:16 pm
curious
Does the entropy here have anything do with information?
16 August, 2018 at 9:19 am
Tatenda Kubalalika
Dear Prof. Tao, according to equation of your paper with Prof. Rodgers, “the de Bruijn-newman constant is nonnegative”, the de Bruijn-Newman constant seems to be equal to
of your paper with Prof. Rodgers, “the de Bruijn-newman constant is nonnegative”, the de Bruijn-Newman constant seems to be equal to 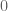 .
.
Indeed, for , we have
, we have
Notice that the right-hand side is invariant under the transformation , thus we have
, thus we have
for all . Suppose that
. Suppose that  for some real
for some real  hence
hence  . But we know by a result of Rodgers and Tao that
. But we know by a result of Rodgers and Tao that  for any
for any  and
and  . Thus we arrive at a contradiction,, which entails that our supposition must be false, and the desired result follows.
. Thus we arrive at a contradiction,, which entails that our supposition must be false, and the desired result follows. 
16 August, 2018 at 2:30 pm
Terence Tao
Unfortunately, the identity (1) is only valid for (as you point out), hence the identity (2) is only valid when
(as you point out), hence the identity (2) is only valid when  , that is to say it is only established in the case
, that is to say it is only established in the case  (where it is trivial). Actually, one can check numerically that (2) is false in general.
(where it is trivial). Actually, one can check numerically that (2) is false in general.
16 August, 2018 at 11:59 pm
Anonymous
Since in (1) (for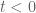 )
)  can be replaced by
can be replaced by  , is it possible that this modification of (1) (with the resulting branch point at
, is it possible that this modification of (1) (with the resulting branch point at  due to
due to  ) still holds for some analytic continuation (with respect to
) still holds for some analytic continuation (with respect to  ) of the modified integral ?
) of the modified integral ?
17 August, 2018 at 6:23 pm
Terence Tao
For positive t, one has
(see the equation before (35) in https://github.com/km-git-acc/dbn_upper_bound/blob/master/Writeup/debruijn.pdf ).
16 August, 2018 at 2:50 pm
Tatenda Kubalalika
Thank you for your response. Do you have any specific $t$ (or t’s) in mind for which (2) is false ? Because it seems to me that $H_{t}(z)$ is the Fourier transform of $\phi(t)e^{zt^2}$, which is an even function. This seems to imply that $H_t$ should also be even. That is, $H_{t}(z)=H_{-t}(z)$ for all real $t$. Of course, my reasoning could be flawed.
16 August, 2018 at 4:28 pm
TK
My mistake indeed in the last comment: i made a typo in the above Fourier transform, which invalidates the argument.
24 August, 2018 at 2:45 am
Tate. I. K
Indeed, the de Bruijn-Newman constant could be equal to zero.
Suppose there exists some pair of real numbers with
of real numbers with  , such that
, such that . It is a classical fact that
. It is a classical fact that 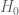 as many real zeros, and let
as many real zeros, and let  be one such zero, where
be one such zero, where  is some real number. That is,
is some real number. That is,  We shall refer to this as equation
We shall refer to this as equation  . Combining equations
. Combining equations  and
and  yields
yields
 We shall refer to this as equation
We shall refer to this as equation  As noted in Rodgers and Tao’s paper (page 3), one can view
As noted in Rodgers and Tao’s paper (page 3), one can view  as the evolution of
as the evolution of  under the backwards heat equation
under the backwards heat equation  , where
, where 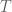 denotes the time. Hence from equation
denotes the time. Hence from equation  we deduce that,“one can view
we deduce that,“one can view  as the EVOLUTION of
as the EVOLUTION of  ” But this quoted statement is meaningless, since both
” But this quoted statement is meaningless, since both  and
and  represent the same time
represent the same time  .
.
$\latex H_{T}(z)=0.$ We shall refer to this as equation
We therefore conclude that our supposition must be false, and the desired result follows. $\square$ equal to zero.
24 August, 2018 at 2:20 pm
Terence Tao
(a) There certainly do exist pairs of real numbers with
of real numbers with  and
and  . In fact, it is a result of Ki, Kim and Lee that for
. In fact, it is a result of Ki, Kim and Lee that for  , there are infinitely many zeroes of
, there are infinitely many zeroes of  , all but finitely many of which are real.
, all but finitely many of which are real.
(b) You have only shown that the equation holds for a single value of
holds for a single value of  , not for all
, not for all  . The evolution of the heat equation does not depend only on the pointwise value of the initial data at a single value of
. The evolution of the heat equation does not depend only on the pointwise value of the initial data at a single value of  , but on the values at all other positions as well (the heat equation has infinite speed of propagation).
, but on the values at all other positions as well (the heat equation has infinite speed of propagation).
24 August, 2018 at 2:57 am
Anonymous commenter.
@Tate. I. K, it really seems that you have demonstrated that . However, your argument is suspiciously short. It will be truly strange if such a long-standing problem as the RH could have such a short solution. I suggest that you submit your work to a formal journal, and goodluck !
. However, your argument is suspiciously short. It will be truly strange if such a long-standing problem as the RH could have such a short solution. I suggest that you submit your work to a formal journal, and goodluck !
28 April, 2022 at 12:43 pm
Brian C. Hall
In Section 2.3 of a recent preprint of mine with Ching-Wei Ho, we studied (essentially) this evolution from a random matrix point of view. Suppose, for example, that you start with the characteristic polynomial of a Brownian motion in the unitary group and then evolve toward negative time. We conjecture that the roots will rapidly move off the unit circle and that they will eventually resemble the eigenvalues of a Brownian motion in the general linear group. See https://arxiv.org/abs/2202.09660