[Note: the content of this post is standard number theoretic material that can be found in many textbooks (I am relying principally here on Iwaniec and Kowalski); I am not claiming any new progress on any version of the Riemann hypothesis here, but am simply arranging existing facts together.]
The Riemann hypothesis is arguably the most important and famous unsolved problem in number theory. It is usually phrased in terms of the Riemann zeta function , defined by
for and extended meromorphically to other values of
, and asserts that the only zeroes of
in the critical strip
lie on the critical line
.
One of the main reasons that the Riemann hypothesis is so important to number theory is that the zeroes of the zeta function in the critical strip control the distribution of the primes. To see the connection, let us perform the following formal manipulations (ignoring for now the important analytic issues of convergence of series, interchanging sums, branches of the logarithm, etc., in order to focus on the intuition). The starting point is the fundamental theorem of arithmetic, which asserts that every natural number has a unique factorisation
into primes. Taking logarithms, we obtain the identity
for any natural number , where
is the von Mangoldt function, thus
when
is a power of a prime
and zero otherwise. If we then perform a “Dirichlet-Fourier transform” by viewing both sides of (1) as coefficients of a Dirichlet series, we conclude that
formally at least. Writing , the right-hand side factors as
whereas the left-hand side is (formally, at least) equal to . We conclude the identity
(formally, at least). If we integrate this, we are formally led to the identity
or equivalently to the exponential identity
which allows one to reconstruct the Riemann zeta function from the von Mangoldt function. (It is instructive exercise in enumerative combinatorics to try to prove this identity directly, at the level of formal Dirichlet series, using the fundamental theorem of arithmetic of course.) Now, as has a simple pole at
and zeroes at various places
on the critical strip, we expect a Weierstrass factorisation which formally (ignoring normalisation issues) takes the form
(where we will be intentionally vague about what is hiding in the terms) and so we expect an expansion of the form
Note that
and hence on integrating in we formally have
and thus we have the heuristic approximation
Comparing this with (3), we are led to a heuristic form of the explicit formula
When trying to make this heuristic rigorous, it turns out (due to the rough nature of both sides of (4)) that one has to interpret the explicit formula in some suitably weak sense, for instance by testing (4) against the indicator function to obtain the formula
which can in fact be made into a rigorous statement after some truncation (the von Mangoldt explicit formula). From this formula we now see how helpful the Riemann hypothesis will be to control the distribution of the primes; indeed, if the Riemann hypothesis holds, so that for all zeroes
, it is not difficult to use (a suitably rigorous version of) the explicit formula to conclude that
as , giving a near-optimal “square root cancellation” for the sum
. Conversely, if one can somehow establish a bound of the form
for any fixed , then the explicit formula can be used to then deduce that all zeroes
of
have real part at most
, which leads to the following remarkable amplification phenomenon (analogous, as we will see later, to the tensor power trick): any bound of the form
can be automatically amplified to the stronger bound
with both bounds being equivalent to the Riemann hypothesis. Of course, the Riemann hypothesis for the Riemann zeta function remains open; but partial progress on this hypothesis (in the form of zero-free regions for the zeta function) leads to partial versions of the asymptotic (6). For instance, it is known that there are no zeroes of the zeta function on the line , and this can be shown by some analysis (either complex analysis or Fourier analysis) to be equivalent to the prime number theorem
see e.g. this previous blog post for more discussion.
The main engine powering the above observations was the fundamental theorem of arithmetic, and so one can expect to establish similar assertions in other contexts where some version of the fundamental theorem of arithmetic is available. One of the simplest such variants is to continue working on the natural numbers, but “twist” them by a Dirichlet character . The analogue of the Riemann zeta function is then the https://en.wikipedia.org/wiki/Multiplicative_function, the equation (1), which encoded the fundamental theorem of arithmetic, can be twisted by
to obtain
and essentially the same manipulations as before eventually lead to the exponential identity
which is a twisted version of (2), as well as twisted explicit formula, which heuristically takes the form
for non-principal , where
now ranges over the zeroes of
in the critical strip, rather than the zeroes of
; a more accurate formulation, following (5), would be
(See e.g. Davenport’s book for a more rigorous discussion which emphasises the analogy between the Riemann zeta function and the Dirichlet -function.) If we assume the generalised Riemann hypothesis, which asserts that all zeroes of
in the critical strip also lie on the critical line, then we obtain the bound
for any non-principal Dirichlet character , again demonstrating a near-optimal square root cancellation for this sum. Again, we have the amplification property that the above bound is implied by the apparently weaker bound
(where denotes a quantity that goes to zero as
for any fixed
). Next, one can consider other number systems than the natural numbers
and integers
. For instance, one can replace the integers
with rings
of integers in other number fields
(i.e. finite extensions of
), such as the quadratic extensions
of the rationals for various square-free integers
, in which case the ring of integers would be the ring of quadratic integers
for a suitable generator
(it turns out that one can take
if
, and
if
). Here, it is not immediately obvious what the analogue of the natural numbers
is in this setting, since rings such as
do not come with a natural ordering. However, we can adopt an algebraic viewpoint to see the correct generalisation, observing that every natural number
generates a principal ideal
in the integers, and conversely every non-trivial ideal
in the integers is associated to precisely one natural number
in this fashion, namely the norm
of that ideal. So one can identify the natural numbers with the ideals of
. Furthermore, with this identification, the prime numbers correspond to the prime ideals, since if
is prime, and
are integers, then
if and only if one of
or
is true. Finally, even in number systems (such as
) in which the classical version of the fundamental theorem of arithmetic fail (e.g.
), we have the fundamental theorem of arithmetic for ideals: every ideal
in a Dedekind domain (which includes the ring
of integers in a number field as a key example) is uniquely representable (up to permutation) as the product of a finite number of prime ideals
(although these ideals might not necessarily be principal). For instance, in
, the principal ideal
factors as the product of four prime (but non-principal) ideals
,
,
,
. (Note that the first two ideals
are actually equal to each other.) Because we still have the fundamental theorem of arithmetic, we can develop analogues of the previous observations relating the Riemann hypothesis to the distribution of primes. The analogue of the Riemann hypothesis is now the Dedekind zeta function
where the summation is over all non-trivial ideals in . One can also define a von Mangoldt function
, defined as
when
is a power of a prime ideal
, and zero otherwise; then the fundamental theorem of arithmetic for ideals can be encoded in an analogue of (1) (or (7)),
which leads as before to an exponential identity
and an explicit formula of the heuristic form
in analogy with (5) or (10). Again, a suitable Riemann hypothesis for the Dedekind zeta function leads to good asymptotics for the distribution of prime ideals, giving a bound of the form
where is the conductor of
(which, in the case of number fields, is the absolute value of the discriminant of
) and
is the degree of the extension of
over
. As before, we have the amplification phenomenon that the above near-optimal square root cancellation bound is implied by the weaker bound
where denotes a quantity that goes to zero as
(holding
fixed). See e.g. Chapter 5 of Iwaniec-Kowalski for details.
As was the case with the Dirichlet -functions, one can twist the Dedekind zeta function example by characters, in this case the Hecke characters; we will not do this here, but see e.g. Section 3 of Iwaniec-Kowalski for details.
Very analogous considerations hold if we move from number fields to function fields. The simplest case is the function field associated to the affine line and a finite field
of some order
. The polynomial functions on the affine line
are just the usual polynomial ring
, which then play the role of the integers
(or
) in previous examples. This ring happens to be a unique factorisation domain, so the situation is closely analogous to the classical setting of the Riemann zeta function. The analogue of the natural numbers are the monic polynomials (since every non-trivial principal ideal is generated by precisely one monic polynomial), and the analogue of the prime numbers are the irreducible monic polynomials. The norm
of a polynomial is the order of
, which can be computed explicitly as
Because of this, we will normalise things slightly differently here and use in place of
in what follows. The (local) zeta function
is then defined as
where ranges over monic polynomials, and the von Mangoldt function
is defined to equal
when
is a power of a monic irreducible polynomial
, and zero otherwise. Note that because
is always a power of
, the zeta function here is in fact periodic with period
. Because of this, it is customary to make a change of variables
, so that
and is the renormalised zeta function
We have the analogue of (1) (or (7) or (11)):
which leads as before to an exponential identity
analogous to (2), (8), or (12). It also leads to the explicit formula
where are the zeroes of the original zeta function
(counting each residue class of the period
just once), or equivalently
where are the reciprocals of the roots of the normalised zeta function
(or to put it another way,
are the factors of this zeta function). Again, to make proper sense of this heuristic we need to sum, obtaining
As it turns out, in the function field setting, the zeta functions are always rational (this is part of the Weil conjectures), and the above heuristic formula is basically exact up to a constant factor, thus
for an explicit integer (independent of
) arising from any potential pole of
at
. In the case of the affine line
, the situation is particularly simple, because the zeta function
is easy to compute. Indeed, since there are exactly
monic polynomials of a given degree
, we see from (14) that
so in fact there are no zeroes whatsoever, and no pole at either, so we have an exact prime number theorem for this function field:
Among other things, this tells us that the number of irreducible monic polynomials of degree is
.
We can transition from an algebraic perspective to a geometric one, by viewing a given monic polynomial through its roots, which are a finite set of points in the algebraic closure
of the finite field
(or more suggestively, as points on the affine line
). The number of such points (counting multiplicity) is the degree of
, and from the factor theorem, the set of points determines the monic polynomial
(or, if one removes the monic hypothesis, it determines the polynomial
projectively). These points have an action of the Galois group
. It is a classical fact that this Galois group is in fact a cyclic group generated by a single element, the (geometric) Frobenius map
, which fixes the elements of the original finite field
but permutes the other elements of
. Thus the roots of a given polynomial
split into orbits of the Frobenius map. One can check that the roots consist of a single such orbit (counting multiplicity) if and only if
is irreducible; thus the fundamental theorem of arithmetic can be viewed geometrically as as the orbit decomposition of any Frobenius-invariant finite set of points in the affine line.
Now consider the degree finite field extension
of
(it is a classical fact that there is exactly one such extension up to isomorphism for each
); this is a subfield of
of order
. (Here we are performing a standard abuse of notation by overloading the subscripts in the
notation; thus
denotes the field of order
, while
denotes the extension of
of order
, so that we in fact have
if we use one subscript convention on the left-hand side and the other subscript convention on the right-hand side. We hope this overloading will not cause confusion.) Each point
in this extension (or, more suggestively, the affine line
over this extension) has a minimal polynomial – an irreducible monic polynomial whose roots consist the Frobenius orbit of
. Since the Frobenius action is periodic of period
on
, the degree of this minimal polynomial must divide
. Conversely, every monic irreducible polynomial of degree
dividing
produces
distinct zeroes that lie in
(here we use the classical fact that finite fields are perfect) and hence in
. We have thus partitioned
into Frobenius orbits (also known as closed points), with each monic irreducible polynomial
of degree
dividing
contributing an orbit of size
. From this we conclude a geometric interpretation of the left-hand side of (18):
The identity (18) thus is equivalent to the thoroughly boring fact that the number of -points on the affine line
is equal to
. However, things become much more interesting if one then replaces the affine line
by a more general (geometrically) irreducible curve
defined over
; for instance one could take
to be an ellpitic curve
for some suitable , although the discussion here applies to more general curves as well (though to avoid some minor technicalities, we will assume that the curve is projective with a finite number of
-rational points removed). The analogue of
is then the coordinate ring of
(for instance, in the case of the elliptic curve (20) it would be
), with polynomials in this ring producing a set of roots in the curve
that is again invariant with respect to the Frobenius action (acting on the
and
coordinates separately). In general, we do not expect unique factorisation in this coordinate ring (this is basically because Bezout’s theorem suggests that the zero set of a polynomial on
will almost never consist of a single (closed) point). Of course, we can use the algebraic formalism of ideals to get around this, setting up a zeta function
and a von Mangoldt function as before, where
would now run over the non-trivial ideals of the coordinate ring. However, it is more instructive to use the geometric viewpoint, using the ideal-variety dictionary from algebraic geometry to convert algebraic objects involving ideals into geometric objects involving varieties. In this dictionary, a non-trivial ideal would correspond to a proper subvariety (or more precisely, a subscheme, but let us ignore the distinction between varieties and schemes here) of the curve
; as the curve is irreducible and one-dimensional, this subvariety must be zero-dimensional and is thus a (multi-)set of points
in
, or equivalently an effective divisor
of
; this generalises the concept of the set of roots of a polynomial (which corresponds to the case of a principal ideal). Furthermore, this divisor has to be rational in the sense that it is Frobenius-invariant. The prime ideals correspond to those divisors (or sets of points) which are irreducible, that is to say the individual Frobenius orbits, also known as closed points of
. With this dictionary, the zeta function becomes
where the sum is over effective rational divisors of
(with
being the degree of an effective divisor
), or equivalently
The analogue of (19), which gives a geometric interpretation to sums of the von Mangoldt function, becomes
thus this sum is simply counting the number of -points of
. The analogue of the exponential identity (16) (or (2), (8), or (12)) is then
and the analogue of the explicit formula (17) (or (5), (10) or (13)) is
where runs over the (reciprocal) zeroes of
(counting multiplicity), and
is an integer independent of
. (As it turns out,
equals
when
is a projective curve, and more generally equals
when
is a projective curve with
rational points deleted.)
To evaluate , one needs to count the number of effective divisors of a given degree on the curve
. Fortunately, there is a tool that is particularly well-designed for this task, namely the Riemann-Roch theorem. By using this theorem, one can show (when
is projective) that
is in fact a rational function, with a finite number of zeroes, and a simple pole at both
and
, with similar results when one deletes some rational points from
; see e.g. Chapter 11 of Iwaniec-Kowalski for details. Thus the sum in (22) is finite. For instance, for the affine elliptic curve (20) (which is a projective curve with one point removed), it turns out that we have
for two complex numbers depending on
and
.
The Riemann hypothesis for (untwisted) curves – which is the deepest and most difficult aspect of the Weil conjectures for these curves – asserts that the zeroes of lie on the critical line, or equivalently that all the roots
in (22) have modulus
, so that (22) then gives the asymptotic
where the implied constant depends only on the genus of (and on the number of points removed from
). For instance, for elliptic curves we have the Hasse bound
As before, we have an important amplification phenomenon: if we can establish a weaker estimate, e.g.
then we can automatically deduce the stronger bound (23). This amplification is not a mere curiosity; most of the proofs of the Riemann hypothesis for curves proceed via this fact. For instance, by using the elementary method of Stepanov to bound points in curves (discussed for instance in this previous post), one can establish the preliminary bound (24) for large , which then amplifies to the optimal bound (23) for all
(and in particular for
). Again, see Chapter 11 of Iwaniec-Kowalski for details. The ability to convert a bound with
-dependent losses over the optimal bound (such as (24)) into an essentially optimal bound with no
-dependent losses (such as (23)) is important in analytic number theory, since in many applications (e.g. in those arising from sieve theory) one wishes to sum over large ranges of
.
Much as the Riemann zeta function can be twisted by a Dirichlet character to form a Dirichlet -function, one can twist the zeta function on curves by various additive and multiplicative characters. For instance, suppose one has an affine plane curve
and an additive character
, thus
for all
. Given a rational effective divisor
, the sum
is Frobenius-invariant and thus lies in
. By abuse of notation, we may thus define
on such divisors by
and observe that is multiplicative in the sense that
for rational effective divisors
. One can then define
for any non-trivial ideal
by replacing that ideal with the associated rational effective divisor; for instance, if
is a polynomial in the coefficient ring of
, with zeroes at
, then
is
. Again, we have the multiplicativity property
. If we then form the twisted normalised zeta function
then by twisting the previous analysis, we eventually arrive at the exponential identity
in analogy with (21) (or (2), (8), (12), or (16)), where the companion sums are defined by
where the trace of an element
in the plane
is defined by the formula
In particular, is the exponential sum
which is an important type of sum in analytic number theory, containing for instance the Kloosterman sum
as a special case, where . (NOTE: the sign conventions for the companion sum
are not consistent across the literature, sometimes it is
which is referred to as the companion sum.)
If is non-principal (and
is non-linear), one can show (by a suitably twisted version of the Riemann-Roch theorem) that
is a rational function of
, with no pole at
, and one then gets an explicit formula of the form
for the companion sums, where are the reciprocals of the zeroes of
, in analogy to (22) (or (5), (10), (13), or (17)). For instance, in the case of Kloosterman sums, there is an identity of the form
for all and some complex numbers
depending on
, where we have abbreviated
as
. As before, the Riemann hypothesis for
then gives a square root cancellation bound of the form
for the companion sums (and in particular gives the very explicit Weil bound for the Kloosterman sum), but again there is the amplification phenomenon that this sort of bound can be deduced from the apparently weaker bound
As before, most of the known proofs of the Riemann hypothesis for these twisted zeta functions proceed by first establishing this weaker bound (e.g. one could again use Stepanov’s method here for this goal) and then amplifying to the full bound (28); see Chapter 11 of Iwaniec-Kowalski for further details.
One can also twist the zeta function on a curve by a multiplicative character by similar arguments, except that instead of forming the sum
of all the components of an effective divisor
, one takes the product
instead, and similarly one replaces the trace
by the norm
Again, see Chapter 11 of Iwaniec-Kowalski for details.
Deligne famously extended the above theory to higher-dimensional varieties than curves, and also to the closely related context of -adic sheaves on curves, giving rise to two separate proofs of the Weil conjectures in full generality. (Very roughly speaking, the former context can be obtained from the latter context by a sort of Fubini theorem type argument that expresses sums on higher-dimensional varieties as iterated sums on curves of various expressions related to
-adic sheaves.) In this higher-dimensional setting, the zeta function formalism is still present, but is much more difficult to use, in large part due to the much less tractable nature of divisors in higher dimensions (they are now combinations of codimension one subvarieties or subschemes, rather than combinations of points). To get around this difficulty, one has to change perspective yet again, from an algebraic or geometric perspective to an
-adic cohomological perspective. (I could imagine that once one is sufficiently expert in the subject, all these perspectives merge back together into a unified viewpoint, but I am certainly not yet at that stage of understanding.) In particular, the zeta function, while still present, plays a significantly less prominent role in the analysis (at least if one is willing to take Deligne’s theorems as a black box); the explicit formula is now obtained via a different route, namely the Grothendieck-Lefschetz fixed point formula. I have written some notes on this material below the fold (based in part on some lectures of Philippe Michel, as well as the text of Iwaniec-Kowalski and also this book of Katz), but I should caution that my understanding here is still rather sketchy and possibly inaccurate in places.
— 1. l-adic sheaves and the etale fundamental group —
From the point of view of applications to analytic number theory, one can view Deligne’s theorems as providing bounds of square root cancellation type for various sums of the form
where is some (quasi-projective) curve (or possibly a higher dimensional variety), and
is a certain type of “structured” function on the set
of
-rational points on
, such that
is not entirely degenerate (e.g. constant). In particular, Deligne’s results allow one to obtain square root cancellation bounds of the form
for certain non-degenerate structured functions defined on
except at a few points where
is “singular”, and the restricted sum
denotes a sum over the non-singular points of
.
The class of functions that can be treated by Deligne’s machinery is very general. The Weil conjectures for curves (and twisted curves) already allows one to obtain bounds of the shape (29) for several useful classes of functions , such as phases
of rational functions, multiplicative characters , or products of the two. Deligne’s results enlarge this class of functions to include Fourier transforms of existing structured functions, such as
in fact the class of structured functions is closed under a large number of operations, such as addition, multiplication, convolution or pullback, making it an excellent class to use in analytic number theory applications. The situation here is not dissimilar to that of characters of finite-dimensional representations
of some group
, in that the class of characters is also closed under basic operations such as addition and multiplication (which correspond to tensor sum and tensor product of representations). Indeed, the formal definition of a structured function will involve such a finite-dimensional representation, but with two technical details: the vector space
is not exactly defined over the complex numbers, but instead defined over the
-adic numbers for some prime
coprime to
, and also the group
is going to be the étale fundamental group
of
.
We first describe (in somewhat vague terms) what the étale fundamental group of a connected variety
(or more generally, a connected Noetherian scheme) defined over a field
. Crucially, we do not require the underlying field
to be algebraically closed, and in our applications
will in fact be the finite field
. The étale fundamental group is the common generalisation of the (profinite completion of the) topological fundamental group
(applied to, say, a smooth complex variety), and of the absolute Galois group
of a field
. (This point of view is nicely presented in this recent book of Szamuely.) To explain this, we first consider the topological fundamental group
of a smooth connected manifold
at some base point
(the choice of which is not too important if one is willing to view the fundamental group up to conjugacy). This group is conventionally defined in terms of loops in
based at
, but the notion of a loop does not make much sense in either Galois theory or algebraic geometry. Fortunately, as observed by Grothendieck, there is an alternate way to interpret this fundamental group as follows. Let
be any covering space of
, with covering map
; then above the base point
there is a discrete fibre
, and given any point
in this fibre, every loop based at
lifts by monodromy to a path starting at
and ending at another point in the fibre
. The endpoint is not affected by homotopy of the path, so this leads to an action
of the fundamental group
(or more precisely, of the opposite group
to this fundamental group, but never mind this annoying technicality) on the fibre
above
of any covering space. For instance, if we take the
-fold cover
of the unit circle by itself formed by multplying by a natural number
, then the fibre may be identified with
, and the fundamental group
acts on this fibre by translation.
The actions of the fundamental group are natural in the following sense: given a morphism between two covering spaces
,
of
(so that
), then the action of the fundamental group is intertwined by
, thus
for any
and
. Conversely, every collection of actions on fibres
that is natural in the above sense arises from a unique element of the fundamental group
; this can be easily seen by working with the universal cover
of
, of which all other (connected) covers are quotients, and on whose fibre the fundamental group acts freely and transitively. Thus, one could define the fundamental group
as the group of all possible collections of isomorphisms on the fibres
above
which are natural in the above sense. (In category-theoretic terms,
is the group of natural isomorphisms of the fibre functor that maps covers
to fibres
.)
There is an analogous way to view the absolute Galois group of a field
. For simplicity we shall only discuss the case of perfect fields (such as finite fields) here, in which case there is no distinction between the separable closure
and the algebraic closure
, although the discussion below can be extended to the general case (and from a scheme-theoretic viewpoint it is in fact natural to not restrict oneself to the perfect case). The analogue of the covering spaces
of the manifold
are the finite extensions
of
. Here, one encounters a “contravariance” problem in pursuing this analogy: for covering spaces, we have a map
from the covering space
to the base space
; but for field extensions, one instead has an inclusion
from the base field to the extension field. To make the analogy more accurate, one has to dualise, with the role of the covering space
being played not by the extension
, but rather by the set
of all field embeddings of
into the algebraic closure
(cf. the Yoneda lemma). (There is nothing too special about the algebraic closure
here; any field which is in some sense “large enough” to support lots of embeddings of
would suffice.) This set projects down to
, which has a canonical point
, namely the standard embedding of
in
; the fibre of
at
is then the set
of field embeddings of
to
that fix
. It is a basic fact of Galois theory that if
is an extension of
of degree
, then this fibre
is a finite set of cardinality
(for perfect fields, this can be easily deduced from the primitive element theorem). The Galois group
then acts on these fibres
by left-composition, and one can verify that the action of a given Galois group element
is natural in the same category-theoretic sense as considered previously. Conversely, because the algebraic closure
of
can be viewed as the direct limit of finite extensions of
, one can show that every natural isomorphism of these fibres (or more precisely, the fibre functor from
(or
) to
) comes from exactly one element of the Galois group
.
Now we can define the étale fundamental group of a general (connected, Noetherian) scheme
with a specified base point
. (Actually, one minor advantages of schemes is that they come with a canonical point to pick here, namely the generic point, although the dependence on the base point is not a major issue here in any event.) The analogue of covering spaces or finite extensions are now the finite étale covers
of
: morphisms from another scheme
to
that are étale (which, roughly, is like saying
is a local diffeomorphism) and finite (roughly, this means that
locally looks like the product of
with a finite set). Unlike the previous two contexts, in which a universal covering object was available, the category of finite étale covers of a given scheme
usually does not have a universal object. (One can already see this in the category of algebraic Riemann surfaces: the universal cover of the punctured plane
ought to be the complex plane
with covering map given by the exponential map
; this is what happens in the topological setting, but it is not allowed in the algebraic geometry setting because the exponential map is not algebraic.) Nevertheless, one can still define the étale fundamental group without recourse to a universal object, again by using actions on fibres
. Namely, the étale fundamental group
consists of all objects
which act by permutation on the fibres
above
of every finite cover of
, in such a way that this action is natural in the category-theoretic sense. (To actually construct the étale fundamental group as a well-defined set requires a small amount of set-theoretic care, because strictly speaking the class of finite étale covers of
is only a class and not a set; but one can start with one representative from each equivalence class of finite étale covers first, with some designated morphisms between them with which to enforce the naturality conditions, and build the fundamental group from there by an inverse limit construction; see e.g. Szamuely’s book for details.) As the étale fundamental group is defined through its actions on finite sets rather than arbitrary discrete sets, it will automatically be a profinite group, and so differs slightly from the topological fundamental group in that regard. For instance, the punctured complex plane
has a topological fundamental group of
, but has an étale fundamental group of
– the profinite integers, rather than the rational integers. More generally, for complex varieties, the étale fundamental group is always the profinite completion of the topological fundamental group (this comes from a deep connection between complex geometry and algebraic geometry known as the Riemann existence theorem), but the situation can be more complicated in finite characteristic or in non-algebraically closed fields, due to the existence of étale finite covers that do not arise from classical topological covers. For instance, the étale fundamental group of a perfect field
(which one can view geometrically as a point over
) turns out to be the absolute Galois group of
.
The étale fundamental group is functorial: every morphism of schemes gives rise to a homomorphism
of fundamental groups. Among other things, this gives rise to a short exact sequence
whenever is a variety defined over a perfect field
(and hence also defined over its algebraic closure
, via base change) which is geometrically connected (i.e. that
is connected). (Again, it is more natural from a scheme-theoretic perspective to not restrict to the perfect case here, but we will do so here for sake of concreteness.) The groups
and
are known as the arithmetic fundamental group and geometric fundamental group of
respectively. The latter should be viewed as a profinite analogue of the topological fundamental group of (a complex model of)
; this intuition is quite accurate in characteristic zero (due to the Riemann existence theorem mentioned earlier), but only partially accurate in positive characteristic
(basically, one has to work with the prime-to-
components of these groups in order to see the correspondence). (See for instance these notes of Milne for further discussion.)
The étale fundamental group can also be described “explicitly” in terms of Galois groups as follows. [Caution: I am not 100% confident in the accuracy of the assertions in this paragraph.] Let
be the function field on
, and let
be its separable closure, so that one can form the Galois group
. For any closed point
of
(basically, an orbit of
), we can form a local version
of
(the Henselization of the discrete valuation ring associated to
, which roughly speaking captures the formal power series around
), and a local version
of the Galois group, known as the decomposition group at
. As
embeds into
,
embeds into
. Inside
is the inertia group
, defined (I think) as the elements of
which stabilise the residue field of
. Informally, this group measures the amount of ramification present at
. One can then identify the arithmetic fundamental group
with the quotient of
by the normal subgroup
generated (as a normal subgroup) by all the inertia groups of closed points; informally, the étale fundamental group describes the unramified Galois representations of
. The geometric fundamental group has a similar description, but with
replaced by the smaller group
.
(Note: as pointed out to me by Brian Conrad, one can also identify with
where
is the maximal Galois extension of
which is unramified at the discrete valuations corresponding to all the closed points of
. A similar description can be given for higher-dimensional schemes
, if one replaces closed points with codimension-1 points, thanks to Abhyankar’s lemma.)
We have seen that fundamental groups (or absolute Galois groups) act on discrete sets, and specifically on the fibres of covering spaces (or field extensions, or étale finite covers). However, fundamental groups also naturally act on other spaces, and in particular on vector spaces over various fields. For instance, suppose one starts with a connected complex manifold
and considers the holomorphic functions on this manifold. Typically, there are very few globally holomorphic functions on
(e.g. if
is compact, then Liouville’s theorem will force a globally holomorphic function to be constant), so one usually works instead with locally holomorphic functions, defined on some open subset
of
. These local holomorphic functions then form a sheaf
over
, with a vector space
of holomorphic functions on
being attached to each open set
, as well as restriction maps from
to
for every open subset
of
which obey a small number of axioms which I will not reproduce here (see e.g. the Wikipedia page on sheaves for the list of sheaf axioms).
Now let be a base point in
. We can then associate a natural complex vector space
to
, namely the space of holomorphic germs at
(the direct limit of
for neighbourhoods
of
). Any loop based at
then induces a map from
to itself, formed by starting with a germ at
and performing analytic continuation until one returns to
. As analytic continuation is a linear operation, this map from
to itself is linear; it is also invertible by reversing the loop, so it lies in the general linear group
. From the locally unique nature of analytic continuation, this map is not affected by homotopy of the loop, and this therefore gives a linear representation
of the fundamental group. (Actually, to be pedantic, it gives a representation of the opposite group
, due to the usual annoyance that composition of functions works in the reverse order from concatenation of paths, but let us ignore this minor technicality.)
Of course, one can perform the same sort of construction for other sheaves over of holomorphic sections of various vector bundles (using the stalk of the sheaf at
for the space of germs), giving rise to other complex linear representations of the fundamental group. In analogy with this, we will define the notion of a certain type of sheaf over a variety
defined over a finite field
in terms of such representations. Due to the profinite nature of the étale fundamental group, we do not work with complex representations, but rather with
-adic representations, for some prime
that is invertible in
. However, as the
-adics have characteristic zero, we can always choose an embedding
into the complex numbers, although it is not unique (and.
We can now give (a special case of) the definition of an -adic sheaf:
Definition 1 (Lisse sheaf) Let
be a non-empty affine curve defined over a finite field
, and let
be a prime not equal to to the characteristic
of
(i.e.
is invertible in
). An
-adic lisse sheaf
over
(also known as an
-adic local system) is a continuous linear representation
of the arithmetic fundamental group of
, where
is a finite-dimensional vector space over the
–adics
. (Here, the continuity is with respect to the profinite topology on
and the
-adic topology on
.) We refer to
as the fibre of the sheaf. The dimension of
is called the rank of the sheaf.
One can define more general -adic sheaves (not necessarily lisse) over more general schemes, but the definitions are more complicated, and the lisse case already suffices for many analytic number theory applications. (However, even if one’s applications only involve lisse sheaves, it is natural to generalise to arbitrary sheaves when proving the key theorems about these sheaves, in particular Deligne’s theorems.)
As we see from the above definition, lisse sheaves are essentially just a linear representation of the arithmetic fundamental group (and hence also of the geometric fundamental group). As such, one can directly import many representation-theoretic concepts into the language of -adic lisse sheaves. For instance, one can form the direct sum
and direct product
of lisse sheaves by using the representation-theoretic direct sum and direct product, and one can take the contragradient sheaf
of a sheaf
by replacing the representation
with its inverse transpose. Morphisms
of the underlying curve give rise to a pullback operation
from sheaves
over
to sheaves
of
. (There is also an important pushforward operation, but it is much more difficult to define and study.) We also have the notion of a trivial sheaf (in which
is the identity), an irreducible sheaf (which cannot be decomposed as an extension of a lower rank sheaf), a semisimple sheaf (a sheaf which factors as the direct sum of irreducibles), or an isotypic sheaf (the direct sum of isomorphic sheaves). By replacing the arithmetic fundamental group with its geometric counterpart, one also has geometric versions of many of the above concepts, thus for instance one can talk about geometrically irreducible sheaves, geometrically semisimple sheaves, etc.
Now let be a closed point in
of degree
, with its associated decomposition group
and inertia group
. The quotient
can be viewed as the arithmetic fundamental group of
, or equivalently the absolute Galois group of the residue field at
, and this quotient embeds into the arithmetic fundamental group
of
since
embeds into
. On the other hand, as
has degree
, the residue field is isomorphic to the degree
extension
of
, so
is isomorphic to the absolute Galois group of
. This latter group is generated (topologically) by the arithmetic Frobenius map
, and also by its inverse, known as the geometric Frobenius map. So the geometric Frobenius map is well defined (up to conjugacy) as an element of
and hence
. By abuse of notation, we will refer to elements of this conjugacy class in
as
, bearing in mind that this object is only defined up to conjugacy. If we have a lisse
-adic sheaf
, then
is defined up to conjugation, which implies that the trace
on
is well-defined as an element of
. (Actually, a technical point: one should restrict the trace from
to the subspace
fixed by the inertia group of
, but as long as there is no ramification at
, this is all of
; we will ignore this technicality, as in practice we will delete the points of
in which ramification occurs.) Fixing some embedding
, we can then form the trace function
which is a function from to
, and in particular a function from
to
. (A certain subclass of) these trace functions will serve as the “structured” functions mentioned at the start of this section.
Now an important definition. For each unramified closed point ,
is an invertible linear transformation on the vector space
, which has dimension
equal to the rank of
. In particular, this transformation has
eigenvalues
(depending on
, of course) in
, and hence in
after selecting an embedding
. We say that the sheaf
is pure of weight
for some real number
if all of these eigenvalues (and their Galois conjugates) have magnitude exactly
, where
is the residue field at
. There is also the weaker concept of being mixed of weight
, in which the magnitude of the eigenvalues and their conjugates is merely assumed to be bounded above by
. (A technical remark: this upper bound are initially only assumed for unramified closed points, but a result of Deligne allows one to extend this upper bound to ramified points also.) If the sheaf is pure or mixed of weight
, then one clearly has the pointwise bound
in particular, for sheaves of weight zero and bounded rank, the trace function is .
The trace functions resemble characters of representations. For instance, taking the direct sum or product of two sheaves results in taking the sum or product of the two trace functions. If two sheaves have weight
, then their direct sum has weight
as well, while if two sheaves have weights
, then their direct product has weight
. Taking the contragradient
of a sheaf of weight
results in a sheaf of weight
; in the weight zero case, the trace function simply gets conjugated. Pulling back a sheaf by some morphism of curves preserves the weight of that sheaf, and pulls back the trace functions accordingly.
It is a convenient fact that pure sheaves automatically have a “geometric semisimplification” which is a pure sheaf of the same weight, and whose trace function is identical to that of the original sheaf. Furthermore, the geometrically irreducible components of the geometrically semisimple sheaf have the same weight as the original sheaf. Because of this, one can often reduce to the study of geometrically irreducible pure sheaves.
In practice, one can normalise the weight of a pure or mixed sheaf to zero by the following simple construction. Given any algebraic integer over the
-adics, we can define the Tate sheaf associated to
to be the unique rank one continuous representation
that acts trivially on the geometric fundamental group, and maps the Frobenius map
of
to
. If we set
, then this is a pure sheaf of weight
, and the associated trace function
is equal to
; it is geometrically trivial but arithmetically non-trivial (if
), and conversely all geometrically trivial and geometrically semisimple sheaves come from direct sums of Tate sheaves. Given any other pure or mixed sheaf
of some weight
, one can then tensor with the Tate sheaf of weight
to create a pure or mixed sheaf
of weight
, which at the level of trace functions amounts to multiplying the trace function by
. In particular, setting
one can perform a “Tate twist” to normalise these sheaves to be of weight zero.
There is also the notion of the “complexity” of an -adic sheaf, measured by a quantity known as the conductor of the sheaf. This quantity is a bit complicated to define here, but basically it incorporates the genus of the underlying curve
, the rank of the sheaf, the number of singularities of the sheaf, and something called the Swan conductor at each singularity of that sheaf; bounding the conductor then leads to a bound on all of these quantities. The conductor behaves well with respect to various sheaf-theoretic operations; for instance the direct sum or product of sheaves of bounded conductor will also be a sheaf of bounded conductor. I’ll use “bounded complexity” in place of “bounded conductor” in the text that follows.
The “structured functions” mentioned at the start of this section on a curve are then precisely the trace functions
associated to sheaves on open dense subsets
of this curve
formed by deleting a bounded number of points at most from
, which are pure of weight zero and of bounded complexity. As discussed above, this class of functions is closed under pointwise sum, pointwise product, complex conjugation, and pullback, and are also pointwise bounded. It is also a deep fact (essentially due to Deligne, Laumon, and Katz) that this class is closed under other important analytic operations, such as Fourier transform and convolution.
Now we give some basic examples of structured functions, which can be combined with each other using the various closure properties of such functions discussed above. First we show how any additive character can be interpreted as an structured function on the affine line
. The affine line
is covered by itself via the finite étale covering map
defined by
. The fibre of this map at
is just the field
, and so the arithmetic fundamental group
acts on
. One can show that this action is a translation action (because of the translation symmetry of this covering space), and so we have a map from
to
, which on composition with
(and pulling back to
) gives a rank one sheaf, called the Artin-Schrier sheaf associated to
. The trace function here is just
, and this is clearly a pure sheaf of weight
; it also has bounded complexity (indeed, the genus is zero and the only singularity is at
, and the Swan conductor there can be computed to be
).
In a similar vein, any multiplicative character can be viewed as an structured function on the multiplciative group
by a similar construction, using
instead of
(which is still an étale covering map, thanks to a baby case of Hilbert’s Theorem 90), giving rise to a rank one, bounded complexity pure sheaf of weight
on
known as the Kummer sheaf, whose trace function is just
.
These two examples, combined with the closure operations defined previously, already give a large number of useful structured functions, such as the function on the affine line with boundedly many points removed, where
are on that affine line. But there is a deep and powerful additional closure property due to Deligne, Laumon, and Katz: if
is a pure sheaf of weight zero on the affine line (with boundedly many points removed) of bounded complexity that does not contain any Artin-Schrier components, and
is a non-trivial additive character, then there is a “Fourier transform”
of
, which is another pure sheaf of weight zero and bounded complexity with no Artin-Schrier components, with the property that the trace function of
is the Fourier transform of the trace function of
with respect to
on
:
See Theorem 8.2.3 of this book of Katz for details. (The construction here is analogous to that used in the Fourier-Mukai transform, although I do not know how tight this analogy is.) This closure under Fourier transforms also implies a closure property with respect to convolutions, by the usual intertwining relationship between convolution and multiplication provided by the Fourier transform. Using these additional closure properties, one can now add many new and interesting examples of structured functions, such as the normalised Kloosterman sums
or more generally the hyper-Kloosterman sums
for some non-principal additive character . These can then be combined with the previous examples of structured functions as before, for instance Kloosterman correlations
would now also be examples of structured functions.
We have now demonstrated that the class of structured functions contains many examples of interest to analytic number theory, but we have not yet done anything with this class, in particular we have not obtained any control on “exponential sums” such as
beyond the trivial bound of that comes from the pointwise bound on
(and the elementary “Schwarz-Zippel” fact that a bounded complexity curve has at most
points over
). However, such control can be obtained through the important Grothendieck-Lefschetz fixed point formula
for any , where
are the
-adic cohomology groups with compact support in
and coefficients in
. These groups are defined through the general homological algebra machinery of derived categories (but can also be interpreted using either Galois cohomology or sheaf cohomology), and I do not yet have a sufficiently good understanding of these topics to say much more about these groups, other than that they turn out to be finite-dimensional vector spaces over
, and carry an action of the (geometric) Frobenius map of
. (In fact they have a richer structure than this, being sheaves over
; this is useful when trying to iterate Deligne’s theorem to control higher-dimensional exponential sums, but we won’t directly use this structure here.) This formula is analogous to the explicit formulae (5), (10), (13), (17), (22), (26), (27) from the introduction, and in fact easily implies the latter four explicit formulae. Specialising to the case
, we see that the sum (30) takes the form
To proceed further, we need to understand the eigenvalues of the Frobenius map on these cohomology groups (and we also need some control on the dimensions of these groups, i.e. on Betti numbers). This can be done by the following deep result of Deligne, essentially the main result in his second proof of the Weil conjectures:
Theorem 2 (Deligne’s Weil II) If
is a lisse
-adic sheaf, pure of weight
, and
, then any eigenvalue of Frobenius on
has magnitude at most
, as does any of its Galois conjugates.
If we form the zeta function
in analogy with (2), (8), (12), (16), (21), or (25), Deligne’s theorem is equivalent to the Riemann hypothesis for , or at least to the “important” half of that hypothesis, namely that the zeroes have magnitude at most
. In many cases, one can use Poincaré duality to derive a functional equation for
which shows that the zeroes in fact have magnitude exactly
, but for the purposes of upper bounds on exponential sums, it is only the upper bound on the zeroes which is relevant. Interestingly, once one has Deligne’s theorem, the zeta function
plays very little role in applications; however, the zeta function is used to some extent in the proof of Deligne’s theorem. (In particular, my understanding is that Deligne establishes a preliminary zero-free region for this zeta function analogous to the classical zero-free region for the Riemann zeta function, which he then amplifies using a device similar to the amplification tricks mentioned previously.)
From Deligne’s theorem we conclude an important upper bound for (30) for structured functions:
To use this bound, we need bounds on the dimensions of the the cohomology groups, and we need the cohomology group to be trivial in order to get a non-trivial bound on the exponential sum
.
As is usual in cohomology, the extreme cohomology groups are relatively easy to compute; for instance, if
is affine
can be shown to vanish, and
can be shown to vanish when
is geometrically irreducible and non-trivial. In any case, when
has bounded complexity, both of these groups have bounded dimension. This leads to the bound
when is geometrically irreducible and non-trivial with bounded complexity. Finally, to control the dimension of
, one uses a variant of the Grothendieck-Lefschetz formula, namely the Euler-Poincaré formula
where is the rank of
,
is the geometric Euler characteristic of
(i.e.
, where
is the number of points
omits from its projective closure
), and
are the Swan conductors. (A side note: this identity formally suggests that there is some extension of the Grothendieck-Lefschetz formula to the
case, with the right-hand side of (32) being interpretable as some sort of sum over the “field with one element“, whatever that means. I wonder if such an interpretation has been fleshed out further?) All the quantities on the right-hand side of (32) are bounded if
has bounded complexity (basically by the definition of complexity), so we conclude that
has bounded dimension if
has bounded complexity. (Here we are relying on the fact that
is one-dimensional, so that there is only one “difficult” Betti number to understand, which can then be recovered through the Euler characteristic; the situation is more complicated, though still reasonably well under control, in higher dimensions.) So we finally recover the square root cancellation bound
whenever is geometrically irreducible and geometrically non-trivial. We thus obtain the more general bound
for any geometrically semisimple lisse sheaf of bounded complexity and pure of weight
, where
is an algebraic integer reflecting the Tate twists present in the geometrically trivial component of
(in particular,
if there is no such component). Thus we have a strong “structure vs randomness” dichotomy for this class of functions: either
has a geometrically trivial component, or else
exhibits square root cancellation. Informally, we are guaranteed square root cancellation for structured functions unless there is a clear geometric reason why such cancellation is not available.
From Schur’s lemma, we then conclude the almost orthogonality relation
for two geometrically irreducible sheaves of bounded complexity and weight
, where
is
when
are geometrically isomorphic, and
otherwise, and
is an algebraic integer measuring the Tate twists in the geometric isomorphism between
and
(in particular
when
). This gives a useful dichotomy: two irreducible structured functions on a curve with boundedly many points removed are either multiples of each other by a root of unity (after restricting to their common domain of definition), or else have an inner product of
. (Among other things, this provides polynomial bounds on the number of distinct structured functions of bounded complexity, by using the Kabatjanskii-Levenstein bound mentioned in the previous post.)
A typical application of this dichotomy is to correlations of the form of some structured function
(where the asterisk denotes a restriction to those
that avoid the singularities of
); if
is prime, one can show that this correlation is
for all non-zero
, unless
correlates with a linear phase (i.e. it has an Artin-Schrier component). In a similar fashion,
can be shown to be
for all non-zero
and any
, unless
correlates with a quadratic phase. These facts are reminiscent of the inverse theorems in the theory of the Gowers uniformity norms, but in the case of structured functions one gets extremely good bounds (either perfect correlation, or square root cancellation). A bit more generally, one can study correlations of the form
, where
is a fractional linear transformation, leading to an analysis of the automorphy group of
with respect to the
action; see this note of Fouvry, Kowalski and Michel for details.

107 comments
Comments feed for this article
25 January, 2015 at 12:14 pm
hiklicepleh
You can get a good estimate for the .
.
27 March, 2015 at 12:12 am
gninrepoli
27 May, 2015 at 5:54 am
tai
I solve Riemann Hypothesis.
Please see it.
http://vixra.org/abs/1403.0184
15 August, 2015 at 10:51 pm
A wave equation approach to automorphic forms in analytic number theory | What's new
[…] e.g. this previous post for a discussion of this bound) to arrive at the […]
27 September, 2015 at 7:00 am
tai
I rewrite the paper.Please see it.
http://vixra.org/abs/1508.0122
17 November, 2015 at 9:18 am
Anonymous
Riemann Hypothesis (proven)
Two of the statements of Riemann.
1º- The series for the zeta function will have the particularity of (s= 1).
2º- Is very likely that the roots of a are real.
are real.
is to say: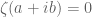
with: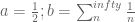
Indicated the beginning of a of the series for
15 November, 2016 at 7:37 am
gninrepoli
Is there an equivalent statement of the Riemann hypothesis in Quantum Theory (Quantum Field Theory, Quantum Mechanics, etc.)? If there is a statement in the Quantum Theory, which is logically equivalent to statement. Then this statement is independent of
statement. Then this statement is independent of  ?
?
We know that RH is equivalent to a statement. Also we know that: “If a
statement. Also we know that: “If a  statement is independent of
statement is independent of  , then it is true”.
, then it is true”.
19 November, 2016 at 1:33 pm
gninrepoli
I think that the sum of prime numbers are the imprint of some sequences +,-,+,-,+,-,+,-,+,- with continious function(‘s) ( ). If this is true, then an error in the formula must be symmetrical. My assumption is based on Perron’s formula, and the sums of the form
). If this is true, then an error in the formula must be symmetrical. My assumption is based on Perron’s formula, and the sums of the form  .
.
19 November, 2016 at 4:35 pm
Anonymous
Of course, the Riemann Hypothesis is true!
Reference links:
https://www.researchgate.net/publication/300068776_Proof_of_Riemann_Hypothesis;
https://www.researchgate.net/post/Why_is_the_Riemann_Hypothesis_true2
27 November, 2016 at 6:54 pm
Anonymous
The Riemann Hypothesis (RH) is true!
It’s a SIN to think otherwise.
Q1. Where are all the primes in the critical strip, [0, 1] ?
Q2. Where are all the powers of primes in the critical strip, [0, 1]?
Q3. How are prime numbers and the nontrivial zeros of the Riemann zeta function connected?
Hints:
Please consider the Fundamental Theorem of Arithmetic, the Generalized Fundamental Theorem of Algebra, the Harmonic Series, and the very important PRIME NUMBER THEOREM since we are counting primes and predicting primes approximately.
If one can answer the above questions, then one understands why the Riemann Hypothesis is true!
Reference link: https://www.researchgate.net/post/Why_is_the_Riemann_Hypothesis_true2
27 November, 2016 at 8:04 pm
Anonymous
Hint for Q1: 1/2 , 1/3, 1/5, 1/7, 1/11, …., 1/p for some prime distinct number, p.
Hint for Q2: We have 1/n where n = ∏(p_i)^k_i over distinct prime numbers, p_i, for some integer, k_i ≥ 1 .
Note: p_1 = 2, p_2 = 3, p_3 = 5, …
Hint for Q3: Prime Number Theorem …
20 February, 2017 at 11:20 am
The Fontaine-Winterberger theorem: going full tilt | Hard Arithmetic
[…] For a taste of the veracity of this claim I would highly recommend reading this excellent post of Terry […]
11 March, 2017 at 7:35 am
Remer
Dear Prof. Tao,
I hope you are doing well.
I’m interested in this topic (Riemann hypothesis- which I believe it’s true) and since I love finding patterns this made me comment.
I know how busy you are but just in case you have time then I greatly appreciate it.
Actually I have difficulties to how I will start since I’m a novice in this area.
Let me say that I was motivated in writing this comment by the story of James Lovelock, one of the scientist invited by NASA for the search of life in Mars, all of the great minds were gathered for analyzing tools for detecting life/organism, then James Lovelock spoke-out his doubt (What if) this is not the way to detect life… then they realize (I’m not good in English but for those who are interested on the story you can find it in youtube).
I know I don’t have the right to say, but What If we just overlook some simple solution of Reimann. What if we need to look simply at once that the Riemann’s zeta function: enable the separation of composite numbers (to the left plane) and prime numbers (to the critical strip) that extracted from Euler equation at the right of the complex plane. That is the zeros of Riemann’s zeta function give us the properties of real numbers located on the corresponding plane – it just happens there is.
In my works, I named the Complex plane of Riemann by:
1st part where R(s)>1: the Composite and Prime number zone
2nd part where 0<R(s)<1: Prime number zone
3rd part where R(s)<0: Composite number zone
Let me start in 3rd part where the value of is R(s)<0
I have named it since I’ve found connections between the trivial zeros (2,4,6,8..) of the function to the composite numbers.
I define a number as:
1. All natural numbers can be represented by a series of ratio of numbers (which carried its divisibility information), I call it “Spine” (I likely to compare it as their DNA). That is in order for a number to be composite its Spine should contain(s) either or combinations of 2,4,6.. (trivial zeros) – I can show it with formula
2.The Spine of all natural numbers follows the cubic equations – I can prove and illustrate it
By the way I’m not sure if I can show you exactly my works here because I have to put some formulas and it will be supported by tables of numbers and drawings to show the behavior, especially in Prime number zone.
Hopefully there's a link to where I can send my works, that’s if you find it relevant.
Remer
13 March, 2017 at 9:35 am
Remer
Dear Prof. Tao,
I know how busy you are but just in case you have time then I greatly appreciate it.
I hope I’m not annoying here, for continuing my claimed in my previous post.
(Continuing at Composite number zone : R(s)<0)
I only consider odd numbers for obvious reason
Let me redefined my 1st claimed
1. All natural numbers (odd) can be represented by a series of ratio of numbers carrying its divisibility information; I call it “Spine” (I likely to compare it as their DNA). That is in order for a number to be composite its Spine should contain(s) either or combination of 2, 4, 6… (trivial zeros)
Let’s consider any composite number, P.
(Ex.1) P=9: its Spine can be shown as 5/4
6/3 = 2
7/2
(Ex.2) P=15: its Spine can be shown as 8/7
9/6
10/5 = 2
11/4
12/3 = 4
13/2
(Ex.3) P=21: its Spine can be shown as 11/10
12/9
13/8
14/7 = 2
15/6
16/5
17/4
18/3 = 6
19/2
Anyone may wish to try it to all odd composite numbers, as long as you will maintain the Spine’s Pattern, you will come out with the same result.
• Trivial zeros are the imprint(s) of Composite’s Spine (any pattern lovers may conclude therefore that Non-trivial zeros are the imprint of Prime number’s Spine – yes, but its Spine is so unique that it only follows the rules inside the critical strip- I will illustrate it)
Pattern of Composite’s Spine
o let a= ath place of the odd number (P)
o that is P=2a+1
o sequence = (a+1)/a , (a+2)/(a-1) , (a+3)/(a-2) , (a+4)/(a-3)… (a+n)/2
o the denominator begins at “a” and ends at “2” (there’s a pattern why it should begins and terminate here, which I think unnecessary to explain)
The Composite’s Spine can help us to do
o Primality testing
o Prime sieving (I can illustrate it)
We can say that a number is composite if it satisfies to
[(a+1+n)/(a-n)] = m or to [P/(a-n)]-1 =m
where:
n= 1, 2, 3, 4…. any natural number {(n-1)th place of the number sequence)}
m= 2, 4, 6…. any the trivial zeros,
a= ath place of the odd number (P), That is P=2a+1
This is how beautifully a number can be interpreted (giving hope for non- technical person, like me, to explore) and I hope that there will be someone (mathematician) who will give progress in this insight.
Remer Catacutan
3 April, 2017 at 1:52 am
MatjazG
I am curious as to your thoughts on the recent progress in solving the Riemann hypothesis via the Hilbert-Pólya conjecture described in this Physical Review Letters article:
C. M. Bender, Dorje C. Brody, and Markus P. Müller, Hamiltonian for the Zeros of the Riemann Zeta Function, Phys. Rev. Lett. 188, 130201 (2017)
DOI: https://doi.org/10.1103/PhysRevLett.118.130201
Abstract:
A Hamiltonian operator H is constructed with the property that if the eigenfunctions obey a suitable boundary condition, then the associated eigenvalues correspond to the nontrivial zeros of the Riemann zeta function. The classical limit of H is 2xp, which is consistent with the Berry-Keating conjecture. While H is not Hermitian in the conventional sense, iH is PT symmetric with a broken PT symmetry, thus allowing for the possibility that all eigenvalues of H are real. A heuristic analysis is presented for the construction of the metric operator to define an inner-product space, on which the Hamiltonian is Hermitian. If the analysis presented here can be made rigorous to show that H is manifestly self-adjoint, then this implies that the Riemann hypothesis holds true.
–
Is there hope that this could lead to something substantial?
22 April, 2017 at 2:09 am
int.math
I have found that:
 .
.
Does anyone know equivalent results?
(η(s):dirichlet eta function)
25 April, 2017 at 1:44 am
int.math
I have also found a similar relation with Riemann zeta function:
 .
.
26 April, 2017 at 7:49 am
int.math
Please, can someone check this:
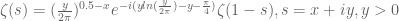
27 April, 2017 at 4:08 am
Anonymous
It seems that Stirling’s approximation(!) for the Gamma function was used in the Zeta functional equation (anyway, it is not an exact identity.)
25 May, 2017 at 9:45 am
David Cole
“If you can’t explain simply, you don’t understand it well enough.” — Albert Einstein.
What does the Riemann Hypothesis (RH) mean?
RH confirms the existence of prime numbers in an optimal way. Or rather, for all positive integers, k > 1, there exists a prime number, p, which divides k such that either p = k or p ≤ sqrt(k) = k^(1/2) where RH states the exponent of k is 1/2.
Please keep that fundamental fact in mind when discussing the truth of RH.
Reference link:
https://www.researchgate.net/post/Why_is_the_Riemann_Hypothesis_true2.
.
28 May, 2017 at 1:36 pm
David Cole
Does the nth non-trivial simple zero of the Riemann zeta function indicate the nth prime, p_n, occurs as a prime factor in all multiples of p_n?
30 May, 2017 at 7:55 am
David Cole
Hmm. The short answer is a resounding yes! Wow! The great Riemann saw it all.
Reference link:
‘On the Number of Prime Numbers less than a
Given Quantity.(Ueber die Anzahl der Primzahlen unter einer
gegebenen Grosse.) ‘,
Click to access ezeta.pdf
31 May, 2017 at 8:38 am
David Cole
FYI:
Please an answer at link:
https://www.researchgate.net/post/Does_the_nth_nontrivial_simple_zero_of_the_Riemann_zeta_function_indicate_the_nth_prime_p_n_occurs_as_a_prime_factor_in_all_multiples_of_p_n
7 June, 2018 at 3:15 am
Heat flow and zeroes of polynomials II: zeroes on a circle | What's new
[…] , then, as famously proven by Weil, the associated local zeta function (as defined for instance in this previous blog post) is known to take the […]
1 July, 2018 at 2:57 am
Pallav Goyal
The summand in identity (2) isn’t defined when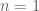 , so maybe the sum should start from
, so maybe the sum should start from  ?
?
1 July, 2018 at 6:52 am
Anonymous
Since , it seems that the first summand is
, it seems that the first summand is  .
.
2 July, 2018 at 1:35 am
Pallav Goyal
Yeah. I guess the meaning of the expression is clear as such, this is just a pedantic correction.
14 January, 2019 at 1:50 am
Anonymous
I have always liked this image,http://en.wikipedia.org/wiki/Image:Zeta_polar.svg, but could someone explain it? Is important or useful? Hides the secret of RH? Has some modular arithmetica?
18 August, 2019 at 12:21 am
Anonymous
This may seem like a stupid question, but what exactly does the Riemann hypothesis mean for the prime numbers? I mean the twin prime conjecture just means that there are infinitely many pairs of primes with difference 2, is there such a straightforward formulation for the consequences of the Riemann hypothesis?
9 November, 2019 at 2:17 pm
Rex
Dear Terry,
Your definition of mixed sheaf seems to be a priori weaker than the usual one (there exists a finite filtration of subsheaves $\mathscr{F}_1 \subset \cdots \subset \mathscr{F}_n = \mathscr{F}$ such that the successive quotients are pure). Does it turn out to be equivalent? If so, is this easy to see?
5 July, 2021 at 2:43 pm
How do you work in midage?
How are you able to do outstanding research in late 40s? Do you have any learning disabilities because of midage? Is there immunity to midage debilitation?
18 February, 2022 at 3:15 pm
Daniel
You are all welcome to comment on my paper “On the Riemann hypothesis” at https://vixra.org/pdf/2004.0533v3.pdf
26 November, 2022 at 9:44 am
Sal Daouairi
Great summary subject from Terrence, finaly the conjecture “Riemann Hypothesis” Solved few day ago 11/25/2022 in a
peer reviewed journal under link:
10.5923.j.ijtmp.20221202.03.pdf
7 February, 2023 at 9:58 am
wired for RH
Is there any plans for you to do a video on Riemann hypothesis as in https://twitter.com/WIRED/status/1620195277456941061?