We now turn to the local existence theory for the initial value problem for the incompressible Euler equations
For sake of discussion we will just work in the non-periodic domain ,
, although the arguments here can be adapted without much difficulty to the periodic setting. We will only work with solutions in which the pressure
is normalised in the usual fashion:
Formally, the Euler equations (with normalised pressure) arise as the vanishing viscosity limit of the Navier-Stokes equations
that was studied in previous notes. However, because most of the bounds established in previous notes, either on the lifespan of the solution or on the size of the solution itself, depended on
, it is not immediate how to justify passing to the limit and obtain either a strong well-posedness theory or a weak solution theory for the limiting equation (1). (For instance, weak solutions to the Navier-Stokes equations (or the approximate solutions used to create such weak solutions) have
lying in
for
, but the bound on the norm is
and so one could lose this regularity in the limit
, at which point it is not clear how to ensure that the nonlinear term
still converges in the sense of distributions to what one expects.)
Nevertheless, by carefully using the energy method (which we will do loosely following an approach of Bertozzi and Majda), it is still possible to obtain local-in-time estimates on (high-regularity) solutions to (3) that are uniform in the limit . Such a priori estimates can then be combined with a number of variants of these estimates obtain a satisfactory local well-posedness theory for the Euler equations. Among other things, we will be able to establish the Beale-Kato-Majda criterion – smooth solutions to the Euler (or Navier-Stokes) equations can be continued indefinitely unless the integral
becomes infinite at the final time , where
is the vorticity field. The vorticity has the important property that it is transported by the Euler flow, and in two spatial dimensions it can be used to establish global regularity for both the Euler and Navier-Stokes equations in these settings. (Unfortunately, in three and higher dimensions the phenomenon of vortex stretching has frustrated all attempts to date to use the vorticity transport property to establish global regularity of either equation in this setting.)
There is a rather different approach to establishing local well-posedness for the Euler equations, which relies on the vorticity-stream formulation of these equations. This will be discused in a later set of notes.
— 1. A priori bounds —
We now develop some a priori bounds for very smooth solutions to Navier-Stokes that are uniform in the viscosity . Define an
function to be a function that lies in every
space; similarly define an
function to be a function that lies in
for every
. Given divergence-free
initial data
, an
mild solution
to the Navier-Stokes initial value problem (3) is a solution that is an
mild solution for all
. From the (non-periodic version of) Corollary 40 of Notes 1, we know that for any
divergence-free initial data
, there is unique
maximal Cauchy development
, with
infinite if
is finite.
Here are our first bounds:
Theorem 1 (A priori bound) Let
be an
maximal Cauchy development to (3) with initial data
.
- (i) For any integer
, we have
Furthermore, if
for a sufficiently small constant
depending only on
, then
- (ii) For any
and integer
, one has
The hypothesis that is integer can be dropped by more heavily exploiting the theory of paraproducts, but we shall restrict attention to integer
for simplicity.
We now prove this theorem using the energy method. Using the Navier-Stokes equations, we see that and
all lie in
for any
; an easy iteration argument then shows that the same is true for all higher derivatives of
also. This will make it easy to justify the differentiation under the integral sign that we shall shortly perform.
Let be an integer. For each time
, we introduce the energy-type quantity
Here we think of as taking values in the Euclidean space
. This quantity is of course comparable to
, up to constants depending on
. It is easy to verify that
is continuously differentiable in time, with derivative
where we suppress explicit dependence on in the integrand for brevity. We now try to bound this quantity in terms of
. We expand the right-hand side in coordinates using (3) to obtain
where
For , we can integrate by parts to move the
operator onto
and use the divergence-free nature
of
to conclude that
. Similarly, we may integrate by parts for
to move one copy of
over to the other factor in the integrand to conclude
so in particular (note that as we are seeking bounds that are uniform in
, we can’t get much further use out of
beyond this bound). Thus we have
Now we expand out using the Leibniz rule. There is one dangerous term, in which all the derivatives in
fall on the
factor, giving rise to the expression
But we can locate a total derivative to write this as
and then an integration by parts using as before shows that this term vanishes. Estimating the remaining contributions to
using the triangle inequality, we arrive at the bound
At this point we now need a variant of Proposition 35 from Notes 1:
Exercise 2 Let
be integers. For any
, show that
(Hint: for
or
, use Hölder’s inequality. Otherwise, use a suitable Littlewood-Paley decomposition.)
Using this exercise and Hölder’s inequality, we see that
By Gronwall’s inequality we conclude that
for any and
, which gives part (ii).
Now assume . Then we have the Sobolev embedding
which when inserted into (4) yields the differential inequality
or equivalently
for some constant (strictly speaking one should work with
for some small
which one sends to zero later, if one wants to avoid the possibility that
vanishes, but we will ignore this small technicality for sake of exposition.) Since
, we conclude that
stays bounded for a time interval of the form
; this, together with the blowup criterion that
must go to infinity as
, gives part (i).
As a consequence, we can now obtain local existence for the Euler equations from smooth data:
Corollary 3 (Local existence for smooth solutions) Let
be divergence-free. Let
be an integer, and set
Then there is a smooth solution
,
to (1) with all derivatives of
in
for appropriate
. Furthermore, for any integer
, one has
Proof: We use the compactness method, which will be more powerful here than in the last section because we have much higher regularity uniform bounds (but they are only local in time rather than global). Let be a sequence of viscosities going to zero. By the local existence theory for Navier-Stokes (Corollary 40 of Notes 1), for each
we have a maximal Cauchy development
,
to the Navier-Stokes initial value problem (3) with viscosity
and initial data
. From Theorem 1(i), we have
for all
(if
is small enough), and
for all . By Sobolev embedding, this implies that
and then by Theorem 1(ii) one has
for every integer . Thus, for each
,
is bounded in
, uniformly in
. By repeatedly using (3) and product estimates for Sobolev spaces, we see the same is true for
, and for all higher derivatives of
. In particular, all derivatives of
are equicontinuous.
Using weak compactness (Proposition 2 of Notes 2), one can pass to a subsequence such that converge weakly to some limits
, such that
and all their derivatives lie in
on
; in particular,
are smooth. From the Arzelá-Ascoli theorem (and Proposition 3 of Notes 2),
and
converge locally uniformly to
, and similarly for all derivatives of
. One can then take limits in (3) and conclude that
solve (1). The bound (5) follows from taking limits in (6).
Remark 4 We are able to easily pass to the zero viscosity limit here because our domain
has no boundary. In the presence of a boundary, we cannot freely differentiate in space as casually as we have been doing above, and one no longer has bounds on higher derivatives on
and
near the boundary that are uniform in the viscosity. Instead, it is possible for the fluid to form a thin boundary layer that has a non-trivial effect on the limiting dynamics. We hope to return to this topic in a future set of notes.
We have constructed a local smooth solution to the Euler equations from smooth data, but have not yet established uniqueness or continuous dependence on the data; related to the latter point, we have not extended the construction to larger classes of initial data than the smooth class . To accomplish these tasks we need a further a priori estimate, now involving differences of two solutions, rather than just bounding a single solution:
Theorem 5 (A priori bound for differences) Let
, let
be an integer, and let
be divergence-free with
norm at most
. Let
where
is sufficiently small depending on
. Let
and
be an
solution to (1) with initial data
(this exists thanks to Corollary 3), and let
and
be an
solution to (1) with initial data
. Then one has
Note the asymmetry between and
in (8): this estimate requires control on the initial data
in the high regularity space
in order to be usable, but has no such requirement on the initial data
. This asymmetry will be important in some later applications.
Proof: From Corollary 3 we have
Now we need bounds on the difference . Initially we have
, where
. To evolve later in time, we will need to use the energy method. Subtracting (1) for
and
, we have
By hypothesis, all derivatives of and
lie in
on
, which will allow us to justify the manipulations below without difficulty. We introduce the low regularity energy for the difference:
Arguing as in the proof of Theorem 1, we see that
where
As before, the divergence-free nature of ensures that
vanishes. For
, we use the Leibniz rule and again extract out the dangerous term
which again vanishes by integration by parts. We then use the triangle inequality to bound
The key point here is that at most derivatives are being applied to
at any given time, although the full
derivatives may also hit
or
. Using Exercise 2 and Hölder, we may bound the above expression by
which by Sobolev embedding gives
Applying (9) and Gronwall’s inequality, we conclude that
for , and (7) follows.
Now we work with the high regularity energy
Arguing as before we have
Using Exercise 2 and Hölder, we may bound this by
Using Sobolev embedding we thus have
By the chain rule, we obtain
(one can work with in place of
and then send
later if one wishes to avoid a lack of differentiability at
). By Gronwall’s inequality, we conclude that
for all , and (8) follows.
By specialising (7) (or (8)) to the case where , we see the solution constructed in Corollary 3 is unique. Now we can extend to wider classes of initial data than
initial data. The following result is essentially due to Kato and to Swann (with a similar result obtained by different methods by Ebin-Marsden):
Proposition 6 Let
be an integer, and let
be divergence-free. Set
where
is sufficiently small depending on
. Let
be a sequence of divergence-free vector fields converging to
in
norm (for instance, one could apply Littlewood-Paley projections to
). Let
,
be the associated solutions to (1) provided by Corollary 3 (these are well-defined for
large enough). Then
and
converge in
norm on
to limits
,
respectively, which solve (1) in a distributional sense.
Proof: We use a variant of Kato’s argument (see also the paper of Bona and Smith for a related technique). It will suffice to show that the form a Cauchy sequence in
, since the algebra properties of
then give the same for
, and one can then easily take limits (in this relatively high regularity setting) to obtain the limiting solution
that solves (1) in a distributional sense.
Let be a large dyadic integer. By Corollary 3, we may find an
solution
be the solution to the Euler equations (1) with initial data
(which lies in
). From Theorem 5, one has
Applying the triangle inequality and then taking limit superior, we conclude that
But by Plancherel’s theorem and dominated convergence we see that
as , and hence
giving the claim.
Remark 7 Since the sequence
can converge to at most one limit
, we see that the solution
to (1) is unique in the class of distributional solutions that are limits of smooth solutions (with initial data of those solutions converging to
in
). However, this leaves open the possibility that there are other distributional solutions that do not arise as the limits of smooth solutions (or as limits of smooth solutions whose initial data only converge to
in a weaker sense). It is possible to recover some uniqueness results for fairly weak solutions to the Euler equations if one also assumes some additional regularity on the fields
(or on related fields such as the vorticity
). In two dimensions, for instance, there is a celebrated theorem of Yudovich that weak solutions to 2D Euler are unique if one has an
bound on the vorticity. In higher dimensions one can also obtain uniqueness results if one assumes that the solution is in a high-regularity space such as
,
. See for instance this paper of Chae for an example of such a result.
Exercise 8 (Continuous dependence on initial data) Let
be an integer, let
, and set
, where
is sufficiently small depending on
. Let
be the closed ball of radius
around the origin of divergence-free vector fields
in
. The above proposition provides a solution
to the associated initial value problem. Show that the map from
to
is a continuous map from
to
.
Remark 9 The continuity result provided by the above exercise is not as strong as in Navier-Stokes, where the solution map is in fact Lipschitz continuous (see e.g., Exercise 43 of Notes 1). In fact for the Euler equations, which is classified as a “quasilinear” equation rather than a “semilinear” one due to the lack of the dissipative term
in the equation, the solution map is not expected to be uniformly continuous on this ball, let alone Lipschitz continuous. See this previous blog post for some more discussion.
Exercise 10 (Maximal Cauchy development) Let
be an integer, and let
be divergence free. Show that there exists a unique
and unique
,
with the following properties:
- (i) If
and
is divergence-free and converges to
in
norm, then for
large enough, there is an
solution
to (1) with initial data
on
, and furthermore
and
converge in
norm on
to
.
- (ii) If
, then
as
.
- (iii) If
, then we have the weak Beale-Kato-Majda criterion
Furthermore, show that
do not depend on the particular choice of
, in the sense that if
belongs to both
and
for two integers
then the time
and the fields
produced by the above claims are the same for both
and
.
We will refine part (iii) of the above exercise in the next section. It is a major open problem as to whether the case (i.e., finite time blowup) can actually occur. (It is important here that we have some spatial decay at infinity, as represented here by the presence of the
norm; when the solution is allowed to diverge at spatial infinity, it is not difficult to construct smooth solutions to the Euler equations that blow up in finite time; see e.g., this article of Stuart for an example.)
Remark 11 The condition
that recurs in the above results can be explained using the heuristics from Section 5 of Notes 1. Assume that a given time
, the velocity field
fluctuates at a spatial frequency
, with the fluctuations being of amplitude
. (We however permit the velocity field
to contain a “bulk” low frequency component which can have much higher amplitude than
; for instance, the first component
of
might take the form
where
is a quantity much larger than
.) Suppose one considers the trajectories of two particles
whose separation at time zero is comparable to the wavelength
of the frequency oscillation. Then the relative velocities of
will differ by about
, so one would expect the particles to stay roughly the same distance from each other up to time
, and then exhibit more complicated and unpredictable behaviour after that point. Thus the natural time scale
here is
, so one only expects to have a reasonable local well-posedness theory in the regime
On the other hand, if
lies in
, and the frequency
fluctuations are spread out over a set of volume
, the heuristics from the previous notes predict that
The uncertainty principle predicts
, and so
Thus we force the regime (11) to occur if
, and barely have a chance of doing so in the endpoint case
, but would not expect to have a local theory (at least using the sort of techniques deployed in this section) for
.
Exercise 12 Use similar heuristics to explain the relevance of quantities of the form
that occurs in various places in this section.
Because the solutions constructed in Exercise 10 are limits (in rather strong topologies) of smooth solutions, it is fairly easy to extend estimates and conservation laws that are known for smooth solutions to these slightly less regular solutions. For instance:
Exercise 13 Let
be as in Exercise 10.
- (i) (Energy conservation) Show that
for all
.
- (ii) Show that
for all
.
Exercise 14 (Vanishing viscosity limit) Let the notation and hypotheses be as in Corollary 3. For each
, let
,
be the solution to (3) with this choice of viscosity and with initial data
. Show that as
,
and
converge locally uniformly to
, and similarly for all derivatives of
and
. (In other words, there is actually no need to pass to a subsequence as is done in the proof of Corollary 3.) Hint: apply the energy method to control the difference
.
Exercise 15 (Local existence for forced Euler) Let
be divergence-free, and let
, thus
is smooth and for any
and any integer
and
,
. Show that there exists
and a smooth solution
to the forced Euler equation
Note: one will first need a local existence theory for the forced Navier-Stokes equation. It is also possible to develop forced analogues of most of the other results in this section, but we will not detail this here.
— 2. The Beale-Kato-Majda blowup criterion —
In Exercise 10 we saw that we could continue solutions,
to the Euler equations indefinitely in time, unless the integral
became infinite at some finite time
. There is an important refinement of this blowup criterion, due to Beale, Kato, and Majda, in which the tensor
is replaced by the vorticity two-form (or vorticity, for short)
that is to say is essentially the anti-symmetric component of
. Whereas
is the tensor field
is the anti-symmetric tensor field
Remark 16 In two dimensions,
is essentially a scalar, since
and
. As such, it is common in fluid mechanics to refer to the scalar field
as the vorticity, rather than the two form
. In three dimensions, there are three independent components
of the vorticity, and it is common to view
as a vector field
rather than a two-form in this case (actually, to be precise
would be a pseudovector field rather than a vector field, because it behaves slightly differently to vectors with respect to changes of coordinate). With this interpretation, the vorticity is now the curl of the velocity field
. From a differential geometry viewpoint, one can view the two-form
as an antisymmetric bilinear map from vector fields
to scalar functions
, and the relation between the vorticity two-form
and the vorticity (pseudo-)vector field
in
is given by the relation
for arbitrary vector fields
, where
is the volume form on
, which can be viewed in three dimensions as an antisymmetric trilinear form on vector fields. The fact that
is a pseudovector rather than a vector then arises from the fact that the volume form changes sign upon applying a reflection.
The point is that vorticity behaves better under the Euler flow than the full derivative . Indeed, if one takes a smooth solution to the Euler equation in coordinates
and applies to both sides, one obtains
If one interchanges and then subtracts, the pressure terms disappear, and one is left with
which we can rearrange using the material derivative as
Writing and
, this becomes the vorticity equation
The vorticity equation is particularly simple in two and three dimensions:
Exercise 17 (Transport of vorticity) Let
be a smooth solution to Euler equation in
, and let
be the vorticity two-form.
- (i) If
, show that
- (ii) If
, show that
where
is the vorticity pseudovector.
Remark 18 One can interpret the vorticity equation in the language of differential geometry, which is a more covenient formalism when working on more general Riemann manifolds than
. To be consistent with the conventions of differential geometry, we now write the components of the velocity field
as
rather than
(and the coordinates of
as
rather than
). Define the covelocity
-form
as
where
is the Euclidean metric tensor (in the standard coordinates,
is the Kronecker delta, though
can take other values than
if one uses a different coordinate system). Thus in coordinates,
; the covelocity field is thus the musical isomorphism applied to the velocity field. The vorticity
-form
can then be interpreted as the exterior derivative of the covelocity, thus
or in coordinates
The Euler equations can be rearranged as
where
is the Lie derivative along
, which for
-forms is given in coordinates as
and
is the modified pressure
If one takes exterior derivatives of both sides of (14) using the basic differential geometry identities
and
, one obtains the vorticity equation
where the Lie derivative for
-forms is given in coordinates as
and so we recover (13) after some relabeling.
We now present the Beale-Kato-Majda condition.
Theorem 19 (Beale-Kato-Majda) Let
be an integer, and let
be divergence free. Let
,
be the maximal Cauchy development from Exercise 10, and let
be the vorticity.
The double exponential in (i) is not a typo! It is an open question though as to whether this double exponential bound can be at all improved, even in the simplest case of two spatial dimensions.
We turn to the proof of this theorem. Part (ii) will be implied by part (i), since if is finite then part (i) gives a uniform bound on
as
, preventing finite time blowup. So it suffices to prove part (i). To do this, it suffices to do so for
solutions, since one can then pass to a limit (using the strong continuity in
) to establish the general case. In particular, we can now assume that
are smooth.
We would like to convert control on back to control of the full derivative
. If one takes divergences
of the vorticity using (12) and the divergence-free nature
of
, we see that
Thus, we can recover the derivative from the vorticity by the formula
where one can define via the Fourier transform as a multiplier bounded on every
space.
If the operators were bounded in
, then we would have
and the claimed bound (15) would follow from Theorem 1(ii) (with one exponential to spare). Unfortunately, is not quite bounded on
. Indeed, from Exercise 18 of Notes 1 we have the formula
for any test function and
, where
is the singular kernel
If one sets to be a (smooth approximation) to the signum
restricted to an annulus
, we conclude that the operator norm of
is at least as large as
But one can calculate using polar coordinates that this expression diverges like in the limit
,
, giving unboundedness.
As it turns out, though, the Gronwall argument used to establish Theorem 1(ii) can just barely tolerate an additional “logarithmic loss” of the above form, albeit at the cost of worsening the exponential term to a double exponential one. The key lemma is the following result that quantifies the logarithmic divergence indicated by the previous calculation, and is similar in spirit to a well known inequality of Brezis and Wainger.
Lemma 20 (Near-boundedness of
) For any
, one has
The lower order terms will be easily dealt with in practice; the main point is that one can almost bound the
norm of
by that of
, up to a logarithmic factor.
Proof: By a limiting argument we may assume that (and hence
are test functions. We apply Littlewood-Paley decomposition to write
and hence by the triangle inequality we may bound the left-hand side of (17) by
where we omit the domain and range from the function space norms for brevity.
By Bernstein’s inequality we have
Also, from Bernstein and Plancherel we have
and hence by geometric series we have
for any . This gives an acceptable contribution if we select
. This leaves
remaining values of
to control, so if one can bound
for each and a test function
, we will be done.
Observe from applying the scaling (that is, replacing
with
that to prove (18) for all
it suffices to do so for
. By Fourier analysis, the function
is the convolution of
with the inverse Fourier transform
of the function
This function is a test function, so is a Schwartz function, and the claim now follows from Young’s inequality.
We return now to the proof of (15). We adapt the proof of Proposition 1(i). As in that proposition, we introduce the higher energy
We no longer have the viscosity term as , but that term was discarded anyway in the analysis. From (4) we have
Applying (16), (17) one thus has
From Exercise 13 one has
By the chain rule, one then has
and hence by Gronwall’s inequality one has
The claim (15) follows.
Remark 21 The Beale-Kato-Majda criterion can be sharpened a little bit, by replacing the sup norm
with slightly smaller norms, such as the bounded mean oscillation (BMO) norm of
, basically by improving the right-hand side of Lemma 20 slightly. See for instance this paper of Planchon and the references therein.
Remark 22 An inspection of the proof of Theorem 19 reveals that the same result holds if the Euler equations are replaced by the Navier-Stokes equations; the energy estimates acquire an additional “
” term by doing so (as in the proof of Proposition 1), but the sign of that term is favorable.
We now apply the Beale-Kato-Majda criterion to obtain global well-posedness for the Euler equations in two dimensions:
Theorem 23 (Global well-posedness) Let
be as in Exercise 10. If
, then
.
This theorem will be immediate from Theorem 19 and the following conservation law:
Proposition 24 (Conservation of vorticity distribution) Let
be as in Exercise 10 with
. Then one has
for all
and
.
Proof: By a limiting argument it suffices to show the claim for , thus we need to show
By another limiting argument we can take to be an
solution. By the monotone convergence theorem (and Sobolev embedding), it suffices to show that
whenever is a test function that vanishes in a neighbourhood of the origin
. Note that as
and all its derivatives are in
on
for every
, it is Lipschitz in space and time, which among other things implies that the level sets
are compact for every
, and so
is smooth and compactly supported in
. We may therefore may differentiate under the integral sign to obtain
where we omit explicit dependence on for brevity. By Exercise 17(i), the right-hand side is
which one can write as a total derivative
which vanishes thanks to integration by parts and the divergence-free nature of . The claim follows.
The above proposition shows that in two dimensions, is constant, and so the integral
cannot diverge for finite
. Applying Theorem 19, we obtain Theorem 23. We remark that global regularity for two-dimensional Euler was established well before the Beale-Kato-Majda theorem, starting with the work of Wolibner.
One can adapt this argument to the Navier-Stokes equations:
Exercise 25 Let
be an integer, let
, let
be divergence-free, and let
,
be a maximal Cauchy development to the Navier-Stokes equations with initial data
. Let
be the vorticity.
- (i) Establish the vorticity equation
.
- (ii) Show that
for all
and
. (Note: to adapt the proof of Proposition 12, one should restrict attention to functions
that are convex on the range of
on, say,
. The
case of this inequality can also be established using the maximum principle for parabolic equations.)
- (iii) Show that
.
Remark 26 There are other ways to establish global regularity for two-dimensional Navier-Stokes (originally due to Ladyzhenskaya); for instance, the
bound on the vorticity in Exercise 25(ii), combined with energy conservation, gives a uniform
bound on the velocity field, which can then be inserted into (the non-periodic version of) Theorem 38 of Notes 1.
Remark 27 If
solve the Euler equations on some time interval
with initial data
, then the time-reversed fields
solve the Euler equations on the reflected interval
with initial data
. Because of this time reversal symmetry, the local and global well-posedness theory for the Euler equations can also be extended backwards in time; for instance, in two dimensions any
divergence free initial data
leads to an
solution to the Euler equations on the whole time interval
. However, the Navier-Stokes equations are very much not time-reversible in this fashion.

23 comments
Comments feed for this article
9 October, 2018 at 9:57 pm
Anonymous
There is no expression in (2).
[Corrected, thanks – T.]
10 October, 2018 at 11:19 am
Anonymous
Dear Terry,
Great post! I have a question on Remark 7. It seems to be an open problem if two dimensional Euler equation has unique weak solution assuming only L^p bound on the vorticity, for p<\infty.
[Oops, I meant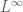 here; now corrected. -T]
here; now corrected. -T]
12 October, 2018 at 12:49 am
yasin şale
Dear Terry,
I would like to read your opinions about the proof of Riemann Hypothesis given by M. Atiyah.
Best regards.
12 October, 2018 at 9:46 pm
Anonymous
Well, I can replace Pro Tao to response your question.According to our observation, Pro Tao seems to be difficult to answer your problem for public,if you meet him in private , he is willing to reply.Because there are many sensitive reasons,although he holds proofs of RH in your hands.On RH,he has 5 ways to approach to RH,every solution seems to constrast to Atiyah’s proof.The second reson , Pro.Tao is the member of Royal committee in England,while Atiyah is also a professor in England.The third reason, he is very old if compare to Tao,so he must respect to Atiyah.According to me,Clay millenium committee will invites Tao to remark Atiyah’sproof,because Pro Tao is the expert on RH,and only members in Clay institue know Atiyah’sproof right or wrong.
12 October, 2018 at 11:39 pm
Anonymous
In order to check Atiyah’s claimed proof of RH, in addition of being expert on RH, it is even more important to be an expert on Todd function and its related functional equations (e.g. Hirzebruch functional equation) on which Atiyah’s claimed proof is based.
13 October, 2018 at 2:13 am
Anonymous
Hello. You must see the comments on the entry “Polymath15, tenth thread: numerics update.”6 September 2018
27 October, 2018 at 5:40 pm
far zeebra
This is mere child’s play. What does the Barrett Series converge to?
The Barrett Series:
1-1/2-(1/2)^2 + (1/2)^3 – (1/2)^4 -(1/2)^5 + (1/2)^6 – (1/2)^7 -(1/2)^8 +(1/2)^9 …
31 October, 2018 at 10:29 pm
YNWA
Dear all, you might be interested in this question concerning the Riemann zeta function on MathOverflow: https://mathoverflow.net/q/314310/130815
2 November, 2018 at 7:32 am
Anonymous
Dear Terry,
Terry Tao-my lovely friend.You have never mett me,but you have a immortal friendliness- a friendliness without border,nothing and anyone can compare it.I am far away with you,I always follow every your step in your jobs.You can image that I am a sattelite.I always support you.In brief, under this great sky,you are lucky to have me,I confirm many times I am the only close friend to you.I know you very well like a clear mirror.No one in the world know that you have good enough on twin prime,navier stokes,birch swinnerton Dyer ,hodge cọnecture,yang mills,collatz conjecture,goldbach,riemann p vs np.But you are stiil silent .You do not want to boast.I like you this point:humble;good virture,patient,gentle,good heart,you have also the sixth sense;you know what someone is doing,but you keep silent.I know that after I write these sentences,many people reject me.Not sense to me.they are still under me with a suppernature head
16 November, 2018 at 2:28 am
Hans
So looking forward for part 4 :-)
21 November, 2018 at 1:05 am
Sergei Ofitserov
Dear Terence Tao! I am sorry by long silence. I am in shock! That no problem of publication! I am know, how to correct your equations outside of Riman hypothesis by theme Nanvier-Stokes. I am is your mate!! We is mutually dependent in following steps. In front transparent simultaneous decision of five sums of millennium! Class N=NP ?? for the time present questionable. I agree able to arrive to you, but how?? My means hardly that’s enough(suffice) only go to airport. But what your position in that situation?? Thanks. Sergei.
15 December, 2018 at 11:44 am
Anonymous
In the proof of Theorem 5, in defining the energy , should the summand be the L^2-norm squared of
, should the summand be the L^2-norm squared of 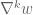 , rather than the dot product of
, rather than the dot product of 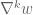 and
and  ?
?
[Corrected, thanks – T.]
8 January, 2019 at 3:12 pm
255B, Notes 2: Onsager’s conjecture | What's new
[…] amount of energy at frequencies is at most . On the other hand, by the heuristics in Remark 11 of 254A Notes 3, the time needed for the portion of the solution at frequency to evolve to a higher frequency […]
16 April, 2019 at 7:17 am
Anonymous
Thanks for the excellent notes. A couple of comments:
1) The definition of E^s around the middle of Theorem 5 is a typo (the limit of the sum should be s, and there shouldn’t be a \partial_t on w).
[Corrected, thanks – T.]
2) Aren’t the distributional solutions constructed in Proposition 6 actually strong since \partial_t u \in H^{s-1} ?
[Depends to some extent on what one means by “strong solution”, but yes, there should be enough regularity to verify that the Euler equations hold in a classical sense using classical derivatives here, though in practice this turns out to not be important so long as one knows that the solution is at least the limit of classical solutions.]
16 April, 2019 at 7:28 am
Anonymous
In the proof of Proposition 6, there seems to be a couple of typos: 1) after taking the limsup and using the triangle inequality, v^{(m)} should be u^{(m)} (two instances).
[Corrected, thanks – T.]
2) We only have (and only need) a uniform upper bound on N^{-1} \|P_{\leq N} u_0 \|_{H^{s+1}}
[Actually, I believe we do have convergence to zero in this case also, even though I agree boundedness would already be sufficient. -T]
23 April, 2019 at 10:15 am
Anonymous
In the proof of Lemma 20 (forth and fifth display), d/2-s-1 should be d/2+1-s. Later appearances are correct.
[Corrected, thanks – T.]
18 June, 2021 at 4:52 am
Ning
In the proof of Corollary 3, you used Proposition 2,3 in notes 2 and the Arzela-Ascoli theorem.
It seems that for the Proposition 2, you meant to take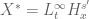 , and the assumption of Proposition 2 is satisfied since
, and the assumption of Proposition 2 is satisfied since  is a subset of
is a subset of 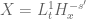 , which is separable by the fact that its dual
, which is separable by the fact that its dual 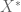 is separable.
is separable.
But for the Proposition 3 and Arzela Ascoli theorem, I’m confused about how you take and which version of Arzela Ascoli you used here?
and which version of Arzela Ascoli you used here?
And the result you get from Proposition 3 confused me a lot. Why the weak convergence which you obtained from Proposition 2 is not sufficient to know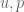 are solutions to (3) by pairing (3) with test functions, taking limit, and by the smoothness of
are solutions to (3) by pairing (3) with test functions, taking limit, and by the smoothness of 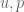 to know they are classical solutions?
to know they are classical solutions?
19 June, 2021 at 10:38 am
Terence Tao
On each ball , one can use the compact embedding of
, one can use the compact embedding of ![L^\infty_t H^{s'}_x([0,T] \times B(0,n))](https://s0.wp.com/latex.php?latex=L%5E%5Cinfty_t+H%5E%7Bs%27%7D_x%28%5B0%2CT%5D+%5Ctimes+B%280%2Cn%29%29&bg=ffffff&fg=545454&s=0&c=20201002) into
into ![L^\infty_t L^\infty_x([0,T] \times B(0,n))](https://s0.wp.com/latex.php?latex=L%5E%5Cinfty_t+L%5E%5Cinfty_x%28%5B0%2CT%5D+%5Ctimes+B%280%2Cn%29%29&bg=ffffff&fg=545454&s=0&c=20201002) (Rellich compactness) and Proposition 3 to obtain a subsequence that converges strongly in
(Rellich compactness) and Proposition 3 to obtain a subsequence that converges strongly in ![L^\infty_t L^\infty_x([0,T] \times B(0,n))](https://s0.wp.com/latex.php?latex=L%5E%5Cinfty_t+L%5E%5Cinfty_x%28%5B0%2CT%5D+%5Ctimes+B%280%2Cn%29%29&bg=ffffff&fg=545454&s=0&c=20201002) for each
for each  . Passing to subsequences once for each
. Passing to subsequences once for each  and then extracting the diagonal sequence (Arzela-Ascoli argument) one obtains a subsequence that converges strongly in
and then extracting the diagonal sequence (Arzela-Ascoli argument) one obtains a subsequence that converges strongly in ![L^\infty_t L^\infty_x([0,T] \times B(0,n))](https://s0.wp.com/latex.php?latex=L%5E%5Cinfty_t+L%5E%5Cinfty_x%28%5B0%2CT%5D+%5Ctimes+B%280%2Cn%29%29&bg=ffffff&fg=545454&s=0&c=20201002) for all
for all  , i.e., converges locally uniformly.
, i.e., converges locally uniformly.
It is also possible to proceed here purely via distributional limits as you suggest since the weak-strong uniqueness one needs is indeed easy at this high level of regularity.
18 June, 2021 at 5:32 am
Ning
In Remark 4, you said that `In the presence of a boundary, we cannot freely differentiate in space as casually as we have been doing above’
Is that because we do not have the prior bound like that in Theorem 1, then we could not get the desired boundedness? I did not quite understand what you mean by casually differentiating in space.
19 June, 2021 at 10:42 am
Terence Tao
Once one is working in a domain with boundary, then one has to be careful because there are now several inequivalent notions of derivative one can use. For instance, consider the constant function
with boundary, then one has to be careful because there are now several inequivalent notions of derivative one can use. For instance, consider the constant function  on
on  . Naively this function has gradient zero. But if instead one extends this function by zero to all of
. Naively this function has gradient zero. But if instead one extends this function by zero to all of 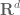 to obtain the indicator function
to obtain the indicator function  then the (weak) gradient of this function is instead a (vector-valued) distribution on the boundary
then the (weak) gradient of this function is instead a (vector-valued) distribution on the boundary 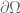 . Related to this, there are now several inequivalent Sobolev spaces
. Related to this, there are now several inequivalent Sobolev spaces 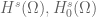 , etc. that one can define on
, etc. that one can define on  , associated with different boundary conditions, and partial differentiation operations (such as the Laplacian) do not necessarily preserve these boundary conditions. (Also, it is not always true that test functions
, associated with different boundary conditions, and partial differentiation operations (such as the Laplacian) do not necessarily preserve these boundary conditions. (Also, it is not always true that test functions 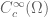 are dense in these spaces, which causes additional complications.) The book by Constantin and Foias on Navier-Stokes equations for instance treats these issues in some detail.
are dense in these spaces, which causes additional complications.) The book by Constantin and Foias on Navier-Stokes equations for instance treats these issues in some detail.
19 October, 2021 at 3:44 pm
Kevin Hu
Hi Dr. Tao, for the expression of \p_tE(t) right below the proof of Lemma 20, I think the indices are inconsistent.
[Corrected, thanks – T.]
25 October, 2021 at 3:43 am
Daniel Eriksson
Before Remark 21, when we apply Gronwall shouldn’t there be an exponential factor on both terms, exp(O_{s,d}||omega||)_{L1Linf})(log(2+E(0))+T(||u_0||_{L^2}+1))?
[Corrected, thanks – T.]
27 October, 2021 at 7:55 am
Lorenzo Pompili
Dear Professor Tao, in the proof of Lemma 20: there should be
in the proof of Lemma 20: there should be  instead of
instead of 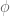 (same thing for the very next sentence).
(same thing for the very next sentence).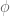 a generic function in order to state and prove the estimate, but
a generic function in order to state and prove the estimate, but 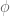 is also the name of the test function that appears in the definition of the Littlewood-Paley projections. I would suggest to use another symbol, as the two appear quite close to each other and that can generate some confusion.
is also the name of the test function that appears in the definition of the Littlewood-Paley projections. I would suggest to use another symbol, as the two appear quite close to each other and that can generate some confusion.
I think there is a typo in the definition of
Also, in formula (18) and right after that, I think you are calling
[Corrected, thanks – T.]