In the previous set of notes we developed a theory of “strong” solutions to the Navier-Stokes equations. This theory, based around viewing the Navier-Stokes equations as a perturbation of the linear heat equation, has many attractive features: solutions exist locally, are unique, depend continuously on the initial data, have a high degree of regularity, can be continued in time as long as a sufficiently high regularity norm is under control, and tend to enjoy the same sort of conservation laws that classical solutions do. However, it is a major open problem as to whether these solutions can be extended to be (forward) global in time, because the norms that we know how to control globally in time do not have high enough regularity to be useful for continuing the solution. Also, the theory becomes degenerate in the inviscid limit .
However, it is possible to construct “weak” solutions which lack many of the desirable features of strong solutions (notably, uniqueness, propagation of regularity, and conservation laws) but can often be constructed globally in time even when one us unable to do so for strong solutions. Broadly speaking, one usually constructs weak solutions by some sort of “compactness method”, which can generally be described as follows.
- Construct a sequence of “approximate solutions” to the desired equation, for instance by developing a well-posedness theory for some “regularised” approximation to the original equation. (This theory often follows similar lines to those in the previous set of notes, for instance using such tools as the contraction mapping theorem to construct the approximate solutions.)
- Establish some uniform bounds (over appropriate time intervals) on these approximate solutions, even in the limit as an approximation parameter is sent to zero. (Uniformity is key; non-uniform bounds are often easy to obtain if one puts enough “mollification”, “hyper-dissipation”, or “discretisation” in the approximating equation.)
- Use some sort of “weak compactness” (e.g., the Banach-Alaoglu theorem, the Arzela-Ascoli theorem, or the Rellich compactness theorem) to extract a subsequence of approximate solutions that converge (in a topology weaker than that associated to the available uniform bounds) to a limit. (Note that there is no reason a priori to expect such limit points to be unique, or to have any regularity properties beyond that implied by the available uniform bounds..)
- Show that this limit solves the original equation in a suitable weak sense.
The quality of these weak solutions is very much determined by the type of uniform bounds one can obtain on the approximate solution; the stronger these bounds are, the more properties one can obtain on these weak solutions. For instance, if the approximate solutions enjoy an energy identity leading to uniform energy bounds, then (by using tools such as Fatou’s lemma) one tends to obtain energy inequalities for the resulting weak solution; but if one somehow is able to obtain uniform bounds in a higher regularity norm than the energy then one can often recover the full energy identity. If the uniform bounds are at the regularity level needed to obtain well-posedness, then one generally expects to upgrade the weak solution to a strong solution. (This phenomenon is often formalised through weak-strong uniqueness theorems, which we will discuss later in these notes.) Thus we see that as far as attacking global regularity is concerned, both the theory of strong solutions and the theory of weak solutions encounter essentially the same obstacle, namely the inability to obtain uniform bounds on (exact or approximate) solutions at high regularities (and at arbitrary times).
For simplicity, we will focus our discussion in this notes on finite energy weak solutions on . There is a completely analogous theory for periodic weak solutions on
(or equivalently, weak solutions on the torus
which we will leave to the interested reader.
In recent years, a completely different way to construct weak solutions to the Navier-Stokes or Euler equations has been developed that are not based on the above compactness methods, but instead based on techniques of convex integration. These will be discussed in a later set of notes.
— 1. A brief review of some aspects of distribution theory —
We have already been using the concept of a distribution in previous notes, but we will rely more heavily on this theory in this set of notes, so we pause to review some key aspects of the theory. A more comprehensive discussion of distributions may be found in this previous blog post. To avoid some minor subtleties involving complex conjugation that are not relevant for this post, we will restrict attention to real-valued (scalar) distributions here. (One can then define vector-valued distributions (taking values in a finite-dimensional vector space) as a vector of scalar-valued distributions.)
Let us work in some non-empty open subset of a Euclidean space
(which may eventually correspond to space, time, or spacetime). We recall that
is the space of (real-valued) test functions
. It has a rather subtle topological structure (see previous notes) which we will not detail here. A (real-valued) distribution
on
is a continuous linear functional
from test functions
to the reals
. (This pairing
may also be denoted
or
in other texts.) There are two basic examples of distributions to keep in mind:
- Any locally integrable function
gives rise to a distribution (which by abuse of notation we also call
) by the formula
.
- Any Radon measure
gives rise to a distribution (which we will again call
) by the formula
. For instance, if
, the Dirac mass
at
is a distribution with
.
As a general principle, any “linear” operation that makes sense for “nice” functions (such as test functions) can also be defined for distributions, but any “nonlinear” operation is unlikely to be usefully defined for arbitrary distributions (though it may still be a good concept to use for distributions with additional regularity). For instance, one can take a partial derivative (known as the weak derivative) of any distribution
by the definition
Exercise 1 Letbe a connected open subset of
. Let
be a distribution on
such that
in the sense of distributions for all
. Show that
is a constant, that is to say there exists
such that
in the sense of distributions.
A sequence of distributions is said to converge in the weak-* sense or converge in the sense of distributions to another distribution
if one has
The linear operations alluded to above tend to be continuous in the distributional sense. For instance, it is easy to see that if , then
for all
, and
for any smooth
; similarly, if
,
, and
,
are sequences of real numbers, then
.
Suppose that one places a norm or seminorm on
. Then one can define a subspace
of the space of distributions, defined to be the space of all distributions
for which the norm
We have the following version of the Banach-Alaoglu theorem which allows us to easily create sequences that converge in the sense of distributions:
Proposition 2 (Variant of Banach-Alaoglu) Suppose thatis a norm or seminorm on
which makes the space
separable. Let
be a bounded sequence in
. Then there is a subsequence of the
which converges in the sense of distributions to a limit
.
Proof: By hypothesis, there is a constant such that
It is important to note that there is no uniqueness claimed for ; while any given subsequence of the
can have at most one limit
, it is certainly possible for different subsequences to converge to different limits. Also, the proposition only applies for spaces
that have preduals
; this covers many popular function spaces, such as
spaces for
, but omits endpoint spaces such as
or
. (For instance, approximations to the identity are uniformly bounded in
, but converge weakly to a Dirac mass, which lies outside of
.)
From definition we see that if , then we have the Fatou-type lemma
- (Escape to spatial infinity) If
is a non-zero test function, and
is a sequence in
going to infinity, then the translations
of
converge in the sense of distributions to zero, even though they will not go to zero in many function space norms (such as
).
- (Escape to frequency infinity) If
is a non-zero test function, and
is a sequence in
going to infinity, then the modulations
of
converge in the sense of distributions to zero (cf. the Riemann-Lebesgue lemma), even though they will not go to zero in many function space norms (such as
).
- (Escape to infinitely fine scales) If
,
is a sequence of positive reals going to infinity, and
, then the sequence
converges in the sense of distributions to zero, but will not go to zero in several function space norms (e.g.
with
).
- (Escape to infinitely coarse scales) If
,
is a sequence of positive reals going to zero, and
, then the sequence
converges in the sense of distributions to zero, but will not go to zero in several function space norms (e.g.
with
).
Related to this loss of mass phenomenon is the important fact that the operation of pointwise multiplication is generally not continuous in the distributional topology: and
does not necessarily imply
in general (in fact in many cases the products
or
might not even be well-defined). For instance:
- Using the escape to frequency infinity example, the functions
converge in the sense of distributions to zero, but their squares
instead converge in the sense of distributions to
, as can be seen from the double angle formula
.
- Using the escape to infinitely fine scales example, the functions
converge in the sense of distributions to zero, but their squares
will not if
.
One way to recover continuity of pointwise multiplication is to somehow upgrade distributional convergence to stronger notions of convergence. For instance, from Hölder’s inequality one sees that if converges strongly to
in
(thus
and
both lie in
, and
goes to zero), and
converges strongly to
in
, then
will converge strongly in
to
, where
.
One key way to obtain strong convergence in some norm is to obtain uniform bounds in an even stronger norm – so strong that the associated space embeds compactly in the space associated to the original norm. More precisely
Proposition 3 (Upgrading to strong convergence) Letbe two norms on
, with associated spaces
of distributions. Suppose that
embeds compactly into
, that is to say the closed unit ball in
is a compact subset of
. If
is a bounded sequence in
that converges in the sense of distributions to a limit
, then
converges strongly in
to
as well.
Proof: By the Urysohn subsequence principle, it suffices to show that every subsequence of has a further subsequence that converges strongly in
to
. But by the compact embedding of
into
, every subsequence of
has a further subsequence that converges strongly in
to some limit
, and hence also in the sense of distributions to
by definition of the
norm. But thus subsequence also converges in the sense of distributions to
, and hence
, and the claim follows.
— 2. Simple examples of weak solutions —
We now study weak solutions for some very simple equations, as a warmup for discussing weak solutions for Navier-Stokes.
We begin with an extremely simple initial value problem, the ODE
Exercise 4 Letbe locally integrable functions (extended by zero to all of
), and let
. Show that the following are equivalent:
Now let be a finite dimensional vector space, let
be a continuous function, let
, and consider the initial value problem
Exercise 5 Letbe finite dimensional, let
be continuous, let
, and let
be locally bounded and measurable. Show that the following are equivalent:
In particular, if the ODE initial value problem (5) exhibits finite time blowup for its (unique) classical solution, then it will also do so for weak solutions (with exactly the same blouwp time). This will be in contrast with the situation for PDE, in which it is possible for weak solutions to persist beyond the time in which classical solutions exist.
Now we give a compactness argument to produce weak solutions (which will then be classical solutions, by the above exercise):
Proposition 6 (Weak existence) Letbe a finite dimensional vector space, let
, let
, and let
be a continuous function. Let
be the time
Then there exists a continuously differentiable solution
to the initial value problem (5) on
.
Proof: By construction, we have
In contrast to the Picard theory when is Lipschitz, Proposition 6 does not assert any uniqueness of the solution
to the initial value problem (5). And in fact uniqueness often fails once the Lipschitz hypothesis is dropped! Consider the simple example of the scalar initial value problem
Exercise 7 Let. For each
, let
denote the function
- (i) Show that each
is Lipschitz continuous, and the
converge uniformly to the function
as
.
- (ii) Show that the solution
to the initial value problem
is given by
for
and
for
.
- (iii) Show that as
,
converges locally uniformly to the function
.
Now we give a simple example of a weak solution construction for a PDE, namely the linear transport equation
where the initial data
Suppose for the moment that are smooth, with
bounded. Then one can solve this problem using the method of characteristics. For any
, let
denote the solution to the initial value problem
Exercise 8 Let the assumptions be as above.
- (i) Show the semigroup property
for all
.
- (ii) Show that
is a homeomorphism for each
.
- (iii) Show that for every
,
is differentiable, and the derivative
obeys the linear initial value problem
(Hint: while this system formally can be obtained by differentiating (10) in
, this formal differentiation requires rigorous justification. One can for instance proceed by first principles, showing that the Newton quotients
approximately obey this equation, and then using a Gronwall inequality argument to compare this approximate solution to an exact solution.)
- (iv) Show that
is a
diffeomorphism for each
; that is to say,
and its inverse are both continuously differentiable.
- (v) Show that
is a smooth diffeomorphism (that is to say
and its inverse are both smooth). (Caution: one may require a bit of planning to avoid the proof becoming extremely long and tedious.)
From (10) and the chain rule we have the identity
Now we drop the hypothesis that is bounded. One can no longer assume that the trajectories
are globally defined, or even that they are defined for a positive time independent of the starting point
. Nevertheless, we have
Proposition 9 (Weak existence) Letbe smooth, and let
be smooth and bounded. Then there exists a bounded measurable function
which weakly solves (10) in the sense that
in the sense of distributions on
) (extending
by zero outside of
), or equivalently that
for any
. Furthermore we have
Proof: By multiplying by appropriate smooth cutoff functions, we can express
as the locally uniform limit of smooth bounded functions
with
equal to
on (say)
. By the preceding discussion, for each
we have a smooth global solution
to the initial value problem
The following exercise shows that while one can construct global weak solutions, there is significant failure of uniqueness and persistence of regularity:
Exercise 10 Set, thus we are solving the ODE
- (i) If
are bounded measurable functions, show that the function
defined by
for
and
for
is a weak solution to (14) with initial data
for
and
for
. (Note that one does not need to specify these functions at
, since this describes a measure zero set.)
- (ii) Suppose further that
, and that
is smooth and compactly supported in
. Show that the weak solution described in (i) is the solution constructed by Proposition 9.
- (iii) Show that there exist at least two bounded measurable weak solutions to (14) with initial data
, thus showing that weak solutions are not unique. (Of course, at most one of these solutions could obey the inequality (12), so there are some weak solutions that are not constructible using Proposition 9.) Show that this lack of uniqueness persists even if one also demands that the weak solutions be smooth; conversely, show that there exist weak solutions with initial data
that are discontinuous.
Remark 11 As the above example illustrates, the loss of mass phenomenon for weak solutions arises because the approximants to those weak solutions “escape to infinity”in the limit, similarly, the loss of uniqueness phenomenon for weak solutions arises because the approximants “come from infinity” in the limit. In this particular case of a transport equation, the infinity is spatial infinity, but for other types of PDE it can be possible for approximate solutions to escape from, or come from, other types of infinity, such as frequency infinity, fine scale infinity, or coarse scale infinity. (In the former two cases, the loss of mass phenomenon will also be closely related to a loss of regularity in the weak solution.) Eliminating these types of “bad behaviour” for weak solutions is morally equivalent to obtaining uniform bounds for the approximating solutions that are strong enough to prevent such solutions from having a significant presence near infinity; in the case of Navier-Stokes, this basically corresponds to controlling such solutions uniformly in subcritical or critical norms.
— 3. Leray-Hopf weak solutions —
We now adapt the above formalism to construct weak solutions to the Navier-Stokes equations, following the fundamental work of Leray, who constructed such solutions on ,
(as before, we discard the
case as being degenerate). The later work of Hopf extended this construction to other domains, but we will work solely with
here for simplicity.
In the previous set of notes, several formulations of the Navier-Stokes equations were considered. For smooth solutions (with suitable decay at infinity, and in some cases a normalisation hypothesis on the pressure also), these formulations were shown to be essentially equivalent to each other. But at the very low level of regularity that weak solutions are known to have, these different formulations of Navier-Stokes are no longer obviously equivalent. As such, there is not a single notion of a “weak solution to the Navier-Stokes equations”; the notion depends on which formulation of these equations one chooses to work with. This leads to a number of rather technical subtleties when developing a theory of weak solutions. We will largely avoid these issues here, focusing on a specific type of weak solution that arises from our version of Leray’s construction.
It will be convenient to work with the formulation
Exercise 12 (Non-endpoint Sobolev embedding theorem) Letbe such that
. Show that for any
, one has
with
(Hint: this non-endpoint case can be proven using the Littlewood-Paley projections from the previous set of notes.) The endpoint case
of the Sobolev embedding theorem is also true (as long as
), but the proof requires the Hardy-Littlewood-Sobolev fractional integration inequality, which we will not cover here; see for instance these previous lecture notes.
We conclude that there is some for which
Next, we invoke the following result from harmonic analysis:
Proposition 13 (Boundedness of the Leray projection) For any, one has the bound
for all
. In particular,
has a unique continuous extension to a linear map from
to itself.
For , this proposition follows easily from Plancherel’s theorem. For
, the proposition is more non-trivial, and is usually proven using the Calderón-Zygmund theory of singular integrals. A proof can be found for instance in Stein’s “Singular integrals“; we shall simply assume it as a black box here. We conclude that for
in the regularity class (16), we have
We can now state a form of Leray’s theorem:
Theorem 14 (Leray’s weak solutions) Letbe divergence free (in the sense of distributions), and let
. Then there exists a weak solution
to the initial value problem (15). Furthermore,
obeys the energy inequality
for almost every
.
We now prove this theorem using the same sort of scheme that was used previously to construct weak solutions to other equations. We first need to set up some approximate solutions to (15). There are many ways to do this – the traditional way being to use some variant of the Galerkin method – but we will proceed using the Littlewood-Paley projections that were already introduced in the previous set of notes. Let be a sequence of dyadic integers going to infinity. We consider solutions
to the initial value problem
The Fujita-Kato theory of mild solutions for (15) from the previous set of notes can be easily adapted to the initial value problem (19), because the projections are bounded on all the function spaces of interest. Thus, for any
, and any divergence-free
, we can define an
-mild solution to (15) on a time interval
to be a function
in the function space
The next step is to ensure that the approximate solutions exist globally in time, that is to say that
. We can do this by exploiting the energy conservation law for this equation. Indeed for any time
, define the energy
Now we need to start taking limits as . For this we need uniform bounds. Returning to the energy identity (20), we have the uniform bounds
Now we work on verifying the energy inequality (18). Let be a test function with
which is non-increasing on
. From (20) and integration by parts we have
It remains to show that is a weak solution of (15), that is to say that (17) holds in the sense of spacetime distributions. Certainly the smooth solution
of (19) will also be a weak solution, thus
At this point it is tempting to just take distributional limits of both sides of (22) to obtain (17). Certainly we have the expected convergence for the linear components of the equation:
Let’s try to simplify the task of proving (23). The partial derivative operator is continuous with respect to convergence in distributions, so it suffices to show that
It thus suffices to show that converges in the sense of distributions to
, thus one wants
Let be a dyadic integer, then we can split
We already know that goes to zero in the sense of distributions, so (as Proposition 3 indicates) the main difficulty is to obtain compactness of the sequence. The
operator localises in spatial frequency, and the restriction to
localises in both space and time, however there is still the possibility of escaping to temporal frequency. To prevent this, we need some sort of equicontinuity in time. For this, we may turn to the equation (19) obeyed by
. Applying
, we see that
Exercise 15 (Rellich compactness theorem) Letbe such that
.
- (i) Show that if
is a bounded sequence in
that converges in the sense of distributions to a limit
, then there is a subsequence
which converges strongly in
to
(thus, for any compact set
, the restrictions of
to
converge strongly in
to the restriction of
to
).
- (ii) Show that for any compact set
, the linear map
defined by setting
to be the restriction of
to
is a compact linear map.
- (iii) Show that the above two claims fail at the endpoint
(which of course only occurs when
).
The weak solutions constructed by Theorem 14 have additional properties beyond the ones listed in the above theorem. For instance:
Exercise 16 Letbe as in Theorem 14, and let
be a weak solution constructed using the proof of Theorem 14.
- (i) Show that
is divergence-free in the sense of spacetime distributions.
- (ii) (Note: this exercise is tricky.) Assume
. Show that the weak solution
obeys a local energy inequality
for all
. (Hint: compute the time derivative of
, where
is a smooth cutoff supported on
that equals one in
, and use Sobolev inequalities and Hölder to control the various terms that arise from integration by parts; one will need to expand out the Leray projection and use the fact that
is bounded on every
space for
.) Using this inequality, show that there is a measure zero subset
of
such that one has the energy inequality
for all
with
. Furthermore, show that for all
, the time-shifted function
defined by
is a weak solution to the initial value problem (15) with initial data
. (The arguments here can be extended to dimensions
, but it is open for
whether one can construct Leray-Hopf solutions obeying the strong energy inequality.)
- (iii) Show that after modifying
on a set of measure zero, the function
is continuous for any
. (Hint: first establish this when
is a test function.)
We will discuss some further properties of the Leray weak solutions in later notes.
— 4. Weak-strong uniqueness —
If is a (non-zero) element in a Hilbert space
, and
is another element obeying the inequality
This basic argument has many variants. Here are two of them:
Exercise 17 (Weak convergence plus norm bound equals strong convergence (Hilbert spaces)) Letbe an element of a Hilbert space
, and let
be a sequence in
which weakly converges to
, that is to say that
for all
. Show that the following are equivalent:
- (i)
.
- (ii)
.
- (iii)
converges strongly to
.
Exercise 18 (Weak convergence plus norm bound equals strong convergence (norms)) Let
be a measure space, let
be an absolutely integrable non-negative function, and let
be a sequence of absolutely integrable non-negative functions that converge pointwise to
. Show that the following are equivalent:
(Hint: express
- (i)
.
- (ii)
.
- (iii)
converges strongly in
to
.
and
in terms of the positive and negative parts of
. The latter can be controlled using the dominated convergence theorem.)
Exercise 19 Letbe as in Theorem 14, and let
be a weak solution constructed using the proof of Theorem 14. Show that (after modifying
on a set of measure zero if necessary),
converges strongly in
to
as
. (Hint: use Exercise 16(iii) and Exercise 17.)
Now we give a variant relating to weak and strong solutions of the Navier-Stokes equations.
Proposition 20 (Weak-strong uniqueness) Letbe an
mild solution to the Navier-Stokes equations (15) for some
,
, and
with
. Let
be a weak solution to the Navier-Stokes equation with
and
which obeys the energy inequality (18) for almost all
. Then
and
agree almost everywhere on
.
Roughly speaking, this proposition asserts that weak solutions obeying the energy inequality stay unique as long as a strong solution exists (in particular, it is unique whenever it is regular enough to be a strong solution). However, once a strong solution reaches the end of its maximal Cauchy development, there is no further guarantee of uniqueness for the rest of the weak solution. Also, there is no guarantee of uniqueness of weak solutions if the energy inequality is dropped, and indeed there is now increasing evidence that uniqueness is simply false in this case; see for instance this paper of Buckmaster and Vicol for recent work in this direction. The conditions on can be relaxed somewhat (in particular, it is possible to drop the condition
), though they still need to be “subcritical” or “critical” in nature; see for instance the classic papers of Prodi, of Serrin, and of Ladyzhenskaya, which show that weak solutions on
obeying the energy inequality are necessarily unique and smooth (after time
) if they lie in the space
for some exponents
with
and
; the endpoint case
was worked out more recently by Escauriaza, Seregin, and Sverak. For a recent survey of weak-strong uniqueness results for fluid equations, see this paper of Wiedemann.
Proof: Before we give the formal proof, let us first give a non-rigorous proof in which we pretend that the weak solution can be manipulated like a strong solution. Then we have
Now we begin the rigorous proof, in which is only known to be a weak solution. Here, we do not directly manipulate the difference equation, but instead carefully use the equations for
and
as a substitute. Define
and
as before. From the cosine rule we have
Now we work on the integral . Because we only know
to solve the equation
By hypothesis, we have
The integral can be rewritten using integration by parts as
(noting that there is enough regularity to justify the integration by parts by the usual limiting argument); expressing
as a total derivative
and integrating by parts again using the divergence-free nature of
, we see that this expression vanishes. Similarly for the
term. Now we eliminate the remaining terms which are linear in
:
One application of weak-strong uniqueness results is to give (in the case at least) partial regularity on the weak solutions constructed by Leray, in that the solutions
agree with smooth solutions on large regions of spacetime – large enough, in fact, to cover all but a measure zero set of times
. Unfortunately, the complement of this measure zero set could be disconnected, and so one could have different smooth solutions agreeing with
at different epochs, so this is still quite far from an assertion of global regularity of the solution. Nevertheless it is still a non-trivial and interesting result:
Theorem 21 (Partial regularity) Let. Let
be as in Theorem 14, and let
be a weak solution constructed using the proof of Theorem 14.
- (i) (Eventual regularity) There exists a time
such that (after modification on a set of measure zero), the weak solution
on
agrees with an
mild solution on
with initial data
(where we time shift the notion of a mild solution to start at
instead of
).
- (ii) (Epochs of regularity) There exists a compact exceptional set
of measure zero, such that for any time
, there is a time interval
containing
in its interior such that
on
agrees almost everywhere whtn an
mild solution on
with initial data
.
Proof: (Sketch) We begin with (i). From (18), the norm of
and the
norm of
are finite. Thus, for any
, one can find a positive measure set of times
such that
Now we look at (ii). In view of (i) we can work in a fixed compact interval . Let
be a time, and let
be a sufficiently small constant. If there is a positive measure set of times
for which
The above argument in fact shows that the exceptional set in part (ii) of the above theorem will have upper Minkowski dimension at most
(and hence also Hausdorff dimension at most
). There is a significant strengthening of this partial regularity result due to Caffarelli, Kohn, and Nirenberg, which we will discuss in later notes.

48 comments
Comments feed for this article
2 October, 2018 at 5:56 pm
Quanling Deng
Reblogged this on gonewithmath.
3 October, 2018 at 3:44 am
Gabriel Apolinario
These notes are a great resource.
Terry, there’s a missing word in the first paragraph: “are not high enough regularity”
[Reworded – T.]
3 October, 2018 at 6:16 am
Dr. Anil Pedgaonkar
Why maths people are left with old topics like fluid mechanics while topics like relativity theory string theory quantum theory are with physics
3 October, 2018 at 9:14 am
Anonymous
Turbulence is still not well understood and since we live in turbulent times it may become a contemporary subject.
4 October, 2018 at 10:53 pm
Anonymous
No doubt you are aware of https://en.wikipedia.org/wiki/Straw_man in your post, but let us overlook that. The reason why fluid mechanics, in particular Navier-Stokes equations, is mathematically interesting is that its behavior is not well-understood, even though its formulation is extremely simple. Anyone with modest math education can “understand” the governing equations, but no-one knows whether they are well-posed for arbitrarily long time intervals. Certainly there are open problems and plenty of theory building to be done in string theory and other fields practiced by “big bad physicists” where the problem setting itself is more complicated, but one is simply less surprised to encounter unsolved problems in more complicated settings. Moreover, all the fields you mentioned belong to mathematical physics and are under active research by quite a few well-trained people who consider themselves primarily as mathematicians.
4 October, 2018 at 11:26 pm
Juha-Matti Perkkiö
Prof. Tao,
the recent polymath-projects discussed in this blog have been very inspiring and seem to be rather efficient when their goals are set properly. Could there be a case for some kind of mixed analysis/numerical analysis/computational project to gain some insight on Navier-Stokes? What comes to mind is for example to generate solutions with H^2- or H^1-norm growing as fast as possible/decaying as slow as possible or perhaps to generate solutions decaying as fast as possible in some relevant weaker norm like L^2. I am aware that even the existence of suitable quantitative criteria for the reliability of such numerical experiments is not self-evident, but perhaps there are some.
5 October, 2018 at 12:44 pm
Sam
Apologies, I must be missing something basic, but why do the bounds on the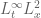 norm of
norm of  and
and  -norm of
-norm of 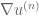 imply an
imply an  bound on
bound on  ?
?
5 October, 2018 at 12:45 pm
Sam
Sorry, I should specify that I’m talking about estimate (21).
5 October, 2018 at 2:23 pm
Terence Tao
This was a typo: it has been corrected to .
.
7 October, 2018 at 1:55 am
Sam
Ah, yes, that makes sense. Thanks!
7 October, 2018 at 5:14 am
Huang
Terry,I am Chinese. I have a new opinion about Callatz Conjecture. How can I send it to you?
8 October, 2018 at 9:29 am
Anonymous
Are you Huang Deren mathematician?
8 October, 2018 at 4:18 pm
Huang
No
9 October, 2018 at 12:44 pm
254A, Notes 3: Local well-posedness for the Euler equations | What's new
[…] weak compactness (Proposition 2 of Notes 2), one can pass to a subsequence such that converge weakly to some limits , such that and all […]
8 November, 2018 at 5:48 am
Stefan
As a double major in theoretical physics/theoretical computer science, I’m very intersted in this.
Does anybody know if this is related to “Homotopy Analysis Method in Nonlinear Differential Equations” and “Liao’s Method of Directly Defining the Inverse Mapping (MDDiM).”?
https://www.researchgate.net/publication/266832165_Homotopy_Analysis_Method_in_Nonlinear_Differential_Equations
https://link.springer.com/article/10.1007/s11075-015-0077-4
Anyway, since reading the post about ultrafilters and hierarchical infinitesimals, I feel that more boundries between physics and computer science could be broken and new solutions be found.
I think it is about time to solve the crisis in physics
8 November, 2018 at 3:39 pm
Anonymous
In physics, the subjective(!) description “more beautiful” for a desired feature of a better new theory should be replaced (or interpreted) by the objective(!) description “more symmetrical”. It is interesting to observe that each new physical theory is indeed “more symmetrical” (i.e. invariant under a larger group of transformations) – leading to (the already observed) microscopic “fearfull symmetry” for all known elementary particles interactions, and also macroscopically for gravitation.
9 December, 2018 at 2:32 pm
254A, Supplemental: Weak solutions from the perspective of nonstandard analysis (optional) | What's new
[…] a Notes 2, we reviewed the classical construction of Leray of global weak solutions to the Navier-Stokes […]
16 December, 2018 at 2:37 pm
255B, Notes 1: The Lagrangian formulation of the Euler equations | What's new
[…] Despite the popularity of the initial condition (4), we will try to keep conceptually separate the Eulerian space from the Lagrangian space , as they play different physical roles in the interpretation of the fluid; for instance, while the Euclidean metric is an important feature of Eulerian space , it is not a geometrically natural structure to use in Lagrangian space . We have the following more general version of Exercise 8 from 254A Notes 2: […]
23 February, 2019 at 10:28 am
Guilherme Rezende
You have tried solutions in the form: with
with 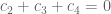 and
and  ? they work
? they work
2 April, 2019 at 6:42 pm
Zaher
In the discussion following (24), it is said that {u^{(n)}} is bounded in {L^\infty_t L^p_x}, uniformly in {n}, for some {2 < p < \infty}. But we only have uniform {L_2 H^1} control which would give {L_t^2 L_x^p}. As a consequence, {F_j^N} is uniformly bounded in {L_t^1 L_x^{p/2}}. This does not affect the argument, apart from some apparent typos.
[Corrected, thanks – T.]
13 April, 2019 at 4:23 am
Anonymous
If one considers the Dirichlet boundary conditions on a bounded domain, does the Leray projection preserve the boundary condition?
7 August, 2019 at 6:25 am
Martin
Hello, I am interested in the solutions of the Navier-Stokes equations. ,
,  are two weak Leray solutions for the 3D Navier-Stokes equations with
are two weak Leray solutions for the 3D Navier-Stokes equations with
 (1)
(1)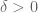 ,
,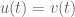 for all
for all ![t\in[0,\delta]](https://s0.wp.com/latex.php?latex=t%5Cin%5B0%2C%5Cdelta%5D&bg=ffffff&fg=545454&s=0&c=20201002) (2).
(2).
Is a weak solution for the 3D Navier-Stokes equations locally unique?
If
Then there is a small
such that
Is it true that (1) implies (2) using weak continuity, energy inequality?
7 August, 2019 at 7:31 am
Terence Tao
I am not aware of such a result (and this would likely be of comparable difficulty as establishing global uniqueness for Leray-Hopf solutions, which is not universally believed to be true). It is true however that will converge strongly to zero in
will converge strongly to zero in 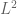 as
as 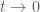 (possibly after modifying the weak solution on a measure zero set of times), thanks to Exercise 19. And weak-strong uniqueness will kick in if one of the weak solutions
(possibly after modifying the weak solution on a measure zero set of times), thanks to Exercise 19. And weak-strong uniqueness will kick in if one of the weak solutions  is strong.
is strong.
7 August, 2019 at 1:24 pm
Martin
We assume that the following assertion is true:![[a,T]](https://s0.wp.com/latex.php?latex=%5Ba%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) , with
, with  corresponding to the same data
corresponding to the same data  .
.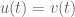 almost everywhere on
almost everywhere on ![[a,T]](https://s0.wp.com/latex.php?latex=%5Ba%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.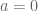 .
.
Let u, v two weak Leray solutions of the 3D Navier-Stokes equations on
Then
Is this an uniqueness result for weak Leray solutions of the 3D Navier-Stokes equations ?
Or, It must to extend this to
8 August, 2019 at 7:08 am
Terence Tao
This would depend rather sensitively on how one actually defines the notion of a “weak Leray solution on![[a,T]](https://s0.wp.com/latex.php?latex=%5Ba%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) “. For instance, would one require the energy inequality (18) to hold starting from time
“. For instance, would one require the energy inequality (18) to hold starting from time  , or from time
, or from time  ? Similarly for the distributional initial value condition (17). With weak solutions one has to be very careful with the precise definitions and hypotheses, as it is very easy to make subtle errors in one’s reasoning otherwise by blindly applying a fact that is true for classical solutions to one or more weak solutions. For instance, depending on how precisely one defines a “Leray weak solution”, the time translation
? Similarly for the distributional initial value condition (17). With weak solutions one has to be very careful with the precise definitions and hypotheses, as it is very easy to make subtle errors in one’s reasoning otherwise by blindly applying a fact that is true for classical solutions to one or more weak solutions. For instance, depending on how precisely one defines a “Leray weak solution”, the time translation  of a Leray weak solution
of a Leray weak solution  may not itself be a Leray weak solution, even though the corresponding fact for classical solutions is trivially true.
may not itself be a Leray weak solution, even though the corresponding fact for classical solutions is trivially true.
3 June, 2020 at 6:36 am
Antoine
At the end of the lecture, you said that you would cover the Caffarelli-Kohn-Nirenberg theorem, which I would like to read about. However, the later notes only cover Euler equations related topics. Do you stil plan on writing notes on this matter?
[No – T.]
17 October, 2020 at 3:59 pm
Anonymous
Before Exercise 4:
Thanks to the fundamental theorem of calculus for locally integrable functions, we still recover the unique solution (16):
and also in Exercise 4(ii):
One has (16) for almost all .
.
“(16)” is linked to equation (3).
[Corrected, thanks – T.]
20 October, 2020 at 3:37 pm
Anonymous
At the level of set function, a function![u:[0,T]\times \mathbf{R}^d\to\mathbf{R}](https://s0.wp.com/latex.php?latex=u%3A%5B0%2CT%5D%5Ctimes+%5Cmathbf%7BR%7D%5Ed%5Cto%5Cmathbf%7BR%7D&bg=ffffff&fg=545454&s=0&c=20201002) can be always interpreted as
can be always interpreted as
![u:[0,T]\to X](https://s0.wp.com/latex.php?latex=u%3A%5B0%2CT%5D%5Cto+X&bg=ffffff&fg=545454&s=0&c=20201002) where
where  is the set of functions from
is the set of functions from  to
to 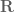 and
and 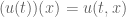 .
.
If one puts extra assumptions on so that
so that  for all
for all  and
and  is some nice (separable, self-reflexive, …) Banach space, then there are two ways to define the weak partial derivative
is some nice (separable, self-reflexive, …) Banach space, then there are two ways to define the weak partial derivative  .
.
One way is to define it as a distribution on , as in this set of notes, which is a continuous linear functional on
, as in this set of notes, which is a continuous linear functional on  (with the smooth topology). This notion does not depend on the structure of
(with the smooth topology). This notion does not depend on the structure of  mentioned above.
mentioned above.
Another way is that if one knows in addition,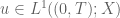 , i.e.,
, i.e.,  is strongly measurable such that
is strongly measurable such that ![\int_{[0,T]}\|u(t)\|_{X}dt<\infty](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5B0%2CT%5D%7D%5C%7Cu%28t%29%5C%7C_%7BX%7Ddt%3C%5Cinfty&bg=ffffff&fg=545454&s=0&c=20201002) , one can define
, one can define 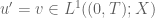 be the "weak derivative of
be the "weak derivative of  where
where

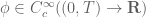 . Here
. Here 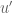 is a continuous functional on
is a continuous functional on 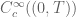 .
.
for all
Are these two notions of "weak derivative" somehow equivalent to each other so that one can always write one in terms of another and safely use them interchangeably?
21 October, 2020 at 11:09 am
Terence Tao
As a general rule, any two “good” notions of weak or strong derivative (or integral, or other standard linear operation) would be expected to coincide on their common domain of definition. One reason for this is that (i) almost all the usual domains of definition admit some nice class of test functions which are dense these domains in suitable topologies; (ii) a “good” interpretation of the operation in question tends to be weakly continuous with respect to these topologies (e.g., as measured in the distributional topology), and (iii) weak limits are unique. It would be a good exercise for you to work out this scheme for the two notions of derivative you describe here to show that they are compatible on the common domain of definition.
21 October, 2020 at 4:23 pm
Anonymous
… by the definition
There is a redundant negative sign.
… Two distributions
I think the subscript is missing in
is missing in 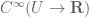 .
.
[Corrected, thanks – T.]
21 October, 2020 at 4:54 pm
Anonymous
Could you elaborate on how Exercise 4 is done by the fundamental theorem of calculus for locally integrable functions?
By definition, (i) is the same as
for every . How does this lead to (3) almost everywhere?
. How does this lead to (3) almost everywhere?
On the other hand, if one assumes (3) almost everywhere, then (*) is true for some special test function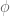 . How does it generalize to every
. How does it generalize to every  ?
?
23 October, 2020 at 7:51 am
Terence Tao
For the first implication, it suffices by the second implication and linearity to verify the case . By the fundamental theorem of calculus, any function in
. By the fundamental theorem of calculus, any function in 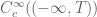 is equal on
is equal on ![[0,T]](https://s0.wp.com/latex.php?latex=%5B0%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) to the derivative of another function on
to the derivative of another function on 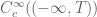 .
.
For the second implication, insert (3) into the left-hand side of (*), then apply Fubini’s theorem and then the fundamental theorem of calculus (the regularity hypotheses on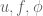 are more than sufficient to justify the formal manipulations).
are more than sufficient to justify the formal manipulations).
21 October, 2020 at 5:07 pm
Anonymous
In section 2, when defining the weak solution using (4), is required to be “locally integrable”. In the more general setting of (5),
is required to be “locally integrable”. In the more general setting of (5),  is said to be “locally bounded”. Are these two notions equivalent?
is said to be “locally bounded”. Are these two notions equivalent?
23 October, 2020 at 7:53 am
Terence Tao
No. For instance if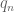 is an enumeration of the rationals then
is an enumeration of the rationals then ![\sum_{n=1}^\infty 2^{n} 1_{[q_n,q_n+4^{-n}]}](https://s0.wp.com/latex.php?latex=%5Csum_%7Bn%3D1%7D%5E%5Cinfty+2%5E%7Bn%7D+1_%7B%5Bq_n%2Cq_n%2B4%5E%7B-n%7D%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) is locally integrable (in fact globally integrable) but not locally bounded. On the other hand all locally bounded functions are locally integrable.
is locally integrable (in fact globally integrable) but not locally bounded. On the other hand all locally bounded functions are locally integrable.
22 October, 2020 at 9:42 am
Anonymous
In the proof of Theorem 14,
 which converges in the sense of spacetime distributions in
which converges in the sense of spacetime distributions in 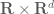 (after extending by zero outside of
(after extending by zero outside of  to a limit
to a limit  , which is in
, which is in ![{L^\infty_t H^1_x([0,T] \times {\bf R}^d \rightarrow {\bf R}^d)}](https://s0.wp.com/latex.php?latex=%7BL%5E%5Cinfty_t+H%5E1_x%28%5B0%2CT%5D+%5Ctimes+%7B%5Cbf+R%7D%5Ed+%5Crightarrow+%7B%5Cbf+R%7D%5Ed%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) for every
for every 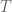 .
.
… This is enough regularity for Proposition 2 to apply, and we can pass to a subsequence of
(A piece of parenthesis is missing and I guess you mean extending by zero outside of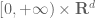 .)
.)
[Typos corrected, also should be
should be  -T.]
-T.]
I try to understand how Banach-Alaoglu (Prop 2) is used here. In particular, what is and what is
and what is  in the argument above?
in the argument above?
[Here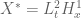 and
and  is the predual space
is the predual space  (or one can use the Riesz representation theorem for Hilbert spaces and take
(or one can use the Riesz representation theorem for Hilbert spaces and take  with the usual Riesz identification). -T.]
with the usual Riesz identification). -T.]
22 October, 2020 at 10:05 am
Anonymous
I’m confused with the topologies on the linear space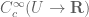 .
.
In the definition of distributions on , there is a “standard” topology
, there is a “standard” topology  on
on 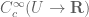 that one defines the continuous linear functionals on
that one defines the continuous linear functionals on 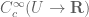 as distributions on
as distributions on  .
.
On the other hand, with a different norm/seminorm on
on 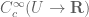 in the hypothesis of Proposition 2, one has different topology
in the hypothesis of Proposition 2, one has different topology  . How does
. How does  compare to
compare to  ? How does one know that element in
? How does one know that element in 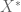 is a “distribution” so that one can talk about “converges in the sense of distributions” in Proposition 2?
is a “distribution” so that one can talk about “converges in the sense of distributions” in Proposition 2?
23 October, 2020 at 12:53 pm
Terence Tao
Virtually every function space norm one works with in analysis, when restricted to test functions, gives a topology that is weaker than the test function topology, hence every linear functional that is continuous with respect to the norm topology will also be continuous with respect to the test function topology, and is hence a distribution.
23 October, 2020 at 4:09 pm
Anonymous
(I tried to post the following comment previously. But I don’t know why it was classified as spam by WordPress…)
In the “approximate solutions” stage of the proof of Theorem 14, what is the purpose of introducing the notion of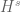 -mild solution to (15) on a time interval
-mild solution to (15) on a time interval ![[0,T]](https://s0.wp.com/latex.php?latex=%5B0%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) ?
?
It is said after the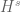 -mild solution definition that
-mild solution definition that
… By a modification of the theory of the previous set of notes, we thus see that there is a maximal Cauchy development
Isn’t being smooth better than being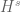 -mild?
-mild?
Later,
… From (19) we know that
why the *smooth* now only lie in
now only lie in ![{C^0_t H^s_x([0,T] \times {\bf R}^d \rightarrow {\bf R}^d)}](https://s0.wp.com/latex.php?latex=%7BC%5E0_t+H%5Es_x%28%5B0%2CT%5D+%5Ctimes+%7B%5Cbf+R%7D%5Ed+%5Crightarrow+%7B%5Cbf+R%7D%5Ed%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) ?
?
23 October, 2020 at 7:38 pm
Terence Tao
Smoothness does not imply decay in space, so a smooth function does not automatically lie in .
.
24 October, 2020 at 6:29 am
Anonymous
In the last big step of the proof of Theorem 14, the problem is reduced to showing (23):
which, by several intermediate steps, is reduced to showing that

 for every fixed
for every fixed 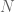 and
and  .
.
strongly in
If one wants to apply Proposition 3 (with some appropriate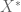 and
and  ) at some point, then it should be that
) at some point, then it should be that 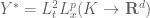 (right?). The sequence itself is not a space, what should
(right?). The sequence itself is not a space, what should 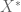 be?
be?
By showing that
and
the later paragraph shows that is equicontinuous in
is equicontinuous in  . In order to apply Arzela-Ascoli theorem, a pointwise bound for
. In order to apply Arzela-Ascoli theorem, a pointwise bound for  is also needed (isn’t it?), is it alluded somewhere?
is also needed (isn’t it?), is it alluded somewhere?
Also, when the Arzela-Ascoli theorem is applied, does one only have a uniformly convergent subsequence of instead of the sequence itself as stated in the penultimate sentence of the proof? Would you elaborate how Proposition 3 is used there?
instead of the sequence itself as stated in the penultimate sentence of the proof? Would you elaborate how Proposition 3 is used there?
25 October, 2020 at 4:08 pm
Terence Tao
Proposition 3 can applied with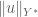 being the sum of the
being the sum of the ![L^2_t L^\infty_x(K \times [0,T])](https://s0.wp.com/latex.php?latex=L%5E2_t+L%5E%5Cinfty_x%28K+%5Ctimes+%5B0%2CT%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) norm of
norm of 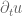 , the
, the ![L^\infty_t L^\infty_x(K \times [0,T])](https://s0.wp.com/latex.php?latex=L%5E%5Cinfty_t+L%5E%5Cinfty_x%28K+%5Ctimes+%5B0%2CT%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) norm of
norm of 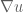 , and the
, and the  norm of
norm of  (to get the lower order term, which in this case vanishes for
(to get the lower order term, which in this case vanishes for  large enough), and
large enough), and ![X^* = L^\infty_t L^\infty_x(K \times [0,T])](https://s0.wp.com/latex.php?latex=X%5E%2A+%3D+L%5E%5Cinfty_t+L%5E%5Cinfty_x%28K+%5Ctimes+%5B0%2CT%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) , with the Arzela-Ascoli theorem giving the required compact embedding. (One can check that these spaces have appropriate preduals
, with the Arzela-Ascoli theorem giving the required compact embedding. (One can check that these spaces have appropriate preduals  ; one can also use the proof of Proposition 3 directly rather than using it as a black box to obtain a similar conclusion, for instance the Urysohn subsequence principle can be used to deal with the subsequence problem you mentioned.)
; one can also use the proof of Proposition 3 directly rather than using it as a black box to obtain a similar conclusion, for instance the Urysohn subsequence principle can be used to deal with the subsequence problem you mentioned.)
29 October, 2020 at 5:36 pm
Anonymous
In the definition (17) of the “weak solution” right before Theorem 14, is the divergence-free condition for hiding somewhere so that one does not need to incorporate it into the definition?
hiding somewhere so that one does not need to incorporate it into the definition?
Does the mentioned definition (17) remain the same if one only considers the spacetime test functions that are (space) divergence-free?.
29 October, 2020 at 6:01 pm
Anonymous
1. If the data is div-free then solutions to this equation are always div-free.
2. The test function here is scalar-valued so this doesn’t make sense. If instead you dot it with a vector-valued test function, the answer is yes because of the Hodge decomposition.
30 October, 2020 at 8:24 am
Anonymous
In the case when is a finite-dimensional vector space, particularly in the definition of “weak solutions” after Exercise 4, the notion of “distributions” seems to be no longer a continuous linear functional on the space
is a finite-dimensional vector space, particularly in the definition of “weak solutions” after Exercise 4, the notion of “distributions” seems to be no longer a continuous linear functional on the space  but a map from
but a map from  to
to  .
.
On the other hand, one can consider the vector-valued test functions![{\boldsymbol \phi}\in [C_c^\infty((-\infty, T))^n]^n](https://s0.wp.com/latex.php?latex=%7B%5Cboldsymbol+%5Cphi%7D%5Cin+%5BC_c%5E%5Cinfty%28%28-%5Cinfty%2C+T%29%29%5En%5D%5En&bg=ffffff&fg=545454&s=0&c=20201002) in the definition of weak solution:
in the definition of weak solution:
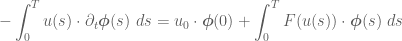
 is endowed with an inner product structure. In this case, one has linear functionals on
is endowed with an inner product structure. In this case, one has linear functionals on ![[C_c^\infty((-\infty, T))^n)]^n](https://s0.wp.com/latex.php?latex=%5BC_c%5E%5Cinfty%28%28-%5Cinfty%2C+T%29%29%5En%29%5D%5En&bg=ffffff&fg=545454&s=0&c=20201002) .
.
where
Are these two notions of weak solutions equivalent? (What if is of infinite-dimensional?)
is of infinite-dimensional?)
30 October, 2020 at 10:43 am
Terence Tao
For finite dimensions the two notions are equivalent, as can be easily be seen by selecting a basis for (e.g., by applying Gram-Schmidt to the inner product) and writing everything in coordinates. For infinite dimensional ranges, different notions of weak solution can in principle differ from each other, though many times in practice one has enough additional bounds on the specific weak solutions one constructs (e.g., by the Leray-Hopf method) that one can establish the weak solvability of the solution in any of the possible senses. Conversely, without such additional bounds the mere property of being weakly solvable is virtually useless, regardless of which specific notion of weak solution one prefers. So in practice the precise definition of weak solution is not of critical importance.
(e.g., by applying Gram-Schmidt to the inner product) and writing everything in coordinates. For infinite dimensional ranges, different notions of weak solution can in principle differ from each other, though many times in practice one has enough additional bounds on the specific weak solutions one constructs (e.g., by the Leray-Hopf method) that one can establish the weak solvability of the solution in any of the possible senses. Conversely, without such additional bounds the mere property of being weakly solvable is virtually useless, regardless of which specific notion of weak solution one prefers. So in practice the precise definition of weak solution is not of critical importance.
7 November, 2020 at 2:15 am
Jakob Moeller
A question about the spaces we need to show convergence of . We know by
. We know by 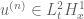 and Sobolev as well as Hölder that
and Sobolev as well as Hölder that  (all on
(all on ![[0,T]](https://s0.wp.com/latex.php?latex=%5B0%2CT%5D&bg=ffffff&fg=545454&s=0&c=20201002) ). It is later stated that
). It is later stated that  is in
is in  . This is a little confusing to me. Shouldn’t it be in
. This is a little confusing to me. Shouldn’t it be in  as before? Especially because we reduce the claim to showing that
as before? Especially because we reduce the claim to showing that  converges strongly in
converges strongly in  to
to  ?
?
[This was a typo, now corrected. -T.]
30 December, 2023 at 6:03 pm
Anonymous
Hello. I have a question about weak-strong uniqueness.
Most textbooks as well as your statement deal with the decaying turbulence only. That is, the external forcing term “f” is set to be zero.
However, it seems to me that your proof of weak-strong uniqueness actually works for any “f” belonging to L^2_t L^2_x.
Could you please tell me your opinion? I also would deeply appreciate if you recommend me any reference.
31 December, 2023 at 10:49 am
Terence Tao
This seems plausible to me, although there are often subtleties with manipulating weak solutions and one would have to go through the proof carefully. I’m afraid I don’t know of a canonical reference for treating weak-strong uniqueness for the inhomogeneous problem, but I would imagine that this problem has been considered by multiple authors in the literature.