We now begin the rigorous theory of the incompressible Navier-Stokes equations
In order for the system (1) to even make sense, one requires some level of regularity on the unknown fields ; this turns out to be a relatively important technical issue that will require some attention later in this set of notes, and we will end up transforming (1) into other forms that are more suitable for lower regularity candidate solution. Our focus here will be on local existence of these solutions in a short time interval
or
, for some
. (One could in principle also consider solutions that extend to negative times, but it turns out that the equations are not time-reversible, and the forward evolution is significantly more natural to study than the backwards one.) The study of Euler equations, in which
, will be deferred to subsequent lecture notes.
As the unknown fields involve a time parameter , and the first equation of (1) involves time derivatives of
, the system (1) should be viewed as describing an evolution for the velocity field
. (As we shall see later, the pressure
is not really an independent dynamical field, as it can essentially be expressed in terms of the velocity field without requiring any differentiation or integration in time.) As such, the natural question to study for this system is the initial value problem, in which an initial velocity field
is specified, and one wishes to locate a solution
to the system (1) with initial condition
The fundamental questions in the local theory of an evolution equation are that of existence, uniqueness, and continuous dependence. In the context of the Navier-Stokes equations, these questions can be phrased (somewhat broadly) as follows:
- (a) (Local existence) Given suitable initial data
, does there exist a solution
to the above initial value problem that exists for some time
? What can one say about the time
of existence? How regular is the solution?
- (b) (Uniqueness) Is it possible to have two solutions
of a certain regularity class to the same initial value problem on a common time interval
? To what extent does the answer to this question depend on the regularity assumed on one or both of the solutions? Does one need to normalise the solutions beforehand in order to obtain uniqueness?
- (c) (Continuous dependence on data) If one perturbs the initial conditions
by a small amount, what happens to the solution
and on the time of existence
? (This question tends to only be sensible once one has a reasonable uniqueness theory.)
The answers to these questions tend to be more complicated than a simple “Yes” or “No”, for instance they can depend on the precise regularity hypotheses one wishes to impose on the data and on the solution, and even on exactly how one interprets the concept of a “solution”. However, once one settles on such a set of hypotheses, it generally happens that one either gets a “strong” theory (in which one has existence, uniqueness, and continuous dependence on the data), a “weak” theory (in which one has existence of somewhat low-quality solutions, but with only limited uniqueness results (or even some spectacular failures of uniqueness) and almost no continuous dependence on data), or no satsfactory theory whatsoever. In the former case, we say (roughly speaking) that the initial value problem is locally well-posed, and one can then try to build upon the theory to explore more interesting topics such as global existence and asymptotics, classifying potential blowup, rigorous justification of conservation laws, and so forth. With a weak local theory, it becomes much more difficult to address these latter sorts of questions, and there are serious analytic pitfalls that one could fall into if one tries too strenuously to treat weak solutions as if they were strong. (For instance, conservation laws that are rigorously justified for strong, high-regularity solutions may well fail for weak, low-regularity ones.) Also, even if one is primarily interested in solutions at one level of regularity, the well-posedness theory at another level of regularity can be very helpful; for instance, if one is interested in smooth solutions in , it turns out that the well-posedness theory at the critical regularity of
can be used to establish globally smooth solutions from small initial data. As such, it can become quite important to know what kind of local theory one can obtain for a given equation.
This set of notes will focus on the “strong” theory, in which a substantial amount of regularity is assumed in the initial data and solution, giving a satisfactory (albeit largely local-in-time) well-posedness theory. “Weak” solutions will be considered in later notes.
The Navier-Stokes equations are not the simplest of partial differential equations to study, in part because they are an amalgam of three more basic equations, which behave rather differently from each other (for instance the first equation is nonlinear, while the latter two are linear):
- (a) Transport equations such as
.
- (b) Diffusion equations (or heat equations) such as
.
- (c) Systems such as
,
, which (for want of a better name) we will call Leray systems.
Accordingly, we will devote some time to getting some preliminary understanding of the linear diffusion and Leray systems before returning to the theory for the Navier-Stokes equation. Transport systems will be discussed further in subsequent notes; in this set of notes, we will instead focus on a more basic example of nonlinear equations, namely the first-order ordinary differential equation
whereA key role in our treatment here will be played by the fundamental theorem of calculus (in various forms and variations). Roughly speaking, this theorem, and its variants, allow us to recast differential equations (such as (1) or (4)) as integral equations. Such integral equations are less tractable algebraically than their differential counterparts (for instance, they are not ideal for verifying conservation laws), but are significantly more convenient for well-posedness theory, basically because integration tends to increase the regularity of a function, while differentiation reduces it. (Indeed, the problem of “losing derivatives”, or more precisely “losing regularity”, is a key obstacle that one often has to address when trying to establish well-posedness for PDE, particularly those that are quite nonlinear and with rough initial data, though for nonlinear parabolic equations such as Navier-Stokes the obstacle is not as serious as it is for some other PDE, due to the smoothing effects of the heat equation.)
One weakness of the methods deployed here are that the quantitative bounds produced deteriorate to the point of uselessness in the inviscid limit , rendering these techniques unsuitable for analysing the Euler equations in which
. However, some of the methods developed in later notes have bounds that remain uniform in the
limit, allowing one to also treat the Euler equations.
In this and subsequent set of notes, we use the following asymptotic notation (a variant of Vinogradov notation that is commonly used in PDE and harmonic analysis). The statement ,
, or
will be used to denote an estimate of the form
(or equivalently
) for some constant
, and
will be used to denote the estimates
. If the constant
depends on other parameters (such as the dimension
), this will be indicated by subscripts, thus for instance
denotes the estimate
for some
depending on
.
— 1. Ordinary differential equations —
We now study solutions to ordinary differential equations (4), focusing in particular on the initial value problem when the initial state is specified. We restrict attention to strong solutions
, in which
is continuously differentiable (
) in the time variable, so that the derivative
in (4) can be interpreted as the classical (strong) derivative, and one has the classical fundamental theorem of calculus
We begin with homogeneous linear equations
One can apply a similar analysis to the differential inequality
where
We continue assuming that for simplicity. From the fundamental theorem of calculus, (7) (and the initial condition
) implies the integral inequality
Lemma 1 (Integral form of Grönwall inequality) Letbe an interval containing
as left endpoint, let
, and let
,
be continuous functions obeying the inequality (10) for all
. Then one has (9) for all
.
Proof: From (10) and the fundamental theorem of calculus, the function is continuously differentiable and obeys the differential inequality
Exercise 2 Relax the hypotheses of continuity onto that of being measurable and bounded on compact intervals. (You will need tools such as the fundamental theorem of calculus for absolutely continuous or Lipschitz functions, covered for instance in this previous set of notes.)
Gronwall’s inequality is an excellent tool for bounding the growth of a solution to an ODE or PDE, or the difference between two such solutions. Here is a basic example, one half of the Picard (or Picard-Lindeöf) theorem:
Theorem 3 (Picard uniqueness theorem) Letbe an interval, let
be a finite-dimensional vector space, let
be a function that is Lipschitz continuous on every bounded subset of
, and let
be continuously differentiable solutions to the ODE (4), thus
on
. If
for some
, then
and
agree identically on
, thus
for all
.
Proof: By translating and
we may assume without loss of generality that
. By splitting
into at most two intervals, we may assume that
is either the left or right endpoint of
; by applying the time reversal symmetry of replacing
by
respectively, and also replacing
by
and
, we may assume without loss of generality that
is the left endpoint of
. Finally, by writing
as the union of compact intervals with left endpoint
, we may assume without loss of generality that
is compact. In particular,
are bounded and hence
is Lipschitz continuous with some finite Lipschitz constant
on the ranges of
and
.
From the fundamental theorem of calculus we have
Remark 4 The same result applies for infinite-dimensional normed vector spaces, at least if one requires
to be continuously differentiable in the strong (Fréchet) sense; the proof is identical.
Exercise 5 (Comparison principle) Letbe a function that is Lipschitz continuous on compact intervals. Let
be an interval, and let
be continuously differentiable functions such that
and
for all
.
- (a) Suppose that
for some
. Show that
for all
with
. (Hint: there are several ways to proceed here. One is to try to verify the hypotheses of Grönwall’s inequality for the quantity
or
.)
- (b) Suppose that
for some
. Show that
for all
with
.
Now we turn to the existence side of the Picard theorem.
Theorem 6 (Picard existence theorem) Letbe a finite dimensional normed vector space, let
, and let
lie in the closed ball
. Let
be a function which has a Lipschitz constant of
on the ball
. If one sets
then there exists a continuously differentiable solution
to the ODE (4) with initial data
such that
for all
.
Note that the solution produced by this theorem is unique on , thanks to Theorem 3. We will be primarily concerned with the case
, in which case the time of existence
simplifies to
.
Proof: Using the fundamental theorem of calculus, we write (4) (with initial condition ) in integral form as
We can view this as a fixed point problem. Let denote the space of continuous functions from
to
. We give this the uniform metric
Remark 7 The proof extends without difficulty to infinite dimensional Banach spaces. Up to a multiplicative constant, the result is sharp. For instance, consider the linear ODE
for some
, with
. Here, the function
is of course Lipschitz with constant
on all of
, and the solution is of the form
, hence
will exit
in time
, which is only larger than the time
given by the above theorem by a multiplicative constant.
We can iterate the Picard existence theorem (and combine it with the uniqueness theorem) to conclude that there is a maximal Cauchy development to the ODE (4) with initial data
, with the solution diverging to infinity (or “blowing up”) at the endpoint
if this endpoint is finite, and similarly for
(thus one has a dichotomy between global existence and finite time blowup). More precisely:
Theorem 8 (Maximal Cauchy development) Letbe a finite dimensional normed vector space, let
, and let
be a function which is Lipschitz on bounded sets. Then there exists
and a continuously differentiable solution
to (4) with
, such that
if
is finite, and
if
is finite. Furthermore,
, and
are unique.
Proof: Uniqueness follows easily from Theorem 3. For existence, let be the union of all the intervals containing
for which there is a continuously differentiable solution to (4) with
. From Theorem 6
contains a neighbourhood of the origin. From Theorem 3 one can glue all the solutions together to obtain a continuously differentiable solution
to (4) with
. If
is contained in
, then by Theorem 6 (and time translation) one could find a solution
to (4) in a neighbourhood of
such that
; by Theorem 3 we must then have
, otherwise we could glue
to
and obtain a solution on a larger domain than
, contradicting the definition of
. Thus
is open, and is of the form
for some
.
Suppose for contradiction that is finite and
does not go to infinity as
. Then there exists a finite
and a sequence
such that
. Let
be the Lipschitz constant of
on
. By Theorem 6, for each
one can find a solution
to (4) on
with
, where
does not depend on
. For
large enough, this and Theorem 6 allow us to extend the solution
outside of
, contradicting the definition of
. Thus we have
when
is finite, and a similar argument gives
when
is finite.
Remark 9 Theorem 6 gives a more quantitative description of the blowup: ifis finite, then for any
, one must have
where
is the Lipschitz constant of
on
. This can be used to give some explicit lower bound on blowup rates. For instance, if
and
behaves like
for some
in the sense that the Lipschitz constant of
on
is
for any
, then we obtain a lower bound
as
, if
is finite, and similarly when
is finite. This type of blowup rate is sharp. For instance, consider the scalar ODE
where
takes values in
and
is fixed. Then for any
, one has explicit solutions on
of the form
where
is a positive constant depending only on
. The blowup rate at
is consistent with (13) and also with (11).
Exercise 10 (Higher regularity) Let the notation and hypotheses be as in Theorem 8. Suppose thatis
times continuously differentiable for some natural number
. Show that the maximal Cauchy development
is
times continuously differentiable. In particular, if
is smooth, then so is
.
Exercise 11 (Lipschitz continuous dependence on data) Letbe a finite-dimensional normed vector space.
- (a) Let
, let
be a function which has a Lipschitz constant of
on the ball
, and let
be the quantity (11). If
, and
are the solutions to (4) with
given by Theorem 6, show that
- (b) Let
be a function which is Lipschitz on bounded sets, let
, and let
be the maximal Cauchy development of (4) with initial data
given by Theorem 6. Show that for any compact interval
containing
, there exists an open neighbourhood
of
, such that for any
, there exists a solution
of (4) with initial data
. Furthermore, the map from
to
is a Lipschitz continuous map from
to
.
Exercise 12 (Non-autonomous Picard theorem) Letbe a finite-dimensional normed vector space, and let
be a function which is Lipschitz on bounded sets. Let
. Show that there exist
and a continuously differentiable function
solving the non-autonomous ODE
for
with initial data
; furthermore one has
if
is finite, and
if
is finite. Finally, show that
are unique. (Hint: this could be done by repeating all of the previous arguments, but there is also a way to deduce this non-autonomous version of the Picard theorem directly from the Picard theorem by adding one extra dimension to the space
.)
The above theory is symmetric with respect to the time reversal of replacing with
and
with
. However, one can break this symmetry by introducing a dissipative linear term, in which case one only obtains the forward-in-time portion of the Picard existence theorem:
Exercise 13 Letbe a finite dimensional normed vector space, let
, and let
lie in the closed ball
. Let
be a function which has a Lipschitz constant of
on the ball
. Let
be the quantity in (11). Let
be a linear operator obeying the dissipative estimates
for all
and
. Show that there exists a continuously differentiable solution
to the ODE
with initial data
such that
for all
.
Remark 14 With the hypotheses of the above exercise, one can also solve the ODE backwards in time by an amount, where
denotes the operator norm of
. However, in the limit as the operator norm of
goes to infinity, the amount to which one can evolve backwards in time goes to zero, whereas the time in which one can evolve forwards in time remains bounded away from zero, thus breaking the time symmetry.
— 2. Leray systems —
Now we discuss the Leray system of equations
whereProceeding purely formally, we could solve this system by taking the divergence of the first equation to conclude that
We first understand the uniqueness theory for this problem. By linearity, this amounts to solving the homogeneous equation when , thus we wish to classify the smooth fields
and
solving the system
By linearity, this implies that (smooth) solutions to the system (15) are only unique up to the addition of an arbitrary harmonic function to
, and the subtraction of the gradient of that harmonic function from
.
We can largely eliminate this lack of uniqueness by imposing further requirements on . For instance, suppose in addition that we require
to all be
-periodic (or periodic for short), thus
Now suppose instead that we only require that and
be
-periodic, but do not require
to be
-periodic. Then we have the freedom to modify
by a harmonic function
which need not be
-periodic, but whose gradient
is
-periodic. Since the gradient of a harmonic function is also harmonic,
has to be constant, and so
is an affine-linear function. Conversely, all affine-linear functions are harmonic, and their gradients are constant and thus also
-periodic. Thus, one has the freedom in this setting to add an arbitrary affine-linear function to
, and subtract the constant gradient of that function from
.
Instead of periodicity, one can also impose decay conditions on the various functions. Suppose for instance that we require the pressure to lie in an space for some
; roughly speaking, this forces the pressure to decay to zero at infinity “on the average”. Then we only have the freedom to modify
by a harmonic function
that is also in the
class (and modify
by the negative gradient of this harmonic function). However, the mean value property of harmonic functions implies that
Having discussed uniqueness, we now turn to existence. We begin with the periodic setting in which are required to be
-periodic and smooth, so that they can also be viewed (by slight abuse of notation) as functions on the torus
. The system (15) is linear and translation-invariant, which strongly suggests that one solve the system using the Fourier transform (which tends to diagonalise linear translation-invariant equations, because the plane waves
that underlie the Fourier transform are the eigenfunctions of translation.) Indeed, we may expand
as Fourier series
We can write the above general solution in a form similar to (16), (17) as
If we require to be
-periodic, but do not require
to be
-periodic, then by the previous uniqueness discussion, the general solution is now
The above discussion was for smooth periodic functions , but one can make the same construction in other function spaces. For instance, recall that for any
, the Sobolev space
consists of those elements
of
whose Sobolev norm
One can argue similarly in the non-periodic setting, as long as one avoids the one-dimensional case which contains some technical divergences. Recall (see e.g., these previous lecture notes on this blog) that functions
have a Fourier transform
, which for
in the dense subclass
of
is defined by the formula
We then define the Sobolev space for
to be the collection of those functions
for which the norm
As in the periodic case we see that we have the bound
Remark 15 (Remark removed due to inaccuracy.)
Exercise 16 (Hodge decomposition) Define the following three subspaces of the Hilbert space:
is the space of all elements of
of the form
(in the sense of distributions) for some
;
is the space of all elements of
that are weakly harmonic in the sense that
(in the sense of distributions).
is the space of all elements
of
which take the form
(with the usual summation conventions) for some tensor
obeying the antisymmetry property
.
- (a) Show that these three spaces are closed subspaces of
, and one has the orthogonal decomposition
This is a simple case of a more general splitting known as the Hodge decomposition, which is available for more general differential forms on manifolds.
- (b) Show that on
, the Leray projection
is the orthogonal projection to
.
- (c) Show that the Leray projection is a non-expansive map on
for all
(that is to say, its operator norm is at most
).
Exercise 17 (Helmholtz decomposition) Define the following two subspaces of the Hilbert space:
is the space of functions
which are divergence-free, by which we mean that
in the sense of distributions.
is the space of functions
which are curl-free, by which we mean that
in the sense of distributions, where
is the rank two tensor with components
.
- (a) Show that these two spaces are closed subspaces of
, and one has the orthogonal decomposition
This is known as the Helmholtz decomposition (particularly in the three-dimensional case
, in which one can interpret
as the curl of
).
- (b) Show that on
, the Leray projection
is the orthogonal projection to
.
- (c) Show that the Leray projection is a non-expansive map on
for all
.
Exercise 18 (Singular integral form of Leray projection) Let. Then the function
is locally integrable and thus well-defined as a distribution.
- (a) For
, show that the distribution
, defined on test functions
by the formula
can be expressed in principal value form as
where
denotes the surface area of the unit sphere
in
and
is the Kronecker delta.
- (b) Conclude in particular the Newtonian potential identity
where (at the risk of a mild notational clash)
is the Dirac delta distribution at
.
- (c) For a test vector field
, establish the explicit form
- (d) Extend part (c) to the case
. (Hint: Replace the role of
with
, in the spirit of the replica trick from physics.)
Remark 19 One can also solve (15) in-based Sobolev spaces for exponents
other than
by using Calderón-Zygmund theory and the singular integral form of the Leray projection given in Exercise 18. However, we will try to avoid having to rely on this theory in these notes.
— 3. The heat equation —
We now turn to the study of the heat equation
on a spacetime region
Formally, the solution to the initial value problem for (23) should be given by , and (by the Duhamel formula (6)) the solution to (24) should similarly be
The first issue is that even if vanishes and
is required to be smooth without any decay hypothesis at infinity, one can have non-uniqueness. The following counterexample is basically due to Tychonoff:
Exercise 20 (Tychonoff example) Letbe a real number, and let
.
- (a) Show that there exists smooth, compactly supported function
, not identically zero, obeying the derivative bounds
for all
and
. (Hint: one can construct
as the convolution of an infinite number of approximate identities
, where each
is supported on an interval of length
, and use the identity
repeatedly. To justify things rigorously, one may need to first work with finite convolutions and take limits.)
- (b) With
as in part (i) show that the function
is well-defined as a smooth function on
that is compactly supported in time, and obeys the heat equation (23) for
without being identically zero.
- (c) Show that the initial value problem to (23) is not unique (for any dimension
) if
is only required to be smooth, even if
vanishes.
Exercise 21 (Kowalevski example)This classic example, due to Sofia Kowalevski, demonstrates the need for some hypotheses on the PDE in order to invoke the Cauchy-Kowaleski theorem.
- (a) Let
be the function
. Show that there does not exist any solution
to (23) that is jointly real analytic in
at
(that is to say, it can be expressed as an absolutely convergent power series in
in a neighbourhood of
).
- (b) Modify the above example by replacing
by a function that extends to an entire function on
(as opposed to
, which has poles at
).
One can recover uniqueness (forwards in time) by imposing some growth condition at infinity. We give a simple example of this, which illustrates a basic tool in the subject, namely the energy method, which is based on understanding the rate of change of various “energy” integrals of integrands which primarily involve quadratic expressions of the solution or its derivatives. The reason for favouring quadratic expressions is that they are more likely to produce integrals with a definite sign (positive definite or negative definite), such as (squares of) norms or higher Sobolev norms of the solution, particularly after suitable application of integration by parts.
Proposition 22 (Uniqueness with energy bounds) Let, and let
be smooth solutions to (24) with common initial data
and forcing term
such that the norm
of
is finite, and similarly for
. Then
.
Proof: As the heat equation (23) is linear, we may subtract from
and assume without loss of generality that
,
, and
. By working with each component separately we may take
.
Let be a non-negative test function supported on
that equals
on
. Let
be a parameter, and consider the “energy” (or more precisely, “local mass”)
A basic rule of thumb in the energy method is this: whenever one is faced with an integral in which one term in the integrand has much lower regularity (or much less control on regularity) than any other, due to a large number of derivatives placed on that term, one should integrate by parts to move one or more derivatives off of that term to other terms in order to make the distribution of derivatives more balanced (which, as we shall see, tends to make the integrals easier to estimate, or to ascribe a definite sign to). Accordingly, we integrate by parts to write
Now we turn to existence for the heat equation, restricting attention to forward in time solutions. Formally, if one solves the heat equation (23), then on taking spatial Fourier transforms
From (27) and Plancherel’s theorem we see that for
is a non-expansive map in (the Schwartz functions of)
, and more generally in
for any
, thus
There is also a smoothing effect:
Exercise 23 (Smoothing effect) Let. Show that
for all
and
.
Exercise 24 (Fundamental solution for the heat equation) Forand
, establish the identity
for almost every
. (Hint: first work with Schwartz functions. Either compute the Fourier transform explicitly, or verify directly that the heat equation initial value problem is solved by the right-hand side.) Conclude in particular that (after modification on a measure zero set if necessary)
is smooth for any
.
Exercise 25 (Ill-posedness of the backwards heat equation) Show that there exists a Schwartz functionwith the property that there is no solution
to (23) with final data
for any
. (Hint: choose
so that the Fourier transform
decays somewhat, but not extremely rapidly. Then argue by contradiction using (27).
Exercise 26 (Continuity in the strong operator topology) For any, let
denote the Banach space of functions
such that for each
,
lies in
and varies continuously and boundedly in
in the strong topology, with norm
Show that if
and
solves the heat equation on
, then
with
Similar considerations apply to the inhomogeneous heat equation (24). If and
are Schwartz for some
, then the function
defined by the Duhamel formula
Exercise 27 (Energy estimates) Let,
, and
be Schwartz functions for some
, and let
be the solution to the equation
with initial condition
given by the Duhamel formula. For any
, establish the energy estimate
in two different ways:
Here of course we are using the norms
- (i) By using the Fourier representation (27) and Plancherel’s formula;
- (ii) By using energy methods as in the proof of Proposition 22. (Hint: first reduce to the case
. You may find the arithmetic mean-geometric mean inequality
to useful.)
and
The energy estimate contains some smoothing effects similar (though not identical) to those in Exercise 23, since it shows that can in principle be one degree of regularity smoother than
(if one averages in time in an
sense, and the viscosity
is not sent to zero), and two degrees of regularity smoother than the forcing term
(with the same caveats). As we shall shortly see, this smoothing effect will allow us to handle the nonlinear terms in the Navier-Stokes equations for the purposes of setting up a local well-posedness theory.
Exercise 28 (Distributional solution) Let, let
, and let
for some
. Let
be given by the Duhamel formula (28). Show that (24) is true in the spacetime distributional sense, or more precisely that
in the sense of spacetime distributions for any test function
supported in the interior of
.
Pretty much all of the above discussion can be extended to the periodic setting:
Exercise 29 Letand
.
- (a) If
is smooth, define
by the formula
where
are the Fourier coefficients of
. Show that
extends continuously to a non-expansive map on
for every
, and that if
then the function
lies in
.
- (b) For
and
, establish the formula
for almost every
, where (by abuse of notation) we identify functions
with
-periodic functions
in the usual fashion.
- (c) If
, and
and
are smooth, show that the function
defined by (28) is smooth and solves the inhomogeneous equation (24) with initial data
, and that this is the unique smooth solution to that initial value problem.
- (d) If
,
, and
and
,
are smooth, and
is the unique smooth solution to the heat equation
with
, establish the energy estimate
- (e) If
,
and
, show that the function
given by (28) is in
and obeys (24) in the sense of spacetime distributions (30).
Remark 30 The heat equation for negative viscositiescan be transformed into a positive viscosity heat equation by time reversal: if
solves the equation
, then
solves the equation
. Thus one can solve negative viscosity heat equations (also known as backwards heat equations) backwards in time, but one tends not to have well-posedness forwards in time. In a similar spirit, if
is positive, one can normalise it to (say)
by an appropriate rescaling of the time variable,
. However, we will generally keep the parameter
non-normalised in preparation for understanding the limit as
.
— 4. Local well-posedness for Navier-Stokes —
We now have all the ingredients necessary to create a local well-posedness theory for the Navier-Stokes equations (1).
We first dispose of the one-dimensional case , which is rather degenerate as incompressible one-dimensional fluids are somewhat boring. Namely, suppose that one had a smooth solution to the one-dimensional Navier-Stokes equations
Now we work in two or higher dimensions , and consider solutions to (1) on the spacetime region
. To begin with, we assume that
is smooth and periodic in space:
for
; we assume
is smooth but do not place any periodicity hypotheses on it. Then, by (1),
is periodic. In particular, for any
and
, the function
has vanishing gradient and is thus constant in
, so that
Note that one can simply omit the constant term from the pressure without affecting the system (1). One can also eliminate the linear term
by the following “generalised Galilean transformation“. If
are as above, and one lets
Once the pressure is normalised, it turns out that one can recover uniqueness (much as was the case with the Leray system):
Theorem 31 (Uniqueness with normalised pressure) Letbe two smooth periodic solutions to (1) on
with normalised pressure such that
. Then
.
Proof: We use the energy method. Write , then subtracting (1) for
from
we see that
is smooth with
For , we observe the total derivative
and integrate by parts to conclude that
Now we turn to existence in the periodic setting, assuming normalised pressure. For various technical reasons, it is convenient to reduce to the case when the velocity field has zero mean. Observe that the right-hand sides
,
of (1) have zero mean on
, thanks to integration by parts. A further integration by parts, using the divergence-free condition
, reveals that the transport term
also has zero mean:
A general rule of thumb is that whenever an integral of a solution to a PDE can be proven to vanish (or be equal to boundary terms) by integration by parts, it is because the integrand can be rewritten in “divergence form” – as the divergence of a tensor of one higher rank. (This is because the integration by parts identity arises from the divergence form
of the expression
.) Thus we expect the transport term
to be in divergence form. Indeed, in components we have
Next, we observe that we can use the Leray projection operator to eliminate the role of the (normalised) pressure. Namely, if
are a smooth periodic solution to (1) with normalised pressure, then on applying
(which preserves divergence-free vector fields such as
and
, but annihilates gradients such as
) we conclude an equation that does not involve the pressure at all:
By Duhamel’s formula (Exercise 29(c)), any smooth solution to the initial value problem (33) with
obeys the Duhamel formula
To obtain existence of smooth periodic solutions (with normalised pressure) to the Navier-Stokes equations with given smooth divergence-free periodic initial data , it thus suffices to find a smooth periodic solution to the integral equation (34). We will achieve this by a two-step procedure:
- (i) (Existence at finite regularity) Construct a solution
to (34) in a certain function space with a finite amount of regularity (assuming that the initial data
has a similarly finite amount of regularity); and then
- (ii) (Propagation of regularity) show that if
is in fact smooth, then the solution constructed in (i) is also smooth.
The reason for this two step procedure is that one wishes to solve (34) using iteration-type methods (which for instance power the contraction mapping theorem that was used to prove the Picard existence theorem); however the function space that one ultimately wishes the solution to lie in is not well adapted for such iteration (for instance, it is not a Banach space, instead being merely a Fréchet space). Instead, we iterate in an auxiliary lower regularity space first, and then “bootstrap” the lower regularity to the desired higher regularity. Observe that the same situation occured with the Picard existence theorem, where one performed the iteration in the low regularity space
, even though ultimately one desired the solution to be continuously differentiable or even smooth.
Of course, to run this procedure, one actually has to write down an explicit function space in which one will perform the iteration argument. Selection of this space is actually a non-trivial matter and often requires a substantial amount of trial and error, as well as experience with similar iteration arguments for other PDE. Often one is guided by the function space theory for the linearised counterpart of the PDE, which in this case is the heat equation (23). As such, the following definition can be at least partially motivated by the energy estimates in Exercise 29(d).
Definition 32 (Mild solution) Let,
, and let
be divergence-free, where
denotes the subspace of
consisting of mean zero functions. An
-mild solution (or Fujita-Kato mild solution to the Navier-Stokes equations with initial data
is a function
in the function space
that obeys the integral equation (34) (in the sense of distributions) for all
. We say that
is a mild solution on
if it is a mild solution on
for every
.
Remark 33 The definition of a mild solution could be extended to those choices of initial datathat are not divergence-free, but then this solution concept no longer has any direct connection with the Navier-Stokes equations, so we will not consider such “solutions” here. Similarly, one could also consider mild solutions without the mean zero hypothesis, but the function space estimates are slightly less favourable in this setting and so we shall restrict attention to mean zero solutions only.
Note that the regularity on places
in
(with plenty of room to spare), which is more than enough regularity to make sense of the right-hand side of (34) in a (spacetime) distributional sense at least. One can also define mild solutions for other function spaces than the one provided here, but we focus on this notion for now, which was introduced in the work of Fujita and Kato. We record a simple compatibility property of mild solutions:
Exercise 34 (Splitting) Let,
, let
be divergence-free, and let
Let
. Show that the following are equivalent:
- (i)
is an
mild solution to the Navier-Stokes equations on
with initial data
.
- (ii)
is an
mild solution to the Navier-Stokes equations on
with initial data
, and the translated function
defined by
is an
mild solution to the Navier-Stokes equations with initial condition
.
To use this notion of a mild solution, we will need the following harmonic analysis estimate:
Proposition 35 (Product estimate) Let, and let
. Then one has
, with the estimate
When this claim follows immediately from Hölder’s inequality. For
the claim is similarly immediate from the Leibniz rule
and the triangle and Hölder inequalities (noting that
is comparable to
. For more general
the claim is not quite so immediate (for instance, when
one runs into difficulties controlling the intermediate term
arising in the Leibniz expansion of
). Nevertheless the bound is still true. However, to prove it we will need to introduce a tool from harmonic analysis, namely Littlewood-Paley theory, and we defer the proof to the appendix.
We also need a simple case of Sobolev embedding:
Exercise 36 (Sobolev embedding)
- (a) If
, show that for any
, one has
with
- (b) Show that the inequality fails at
.
- (c) Establish the same statements with
replaced by
throughout.
In particular, combining this exercise with Proposition 35 we see that for ,
is a Banach algebra:
Now we can construct mild solutions at high regularities .
Theorem 37 (Local well-posedness of mild solutions at high regularity) Let, and let
be divergence-free. Then there exists a time
and an
mild solution
to (34). Furthermore, this mild solution is unique.
The hypothesis is not optimal; we return to this point later in these notes.
Proof: We begin with existence. We can write (34) in the fixed point form
Note that if , then
by (35), which by Exercise 29(d) (and the fact that
commutes with
and is a non-expansive map on
) implies that
. Thus
is a map from
to
. In fact we can obtain more quantitative control on this map. By using Exercise 29(d), (35), and the Hölder bound
Now we show that it is the only mild solution. Suppose for contradiction that there is another mild solution
with the same initial data
. This solution
might not lie in
, but it will lie in
for some
. By the same arguments as above, if
is sufficiently small depending on
then
will be a contraction on
, which implies that
and
agree on
. Now we apply Exercise 34 to advance in time by
and iterate this process (noting that
depends on
but does not otherwise depend on
or
) until one concludes that
on all of
.
Iterating this as in the proof of Theorem 8, we have
Theorem 38 (Maximal Cauchy development) Let, and let
be divergence-free. Then there exists a time
and an
mild solution
to (34), such that if
then
as
. Furthermore,
and
are unique.
In principle, if the initial data belongs to multiple Sobolev spaces
the maximal time of existence
could depend on
(so that the solution exits different regularity classes
at different times). However, this is not the case, because there is an
-independent blowup criterion:
Proposition 39 (Blowup criterion) Letbe as in Theorem 38. If
, then
.
Note from Exercise 36 that is finite for any
. This shows that
is the unique time at which the
norm “blows up” (becomes infinite) and thus
is independent of
.
Proof: Suppose for contradiction that but that the quantity
was finite. Let
be parameters to be optimised in later. We define the norm
We adapt the proof of Theorem 37. Using Exercise 29(d) (and Exercise 34) we have
Corollary 40 (Existence of smooth solutions) Ifis smooth and divergence free then there is a
and a smooth periodic solution
to the Navier-Stokes equations on
with normalised pressure such that if
, then
. Furthermore,
and
are unique.
Proof: As discussed previously, we may assume without loss of generality that has mean zero. As
is periodic and smooth, it lies in
for every
. From the preceding discussion we already have
and a function
that is an
mild solution for every
, and with
if
is finite. It will suffice to show that
is smooth, since we know from preceding discussion that a smooth solution to (33) can be converted to a smooth solution to (1).
By Exercise 29, one has
Remark 41 When, it is a notorious open problem whether the maximal lifespan
given by the above corollary is always infinite.
Exercise 42 (Instantaneous smoothing) Let, let
be divergence-free, and let
be the maximal Cauchy development provided by Theorem 38. Show that
is smooth on
(note the omission of the initial time
). (Hint: first show that
is a
mild solution for arbitrarily small
.)
Exercise 43 (Lipschitz continuous dependence on initial data) Let, let
, and let
be divergence-free. Suppose one has an
mild solution
to the Navier-Stokes equations with initial data
. Show that there in a neighbourhood
of
in (the divergence-free elements of) in
, such that for every
, there exists an
mild solution
to the Navier-Stokes equations with initial data
with the map from
to
Lipschitz continuous (using the
metric for the initial data
and the
metric for the solution
).
Now we discuss the issue of relaxing the regularity condition in the above theory. The main inefficiency in the above arguments is the use of the crude estimate (37), which sacrifices some of the
exponent in time in exchange for extracting a positive power of the lifespan
that can be used to create a contraction mapping, as long as
is small enough. It turns out that by using a different energy estimate than Exercise 29(d), one can avoid such an exchange, allowing one to construct solutions at lower regularity, and in particular at the “critical” regularity of
. Furthermore, in the category of smooth solutions, one can even achieve the desirable goal of ensuring that the time of existence
is infinite – but only provided that the initial data is small. More precisely,
Proposition 44 Letand let
. Then the function
defined by the Duhamel formula
also has mean zero for all
, and obeys the estimates
Proof: By Minkowski’s integral inequality, it will suffice to establish the bounds in the case . The first two norms of the left-hand side are already established by Exercise 29(d), so it remains to establish the estimate
This gives the following small data global existence result, also due to Fujita and Kato:
Theorem 45 (Small data global existence) Suppose thatis divergence-free with norm at most
, where
is a sufficiently small constant depending only on
. Then there exists a
mild solution to the Navier-Stokes equations on
. Furthermore, if
is smooth, then this mild solution is also smooth.
Proof: By working with the rescaled function , we may normalise
. Let
denote the Banach space of functions
Now suppose that is smooth. Let
, and let
be the maximal Cauchy development provided by Theorem 38. For any
, if one defines
Remark 46 Modifications of this argument also allow one to establish local existence ofmild solutions when the initial data
lies in
, but has large norm rather than norm less than
; see Exercise 47 below. However, in this case one does not have a lower bound on the time of existence that depends only on the norm of the data, as was the case with Theorem 37. Further modification of the argument also allows one to extend Theorem 38 to the entire “subcritical” range of regularities
. See the paper of Fujita and Kato for details.
Exercise 47 (Large data critical local existence) Suppose thatis divergence-free. Show that there exists
and a
mild solution to the Navier-Stokes equations on
. Furthermore, if
is smooth, then this mild solution is also smooth. (Hint: By choosing
small enough, one can ensure that the linear evolution
is small in
and
norms. Now run a contraction mapping argument in a space of functions
that are small in
and
norm and bounded in
norm. One will have to carefully choose all the relevant parameters in the right order, and to choose an appropriate weighted metric on this space of functions, in order to actually obtain a contraction.
We now turn attention to the non-periodic case in two and higher dimensions . The theory is largely identical, though with some minor technical differences. Unlike the periodic case, we will not attempt to reduce to the case of
having mean zero (indeed, we will not even assume that
is absolutely integrable, so that the mean might not even be well defined).
In the periodic case, we focused initially on smooth solutions. Smoothness is not sufficient by itself in the non-periodic setting to provide a good well-posedness theory, as we already saw in Section 3 when discussing the linear heat equation; some additional decay at spatial infinity is needed. There is some flexibility as to how much smoothness to prescribe. Let us say that a solution to Navier-Stokes is classical if
and
are smooth, and furthermore
lies in
for every
.
Now we work on normalising the pressure. Suppose is a classical solution. As before we may write the Navier-Stokes equation in divergence form as (32). Taking a further divergence we obtain the equation
Exercise 48 (Uniqueness with normalised pressure) Letbe two smooth classical solutions to (1) on
with normalised pressure such that
. Then
.
We can now define the notion of a Fujita-Kato mild solution as before, except that we replace all mention of the torus
with the Euclidean space
, and omit all requirements for the solution to be of mean zero. As stated in the appendix, the product estimate in Proposition 35 continues to hold in
, so one can obtain the analogue of Theorem 37, Theorem 38, Proposition 39, and Corollary 40 on
by repeating the proofs with the obvious changes; we leave the details as an exercise for the interested reader.
Exercise 49 Establish an analogue of Proposition 44 on, using the homogeneous Sobolev space
defined to be the closure of the Schwartz functions
with respect to the norm
and use this to state and prove an analogue of Theorem 45.
— 5. Heuristics —
There are several further extensions of these types of local and global existence results for smooth solutions, in which the role of the Sobolev spaces here are replaced by other function spaces. For instance, in three dimensions in the non-periodic setting, the role of the critical space
was replaced by the larger critical space
by Kato, and to the even larger space
by Koch and Tataru, who also gave evidence that the latter space essentially the limit of the method; in even larger spaces such as the Besov space
, there are constructions of Bourgain and Pavlovic that demonstrate ill-posedness in the sense of “norm inflation” – solutions that start from arbitrarily small norm data but end up being arbitrarily large in arbitrarily small amounts of time. (This grossly abbreviated history skips over dozens of other results, both positive and negative, in yet further function spaces, such as Morrey spaces or Besov spaces. See for instance the recent text of Lemarie-Rieusset for a survey.)
Rather tham detail these other results, let us present instead a scaling heuristic which can be used to interpret these results (and can clarify why all the positive well-posedness results discussed here involve either “subcritical” or “critical” function spaces, rather than “supercritical” ones). For simplicity we restrict our discussion to the non-periodic setting , although the discussion here could also be adapted without much difficulty to the periodic setting (which effectively just imposes an additional constraint
on the frequency parameter
to be introduced below).
In this heuristic discussion, we assume that any given time , the velocity field
is primarily located at a certain frequency
(or equivalently, at a certain wavelength
) in the sense that the spatial Fourier transform
is largely concentrated in the region
. We also assume that at this time, the solution has an amplitude
, in the sense that
tends to be of order
in magnitude in the region where it is concentrated. (We are deliberately leaving terms such as “concentrated” vague for the purposes of this discussion.) Using this ansatz, one can then heuristically compute the magnitude of various terms in the Navier-Stokes equations (1) or the projected version (33). For instance, if
has amplitude
and frequency
, then
should have amplitude
(and frequency
), since the Laplacian operator
multiplies the Fourier transform
by
; one can also take a more “physical space” viewpoint and view the second derivatives in
as being roughly like dividing out by the wavelength
twice. Thus we see that the viscosity term
in (1) or (33) should have size about
. Similarly, the expression
in (33) should have magnitude
and frequency
(or maybe slightly less due to cancellation), so
and hence
should have magnitude
. The terms
and
in (1) can similarly be computed to have magnitude
. Finally, if the solution oscillates (or blows up) in time in intervals of length
(which one can think of as the natural time scale for the solution), then the term
should have magnitude
.
This leads to the following heuristics:
- If
(or equivalently if
), then the viscosity term
dominates the nonlinear terms in (1) or (33), and one should expect the Navier-Stokes equations to behave like the heat equation (23) in this regime. In particular solutions should exist and maintain (or even improve) their regularity as long as this regime persists. To balance the equation (1) or (33), one expects
, so the natural time scale here is
.
- If
(or equivalently if
), then nonlinear effects dominate, and the behaviour is likely to be quite different to that of the heat equation. One now expects
, so the natural time scale here is
. In particular, one could theoretically have blowup or other bad behaviour after this time scale.
As a general rule of thumb, the known well-posedness theory for the Navier-Stokes equation is only applicable when the hypotheses on the initial data (and on the timescale being considered) is compatible either with the viscosity-dominated regime , or the time-limited regime
. Outside of these regimes, we expect the evolution to be highly nonlinear in nature, and techniques such as the ones in this set of notes, which are primarily based on approximating the evolution by the linear heat flow, are not expected to apply.
Let’s discuss some of the results in this set of notes using these heuristics. Suppose we are given that the initial data is bounded in
norm by some bound
:
Exercise 50 If, make a heuristic argument as to why the optimal lower bound for the time of existence
for the Navier-Stokes equation in terms of the
norm of the initial data
should take the form
In a similar spirit, suppose we have the smallness hypothesis
Finally, if one only controls a supercritical norm such as for some
, this gives a bound on a quantity of the form
, which allows one to leave the viscosity dominated regime
(with plenty of room to spare) when
is large, creating examples of initial data for which the natural time scale can be made arbitrarily small. As
increases (restricting to, say, powers of two), the supercritical norm of these examples decays geometrically, so one can superimpose an infinite number of these examples together, leading to a choice of initial data with arbitrarily small supercritical norm for which the natural time scale is in fact zero. This strongly suggests that there is no good local well-posedness theory at such regularities.
Exercise 51 Discuss the product estimate in Proposition 35, the Sobolev estimate in Exercise 36, and the energy estimates in Exercise 29(d) and Proposition 44 using the above heuristics.
Remark 52 These heuristics can also be used to locate errors in many purported solutions to the Navier-Stokes global regularity problem that proceed through a sequence of estimates on a Navier-Stokes solution. At some point, the estimates have to rule out the scenario that the solutionleaves the viscosity-dominated regime
at larger and larger frequencies
(and at smaller and smaller time scales
), with the time scales converging to zero to achieve a finite time blowup. If the estimates in the proposed solution are strong enough to heuristically rule out this scenario by the end of the argument, but not at the beginning of the argument, then there must be some step inside the argument where one moves from “supercritical” estimates that are too weak to rule out this scenario, to “critical” or “subcritical” estimates which are capable of doing so. This step is often where the error in the argument may be found.
The above heuristics are closely tied to the classification of various function space norms as being “subcritical”, “supercritical”, or “critical”. Roughly speaking, a norm is subcritical if bounding that norm heuristically places one in the linear-dominated regime (which, for Navier-Stokes, is the viscosity-dominated regime) at high frequencies; critical if control of the norm very nearly places one in the linear-dominated regime at high frequencies; and supercritical if control of the norm completely fails to place one in the linear-dominated regime at high frequencies. When the equation in question enjoys a scaling symmetry, the distinction between subcritical, supercritical, and critical norms can be made by seeing how the the top-order component of these norms vary with respect to scaling a function to be high frequency. In the case of the Navier-Stokes equations (1), the scaling is given by the formulae
Typically, if one considers a function space norm of (or of
or
) in the limit
, the top order behaviour will be given by some power
of
. A norm is called subcritical if the exponent
is positive, supercritical if the exponent is negative, and critical if the exponent is zero. For instance, one can calculate the Fourier transform
Another way to phrase this classification is to use dimensional analysis. If we use to denote the unit of length, and
the unit of time, then the velocity field
should have units
, and the terms
and
in (1) then have units
. To be dimensionally consistent, the kinematic viscosity
must then have the units
, and the pressure
should have units
. (This differs from the usual units given in physics to the pressure, which is
where
is the unit of mass; the discrepancy comes from the choice to normalise the density, which usually has units
, to equal
.) If we fix
to be a dimensionless constant such as
, this forces a relation
between the time and length units, so now
and
have the units
and
respectively (compare with (40) and (41)). Of course
will then also have units
. One can then declare a function space norm of
,
, or
to be subcritical if its top order term has units of a negative power of
, supercritical if this is a positive power of
, and critical if it is dimensionless. For instance, the top order term in
is the
norm of
; as
has the units of
, and Lebesgue measure
has the units of
, we see that
has the units of
, giving the same division into subcritical, supercritical, and critical spaces as before.
— 6. Appendix: some Littlewood-Paley theory —
We now prove Proposition 35. By a limiting argument it suffices to establish the claim for smooth . The claim is immediate from Hölder’s inequality when
, so we will assume
. For brevity we shall abbreviate
as
, and similarly for
, etc..
We use the technique of Littlewood-Paley projections. Let be an even bump function (depending only on
) that equals
on
and is supported on
; for the purposes of asymptotic notation, any bound that depends on
can thus be thought of as depending on
instead. For any dyadic integer
(by which we mean an integer that is a power of
), define the Littlewood-Paley projections
on periodic smooth functions
by the formulae
The key point of this decomposition is that the and Sobolev norms of the individual components of this decomposition are easier to estimate than the original function
. The following estimates in particular will suffice for our applications:
Exercise 53 (Basic Littlewood-Paley estimates)
- (a) For any dyadic integer
, show that
where
is the inverse Fourier transform of
on
, and the difference
between the coset
and the shift
is defined in the obvious fashion. In particular if
is real-valued then so is
and
. Conclude the Bernstein inequality
for all smooth functions
, all
and
; in particular
(Recall our convention that constants that depend on
can also be thought of as depending just on
.) By the triangle inequality, the same estimates also hold for
,
.
- (b) For any
, show that
Remark 54 The more advanced Littlewood-Paley inequality, which is usually proven using the Calderón-Zygmund theory of singular integrals, asserts thatfor any
. However, we will not use this estimate here.
We return now to the proof of Proposition 35. Let be as above. By Exercise 53, it suffices to establish the bounds
The estimate (42) follows by dropping (using Exercise 53) and applying Hölder’s inequality, so we turn to (43). We may restrict attention to those terms where
(say) since the other terms can be treated by the same argument used to prove (42).
The basic strategy here is to split the product (or the component
of this product) into paraproducts in which some constraint is imposed between the frequencies of the
and
terms. There are many ways to achieve this splitting; we will use
We begin with (44). We can expand further
There is an essentially identical theory in the non-periodic setting, in which the role of smooth periodic functions are now replaced by Schwartz functions, the Littlewood-Paley projections are now defined as
Exercise 55 (Non-periodic Littlewood-Paley theory) Withnow denoting
instead of
, and similarly for other function spaces, establish the non-periodic analogue of Exercise 53 for Schwartz functions
.
In particular, one obtains the non-periodic analogue of Proposition 35 by repeating the proof verbatim.

92 comments
Comments feed for this article
18 April, 2021 at 1:44 am
Anonymous
I think it seems that Lemma 1 does not need to assume u_0 and u is positive?
[Fair enough; I’ve adjusted the statement appropriately. -T]
23 April, 2021 at 10:15 pm
Ning
Dear Prof. Tao,
In the Part 2 – Leray system of your notes, you said that Fourier transform tends to diagonalize linear translation-invariant equations, because the plane waves $x \mapsto e^{2\pi i k \cdot x}$ that underlie the Fourier transform are the eigenfunctions of translation.
I understood the rigorous proof below, but I did not understand this intuitive insights you presented here. I believe I have seen analogous idea in Sturm-Liouville problem. But I’m wondering what you mean by saying that ‘diagonalize linear translation-invariant equation’? I thought you used the fact that since $e^{2\pi i k \cdot x}$ are the complete eigenbasis of translation in L^2, so they are also eigenbasis for linear translation-invariant operators?
But I’m still confused about this. Could you further explain this? Thanks!
26 April, 2021 at 8:54 am
Terence Tao
Heuristically speaking, a linear operator should be diagonalised by its eigenvectors (there are subtleties if the operator is not normal, but let us ignore this issue for now). Also heuristically speaking, commuting linear operators should have the same bases of eigenvectors (again, there are subtleties when the eigenvalues have multiplicity, but we will ignore this). Since translation has the plane waves as an eigenbasis, these two heuristics predict that any other translation-invariant operator is diagonalised by the plane wave basis. And indeed on taking Fourier transforms, any (reasonable) translation-invariant operator becomes a multiplier operator, which is the continuous version of the operation of multiplying by a diagonal matrix.
28 April, 2021 at 5:37 am
Ning
Thanks for your reply! It makes sense to me now.
24 April, 2021 at 10:07 pm
Ning
Between equation (22) and Remark 15, there is a typo in ‘hence also in the classical sense since {p,F} have rapidly decreasing Fourier transforms and are thus smooth.’
I think it may be instead, and the reason for smoothness may be easier to understand in my view as following:
instead, and the reason for smoothness may be easier to understand in my view as following:
 is in
is in  for any multi-index
for any multi-index  in the setting
in the setting 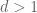 , instead of ‘rapidly decreasing’ since I think
, instead of ‘rapidly decreasing’ since I think  is not in
is not in 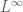 , i.e.
, i.e.  case for rapid decreasing. And actually I’m confused about what does it mean by ‘rapid decreasing of a tempered distribution’.
case for rapid decreasing. And actually I’m confused about what does it mean by ‘rapid decreasing of a tempered distribution’.
Maybe my idea is stupid, but I think it is indeed another way to think about this?
[Text clarified – T.]
25 May, 2021 at 7:50 am
Ning
The paragraph between Remark 33 and Exercise 34 says that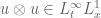 is more than enough regularity to make sense of the right-hand side of (34) in a distributional sense at least.
is more than enough regularity to make sense of the right-hand side of (34) in a distributional sense at least.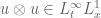 , but how could I verify that RHS of (34) is indeed a well-defined distribution?
, but how could I verify that RHS of (34) is indeed a well-defined distribution?
I got stuck here, there are too many operators here. I knew how
Thanks!
[Verify that the adjoint of the operator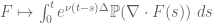 maps test functions to bounded functions. -T]
maps test functions to bounded functions. -T]
27 May, 2021 at 8:54 am
Ning
Thanks for your reply. I think I have know what is the right way to prove this but I want to make sure this is correct. with a test function
with a test function  , then use the form of heat propagator on torus which analogous to that in exercise 24, which allows us to estimate
, then use the form of heat propagator on torus which analogous to that in exercise 24, which allows us to estimate 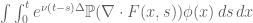 by Young’s inequality for convolution, and then use the symmetry and non-expansive property of
by Young’s inequality for convolution, and then use the symmetry and non-expansive property of  to conclude that it is bounded by
to conclude that it is bounded by 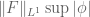 , which verifies that it is a distribution.
, which verifies that it is a distribution.
So actually I think we do not need to calculate an explicit formula for the adjoint, but we use the adjoint to define the distribution in the way similar to the definition of the distributional derivative. We pair
28 May, 2021 at 3:20 am
Ning
In exercise 29(d), I think the assumption should be G:[0,T] \times {\mathbb R}^d/{\mathbb Z}^d \rightarrow {\mathbb R}^{m^2}, and \nabla G should be changed to \nabla\cdot G. Otherwise, the dimension is not consistent.
[Corrected, thanks – T.]
6 June, 2021 at 3:15 am
Ning
Some typos and some points that confused me.
1.In the second line of the proof of Proposition 44, RHS should be LHS.
2.In the proof of Theorem 45, in first the formula to established the bound for \Phi u, \cdot should be \otimes
3.In the third line of the proof of the smooth case in Theorem 45,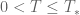 should be
should be 
4.Also in the proof of this smooth case, you missed the subsript 0 of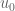 in the norm below
in the norm below
` depends continuously on
depends continuously on  and converges to
and converges to 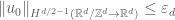 as
as  .'
.'
5.And I think the order in this proof for the smooth case should be reversed somehow.
You may first argue , then conclude that
, then conclude that 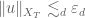 for all
for all  , then
, then  .
.
Instead of putting the argument of to the last.
to the last.
6.In this proof, you use many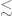 symbols. I think maybe writing these constants explicitly will be more safe for me.You said
symbols. I think maybe writing these constants explicitly will be more safe for me.You said
In particular, {u} lies in {X} with norm {O(C_d \varepsilon_d)}, and so agrees with the fixed point of {\Phi} located previously.
I am confused about why only the big O notation could tells us one agrees with another. Instead, I think we should calculate the constants carefully and find that there is a smaller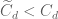 such that
such that  .(After writing out the constants carefully, I found this is the case, but I want to know how could you know only from the big O notation here?)
.(After writing out the constants carefully, I found this is the case, but I want to know how could you know only from the big O notation here?)
7.I'm curious what is it mean by having a dot on in the formulas just below the Exercise 50?
in the formulas just below the Exercise 50?
8.In the last three line of Part 5, the heuristics part, the unit of of
of  , not
, not 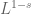
If you could reply when you are free, I will be very happy!
7 June, 2021 at 3:10 pm
Terence Tao
Thanks for the corrections. was a typo, it should have been “at most
was a typo, it should have been “at most  .
.
The dot notation was defined in Exercise 49.
I do not think there is an easy way to jump straight to establishing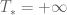 in the small data theory without first obtaining estimates on
in the small data theory without first obtaining estimates on  and
and  norms for various
norms for various  . In particular one does not know a priori that the
. In particular one does not know a priori that the 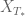 or
or  norms are finite.
norms are finite.
8 June, 2021 at 8:33 am
Ning
Thanks for your reply!
For your last comment, I think after you showed that
For {\varepsilon_d} small enough, this implies that {\|u\|_{X_T} \lesssim_d \varepsilon_d} for all {T} (this is an example of a “continuity argument”).
This did not sufficiently show that $u\in X$ since `all $T$’ here means that all $T<T_*$. Maybe after this, we first show that $T_*=\infty$ would be a fair way for us to conclude $u\in X$.
[Fair enough, I’ve rearranged the order of these sentences. -T]
8 June, 2021 at 8:47 am
Ning
Before Exercise 34, you said $u \otimes u$ is a distribution. Here you mean that it is a space-time distribution or a spatial distribution (when $t$ fixed)?
I think I have verified both by definition, but you did not use the terminology `space-time distribution’ like elsewhere, so I’m wondering what you mean in this context.
[Added a clarification that spacetime distributions are intended here. -T]
15 June, 2021 at 7:51 am
Ning
In the last two equations of Note 1,
You bound
but I think the last inequality is not correct. Maybe we could just using
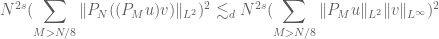
and then summing in N and interchanging summations by the Minkowski’s inequality to get your result.
[Seems fine to me (note that ). -T]
). -T]
3 May, 2022 at 4:33 am
J
Can one use the continuity method to prove Lemma 1?
If one begins with
then one has, by the assumption,
which seems not very helpful.
19 November, 2023 at 9:51 am
Anonymous
Hello. I posted my question on MO https://mathoverflow.net/questions/458716/hs-mild-solution-for-navier-stokes-why-do-we-restrict-attention-to-the-func?noredirect=1#comment1188330_458716
But I guess it is more direct to ask here. In your Remarks 33, what do you mean by estimates being “less favorable” for function spaces with the Fourier zeroth mode included?
I believe that all results and proofs below Definition 32 + Remark 33 (especially local Lipschitz continuity on the initial data) hold “equally valid” even if we do not exclude the Fourier zeroth mode.
Could you please confirm for me?
19 November, 2023 at 11:39 am
Terence Tao
Proposition 44 breaks down if the mode is included (note for instance the negative power of
mode is included (note for instance the negative power of  at the end of the proof).
at the end of the proof).
As a general rule of thumb, for local-in-time theory the zero mode is harmless, but for global-in-time theory the zero mode can cause some minor technical difficulties, due to the heat flow not causing that mode to decay exponentially in time (in contrast to all the other modes).
19 November, 2023 at 12:02 pm
Anonymous
The seroth Fourier mode in the NS problem can be harmlessly set to zero because of the Gallien invariance property. Cheers, Dr Hayes