Rachel Greenfeld and I have just uploaded to the arXiv our announcement “A counterexample to the periodic tiling conjecture“. This is an announcement of a longer paper that we are currently in the process of writing up (and hope to release in a few weeks), in which we disprove the periodic tiling conjecture of Grünbaum-Shephard and Lagarias-Wang. This conjecture can be formulated in both discrete and continuous settings:
Conjecture 1 (Discrete periodic tiling conjecture) Suppose thatis a finite set that tiles
by translations (i.e.,
can be partitioned into translates of
). Then
also tiles
by translations periodically (i.e., the set of translations can be taken to be a periodic subset of
).
Conjecture 2 (Continuous periodic tiling conjecture) Suppose thatis a bounded measurable set of positive measure that tiles
by translations up to null sets. Then
also tiles
by translations periodically up to null sets.
The discrete periodic tiling conjecture can be easily established for by the pigeonhole principle (as first observed by Newman), and was proven for
by Bhattacharya (with a new proof given by Greenfeld and myself). The continuous periodic tiling conjecture was established for
by Lagarias and Wang. By an old observation of Hao Wang, one of the consequences of the (discrete) periodic tiling conjecture is that the problem of determining whether a given finite set
tiles by translations is (algorithmically and logically) decidable.
On the other hand, once one allows tilings by more than one tile, it is well known that aperiodic tile sets exist, even in dimension two – finite collections of discrete or continuous tiles that can tile the given domain by translations, but not periodically. Perhaps the most famous examples of such aperiodic tilings are the Penrose tilings, but there are many other constructions; for instance, there is a construction of Ammann, Grümbaum, and Shephard of eight tiles in which tile aperiodically. Recently, Rachel and I constructed a pair of tiles in
that tiled a periodic subset of
aperiodically (in fact we could even make the tiling question logically undecidable in ZFC).
Our main result is then
Theorem 3 Both the discrete and continuous periodic tiling conjectures fail for sufficiently large. Also, there is a finite abelian group
such that the analogue of the discrete periodic tiling conjecture for
is false.
This suggests that the techniques used to prove the discrete periodic conjecture in are already close to the limit of their applicability, as they cannot handle even virtually two-dimensional discrete abelian groups such as
. The main difficulty is in constructing the counterexample in the
setting.
The approach starts by adapting some of the methods of a previous paper of Rachel and myself. The first step is make the problem easier to solve by disproving a “multiple periodic tiling conjecture” instead of the traditional periodic tiling conjecture. At present, Theorem 3 asserts the existence of a “tiling equation” (where one should think of
and
as given, and the tiling set
is known), which admits solutions, all of which are non-periodic. It turns out that it is enough to instead assert the existence of a system
It is convenient to replace sets by functions, so that this tiling language can be translated to a more familiar language, namely the language of (certain types of) functional equations. The key point here is that the tiling equation
The non-periodic behaviour that we ended up trying to capture was that of a certain “-adically structured function”
associated to some fixed and sufficiently large prime
(in fact for our arguments any prime larger than
, e.g.,
, would suffice), defined by the formula

It turns out that we cannot describe this one-dimensional non-periodic function directly via tiling equations. However, we can describe two-dimensional non-periodic functions such as for some coefficients
via a suitable system of tiling equations. A typical such function looks like this:

A feature of this function is that when one restricts to a row or diagonal of such a function, the resulting one-dimensional function exhibits “-adic structure” in the sense that it behaves like a rescaled version of
; see the announcement for a precise version of this statement. It turns out that the converse is essentially true: after excluding some degenerate solutions in which the function is constant along one or more of the columns, all two-dimensional functions which exhibit
-adic structure along (non-vertical) lines must behave like one of the functions
mentioned earlier, and in particular is non-periodic. The proof of this result is strongly reminiscent of the type of reasoning needed to solve a Sudoku puzzle, and so we have adopted some Sudoku-like terminology in our arguments to provide intuition and visuals. One key step is to perform a shear transformation to the puzzle so that many of the rows become constant, as displayed in this example,

and then perform a “Tetris” move of eliminating the constant rows to arrive at a secondary Sudoku puzzle which one then analyzes in turn:

It is the iteration of this procedure that ultimately generates the non-periodic -adic structure.

32 comments
Comments feed for this article
19 September, 2022 at 11:35 pm
Emmanuel Amiot
Congrats, this is huge. Very nice original ideas.
20 September, 2022 at 2:53 am
Announcing a result on the arXiv – SPP 2026
[…] Today Rachel Greenfeld and Terence Tao announced via the arXiv that they can disprove the periodic tiling conjecture (arXiv:2209.08451). I do not want to discuss here in detail the contents of the conjecture or their approach to disprove it (if you are interested in this, you can read about it on Tao’s blog). […]
20 September, 2022 at 4:26 am
Sébastien Labbé
Sounds very interesting. I also needed to use a similar sheer transformation when studying the structure of Jeandel-Rao aperiodic tilings (doi:10.1007/s00454-019-00153-3). Also, the ““Tetris” move of eliminating the constant rows” reminds of the desubstitution steps performed in the same work. Looking forward for the long version.
20 September, 2022 at 11:32 am
Terence Tao
Thanks for the link! You have helped me realize that this “p-adic structure” that we have in our Sudoku puzzle solutions encoded by tiling are indeed analogous to some type of susbtitution tiling, which in retrospect makes a lot of sense given how substitution tilings are a common device to make aperiodic tilings in other settings. (I don’t think that the tiling our construction ends up producing is literally a substitution tiling, though, but it certainly has some sort of self-similar structure to it…)
20 September, 2022 at 8:54 am
Felix Johan Schistad Jacobsen
Tao, you are famous for knowing lots of different maths. Do you know much about q-series on number theory (something I believe to be a promising field)?
20 September, 2022 at 9:00 am
Anonymous
Is it possible to find also some explicit upper bounds on the minimal “sufficiently large d” in theorem 3 ?
20 September, 2022 at 11:39 am
Terence Tao
In principle all of our constructions are completely explicit, but we made no attempt to optimize the bounds and so I would imagine that a direct execution of our construction would give extremely large dimension bounds (if I had to guess, I’d say something like ). For instance, there is one stage in our argument where we need to encode a constraint of the form
). For instance, there is one stage in our argument where we need to encode a constraint of the form
for all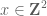 , where
, where 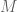 is something of the order of
is something of the order of 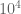 ,
,  are boolean functions, and
are boolean functions, and  is a symmetric set. We proceed here by splitting this constraint into up to
is a symmetric set. We proceed here by splitting this constraint into up to  smaller constraints of the form
smaller constraints of the form
for various coefficients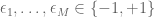 (each of which corresponds to shaving one pair of antipodal corners of the cube
(each of which corresponds to shaving one pair of antipodal corners of the cube  off of the range
off of the range 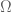 ) and spending a few of of the dimensions
) and spending a few of of the dimensions  to encode each such constraint. This procedure works, but would produce dimensions that are exponential in
to encode each such constraint. This procedure works, but would produce dimensions that are exponential in 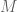 , which is already somewhat large for us. Surely there are more efficient ways to do this, but we decided to use this brute force method as it was relatively simple to implement.
, which is already somewhat large for us. Surely there are more efficient ways to do this, but we decided to use this brute force method as it was relatively simple to implement.
20 September, 2022 at 12:15 pm
Jeremy Rogers
If you don’t mind my asking, why an announcement? Why not just release the full paper in a couple of weeks?
21 September, 2022 at 9:08 am
Anonymous
It is a good practice to announce it first, as a full paper takes much more effort, and time delay. Also, nice to have feedback from others before finishing up the paper. If you have a blog, you may want to do it too.
21 September, 2022 at 10:18 am
Anonymous
So announce it on the blog?
21 September, 2022 at 12:04 pm
Terence Tao
There was some existing interest in this result (which we had announced in some less public channels than this blog), and some of this interest happens to be time-sensitive. On the other hand there is a tradeoff between how hastily we would write the longer paper, and the expositional quality of that paper, so in this case we decided to instead write a shorter announcement first (giving a simplified outline of the argument focusing on the key ideas), and take more time with the full length paper.
21 September, 2022 at 9:22 am
Curious middle aged man
The problem reminds me of the question of whether lattices can have highest packing densities in all dimensions. The analogy being lattices are ‘periodic’ and the fundamental region being a single ’tile’. Can the approach say anything about density of sphere packings in dimensions which are open? In slightly different view point can the concept of multiple ’tiles’ be tied with lattices (multiple lattices) at all?
21 September, 2022 at 12:03 pm
Terence Tao
Our methods are rather specific to the situation in which one has perfect packing with no wasted space, but perhaps one could interpret this result as a negative result that makes it unlikely that there is any sort of general procedure to take a non-periodic tiling and somehow adjust it into a periodic tiling of equal or greater packing density, since our construction gives a counterexample to this when the sphere is replaced by another (much more complex, and most likely non-convex) body. But there could well be special structure specific to the sphere packing problem (as opposed to other tiling problems) in which lattices play a special role. (Certainly the breakthroughs of Viazovska and co-authors on sphere packing in 8 and 24 dimensions are quite specific to this spherically symmetric situation, and do not seem to apply to more general tiling problems.)
21 September, 2022 at 1:12 pm
Craig
I may be seeing a connection that does not exist, but I just now read Bernshteyn’s AMS article on descriptive combinatorics (https://www.ams.org/notices/202209/rnoti-p1496.pdf), and it *looks* like your result might be relevant to the open question 2.14 at the end of the paper?
Your aperiodic tile F can be translated into a locally checkable labeling problem (LCL) by requiring that each region of a given label is in the shape of the tile. I think the existence of a Borel solution might correspond to being able to truncate the p-adic expansion at a finite order, but I’m not certain that I’m even grasping the problem correctly.
22 September, 2022 at 8:46 am
Terence Tao
Yes, there are definitely connections between the discrete or Euclidean tilings consdered here and measurable tiling questions in which one places various descriptive set theory constraints on the sets being tiled. For instance there is a nice paper of Conley, Grebik, and Pikhurko exploring rotational tilings of the sphere in various categories (in the spirit of the Banach-Tarski paradox). In a previous paper of this paper of Grebik, Greenfeld, Rozhon, and myself we were able to demonstrate that there were no non-trivial “factor of iid” tilings of the lattice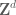 , which is related to the locally checkable condition you mention. It’s a good suggestion to see whether this new construction can help answer some of these questions; we’ll look into it.
, which is related to the locally checkable condition you mention. It’s a good suggestion to see whether this new construction can help answer some of these questions; we’ll look into it.
21 September, 2022 at 5:47 pm
David Speyer
The answer to this question might be “read the paper”, but I’m curious how the reduction from to
to  goes. I see that, if there is a tiling of
goes. I see that, if there is a tiling of  then there is a tiling of
then there is a tiling of  , but you also need to know that, if there is a periodic tiling of
, but you also need to know that, if there is a periodic tiling of  then there is a periodic tiling of
then there is a periodic tiling of  , and that doesn’t seem obvious to me.
, and that doesn’t seem obvious to me.
22 September, 2022 at 8:51 am
Terence Tao
The main trick is to introduce a fundamental domain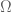 for
for  in
in 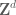 that is “rigid” in the sense that the only way to tile
that is “rigid” in the sense that the only way to tile 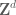 by translates of
by translates of 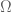 is by a lattice tiling. Such a rigid tile can be created by starting with a standard rectangular box tile and creating some “bumps” on the sides to make it look somewhat like a jigsaw puzzle piece; see Figure 9.1 of our previous paper for an illustration. This trick is already sufficient for the case when the tiling set is a graph of a function, which is basically the situation we have in our paper, but there is a more sophisticated version of this trick which in fact works for arbitrary tilings; this was recently shown by Meyerovitch, Sanadhya, and Solomon, in a paper which should also be appearing shortly.
is by a lattice tiling. Such a rigid tile can be created by starting with a standard rectangular box tile and creating some “bumps” on the sides to make it look somewhat like a jigsaw puzzle piece; see Figure 9.1 of our previous paper for an illustration. This trick is already sufficient for the case when the tiling set is a graph of a function, which is basically the situation we have in our paper, but there is a more sophisticated version of this trick which in fact works for arbitrary tilings; this was recently shown by Meyerovitch, Sanadhya, and Solomon, in a paper which should also be appearing shortly.
22 September, 2022 at 4:36 am
Adrian Fellhauer
I wonder whether the conjecture holds in Euclidean space when one restricts to closed sets (local finiteness then implies via open-ness of the complement that the covering is seamless). It is probably false, because the set Ω may probably chosen to be closed (can’t we just make it a closed hypercube centered at the lattice point? If there aren’t enough corners in the resulting periodic tiling (from the conjecture) to prove that the hypercubes are all centered, we can probably just linearly move the hypercubes into the right position).
22 September, 2022 at 10:46 pm
deleforg
Congratulations for this impressive results, which seems to be the culmination of many years of efforts by you and Rachel Greenfeld, considering your previous papers on the topic. Were you aiming at this result since the beginning or did it come as a surprise?
Do you have any bound on the size of the counter-example tile? Assuming that the constants in your proof could be reduced to non-astronomical values, is there an interpretation of the Z^2 x G_0 tiling that could be “physically realizable”? i.e., does it mean that someone could build a form of 2D tiles with thickness that could translationally pave a thick plane?
25 September, 2022 at 12:07 pm
Terence Tao
Rachel and I have been working on both the positive and negative directions of this conjecture for the past few years, and we were genuinely uncertain which way our analysis on ${\bf Z}^2 \times G_0$ would go. In fact at one point we believed we had positively resolved the periodic tiling conjecture on ${\bf Z}^2 \times G_0$ by combining the structural analysis from our first paper (which focused on positive results) with a strong version of the van der Waerden theorem; but then we found that this “strong version” had a counterexample which involved the p-adic function mentioned in this blog post. It was at this point that we decided to try encoding this p-adic function by the methods from our second paper (which focused on negative results) to get a counterexample, though it took a while to find the “Sudoku puzzle” formalism that would achieve this.
The group that we have is quite far from cyclic and so
that we have is quite far from cyclic and so  is not going to be a quotient of
is not going to be a quotient of  . As such it is unlikely that it can be used to directly provide a physical tiling of a three-dimensional region, unless one somehow “cheats” by using colors or some other device to simulate the additional finite dimensions of
. As such it is unlikely that it can be used to directly provide a physical tiling of a three-dimensional region, unless one somehow “cheats” by using colors or some other device to simulate the additional finite dimensions of  .
.
23 September, 2022 at 7:40 am
Anonymous
Is there any “natural” generalization of this conjecture for some smooth Riemannian manifolds?
23 September, 2022 at 1:41 pm
Anonymous
Dr. Tao:
What class are you teaching this fall? Could one attend it remotely?
[My class this quarter is in-person only. -T]
27 September, 2022 at 7:16 am
N.S.
I think that Conjecture 2 is known to fail for $d=3$,a counterexample was constructed in 1993 by Conway and Danzer. Here it is https://handwiki.org/wiki/Gyrobifastigium#Schmitt.E2.80.93Conway.E2.80.93Danzer_biprism
29 September, 2022 at 5:36 am
anon
That tiling is not using only translations.
28 September, 2022 at 12:42 pm
Chun-Kit Lai
I am excited about the results. I know the answer will be known if I read the paper.
But I would like to know the structure of the counterexamples on $R^d$. Would it be a finite union of hypercubes, like the counterexample of Fuglede’s conjecture? Or it has to make some fractal-type boundaries making it impossible to tile periodically?
1 October, 2022 at 7:51 am
Terence Tao
The continuous example will be a finite union of translates of a fundamental domain of which will be a slightly modified version of a unit cube in order to make it rigid; the unit cube itself is not suitable for transferring counterexamples because the standard lattice tiling by unit cubes is non-rigid (individual rows of cubes can “slide”, and in fact in high dimensions quite weird behaviour can occur, as seen by the breakdown of Keller’s conjecture). A picture of a rigid fundamental domain can be found in Figure 9.1 of our previous paper; it is a finite union of slightly smaller cubes than the unit cube.
which will be a slightly modified version of a unit cube in order to make it rigid; the unit cube itself is not suitable for transferring counterexamples because the standard lattice tiling by unit cubes is non-rigid (individual rows of cubes can “slide”, and in fact in high dimensions quite weird behaviour can occur, as seen by the breakdown of Keller’s conjecture). A picture of a rigid fundamental domain can be found in Figure 9.1 of our previous paper; it is a finite union of slightly smaller cubes than the unit cube.
3 October, 2022 at 1:31 pm
Anonymous
For sufficiently large d,are such counter examples “rare” (in some sense) or not ?
3 October, 2022 at 11:12 pm
Terence Tao
This is an interesting question. There isn’t much literature on what a “typical” tile looks like – for instance I would expect the tiles which are very “rigid” and have only a few tilings much less numerous than those tiles (such as discrete boxes) which are very “non-rigid” and admit a lot of tilings, but I see no way to prove such assertions rigorously (even if one figures out some reasonable metric by which to count these tiles). Even in one dimension (or in a finite group) these sorts of questions seem hard to tackle with our current technology. But certainly once one can find one tile that tiles aperiodically, one can generate a reasonably large family of others, for instance by taking the Cartesian product
that tiles aperiodically, one can generate a reasonably large family of others, for instance by taking the Cartesian product  with an arbitrary tile
with an arbitrary tile  .
.
4 October, 2022 at 4:10 am
Michael R.
Grümbaum = Grünbaum
14 November, 2022 at 11:37 am
Anonymous
How’s this goin?
29 November, 2022 at 8:59 pm
A counterexample to the periodic tiling conjecture | What's new
[…] periodic tiling conjecture“. This is the full version of the result I announced on this blog a few months ago, in which we disprove the periodic tiling conjecture of Grünbaum-Shephard and Lagarias-Wang. […]
29 November, 2022 at 9:33 pm
A counterexample to the periodic tiling conjecture - My Blog
[…] the periodic tiling conjecture“. This is the full version of the result I announced on this blog a few months ago, in which we disprove the periodic tiling conjecture of Grünbaum-Shephard and Lagarias-Wang. The […]