Jon Bennett and I have just uploaded to the arXiv our paper “Adjoint Brascamp-Lieb inequalities“. In this paper, we observe that the family of multilinear inequalities known as the Brascamp-Lieb inequalities (or Holder-Brascamp-Lieb inequalities) admit an adjoint formulation, and explore the theory of these adjoint inequalities and some of their consequences.
To motivate matters let us review the classical theory of adjoints for linear operators. If one has a bounded linear operator for some measure spaces
and exponents
, then one can define an adjoint linear operator
involving the dual exponents
, obeying (formally at least) the duality relation
on
respectively. Using the dual characterization
There is a slightly different way to proceed using Hölder’s inequality. For sake of exposition let us make the simplifying assumption that (and hence also
) maps non-negative functions to non-negative functions, and ignore issues of convergence or division by zero in the formal calculations below. Then for any reasonable function
on
, we have
The first argument also extends to some extent to multilinear operators. For instance if one has a bounded bilinear operator for
then one can then define adjoint bilinear operators
and
obeying the relations
In this paper we observe that the Hölder inequality argument can be modified in the case of Brascamp-Lieb inequalities to obtain a different type of adjoint inequality. (Continuous) Brascamp-Lieb inequalities take the form
The operation of pulling back a function on
by a linear map
to create a function on
has an adjoint pushforward map
, which takes a function on
and basically integrates it on the fibers of
to obtain a “marginal distribution” on
(possibly multiplied by a normalizing determinant factor). The adjoint Brascamp-Lieb inequalities that we obtain take the form
One can derive these adjoint Brascamp-Lieb inequalities from their forward counterparts by a version of the Hölder inequality argument mentioned previously, in conjunction with the observation that the pushforward maps are mass-preserving (i.e., they preserve the
norm on non-negative functions). Conversely, it turns out that the adjoint Brascamp-Lieb inequalities are only available when the forward Brascamp-Lieb inequalities are. In the discrete case the forward and adjoint Brascamp-Lieb constants are essentially identical, but in the continuous case they can (and often do) differ by up to a constant. Furthermore, whereas in the forward case there is a famous theorem of Lieb that asserts that the Brascamp-Lieb constants can be computed by optimizing over gaussian inputs, the same statement is only true up to constants in the adjoint case, and in fact in most cases the gaussians will fail to optimize the adjoint inequality. The situation appears to be complicated; roughly speaking, the adjoint inequalities only use a portion of the range of possible inputs of the forward Brascamp-Lieb inequality, and this portion often misses the gaussian inputs that would otherwise optimize the inequality.
We have located a modest number of applications of the adjoint Brascamp-Lieb inequality (but hope that there will be more in the future):
- The inequalities become equalities at
; taking a derivative at this value (in the spirit of the replica trick in physics) we recover the entropic Brascamp-Lieb inequalities of Carlen and Cordero-Erausquin. For instance, the derivative of the adjoint Loomis-Whitney inequalities at
yields Shearer’s inequality.
- The adjoint Loomis-Whitney inequalities, together with a few more applications of Hölder’s inequality, implies the log-concavity of the Gowers uniformity norms on non-negative functions, which was previously observed by Shkredov and by Manners.
- Averaging the adjoint Loomis-Whitney inequalities over coordinate systems gives reverse
inequalities for the X-ray transform and other tomographic transforms that appear to be new in the literature. In particular, we obtain some monotonicity of the
norms or entropies of the
-plane transform in
(if the exponents
are chosen in a dimensionally consistent fashion).
We also record a number of variants of the adjoint Brascamp-Lieb inequalities, including discrete variants, and a reverse inequality involving norms with
rather than
.

12 comments
Comments feed for this article
30 June, 2023 at 3:59 am
adj
amazing adjoints
30 June, 2023 at 8:03 am
Anonymous
Hi Terry. Love your blog. I want to ask though, why are you linking to mathscinet papers? That severely limits accessibility.
1 July, 2023 at 12:49 pm
Terence Tao
This appears to be a recent change on mathscinet’s end. I would be open to suggestions for alternatives (in particular, a comparison with Zentralblatt or with doi).
30 June, 2023 at 11:36 am
Anonymous
Is it true that whenever the adjoint and forward constants are the same (in some sense indicating “no loss of information”) than the adjoint inequalities are also optimized by gaussians?
1 July, 2023 at 12:47 pm
Terence Tao
Actually, we found that in all non-degenerate cases that gaussians do *not* extremize the adjoint inequality; see Theorem 6.1. For instance, the adjoint Loomis-Whitney inequality is not optimized by gaussians, but instead by indicator functions of boxes (or more generally, Cartesian products ). This is despite the Loomis-Whitney inequality being optimized by gaussians (and with no loss in passing back and forth between the forward and adjoint inequalities). What seems to be going on here is that in order for gaussians to be good test functions for the forward inequality, the
). This is despite the Loomis-Whitney inequality being optimized by gaussians (and with no loss in passing back and forth between the forward and adjoint inequalities). What seems to be going on here is that in order for gaussians to be good test functions for the forward inequality, the  gaussians
gaussians  have to be related to each other in a very specific way; but for the adjoint inequality there is only one input
have to be related to each other in a very specific way; but for the adjoint inequality there is only one input  and the dual functions
and the dual functions  associated to that input are unlikely to obey this specific relation even if
associated to that input are unlikely to obey this specific relation even if  is gaussian.
is gaussian.
For the discrete analogues of these inequalities the situation is different; for both the forward and adjoint inequalities, indicator functions of subspaces serve as extremizers (Theorem 1.14).
2 July, 2023 at 9:11 am
s
Splundiferous
4 July, 2023 at 4:56 am
XG
Great results! Small thing: in the early derivation right after “Then for any reasonable function”, I think that one should replace q by p’.
6 July, 2023 at 1:46 pm
Quadratini Loacker
A small typo: Cordero-Erausquin instead of Cordero-Erasquin.
[Corrected, thanks – T.]
8 July, 2023 at 3:51 am
Tom Courtade
Unless I’m mistaken, a simple observation is that the adjoint BL inequality can be restated in terms of Rényi entropies, in a way that parallels the Cordero–Erausquin dual formulation of the BL inequalities. Namely, for a random vector with density
with density  , the adjoint BL inequality is equivalently restated as
, the adjoint BL inequality is equivalently restated as
for a suitable constant , where $h_p$ denotes the Rényi entropy of order
, where $h_p$ denotes the Rényi entropy of order  . As
. As  tends to Shannon entropy as
tends to Shannon entropy as  , the connection to the Cordero–Erausquin entropic formulation of BL is fairly transparent.
, the connection to the Cordero–Erausquin entropic formulation of BL is fairly transparent.
This rewriting of the adjoint BL inequality also suggests what other “reverse” formulations of the adjoint BL inequality might look like (Question 10.8 in your paper), since we know their dual entropic formulations. For instance, just based on pattern matching, one might conjecture the analogue to Barthe’s inequality would look something like this: For random vectors on
random vectors on  , do we have
, do we have
where the sup is over all couplings of the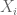 ‘s? Taking
‘s? Taking  would recover Barthe’s inequality.
would recover Barthe’s inequality.
10 July, 2023 at 2:12 pm
Terence Tao
Nice observation! We will add this to the next revision of the ms.
20 July, 2023 at 10:16 am
JojoPizza
Terence tao We need you in the field of Geometric complexity theory. Please contribute your time to advance this important field.
5 August, 2023 at 2:22 pm
Paul Pritchard
Small typo: “various” should be “variants” in the last sentence.
[Corrected, thanks – T.]