I have just uploaded to the arXiv my paper “The convergence of an alternating series of Erdős, assuming the Hardy–Littlewood prime tuples conjecture“. This paper concerns an old problem of Erdős concerning whether the alternating series converges, where
denotes the
prime. The main result of this paper is that the answer to this question is affirmative assuming a sufficiently strong version of the Hardy–Littlewood prime tuples conjecture.
The alternating series test does not apply here because the ratios are not monotonically decreasing. The deviations of monotonicity arise from fluctuations in the prime gaps
, so the enemy arises from biases in the prime gaps for odd and even
. By changing variables from
to
(or more precisely, to integers in the range between
and
), this is basically equivalent to biases in the parity
of the prime counting function. Indeed, it is an unpublished observation of Said that the convergence of
is equivalent to the convergence of
. So this question is really about trying to get a sufficiently strong amount of equidistribution for the parity of
.
The prime tuples conjecture does not directly say much about the value of ; however, it can be used to control differences
for
and
not too large. Indeed, it is a famous calculation of Gallagher that for fixed
, and
chosen randomly from
to
, the quantity
is distributed according to the Poisson distribution of mean
asymptotically if the prime tuples conjecture holds. In particular, the parity
of this quantity should have mean asymptotic to
. An application of the van der Corput
-process then gives some decay on the mean of
as well. Unfortunately, this decay is a bit too weak for this problem; even if one uses the most quantitative version of Gallagher’s calculation, worked out in a recent paper of (Vivian) Kuperberg, the best bound on the mean
is something like
, which is not quite strong enough to overcome the doubly logarithmic divergence of
.
To get around this obstacle, we take advantage of the random sifted model of the primes that was introduced in a paper of Banks, Ford, and myself. To model the primes in an interval such as
with
drawn randomly from say
, we remove one random residue class
from this interval for all primes
up to Pólya’s “magic cutoff”
. The prime tuples conjecture can then be intepreted as the assertion that the random set
produced by this sieving process is statistically a good model for the primes in
. After some standard manipulations (using a version of the Bonferroni inequalities, as well as some upper bounds of Kuperberg), the problem then boils down to getting sufficiently strong estimates for the expected parity
of the random sifted set
.
For this problem, the main advantage of working with the random sifted model, rather than with the primes or the singular series arising from the prime tuples conjecture, is that the sifted model can be studied iteratively from the partially sifted sets arising from sifting primes
up to some intermediate threshold
, and that the expected parity of the
experiences some decay in
. Indeed, once
exceeds the length
of the interval
, sifting
by an additional prime
will cause
to lose one element with probability
, and remain unchanged with probability
. If
concentrates around some value
, this suggests that the expected parity
will decay by a factor of about
as one increases
to
, and iterating this should give good bounds on the final expected parity
. It turns out that existing second moment calculations of Montgomery and Soundararajan suffice to obtain enough concentration to make this strategy work.

28 comments
Comments feed for this article
14 August, 2023 at 9:26 pm
Osama Basta
I have employed the z variant of the transform in my paper https://vixra.org/pdf/2307.0094v1.pdf
and used pi*nlog(n) which is the original form inside the instead of 1/(6x^2) + 1/(4x) which is an approximation of pi(n) the prime counting function.
i found analytically that the first question converges to -0.05
15 August, 2023 at 12:51 am
Anonymous
Is assumption 1.3 (without knowledge of explicit values of the two absolute constants sufficient for the sum to be effectively computable?
sufficient for the sum to be effectively computable?
15 August, 2023 at 5:58 am
Terence Tao
I don’t think I can make the arguments effective without knowing explicit values the constant for Conjecture 1.3, as for any given value of
for Conjecture 1.3, as for any given value of  , this conjecture will trivially hold for some sufficiently large value of
, this conjecture will trivially hold for some sufficiently large value of  depending on
depending on  , so the conjecture has no content non-asymptotically without specifying the constant.
, so the conjecture has no content non-asymptotically without specifying the constant.
15 August, 2023 at 1:12 am
William Maugham
Very.
15 August, 2023 at 7:52 am
Snæ
Kudos.
Just found this conjecture (3 weeks ago) from
Thomas Bloom’s page:
https://www.erdosproblems.com/15
Which only contained the first sentence until your article.
Tried from a computational point of view.
Looking at the differences between the even and odd indices of each result. Then try for a curve fit to determine where the difference could be zero.
Doubt any of my data is of value; at least I improved my programming skills.
It will take some time to digest your paper.
Thanks for the read.
15 August, 2023 at 8:47 am
Anonymous
Prof. Tao:
The proof is based on a conjecture that hasn’t been proven. Is this a good practice? If the conjecture is wrong, then the work would be void.
15 August, 2023 at 8:55 am
Terence Tao
Conditional results are of course not as strong as unconditional results, but the former often arise as a precursor to the latter; a desired result might first be proven assuming one or more standard conjectures, and later work, inspired by this initial conditional result, removes the dependence on these conjectures.
In analytic number theory, many sought after results are extremely difficult to prove unconditionally, so conditional proofs are the next best thing, and can supply heuristic confirmation of the result at least, especially given that many of the standard conjectures in analytic number theory, such as the prime tuples conjecture, are quite firmly believed and have a fair amount of numerical, rigorous, or heuristic supporting evidence in their favor.
Another value of conditional results is that they can highlight the importance of the conjecture being relied upon. Part of the reason that the Riemann hypothesis, for instance, is considered so important is that there is an extremely large number of conditional implications of this hypothesis (and its generalizations) throughout analytic number theory.
Occasionally, one finds that a conjecture conditionally implies a result that one can demonstrate by other means to be false, in which case this automatically disproves the initial conjecture, which is also a noteworthy accomplishment. One reason to pursue conditional implications of the Siegel zero hypothesis, for instance, is to eventually find a way to disprove this hypothesis (which is widely believed to be false, but has proven extremely stubborn to actually eliminate).
15 August, 2023 at 9:27 am
Richard
Tim Gowers has written a nice essay which touches upon conditional proofs, among other practice of practical mathematics research
https://mathstodon.xyz/@wtgowers/110639100049503090
What Makes Mathematicians Believe Unproved Mathematical Statements?
Annals of Mathematics and Philosophy
vol. 1, no 1, 2023
16 August, 2023 at 11:55 am
kodlu
Possibly naive question: Since the Hardy-Littlewood prime $k-$tuples conjecture and the Second Hardy-Littlewood (2HL) conjecture ($\pi(x+y)\leq \pi(x)+\pi(y)$) are contradictory (from memory) I wonder if anything useful could be said about the relationship between 2HL and your new result.
20 August, 2023 at 4:52 am
Terence Tao
Unfortunately the implications here flow in the wrong direction to say anything about the second Hardy-Littlewood conjecture, which as you say is known to be false under the assumption of the prime tuples conjecture. Meanwhile, the result in my paper shows that the Erdos sum is convergent under the assumption of the prime tuples conjecture. The basic takeaway here is that the prime tuples conjecture is a powerful conjecture that allows one to settle (either positively or negatively) many other conjectures involving the primes.
15 August, 2023 at 10:53 am
Anonymous
Sayid observed the sum going from n = 2, not n =10. Is this somehow relevant?
[No. I chose to start most series in my paper from 10 rather than 2 to ensure that both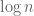 and
and  are positive, but it makes little difference to the convergence. -T]
are positive, but it makes little difference to the convergence. -T]
15 August, 2023 at 10:56 am
Emmanuel Audigé
Hi professor Tao. This are good news.
Finding this question interesting, I think maybe looking the sums over divisors of numbers (-1)^d can help grasping more informations.
16 August, 2023 at 11:54 am
Anonymous
The name Kuperberg does not uniquely define a mathematician, rather there are at least three generations :-)
[First name added to clarify – T.]
17 August, 2023 at 7:16 am
Anonymous
Is it possible by this method to decide the summability of any similar alternating series where is replace by any rational function of
is replace by any rational function of  ?
?
20 August, 2023 at 5:03 am
Terence Tao
It’s possible, but (as with many Erdos questions) the particular question involving is very finely balanced, in the interesting boundary zone between problems that can be resolved by a straightforward application of known methods, and problems which have so many complexities and obstacles that they are significantly more difficult than simpler claims that are still out of reach. The quantity
is very finely balanced, in the interesting boundary zone between problems that can be resolved by a straightforward application of known methods, and problems which have so many complexities and obstacles that they are significantly more difficult than simpler claims that are still out of reach. The quantity  is of size about
is of size about  (which is why, by the way, the series is not absolutely convergent), but the difference between consecutive terms is far smaller:
(which is why, by the way, the series is not absolutely convergent), but the difference between consecutive terms is far smaller:
The second term is monotone decreasing and can be handled by the alternating series test. Heuristically, the prime gap
is monotone decreasing and can be handled by the alternating series test. Heuristically, the prime gap  is of size about
is of size about 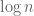 , and so the first term should be of size about
, and so the first term should be of size about  – just barely short of being summable, so one still has to squeeze a little more cancellation out of the sum (which is where the prime tuples conjecture comes in, as this conjecture is known to control the distribution of the prmie gap).
– just barely short of being summable, so one still has to squeeze a little more cancellation out of the sum (which is where the prime tuples conjecture comes in, as this conjecture is known to control the distribution of the prmie gap).
If one repeated this sort of calculation with another expression than , most likely one would either get a sum with terms decaying so fast that it was easy to establish convergence, or a sum whose terms diverged so slowly that convergence was either false, or impossible to prove with existing technology.
, most likely one would either get a sum with terms decaying so fast that it was easy to establish convergence, or a sum whose terms diverged so slowly that convergence was either false, or impossible to prove with existing technology.
Erdos may have made the task of posing productive mathematical questions look effortless, but I believe he must have actually put a lot of prior effort in testing each of his questions against existing methods before releasing them, as the overwhelming majority of them do land in the narrow interesting boundary zone mentioned above.
21 August, 2023 at 7:07 am
Terence Tao
An update: William Banks has informed me that the arguments for in my paper can be adapted to the variant sum
in my paper can be adapted to the variant sum  for any
for any  on the unit circle other than 1. Thus, assuming a strong version of the prime tupoles conjecture, this power series converges on the boundary of its disk of convergence except at
on the unit circle other than 1. Thus, assuming a strong version of the prime tupoles conjecture, this power series converges on the boundary of its disk of convergence except at  where it diverges.
where it diverges.
21 August, 2023 at 12:56 pm
Anonymous
Since the Taylor coefficients of this variant series are quite “noisy”, is it possible that this series has the unit circle as its natural boundary?
of this variant series are quite “noisy”, is it possible that this series has the unit circle as its natural boundary?
23 August, 2023 at 7:19 am
Terence Tao
Nice question! I would also expect the circle to be the natural boundary, in analogy with random power series as you indicate. Proving it rigorously (even with the prime tuples conjecture) could be a challenge though. It morally amounts to getting *lower bounds* on the rate of convergence of (smoothed) partial sums, rather than upper bounds which was the focus of my paper. I’ll add it as an open question in the next revision of the ms.
17 August, 2023 at 8:27 am
Ofir G.
I’d like to point out that the computation of , used in p. 9 of your preprint, has a confusing history. A weak version of it appears in Lemma 2 of Montgomery’s “Primes in arithmetic progressions” (1970), which is also the last chapter of his book “Topics in Multiplicative Number Theory” (1971). It gives
, used in p. 9 of your preprint, has a confusing history. A weak version of it appears in Lemma 2 of Montgomery’s “Primes in arithmetic progressions” (1970), which is also the last chapter of his book “Topics in Multiplicative Number Theory” (1971). It gives  . The sharper estimate with
. The sharper estimate with  was known to Montgomery during the same time. In fact, the lower order term
was known to Montgomery during the same time. In fact, the lower order term  was central for coming up with his Pair Correlation Conjecture (this is alluded to in his paper introducing the conjecture, and also indicated explicitly in Montgomery and Soundararajan's "Beyond Pair Correlation"). A proof of the
was central for coming up with his Pair Correlation Conjecture (this is alluded to in his paper introducing the conjecture, and also indicated explicitly in Montgomery and Soundararajan's "Beyond Pair Correlation"). A proof of the  estimate is given in Croft's "Square-free numbers in arithmetic progressions" (1975). Finally, the estimate
estimate is given in Croft's "Square-free numbers in arithmetic progressions" (1975). Finally, the estimate  for an explicit $C$ was given by Goldston's "Linnik’s theorem on Goldbach numbers in short intervals" (1990) in equation (33), but without proof. A proof of a more general statement was given in Friedlander and Goldston "Variance of distribution of primes in residue classes" (Proposition 3).
for an explicit $C$ was given by Goldston's "Linnik’s theorem on Goldbach numbers in short intervals" (1990) in equation (33), but without proof. A proof of a more general statement was given in Friedlander and Goldston "Variance of distribution of primes in residue classes" (Proposition 3).
[Thanks for the references! These will be incorporated into the next version of the ms. -T]
18 August, 2023 at 4:34 pm
Anonymous
Is it known whether the non-alternating version – just sum of n/p(n) – converges?
20 August, 2023 at 1:05 am
Anonymous
Yes one has divergence.
21 August, 2023 at 12:43 am
Binbin Hu
Just a simple question about the shift operation in the proof of the equivalence of Q1.1 and Q1.2. From my understanding, the shift operation is , and the first term on the right-hand side should be
, and the first term on the right-hand side should be  . (The constant term has absolutely no influence to the valid proof.)
. (The constant term has absolutely no influence to the valid proof.)
[Thanks, this will be corrected in the next revision of the ms. -T]
21 August, 2023 at 7:24 am
Jonathan Baxter
Don’t keep us in suspense…
To what does it converge?
21 August, 2023 at 7:29 am
Jonathan Baxter
Nevermind. Now I read the paper, it’s ~ -0.05. Surprising. Almost cancels. I would have expected something a lot larger (in absolute value).
21 August, 2023 at 7:34 am
Jonathan Baxter
This post has Said’s sum starting at 10, whereas the paper has it starting at 2 (obviously both are correct, but the 10 in this version had me scratching my head).
21 August, 2023 at 11:33 am
Daniel Goldston
This is an amazing proof, especially using the Banks-Ford-Tao large prime gap probability model as tool in the proof. Not directly related to the paper, I want to mention that for the average of the singular series over two-tuples, which is equivalent to the Cesaro mean of the singular series, the error term mentioned in the comments above was improved by Vaughan in 2001 using the zero-free region and also assuming RH he obtained the error term
mentioned in the comments above was improved by Vaughan in 2001 using the zero-free region and also assuming RH he obtained the error term  . Recently Suriajaya and I proved that this error term is
. Recently Suriajaya and I proved that this error term is  . This is on the Arxiv or JNT 227 (2021) 144-157.
. This is on the Arxiv or JNT 227 (2021) 144-157.
[Thanks for the references – these will be added to the next revision of the MS. -T]
31 August, 2023 at 2:05 am
Keiju Sono
Very interesting paper. I found a couple of minor mistakes. I apologize if I am mistaken.
p2. In the definition of the singular series, \nu _{H}(p) should be divided by p.
The last line of p5. The n in the binomial coefficient should be N.
p5. In the proof of Lemma 3.1, f(r+2)-f(r) changes sign when r=(2N-4)/3.
p11. line 5. I think “for some absolute constant c>0” is unnecessary.
[Thanks, this will be corrected in the next revision of the ms – T.]
3 October, 2023 at 3:04 am
Anonymous
I apologize Pr. This is a series of conjectures of my highschool student (Ousmanou Abdou Mohamadou from Cameroon): https://www.researchgate.net/publication/374388548_OUSMANOU's_CONJECTURES_PART_1 Tthe curious conjecture P10: Let p_n be the n^th prime number after the first 2, and p_m be the m^th prime number ( n,m≥4):
for all natural numbers k,r one has |〖p_n〗^2k-〖p_m〗^2r | multiple of 24 . Please could any one help us? thanks. Yannick.
Kouakep’s comment: maybe a quadratic distance between prime numbers, following P10?