Additive combinatorics is largely focused on the additive properties of finite subsets A of an additive group . This group can be finite or infinite, but there is a very convenient trick, the Ruzsa projection trick, which allows one to reduce the latter case to the former. For instance, consider the set
inside the integers
. The integers of course form an infinite group, but if we are only interested in sums of at most two elements of A at a time, we can embed A ininside the finite cyclic group
without losing any combinatorial information. More precisely, there is a Freiman isomorphism of order 2 between the set
in
and the set
in
. One can view the latter version of
as a model for the former version of
. More generally, it turns out that any finite set A in an additive group can be modeled in the above set by an equivalent set in a finite group, and in fact one can ensure that this ambient modeling group is not much larger than A itself if A has some additive structure; see this paper of Ruzsa (or Lemma 5.26 of my book with Van Vu) for a precise statement. This projection trick has a number of important uses in additive combinatorics, most notably in Ruzsa’s simplified proof of Freiman’s theorem.
Given the interest in non-commutative analogues of Freiman’s theorem, it is natural to ask whether one can similarly model finite sets A in multiplicative (and non-commutative) groups using finite models. Unfortunately (as I learned recently from Akshay Venkatesh, via Ben Green), this turns out to be impossible in general, due to an old example of Higman. More precisely, Higman shows:
Theorem 1. There exists an infinite group G generated by four distinct elements a,b,c,d that obey the relations
; (1)
in fact, a and c generate the free group in G. On the other hand, if G’ is a finite group containing four elements a,b,c,d obeying (1), then a,b,c,d are all trivial.
As a consequence, the finite set in G has no model (in the sense of Freiman isomorphisms) in a finite group.
Theorem 1 is proven by a small amount of elementary group theory and number theory, and it was neat enough that I thought I would reproduce it here.
— No non-trivial finite models —
Let’s first show the second part of Theorem 1. The key point is that in a finite group G’, all elements have finite order, thanks to Lagrange’s theorem. From (1) we have
and hence by induction
(2)
for any positive n. One consequence of (2) is that if , then
, and thus
. Applying this with n equal to the order
of b, we conclude that
.
As a consequence, if is divisible by some prime p, then
is divisible by p, which forces p to be odd and
to be divisible by the multiplicative order of 2 modulo p. This is at most p-1 (by Fermat’s little theorem), and so
is divisible by a prime strictly smaller than the prime dividing
. But we can cyclically permute this argument and conclude that
is divisible by an even smaller prime than the prime dividing
, and so forth, creating an infinite descent, which is absurd. Thus none of
can be divisible by any prime, and so a,b,c,d are trivial as claimed.
Remark 1. There is nothing special here about using four generators; the above arguments work with any number of generators (adapting (1) appropriately). But we will need four generators in order to establish the infinite model below.
Remark 2. The above argument also shows that the group G has no non-trivial finite-dimensional linear representation. Indeed, let a, b, c, d be matrices obeying (1), then b is conjugate to , which by the spectral theorem forces the eigenvalues of b to be roots of unity, which implies in particular that
grows at most polynomially in n; similarly for
. Applying (2) we see that
grows at most polynomially in n, which by the Jordan normal form for a implies that a is diagonalisable; since its eigenvalues are roots of unity, it thus has finite order. Similarly for b,c,d. Now apply the previous argument to conclude that a,b,c,d are trivial.
— Existence of an infinite model —
To build the infinite group G that obeys the relations (1), we need the notion of an amalgamated free product of groups.
Recall that the free product of two groups
and
can be defined (up to group isomorphism) in one of three equivalent ways:
- (Relations-based definition)
is the group generated by the disjoint union
of
and
, with no further relations between these elements beyond those already present in
and
separately.
- (Category-theoretic definition)
is a group with homomorphisms from
and
into
, which is universal in the sense that any other group G’ with homomorphisms from
will have these homomorphisms factor uniquely through
.
- (Word-based definition)
is the collection of all words
, where each
lies in either
or
, with no two adjacent
lying in the same
(let’s label
here to be disjoint to avoid notational confusion), with the obvious group operations.
It is not hard to see that all three definitions are equivalent, and that the free product exists and is unique up to group isomorphism.
Example 1. The free product of the free cyclic group with one generator a, and the free cyclic group
with one generator b, is the free (non-abelian) group
on two generators.
We will need a “relative” generalisation of the free product concept, in which the groups are not totally disjoint, but instead share a common subgroup H (or if one wants to proceed more category-theoretically, with a group H that embeds into both
and
). In this situation, we define the amalgamated free product
by one of the following two equivalent definitions:
- (Relations-based definition)
is the group generated by the relative disjoint union
of
and
(which is the same as the disjoint union but with the common subgroup H identified), with no further relations between these elements beyond those already present in
and
separately.
- (Category-theoretic definition)
is a group with homomorphisms from
and
into
that agree on H, which is universal in the sense that any other group G’ with homomorphisms from
that agree on H will have these homomorphisms factor uniquely through
.
Example 2. Let be the group generated by two elements
with one relation
. It is not hard to see that all elements of
can be expressed uniquely as
for some integers n, m, and in particular that
is a free cyclic group. Let
be the group generated by two elements
with one relation
, then again
is a free cyclic group, and isomorphic to the previous copy of H. The amalgamated free product
is then generated by three elements
with two relations
.
It is not hard to see that the above two definitions are equivalent, and that exists and is unique up to group isomorphism. But note that I did not give the word-based definition of the amalgamated free product yet. We will need to do so now; I will use the arguments from this 1954 paper of Neumann (who I briefly overlapped with, actually, at ANU), though the basic result I need here (namely, Corollary 1) dates all the way back to the work of Schreier in 1927.
In order to analyse these groups, we will need to study how they act on various spaces. If G is a group, we define a G-space to be a set X together with an action of G on X (or equivalently, a homomorphism from G to the permutation group
of X). Thus for instance G is itself a G-space. A G-space X is transitive if for every
, there exists
such that
. A morphism from one G-space X to another G-space Y is a map
such that
for all
and
. If a morphism has an inverse that is also a morphism, we say that it is an isomorphism.
The first observation is that a G-space with certain properties will necessarily be isomorphic to G itself.
Lemma 1. (Criterion for isomorphism with G) Let G be a group, and let X be a non-empty transitive G-space, and suppose there is a morphism
from the G-space X to the G-space G. Then
is in fact an isomorphism of G-spaces.
Proof. It suffices to show that is both injective and surjective. To show surjectivity, observe that the image
is G-invariant and non-empty. But the action of G on G is transitive, and so
as desired. To show injectivity, observe from transitivity that if
are distinct elements of X then
for some non-identity
, thus
, thus
, establishing injectivity.
Now we can give the word formulation of the amalgamated free product.
Lemma 2. (Word-based description of amalgamated free product) Let
be two groups with common subgroup H, and let
be the amalgamated free product. Let
,
be some partitions of
into right-cosets of H. Let X be the space of all formal words of the form
, where
, each
lies in either
or
, and no two adjacent
lie in the same
. let
be the obvious evaluation map. Then there is an action of G on X for which
becomes an isomorphism of G-spaces.
Proof. It is easy to verify that and
act separately on X in a manner consistent (via
) with their action on G, and these actions agree on H. Hence the amalgamated free product G also acts on this space and turns
into a morphism of G-spaces. From construction of X we see that the G-action is transitive, and the claim now follows from Lemma 1.
Corollary 1. Let
be two groups with common subgroup H, and let
be the amalgamated free product. Let
and
be such that the cyclic groups
are infinite and have no intersection with H. Then
generate a free subgroup in G.
Proof. By hypothesis (and the axiom of choice), we can find a partition where
contains the infinite cyclic group
, and similarly we can find a partition
. Let X be the space in Lemma 2. Each reduced word formed by
then generates a distinct element of X, and thus (by Lemma 2) a distinct element of G. The claim follows.
Remark 3. The above corollary can also be established by the ping-pong lemma (which is not surprising, since the proof of that lemma uses many of the same ideas, and in particular exploiting an action of G on a space X in order to distinguish various words in G from each other). Indeed, observe that map those words
in X with
into words
with
, and similarly for
, which is the type of hypothesis needed to apply the ping-pong lemma. [Thanks to Ben Green for this observation.]
Now we can finish the proof of Theorem 1. As discussed in Example 2, the group is the amalgamated free product of
and
relative to
. By Corollary 1, a and c generate the free group here, thus
contains
as a subgroup. Similarly, the group
also contains
as a subgroup. We may then form the amalgamated free product
and another application of Theorem 1 shows that b,d generate the free group (and are in particular distinct); similarly a, c are distinct. Finally, the group embeds into
, which embeds into G, and so a, b, are also distinct; cyclically permuting this we conclude that all of the a, b, c, d are distinct as claimed.

9 comments
Comments feed for this article
7 October, 2008 at 3:47 am
ben green
Terry,
Thanks for explaining this! The example is potentially disturbing in that if one aspires towards a Freiman-type theory for arbitrary groups (a theory which would only involve finite sets) then it may be necessary to understand infinite groups and even infinite-dimensional representations.
I say only *potentially* disturbing because there is some hope that a weaker statement holds. Namely, if is a constant and if
is a constant and if  is a set for which
is a set for which 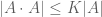 then there is a subset
then there is a subset  with
with 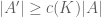 which has a Freiman-isomorphic copy inside some finite group
which has a Freiman-isomorphic copy inside some finite group  . I can’t see it being easy to produce a counterexample to this!
. I can’t see it being easy to produce a counterexample to this!
One cannot hope for to have size comparable to
to have size comparable to  (thus
(thus 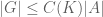 , say) as is the case in the abelian setting. I worked out the slightly painful details of an example a few months ago and have posted it here
, say) as is the case in the abelian setting. I worked out the slightly painful details of an example a few months ago and have posted it here
Click to access nonabelianmodels.pdf
since I don’t have any intention of publishing it.
Best wishes
Ben
7 October, 2008 at 9:54 am
Anonymous
professor tao,
thank you for your well written posts. i am learning a lot of math mainly through your posts.
if it is not too much trouble can you plaese include some references, ideally to books that can
with easy availability. i don’t have access to jstor or a good math library with easy access to
journals.
again thanks for writing up beautiful math.
10 October, 2008 at 9:40 am
Anonymous
In the beginning of the proof of theorem 1: “The key point is that in a finite group G’, all elements have finite order, thanks to Cauchy’s theorem”.
Apart from this fact being obvious, could you explain how it follows from Cauchys theorem?
10 October, 2008 at 11:00 am
Terence Tao
Oops! I meant Lagrange’s theorem rather than Cauchy’s theorem.
11 October, 2008 at 5:01 pm
David Fisher
Hi Terry,
That is a cool example.
A remark: all linear groups are residually finite i.e. have finite quotients
that separate any finite set.
So Remark 2 actually follows from the the fact that G has no finite quotients.
Your proof that G is non-linear is easier than the proof that linear groups
are residually finite.
Best,
David
23 October, 2008 at 8:02 am
Gabor Elek
Gordon and Vershik have a paper that characterizes those groups G such that
all finite subset of G can be modelled in finite groups.
They call these groups LEF (locally finitely embeddable). http://www.esi.ac.at/preprints/esi334.pdf
28 October, 2012 at 11:37 am
van Kampen’s theorem via covering spaces « What’s new
[…] in and using the combinatorial description of the amalgamated free product (which was discussed in this previous blog post). But I recently learned (thanks to the responses to this recent MathOverflow question of mine) […]
10 February, 2014 at 10:02 am
Anon
Joining a little late, but regarding remark 2: every linear group is residually finite, and so the remark follows immediately from the theorem.
20 June, 2016 at 7:48 am
Shtetl-Optimized » Blog Archive » Entanglement without end
[…] have a good intuition for Higman’s group, but if I did, it would come from rereading this post by Terry Tao. Certainly it has no known “physical interpretation” analogous to the […]