One of the most important topological concepts in analysis is that of compactness (as discussed for instance in my Companion article on this topic). There are various flavours of this concept, but let us focus on sequential compactness: a subset E of a topological space X is sequentially compact if every sequence in E has a convergent subsequence whose limit is also in E. This property allows one to do many things with the set E. For instance, it allows one to maximise a functional on E:
Proposition 1. (Existence of extremisers) Let E be a non-empty sequentially compact subset of a topological space X, and let
be a continuous function. Then the supremum
is attained at at least one point
, thus
for all
. (In particular, this supremum is finite.) Similarly for the infimum.
Proof. Let be the supremum
. By the definition of supremum (and the axiom of (countable) choice), one can find a sequence
in E such that
. By compactness, we can refine this sequence to a subsequence (which, by abuse of notation, we shall continue to call
) such that
converges to a limit x in E. Since we still have
, and f is continuous at x, we conclude that f(x)=L, and the claim for the supremum follows. The claim for the infimum is similar.
Remark 1. An inspection of the argument shows that one can relax the continuity hypothesis on F somewhat: to attain the supremum, it suffices that F be upper semicontinuous, and to attain the infimum, it suffices that F be lower semicontinuous.
We thus see that sequential compactness is useful, among other things, for ensuring the existence of extremisers. In finite-dimensional spaces (such as vector spaces), compact sets are plentiful; indeed, the Heine-Borel theorem asserts that every closed and bounded set is compact. However, once one moves to infinite-dimensional spaces, such as function spaces, then the Heine-Borel theorem fails quite dramatically; most of the closed and bounded sets one encounters in a topological vector space are non-compact, if one insists on using a reasonably “strong” topology. This causes a difficulty in (among other things) calculus of variations, which is often concerned to finding extremisers to a functional on a subset E of an infinite-dimensional function space X.
In recent decades, mathematicians have found a number of ways to get around this difficulty. One of them is to weaken the topology to recover compactness, taking advantage of such results as the Banach-Alaoglu theorem (or its sequential counterpart). Of course, there is a tradeoff: weakening the topology makes compactness easier to attain, but makes the continuity of F harder to establish. Nevertheless, if F enjoys enough “smoothing” or “cancellation” properties, one can hope to obtain continuity in the weak topology, allowing one to do things such as locate extremisers. (The phenomenon that cancellation can lead to continuity in the weak topology is sometimes referred to as compensated compactness.)
Another option is to abandon trying to make all sequences have convergent subsequences, and settle just for extremising sequences to have convergent subsequences, as this would still be enough to retain Theorem 1. Pursuing this line of thought leads to the Palais-Smale condition, which is a substitute for compactness in some calculus of variations situations.
But in many situations, one cannot weaken the topology to the point where the domain E becomes compact, without destroying the continuity (or semi-continuity) of F, though one can often at least find an intermediate topology (or metric) in which F is continuous, but for which E is still not quite compact. Thus one can find sequences in E which do not have any subsequences that converge to a constant element
, even in this intermediate metric. (As we shall see shortly, one major cause of this failure of compactness is the existence of a non-trivial action of a non-compact group G on E; such a group action can cause compensated compactness or the Palais-Smale condition to fail also.) Because of this, it is a priori conceivable that a continuous function F need not attain its supremum or infimum.
Nevertheless, even though a sequence does not have any subsequences that converge to a constant x, it may have a subsequence (which we also call
) which converges to some non-constant sequence
(in the sense that the distance
between the subsequence and the new sequence in a this intermediate metric), where the approximating sequence
is of a very structured form (e.g. “concentrating” to a point, or “travelling” off to infinity, or a superposition
of several concentrating or travelling profiles of this form). This weaker form of compactness, in which superpositions of a certain type of profile completely describe all the failures (or defects) of compactness, is known as concentration compactness, and the decomposition
of the subsequence is known as the profile decomposition. In many applications, it is a sufficiently good substitute for compactness that one can still do things like locate extremisers for functionals F – though one often has to make some additional assumptions of F to compensate for the more complicated nature of the compactness. This phenomenon was systematically studied by P.L. Lions in the 80s, and found great application in calculus of variations and nonlinear elliptic PDE. More recently, concentration compactness has been a crucial and powerful tool in the non-perturbative analysis of nonlinear dispersive PDE, in particular being used to locate “minimal energy blowup solutions” or “minimal mass blowup solutions” for such a PDE (analogously to how one can use calculus of variations to find minimal energy solutions to a nonlinear elliptic equation); see for instance this recent survey by Killip and Visan.
In typical applications, the concentration compactness phenomenon is exploited in moderately sophisticated function spaces (such as Sobolev spaces or Strichartz spaces), with the failure of traditional compactness being connected to a moderately complicated group G of symmetries (e.g. the group generated by translations and dilations). Because of this, concentration compactness can appear to be a rather complicated and technical concept when it is first encountered. In this note, I would like to illustrate concentration compactness in a simple toy setting, namely in the space of absolutely summable sequences, with the uniform (
) metric playing the role of the intermediate metric, and the translation group
playing the role of the symmetry group G. This toy setting is significantly simpler than any model that one would actually use in practice [for instance, in most applications X is a Hilbert space], but hopefully it serves to illuminate this useful concept in a less technical fashion.
— Defects of compactness in —
Consider the space
of absolutely summable doubly infinite sequences ; this is a normed vector space generated by the basis vectors
for
(here
is the Kronecker delta). We can place several topologies on this space X:
Definition 1. Let
be a sequence in X (i.e. a sequence of sequences!), and let
be another element in X.
- (Strong topology) We say that
converges to x in the strong topology (or
topology) if the
distance
converges to zero.
- (Intermediate topology) We say that
converges in x in the intermediate topology (or uniform topology) if the
distance
converges to zero.
- (Weak topology) We say that
converges in x in the weak topology (or pointwise topology) if
as
for each m. [Strictly speaking, this only describes the weak topology for bounded sequences, but these are the only sequences we will be considering here.]
Example 1. The sequence for
converges weakly to zero, but is not convergent in the strong or intermediate topologies. The sequence
converges in the intermediate and weak topologies to zero, but is not convergent in the strong topology.
It is easy to see that strong convergence implies intermediate convergence, which in turn implies weak convergence, thus justifying the names “strong”, “intermediate”, and “weak”. For bounded sequences, the intermediate topology can also be described by a number of other norms, e.g. the norm for any
(this is an easy application of Hölder’s inequality).
The space X also has the translation action of the group of integers , defined using the shift operators
for
, defined by the formula
(in particular, is linear with
). This action is continuous with respect to all three of the above topologies. (We give G the discrete topology.)
Inside the infinite-dimensional space X, we let E be the “unit sphere” (though it looks more like an octahedron, actually)
E is clearly invariant under the translation action of G. It is easy to see that E is closed and bounded in the strong topology (or metric). However, it is not closed in the weak topology: the sequence of basis vectors for
converges weakly to the origin 0, which lies outside of E. It is also not closed in the intermediate topology; the sequence
lies in E but converges in the intermediate topology to 0, which lies outside of E.
The failure of closure in the weak topology causes failure of compactness in the strong or intermediate topologies. Indeed, the sequence cannot have any convergent subsequence in those topologies, since the limit of such a subsequence would have to equal its weak limit, which is zero; but
clearly does not converge in either the strong or intermediate topologies to 0. (To put it another way, the embedding of
into
is not compact.)
More generally, for any fixed profile , the “travelling wave” (or “travelling profile”)
for
converges weakly to zero, and so by the above argument has no convergent subsequence in the strong or intermediate topologies. A little more generally still, given any sequence
of integers going off to infinity,
is a sequence in E which has no convergent subsequence in the strong or intermediate topologies. Thus we see that the action of the (non-compact) group G is causing a failure of compactness of E in the strong and intermediate topologies.
Because of the linear nature of the vector space X, one can also create examples of sequences in E with no convergent subsequences by taking superpositions of travelling profiles. For instance, if are two non-negative sequences with
, and
are two sequences of integers which both go off to infinity,
then the superposition
of the two travelling profiles and
will be a sequence in E that continues to converge weakly to zero, and so again has no convergent subsequence in the strong or intermediate topologies.
If and
are not non-negative, then there can be cancellations between
and
, which could cause
to have norm significantly less than 1 (thus straying away from E). However, if one also imposes the asymptotic orthogonality condition
we see that these cancellations vanish in the limit , and so in this case we can build a modified superposition
that lies in E, with converging to zero in the strong and uniform topology, and will once again be a sequence with no convergent subsequence. [If the asymptotic orthogonality condition fails, then one can collapse the superposition of two travelling profiles into a single travelling profile, after passing to a subsequence if necessary. Indeed, if
does not go to infinity, then we can find a subsequence for which
is equal to a constant c, in which case
is equal to a single travelling profile
.] More generally, given any collection
of non-zero elements of X with
(1)
and any sequences of integers obeying the asymptotic orthogonality condition
(2)
for all , we can find a sequence in
that takes the form
(3)
where converges to zero in the intermediate topology. [If one has equality in (1), one can make
converge in the strong topology also.] If
goes off to infinity for at least one j with
non-zero, then this sequence will have no convergent subsequence.
We have thus demonstrated a large number of ways that compactness of E fails in the strong and intermediate topologies. The concentration compactness phenomenon, in this setting, tells us that these are essentially the only ways in which compactness fails in the intermediate topology. More precisely, one has
Theorem 2. (Profile decomposition) Let
be a sequence in E. Then, after passing to a subsequence (which we still call
), there exist
obeying (1), and sequences
of integers obeying (2), such that we have the decomposition (3) where the error
converges to zero in the intermediate topology. Furthermore, we can improve (1) to
(1′)
Remark 2. The situation is vastly different in the strong topology; in this case, virtually every sequence in E fails to have a convergent subsequence (consider for instance the sequence from Example 1), and there are so many different ways a sequence can behave that there is no meaningful profile decomposition. A more quantitative way to see this is via a computation of metric entropy constants (i.e. covering numbers). Pick a small number
(e.g.
) and a large number N, and consider how many balls of radius
in the
norm are needed to cover the unit sphere
in
. A simple volume packing argument shows that this number must grow exponentially in N. On the other hand, if one wants to cover
with the (much larger) balls of radius
in the
topology instead, the number of balls needed grows only polynomially with N. Indeed, after rounding down each coefficient of an element of
to a multiple of
, there are only at most
non-zero coefficients, and so the total number of possibilities for this rounded down approximant is about
. Thus, the metric entropy constants for both the strong and intermediate topologies go to infinity in the infinite dimensional limit
(thus demonstrating the lack of compactness for both), but much more rapidly for the former than for the latter.
— Proof sketch of Theorem 2 —
We now sketch how one would prove Theorem 2. The idea is to hunt down and “domesticate” the large values of , as these are the only obstructions to convergence in the intermediate topology. (I believe the use of the term “domesticate” here is due to Kyril Tintarev.) Each large piece of the
that we capture in this manner will decrease the total “mass” in play, which guarantees that eventually one runs out of such large pieces, at which point one obtains the decomposition (3). [Curiously, the strategy here is very similar to that underlying the structural theorems that arise in additive combinatorics and ergodic theory; I touched upon these analogies before in my Simons lectures.] In this process we rely heavily on the freedom to pass to a subsequence at will, which is useful to eliminate any fluctuations so long as they range over a compact space of possibilities.
Let’s see how this procedure works. We begin with our bounded sequence , whose
norms are all equal to 1. If this sequence already converging to zero in the intermediate topology, we are done (we let j range over the empty set, and set
equal to all of
. So suppose that
are not converging to zero in this topology. Passing to a subsequence if necessary, this implies the existence of an
such that
for all n. Thus we can find integers
such that
for all n, or equivalently that the shifts
have their zero coefficient uniformly bounded below in magnitude by
.
We have used the symmetry group G to move a large component of each of the the origin. Now we take advantage of sequential compactness of the unit ball in the weak topology. This allows one (after passing to another subsequence) to assume that the shifted elements
converge weakly to some limit
; since the
are uniformly non-trivial at the origin, the weak limit
is also; in particular, we have
. Undoing the shift, we have obtained a decomposition
where the residual is such that
converges weakly to zero (thus, in some sense
vanishes asymptotically near
). It is then not difficult to show the “asymptotic orthogonality” relationship
where is a quantity that goes to zero as
; this implies, in particular, that the residual
eventually has mass strictly less than that of the original sequence
:
;
in fact we have the more precise relationship
.
Now we take this residual and repeat the whole process. Namely, if
converges in the intermediate topology to zero, then we are done; otherwise, as before, we can find (after passing to a subsequence)
,
for which
is bounded from below by
at the origin. Because
already converged weakly to zero, one can conclude that
and
must be asymptotically orthogonal in the sense of (2).
Passing to a subsequence again, we can assume that converges weakly to a limit
with mass at least
, leading to a decomposition
where the residual is such that
and
both converge weakly to zero, and has norm
;
in fact we have the more precise relationship
.
One can continue in this vein, extracting more and more travelling profiles on finer and finer subsequences, with residuals
that are getting smaller and smaller. The subsequences involved depend on j, but by the usual Cantor (or Arzelá-Ascoli) diagonalisation argument, one can work with a single sequence throughout. Note that the amounts of mass
that are extracted in this process cannot exceed 1 in total:
(in fact we have the slightly stronger statement (2)). In particular, the
must go to zero as
(the infinite convergence principle!). If the
were selected in a “greedy” manner, this shows that the asymptotic
norm of the residuals
as
must decay to zero as
. Carefully rearranging the epsilons, this gives the decomposition (3) with residual
converging to zero in the intermediate topology, and the verification of the rest of the theorem is routine.
Remark 3. It is tempting to view Theorem 2 as asserting that the space E with the can be “compactified” by throwing in some idealised superposition of profiles that are “infinitely far apart” from each other.
— An application of concentration compactness —
As mentioned in the introduction, one can use the profile decomposition of Theorem 2 as a substitute for compactness in establishing results analogous to Theorem 1. The catch is that one needs more hypotheses on the functional F in order to be able to handle the complicated profiles that come up. It is difficult to formalise the “best” set of hypotheses that would cover all conceivable situations; it seems better to just adapt the general arguments to each individual situation separately. Here is a typical (but certainly not optimal) result of this type:
Theorem 3. Let X, E be as above. Let
be a non-negative function with the following properties:
- (Continuity) F is continuous in the intermediate topology on E.
- (Homogeneity) F is homogeneous of some degree
, thus
for all
and
. (In particular, F(0)=0.)
- (Invariance) F is G-invariant:
for all
and
.
- (Asymptotic additivity) If
are a collection of sequences obeying the asymptotic orthogonality condition (1), and
are such that
, then
and
. More generally, if
is bounded in
and converges to zero in the intermediate topology, then
. (Note that this generalises both 1. and 3.)
Then F is bounded on E, and attains its supremum.
A typical example of a functional F obeying the above properties is
for some .
Proof. We repeat the proof of Theorem 1. Let . Clearly
; we can assume that
, since the claim is trivial when
. As before, we have an extremising sequence
with
. Applying Theorem 2, and passing to a subsequence, we obtain a decomposition (3) with the stated properties. Applying the asymptotic additivity hypothesis 4., we have
and in particular
. (4)
This implies in particular that L is finite.
Now, we use the homogeneity assumption. Since when
, we obtain the bound
. We conclude that
Combining this with (1) we obtain
.
Thus all these inequalities must be equality. Analysing this, we see that all but one of the must vanish, with the remaining
(say
) having norm 1. From (4) we thus have
, and we have obtained the desired extremiser.
[Update, Nov 6: some corrections, in particular with regard to the closure of E in the intermediate topology.]

18 comments
Comments feed for this article
6 November, 2008 at 1:58 am
Jerry Gagelman
Dear Terry,
In keeping with the standards you’ve established on this blog, another excellent post! I’ve noticed one minor correction: in Example 1, I think you meant to say that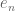 does not converge in the strong or _intermediate_ topologies. However the reason for my comment is the following question. In introducing travelling profiles in the sphere
does not converge in the strong or _intermediate_ topologies. However the reason for my comment is the following question. In introducing travelling profiles in the sphere  in
in 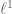 , you said that it “is the action of the (non-compact) group
, you said that it “is the action of the (non-compact) group  causing the failure of compatness of
causing the failure of compatness of  in the strong and weak topologies,” which which would imply that
in the strong and weak topologies,” which which would imply that  has its own topology. Could you please expand on this briefly? E.g., is there a topology on
has its own topology. Could you please expand on this briefly? E.g., is there a topology on  for which the action
for which the action  is continuous in the three topologies on
is continuous in the three topologies on 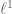 ?
?
Thanks!
Jerry
PS. I’ve also noticed that some formulas in the statment of Theorem 3 are not displayed correctly, but this could just be my browser.
6 November, 2008 at 6:56 am
JC
I’ve also noticed a few typos: the word “thisbv” and “howe”, and there is a non-latexed formula in the paragraph beginning with “Now we take”
6 November, 2008 at 7:27 am
A.P.
Professor Tao
I can’t give up the impression, that the statement, that unite sphere E is closed in intermediate topology is false.
Of course I cannot exclude (and it is actually quite probable), that I make some obvious mistake and something blinds me.
Here is a sequence that concerns me:
Let x(i) be a sequence:
x(i)(0) = (1/2) + (1/2)^i
x(i)(j) = ((1/2) – (1/2)^i)(1/2)^i for j = 1 to (2^i)
x(i)(j) = 0 for j > (2^i) and for j 0 x(i) belongs to E, but
x(i) converges to …,0, 0, 1/2, 0, 0, … in intermediate (uniform) topology.
Regards.
P.S. Great blog. One of the best in known universe.
6 November, 2008 at 10:08 am
Terence Tao
Thanks for the corrections! It is true that E is not closed in the intermediate topology; I have adjusted the discussion to reflect this.
The group G (i.e. the integers) is given the discrete topology; the non-compactness of G is in that case equivalent to the non-finiteness of G. In the situations that occur in actual applications, G is typically something like a translation group (equivalent to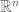 ), a dilation group (equivalent to
), a dilation group (equivalent to 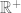 ), an affine group (e.g.
), an affine group (e.g.  ), etc., and again it is the non-compactness which causes all the trouble. (Actions of compact groups such as a rotation group O(n) do not need to be accounted for by a profile decomposition.)
), etc., and again it is the non-compactness which causes all the trouble. (Actions of compact groups such as a rotation group O(n) do not need to be accounted for by a profile decomposition.)
6 November, 2008 at 11:36 am
Dylan Thurston
The whole discussion reminds me of the treatment of pseudo-holomorphic curves in symplectic manifolds with cylindrical ends. There, the standard approach is to go in the direction suggested by your Remark 3: to enlarge the space to make everything honestly compact. In order to make it work, you of course need to take the quotient by the action of the group for the limiting objects, which in this case would mean you no longer have a vector space. In this and similar contexts, trying to deduce what the limits might be to prove a form of concentration compactness seems like it would be harder, as the limits can be fairly complicated.
(This is called Gromov compactness, and one standard reference is Bourgeoi-Eliashberg-Hofer-Wysocki-Zehnder.)
By the way, in condition (2) you probably want to assume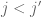 rather than
rather than  .
.
7 November, 2008 at 3:50 am
David Speyer
I am confused by the statement “Now we take advantage of sequential compactness in the weak topology”. Is the point that, even though the unit sphere is neither closed nor compact in the weak topology, the unit ball is both?
Otherwise, a very interesting result! If I were to follow up on Dylan’s analogy, and think like an algebraic geometer, I would want to compactify E to have some extra points that correspond to the limits of these infinite sequences. My first thought is to mimic the Stone-Cech compactification but, rather than using all continuous functions from![E \to [0,1]](https://s0.wp.com/latex.php?latex=E+%5Cto+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) , use only those satisfying the hypothesis of Theorem 3. Is there any use in this?
, use only those satisfying the hypothesis of Theorem 3. Is there any use in this?
7 November, 2008 at 8:37 am
Terence Tao
Dear Dylan and David: Thanks for the corrections and comments! There certainly are close relationships between concentration compactness and, say, bubble tree decompositions, which come up in the analysis of various types of geometric singularities (or other sources of non-compactness); this comes up in harmonic maps and minimal surfaces already, so it makes sense that it would be relevant for pseudoholomorphic curves also.
It sounds plausible that some abstract procedure should be able to compactify E in such a way that concentration compactness can be interpreted as a special case of classical compactness; I would find this reassuring, though it would be more of a psychological advance than a technical one I think (unless it allows one to easily transfer a large number of additional theorems about compact sets, beyond the existence of extremisers, to the concentration-compact setting), and of course it would be nice to have a reasonably “concrete” description of the compactification (one should be adding things like formal superpositions of profiles that have been translated to be “infinitely far apart”). I played around a little with the semigroup structure of the Stone-Cech compactification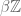 of the underlying group
of the underlying group 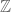 for a while but wasn’t able to get a clean and satisfactory compactification of E out of it.
for a while but wasn’t able to get a clean and satisfactory compactification of E out of it.
7 November, 2008 at 9:54 am
Pedro Lauridsen Ribeiro
Dear Prof. Tao,
I have a more or less complex question that may be related: as you have mentioned at the beginning of this post, the method of concentration compactness has been used in the context of dispersive PDE’s in order to exhibit solutions with a certain blow-up profile. This procedure can even be microlocalised, as shown by L. Tartar and P. Gerard, and fits well with the method of second microlocalisation, used to study the formation of caustics due to nonlinear concentration phenomena.
A curious feature of this method is that it seems to allow one to study oscillatory solutions beyond the formation of focal points and/or caustics. These are the main cause of failure of decay and Strichartz estimates for the linear wave equation with variable coefficients / curved spacetimes (as extensively discussed in recent works by Tataru, his collaborators, and many others). – after all, that’s how lensing works for _physical_ optics! On the physical side, we know from playing around with lenses and paper that the concentration is strongest when the caustic is a single, isolated point (only then can we burn the paper!), and it gets weaker and weaker as one moves away from the unfolding points of more complicated caustics. The “single point caustic” is, however, “structurally unstable”, since it gets lost when we move the lens by the slightest bit, unlike the more complicated one. Mathematically, such a procedure corresponds to perturbing the principal symbol. In curved spacetimes, isolated caustic points due to trapped geodesics (e.g. the photosphere in Schwarzschild spacetime, or the (whole) Einstein static universe) can completely kill any decay / Strichartz estimates if they occur in a more or less uniform fashion throughout spacetime, but also seem to be structurally unstable in the sense above. This leads to the following two questions:
1.) Could it be that, even for the _linear, variable-coefficient_ wave equation, one could find “intermediate” decay /Strichartz norms such that one could establish a “profile decomposition” that describes this weaker dispersion along structurally stable caustics, at least for a given normal form in Arnold’s classification?
2.) By assembling these profiles together for all normal forms, could we perhaps establish a “robust” version of decay / Strichartz estimates w.r.t. perturbations of the metric symbol that could be used for variable coefficient wave equations?
Many thanks in advance.
8 November, 2008 at 11:54 am
reader
Dear Prof.Tao,
i wonder is this idea of profile decomposition related to fourier linear bias?
if so, could you say something more about it. thanks
reader
9 November, 2008 at 5:19 pm
Terence Tao
Dear reader,
Well, there is a broad theme in several areas of analysis that an inverse theorem (that asserts the largeness of some norm or norm-like quantity implies the presence of a specific structure) implies a structure theorem (that asserts that arbitrary objects can be decomposed into a superposition of specific structures, plus an error of small norm). In the case of the concentration compactness result above, the inverse theorem is quite trivial: a function with large norm contains a large component concentrated at a point. But one could similarly start with, say, the inverse theorem that says that a function with large Gowers norm
norm contains a large component concentrated at a point. But one could similarly start with, say, the inverse theorem that says that a function with large Gowers norm 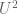 correlates with a Fourier character, and obtain an analogous concentration compactness result that would assert that a sequence of bounded (in
correlates with a Fourier character, and obtain an analogous concentration compactness result that would assert that a sequence of bounded (in  ) functions could be resolved into a superposition of frequency modulated profiles, plus an error with small
) functions could be resolved into a superposition of frequency modulated profiles, plus an error with small 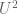 norm; this is close to certain “arithmetic regularity lemmas” that are already used in the additive combinatorics literature.
norm; this is close to certain “arithmetic regularity lemmas” that are already used in the additive combinatorics literature.
10 January, 2009 at 8:38 am
245B, notes 3: L^p spaces « What’s new
[…] Metric structure. We also want to tell whether two functions f, g in a function space V are “near together” or “far apart”. A typical way to do this is to impose a metric on the space . If both a norm and a vector space structure are available, there is an obvious way to do this: define the distance between two functions in to be . (This will be the only type of metric on function spaces encountered in this course. But there are some nonlinear function spaces of importance in nonlinear analysis (e.g. spaces of maps from one manifold to another) which have no vector space structure or norm, but still have a metric.) It is often important to know if the vector space is complete with respect to the given metric; this allows one to take limits of Cauchy sequences, and (with a norm and vector space structure) sum absolutely convergent series, as well as use some useful results from point set topology such as the Baire category theorem. All of these operations are of course vital in analysis. [Compactness would be an even better property than completeness to have, but function spaces unfortunately tend be non-compact in various rather nasty ways, although there are useful partial substitutes for compactness that are available, see e.g. this blog post of mine.] […]
21 April, 2009 at 8:16 pm
An inverse theorem for the bilinear L^2 Strichartz estimate for the wave equation « What’s new
[…] closely related to the theory of concentration compactness and profile decompositions; see this previous blog post of mine for a […]
29 November, 2010 at 12:00 pm
Concentration compactness via nonstandard analysis « What’s new
[…] property in infinite-dimensional spaces. One of these tools is concentration compactness, which was discussed previously on this blog. This can be viewed as a compromise between weak compactness (which is true in very general […]
4 August, 2011 at 6:53 pm
Localisation and compactness properties of the Navier-Stokes global regularity problem « What’s new
[…] translation symmetry that is available for the space . (Concentration compactness is discussed in these previous blog posts.) One then has to deal with sequences of data that are not strongly convergent, […]
27 July, 2012 at 7:42 am
Willie Wong
It appears that the link to “concentration compactness” that points to tosio.toronto… is broken. Does it point to the old dispersive wiki? the correct link probably should be wiki.math.toronto…
[Updated, thanks – T.]
18 January, 2013 at 2:06 am
Compactness in analysis | Shrinklemma
[…] Terence Tao talked about a toy model of concentrated compactness in one of his blogs. […]
8 November, 2018 at 12:35 pm
Debajyoti Choudhuri
” Analysing this, we see that all but one of the x_j must vanish, with the remaining x_j (say x_0) having norm 1″…this comment is to the end of the article. I was wondering as to why this should happen?. I presume there could several other x_j, the sum of whose norm yields 1. Can you please clear this doubt?
21 November, 2018 at 12:06 pm
Terence Tao
If there are some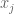 of norm strictly between 0 and 1, then
of norm strictly between 0 and 1, then  would be strictly less than
would be strictly less than  , and the above string of inequalities would give
, and the above string of inequalities would give 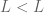 , which is absurd.
, which is absurd.