There are many situations in combinatorics in which one is running some sort of iteration algorithm to continually “improve” some object ; each loop of the algorithm replaces
with some better version
of itself, until some desired property of
is attained and the algorithm halts. In order for such arguments to yield a useful conclusion, it is often necessary that the algorithm halts in a finite amount of time, or (even better), in a bounded amount of time. (In general, one cannot use infinitary iteration tools, such as transfinite induction or Zorn’s lemma, in combinatorial settings, because the iteration processes used to improve some target object
often degrade some other finitary quantity
in the process, and an infinite iteration would then have the undesirable effect of making
infinite.)
A basic strategy to ensure termination of an algorithm is to exploit a monotonicity property, or more precisely to show that some key quantity keeps increasing (or keeps decreasing) with each loop of the algorithm, while simultaneously staying bounded. (Or, as the economist Herbert Stein was fond of saying, “If something cannot go on forever, it must stop.”)
Here are four common flavours of this monotonicity strategy:
- The mass increment argument. This is perhaps the most familiar way to ensure termination: make each improved object
“heavier” than the previous one
by some non-trivial amount (e.g. by ensuring that the cardinality of
is strictly greater than that of
, thus
). Dually, one can try to force the amount of “mass” remaining “outside” of
in some sense to decrease at every stage of the iteration. If there is a good upper bound on the “mass” of
that stays essentially fixed throughout the iteration process, and a lower bound on the mass increment at each stage, then the argument terminates. Many “greedy algorithm” arguments are of this type. The proof of the Hahn decomposition theorem in measure theory also falls into this category. The general strategy here is to keep looking for useful pieces of mass outside of
, and add them to
to form
, thus exploiting the additivity properties of mass. Eventually no further usable mass remains to be added (i.e.
is maximal in some
sense), and this should force some desirable property on
.
- The density increment argument. This is a variant of the mass increment argument, in which one increments the “density” of
rather than the “mass”. For instance,
might be contained in some ambient space
, and one seeks to improve
to
(and
to
) in such a way that the density of the new object in the new ambient space is better than that of the previous object (e.g.
for some
). On the other hand, the density of
is clearly bounded above by
. As long as one has a sufficiently good lower bound on the density increment at each stage, one can conclude an upper bound on the number of iterations in the algorithm. The prototypical example of this is Roth’s proof of his theorem that every set of integers of positive upper density contains an arithmetic progression of length three. The general strategy here is to keep looking for useful density fluctuations inside
, and then “zoom in” to a region of increased density by reducing
and
appropriately. Eventually no further usable density fluctuation remains (i.e.
is uniformly distributed), and this should force some desirable property on
.
- The energy increment argument. This is an “
” analogue of the “
“-based mass increment argument (or the “
“-based density increment argument), in which one seeks to increments the amount of “energy” that
captures from some reference object
, or (equivalently) to decrement the amount of energy of
which is still “orthogonal” to
. Here
and
are related somehow to a Hilbert space, and the energy involves the norm on that space. A classic example of this type of argument is the existence of orthogonal projections onto closed subspaces of a Hilbert space; this leads among other things to the construction of conditional expectation in measure theory, which then underlies a number of arguments in ergodic theory, as discussed for instance in this earlier blog post. Another basic example is the standard proof of the Szemerédi regularity lemma (where the “energy” is often referred to as the “index”). These examples are related; see this blog post for further discussion. The general strategy here is to keep looking for useful pieces of energy orthogonal to
, and add them to
to form
, thus exploiting square-additivity properties of energy, such as Pythagoras’ theorem. Eventually, no further usable energy outside of
remains to be added (i.e.
is maximal in some
sense), and this should force some desirable property on
.
- The rank reduction argument. Here, one seeks to make each new object
to have a lower “rank”, “dimension”, or “order” than the previous one. A classic example here is the proof of the linear algebra fact that given any finite set of vectors, there exists a linearly independent subset which spans the same subspace; the proof of the more general Steinitz exchange lemma is in the same spirit. The general strategy here is to keep looking for “collisions” or “dependencies” within
, and use them to collapse
to an object
of lower rank. Eventually, no further usable collisions within
remain, and this should force some desirable property on
.
Much of my own work in additive combinatorics relies heavily on at least one of these types of arguments (and, in some cases, on a nested combination of two or more of them). Many arguments in nonlinear partial differential equations also have a similar flavour, relying on various monotonicity formulae for solutions to such equations, though the objective in PDE is usually slightly different, in that one wants to keep control of a solution as one approaches a singularity (or as some time or space coordinate goes off to infinity), rather than to ensure termination of an algorithm. (On the other hand, many arguments in the theory of concentration compactness, which is used heavily in PDE, does have the same algorithm-terminating flavour as the combinatorial arguments; see this earlier blog post for more discussion.)
Recently, a new species of monotonicity argument was introduced by Moser, as the primary tool in his elegant new proof of the Lovász local lemma. This argument could be dubbed an entropy compression argument, and only applies to probabilistic algorithms which require a certain collection of random “bits” or other random choices as part of the input, thus each loop of the algorithm takes an object
(which may also have been generated randomly) and some portion of the random string
to (deterministically) create a better object
(and a shorter random string
, formed by throwing away those bits of
that were used in the loop). The key point is to design the algorithm to be partially reversible, in the sense that given
and
and some additional data
that logs the cumulative history of the algorithm up to this point, one can reconstruct
together with the remaining portion
not already contained in
. Thus, each stage of the argument compresses the information-theoretic content of the string
into the string
in a lossless fashion. However, a random variable such as
cannot be compressed losslessly into a string of expected size smaller than the Shannon entropy of that variable. Thus, if one has a good lower bound on the entropy of
, and if the length of
is significantly less than that of
(i.e. we need the marginal growth in the length of the history file
per iteration to be less than the marginal amount of randomness used per iteration), then there is a limit as to how many times the algorithm can be run, much as there is a limit as to how many times a random data file can be compressed before no further length reduction occurs.
It is interesting to compare this method with the ones discussed earlier. In the previous methods, the failure of the algorithm to halt led to a new iteration of the object which was “heavier”, “denser”, captured more “energy”, or “lower rank” than the previous instance of
. Here, the failure of the algorithm to halt leads to new information that can be used to “compress”
(or more precisely, the full state
) into a smaller amount of space. I don’t know yet of any application of this new type of termination strategy to the fields I work in, but one could imagine that it could eventually be of use (perhaps to show that solutions to PDE with sufficiently “random” initial data can avoid singularity formation?), so I thought I would discuss it here.
Below the fold I give a special case of Moser’s argument, based on a blog post of Lance Fortnow on this topic.
Rather than deal with the Lovász local lemma in full generality, I will follow Fortnow and work with a special case of this lemma involving the -satisfiability problem (in conjunctive normal form). Here, one is given a set of boolean variables
together with their negations
; we refer to the
variables and their negations collectively as literals. We fix an integer
, and define a (length
) clause to be a disjunction of
literals, for instance
is a clause of length three, which is true unless is false,
is true, and
is false. We define the support of a clause to be the set of variables that are involved in the clause, thus for instance
has support
. To avoid degeneracy we assume that no clause uses a variable more than once (or equivalently, all supports have cardinality exactly
), thus for instance we do not consider
or
to be clauses.
Note that the failure of a clause reveals complete information about all of the boolean variables in the support; this will be an important fact later on.
The -satisfiability problem is the following: given a set
of clauses of length
involving
boolean variables
, is there a way to assign truth values to each of the
, so that all of the clauses are simultaneously satisfied?
For general , this problem is easy for
(essentially equivalent to the problem of
-colouring a graph), but NP-complete for
(this is the famous Cook-Levin theorem). But the problem becomes simpler if one makes some more assumptions on the set
of clauses. For instance, if the clauses in
have disjoint supports, then they can be satisfied independently of each other, and so one easily has a positive answer to the satisfiability problem in this case. (Indeed, one only needs each clause in
to have one variable in its support that is disjoint from all the other supports in order to make this argument work.)
Now suppose that the clauses are not completely disjoint, but have a limited amount of overlap; thus most clauses in
have disjoint supports, but not all. With too much overlap, of course, one expects satisfability to fail (e.g. if
is the set of all length
clauses). But with a sufficiently small amount of overlap, one still has satisfiability:
Theorem 1 (Lovász local lemma, special case) Suppose that
is a set of length
clauses, such that the support of each clause
in
intersects at most
supports of clauses in
(including
itself), where
is a sufficiently large absolute constant. Then the clauses in
are simultaneously satisfiable.
One of the reasons that this result is powerful is that the bounds here are uniform in the number of variables. Apart from the loss of
, this result is sharp; consider for instance the set
of all
clauses with support
, which is clearly unsatisfiable.
The standard proof of this theorem proceeds by assigning each of the boolean variables
a truth value
independently at random (with each truth value occurring with an equal probability of
); then each of the clauses in
has a positive zero probability of holding (in fact, the probability is
). Furthermore, if
denotes the event that a clause
is satisfied, then the
are mostly independent of each other; indeed, each event
is independent of all but most
other events
. Applying the Lovász local lemma, one concludes that the
simultaneously hold with positive probability (if
is a little bit larger than
), and the claim follows.
The textbook proof of the Lovász local lemma is short but nonconstructive; in particular, it does not easily offer any quick way to compute an actual satisfying assignment for , only saying that such an assignment exists. Moser’s argument, by contrast, gives a simple and natural algorithm to locate such an assignment (and thus prove Theorem 1). (The constant
becomes
rather than
, although the
bound has since been recovered in a paper of Moser and Tardos.)
As with the usual proof, one begins by randomly assigning truth values to
; call this random assignment
. If
satisfied all the clauses in
, we would be done. However, it is likely that there will be some non-empty subset
of clauses in
which are not satisfied by
.
We would now like to modify in such a manner to reduce the number
of violated clauses. If, for instance, we could always find a modification
of
whose set
of violated clauses was strictly smaller than
(assuming of course that
is non-empty), then we could iterate and be done (this is basically a mass decrement argument). One obvious way to try to achieve this is to pick a clause
in
that is violated by
, and modify the values of
on the support of
to create a modified set
that satisfies
, which is easily accomplished; in fact, any non-trivial modification of
on the support will work here. In order to maximize the amount of entropy in the system (which is what one wants to do for an entropy compression argument), we will choose this modification of
randomly; in particular, we will use
fresh random bits to replace the
bits of
in the support of
. (By doing so, there is a small probability (
) that we in fact do not change
at all, but the argument is (very) slightly simpler if we do not bother to try to eliminate this case.)
If all the clauses had disjoint supports, then this strategy would work without difficulty. But when the supports are not disjoint, one has a problem: every time one modifies to “fix” a clause
by modifying the variables on the support of
, one may cause other clauses
whose supports overlap those of
to fail, thus potentially increasing the size of
by as much as
. One could then try fixing all the clauses which were broken by the first fix, but it appears that the number of clauses needed to repair could grow indefinitely with this procedure, and one might never terminate in a state in which all clauses are simultaneously satisfied.
The key observation of Moser, as alluded earlier, is that each failure of a clause for an assignment
reveals
bits of information about
, namely that the exact values that
assigns to the support of
. The plan is then to use each failure of a clause as a part of a compression protocol that compresses
(plus some other data) losslessly into a smaller amount of space. A crucial point is that at each stage of the process, the clause one is trying to fix is almost always going to be one that overlapped the clause that one had just previously fixed. Thus the total number of possibilities for each clause, given the previous clauses, is basically
, which requires only
bits of storage, compared with the
bits of entropy that have been eliminated. This is what is going to force the algorithm to terminate in finite time (with positive probability).
Let’s make the details more precise. We will need the following objects:
- A truth assignment
of
truth values
, which is initially assigned randomly, but which will be modified as the algorithm progresses;
- A long random string
of bits, from which we will make future random choices, with each random bit being removed from
as it is read.
We also need a recursive algorithm , which modifies the string
to satisfy a clause
in
(and, as a bonus, may also make
obey some other clauses in
that it did not previously satisfy). It is defined recursively:
- Step 1. If
already satisfies
, do nothing (i.e. leave
unchanged).
- Step 2. Otherwise, read off
random bits from
(thus shortening
by
bits), and use these to replace the
bits of
on the support of
in the obvious manner (ordering the support of
by some fixed ordering, and assigning the
bit from
to the
variable in the support for
).
- Step 3. Next, find all the clauses
in
whose supports intersect
, and which
now violates; this is a collection of at most
clauses, possibly including
itself. Order these clauses
in some arbitrary fashion, and then apply
to each such clause in turn. (Thus the original algorithm
is put “on hold” on some CPU stack while all the child processes
are executed; once all of the child processes are complete,
then terminates also.)
An easy induction shows that if terminates, then the resulting modification of
will satisfy
; and furthermore, any other clause
in
which was already satisfied by
before
was called, will continue to be satisfied by
after
is called. Thus,
can only serve to decrease the number of unsatisfied clauses
in
, and so one can fix all the clauses by calling
once for each clause in
– provided that these algorithms all terminate.
Each time Step 2 of the Fix algorithm is called, the assignment changes to a new assignment
, and the random string
changes to a shorter string
. Is this process reversible? Yes – provided that one knows what clause
was being fixed by this instance of the algorithm. Indeed, if
are known, then
can be recovered by changing the assignment of
on the support of
to the only set of choices that violates
, while
can be recovered from
by appending to
the bits of
on the support of
.
This type of reversibility does not seem very useful for an entropy compression argument, because while is shorter than
by
bits, it requires about
bits to store the clause
. So the map
is only a compression if
, which is not what is being assumed here (and in any case the satisfiability of
in the case
is trivial from the union bound).
The key trick is that while it does indeed take bits to store any given clause
, there is an economy of scale: after many recursive applications of the fix algorithm, the marginal amount of bits needed to store
drops to merely
, which is less than
if
is large enough, and which will therefore make the entropy compression argument work.
Let’s see why this is the case. Observe that the clauses for which the above algorithm
is called come in two categories. Firstly, there are those
which came from the original list
of failed clauses. Each of these will require
bits to store – but there are only
of them. Since
, the net amount of storage space required for these clauses is
at most. Actually, one can just store the subset
of
using
bits (one for each element of
, to record whether it lies in
or not).
Of more interest is the other category of clauses , in which
is called recursively from some previously invoked call
to the fix algorithm. But then
is one of the at most
clauses in
whose support intersects that of
. Thus one can encode
using
and a number between
and
, representing the position of
(with respect to some arbitrarily chosen fixed ordering of
) in the list of all clauses in
whose supports intersect that of
. Let us call this number the index of the call
.
Now imagine that while the Fix routine is called, a running log file (or history) of the routine is kept, which records
each time one of the original
calls
with
is invoked, and also records the index of any other call
made during the recursive procedure. Finally, we assume that this log file records a termination symbol whenever a
routine terminates. By performing a stack trace, one sees that whenever a Fix routine is called, the clause
that is being repaired by that routine can be deduced from an inspection of the log file
up to that point.
As a consequence, at any intermediate stage in the process of all these fix calls, the original state of the assignment and the random string of bits can be deduced from the current state
of these objects, plus the history
up to that point.
Now suppose for contradiction that is not satisfiable; thus the stack of fix calls can never completely terminate. We trace through this stack for
steps, where
is some large number to be chosen later. After these steps, the random string
has shortened by an amount of
; if we set
to initially have length
, then the string is now completely empty,
. On the other hand, the history
has size at most
, since it takes
bits to store the initial clauses in
,
bits to record all the instances when Step 1 occurs, and every subsequent call to Fix generates a
-bit number, plus possibly a termination symbol of size
. Thus we have a lossless compression algorithm
from
completely random bits to
bits (recall that
and
were chosen randomly, and independently of each other). But since
random bits cannot be compressed losslessly into any smaller space, we have the entropy bound
which leads to a contradiction if is large enough (and if
is larger than an absolute constant). This proves Theorem 1.
Remark 1 Observe that the above argument in fact gives an explicit bound on
, and with a small bit of additional effort, it can be converted into a probabilistic algorithm that (with high probability) computes a satisfying assignment for
in time polynomial in
and
.
Remark 2 One can replace the usage of randomness and Shannon entropy in the above argument with Kolmogorov complexity instead; thus, one sets
to be a string of
bits which cannot be computed by any algorithm of length
, the existence of which is guaranteed as soon as (1) is violated; the proof now becomes deterministic, except of course for the problem of building the high-complexity string, which by their definition can only be constructed quickly by probabilistic methods. This is the approach taken by Fortnow.

46 comments
Comments feed for this article
5 August, 2009 at 4:58 pm
harrison
The link to the Szemeredi regularity lemma is messed up (and I was just about to point out that it’s probably the most famous energy-increment argument in additive combinatorics, too!) [Corrected, thanks – T.]
Apart from that, wonderful exposition! The insight that the failure of an algorithm on X gives you information about X is, of course, nothing new (it underlies the monotonicity arguments as well as many, many others), but Moser’s result is probably the purest use of it I’ve seen.
5 August, 2009 at 5:48 pm
Emmanuel Kowalski
This is very interesting! I can’t help finding some analogy with the problem of constructing large primes, because the application of the Local Lemma seems to have the flavor of a lower-bound sieve argument (getting a probability for the intersection of the complements of events which are close to independent), and we can see the problem of explicit construction of primes as an algorithmic (as opposed to non-constructive) version of sieve…
5 August, 2009 at 7:10 pm
Anonymous
“If something cannot go on forever, it must stop.”
I think Markov should be referenced. See “Markov Principle” on wiki.
5 August, 2009 at 8:45 pm
oguz
Dear All,
I am doing my Ph.D. in probability theory and planning to deal with theoretical computer science too.
Could you please recommend me some introductory books, survey papers, web blogs in that field?
thanks
6 August, 2009 at 4:48 am
nh
Very nice exposition, thank you!
I believe that you can slightly improve that compression argument when it comes to determining the value of M. In fact, to store the initial set of unsatisfied clauses, you can just store one bit for each clause, for |S| bits, instead of O(|S| log |S|) bits.
I didn’t thoroughly check it, but I believe this gets you to the expected linear running time (as in Moser’s result) when you turn the compression argument into a probilistic algorithm.
6 August, 2009 at 9:00 am
Terence Tao
Hmm, heuristically this seems plausible, but even after storing the initial set T, I think one would need another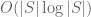 bits to update that set due to the fact that fixing one clause of T may well “accidentally” fix other clauses that were in the queue to be fixed also. It may be though that if one does this carefully enough, one can keep the total entropy cost down to
bits to update that set due to the fact that fixing one clause of T may well “accidentally” fix other clauses that were in the queue to be fixed also. It may be though that if one does this carefully enough, one can keep the total entropy cost down to 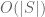 , but it would need to be checked.
, but it would need to be checked.
8 August, 2009 at 2:15 am
Heinrich
The algorithm is “accidentally” fixing many clauses already, namely whenever it reaches Step 1. The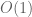 token in the history records this.
token in the history records this.
8 August, 2009 at 7:04 am
Terence Tao
Ah yes, you’re right, so we can eliminate the log after all. I’ve amended the text to reflect this.
6 August, 2009 at 8:53 am
Anonymous
This post is missing an expository tag. [Well spotted! Corrected, thanks – T.]
6 August, 2009 at 11:32 am
proaonuiq
In some cases the hard task is to prove that the monotonicity property, observed experimentally in some cases, holds for all the instances of the problem and it is straightforward to convert this property into a step of the searching algorithm…but the Moser argument seems great.
It is also great how you describe in your posts the hidden mathematical connections: infinite-finite, continuous-discrete, random-structured…
6 August, 2009 at 4:27 pm
Top Posts « WordPress.com
[…] Moser’s entropy compression argument There are many situations in combinatorics in which one is running some sort of iteration algorithm to continually ̶ […] […]
6 August, 2009 at 9:04 pm
Foster Boondoggle
I’m puzzled by the throwaway comment right at the beginning in parentheses, about not being able to use transfinite induction. Isn’t it tautological that an algorithm can’t possibly depend on AC? Any method that essentially uses AC cannot possibly have an algorithm (unless by algorithm one includes waving a wand and saying “presto” at a key point).
My layman’s understanding of AC is that it plays a role similar to that of an oracle in your previous post – you invoke it to “create” an object (such as a non-principal ultrafilter) that cannot be constructed or exhibited by means involving a finite or countable number of steps – otherwise it would be unnecessary.
6 August, 2009 at 9:56 pm
Qiaochu Yuan
You seem to be using “algorithm” to mean “terminating algorithm.” This isn’t the case; for example, there are situations in which we can give an algorithm that produces a sequence which one wants to converge to a point with desirable properties, but it can happen that in order to guarantee convergence we need to index the sequence by an ordinal larger than the natural numbers. Transfinite induction and Zorn’s lemma are tools we use to create “extra steps” to guarantee that our algorithm “terminates.”
6 August, 2009 at 10:02 pm
Foster Boondoggle
I don’t think I mean an algorithm that terminates – e.g., Newton’s method for finding $\sqrt{2}$ is an instance of an algorithm. But isn’t it essential to what we mean by $\it algorithm$ that it be amenable to execution? An algorithm that entails AC is, by hypothesis, $\it not$ executable.
7 August, 2009 at 6:34 am
Terence Tao
Algorithms which involve AC are, by definition, valid (or “executable”, if you will) algorithms in any mathematical universe in which AC holds, and in particular in any model of ZFC. (If one wishes to think algorithmically, one can think of AC as providing a ‘choice function’ oracle in one’s transfinite program. Other axioms of ZFC, such as the axiom of union, axiom of specification, and axiom of infinity, are also needed to set up the architecture needed to “run” a transfinite algorithm, in particular the theory of ordinals, but this is relatively straightforward; see these notes of mine.)
Of course, such an algorithm would not work as stated in the physical universe, but that is not the direct concern of pure mathematics, being instead a topic of computer science (and physics also, to some extent). In particular, transfinite algorithms are not covered by the Church-Turing thesis. (On the other hand, one can convert many (though not all) infinitary algorithms into finitary counterparts which would, in principle, run in the physical universe; see my earlier blog post for further discussion. Furthermore, the independence of AC from the other axioms can often be used to show that a mathematical result obtained using an AC-dependent algorithm, is also necessarily true in the absence of that axiom, even if the algorithm used to prove that result no longer “runs”.)
Thus, for instance, the standard greedy algorithm to locate a basis for an arbitrary vector space (which may be infinite dimensional) can be proven to succeed in any ZFC universe, thanks to Zorn’s lemma, just as Newton’s algorithm to obtain a root of a smooth function from a sufficiently accurate initial guess can be proven to succeed in any model of the reals which obeys the Dedekind completeness axiom (which is part of the standard axiomatisation of the reals, and holds for the standard model of the reals).
7 August, 2009 at 7:41 am
Foster Boondoggle
Thank you Terry. This has been bothering me ever since I saw a solution (by Stan Wagon) to the infinite version of the prisoners guessing each others’ hat colors which involved using a non-principal ultrafilter. (I still think his “solution” was bogus, since the problem statement didn’t mention that the prisoners had access to this choice-function oracle.)
31 July, 2021 at 2:32 am
andreaberdondini
Terence tao I would like to know your answer to this question.
If we roll a ten-sided die a thousand times, what is the average entropy of the generated sequence?
It seems a very easy question, there are 10^1000 possible combinations, each with its own entropy, we just need to take the average.
We get the following value H(X)med=0.9980.
For example, if I toss a coin 3 times I have 2^3=8 possible combinations, each with its own entropy, in this case, H(X)med is:
H(X)med=(H1(X)+H2(X)+H3(X)+H4(X)+H5(X)+H6(X)+H7(X)+H8(X))/8
But, if now we throw the dice once more and calculate the average entropy of 10% of the combinations with less entropy, we get a set equal to the previous 0.1*10^1001 =10^1000.
The entropy value thus obtained is H(X)med2=0.9964.
How can we choose between the two entropy values?
In practice, there are two points of view with which to observe the outcome of the throwing of the dice.
A good way may be to choose the entropy value which multiplied by the length of the sequence gives a smaller value.
0.998*1000=998
0.9964*1001=997.4
Therefore, we should choose the second entropy value.
If we choose the first entropy value, the encoder will take n outputs i.i.d. of the source and maps them on n(H(X)med), in the case of example n=1000.
By choosing the second entropy value, the encoder takes n outputs i.i.d. of the source and maps them to n2(H(X)med2) with n2> n. in the case of example n=1000 and n2=1001.
Starting from an apparently simple question, it is possible to arrive in a not simple situation where we can have different interpretations.
So, I repeat the starting question: If we roll a ten-sided die a thousand times what is the average entropy of the generated sequence?
8 August, 2009 at 2:35 am
Heinrich
Small typo just below inequality (1), “contradiction of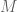 is large enough” should be “.. if
is large enough” should be “.. if 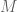 is …”.
is …”.
I am slightly confused about the wording surrounding (1). I take it you mean that inequality (1) holds when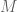 is large enough, but this would mean that we can compress completely random bits, a contradiction. I think the naming (1) an “entropy bound” is slightly misleading, or at least has mislead myself, in that (1) does not a priori estimate the entropy of
is large enough, but this would mean that we can compress completely random bits, a contradiction. I think the naming (1) an “entropy bound” is slightly misleading, or at least has mislead myself, in that (1) does not a priori estimate the entropy of  or that of
or that of  , but compares the two entropy estimates for large
, but compares the two entropy estimates for large 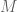 a posterior.
a posterior.
8 August, 2009 at 7:05 am
Terence Tao
Oops; I had the inequality (1) the wrong way around. (Both are true, which is where the contradiction comes from, but yes, the attribution was wrong.)
Thanks for the corrections!
8 August, 2009 at 11:13 am
Pietro Poggi-Corradini
Does the Lovasz local lemma have any connection with the central limit thm?
9 August, 2009 at 11:10 am
Mer
Hi,
I have a question some how related to this post. Suppose, we have a monotonically decreasing function and we want to find its fixed point, i.e., we have an iterative process with x_{n+1}=f(x_n). Now what is interesting to me is not the fixed point itself but the number of iteration to reach this fixed point given a specific starting point. Is there any way to guess/approximate the number of iterations needed? Even if there is not a general way of approximating the number of iterations for a general monotonic function, a hint to special cases is also appreciated.
Thanks
Mer
11 August, 2009 at 8:27 pm
Anonymous
Is it possible to control the $O(1)$ term more precisely and obtain a better bound on $C$, say make it arbitrarily small? Is the LLL argument tight for k-sat, i.e. is there an example of an unsatisfiable instance where each clause intersects at most $2^{k – \log_2 e}$ others?
12 August, 2009 at 1:19 pm
Anonymous
Dear Prof. Tao,
in Theorem 1, what do you mean by ” (including s itself)” ?
thanks [s was supposed to refer to the initial clause; I’ve adjusted the text a little to reflect this. -T.]
12 August, 2009 at 1:26 pm
Anonymous
”…it is likely that there will be some non-empty subset T of clauses in S which are not satisfied by S.”
the last S should be A.
thanks [Corrected, thanks – T.]
14 August, 2009 at 1:59 am
Math World | Moser’s entropy compression argument
[…] Here is the original post: Moser’s entropy compression argument […]
7 October, 2009 at 3:33 pm
piotr
Is the LLL argument tight for k-sat, i.e. is there an example of an unsatisfiable instance where each clause intersects at most $2^{k – \log_2 e}$ others?
Not exactly tight, but quite close. I think this is the best construction of k-sat instances that are unsatisfied and have have variable occurences:
@article{hoory:523,
author = {Shlomo Hoory and Stefan Szeider},
collaboration = {},
title = {A Note on Unsatisfiable k-CNF Formulas with Few Occurrences per Variable},
publisher = {SIAM},
year = {2006},
journal = {SIAM Journal on Discrete Mathematics},
volume = {20},
number = {2},
pages = {523-528},
keywords = {unsatisfiable CNF formulas; NP-completeness; occurrence of variables},
url = {http://link.aip.org/link/?SJD/20/523/1},
doi = {10.1137/S0895480104445745}
}
26 January, 2010 at 12:05 pm
Konstantinos Panagiotou
Thanks for the great post.
Do you think that this approach could be extended to show that any call to FIX terminates after, say, O(log S) recursive calls with high probability? This might not be interesting in the case of the local lemma, but I think it would be great for other applications: think for example of a dynamic data structure in an online setting, where we want to bound the maximum time that a query can take.
I’m not sure if the original proof of Moser gives this result, but Joel Spencer’s version of it gives it (if I recall correctly).
26 January, 2010 at 10:51 pm
Shiva
The bitmask representing the initially violate clause is precisely |S| long, so can O(|S|) be simplified to |S| in the last paragraph?
18 July, 2010 at 6:27 pm
AJ
Great exposition!!!
16 February, 2011 at 9:50 am
Seminare SS 2011 « ………. DOT's blog ……….
[…] Lovász Local Lemma: Hier und hier […]
14 June, 2011 at 12:53 pm
Tentative Plans and Belated Updates II | Combinatorics and more
[…] These are also good times for other areas of combinatorics. I described some startling developments (e.g., here and here and here) and there is more. There were a few posts (here and here) on the Cup Set Problem. Recently David Bateman and Nets Katz improved, after many years, the Roth-Meshulam bound. See these two posts on Gowers’s blog (I,II). Very general theorems discovered independently by David Conlon and Tim Gowers and by Matheas Schacht show that many theorems (such as Ramsey’s theorem or Turan’s theorem) continue to hold for substructures of sparse random sets. Louis Esperet, Frantisek Kardos, Andrew King, Daniel Kral, and Serguei Norine proved the Lovasz-Palmer conjecture. They showed that every cubic bridgeless graph G has at least perfect matchings. The concept of flag algebras, discovered by Rasborov, is an extremely useful tool for extremal set theory. It has led to solutions of several problems and seems to bring us close to a solution of Turan’s Conjecture (which we discussed here and here.) For example, it led to the solution by Hamed Hatami, Jan Hladký, Daniel Král, Serguei Norine, and Alexander Razborov of the question on the maximum number of pentagons in triangle-free graphs. Hamed Hatami found a structure theorem for Boolean functions with coarse thresholds w.r.t. small probabilities. This extends and sharpens results by Ehud Friedgut and Jean Bourgain. I finally caught up (thanks to Reshef Meir) with Moser-Tardos result giving a new algorithmic proof for Lovasz local lemma. Amazing! You can read about it here. […]
3 February, 2012 at 8:28 pm
How to measure a vector’s quality of having less negative entries. | Help me on math , homework, math activities
[…] iterative algorithm which continually improves some vector $mathbf{v}$. Borrowing expressions from Terry Tao’s blog, each loop of my algorithm replaces $mathbf{v}$ with some better version $mathbf{v}'$ of […]
12 February, 2012 at 11:36 am
How to measure a vector's quality of having less negative entries. | Q&A System
[…] iterative algorithm which continually improves some vector $mathbf{v}$. Borrowing expressions from Terry Tao’s blog, every loop of my algorithm replaces $mathbf{v}$ with some an exceptional offer better edition […]
26 April, 2012 at 3:33 am
ThankYou
Hi,
could you please check your code for the “entropy bound” again? I cannot see any formula between “…we have the entropy bound” and “which leads to a contradiction…”.
Thank You!
[Fixed, thanks – T.]
19 October, 2012 at 6:54 am
Surya
Dear Prof. Tao
Is there a way to see why the random improvements are producing an assignment even though the Lovasz Local Lemma seems to be capable of producing occurrence of extremely rare events. Randomised and local choices generally tend to work only when the event of interest occurs with significant probability.
Thank you.
19 October, 2012 at 7:52 am
Terence Tao
I would classify Moser’s algorithm as a semi-random method rather than a random method; the iterative modifications made are not intended to disperse the solution uniformly across the configuration space, but are deliberately engineered to move the proposed solution closer to a true solution by reducing the number of visible “local errors”. The randomness is mostly present to avoid getting stuck in some sort of local minimum (cf. annealing methods in variational problems), and of course is also crucial in the theoretical guarantee that a solution must eventually be detected with positive probability.
11 November, 2013 at 8:58 pm
tap1cse
Can you please clarify how that constant term becomes 3?
Thanks in advance.
22 December, 2014 at 6:42 pm
Quantum Lovasz Local Lemma | Pieces
[…] we sketch the core idea of the termination proof for Algorithm 1, and refer interested readers to Terence Tao’s blog post, which covers more […]
10 June, 2015 at 5:32 am
Quantum Lovasz Local Lemma | Pieces
[…] we sketch the core idea of the termination proof for Algorithm 1, and refer interested readers to Terence Tao’s blog post, which covers more detail. Notice that at each call to FIX, we have as input $latex {(R, A, […]
18 September, 2015 at 4:46 pm
The logarithmically averaged Chowla and Elliott conjectures for two-point correlations; the Erdos discrepancy problem | What's new
[…] reminiscent of the “entropy compression argument” of Moser and Tardos, discussed in this previous post). This argument, which is a simple consequence of the Shannon entropy inequalities, can be viewed […]
26 July, 2018 at 11:16 pm
D.S.
There is one additional somewhat critical detail missing in this proof. The encoder and decoder for the lossless compression has the formula (that is, the set S of clauses) “built into” it (for example, it needs to consult this to encode/decode some clause as the t-th neighbor of some other clause during a recursive call to Fix). This is not a problem, however, and can be handled in one of two ways: pay for it in the LHS of the key inequality (1) by throwing in an additional |S| k log n term, which will weaken the bound on M by a tiny bit; or (2) use a stronger version of the entropy compression bound asserting that even if the encoder/decoder has a fixed string of this length hardwired into it, n + Mk bits can’t be compressed to n + O(|S|) + M(k – C + O(1)) bits on average. (In the Fortnow version, this is captured elegantly if opaquely by writing “Fix a Kolmogorov random string x of length n+sk (random relative to φ, k, s, r, m and n) ” [I’m referring to the “relative to φ” part here].
7 December, 2019 at 7:58 am
Terence Tao
Yes, but no matter how many bits of deterministic information the encoder and decoder have access to, it is still not possible to losslessly encode random bits into
random bits into 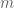 bits for any fixed
bits for any fixed 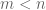 , simply because the number
, simply because the number 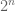 of possible values of the input exceeds the number
of possible values of the input exceeds the number  of the number of possible outputs, and no decoder can overcome the collision that is then forced by the pigeonhole principle regardless of how much deterministic information (independent of the input) that the decoder has access to.
of the number of possible outputs, and no decoder can overcome the collision that is then forced by the pigeonhole principle regardless of how much deterministic information (independent of the input) that the decoder has access to.
20 July, 2020 at 4:31 pm
The sunflower lemma via Shannon entropy | What's new
[…] The argument bears some resemblance to the “entropy compression method” discussed in this previous blog post; there may be a way to more explicitly express the argument below in terms of that method. (There […]
7 September, 2020 at 10:24 pm
Anonymous
Are there instances where these kind of monotonicity arguments are used to prove lower bounds?
12 April, 2021 at 1:50 pm
Typo?
The end of the paragraph starting with “Each time Step 2 of the Fix algorithm…” should be changed to “…bits of A’ on the support of s.”
[Corrected, thanks – T.]
19 May, 2021 at 3:04 pm
Entropy Estimation via Two Chains: Streamlining the Proof of the Sunflower Lemma – Theory Dish
[…] We need the following useful lemmas about Shannon entropy. We omit their proofs here as they can be found in Tao’s blog post, where many basic properties of Shannon entropy are also discussed. (We also highly recommend Tao’s other blog posts about Shannon entropy and the entropy compression argument.) […]