A large portion of analytic number theory is concerned with the distribution of number-theoretic sets such as the primes, or quadratic residues in a certain modulus. At a local level (e.g. on a short interval ), the behaviour of these sets may be quite irregular. However, in many cases one can understand the global behaviour of such sets on very large intervals, (e.g.
), with reasonable accuracy (particularly if one assumes powerful additional conjectures, such as the Riemann hypothesis and its generalisations). For instance, in the case of the primes, we have the prime number theorem, which asserts that the number of primes in a large interval
is asymptotically equal to
; in the case of quadratic residues modulo a prime
, it is clear that there are exactly
such residues in
. With elementary arguments, one can also count statistics such as the number of pairs of consecutive quadratic residues; and with the aid of deeper tools such as the Weil sum estimates, one can count more complex patterns in these residues also (e.g.
-point correlations).
One is often interested in converting this sort of “global” information on long intervals into “local” information on short intervals. If one is interested in the behaviour on a generic or average short interval, then the question is still essentially a global one, basically because one can view a long interval as an average of a long sequence of short intervals. (This does not mean that the problem is automatically easy, because not every global statistic about, say, the primes is understood. For instance, we do not know how to rigorously establish the conjectured asymptotic for the number of twin primes in a long interval
, and so we do not fully understand the local distribution of the primes in a typical short interval
.)
However, suppose that instead of understanding the average-case behaviour of short intervals, one wants to control the worst-case behaviour of such intervals (i.e. to establish bounds that hold for all short intervals, rather than most short intervals). Then it becomes substantially harder to convert global information to local information. In many cases one encounters a “square root barrier”, in which global information at scale (e.g. statistics on
) cannot be used to say anything non-trivial about a fixed (and possibly worst-case) short interval at scales
or below. (Here we ignore factors of
for simplicity.) The basic reason for this is that even randomly distributed sets in
(which are basically the most uniform type of global distribution one could hope for) exhibit random fluctuations of size
or so in their global statistics (as can be seen for instance from the central limit theorem). Because of this, one could take a random (or pseudorandom) subset of
and delete all the elements in a short interval of length
, without anything suspicious showing up on the global statistics level; the edited set still has essentially the same global statistics as the original set. On the other hand, the worst-case behaviour of this set on a short interval has been drastically altered.
One stark example of this arises when trying to control the largest gap between consecutive prime numbers in a large interval . There are convincing heuristics that suggest that this largest gap is of size
(Cramér’s conjecture). But even assuming the Riemann hypothesis, the best upper bound on this gap is only of size
, basically because of this square root barrier. This particular instance of the square root barrier is a significant obstruction to the current polymath project “Finding primes“.
On the other hand, in some cases one can use additional tricks to get past the square root barrier. The key point is that many number-theoretic sequences have special structure that distinguish them from being exactly like random sets. For instance, quadratic residues have the basic but fundamental property that the product of two quadratic residues is again a quadratic residue. One way to use this sort of structure to amplify bad behaviour in a single short interval into bad behaviour across many short intervals. Because of this amplification, one can sometimes get new worst-case bounds by tapping the average-case bounds.
In this post I would like to indicate a classical example of this type of amplification trick, namely Burgess’s bound on short character sums. To narrow the discussion, I would like to focus primarily on the following classical problem:
Problem 1 What are the best bounds one can place on the first quadratic non-residue
in the interval
for a large prime
?
(The first quadratic residue is, of course, ; the more interesting problem is the first quadratic non-residue.)
Probabilistic heuristics (presuming that each non-square integer has a 50-50 chance of being a quadratic residue) suggests that should have size
, and indeed Vinogradov conjectured that
for any
. Using the Pólya-Vinogradov inequality, one can get the bound
(and can improve it to
using smoothed sums); combining this with a sieve theory argument (exploiting the multiplicative nature of quadratic residues) one can boost this to
. Inserting Burgess’s amplification trick one can boost this to
for any
. Apart from refinements to the
factor, this bound has stood for five decades as the “world record” for this problem, which is a testament to the difficulty in breaching the square root barrier.
Note: in order not to obscure the presentation with technical details, I will be using asymptotic notation in a somewhat informal manner.
— 1. Character sums —
To approach the problem, we begin by fixing the large prime and introducing the Legendre symbol
, defined to equal
when
is divisible by
,
when
is an invertible quadratic residue modulo
, and
when
is an invertible quadratic non-residue modulo
. Thus, for instance,
for all
. One of the main reasons one wants to work with the function
is that it enjoys two easily verified properties:
-
is periodic with period
.
- One has the total multiplicativity property
for all integers
.
In the jargon of number theory, is a Dirichlet character with conductor
. Another important property of this character is of course the law of quadratic reciprocity, but this law is more important for the average-case behaviour in
, whereas we are concerned here with the worst-case behaviour in
, and so we will not actually use this law here.
An obvious way to control is via the character sum
From the triangle inequality, we see that this sum has magnitude at most . If we can then obtain a non-trivial bound of the form
for some , this forces the existence of a quadratic nonresidue less than or equal to
, thus
. So one approach to the problem is to bound the character sum (1).
As there are just as many residues as non-residues, the sum (1) is periodic with period and we obtain a trivial bound of
for the magnitude of the sum. One can achieve a non-trivial bound by Fourier analysis. One can expand
where are the Fourier coefficients of
:
As there are just as many quadratic residues as non-residues, , so we may drop the
term. From summing the geometric series we see that
where is the distance from
to the nearest integer (
or
); inserting these bounds into (1) and summing what is essentially a harmonic series in
we obtain
Now, how big is ? Taking absolute values, we get a bound of
, but this gives us something worse than the trivial bound. To do better, we use the Plancherel identity
which tells us that
This tells us that is small on the average, but does not immediately tell us anything new about the worst-case behaviour of
, which is what we need here. But now we use the multiplicative structure of
to relate average-case and worst-case behaviour. Note that if
is coprime to
, then
is a scalar multiple of
by a quantity
of magnitude
; taking Fourier transforms, this implies that
and
also differ by this factor. In particular,
. As
was arbitrary, we thus see that
is constant for all
coprime to
; in other words, the worst case is the same as the average case. Combining this with the Plancherel bound one obtains
, leading to the Pólya-Vinogradov inequality
(In fact, a more careful computation reveals the slightly sharper bound ; this is non-trivial for
.)
Remark 1 Up to logarithmic factors, this is consistent with what one would expect if
fluctuated like a random sign pattern (at least for
comparable to
; for smaller values of
, one expects instead a bound of the form
, up to logarithmic factors). It is conjectured that the
factor can be replaced with a
factor, which would be consistent with the random fluctuation model and is best possible; this is known for GRH, but unconditionally the Pólya-Vinogradov inequality is still the best known. (See however this paper of Granville and Soundararajan for an improvement for non-quadratic characters
.)
A direct application of the Pólya-Vinogradov inequality gives the bound . One can get rid of the logarithmic factor (which comes from the harmonic series arising from (3)) by replacing the sharp cutoff
by a smoother sum, which has a better behaved Fourier transform. But one can do better still by exploiting the multiplicativity of
again, by the following trick of Vinogradov. Observe that not only does one have
for all
, but also
for any
which is
-smooth, i.e. is the product of integers less than
. So even if
is significantly less than
, one can show that the sum (1) is large if the majority of integers less than
are
-smooth.
Since every integer less than
is either
-smooth (in which case
), or divisible by a prime
between
and
(in which case
is at least
), we obtain the lower bound
Clearly, and
. The total number of primes less than
is
by the prime number theorem, thus
Using the classical asymptotic for some absolute constant
(which basically follows from the prime number theorem, but also has an elementary proof), we conclude that
If for some fixed
, then the expression in brackets is bounded away from zero for
large; in particular, this is incompatible with (2) for
large enough. As a consequence, we see that if we have a bound of the form (2), then we can conclude
for all
; in particular, from the Pólya-Vinogradov inequality one has
for all , or equivalently that
. (By being a bit more careful, one can refine this to
.)
Remark 2 The estimates on the Gauss-type sums
are sharp; nevertheless, they fail to penetrate the square root barrier in the sense that no non-trivial estimates are provided below the scale
. One can also see this barrier using the Poisson summation formula, which basically gives a formula that (very roughly) takes the form
for any
, and is basically the limit of what one can say about character sums using Fourier analysis alone. In particular, we see that the Pólya-Vinogradov bound is basically the Poisson dual of the trivial bound. The scale
is the crossing point where Poisson summation does not achieve any non-trivial modification of the scale parameter.
— 2. Average-case bounds —
The Pólya-Vinogradov bound establishes a non-trivial estimate (1) for significantly larger than
. We are interested in extending (1) to shorter intervals.
Before we address this issue for a fixed interval , we first study the average-case bound on short character sums. Fix a short length
, and consider the shifted sum
where is a parameter. The analogue of (1) for such intervals would be
For very small (e.g.
for some small
), we do not know how to establish (5) for all
; but we can at least establish (5) for almost all
, with only about
exceptions (here we see the square root barrier again!).
More precisely, we will establish the moment estimates
for any positive even integer . If
is not too tiny, say
for some
, then by applying (6) for a sufficiently large
and using Chebyshev’s inequality (or Markov’s inequality), we see (for any given
) that one has the non-trivial bound
for all but at most values of
.
To see why (6) is true, let us just consider the easiest case . Squaring both sides, we expand (6) as
We can write as
. Writing
, and using the periodicity of
, we can rewrite the left-hand side as
where we have abused notation and identified the finite field with
.
For , the inner average is
. For
non-zero, we claim the bound
which is consistent with (and is in fact slightly stronger than) what one would get if was a random sign pattern; assuming this bound gives (6) for
as required.
The bound (7) can be established by quite elementary means (as it comes down to counting points on the hyperbola , which can be done by transforming the hyperbola to be rectangular), but for larger values of
we will need the more general estimate
whenever is a polynomial over
of degree
which is not a constant multiple of a perfect square; this can be easily seen to give (6) for general
.
An equivalent form of (8) is that the hyperelliptic curve
contains points. This fact follows from a general theorem of Weil establishing the Riemann hypothesis for curves over function fields, but can also be deduced by a more elementary argument of Stepanov, using the polynomial method, which we now give here. (This arrangement of the argument is based on the exposition in the book by Iwaniec and Kowalski.)
By translating the variable we may assume that
is non-zero. The key lemma is the following. Assume
large, and take
to be an integer comparable to
(other values of this parameter are possible, but this is the optimal choice). All polynomials
are understood to be over the field
(i.e. they lie in the polynomial ring
), although indeterminate variables
need not lie in this field.
Lemma 2 There exists a non-zero polynomial
of one indeterminate variable
over
of degree at most
which vanishes to order at least
at every point
for which
is a quadratic residue.
Note from the factor theorem that can vanish to order at least
at at most
points, and so we see that
is an invertible quadratic residue for at most
values of
. Multiplying
by a quadratic non-residue and running the same argument, we also see that
is an invertible quadratic non-residue for at most
values of
, and (8) (or the asymptotic for the number of points in (9)) follows.
We now prove the lemma. The polynomial will be chosen to be of the form
where are polynomials of degree at most
in
, and degree at most
in
, where
is a large constant (depending on
) to be chosen later (these parameters have been optimised for the argument that follows). Since
has degree at most
, such a
will have degree
as required. We claim (for suitable choices of ) that
- (a) The degrees are small enough that
is a non-zero polynomial whenever
are non-zero polynomials; and
- (b) The degrees are large enough that there exists a non-trivial choice of
and
that
vanishes to order at least
whenever
is such that
is a quadratic residue.
Claims (a) and (b) together establish the lemma.
We first verify (a). We can cancel off the initial factor, so that we need to show that
does not vanish when at least one of
is not vanishing. We may assume that
are not both divisible by
, since we could cancel out a common factor of
otherwise.
Suppose for contradiction that the polynomial vanished, which implies that
modulo
. Squaring and multiplying by
, we see that
But over and modulo
,
by Fermat’s little theorem. Observe that
and
both have degree at most
, and so we can remove the
modulus and conclude that
over
. But this implies (by the fundamental theorem of arithmetic for
) that
is a constant multiple of a square, a contradiction. (Recall that
is non-zero, and that
and
are not both zero.)
Now we prove (b). Let be such that
is a quadratic residue, thus
by Fermat’s little theorem. To get vanishing to order
, we need
for all . (Of course, we cannot define derivatives using limits and Newton quotients in this finite characteristic setting, but we can still define derivatives of polynomials formally, thus for instance
, and enjoy all the usual rules of calculus, such as the product rule and chain rule.)
Over , the polynomial
has derivative zero. If we then compute the derivative in (10) using many applications of the product and chain rule, we see that the left-hand side of (10) can be expressed in the form
where are polynomials of degree at most
in
and at most
in
, whose coefficients depend in some linear fashion on the coefficients of
and
. (The exact nature of this linear relationship will depend on
, but this will not concern us.) Since we only need to evaluate this expression when
and
(by Fermat’s little theorem), we thus see that we can verify (10) provided that the polynomial
vanishes identically. This is a polynomial of degree at most
and there are possible values of
, so this leads to
linear constraints on the coefficients of and
to satisfy. On the other hand, the total number of these coefficients is
For large enough, there are more coefficients than constraints, and so one can find a non-trivial choice of coefficients obeying the constraints (10), and (b) follows.
Remark 3 If one optimises all the constants here, one gets an upper bound of basically
for the deviation in the number of points in (9). This is only a little worse than the sharp bound of
given from Weil’s theorem, where
is the genus; however, it is possible to boost the former bound to the latter by using a version of the tensor power trick (generalising
to
and then letting
) combined with the theory of Artin L-functions and the Riemann-Roch theorem. This is (very briefly!) sketched in the Tricki article on the tensor power trick.
Remark 4 Once again, the global estimate (8) is very sharp, but cannot penetrate below the square root barrier, in that one is allowed to have about
exceptional values of
for which no cancellation exists. One expects that these exceptional values of
in fact do not exist, but we do not know how to do this unless
is larger than
(so that the Burgess bounds apply).
— 3. The Burgess bound —
The average case bounds in the previous section give an alternate demonstration of a non-trivial estimate (1) for , which is just a bit weaker than what the Pólya-Vinogradov inequality gives. Indeed, if (1) failed for such an
, thus
then by taking a small (e.g.
) and covering
by intervals of length
, we see (from a first moment method argument) that
for a positive fraction of the in
. But this contradicts the results of the previous section.
Burgess observed that by exploiting the multiplicativity of one last time to amplify the above argument, one can extend the range for which (1) can be proved from
to also cover the range
. The idea is not to cover
by intervals of length
, but rather by arithmetic progressions
of length
, where
and
. Another application of the first moment method then shows that
for a positive fraction of the in
and
in
(i.e.
such pairs
).
For technical reasons, it will be inconvenient if and
have too large of a common factor, so we pause to remove this possibility. Observe that for any
, the number of pairs
which have
as a common factor is
. As
is convergent, we may thus remove those pairs which have too large of a common factor, and assume that all pairs
have common factor
at most (so are “almost coprime”).
Now we exploit the multiplicativity of to write
as
, where
is a residue which is equal to
mod
. Dividing out by
, we conclude that
for pairs
.
Now for a key observation: the values of
arising from the pairs
are mostly disjoint. Indeed, suppose that two pairs
generated the same value of
, thus
. This implies that
. Since
, we see that
do not exceed
, so we may remove the modulus and conclude that
. But since we are assuming that
and
are almost coprime, we see that for each
there are at most
values of
for which
. So the
‘s here only overlap with multiplicity
, and we conclude that (11) holds for
values of
. But comparing this with the previous section, we obtain a contradiction unless
. Setting
to be a sufficiently small power of
, we obtain Burgess’s result that (1) holds for
for any fixed
.
Combining Burgess’s estimate with Vinogradov’s sieving trick we conclude the bound for all
, which is the best bound known today on the least quadratic non-residue except for refinements of the
error term.
Remark 5 There are many generalisations of this result, for instance to more general characters (with possibly composite conductor), or to shifted sums (4). However, the
type exponent has not been improved except with the assistance of powerful conjectures such as the generalised Riemann hypothesis.

27 comments
Comments feed for this article
18 August, 2009 at 5:36 pm
Joshua Zelinsky
“…but also ${\chi(n) = +1}$ for any $n$ which is $n_p$-smooth, i.e. is the product of integers less than or equal to $n_p$.” Shouldn’t that be $n_p -1$ smooth? [Corrected, thanks – T.]
19 August, 2009 at 3:38 am
charav
Professor Tao,
how we define a number-theoretic set?
Thanks for your time,
Christian
19 August, 2009 at 11:46 am
Terence Tao
By “number-theoretic set”, I simply mean a set which is of interest to number-theorists.
19 August, 2009 at 10:44 am
Gil Kalai
Some look on amplification in various areas of science and in tcs can be found in these two posts of Dick Lipton http://rjlipton.wordpress.com/2009/08/10/the-role-of-amplifiers-in-science/
http://rjlipton.wordpress.com/2009/08/13/amplifying-on-the-pcr-amplifier/
20 August, 2009 at 2:04 pm
K
I think the bound in (3) should be rather than
rather than  . [Corrected, thanks. -T]
. [Corrected, thanks. -T]
21 August, 2009 at 1:54 pm
Efthymios Sofos
There exists an elementary argument which shows the inequality
 . Defining an integer m by
. Defining an integer m by
 , we deduce that
, we deduce that 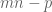 lies between 0 and n.
lies between 0 and n.
By the definition of n, m is not a quadratic residue, therefore
which yields the stated inequality.
24 August, 2009 at 11:43 pm
RK
In a different direction, one can look at this problem on average over the prime p, using the large sieve. Fix . Linnik showed that the number of primes
. Linnik showed that the number of primes  with
with 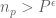 is bounded.
is bounded.
7 September, 2009 at 9:31 am
Boris
That is a very nice explanation of Stepanov’s argument. The trick of getting the extra variables by using the Frobenius map x|->x^p is really cool. It is similar to Thue’s trick from the proof of his famous result on the Diophantine approximations to algebraic numbers, where instead of the exact equality x=x^p, that is used here, he used two very good approximations to the same algebraic number.
A request: can you please increase the size of the images you use for mathematical equations. Currently, a single letter is 7px by 7px, which is really hard on the eyes. Since the images are scalar, scaling these tiny letters up yields images that are even more straining on the eyes. Thank you.
29 September, 2009 at 7:56 am
other
Bourgain has recently found many ways around the square root barrier; see:
1. Bourgain-Glibichuk-Konyagin, Bourgain-Chang: character sums over multiplicative groups
2. Bourgain: 2-source extractors
3. Bourgain: affine extractors
These are all based on the sum-product theorem.
30 September, 2009 at 2:26 am
Seva
Dear Terry,
Could you indicate the exact form of the identity you mention in Remark 2?
As a more rhetorical question, I wonder whether it is possible to improve
 for
for  with some
with some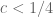 . Using Vinogradov's trick, one would automatically
. Using Vinogradov's trick, one would automatically in the least quadratic
in the least quadratic
Burgess’ result showing that, for some smoothening function $\psi$, we have
constant
improve then the exponent
non-residue estimate.
Several tiny corrections on this occasion. "Consecutive pairs" in the first
 ; fortunately, there is an easy fix-up. For part (b), to get
; fortunately, there is an easy fix-up. For part (b), to get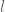 it suffices for (10) to hold for all
it suffices for (10) to hold for all 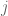
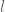 .
.
paragraph should be "pairs of consecutive"; to count such pairs one does not
need Weil or anything that deep, this goes by a very simple computation.
Similarly, one does not need Chebyshev's inequality (whatever it means in
this context) to derive conclusions from (6), this follows by "plain Markov".
For the proof of Lemma 2, part (a), an issue to address is the case where
vanishing of order
strictly less than
30 September, 2009 at 4:06 pm
Terence Tao
Thanks for the corrections!
Regarding Remark 2, the Fourier transform of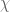 is (up to a constant phase)
is (up to a constant phase)  , hence by Parseval
, hence by Parseval 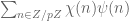 is a constant phase times
is a constant phase times  (I may have dropped a conjugation sign here, but it is not particularly relevant). If one chooses
(I may have dropped a conjugation sign here, but it is not particularly relevant). If one chooses 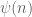 to be a smooth function adapted to the interval
to be a smooth function adapted to the interval 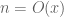 , then its Fourier transform will be mostly adapted to the interval
, then its Fourier transform will be mostly adapted to the interval  by the uncertainty principle, which leads to the heuristic relationship indicated in the text.
by the uncertainty principle, which leads to the heuristic relationship indicated in the text.
In harmonic analysis, Chebyshev’s inequality is often used to refer to the L^p version of Markov’s inequality (rather than just the L^2 version, which is the probability theorist’s version). I’ve now referenced both here.
Smoothing the sum can’t hurt, but in this particular case I don’t think it helps either. The sum from 1 to H in the Burgess argument ultimately just gets summed in absolute value, so smoothing this sum doesn’t really make it much smaller (there is no cancellation from oscillation to exploit, e.g. from Fourier analysis, which is the place where smoothing really helps.)
17 December, 2009 at 8:03 pm
Math websites falling into disuse? « What Is Research?
[…] Tricki also hasn’t been mentioned on Gowers’ blog since June 25, 2009 and on Terence Tao’s blog since August 2009. […]
1 August, 2010 at 12:45 pm
Theorem 33: the size of Gauss sums « Theorem of the week
[…] difficult to say precise things about the distribution of the quadratic residues (Tao has a nice post about some ideas about this), but this evaluation of the Gauss sum gives some information that […]
15 March, 2011 at 8:55 am
Sungjin Kim
Dear Professor Tao,
If chi is a Legendre symbol, (7) follows easily by replacing (n/p) by (n*/p). Even we get strong result, the sum (7) becomes -1. Also, the n_p << sqrt (p) bound can be obtained by much simpler way, it is in
http://number.subwiki.org/wiki/Smallest_quadratic_nonresidue_is_less_than_square_root_plus_one
Sincerely,
Sungjin Kim
7 July, 2011 at 10:52 am
On the number of solutions to 4/p = 1/n_1 + 1/n_2 + 1/n_3 « What’s new
[…] in which one or two of the are divisible by , with the other denominators being coprime to . (Of course, one can still get representations of by starting with a representation of and dividing by , but such representations are is not of the above form.) This shows that any attempt to establish the Erdös-Straus conjecture by manually constructing as a function of must involve a technique which breaks down if is replaced by (for instance, this rules out any approach based on using polynomial combinations of and dividing into cases based on residue classes of in small moduli). Part of the problem here is that we do not have good bounds that prevent a prime from “spoofing” a perfect square to all small moduli (say, to all moduli less than a small power of ); this problem is closely related (via quadratic reciprocity) to Vinogradov’s conjecture on the least quadratic nonresidue, discussed in this previous blog post. […]
8 July, 2011 at 4:59 am
Ian M.
In the line following equation (2), you write quadratic residue where I think you mean quadratic nonresidue. [Corrected, thanks – T.]
30 September, 2011 at 5:41 am
Jack D'Aurizio
What is known about the short sum![S=\sum_{p\in [q^{D/C},q^D]}\frac{\chi(p)}{p}](https://s0.wp.com/latex.php?latex=S%3D%5Csum_%7Bp%5Cin+%5Bq%5E%7BD%2FC%7D%2Cq%5ED%5D%7D%5Cfrac%7B%5Cchi%28p%29%7D%7Bp%7D&bg=ffffff&fg=545454&s=0&c=20201002) where
where  is a big prime,
is a big prime, 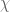 is the nonprincipal real character modulus
is the nonprincipal real character modulus  ,
,  is a real number a little bigger than
is a real number a little bigger than  and
and  ?
?
If was
was  (or even bounded by a small constant), there would be significant improvements in the Vinogradov’s amplification trick. However,
(or even bounded by a small constant), there would be significant improvements in the Vinogradov’s amplification trick. However,  is rather too short…
is rather too short…![J=[q^{D/C},q^D]\cap\mathcal{P}](https://s0.wp.com/latex.php?latex=J%3D%5Bq%5E%7BD%2FC%7D%2Cq%5ED%5D%5Ccap%5Cmathcal%7BP%7D&bg=ffffff&fg=545454&s=0&c=20201002) , one has
, one has
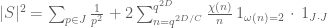
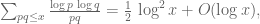
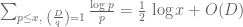
 ?
?
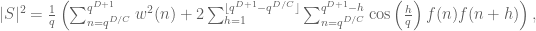
 .
. has mean zero on intervals of length
has mean zero on intervals of length  , and
, and  is relatively small and supported on q-smooth numbers. However, reasonable bounds seem very hard to achieve also in this case, since there are a huge number of sums, and the least of them have too few terms to hope in some cancellation.
is relatively small and supported on q-smooth numbers. However, reasonable bounds seem very hard to achieve also in this case, since there are a huge number of sums, and the least of them have too few terms to hope in some cancellation.

 . Again, by expressing character values as Gauss sums and by switching the order of summation,
. Again, by expressing character values as Gauss sums and by switching the order of summation,
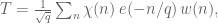

 ), almost-multiplicative weight-function, supported on q-smooth numbers and
), almost-multiplicative weight-function, supported on q-smooth numbers and

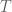 by Poisson summation, maybe using the results of Maier, De La Breteche and Tenenbaum on exponential sums over smooth numbers?
by Poisson summation, maybe using the results of Maier, De La Breteche and Tenenbaum on exponential sums over smooth numbers?
By naming
that is slighly larger and supported on almost primes: is it possible to apply some weaker version of the Selberg formulas
in the unlucky case
In alternative, it is possible to express every value of the character as a Gauss sum and use Weyl difference method to state:
where
Here
As a third way, one could try to deal with
that exhibits a strong connection with
one has
where
is a small (
is a Gauss sum on intervals of length q. Is it possible to bound
elianto84@gmail.com
University of Pisa
30 September, 2011 at 6:11 am
Jack D'Aurizio
The problem of bounding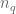 , the least quadratic non-residue modulus, without assuming GRH, is indeed very challenging.
, the least quadratic non-residue modulus, without assuming GRH, is indeed very challenging.
I’m asking myself, too, if there is a way to deeper exploit quadratic reciprocity.
By assuming the independence of the values taken by the Legendre symbol modulus q over primes, one would expect to have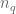 bounded by some (potentially huge) power of
bounded by some (potentially huge) power of  .
.
Moreover, if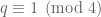 and, for some prime
and, for some prime  ,
,
 , then the prime number
, then the prime number  is a quadratic non-residue modulus q.
is a quadratic non-residue modulus q.
Is there a way to exploit the Lovasz Local Lemma in the last setting?
31 August, 2012 at 5:02 pm
The Lang-Weil bound « What’s new
[…] for plane curves. For hyper-elliptic curves, an elementary proof (due to Stepanov) is discussed in this previous post. For general plane curves, the first proof was by Weil (leading to his famous Weil conjectures); […]
22 June, 2013 at 7:39 am
Bounding short exponential sums on smooth moduli via Weyl differencing | What's new
[…] any fixed integer , assuming that is square-free (for simplicity) and of polynomial size; see this previous post for a discussion of the Burgess argument. This is non-trivial for as small as […]
27 October, 2014 at 9:22 pm
The Elliott-Halberstam conjecture implies the Vinogradov least quadratic nonresidue conjecture | What's new
[…] any fixed . See this previous post for a proof of these […]
8 February, 2016 at 12:50 pm
Anonymous
I don’t really understand the second half of this:
“Note that if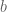 is coprime to
is coprime to 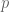 , then
, then  is a scalar multiple of
is a scalar multiple of 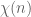 by a quantity
by a quantity  of magnitude
of magnitude 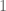 ; taking Fourier transforms, this implies that
; taking Fourier transforms, this implies that  and
and 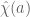 also differ by this factor. “
also differ by this factor. “
8 February, 2016 at 8:38 pm
Terence Tao
If is the Fourier transform of
is the Fourier transform of 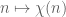 , then
, then  is the Fourier transform of
is the Fourier transform of 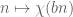 , as can be seen by a simple change of variables
, as can be seen by a simple change of variables  .
.
23 September, 2016 at 10:19 pm
kodlu
Could you please give a reference to the generalisation of the Burgess bound to shifted sums as in (4)?
24 September, 2016 at 7:35 am
Terence Tao
See e.g. Theorem 12.6 of Iwaniec-Kowalski.
24 April, 2018 at 8:10 am
On the Cramér-Granville Conjecture and finding prime pairs whose difference is 666 BootMath
[…] The least quadratic nonresidue, and the square root barrier […]
9 May, 2018 at 11:13 am
Breaking the Square root Barrier via the Burgess Bound | George Shakan
[…] analytic number theory and such a result would have wide applications. For instance, it would solve the Vinogradov least square problem. It would also have implications to sub–convexity bounds of –fucntions, […]