Let be a finite field, with algebraic closure
, and let
be an (affine) algebraic variety defined over
, by which I mean a set of the form
for some ambient dimension , and some finite number of polynomials
. In order to reduce the number of subscripts later on, let us say that
has complexity at most
if
,
, and the degrees of the
are all less than or equal to
. Note that we do not require at this stage that
be irreducible (i.e. not the union of two strictly smaller varieties), or defined over
, though we will often specialise to these cases later in this post. (Also, everything said here can also be applied with almost no changes to projective varieties, but we will stick with affine varieties for sake of concreteness.)
One can consider two crude measures of how “big” the variety is. The first measure, which is algebraic geometric in nature, is the dimension
of the variety
, which is an integer between
and
(or, depending on convention,
,
, or undefined, if
is empty) that can be defined in a large number of ways (e.g. it is the largest
for which the generic linear projection from
to
is dominant, or the smallest
for which the intersection with a generic codimension
subspace is non-empty). The second measure, which is number-theoretic in nature, is the number
of
-points of
, i.e. points
in
all of whose coefficients lie in the finite field, or equivalently the number of solutions to the system of equations
for
with variables
in
.
These two measures are linked together in a number of ways. For instance, we have the basic Schwarz-Zippel type bound (which, in this qualitative form, goes back at least to Lemma 1 of the work of Lang and Weil in 1954).
Lemma 1 (Schwarz-Zippel type bound) Let
be a variety of complexity at most
. Then we have
.
Proof: (Sketch) For the purposes of exposition, we will not carefully track the dependencies of implied constants on the complexity , instead simply assuming that all of these quantities remain controlled throughout the argument. (If one wished, one could obtain ineffective bounds on these quantities by an ultralimit argument, as discussed in this previous post, or equivalently by moving everything over to a nonstandard analysis framework; one could also obtain such uniformity using the machinery of schemes.)
We argue by induction on the ambient dimension of the variety
. The
case is trivial, so suppose
and that the claim has already been proven for
. By breaking up
into irreducible components we may assume that
is irreducible (this requires some control on the number and complexity of these components, but this is available, as discussed in this previous post). For each
, the fibre
is either one-dimensional (and thus all of
) or zero-dimensional. In the latter case, one has
points in the fibre from the fundamental theorem of algebra (indeed one has a bound of
in this case), and
lives in the projection of
to
, which is a variety of dimension at most
and controlled complexity, so the contribution of this case is acceptable from the induction hypothesis. In the former case, the fibre contributes
-points, but
lies in a variety in
of dimension at most
(since otherwise
would contain a subvariety of dimension at least
, which is absurd) and controlled complexity, and so the contribution of this case is also acceptable from the induction hypothesis.
One can improve the bound on the implied constant to be linear in the degree of (see e.g. Claim 7.2 of this paper of Dvir, Kollar, and Lovett, or Lemma A.3 of this paper of Ellenberg, Oberlin, and myself), but we will not be concerned with these improvements here.
Without further hypotheses on , the above upper bound is sharp (except for improvements in the implied constants). For instance, the variety
where are distict, is the union of
distinct hyperplanes of dimension
, with
and complexity
; similar examples can easily be concocted for other choices of
. In the other direction, there is also no non-trivial lower bound for
without further hypotheses on
. For a trivial example, if
is an element of
that does not lie in
, then the hyperplane
clearly has no -points whatsoever, despite being a
-dimensional variety in
of complexity
. For a slightly less non-trivial example, if
is an element of
that is not a quadratic residue, then the variety
which is the union of two hyperplanes, still has no -points, even though this time the variety is defined over
instead of
(by which we mean that the defining polynomial(s) have all of their coefficients in
). There is however the important Lang-Weil bound that allows for a much better estimate as long as
is both defined over
and irreducible:
Theorem 2 (Lang-Weil bound) Let
be a variety of complexity at most
. Assume that
is defined over
, and that
is irreducible as a variety over
(i.e.
is geometrically irreducible or absolutely irreducible). Then
Again, more explicit bounds on the implied constant here are known, but will not be the focus of this post. As the previous examples show, the hypotheses of definability over and geometric irreducibility are both necessary.
The Lang-Weil bound is already non-trivial in the model case of plane curves:
Theorem 3 (Hasse-Weil bound) Let
be an irreducible polynomial of degree
with coefficients in
. Then
Thus, for instance, if , then the elliptic curve
has
-points, a result first established by Hasse. The Hasse-Weil bound is already quite non-trivial, being the analogue of the Riemann hypothesis for plane curves. For hyper-elliptic curves, an elementary proof (due to Stepanov) is discussed in this previous post. For general plane curves, the first proof was by Weil (leading to his famous Weil conjectures); there is also a nice version of Stepanov’s argument due to Bombieri covering this case which is a little less elementary (relying crucially on the Riemann-Roch theorem for the upper bound, and a lifting trick to then get the lower bound), which I briefly summarise later in this post. The full Lang-Weil bound is deduced from the Hasse-Weil bound by an induction argument using generic hyperplane slicing, as I will also summarise later in this post.
The hypotheses of definability over and geometric irreducibility in the Lang-Weil can be removed after inserting a geometric factor:
Corollary 4 (Lang-Weil bound, alternate form) Let
be a variety of complexity at most
. Then one has
where
is the number of top-dimensional components of
(i.e. geometrically irreducible components of
of dimension
) that are definable over
, or equivalently are invariant with respect to the Frobenius endomorphism
that defines
.
Proof: By breaking up a general variety into components (and using Lemma 1 to dispose of any lower-dimensional components), it suffices to establish this claim when
is itself geometrically irreducible. If
is definable over
, the claim follows from Theorem 2. If
is not definable over
, then it is not fixed by the Frobenius endomorphism
(since otherwise one could produce a set of defining polynomials that were fixed by Frobenius and thus defined over
by using some canonical basis (such as a reduced Grobner basis) for the associated ideal), and so
has strictly smaller dimension than
. But
captures all the
-points of
, so in this case the claim follows from Lemma 1.
Note that if is reducible but is itself defined over
, then the Frobenius endomorphism preserves
itself, but may permute the components of
around. In this case,
is the number of fixed points of this permutation action of Frobenius on the components. In particular,
is always a natural number between
and
; thus we see that regardless of the geometry of
, the normalised count
is asymptotically restricted to a bounded range of natural numbers (in the regime where the complexity stays bounded and
goes to infinity).
Example 1 Consider the variety
for some non-zero parameter
. Geometrically (by which we basically mean “when viewed over the algebraically closed field
“), this is the union of two lines, with slopes corresponding to the two square roots of
. If
is a quadratic residue, then both of these lines are defined over
, and are fixed by Frobenius, and
in this case. If
is not a quadratic residue, then the lines are not defined over
, and the Frobenius automorphism permutes the two lines while preserving
as a whole, giving
in this case.
Corollary 4 effectively computes (at least to leading order) the number-theoretic size of a variety in terms of geometric information about
, namely its dimension
and the number
of top-dimensional components fixed by Frobenius. It turns out that with a little bit more effort, one can extend this connection to cover not just a single variety
, but a family of varieties indexed by points in some base space
. More precisely, suppose we now have two affine varieties
of bounded complexity, together with a regular map
of bounded complexity (the definition of complexity of a regular map is a bit technical, see e.g. this paper, but one can think for instance of a polynomial or rational map of bounded degree as a good example). It will be convenient to assume that the base space
is irreducible. If the map
is a dominant map (i.e. the image
is Zariski dense in
), then standard algebraic geometry results tell us that the fibres
are an unramified family of
-dimensional varieties outside of an exceptional subset
of
of dimension strictly smaller than
(and with
having dimension strictly smaller than
); see e.g. Section I.6.3 of Shafarevich.
Now suppose that ,
, and
are defined over
. Then, by Lang-Weil,
has
-points, and by Schwarz-Zippel, for all but
of these
-points
(the ones that lie in the subvariety
), the fibre
is an algebraic variety defined over
of dimension
. By using ultraproduct arguments (see e.g. Lemma 3.7 of this paper of mine with Emmanuel Breuillard and Ben Green), this variety can be shown to have bounded complexity, and thus by Corollary 4, has
-points. One can then ask how the quantity
is distributed. A simple but illustrative example occurs when
and
is the polynomial
. Then
equals
when
is a non-zero quadratic residue and
when
is a non-zero quadratic non-residue (and
when
is zero, but this is a negligible fraction of all
). In particular, in the asymptotic limit
,
is equal to
half of the time and
half of the time.
Now we describe the asymptotic distribution of the . We need some additional notation. Let
be an
-point in
, and let
be the connected components of the fibre
. As
is defined over
, this set of components is permuted by the Frobenius endomorphism
. But there is also an action by monodromy of the fundamental group
(this requires a certain amount of étale machinery to properly set up, as we are working over a positive characteristic field rather than over the complex numbers, but I am going to ignore this rather important detail here, as I still don’t fully understand it). This fundamental group may be infinite, but (by the étale construction) is always profinite, and in particular has a Haar probability measure, in which every finite index subgroup (and their cosets) are measurable. Thus we may meaningfully talk about elements drawn uniformly at random from this group, so long as we work only with the profinite
-algebra on
that is generated by the cosets of the finite index subgroups of this group (which will be the only relevant sets we need to measure when considering the action of this group on finite sets, such as the components of a generic fibre).
Theorem 5 (Lang-Weil with parameters) Let
be varieties of complexity at most
with
irreducible, and let
be a dominant map of complexity at most
. Let
be an
-point of
. Then, for any natural number
, one has
for
values of
, where
is the random variable that counts the number of components of a generic fibre
that are invariant under
, where
is an element chosen uniformly at random from the étale fundamental group
. In particular, in the asymptotic limit
, and with
chosen uniformly at random from
,
(or, equivalently,
) and
have the same asymptotic distribution.
This theorem generalises Corollary 4 (which is the case when is just a point, so that
is just
and
is trivial). Informally, the effect of a non-trivial parameter space
on the Lang-Weil bound is to push around the Frobenius map by monodromy for the purposes of counting invariant components, and a randomly chosen set of parameters corresponds to a randomly chosen loop on which to perform monodromy.
Example 2 Let
and
for some fixed
; to avoid some technical issues let us suppose that
is coprime to
. Then
can be taken to be
, and for a base point
we can take
. The fibre
– the
roots of unity – can be identified with the cyclic group
by using a primitive root of unity. The étale fundamental group
is (I think) isomorphic to the profinite closure
of the integers
(excluding the part of that closure coming from the characteristic of
). Not coincidentally, the integers
are the fundamental group of the complex analogue
of
. (Brian Conrad points out to me though that for more complicated varieties, such as covers of
by a power of the characteristic, the etale fundamental group is more complicated than just a profinite closure of the ordinary fundamental group, due to the presence of Artin-Schreier covers that are only ramified at infinity.) The action of this fundamental group on the fibres
can given by translation. Meanwhile, the Frobenius map
on
is given by multiplication by
. A random element
then becomes a random affine map
on
, where
chosen uniformly at random from
. The number of fixed points of this map is equal to the greatest common divisor
of
and
when
is divisible by
, and equal to
otherwise. This matches up with the elementary number fact that a randomly chosen non-zero element of
will be an
power with probability
, and when this occurs, the number of
roots in
will be
.
Example 3 (Thanks to Jordan Ellenberg for this example.) Consider a random elliptic curve
, where
are chosen uniformly at random, and let
. Let
be the
-torsion points of
(i.e. those elements
with
using the elliptic curve addition law); as a group, this is isomorphic to
(assuming that
has sufficiently large characteristic, for simplicity), and consider the number of
points of
, which is a random variable taking values in the natural numbers between
and
. In this case, the base variety
is the modular curve
, and the covering variety
is the modular curve
. The generic fibre here can be identified with
, the monodromy action projects down to the action of
, and the action of Frobenius on this fibre can be shown to be given by a
matrix with determinant
(with the exact choice of matrix depending on the choice of fibre and of the identification), so the distribution of the number of
-points of
is asymptotic to the distribution of the number of fixed points
of a random linear map of determinant
on
.
Theorem 5 seems to be well known “folklore” among arithmetic geometers, though I do not know of an explicit reference for it. I enjoyed deriving it for myself (though my derivation is somewhat incomplete due to my lack of understanding of étale cohomology) from the ordinary Lang-Weil theorem and the moment method. I’m recording this derivation later in this post, mostly for my own benefit (as I am still in the process of learning this material), though perhaps some other readers may also be interested in it.
Caveat: not all details are fully fleshed out in this writeup, particularly those involving the finer points of algebraic geometry and étale cohomology, as my understanding of these topics is not as complete as I would like it to be.
Many thanks to Brian Conrad and Jordan Ellenberg for helpful discussions on these topics.
— 1. The Stepanov-Bombieri proof of the Hasse-Weil bound —
We now give (most of) the Stepanov-Bombieri proof of Theorem 3, following the exposition of Bombieri (see also these lecture notes of Kowalski, focusing on the model case of curves of the form ). In this section all implied constants are allowed to depend on the degree
of the polynomial
.
Let be the
-points of the curve
; the hypothesis that
is irreducible means that the curve
is also irreducible. Our task is to establish the upper bound
For technical reasons, we only prove these bounds directly when is a perfect square; the general case then follows by using the explicit formula for
as a function of
and the tensor power trick, as explained in this previous post.
Now we prove the upper bound. One uses Stepanov’s polynomial method (discussed in these previous blog posts, for a somewhat different set of applications). The basic idea here is to bound the size of a finite set by constructing a non-trivial polynomial of controlled degree that vanishes to high order at each point of
. Stepanov’s original argument projected the curve
onto an affine line
so that one could use ordinary one-dimensional polynomials, but Bombieri’s approach works directly on the curve
. For this it becomes convenient to work in the language of divisors of rational functions, rather than zeroes of polynomials (and also it becomes slightly more convenient to work projectively rather than affinely, though I will gloss over this minor detail). Given a rational function
on the curve
(with coefficients in
) that is not identically zero or identically infinite on
, one can define the divisor
to be the formal sum
of the zeroes and poles
of
on
, weighted by the multiplicity
of the zero or pole (with poles being viewed as having negative multiplicity; one has to be a little careful defining multiplicity at singular points of
, but this can be done by using a sufficiently algebraic formalism). The irreducibility of
(which, of course, must be used at some juncture to prove the Hasse-Weil bound) ensures that this formal sum only has finitely many non-zero terms. One can show that the total signed multiplicities of zeroes and poles of
always add up to zero:
. (This generalises the fundamental theorem of algebra, which is the case when
is a projective line.)
Fix a point of
(which one can think of as being at infinity), and for each degree
, let
be the space of those rational functions
which are either zero, or have
, i.e.
has a pole of order
at
but no other poles; this generalises the space of polynomials of degree at most
, which corresponds to the case when
is a projective line and
is the point at infinity. It is easy to see that
is a vector space (over
), which is non-decreasing in
. In the case when
is a line, this space clearly has dimension
. The Riemann-Roch theorem is the generalisation of this to the case of a general curve. In its most precise form, it asserts the identity
where is the genus of
, and
is the canonical divisor of
(i.e. the divisor of the canonical line bundle of
). For our application, we will need two specific corollaries of the Riemann-Roch theorem, coming from the non-negativity and monotonicity properties of
. The first is the Riemann inequality
(so in particular ), and the second is the inequality
for all . In particular, if we set
to be the set of all degrees
such that
, then
consists of all but at most
elements of the natural numbers, and we can find a sequence
of rational functions on
with
(i.e.
has a pole of order exactly
at
and no other poles), with each
being spanned by the
with
. The
can be viewed as a generalisation of the standard monomial basis
of the polynomials of one variable. A key point here is that the degrees of this basis are all distinct; this will be crucial later on for ensuring that the polynomial we will be using for Stepanov’s method does not vanish identically.
We will not prove the Riemann-Roch theorem here, and simply assume it (and its consequences) as a black box. Next, we consider the Frobenius map defined by
. As
is defined over
, this map preserves
, and the fixed points of this map are precisely the
-points of
.
The plan is now to find a non-trivial element for some controlled
that vanishes to order at least
at each fixed point of
on
for some
. As the total number of zeroes and poles of
must agree, this forces
and by optimising the parameters this should lead to (1).
The trick is to pick rational functions of a specific form, namely
where is a parameter to be optimised later, and for each
,
lies in
for another parameter
to be optimised in later. We also pick
to divide
, thus
is a power of the characteristic
of
that is less than or equal to
. There are several reasons to working with polynomials of this form. The first is that because of the Frobenius endomorphism identity
, and
divides
by hypothesis, each term in
is an
power, and hence (since
in characteristic
)
is itself the
power of some rational function. As such, whenever
vanishes at a point, it automatically vanishes to order at least
.
Secondly, in order for to vanish at every fixed point of the Frobenius map on
(and thus vanish to order
at each such point, by the above discussion), it is of course necessary and sufficient that the rational function
This is a constraint on the which is linear over
(because the map
is linear over
, though not over
), and so we can try to enforce this constraint by linear algebra. Note that if each
lies in
, then the rational function on the left-hand side of of (4) lies in
, so the vanishing (4) imposes
homogeneous linear constraints (possibly dependent) over
on the
, where
. On the other hand, the dimension (over
) of the space of all possible
is
Thus, by linear algebra, we can find a collection of , not all zero, obeying (4) as long as we have
We are not done yet, because even if the are are not all zero, it is conceivable that the combined function (3) could still vanish. But observe that if
is the largest index for which
is non-zero, then the rational function
has a pole of order at least
at
, and all the other terms have a pole of order at most
(here it is crucial that the
have poles of different orders at
, thanks to Riemann-Roch). So as long as we have
we have that does not vanish identically. As it vanishes to degree at least
at every point of
, and lies in
, and so we obtain the upper bound
Now we optimise in the parameters subject to the constraints (5), (6). As
is assumed to be a perfect square and is sufficiently large, then a little work shows that one can satisfy the constraints with
,
, and
for some sufficiently large
, leading to the desired bound (1).
Remark 1 When
is not a perfect square, but is not a prime, one can still choose other values of
and obtain a weaker version of (1) that is still non-trivial. But it is curious that Bombieri’s version of Stepanov’s argument breaks down completely when
has prime order. As mentioned previously, one can still recover this case a posteriori by the tensor product trick, but this requires the explicit formula for
which is not exactly trivial. On the other hand, other versions of Stepanov’s argument (such as the one given in this previous blog post) do work in the prime order case, so this obstruction may be purely artificial in nature.
Now we need to pass from the upper bound (1) to the lower bound (2). In model cases, such as curves of the form with
not divisible by the characteristic of
, one can proceed by observing that the multiplicative group
foliates into
cosets
of the subgroup
of
powers. Because of this, we see that the union
of the curves
contains exactly
-points on all but
vertical lines
,
, and hence the union has cardinality
-points. (In other words, the projection
from
to
is generically
-to-one. Also, as the
are all dilations of
, they will be irreducible if
is, and thus by (1) they each have at most
-points; from subtracting all but one of the curves from
we then see that each of the
has at least
-points also. As we can take one of the
to be the identity, the claim (2) follows in this case. The general case follows in a similar fashion, using Galois theory to lifting a general curve
to another curve
whose projection to some coordinate line
has fixed multiplicity (basically by ensuring that the function field of the former is a Galois extension of the function field of the latter); see Bombieri’s paper for details.
— 2. The proof of the Lang-Weil bound —
Now we prove the Lang-Weil bound. We allow all implied constants to depend on the complexity bound , and will ignore the issues of how to control the complexity of the various algebraic objects that arise in our analysis (as before, one can obtain such bounds more or less “for free” from an ultraproduct argument, if desired).
The proof proceeds by induction on the dimension of the variety
. The first non-trivial case occurs at dimension one. If
is a plane curve (so
, and the ambient dimension is
), then the claim follows directly from the Hasse-Weil bound. If
is a higher-dimensional curve, we can use resultants to eliminate all but two of the variables (or, alternatively, one can apply the primitive element theorem to the function field of the curve), and convert the curve to a birationally equivalent (over
) plane curve, to reduce to the plane curve case (noting that the singular points of the birational transformation only influence the number of
-points by
at most).
Now suppose inductively that , and that the claim has already been proven for irreducible varieties of dimension
. The induction step is then based on the following two parallel facts about hyperplane slicing, the first in the algebraic geometric category, and the second in the combinatorial category:
Lemma 6 (Bertini’s theorem) Let
be an irreducible variety in
of dimension at least two. Then, for a generic affine hyperplane
(over
), the slice
is an irreducible variety of dimension
.
Lemma 7 (Random sampling) Let
be a subset of
for some
. Then, for a affine hyperplane
(defined over
) chosen uniformly at random, the random variable
has mean
and variance
. In particular, by Chebyshev’s inequality, the median value of
is
.
Let us see how the two lemmas conclude the induction. There are different affine hyperplanes
over
. The set of hyperplanes
over
for which
fails to be an irreducible variety of dimension
is, by Bertini’s theorem, a proper algebraic variety in the Grassmannian space, which one can show to have bounded complexity; and so by Lemma 1, only
of all such hyperplanes over
fall into this variety. For the remaining
such hyperplanes, we may apply the induction hypothesis and conclude that
. In particular, if
is an affine hyperplane chosen uniformly at random, then the median value of
is
. But this is consistent with Lemma 7 only when
, closing the induction.
Remark 2 One can also proceed without the variance bound in Lemma 7 by using Lemma 1 as a crude estimate for
for the exceptional
, after first making an easy reduction to the case where
is not already contained inside a single hyperplane. However, I think the variance bound is illuminating, as it illustrates the concentration of measure that occurs when
becomes much larger than
, which only occurs in dimensions two and higher. In contrast, if one attempts to slice a curve by a hyperplane, one typically gets zero or multiple points, so there is no concentration of measure and irreducibility usually fails. So the slicing method can reduce the dimension of
down to one, but not to zero, so the need to invoke Hasse-Weil cannot be avoided by this method.
We first show Lemma 7, which is a routine first and second moment calculation. Any given point in
lies in precisely
of the hyperplanes
, so summing in
we obtain
. Next, any two distinct points
in
lie in
of the hyperplanes
, and so
giving the variance bound.
Now we show Bertini’s theorem. A dimension count shows that the space of pairs where
is a hyperplane and
is a singular point of
in
has dimension at most
, and so for a generic hyperplane, the space of singular points of
in
is contained in a variety of dimension at most
. Similarly, the space of pairs
where
is a smooth point of
and
is a hyperplane containing the tangent space to
at
is at most
, and so the space of smooth points of
in
whose tangent space is not transverse to a generic
also has dimension at most
. Thus, for generic
, the slice
is a
-dimensional variety, which is generically comes from smooth points of
whose tangent space is transverse to
. The remaining task is to establish irreducibility for generic
. As irreducibility is an algebraic condition,
is either generically irreducible or generically reducible. Suppose for contradiction that
is generically reducible. Consider the set
of triples
where
are distinct smooth points of
, and
is a hyperplane through
that is transverse to the tangent spaces of both
and
, with
reducible. This is a quasiprojective variety of dimension
. It can be decomposed into two top-dimensional components: one where
lie in the same component of
, and one where they lie in distinct components. (The hypothesis
is crucial to ensure that the first component is non-empty.) As such,
is disconnected in the Zariski topology. On the other hand, for fixed
, the set of all
contributing to
is connected, while the set of all distinct smooth pairs
is also connected, and so
(and hence is closure) is also connected, a contradiction.
Remark 3 See also page 174 of Griffiths-Harris for a slight variant of this argument (thanks to Jordan Ellenberg for pointing this out). In that reference, it is also noted that the claim can also be derived from the Lefschetz hyperplane theorem in the case that
is smooth.
— 3. Lang-Weil with parameters —
Now we prove Theorem 5. Again we allow all implied constants to depend on the complexity parameter , and gloss over the task of making sure that all algebraic objects have complexity
.
We will proceed by the moment method. Observe that is a bounded natural number random variable, so to show that
has the asymptotic distribution of
up to errors of
, it suffices to show that
for any fixed natural number , or equivalently (by the Lang-Weil bound for
and for the fibres
)
Fix . We form the
-fold fibre product
of
over
, consisting of all
-tuples
such that
lies in
. This fibre product is a quasiprojective variety of dimension
, is defined over
, and the left-hand side of (7) is precisely equal to the number of
-points of
. Thus, by the Lang-Weil bound for
, it suffices to show that
i.e. that has precisely
top-dimensional components which are Frobenius-invariant.
We will in fact prove a more general statement: if is any dominant map which has smooth unramified fibres on
, then the number
of top-dimensional components of
that are Frobenius-invariant is equal to the expected number of top-dimensional components of
on a generic fibre
, where
is selected uniformly at random from
. Specialising this to the fibre product
(noting that the generic fibre of
is just the
-fold Cartesian power of the generic fibre of
, and similarly for the action of Frobenius and the fundamental group), we obtain the claim.
Now we prove this more general statement. By decomposing into irreducible components, we may certainly assume that is irreducible. If
is not Frobenius-invariant, then
is generically disjoint from
and so there certainly can be no components of
that are fixed by
. Thus we may assume that
is Frobenius-invariant (i.e. defined over
). Then the situation becomes very close to that of Burnside’s lemma. If there are
components
of
, the connectedness of
implies that the fundamental group
acts transitively on these components, and so for any single component
and uniformly chosen
,
will be uniformly distributed amongst the
, as will
. In particular, each
has a
chance of being a fixed point of
, so the expected number of fixed points of
is
as requred.
Exercise 1 Obtain the following extension of Corollary 5: if one has
different dominant maps
of varieties
of complexity
, with unramified, non-singular fibres on
, then the joint distribution of
converges in distribution to the joint distribution of
, where each
is the number of fixed points of
on the components of a generic fibre, where
is independent of
and drawn uniformly from
.
Remark 4 While the moment computation is simple and cute, I would be interested in seeing either a heuristic or rigorous explanation of Theorem 5 (or Exercise 1) that did not proceed through moments. The theorem seems to be asserting a statement roughly of the following form (ignoring for now the fact that paths do not actually make much sense in positive characteristic): if one takes a random path
in
connecting two random
-points, then the loop
behaves as if it is distributed uniformly in the fundamental group of
(or
, for any lower-dimensional set
). But I do not know how to make this heuristic precise.

19 comments
Comments feed for this article
12 September, 2012 at 3:36 pm
Definable subsets over (nonstandard) finite fields, and almost quantifier elimination « What’s new
[…] the small characteristic case); for instance, in conjunction with the Lang-Weil bound discussed in this recent blog post, it shows that any non-empty definable subset of a nonstandard finite field has a nonstandard […]
14 November, 2012 at 9:41 am
Expanding polynomials over finite fields of large characteristic, and a regularity lemma for definable sets « What’s new
[…] in particular the Lang-Weil bound on counting points in varieties over a finite field (discussed in this previous blog post), and also the theory of the etale fundamental group. Let me try to briefly explain why this is the […]
12 June, 2013 at 2:13 pm
Estimation of the Type I and Type II sums | What's new
[…] can show (e.g. using Stepanov’s method, cf. this previous post) that the number of this points on this curve is equal to , leading to the […]
25 October, 2013 at 7:48 am
Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory | What's new
[…] for instance, it plays a key role in the proof of Baker’s theorem in transcendence theory, or Stepanov’s method in giving an elementary proof of the Riemann hypothesis for finite fields ov…; in combinatorics, the nullstellenatz of Alon is also another relatively early use of the […]
29 October, 2013 at 8:09 pm
A spectral theory proof of the algebraic regularity lemma | What's new
[…] using the Lang-Weil bound and some facts about the étale fundamental group. It was the reliance on the latter which […]
1 February, 2014 at 12:57 am
Mrinmoy Datta
I would like to ask you if the Lang Weil, or Hasse Weil bounds are attained by some variety.
1 February, 2014 at 8:10 am
Terence Tao
The Hasse-Weil bound can come arbitrarily close to being sharp, thanks to the Sato-Tate conjecture, which has now been verified for large families of elliptic curves. The situation with Lang-Weil in higher dimensions is more delicate: in principle, the theorems of Deligne give much more precise error terms (full square root cancellation), but this requires some algebraic geometry vanishing conditions (certain cohomology groups have to vanish) which I don’t understand very well.
2 May, 2014 at 5:54 pm
The Bombieri-Stepanov proof of the Hasse-Weil bound | What's new
[…] discussed Bombieri’s proof of Theorem 2 in this previous post (in the special case of hyperelliptic curves), but now wish to present the full proof, with some […]
22 February, 2015 at 4:09 am
First Bourbaki seminar of 2015 (I): Harari’s talk | Disquisitiones Mathematicae
[…] bad fibers. The reason for this fact is that if is split, then one can show (with the aid of the Lang-Weil estimate and Hensel’s lemma) that for almost all places […]
11 May, 2015 at 8:11 am
gilleslachaud
It may be worthwhile to specify that there are precise values (for affine or projective algebraic sets) of the implied constants in Lemma 1, see
arXiv:1405.3027v2 and the references therein.
13 June, 2016 at 12:51 pm
nonononoas
Dear Terry, I was wondering if you have any idea on how the function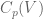 distributes as
distributes as  ranges over all large primes. For example, if
ranges over all large primes. For example, if 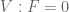 is an affine hypersurface, with
is an affine hypersurface, with  irreducible over
irreducible over 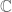 , then does the limit
, then does the limit  exist ?
exist ?
14 June, 2016 at 9:18 am
Terence Tao
In the one-dimensional case at least I believe the Chebotarev density theorem is supposed to answer these questions, though I am not an expert on this topic. The higher dimensional case might also be treatable by this theorem or a variant thereof. The general heuristic here is that the action of the Frobenius map should be as “equidistributed” as possible subject to whatever algebraic constraints that map has to obey.
14 June, 2016 at 9:29 am
nonononoas
Thanks!
5 November, 2019 at 8:47 pm
Anonymous
Dear Terry,
I have a question about one application of the above bounds. (e.g. Lang Weil)
Suppose you want to count the number of integer solutions of a polynomial equation e.g. f(x,y) = 0, where |x|< H, |y|<H. Then, one attempt is to first consider mod p to first count the number of solutions in F_p by using the bounds in your post, and then apply large Sieve.
However, the upper bound you can get in this way may not be good. One issue is that in Lang Weil bound, the degree of the polynomial f(x,y) is not important, it goes to the 'complexity'. However, the degree might be important when you are counting over integers.
Do you know any tools, in general, to deal with this issue?
12 November, 2019 at 6:20 pm
Terence Tao
Well, counting integer points to polynomial equations is a hugely difficult problem in general, thanks to Matiyasevich’s theorem. While sieving can give some bounds, other methods such as the determinant method are often more effective in practice. If the equations have additive structure then the circle method and its variants can give good bounds; there are many further techniques in arithmetic geometry and Diophantine geometry that can also be useful here, though I am not an expert on these matters.
27 February, 2020 at 6:32 am
Anonymous
About the Lang-Weil estimate, I would like to know how the Lang-Weil constant depends on the degree of varieties. More precisely, I proposed such a question: https://mathoverflow.net/questions/352053/density-of-rational-points-over-finite-fields-an-estimate-of-lang-weil-constant
31 January, 2022 at 9:57 am
Jonathan Love
Thank you for this very interesting and helpful write-up! I have a question about one of the steps:
“The set of hyperplanes {H} over {\overline{F}} for which {V \cap H} fails to be an irreducible variety of dimension {\hbox{dim}(V)} is, by Bertini’s theorem, a proper algebraic variety in the Grassmannian space, which one can show to have bounded complexity”
How can one show that this variety has bounded complexity? I’ve seen some very tight bounds on the dimension (for instance Poonen and Slavov’s 2020 paper using the statistical methods described in this post) but I don’t see a natural way to bound, for example, the degree. Even just a rough sketch or pointer would be very helpful.
1 February, 2022 at 12:15 pm
Terence Tao
As the degree of is bounded, there are only a bounded number of ways in which
is bounded, there are only a bounded number of ways in which  can be reducible (e.g., it could split into the union of a degree five and a degree seven subvariety), and each of these can be described via a bounded complexity system of equations. Alternatively, one can get an ineffective bound using ultraproducts, as in https://terrytao.wordpress.com/2010/01/30/the-ultralimit-argument-and-quantitative-algebraic-geometry/
can be reducible (e.g., it could split into the union of a degree five and a degree seven subvariety), and each of these can be described via a bounded complexity system of equations. Alternatively, one can get an ineffective bound using ultraproducts, as in https://terrytao.wordpress.com/2010/01/30/the-ultralimit-argument-and-quantitative-algebraic-geometry/
1 February, 2022 at 4:16 pm
Jonathan Love
Ah that makes sense, thank you!