Define a partition of to be a finite or infinite multiset
of real numbers in the interval
(that is, an unordered set of real numbers in
, possibly with multiplicity) whose total sum is
:
. For instance,
is a partition of
. Such partitions arise naturally when trying to decompose a large object into smaller ones, for instance:
- (Prime factorisation) Given a natural number
, one can decompose it into prime factors
(counting multiplicity), and then the multiset
is a partition of
.
- (Cycle decomposition) Given a permutation
on
labels
, one can decompose
into cycles
, and then the multiset
is a partition of
.
- (Normalisation) Given a multiset
of positive real numbers whose sum
is finite and non-zero, the multiset
is a partition of
.
In the spirit of the universality phenomenon, one can ask what is the natural distribution for what a “typical” partition should look like; thus one seeks a natural probability distribution on the space of all partitions, analogous to (say) the gaussian distributions on the real line, or GUE distributions on point processes on the line, and so forth. It turns out that there is one natural such distribution which is related to all three examples above, known as the Poisson-Dirichlet distribution. To describe this distribution, we first have to deal with the problem that it is not immediately obvious how to cleanly parameterise the space of partitions, given that the cardinality of the partition can be finite or infinite, that multiplicity is allowed, and that we would like to identify two partitions that are permutations of each other
One way to proceed is to random partition as a type of point process on the interval
, with the constraint that
, in which case one can study statistics such as the counting functions
(where the cardinality here counts multiplicity). This can certainly be done, although in the case of the Poisson-Dirichlet process, the formulae for the joint distribution of such counting functions is moderately complicated. Another way to proceed is to order the elements of in decreasing order
with the convention that one pads the sequence by an infinite number of zeroes if
is finite; this identifies the space of partitions with an infinite dimensional simplex
However, it turns out that the process of ordering the elements is not “smooth” (basically because functions such as and
are not smooth) and the formulae for the joint distribution in the case of the Poisson-Dirichlet process is again complicated.
It turns out that there is a better (or at least “smoother”) way to enumerate the elements of a partition
than the ordered method, although it is random rather than deterministic. This procedure (which I learned from this paper of Donnelly and Grimmett) works as follows.
- Given a partition
, let
be an element of
chosen at random, with each element
having a probability
of being chosen as
(so if
occurs with multiplicity
, the net probability that
is chosen as
is actually
). Note that this is well-defined since the elements of
sum to
.
- Now suppose
is chosen. If
is empty, we set
all equal to zero and stop. Otherwise, let
be an element of
chosen at random, with each element
having a probability
of being chosen as
. (For instance, if
occurred with some multiplicity
in
, then
can equal
with probability
.)
- Now suppose
are both chosen. If
is empty, we set
all equal to zero and stop. Otherwise, let
be an element of
, with ech element
having a probability
of being chosen as
.
- We continue this process indefinitely to create elements
.
We denote the random sequence formed from a partition
in the above manner as the random normalised enumeration of
; this is a random variable in the infinite unit cube
, and can be defined recursively by the formula
with drawn randomly from
, with each element
chosen with probability
, except when
in which case we instead have
Note that one can recover from any of its random normalised enumerations
by the formula
with the convention that one discards any zero elements on the right-hand side. Thus can be viewed as a (stochastic) parameterisation of the space of partitions by the unit cube
, which is a simpler domain to work with than the infinite-dimensional simplex mentioned earlier.
Note that this random enumeration procedure can also be adapted to the three models described earlier:
- Given a natural number
, one can randomly enumerate its prime factors
by letting each prime factor
of
be equal to
with probability
, then once
is chosen, let each remaining prime factor
of
be equal to
with probability
, and so forth.
- Given a permutation
, one can randomly enumerate its cycles
by letting each cycle
in
be equal to
with probability
, and once
is chosen, let each remaining cycle
be equalto
with probability
, and so forth. Alternatively, one traverse the elements of
in random order, then let
be the first cycle one encounters when performing this traversal, let
be the next cycle (not equal to
one encounters when performing this traversal, and so forth.
- Given a multiset
of positive real numbers whose sum
is finite, we can randomly enumerate
the elements of this sequence by letting each
have a
probability of being set equal to
, and then once
is chosen, let each remaining
have a
probability of being set equal to
, and so forth.
We then have the following result:
Proposition 1 (Existence of the Poisson-Dirichlet process) There exists a random partition
whose random enumeration
has the uniform distribution on
, thus
are independently and identically distributed copies of the uniform distribution on
.
A random partition with this property will be called the Poisson-Dirichlet process. This process, first introduced by Kingman, can be described explicitly using (1) as
where are iid copies of the uniform distribution of
, although it is not immediately obvious from this definition that
is indeed uniformly distributed on
. We prove this proposition below the fold.
An equivalent definition of a Poisson-Dirichlet process is a random partition with the property that
where is a random element of
with each
having a probability
of being equal to
,
is a uniform variable on
that is independent of
, and
denotes equality of distribution. This can be viewed as a sort of stochastic self-similarity property of
: if one randomly removes one element from
and rescales, one gets a new copy of
.
It turns out that each of the three ways to generate partitions listed above can lead to the Poisson-Dirichlet process, either directly or in a suitable limit. We begin with the third way, namely by normalising a Poisson process to have sum :
Proposition 2 (Poisson-Dirichlet processes via Poisson processes) Let
, and let
be a Poisson process on
with intensity function
. Then the sum
is almost surely finite, and the normalisation
is a Poisson-Dirichlet process.
Again, we prove this proposition below the fold. Now we turn to the second way (a topic, incidentally, that was briefly touched upon in this previous blog post):
Proposition 3 (Large cycles of a typical permutation) For each natural number
, let
be a permutation drawn uniformly at random from
. Then the random partition
converges in the limit
to a Poisson-Dirichlet process
in the following sense: given any fixed sequence of intervals
(independent of
), the joint discrete random variable
converges in distribution to
.
Finally, we turn to the first way:
Proposition 4 (Large prime factors of a typical number) Let
, and let
be a random natural number chosen according to one of the following three rules:
- (Uniform distribution)
is drawn uniformly at random from the natural numbers in
.
- (Shifted uniform distribution)
is drawn uniformly at random from the natural numbers in
.
- (Zeta distribution) Each natural number
has a probability
of being equal to
, where
and
.
Then
converges as
to a Poisson-Dirichlet process
in the same fashion as in Proposition 3.
The process was first studied by Billingsley (and also later by Knuth-Trabb Pardo and by Vershik, but the formulae were initially rather complicated; the proposition above is due to of Donnelly and Grimmett, although the third case of the proposition is substantially easier and appears in the earlier work of Lloyd. We prove the proposition below the fold.
The previous two propositions suggests an interesting analogy between large random integers and large random permutations; see this ICM article of Vershik and this non-technical article of Granville (which, incidentally, was once adapted into a play) for further discussion.
As a sample application, consider the problem of estimating the number of integers up to
which are not divisible by any prime larger than
(i.e. they are
–smooth), where
is a fixed real number. This is essentially (modulo some inessential technicalities concerning the distinction between the intervals
and
) the probability that
avoids
, which by the above theorem converges to the probability
that
avoids
. Below the fold we will show that this function is given by the Dickman function, defined by setting
for
and
for
, thus recovering the classical result of Dickman that
.
I thank Andrew Granville and Anatoly Vershik for showing me the nice link between prime factors and the Poisson-Dirichlet process. The material here is standard, and (like many of the other notes on this blog) was primarily written for my own benefit, but it may be of interest to some readers. In preparing this article I found this exposition by Kingman to be helpful.
Note: this article will emphasise the computations rather than rigour, and in particular will rely on informal use of infinitesimals to avoid dealing with stochastic calculus or other technicalities. We adopt the convention that we will neglect higher order terms in infinitesimal calculations, e.g. if is infinitesimal then we will abbreviate
simply as
.
— 1. Constructing the Poisson-Dirichlet process —
We now prove Proposition 2, which of course also implies Proposition 1.
Let , and let
be as in Proposition 2. We note that
, so if one wished, one could normalise
. However, for minor technical reasons it will be convenient to allow
to to be arbitrary.
We first understand the law of the sum of the Poisson process
.
Lemma 5 Let
be as in Proposition 2. Then
is an exponential variable with probability distribution
. In particular,
is almost surely finite.
Proof: Taking Laplace transforms, it suffices to show that
for all . We come the left-hand side by an informal argument using infinitesimals, leaving the rigorous version of the argument as an exercise to the reader. Partitioning
into infinitesimal intervals
, we expect each interval
to contain exactly one element of
with probability about
, and to contain two or more elements with negligible probability. We can then write
(ignoring higher order terms) and thus
and thus on sending to zero
The quantity vanishes when
and has an
-derivative of
, so on integrating we have
and (3) follows.
The same analysis can be performed for Poisson processes with more general intensity functions, leading to Campbell’s theorem. However, the exponential nature of leads to an important decoupling property:
Proposition 6 Let
be as in Proposition 2. Then the random variable
and the normalisation
are independent.
Proof: Let be disjoint infinitesimal intervals in
, and let
be another infinitesimal interval in
, with
infinitesimal compared with
. We compute the probability of of the (infinitesimal) event
that
lies in
and each of
is occupied by an element of
; our goal is to show that this probability decouples into the product of a function of
and a function of the
. This event
is (up to higher order errors) empty if
, and is otherwise equal to the event that each of the
is occupied by an element
of
, and that the sum
of the remaining elements lies in
. By definition of Poisson process, the former event occurs with probability
Once we condition on this event, is again a Poisson process of intensity
, so by Lemma 5
is an exponential variable of parameter
, so it lies in
with probability
Since is infinitesimally close to
, we conclude that the probability of
is
giving the claim.
Note that the above calculation in fact computes the -point intensity function of
as
We can now show the Poisson-Dirichlet property (2):
Proposition 7 Let
, and let
be a random element, with each
having a probability
of equalling
. Then
is distributed uniformly in
, and after one conditions on the value of
,
has the same distribution as
.
Proof: We first establish that is distributed uniformly in
. Consider the event
that
lies in an infinitesimal interval
for some
. This requires the interval
to contain an element
of
, which occurs with probability
, and then there is a probability
that this element will be selected as
. Thus
has probability
, giving the claim of uniform distribution.
Now consider the probability of the event that
lies in
, and that
meets each of the disjoint infinitesimal
, where we choose
to be infinitesimal compared with
. This event is empty if
, and is otherwise equal (up to higher order errors) as the event that
and that
meets each of the
. By (4) for
applied at
, we conclude that
occurs with probability
which simplifies to
If we condition out by which has probability
, we recover the same
-point correlation function (4) as
, and the claim follows.
Remark 8 As a crude zeroth approximation to the process
, one can consider the Poisson process
on
with intensity function
. By (4), this process has the same
-point intensity function as the true Poisson-Dirichlet process
, but has the wrong higher point correlation functions (the cutoff
is replaced by
). Related to this,
is not a partition in general as there is no reason why
should equal
. Nevertheless, this zeroth approximation can be used as a crude heuristic in some cases. In the number theoretic setting, it corresponds to a Cramer-type random model in which each prime
less than a “typical” number
has an independent probability of
of dividing
.
Remark 9 If one starts with a Poisson process
of intensity
for some parameter
and normaliises it as above, one arrives at a more general Poisson-Dirichlet process whose enumeration variables
are distributed according to a beta distribution rather than the uniform distribution.
— 2. Cycle decomposition of random permutations —
The proof of Proposition 3 is essentially immediate from the following claim:
Proposition 10 Let
and
be as in Proposition 3. Let
be a random element of
, with each
occuring with probability
. Then
is distributed uniformly among the multiples
of
, and after conditioning on a given value
of
,
has the distribution of
.
Heuristically at least, in the limit , this proposition asserts that the limiting distribution of the
obeys the defining relation (2) of the Poisson-Dirichlet process. It is not difficult to make this argument rigorous, but we leave this as an exercise to the reader.
Proof: We first compute the probability that is equal to
. Using the cycle interpretation of the enumeration of
, this is equal to the probability that a randomly chosen element of
lies in a cycle of
of length
. By permutation symmetry, it suffices to compute the probability that
lies in a cycle of length
. To count the number of permutations
with this property, observe from direct counting that there are
ways to select the cycle of length
containing
, and once this cycle is chosen there are
ways to select the rest of the permutation
, leading to
ways in all. Dividing by the total number
of permutations, we see that the cycle length
occurs with probability
, giving the required uniform distribution.
The same analysis shows that once one fixes the cycle of length that contains
, the partition associated to the remaining cycles has the distribution of
. Averaging over all the cycles of length
containing
, we obtain the second claim of the proposition.
— 3. Asymptotics of prime divisors —
We now prove Proposition 4. We first give a simple argument of Lloyd (as described by Kingman), which handles the much smoother (and hence much easier) third case of the theorem. In this case one can take advantage of Euler product factorisation. Indeed, if we define to be the point process of primes defined by setting each prime
to occur with multiplicity
in
with probability
, independently in
, then we see from the fundamental theorem of arithmetic and the Euler product
that the random variable
has the same distribution as
, where the product is with multiplicity. Setting
and
, we thus see that the point process
associated to the prime divisors of this random number
is the same process as
. On the other hand, it is easy to see (from the same Mertens’ theorem calculation in the introduction) that in the limit as
(or
), the point process
converges (in the sense of Theorem 3) to the Poisson process with intensity
, and the claim follows in this case from Proposition 2.
Now we prove the theorem in the first and second cases. Here, the Euler product factorisation is not available (unless one allows to be complex and uses something like Perron’s formula, but this turns the probabilities involved into complex numbers, and it is difficult to see how this can be made at all rigorous). Instead, we use (a slightly informal version of) the argument of Donnelly and Grimmett. The key proposition is the following analogue of Proposition 11, stated slightly informally:
Proposition 11 Let
be as in the first or second case of Proposition 4. Let
be a random prime factor of
, with each prime factor
of
having a probability of
of being chosen as
. Then the distribution of
converges in the vague topology to the uniform distribution as
. Also, if one conditions on a specific value
of
, then
has the same distribution as
(up to negligible errors).
Again, upon taking logarithms and sending we conclude, heuristically at least, that the limiting distribution of
converges to a process that obeys (2) and is thus a Poisson-Dirichlet process. Again, one can make this argument rigorous; see the paper of Donnelly and Grimmett for details.
Proof: (Informal) For sake of concreteness let us work with the second case of Proposition 4, as the first case is similar (and also follows from the second case by a dyadic decomposition). We compute the probability that is equal to a given prime
, and
equal to a given multiple
of
. This requires
lies in
, and occurs with probability about
(This is slightly inaccurate in the case that is also divisible by
, but this event is negligible in the limit
).
Summing in , we see that
is equal to
with probability about
, and that once one conditions on the event
, one essentially recovers the distribution of
. Finally, the probability that
lies in
is essentially
which by Mertens’ theorems is asymptotic to , and the claim follows.
Remark 12 The same argument also works when
is drawn from the zeta distribution. Comparing this with Lloyd’s argument, this gives another proof of Proposition 2 (although ultimately it is just a discrete version of the previous, continuous, proof).
Remark 13 A variant of Proposition 4 of relevance to the polymath8 project; if instead of selecting
uniformly at random from
, one instead performs a weighted distribution where each
has a probability
of being chosen as
for some fixed
, where
is the number of prime factors of
, then the same argument shows that
is now asymptotic to a generalised Poisson-Dirichlet process in which the coordinates
of the random enumeration remain independent, but now have the probability density function of
rather than the uniform distribution. (This distribution is in fact of the form in Remark 9, with
replaced by
.) In particular, when
is large, the elements of
tend to cluster near the origin (most elements will have magnitude
), which helps explain the Motohashi-Pintz-Zhang phenomenon that when sieving for
-tuples, the majority of moduli that one encounters in the sieve are quite smooth (or at least densely divisible).
— 4. Dickman’s function —
Let be the probability that the Poisson-Dirichlet process
has no element larger than
. Clearly
for
; it is also not difficult to show that
is continuous. It thus suffices to verify the delay-differential equation
for
.
Let . If we let
be the
process from Proposition 2, and
, we see that
is equal to the probability that
for all
. Taking (backwards) Newton quotients, we then conclude that
is equal to the probability that
for all
, and that
for the largest element
of
.
For any real number , let
denote the event that
,
for all
, and that
, where
is infinitesimal compared with
. This is essentially the same as the event that
contains an element
in
, that
for all
, and that
. The first event occurs with probability
. Conditioning on this event,
is still a Poisson process with intensity
with sum
. By Lemma 5, the random variable
is exponential with parameter
and indepenent of the process
. Thus the remaining two events defining
are conditionally independent, with the former occuring with probability
and the latter with probability
. Thus the total probability that
occurs is
which simplifies to ; integrating in
, we conclude that
is equal to
, and the claim follows.
Remark 14 Using (4) and the inclusion-exclusion formula, one also has the integral expression
for
, with the convention that the
term is
; note that the summands vanish for
and so only finitely many terms in this expression need to be evaluated. This gives another way to verify the delay-differential equation
.

27 comments
Comments feed for this article
24 September, 2013 at 7:05 am
arch1
In step 2 of the enumeration procedure, why isn’t the probability of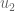 equaling
equaling  instead
instead 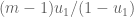 , since there are
, since there are  instances of
instances of  remaining in the multiset at that point, each of which has probability
remaining in the multiset at that point, each of which has probability  of being chosen?
of being chosen?
[Oops, that was a careless mistake; fixed now, thanks. -T.]
24 September, 2013 at 5:53 pm
D
The steps 2–4 do not agree with the reconstruction in formula (1). When you pick u_1, do you divide remaining points by 1-u_1? In other words, u_2 does not come from the original list \Sigma, but from a rescaled list?
[Oops, you’re right; the way it was written was completely confusing. I hope I’ve fixed it now – T.]
26 September, 2013 at 5:19 am
arch1
In the recursive formula for Enum, should the multiplier therefore be ?
?
[Corrected, thanks – T.]
12 February, 2020 at 9:52 pm
Peleg Michaeli پليج (@pelegmichaeli)
I think this is still written wrongly, or at least unclear. Suppose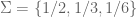 , and suppose
, and suppose 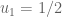 . Then
. Then 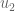 is chosen from
is chosen from 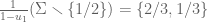 . Now suppose
. Now suppose 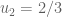 . You probably don’t want to have
. You probably don’t want to have 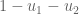 in the denominator in step 3.
in the denominator in step 3.
[Corrected, thanks – T.]
25 September, 2013 at 9:57 am
David
This Poisson-Dirichlet process is PD(1) in a more general family PD(t), see page 99 of Poisson processes by Kingman. The same construction, only the uniform distribution is replaced by Beta(1,t) distribution. The process PD(t) itself is PD(0,t) in more general family PD(a,t) in the paper of Pitman and Yor.
25 September, 2013 at 9:59 am
D
In Proposition 6, equality sign is missing in {\Sigma_N(\Gamma_a) = \frac{1}{S} \cdot \Gamma_a}.
[Corrected, thanks – T.]
25 September, 2013 at 11:04 am
❧ ✲ ❂ ❂ ✲✳ ✴ ✶ ❂✯❀
In Proposition 4, \Sigma_{PD} is \Sigma_{PF}.
[Corrected, thanks – T.]
25 September, 2013 at 6:44 pm
D
In the case of Zeta distribution, the comment after the proof of Theorem 1 in Kingman’s paper implies that (asymptotically in x) multiplicities of any finite number of largest prime divisors are equal to one. I am assuming this also holds in the case 1 of Uniform distribution, so is it some basic result in number theory that the density of numbers with this property is equal to one? How can the number of largest prime divisors grow with x so that one still has this property?
25 September, 2013 at 8:01 pm
Terence Tao
Yes, it is rare for a large number to be divisible by a large prime with multiplicity more than one. This is basically because the sum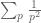 is convergent, so that the sum
is convergent, so that the sum 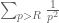 goes to zero as
goes to zero as 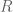 goes to infinity. Thus, the proportion of numbers which are divisible by the square of a prime greater than
goes to infinity. Thus, the proportion of numbers which are divisible by the square of a prime greater than 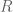 goes to zero as
goes to zero as 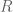 goes to infinity. Among other things, this shows that the set of numbers whose largest
goes to infinity. Among other things, this shows that the set of numbers whose largest  prime factors occur with multiplicity one, has density one for any fixed
prime factors occur with multiplicity one, has density one for any fixed  .
.
5 October, 2013 at 3:36 pm
vcp
In the first sentence following the box containing Proposition 4, “by first done” can be deleted.
[Corrected, thanks – T.]
15 October, 2013 at 8:37 pm
thichchaytron
It very difficulty with me :(
17 October, 2013 at 12:28 pm
X
I think that there are some typos in section 1: Resp. 2 and 3 equations below (3), the left-hand side should be E exp(-sS), not E exp(-tS)
Also, “Theorem 2/3” should be “as in Proposition 2/3”
[Corrected, thanks – T.]
5 November, 2013 at 1:17 pm
Anita
Is it trivial that if they are non-zero and sums to 1, the multiset must be countable?
6 November, 2013 at 10:47 pm
Anita
Of course it is, ignore this.
13 November, 2013 at 3:30 am
Grigory F
Typo in the third line after equation (1):![[0,1]^n](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5En&bg=ffffff&fg=545454&s=0&c=20201002) should read
should read ![[0,1]^{\bf N}](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E%7B%5Cbf+N%7D&bg=ffffff&fg=545454&s=0&c=20201002) instead.
instead.
[Corrected, thanks – T.]
21 November, 2013 at 5:33 pm
Sary D
Some signs should probably be swapped in section 4 : $u\rho'(u)=-\rho(u-1)$ and probability $-du\rho'(u)$, since rho is decreasing.
I love reading your blog !
[Corrected, thanks – T.]
14 March, 2014 at 11:16 am
The Chinese Restaurant Process | Eventually Almost Everywhere
[…] The Poisson-Dirichlet process, and large prime factors of a random number (terrytao.wordpress.com) […]
14 March, 2014 at 11:17 am
Urns and the Dirichlet Distribution | Eventually Almost Everywhere
[…] The Poisson-Dirichlet process, and large prime factors of a random number (terrytao.wordpress.com) […]
15 July, 2015 at 2:44 pm
Cycles of a random permutation, and irreducible factors of a random polynomial | What's new
[…] If is a randomly selected large integer of size , and is a randomly selected prime factor of (with each index being chosen with probability ), then is approximately uniformly distributed between and . (See Proposition 9 of this previous blog post.) […]
18 March, 2016 at 12:07 am
saroj
can any body give me the proof of ”(estimation of s^(2/B))<infinite''????
16 August, 2018 at 10:40 am
Karl Keppler
Dickman function arises in a problem proposed here:
https://math.stackexchange.com/questions/2130264/sum-of-random-decreasing-numbers-between-0-and-1-does-it-converge
31 October, 2018 at 8:53 am
Martin
Hi Terry!
Your blog post asked what’s new in prime numbers. I have something I think is new I would like to show you and the readers of your blog. I hope you don’t mind and are gracious enough to post this.
Kind regards,
Martin
Claim: “All prime numbers can be transformed into an integer sequence equivalent to one-half the sum of the first 2n + 1 primes.”
Proof:
1) Sum each consecutive pair of prime numbers (i.e. 2,3 then 3,5, etc.)
2) Subtract the difference between the two numbers.
3) Divide the result by 4.
4) Keep a continual sum from step 3.
5) At odd intervals the continual sum is equivalent to 1/2 half the sum of the first 2n + 1 primes.
1, 5, 14, 29, 50, 80, 119, 164, 220, 284, 356, 437, 530, 632, 740, 860, 994, 1138, 1292, 1457, 1633, 1819, 2014, 2219, 2444, 2675, 2915, 3169, 3435
30 December, 2019 at 8:53 am
Separating big sticks from little sticks, and applications – Random Permutations
[…] Tao on the stick-breaking process, or the Poisson–Dirichlet process (which is essentially the same); […]
30 March, 2020 at 9:37 am
Noam
I think there is a mistake in the calculation of the integral that appears in the proof that S is an exponential variable – I believe it should be log(a/(s+a)) and not – log(s+a).
[Corrected, thanks – T.]
3 October, 2020 at 7:38 am
Will
Some kind of malformed formatting tag in the proof of Proposition 7 has gone mad with power and underlined half this post.
[Corrected, thanks – T.]
6 March, 2024 at 9:35 am
Anonymous
This is a wonderful blog post and I really enjoyed the read! However, I am struggling to understand few things regarding the proof of Lemma 5.
– Given the definition of exponential r.v. in the lemma, shouldn’t we show – in (3) – that its Laplace transform is a/(s+a)?
– Why is \Gamma_a=a\Gamma_1? Already by checking the expectation of the two processes, the integrand looks different.
– I don’t understand how can we rewrite the Laplace transform of S as the product in the third equation of the proof for Lemma 5. Isn’t S given by a Poisson binomial distribution?
Thanks in advance for the clarifications. FZ
17 March, 2024 at 6:14 pm
Terence Tao
1. This was a typo, now corrected. should be
should be 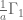 .
.
2. This was also a typo:
3. The Laplace transform (aka moment generating function) of a sum of independent random variables is the product of the Laplace transform of the individual variables.