A core foundation of the subject now known as arithmetic combinatorics (and particularly the subfield of additive combinatorics) are the elementary sum set estimates (sometimes known as “Ruzsa calculus”) that relate the cardinality of various sum sets
and difference sets
as well as iterated sumsets such as ,
, and so forth. Here,
are finite non-empty subsets of some additive group
(classically one took
or
, but nowadays one usually considers more general additive groups). Some basic estimates in this vein are the following:
Lemma 1 (Ruzsa covering lemma) Let
be finite non-empty subsets of
. Then
may be covered by at most
translates of
.
Proof: Consider a maximal set of disjoint translates of
by elements
. These translates have cardinality
, are disjoint, and lie in
, so there are at most
of them. By maximality, for any
,
must intersect at least one of the selected
, thus
, and the claim follows.
Lemma 2 (Ruzsa triangle inequality) Let
be finite non-empty subsets of
. Then
.
Proof: Consider the addition map from
to
. Every element
of
has a preimage
of this map of cardinality at least
, thanks to the obvious identity
for each
. Since
has cardinality
, the claim follows.
Such estimates (which are covered, incidentally, in Section 2 of my book with Van Vu) are particularly useful for controlling finite sets of small doubling, in the sense that
for some bounded
. (There are deeper theorems, most notably Freiman’s theorem, which give more control than what elementary Ruzsa calculus does, however the known bounds in the latter theorem are worse than polynomial in
(although it is conjectured otherwise), whereas the elementary estimates are almost all polynomial in
.)
However, there are some settings in which the standard sum set estimates are not quite applicable. One such setting is the continuous setting, where one is dealing with bounded open sets in an additive Lie group (e.g. or a torus
) rather than a finite setting. Here, one can largely replicate the discrete sum set estimates by working with a Haar measure in place of cardinality; this is the approach taken for instance in this paper of mine. However, there is another setting, which one might dub the “discretised” setting (as opposed to the “discrete” setting or “continuous” setting), in which the sets
remain finite (or at least discretisable to be finite), but for which there is a certain amount of “roundoff error” coming from the discretisation. As a typical example (working now in a non-commutative multiplicative setting rather than an additive one), consider the orthogonal group
of orthogonal
matrices, and let
be the matrices obtained by starting with all of the orthogonal matrice in
and rounding each coefficient of each matrix in this set to the nearest multiple of
, for some small
. This forms a finite set (whose cardinality grows as
like a certain negative power of
). In the limit
, the set
is not a set of small doubling in the discrete sense. However,
is still close to
in a metric sense, being contained in the
-neighbourhood of
. Another key example comes from graphs
of maps
from a subset
of one additive group
to another
. If
is “approximately additive” in the sense that for all
,
is close to
in some metric, then
might not have small doubling in the discrete sense (because
could take a large number of values), but could be considered a set of small doubling in a discretised sense.
One would like to have a sum set (or product set) theory that can handle these cases, particularly in “high-dimensional” settings in which the standard methods of passing back and forth between continuous, discrete, or discretised settings behave poorly from a quantitative point of view due to the exponentially large doubling constant of balls. One way to do this is to impose a translation invariant metric on the underlying group
(reverting back to additive notation), and replace the notion of cardinality by that of metric entropy. There are a number of almost equivalent ways to define this concept:
Definition 3 Let
be a metric space, let
be a subset of
, and let
be a radius.
- The packing number
is the largest number of points
one can pack inside
such that the balls
are disjoint.
- The internal covering number
is the fewest number of points
such that the balls
cover
.
- The external covering number
is the fewest number of points
such that the balls
cover
.
- The metric entropy
is the largest number of points
one can find in
that are
-separated, thus
for all
.
It is an easy exercise to verify the inequalities
for any , and that
is non-increasing in
and non-decreasing in
for the three choices
(but monotonicity in
can fail for
!). It turns out that the external covering number
is slightly more convenient than the other notions of metric entropy, so we will abbreviate
. The cardinality
can be viewed as the limit of the entropies
as
.
If we have the bounded doubling property that is covered by
translates of
for each
, and one has a Haar measure
on
which assigns a positive finite mass to each ball, then any of the above entropies
is comparable to
, as can be seen by simple volume packing arguments. Thus in the bounded doubling setting one can usually use the measure-theoretic sum set theory to derive entropy-theoretic sumset bounds (see e.g. this paper of mine for an example of this). However, it turns out that even in the absence of bounded doubling, one still has an entropy analogue of most of the elementary sum set theory, except that one has to accept some degradation in the radius parameter
by some absolute constant. Such losses can be acceptable in applications in which the underlying sets
are largely “transverse” to the balls
, so that the
-entropy of
is largely independent of
; this is a situation which arises in particular in the case of graphs
discussed above, if one works with “vertical” metrics whose balls extend primarily in the vertical direction. (I hope to present a specific application of this type here in the near future.)
Henceforth we work in an additive group equipped with a translation-invariant metric
. (One can also generalise things slightly by allowing the metric to attain the values
or
, without changing much of the analysis below.) By the Heine-Borel theorem, any precompact set
will have finite entropy
for any
. We now have analogues of the two basic Ruzsa lemmas above:
Lemma 4 (Ruzsa covering lemma) Let
be precompact non-empty subsets of
, and let
. Then
may be covered by at most
translates of
.
Proof: Let be a maximal set of points such that the sets
are all disjoint. Then the sets
are disjoint in
and have entropy
, and furthermore any ball of radius
can intersect at most one of the
. We conclude that
, so
. If
, then
must intersect one of the
, so
, and the claim follows.
Lemma 5 (Ruzsa triangle inequality) Let
be precompact non-empty subsets of
, and let
. Then
.
Proof: Consider the addition map from
to
. The domain
may be covered by
product balls
. Every element
of
has a preimage
of this map which projects to a translate of
, and thus must meet at least
of these product balls. However, if two elements of
are separated by a distance of at least
, then no product ball can intersect both preimages. We thus see that
, and the claim follows.
Below the fold we will record some further metric entropy analogues of sum set estimates (basically redoing much of Chapter 2 of my book with Van Vu). Unfortunately there does not seem to be a direct way to abstractly deduce metric entropy results from their sum set analogues (basically due to the failure of a certain strong version of Freiman’s theorem, as discussed in this previous post); nevertheless, the proofs of the discrete arguments are elementary enough that they can be modified with a small amount of effort to handle the entropy case. (In fact, there should be a very general model-theoretic framework in which both the discrete and entropy arguments can be processed in a unified manner; see this paper of Hrushovski for one such framework.)
It is also likely that many of the arguments here extend to the non-commutative setting, but for simplicity we will not pursue such generalisations here.
— 1. Approximate groups —
In discrete sum set theory, a key concept is that of a -approximate group – a finite symmetric subset
of
containing the origin such that
is covered by at most
translates of
. The analogous concept here will be that of a
-approximate group: a precompact symmetric subset
of
containing the origin such that
is covered by at most
copies of
. Such sets obey good iterated doubling properties; for instance,
is covered by at most
copies of
for any
. They can be generated from sets of small tripling:
Lemma 6 Let
be a precompact non-empty subset of
, and let
. If
or
, then
is a
-approximate group.
Proof: From Lemma 5 we have
(for an appropriate choice of sign) and
and thus by Lemma 4, may be covered by at most
copies of
, giving the claim.
— 2. From small doubling to small tripling or quadrupling —
As we saw above, Lemma 5 and Lemma 4 are already very powerful once one has some sort of control on triple or higher sums such as ,
, or
. But if only controls a double sum such as
or
, it is a bit trickier to proceed. Here is one estimate (somewhat analogous to Proposition 2.18 from my book with Van Vu, but with slightly worse numerology):
Lemma 7 Let
be a precompact non-empty subset of
, and let
. If
, then
.
One can combine this lemma with Lemma 5 to obtain similar conclusions starting with a hypothesis on rather than
; we leave this to the interested reader. Of course, the conclusion can also be combined with Lemma 6; we again leave this as an exercise.
Proof: Write . Then
, so we may find a
-separated subset
of
with
. By hypothesis, we may cover
by balls
with
. Call a centre
popular if
contains at least
differences
with
(counting multiplicity), and let
denote the set of popular centres. Then at most
of the
pairs
have
lying in an unpopular ball
, thus we have
for at least
pairs
in
. Thus, by the pigeonhole principle, there exists
such that at least
elements of
lie in
. Thus
and thus
Next, for any , we consider the set
of pairs
such that
. We may write
for some and
. By definition of
, we can find distinct pairs
for
with
such that
for all
. As
is
-separated and
has diameter at most
, the
must be distinct in
, and similarly for the
. We then have
for . Each
lies in
and is thus lies in
for some
, and similarly
for some
. Then
and so . Also, since
and the
are
-separated, we see that the
are distinct as
varies. We conclude that
. On the other hand, the total number of pairs
is
, and any two
-separated points
in
generate disjoint sets
. We conclude that there can be at most
-separated points in
, thus
and thus
By Lemma 5 and (1), we conclude that
and the claim follows.
— 3. The Balog-Szemeredi-Gowers lemma —
One of the most difficult, but powerful, components of the elementary sum set theory is the tool now known as the Balog-Szemerédi-Gowers lemma, which converts control on partial sumsets (or equivalently, lower bounds on “additive energy”) to control on total sumsets, after suitable refinements of the sets. Here is one metric entropy version of this lemma.
Lemma 8 (Balog-Szemerédi-Gowers) Let
and
, and let
be precompact subsets of
. Suppose that
and
where we endow
with the sup norm metric. Then there exist subsets
,
of
respectively with
and
Again, this lemma may be usefully combined with the previous sum set estimates, much as was done in my book with Van Vu; I leave the details to the interested reader.
Proof: Let ,
be maximal
-separated subsets of
respectively, thus
, and similarly
.
By hypothesis, we can find at least quadruples
which are
-separated in
, such that
for all such quadruples. By construction of , each such quadruple can be associated to a nearby quadruple
with
and thus by the triangle inequality
Also by the triangle inequality we see that each can be associated to at most one of the quadruples
, and as the
are
-separated, the
are
-separated. We conclude that there is a set of at least
quadruples
in
obeying (2) that are
-separated.
Call a pair popular if there are at least
of the above quadruples
in
obeying (2) with the indicated first two coefficients. The unpopular pairs
absorb at most
of the
quadruples, so at least
of the quadruples are associated to popular pairs
. On the other hand, as the quadruples are
-separated, we see from (2) and the triangle inequality that for each
there is at most one
giving rise to a quadruple
. Thus each
can be associated to at most
quadruples, and we conclude that the set
of popular pairs
has size at least
. In particular this shows that
.
We now apply the graph-theoretic Balog-Szemerédi-Gowers lemma (see Corollary 6.19 of my book with Van Vu) to conclude that there exists a subset of
and
of
with
such that for every and
there exist
pairs
such that
lie in
. Since
was already
-separated, we conclude that
Now fix and
, and let
be one of the above
pairs. As
is popular, we can thus find
pairs
such that
furthermore, the lie in an
-separated set. Similarly, we can find
pairs
and
pairs
such that
with the and
also lying in an
-separated set. In particular, we see that given
,
uniquely determine
, and
uniquely determine
, so a single sextuple
can arise from at most one pair
; in particular, we see that
sextuples are associated to each pair
. Taking alternating combinations of (3), (4), (5) we see that
In particular, if and
are two pairs in
with
at least
apart, then a single sextuple
can be associated to at most one of these pairs. Since the number of sextuples is at most
, we conclude that there are at most
pairs
with
-separated differences
, thus
as required.

20 comments
Comments feed for this article
19 March, 2014 at 6:44 pm
Anonymous
Is there a typo in the definition of difference sets?
[Corrected, thanks – T.]
19 March, 2014 at 10:18 pm
domotorp
In proof of Lemma 1, {|A|} should be {|B|}.
[Corrected, thanks – T.]
19 March, 2014 at 11:50 pm
domotorp
Another typo above Def 3: odubling
[Corrected, thanks – T.]
20 March, 2014 at 12:26 am
domotorp
And at the end of Def 3 there is an extra {itemize}
[Corrected, thanks – T.]
20 March, 2014 at 12:30 am
domotorp
Closing parenthesis missing from para above lemma 4.
[Corrected, thanks – T.]
19 March, 2014 at 11:56 pm
domotorp
The internal covering number, {N^{int}_r(E)}, might decrease in E – consider r=3 and E={0,2,4} and E’={0,4}.
[Corrected, thanks – T.]
20 March, 2014 at 4:55 am
kyle
I think there are some typos in the proof of lemma 1. For example, I think the maximal set that is chosen should be a subset of A, not a subset of B as stated. I also agree with the earlier comment by domotorp that the cardinality of each of these translates is |B|, not |A|.
20 March, 2014 at 4:56 am
kyle
Sorry, didn’t mean to post a reply under this comment.
20 March, 2014 at 4:54 am
chorasimilarity
Kind of being in this frame of “discretized”, but not discrete, nor continuous, in arXiv:1304.3358 there is a very simple note about a “geometric Ruzsa triangle intequality”, which does not even use group operations, maybe is of some interest here.
20 March, 2014 at 1:06 pm
Pascal
Is there a version of the basic results of additive combinatorics for multisets rather than sets, or even better for multisets where negative cardinalities are allowed?
If this looks like a baroque idea, note that there is a quite natural interpretation: if c_a denotes the mulitplicity of element a, we can represent a multiset by the polynomial sum_a c_a X^a. Taking a sum set A+B then amounts to multiplying the 2 corresponding polynomials.
20 March, 2014 at 3:46 pm
Terence Tao
There is a closely analogous theory to discrete sumset theory for random variables, with Shannon entropy taking the place of cardinality: see http://www.ams.org/mathscinet-getitem?mr=2647496 . For signed functions, the appropriate tool is Fourier analysis and convolution, for which there are certainly a lot of estimates available (though once one gives up positivity, many of the more combinatorial estimates in the sumset theory no longer have good analogues).
27 March, 2014 at 2:35 am
Geoff Sang
Hi Terence,
I am a year 9 student from Western Australia, and I find your blog very fascinating. The school maths I do are easy however I know that there are many more students better than I am.
I have never done complicated maths before like the Australian Maths Olympiad (unlike you when you were my age), but now I am starting to learn the fundamentals. Proof has always been an obstacle when I do competitions (e.g. The Western Australian Junior Mathematical Olympiad). How could I practice proof and also understand a question better when doing competitions?
Thank you,
Geoff Sang
21 March, 2014 at 5:05 pm
arch1
In the proof of Lemma 1 should “lie in |A + B|” be “lie in A + B”?
[Corrected, thanks – T.]
25 March, 2014 at 5:59 am
arch1
In the orthogonal nxn matrix example: “…let A be the matrices obtained by starting with an orthogonal matrix in On(R) and rounding each coefficient to the nearest multiple of epsilon…. This is a finite set (whose cardinality grows as [epsilon goes to 0] like a certain negative power of epsilon).”
The above recipe seems to me to produce exactly one matrix, regardless of epsilon’s value, so I must be missing something real basic. Can someone help?
[Reworded for clarity – T.]
28 March, 2014 at 8:09 am
MrCactu5 (@MonsieurCactus)
It looks like you are describing some sort of generalized Hamming Code? For noisy channel coding the “buzzwords” should be a certain Hammin distance apart.
At this point I am taking a step back and reading through your book with Van Vu.
29 May, 2014 at 9:15 am
Anonymous
Prof. Tao,
In general, we can not replace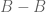 by
by  in Ruzsa’s covering lemma without some sort of loss. That is showed in an exercise in the book of you and Prof. Vu. If
in Ruzsa’s covering lemma without some sort of loss. That is showed in an exercise in the book of you and Prof. Vu. If 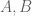 are finite subsets of integers, is it true that we can cover
are finite subsets of integers, is it true that we can cover  by at most
by at most  (
( ) translates of
) translates of  ? I did some simulations, and no counterexample was found.
? I did some simulations, and no counterexample was found.
Best,
Jiange
29 May, 2014 at 11:57 am
Terence Tao
Unfortunately not; one can take a counterexample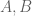 in a finite group such as
in a finite group such as  (e.g. the one in Exercise 2.4.1 of my book with Van), and “transfer” it to the integers by considering a set such as
(e.g. the one in Exercise 2.4.1 of my book with Van), and “transfer” it to the integers by considering a set such as  and
and  , where
, where  is much larger than
is much larger than  . This modifies the covering number by a factor of 2 or so, but the failure in
. This modifies the covering number by a factor of 2 or so, but the failure in  of the naive Ruzsa covering lemma is by an arbitrarily large constant, so it can also create an arbitrarily large failure of that covering lemma in the integers.
of the naive Ruzsa covering lemma is by an arbitrarily large constant, so it can also create an arbitrarily large failure of that covering lemma in the integers.
2 May, 2018 at 8:25 am
Anonymous
Typo: is slightly more convenient than the other notions of metric entropy, so we will abbreviate
is slightly more convenient than the other notions of metric entropy, so we will abbreviate  ”
” is slightly more convenient than the other notions of metric entropy, so we will abbreviate
is slightly more convenient than the other notions of metric entropy, so we will abbreviate  ” (The difference is in the superscript.)
” (The difference is in the superscript.)
In the paragraph following Definition 3,
“…the external covering number
should be
“…the external covering number
I think.
26 April, 2019 at 11:48 am
aetjmaison
In your definitions of entropies, are the balls open? If they are closed, should the inequality be strict in the definition of r-separation? Thank you.
26 April, 2019 at 4:29 pm
Terence Tao
It doesn’t make too much difference to the arguments, but in my post the balls are open, and I believe all the statements in the post are valid with non-strict inequality in the definition of separation.