Last updated: Feb 24, 2024
An introduction to measure theory
Terence Tao2011; 206 pp; hardcover
ISBN-10: 0-8218-6919-1
ISBN-13: 978-0-8218-6919-2
Graduate Studies in Mathematics, vol. 126
This continues my series of books derived from my blog. The preceding books in this series were “Structure and Randomness“, “Poincaré’s legacies“, and “An epsilon of room“. It is based primarily on these lecture notes.
An online version of the text can be found here. The official AMS page for the book is here. There is no solution guide for this text.
The book has been reviewed for the American Mathematical Monthly by Takis Konstantopoulos, and also reviewed for the Mathematical Association of America by Mihaela Poplicher.
Errata:
- Page 2: In the first paragraph, “same area” should be “same measure”. In the third paragraph, “
is indeterminate” should be “
vanishes by our conventions”
- Page 6: In Remark 1.1.3, “Exercise!” should be “exercise!”.
- Page 8: In the first paragraph, “or even a rotated box” should be a separate sentence: “A rectangle with sides parallel to the axes is elementary, but most rotations of that rectangle will not be.”
- Page 10: In Exercise 1.1.14, “epsilon entropy” is a slightly more accurate description here than “metric entropy”.
- Page 11: In Exercise 1.1.19, add “Generalise this result to the case when
is Jordan measurable instead of elementary”. In Exercise 1.1.18(4), the second
should be in boldface.
- Page 14: In Exercise 1.1.24(3), “Jordan measurable of” should be “Jordan measurable subset of”.
- Page 15: In Section 1.2, (iii), “inner and Jordan outer” should be “Jordan inner and outer”.
- Page 17: Exercise 1.1.13 should be Exercise 1.1.5. In the last paragraph, “In the notes below” should be “In the rest of this section”.
- Page 19: “assigment” should be “assignment”, and “of element of” should be “of elements of”.
- Page 20: In the first paragraph, “Vol I” should be “Vol. I”
- Page 21 Remark 1.2.7: “proof this” should be “proof of this”.
- Page 27: In the proof of Lemma 1.2.13(v), (iv) should be (vi). In the proof of Lemma 1.2.13(vi), the phrases “By countable additivity” and “this implies that
is contained
” should be interchanged.
- Page 29: In the hint for Exercise 1.2.10: “conclude that
is homeomorphic …” should be “conclude that the set of endpoints of the intervals is homeomorphic …”, and “infinitely many closed intervals” should be “countably many closed intervals”.
- Page 32: In Exercise 1.2.13(ii), insert “Let
,
be as in part (i).”
- Page 34: In Exercise 1.2.22(i), “Lebesgue measure” should be “Lebesgue outer measure”.
- Page 35: In Exercise 1.2.24(i), “a equivalence” should be “an equivalence”.
- Page 36: In Exercise 1.2.25 and the following paragraph, “continuously differentiable” may be weakened to “Lipschitz continuous”.
- Page 40: Near the end of the second paragraph, the reference to
should be deleted.
-
Page 42: On line 12, “indicator function of these sets” should be “indicator functions of these sets”. In Definition 1.3.3, “a unsigned” should be “an unsigned”.
- Page 45: In Definition 1.3.6, “said to be absolutely integrable of” should be “said to be absolutely integrable if”. Before this definition, “absolutely Lebesgue” should be “absolutely convergent Lebesgue”.
- Page 46: In the hint for Exercise 1.3.2, “the second inequality” should be “the second equality”.
- Page 50: In Exercise 1.3.3(iii), “unsigned measurable functions” should be “at most countable family of unsigned measurable functions”.
- Page 52: In Exercise 1.3.8, both (iii) and (iv): “an” should be “a”. After Exercise 1.3.8, add the following question: Suppose that
is measurable, and
is a surjective linear map. Show that
is also measurable. (Hint: uses Exercises 1.2.21 and 1.2.22.) What happens if the requirement that
be surjective is dropped?”.
- Page 58: In Exercise 1.3.21, “greatest integer less than” should be “greatest integer less than or equal to”.
- Page 60: At the end of Theorem 1.3.20, add “We call a function compactly supported if its support is contained in a compact set.”
- Page 64: In the proof of Theorem 1.3.28,
and
should both be
,
should be
, and the sentence fragment “, and the same is true for local uniform limits (because continuity is a local property)” should be deleted.
- Page 67: In Definition 1.4.1, “
of
” should be “
of subsets of
“. “a sub-algebra of” should be moved from the fragment “
is finer than…” to “
is coarser than”.
- Page ???: In Exercise 1.4.3, “if and only if exists a bijection” should be “if and only if there exists a bijection”.
- Page 68, Example 1.4.7: “finer… atomic algebra” should be “finer … atomic algebras”, and “one or more” should be “zero or more”. At the end of Example 1.4.4, the period should be outside the parenthesis.
- Page 70, Exercise 1.4.9, (ii): “either” should be “are either”. In Exercise 1.4.7,
should be
.
- Page 72, line 1: “only holds if and only if” should be “holds if and only if”.
- Page 73, Remark 1.4.17: “so that
” should be “so that
is the Borel
-algebra”. In Exercise 1.4.15,
should be
.
- Page 74, Section 1.4.3, l. 2: “a sigma-algebra a measurable space” should be “a measurable space”. In Remark 1.4.18, delete the left parenthesis before “Indeed”.
- Page 75: In Exercise 1.4.20, “Boolean
-algebra” should be “Boolean algebra”.
- Page 77: In Example 1.4.29, “Exercise 1.4.22” should be “Example 1.4.22”.
- Page 81: In Definition 1.4.31 and Exercise 1.4.32, “a measurable space
” should be “a measure space
“. In Exercise 1.4.33 (iv), the reference to Exercise 1.3.2 instead of Exercise 1.1.2. The definition of almost everywhere should be moved to before Exercise 1.4.31 where it is first used.
- Page 83: In Exercise 1.4.35 (ix,x), “Horizontal” and “Vertical” should be interchanged.
- Page 84: In the proof of Theorem 1.4.37, “horizontal” and “vertical” should be interchanged.
- Page 85: In Exercise 1.4.39, “Exercise 1.4.26” should be “Example 1.4.26”.
- Page 86: After Definition 1.4.38, add to the following paragraph “Clearly, this definition…” the sentence “As in that definition, one can extend the integral to measurable functions that are
-almost everywhere defined, rather than everywhere defined.”
- Page 87: Replace the second half of the last sentence of Example 1.4.40 by “but the support of the
are becoming increasingly wide, and so Exercise 1.4.41 does not apply”. In Example 1.4.41, “converges pointwise to
” should be “converges pointwise to
“.
- Page 88: In the proof of Theorem 1.4.43, “vertical truncation” should be “horizontal truncation”.
- Page 91: In the first paragraph of the proof of Theorem 1.4.48,
should be
.
- Page 96: In Exercise 1.5.1,
may be replaced by
.
- Page 97: The final sentence of Remark 1.5.6 is redundant (it already appears in page 96) and can be deleted.
- Page 99: In the fourth line of Section 1.5.2, “a measurable set” should be “an indicator function of a measurable set”.
- Page 100: In Exercise 1.5.3(iii), replace the condition after “if and only if” by “
as
“. Similarly in (vi), replace the condition after “if and only if” by “
as
“. In 1.5.3 (vii) “converges in
norm” should be “converges in
norm to zero”.
- Page 103, Section 1.5.5, line 4: “examples shows” should be “examples show”. In the second paragraph of Section 1.5.5,
should take values in
, rather than
. In Exercise 1.5.9, “using Exercise 1.5.6” should be “using Exercise 1.5.8”.
- Page 104: In Exercise 1.5.10, the dominated convergence theorem should be used instead of the monotone convergence theorem.
- Page ???: The definition of uniform integrability in Definition 1.5.11 is a little weaker than the commonly accepted one in the case of infinite measure spaces. The blog post associated to this section contains the corrected version (with attendant changes to some subsequent material).
- Page 106: In the second display after (1.17),
should just be
.
- Page 107: In Exercise 1.5.19, a comma is missing between “almost uniformly” and “pointwise”.
- Page 108, line 5: a right parenthesis is missing before “is commonly used”. At the start of Section 1.6, add “Throughout this section, the notions of measurability and “almost everywhere” are understood to be with respect to Lebesgue measure.”
- Page 112: For Theorem 1.6.11 and Exercise 1.6.5, “definite integral” should be “indefinite integral” (because the endpoint
is allowed to vary). In Theorem 1.6.11,
should be
.
- Page 114 3rd paragraph, line 3: the symbol
should be an
. In the third display from bottom,
should be
. In the proof of Proposition 1.6.13, “Applying Littlewood’s second principle … to …
” should be “Applying Littlewood’s second principle … to …
“.
- Pages 115-116, Exercise 1.6.9: The second item here should be labeled (ii) (and the third should be labeled (iii)). In Remark 1.6.15, “equal to 2” should be “equal to 4”, and “if one force” should be “if one wishes to force”.
- Page 117: In the paragraph after (1.24), “
is sufficiently close to
” should be “
is sufficiently close to
“.
- Page 118: In Lemma 1.6.17(ii),
should be
, and similarly for the second display after (1.25).
- Page 119: Near the bottom of the page, “Corollary 1.6.5” should be “Exercise 1.6.5”. In the second paragraph, replace “but not
” with “but is disjoint from
(since
for all
)”, and
should be
.
- Page 120, Exercise 1.6.13: “Lemma 1.6.16” should be “Exercise 1.6.12”, and the hypothesis
should be added.
- Page 121: Before Exercise 1.6.14, “Lebesgue point for
” should be “Lebesgue point for
“.
- Page 122: In Remark 1.6.21, the fragment
should be deleted. In Theorem 1.6.20, the second integral should be over
rather than
.
- Page 124: In the first and second displays, the integrals over
should instead be over
.
- Page 125, Exercise 1.6.21: “Besicovich” should be “Besicovitch”; part (i) should be
and
as opposed to
and
. In part (ii) of this exercise,
should be
. In the hint for the exercise, “the the” should be “the”. In Exercise 1.6.22, “positive length” should be “positive finite length”. In Exercise 1.6.20, the integral over
should instead be over
.
- Page 127: In Exercise 1.6.27(iii), add the parenthetical “In fact one can take
.”
- Page ???: In the proof of Lemma 1.6.28, “
is contained” should be “
is contained”
- Page 128, Section 1.6.3, line 4: “continuous not differentiable” should be “continuous but not differentiable”. In Exercise 1.6.28(ii), delete “8-dyadic”, and replace “n” with “m” throughout to reduce confusion. Also, replace
with
, and replace
with
throughout the exercise.
- Page 129: In part (iv), “lower right derivative” should be “lower left derivative”. Afterwards, “rather than on the endpoints” should be “rather than on the real line”. After Exercise 1.6.30, “four derivatives” should be “four Dini derivatives”.
- Page 130: In the second to last line (in the proof of Lemma 1.6.26),
should be
. Similarly, on page 132 in the proof of Lemma 1.6.28,
should be
and
should similarly be
.
- Page 131-132:
and
should be
and
respectively throughout. In the second display,
should be
. At the end of Exercise 1.6.31, add a right parenthesis. In the paragraph preceding Definition 1.6.30, remove the period after Lemma 1.6.26.
- Page 133: In the proof of Lemma 1.6.31,
should be
. At the end of the proof, add that by continuity of
, one can assume that
avoid the jumps.
- Page 134: On the eighth line: “
is discontinuous” should be “
is discontinuous”.
- Page ???: In the proof of Theorem 1.6.25, in the display, Lebesgue measure
is missing on the left-hand side.
- Page 135: Before Definition 1.6.33, “absolutely convergent functions” should be “absolutely integrable functions”. After the first display, “four Dini derivatives” should be “three Dini derivatives”. In Definition 1.6.33,
should be
, and similarly on p. 136, 137. “Since
is almost everywhere differentiable” should be “Since
is almost everywhere differentiable”.
- Page 137: In the second paragraph, “it suffices to (by writing
to show that
” should be “it suffices (by writing
) to show that
“. “is a monotone increasing function” -> “is a monotone non-decreasing function”, and “for all $a \leq b$” should be stated after the second display.
- Page 141: in the definition (i) after Remark 1.6.38, “contains
” should be “whose closure contains
“.
- Page 144: In the third paragraph of the proof of the rising sun lemma (Lemma 1.6.17),
should be
in the definition of
and in the next two occurrences (i.e. “
but not
” should be
but not
“, and “
” should be
“.
- Page ???: In Exercise 1.6.47, the last two parts of the exercise should be numbered (vii) and (viii) rather than (1) and (2).
- Page 145, bottom: “
exists” should be “
exists”. After Exercise 1.6.52, “ensure the almost everywhere existence” should be “ensure the absolute integrability of the derivative”.
- Pages 149-152: In Section 1.7.1, “Caratheodory extension theorem” should be “Caratheodory lemma” throughout.
- Page 150, Exercise 1.7.2: “Lebesgue outer measurable” should be ” the Lebesgue outer measure”
- Page 151: In the last two displays, and in the first display on the next page,
may be simplified to
. In the second paragraph, “a disjoint sequence of” should be “a sequence of disjoint”.
- Page 156: In Theorem 1.7.9,
should be
. In the second paragraph of the proof of this theorem, before “, adopting the obvious conventions”, add “to be the required value of
given by (1.33) (e.g.,
)”.
- Page 157: Before (1.35), replace “By subadditivity, it suffices to show that” with “By finite additivity, we have
for any
, so it suffices to show that”. In the second display after (1.35), the right-hand side should be
rather than
. In the second and third paragraphs, “Exercise!” should be “exercise!”. “We suppose that
” should be “We suppose that
“.
- Page 158: Throughout this page, “Exercise!” should be “exercise!”.
- Page 159: In Exercise 1.7.13, add a right parenthesis after “absolutely integrable”.
- Page 160: In Exercise 1.7.14(ii), “delta functions” should be “Dirac measures” for consistency. In the first line,
should be
.
- Page 161: In Exercise 1.7.18 (i), $latex Y \in B_Y$ should be
. In the second display,
should be
- Page 162: Exercise 1.7.19(ii) is not correct as stated and should be deleted.
- Page 163: In the third paragraph of the proof of Proposition 1.7.11,
should be
.
- Page 164: “integrate in
” should be “integrate in
“.
- Page 165, Exercise 1.7.21: Add the line: “In particular,
and
are isomorphic as measure spaces and can thus safely be denoted as
.” In the definition of a monotone class, “is a collection” should be “to be a collection”. In Example 1.7.13,
should be
. In Exercise 1.7.21, “
-finite sets” should be “
-finite measure spaces”.
- Page 167: The sentence preceding Theorem 1.7.18 should be deleted.
- Page 168, in (1.37), the third integral should have X and Y interchanged (as well as the measures
and
). In the proof of Theorem 1.7.18, Exercise 1.4.28 should be Exercise 1.4.26.
- Page 169: In Exercise 1.7.22, “the counting measure (…)
” should be “the counting measure
(…)”. In the second line of (1.38), the integral should be over
rather than
, and
should be
. In the seventh line from the bottom, “equal to one for every
” should be “equal to one for every
“.
- Page 170: In Exercise 1.7.23, the right-hand side of the display should read
rather than
. Also, “exist and are absolutely integrable” should be “exist as absolutely integrable integrals” (two occurrences). In the statement of Theorem 1.7.21(iii), the second appearance of
should instead be
. In Remark 1.7.22, “
-finite setting” should be “non-
-finite setting”.
- Page 171: In Exercise 1.7.24, “Show that if” should be “Show that”.
- Page 175: In the last complete paragraph, “for thus purpose” should be “for this purpose”.
- Page 187: In the display before Remark 2.2.3,
should be
.
- Page 188: After (2.2),
should just be
.
- Page 189: In the second paragraph, a comma is missing between “For
” and “
is clearly”. In the third paragraph, “
is a null set” should be “
is a null set”. In the fourth paragraph, “
is rational” should be “
is countable”. In the definition of
,
should be
. The definition of F-volume is missing the text “to equal the right-hand side of (1.33)”; also, one could replace “F-volume” by “F-length” to be more descriptive.
- Page 191: The modified function
should take values in
rather than
.
- Page 194: In the final sentence of Section 2.3,
should be
for notational consistency.
- Page 195: In Exercise 2.4.1(3),
should be
. In Exercise 2.4.1(8),
should be
.
- Page 197: In the final display,
should be defined as
rather than
. On the first display of the next page, the first occurrence of
should be
, and the final
should just be
. In the seventh paragraph,
should be
.
- Page 205: The index entry for “restriction (measure)” should point to Example 1.4.25 rather than Exercise 1.4.35 (which could instead be referenced by “restriction (function)”.

115 comments
Comments feed for this article
23 June, 2021 at 12:55 am
Anonymous
Thank you for posting many books and lecture notes of yours.
1 July, 2021 at 6:55 am
Zijin Liu
Dear Professor Tao,
In the pdf version, page 159, the proof of lemma 1.6.28, “ whenever
whenever  ” should be “
” should be “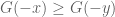 whenever
whenever  ” (because of the rising sun lemma)
” (because of the rising sun lemma)
[This is already noted in the errata – T.]
2 December, 2021 at 1:41 pm
Anonymous
I don’t think this comment is quite the erratum mentioned on Page 130? The relevant bullet point only mentions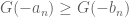 not
not 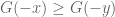
[Corrected, thanks – T.]
11 September, 2021 at 1:09 am
Yaver Gulusoy
Dear Prof. Tao,
Page 157: in the sentence before the third display, “we suppose that ” should be “we suppose that
” should be “we suppose that  “.
“.
[Erratum added, thanks – T.]
12 September, 2021 at 6:36 am
Batuhan Bayır
Dear Tao,
After definition 1.3.2 (in draft edition, page 50) you said Simp$^{+}$($R^{d}$) is $[0,+\infty]$-module. $R=[0,+\infty]$ is not ring, because we don’t have additive inverses of elements in this set. So I think we don’t have $R=[0,+\infty]$-module structure.
[Modules can also be defined over semirings: see https://en.wikipedia.org/wiki/Module_(mathematics)#Generalizations -T.]
14 September, 2021 at 8:09 pm
Anonymous
Hi Prof. Tao,
Here are two errata (page count following print book):
page 11, Exercise 1.1.18(4): The Q in the definition of the set of bullets is typeset incorrectly.
page 50, Exercise 1.3.3(iii): one should add the additional requirement that the set of unsigned measurable functions is countable.
Thanks.
[Errata added, thanks – T.]
13 October, 2021 at 5:34 pm
Zhiyuan Luo
Hi Prof. Tao,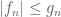 ” should be “
” should be “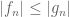 ”.
”.
Page 96: Exercise 1.5.1 (iii), “
Page 135: “Since is almost everywhere differentiable ” should be “Since
is almost everywhere differentiable ” should be “Since 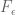 is almost everywhere differentiable” .
is almost everywhere differentiable” .
Page 137: In the proof, “this is a monotone increasing function” should be “this is a monotone nondecreasing function”, and it would be better if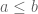 is explicitly stated in the proof.
is explicitly stated in the proof.
Page 189: “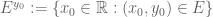 ” should be “
” should be “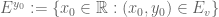 ”.
”.
Page 191: “let be the modified function” should be “let
be the modified function” should be “let 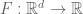 be the modified function”.
be the modified function”.
Page numbers correspond to printed book.
[Errata added, thanks – T.]
3 November, 2021 at 10:16 am
Zane Li
This is not really an errata, but in Section 1.4 only and starting with Exercise 1.4.33, the printed version number is off by one from the online preliminary version of the textbook. More precisely, Exercise 1.4.33 in the printed version is Exercise 1.4.34 in the online preliminary version. This continues on to the last exercise, Exercise 1.4.50 in the printed version which is Exercise 1.4.51 in the online preliminary version.
1 April, 2022 at 8:01 am
kent
I have a question about Example 1.4.7 on page 82, in the manuscript that is posted online.
It is the example that introduces atomic algebras. I am wondering if the sentence that says “…is the collection of all sets that can be represented as the union of one or more atoms.”. I am wondering if it should be “zero or more”, instead of “one or more”. I ask because if we take $X = \{0,1\}$ and $A_0 = {0}$ and $A_1 = {1}$. Then every union of one or more these disjoint sets will be nonempty, so the empty set isn’t obtainable.
I really appreciate the book. Thanks.
[Corrected, thanks – T.]
1 April, 2022 at 8:14 am
Kent
A small issue with Exercise 1.4.3 on page 83 “if and only if exists
a bijection” should probably be “if and only if THERE exists a bijection”.
[Correction added, thanks – T.]
5 April, 2022 at 2:05 pm
Kent
I think there is a small issue with an exercise. It is exercise 1.2.10 on page 35 in the manuscript that is posted online. It is the exercise about the impossibility of expressing as the countable union of disjoint closed intervals. In the hint, it says, “… assume for the sake of contradiction, that
as the countable union of disjoint closed intervals. In the hint, it says, “… assume for the sake of contradiction, that  is the union of infinitely many closed intervals,…” I think it should probably be “union of countably many closed intervals”.
is the union of infinitely many closed intervals,…” I think it should probably be “union of countably many closed intervals”.
[Erratum added, thanks – T.]
6 April, 2022 at 3:09 pm
Kent
There is something you might want to look at. It is the exercise about the Cantor function, Exercise 1.6.47 on page 170 in the manuscript you posted online. The numbering for the steps of the exercise change from roman numeral 1(i) to roman numeral 6(vi) but then switches to arabic numerals for the next two steps.
[Erratum added, thanks – T.]
24 May, 2022 at 5:21 am
jameswang98
I am not a mathematician. The following confuses me much. In page 16, “The Jordan outer measure is the infimal cost required to cover E by a finite union of boxes.” why “finite” ? by the definition:
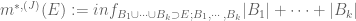 ,
,
 could be any in
could be any in  , so it could be infinite.
, so it could be infinite.
could any one kindly give some explanation ?
[Infinity is not part of the natural number system – T.]
24 May, 2022 at 9:37 am
Anonymous
That’s the definition of being Jordan measurable. Jordan measure is only defined on simple sets, i.e. sets that can be covered by finite union of boxes. It might well be true that you could cover it by infinite number of boxes, but that’s not the point.
25 May, 2022 at 9:48 pm
Anonymous
Is the explanation wrong, or simply not answering the question?
26 May, 2022 at 8:28 am
Aditya Guha Roy
I don’t know if I understood your doubt correctly or not, but let me write on the basis of the impression I developed by reading your comment.
We are looking at the set of all and only those coverings of a set using boxes where only a finite number of boxes are being used. It could very well happen that such a set admits a covering using infinitely many boxes, but we are not bothered by that.
Then we take the infimum as mentioned and we are done.
(PS: while it is true that there are infinitely many natural numbers, infinity is not a part of the natural number system.
A few years back, I had a strange encounter with a friend on a similar topic. My friend who at that time was studying a non-mathematics course, came across the notion of countable and uncountable sets and developed the impression that the power set of natural numbers should be countable. He argued that we consider the set of all subsets of the natural numbers, and then he went on to multiply the elements in each such set, he had the impression that since multiplying natural numbers produce another natural number so the product of the elements of any such set should also give a natural number. Of course, this is wrong, because at the first place we do not even have a well-defined notion of multiplying infinitely many natural numbers inside the natural number system.)
Hope this helps!
29 May, 2022 at 1:34 am
jameswang98
Jordan measure is equivalent with Riemann integral and Lebesgue measure is equivalent with Lebesgue integral. The reason that Lebesgue measure is more powerful than Jordan measure is that Lebesgue measure uses countable covers instead of finite covers. This is inferred by the book. But actually, Riemann’s partitions could be infinite, so does Jordan measure. That is what really confuse me.
29 May, 2022 at 5:54 am
jameswang98
Now, I understand it. is infinite, but its elements are not, whatever how big they are.
is infinite, but its elements are not, whatever how big they are.
29 May, 2022 at 11:16 am
Anonymous
You need to take an introductory math course on proofs.
1 June, 2022 at 11:56 am
Anonymous
On page 2, the middle of the third paragraph, you said that is indeterminate. But the convention has already been chosen, i.e.
is indeterminate. But the convention has already been chosen, i.e.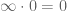 . Is this an error?
. Is this an error?
[Erratum added, thanks – T.]
1 June, 2022 at 12:17 pm
Anonymous
In the proof of Tonelli’s theorem for series [Theorem0.0.2], Let F be any finite sumset of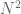 , then
, then
Isn’t the RHS just an expansion (or definition) of the LHS? Are you using the logic that if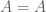 , then
, then  ? or maybe something deeper?
? or maybe something deeper?
2 June, 2022 at 1:38 pm
Terence Tao
No, because if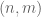 is a pair in
is a pair in  that does not lie in
that does not lie in  , then
, then 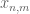 will appear as a term in the RHS but not the LHS.
will appear as a term in the RHS but not the LHS.
2 June, 2022 at 2:20 pm
Anonymous
Dr. Tao:
On page 5 of the book, you introduced the formula for measure of an elementary set $I$ as a limit of a discrete normalized cardinality:
One could prove it by brute force, but how to think of the formula intuitively? wlog, let , then by Archimedean property, there exists
, then by Archimedean property, there exists 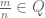 such that
such that  . If we fix
. If we fix  and consider all integers
and consider all integers 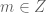 , and count the number of those integers divide
, and count the number of those integers divide  that lies between
that lies between  and
and 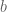 , then normalize it by $n$, and take the limit as
, then normalize it by $n$, and take the limit as  , to get the quantity
, to get the quantity  . By taking the limit, we are turning a discrete argument into a continuous one, since
. By taking the limit, we are turning a discrete argument into a continuous one, since 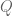 is dense in
is dense in  , we are essentially consider all the rationals in the interval
, we are essentially consider all the rationals in the interval 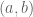 . Is this the right interpretation? Also not sure about the normalization part. What is your opinion?
. Is this the right interpretation? Also not sure about the normalization part. What is your opinion?
3 June, 2022 at 9:34 am
Terence Tao
As intuition, think about how one can approximately measure the length of an interval with a ruler by counting the number of ticks of the ruler that lie within the interval when one lines up the ruler. Using a finer scale of ticks (e.g., one separated by millimeters, rather than by centimeters or inches) will lead to a more precise measurement of length.
3 June, 2022 at 11:20 am
Anonymous
This is a great idea. We can think of as the unit we use to measure the interval. Since the length of an interval is an intrinsic quantity, and is independent of the scale of the ruler we use, thus we should normalize it. Thanks you!
as the unit we use to measure the interval. Since the length of an interval is an intrinsic quantity, and is independent of the scale of the ruler we use, thus we should normalize it. Thanks you!
3 July, 2022 at 2:27 pm
Joshua
This is my take on the normalization part:
I would interpret (1/N) as a constituent of the length we’re trying to approximate. We’re going to multiply (1/N) several times to get the desired length of interval I.
Wlog, the interval we work with will has the form of I= (a,b), whose length is b-a. To simplify the argument later, we define another interval O =( 0,b-a), which has same length as I=(a,b)
If the formula works for the original, it will also work for O.
Denote the real length of O by Length. Denote quantity after the lim part in the RHS of the original formular by Approx . Given any N>0 we have:
Length – Approx(N) ≤ 1/N
Which means, given any N>0, the formular aways underestimates the real value of |O| by an error not exceeding 1/N.
Why:
The Approx(N) has two parts:
The 1/N
And the cardinality of a finite set
1/N can be understood as the unit that we’re using to measure |O|
Starting from 0, we see that the Approx(N) indicates exactly how many units 1/N that we can spread out that are still within the interval O.
Example N=5, and O=(0,1): we have the 1/5 units as: 0, 1/5 , 2/5 , … 5/5, ..1000/5…… Clearly, because we are having an open interval, there will never be exactly 5 units 1/5 that fit in an interval O=(0,1), there will only be 4 of them and hence, we multiple 4 by 1/5 to get Approx(5)=4/5 (underestimating)
Therefore, the formular is actually approximating the real length of an interval. The 1/N part is the unit length and the cardinality part counts how many 1/N that lay between a and b. The bigger N, the smaller error part 1/N.
25 June, 2022 at 1:21 am
Real Analisis 2.0 – Icey の塔
[…] Tao 的 An Introduction to Measure Theory […]
2 October, 2022 at 4:56 am
Real Analysis 1+ – Icey One
[…] 最后推荐一本 Tao 的 An Introduction to Measure Theory 虽然我没有仔细看,但是写的很有趣,观点很奇特。 […]
30 December, 2022 at 11:21 am
Kent VV
I have a question about exercise 1.11 on page 10. It is the question that culminates in showing that the linear image of a Jordan measurable set is Jordan measurable. I am running into the weeds in the first part if don’t assume that the linear transformation is non-singular.
In this case it is easy to show that the map in the hint is finitely-additive, but in the singular case, it seems a different argument is required.
I appreciate your help.
30 December, 2022 at 11:22 am
Kent VV
I realize I never asked a question. Do I need to treat the singular case and non-singular case separately? Is there something I am overlooking?
30 August, 2023 at 3:21 pm
Jas, the Physicist
I’m working on Exercise 1.1.3, where I show that there exists a c such that m'(E) = cm(E) but I’m not sure how to start the proof formally.
I wrote “Let E be an elementary set and let m’ be a measure that satisfies the given properties…”
I don’t know what to do with the hint or why I would think to use it. Another friend of mine said “use the set of irrationals and the set of rationals” but that also is confusing me.
I’m sorry I don’t know how to formulate a good question because I’m not sure what I am proving. Why does it matter that the elementary measure is unique up to some constant? What is a good geometric example of this?
My thoughts were “you can measure a table in inches, meters or feet but its length is still the same.”
3 September, 2023 at 1:09 pm
Terence Tao
This is actually a good analogy. Imagine there are two friends, one of which has a ruler m that measures length in some traditional unit, such as meters, and the other friend has a ruler m’ measuring in mystery unit (let’s say Atlantean inches). But both rulers have their unit markings equally spaced (representing the translation invariance and additivity axioms). How can one then conclude that the length measurements for both units must differ by a multiplicative constant ? Hint: get both friends to measure a meter length stick to determine the constant
? Hint: get both friends to measure a meter length stick to determine the constant  , then figure out what would happen if they both measured, say, a centimeter fragment of that stick. Then work out what happens if measuring a stick that is, say, 37 centimeters long (or more generally, a length that is a rational number of meters).
, then figure out what would happen if they both measured, say, a centimeter fragment of that stick. Then work out what happens if measuring a stick that is, say, 37 centimeters long (or more generally, a length that is a rational number of meters).
21 January, 2024 at 8:27 pm
Anonymous
Dear Professor Tao,
Will a new edition of the book : ‘An introduction to measure theory,’ be coming out in the coming years?
12 February, 2024 at 4:13 pm
Anonymous
Hey. There is a quadratic typo on p.19, line 1: “which is an assigment \( E \mapsto m^{\ast}(E) \) of element of \( [0,+\infty] \)”. (assigNment, of elementS of ).
Sincerely, Robin.
[Errata added, thanks – T.]
13 February, 2024 at 5:02 am
Anonymous
Should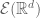 in Exercise 1.4.7, p.70, be
in Exercise 1.4.7, p.70, be ![\overline{\mathcal{E}(\mathbb{R}^d] }](https://s0.wp.com/latex.php?latex=%5Coverline%7B%5Cmathcal%7BE%7D%28%5Cmathbb%7BR%7D%5Ed%5D+%7D&bg=ffffff&fg=545454&s=0&c=20201002) ? (cf. p.7 and p.68 for occurence of these symbols).
? (cf. p.7 and p.68 for occurence of these symbols).
[Erratum added, thanks – T.]