Last updated Apr 2, 2024
Topics in random matrix theory.
Terence TaoPublication Year: 2012
ISBN-10: 0-8218-7430-6
ISBN-13: 978-0-8218-7430-1
Graduate Studies in Mathematics, vol. 132
American Mathematical Society
This continues my series of books derived from my blog. The preceding books in this series were “Structure and Randomness“, “Poincaré’s legacies“, “An epsilon of room“, and “An introduction to measure theory“.
A draft version of the MS can be found here (last updated, Aug 23, 2011; note that the page numbering there differs from that of the published version). It is based primarily on these lecture notes.
Pre-errata (errors in the draft that were corrected in the published version):
- p. 20: In Exercise 1.1.11(i), “if and only for” should be “if and only if for”.
- p. 21: In Exercise 1.1.18, in the definition of convexity,
should be
.
- p. 46: In Exercise 1.3.16, Weilandt should be Wielandt. Similarly on p. 47 after Exercise 1.3.9, in Exercise 1.3.22(v) on page 53, on page 137 before (2.82), on page 184 after (2.129), and on page 208 before 2.6.6. Also, before (1.66), the supremum should be over
rather than
.
- p. 72: All occurrences of
on this page should be
.
- p. 183: The formula (2.127) should be attributed to Dyson ( The three fold way, J. Math. Phys. vol. 3 (1962) pgs. 1199-1215) rather than to Ginibre. Similarly on pages 251, 259, and 265.
- p. 225-226: U should be U_0 (several occurrences). Also,
should be
and
should be
.
- p. 225, Section 2.8.2: right parenthesis should be added after “sufficient decay at infinity.”
- p. 228, just before (2.179): “g_n” should be “f_n”
- p. 231: “lets ignore” should be “lets us ignore”
- p. 258: In the second paragraph,
should be
, and
should be
.
- Page 6: In parts (iii), (iv) of Lemma 1.1.3, “the
” should be “then
“.
- Page 16: In Example 1.1.9, the Poisson distribution should be classified as having sub-exponential tail rather than being sub-Gaussian.
- Page 17: In Exercise 1.1.5,
should be
.
- Page 18: Exercise 1.1.10 is incorrect as stated. Replace the second sentence with “Show that there exists a random variable
(on the sample space
) taking values in
, such that
is equal almost surely to an extension of
(to the sample space
), and
is equal almost surely to an extension of
(to the sample space
).
- Page 22: In Exercise 1.1.18(ii), the requirement that the
take values in
should be dropped.
- Page 29, In Definition 1.1.23,
should lie in
rather than
.
- Page 32: In Definition 1.1.29, Remark 1.1.30, and Exercise 1.1.25, “
-compact” should be “
-compact and locally compact”.
- Page 37: After (1.49), “uniform lower bound” should be “uniform upper bound”, and after the second line of the following display,
should be
.
- Page 41: In the proof of Theorem 1.3.1,
should strictly speaking be
(though it makes no difference to the remainder of the argument).
- Page 41: In Exercise 1.3.1,
should be
.
- Page 45: “But, from (1.57)” should be “But, from (1.58)”.
- Page 49: After (1.72),
should be
, and “orthogonal” should be “orthogonal (using the real part of the inner product)”.
- Page 51: In Section 1.3.6, the role of rows and columns should be reversed in “at least as many rows as columns”.
- Page 53: In Exercise 1.3.22 (vii), (viii), the eigenvalues
should be replaced by singular values
.
- Page 60?: Just before (2.8),
should be
.
- Page 61: In the proof of Theorem 2.1.3,
should be
throughout (three occurrences), and
should be
. Also, the reference to (2.9) here may be replaced by (2.10). In the second last line of the proof of Lemma 2.1.2, a closing parenthesis is missing.
- Page 68: In the last display of Proposition 2.1.9,
should be
. The definitions of
and
are missing absolute value signs (they should be
and
respectively). Also,
should be
.
- Page 69: In Theorem 2.1.10,
should be
. In (2.15),
should be
.
- Page 70: The footnote “Note that we must have
…” should read “Note that we should take
if we wish to allow the variance to actually be able to attain the value
“. The condition
after (2.8) sohuld be
.
- Page 74: In the proof of Lemma 2.1.14,
should be
(two times).
- Page 74: In the proof of Lemma 2.1.15,
should be
, and
should be “one of
or
“.
- Page 76: In the proof of Lemma 2.1.16, after (2.24), the expectation in the next two expressions should instead be conditional expectation with respect to
.
- Page 81: In Remark 2.2.2, “central limit” should be “central limit theorem”
- Page ???: In Lemma 2.3.1,
should be
.
- In Section 2.4: all references to the “circular law” should be to the “semi-circular law”.
- Page 88: At and just before (2.4.1),
should be
. (Also to avoid having to deal with distributions, one should temporarily truncate
to, say,
and then let
go to infinity at the end of the argument.) In the display after (2.40),
should be
. Just before the last display in the proof of Theorem 2.2.8,
should be
.
- Page 90: In Theorem 2.2.9(i), k should range in 1,2,3,… rather than 0,1,2,… .
- Page 95: In the first display of the proof of Theorem 2.2.11,
should be
.
- Page 97: Near the end of Section 2.2.5: [TaVuKr2010] should be [TaVu2009b].
- Page 98: In the proof of Theorem 2.2.13,
should be assumed to be Lipschitz and not just continuous.
- Page 99: In the final display, every term should have an expectation symbol
attached to it.
- Page 107: After (2.58),
should be
(two occurrences).
- Page 113: Before (2.62), the
symbol should be
.
- Page 114: In Proposition 2.3.10,
should be
(two occurrences).
- Page 117: In item (ii) i the list after (2.69), the condition
should be added.
- Page 126, second line: the
error term needs to be improved to
.
- Page 127: In the proof of Lemma 2.3.22, the first arrival can be either a fresh leg or a high multiplicity edge, not simply a fresh leg as stated in the text. However, this does not affect the rest of the argument.
- Page 128: For each non-innovative leg, one also needs to record a leg that had already departed from the vertex that one is revisiting; this increases the total combinatorial cost here from
to
(and the first display should be similarly adjusted). However, the rest of the argument remains unchanged. In the last display and the first display of the next page,
should be
.
- Page 130: The statement “(2.76) holds” should read “(2.76) fails”.
- Page ???: In the paragraph before Remark 2.4.1, it should be stated that
is equipped with the vague topology, and can be viewed as a measurable subset of the compact space
of probability measures on the compactification
.
- Page ???: In the definition of the Stieltjes transform before (2.90),
should be
.
- Page 157: In the discussion of classical independence in Section 2.5, “all of
vanishes” should be “
both vanish”.
- Page 170: Before Exercise 2.5.10, the constraint
should be
.
- Page 174: In Exercise 2.5.15, the additional hypothesis that X and Y are self-adjoint should be added. In Exercise 2.5.16, add “Show more generally that
and
are freely independent for any polynomials
.
- Page 175: In the second display, an extra right parenthesis should be added to the left-hand side.
- Page 176: In the proof of Lemma 2.5.20,
should be
. Also,
should be
.
- Page 181: The formulae for
in Exercises 2.5.20 and Exercises 2.5.21 should be swapped with each other. Also, the formula for the third cumulant
is incorrect; this quantity is in fact equal to the third free cumulant
(but
and
are not equal in general).
- Page 183: In (2.127), the factor
is missing from the denominator.
- Page 184: In the paragraph before (2.128), “eigenvalues of
” should be “eigenvalues of
“.
- Page 187-188: The derivation of the Ginibre formula requires modification, because the claim that the space of upper triangular matrices is preserved with respect to conjugation by permutation matrices is incorrect. Instead, the given data
needs to be replaced by a pair consisting of the random matrix
, together with a random enumeration
of the eigenvalues of
, and the factorisation
is then subjected to the constraint that
has diagonal entries
in that order. (To put it another way, one works in an n!-fold cover of the space of matrices with simple spectrum.) One then performs the analysis in the text, with the enumeration of the eigenvalues of a perturbation of
understood to be the one associated with the diagonal entries of
. (Details may be found at the associated blog entry for this section.)
- Page 189: In the second paragraph,
should be
.
- Page 191: In the last line in the paragraph after (2.137),
should be
.
- Page 192: In Footnote 52 to Section 2.6.3, the exponent
should be
instead.
- Page 199: In (2.161),
should be
.
- Page 200: In the definition of
, the first factor of
should be
. In the eigenfunction equation for
,
should be
.
- Page 201: In (2.162),
should be
.
- Page 203: In Exercise 2.6.6, a factor of
is missing in the
error term, and
should be
. In the penultimate display,
should be
.
- Page 206: In Remark 2.6.8, the
denominator in the first display should instead be in the numerator, and similarly for (2.169); the
denominator two displays afterwards should similarly be
.
- Page 212: For the application of Markov’s inequality and through to the next page, all appearances of
should be replaced by
, and “for at least
values of
” should be “for at least
values of
. Any appearance of
should instead be
.
- Page 213: In Exercise 2.7.1,
should be
, the condition
should be
, the final bound should be
rather than
, and
should be
. The definition of incompressibility should be
, with
to be chosen later, in the next display
should be
, and “within
…
positions” on the next paragraph should be “within
…
positions”. Finally, in footnote 58, the summation should go up to
rather than to
in both occurrences. Just before this exercise,
and
should go up to
rather than
(with some corresponding changes within the exercise).
- Page 214:
should be
(two occurrences), and
should be
in Exercise 2.7.2.
- Page 215: In the last line “Proposition 2.7.3” should be “Proposition 2.7.3 and (2.172)”, and on the next page,
should be
(two occurrences). Somewhat previously, the entropy cost of
should just be
.
- Page 216: In the treatment of the incompressible case, every row
shuold be replaced instead with the corresponding column
.
- Page 217: In Exercise 2.7.3,
should be
. “
” should be “
is comparable to
.” “eigenvalues
” should be “singular values
.
- Page 218. After the first complete sentence, add “This of course contains the event that
.”
- Page 220: In Section 2.7.5, all occurrences of
should be
.
- Page 223, in Theorem 2.8.1: add “in the vague topology” after “converges”.
- Page 225: In Section 2.8.2, all integrals should be over
rather than
. In Exercise 2.8.3, it should be noted that
is interpreted in a principal value sense.
- Pages 226-227: All occurrences of
should be
.
- Page 228: All occurrences of “operator norm” should be “spectral radius”.
- Page ???: In Theorem 2.8.3, add the hypotheses that
almost surely, and that
is compactl supported.
- Page 237: In Proposition 3.1.5, “same distribution as
” should be “same distribution as
. Similarly in Proposition 3.1.16.
- Page 246 The statement and proof of Theorem 3.1.16 have a number of issues. A corrected version can be found at this blog post.
- Page 251: In Exercise 3.1.11,
should be
. In (3.12) and the preceding display,
should be
.
- Page ???: In the last part of Section 2, the threshold
for
should be
, and the factors of
should similarly be
.
- Page 267: In the display after “Hermite polynomial”,
should be
.
- Page 269: In Section 3.4.2, the expansion into Haar coefficients of
should instead be of
.

85 comments
Comments feed for this article
21 February, 2018 at 7:25 am
Daniel Virosztek
Dear Prof. Tao, and
and 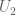 but I also noted that the same argument can be used to show the free independence of
but I also noted that the same argument can be used to show the free independence of  and
and 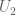 if we consider almost the same situation but we replace the free group
if we consider almost the same situation but we replace the free group  (generated by
(generated by  ) by the free Abelian group
) by the free Abelian group 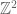 (generated by
(generated by  ).
). on
on  is freely independent from itself, or (which is more or less the same) the classical random variable drawn uniformly at random from the unit circle of the complex plain (let us denote it by
is freely independent from itself, or (which is more or less the same) the classical random variable drawn uniformly at random from the unit circle of the complex plain (let us denote it by 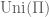 for further use) is freely independent from itself.
for further use) is freely independent from itself. is a faithful non-commutative probability space (which is, in fact, commutative), and
is a faithful non-commutative probability space (which is, in fact, commutative), and  and
and  are freely independent if
are freely independent if  They also commute, but none of them is equal to a scalar.
They also commute, but none of them is equal to a scalar. are replaced by
are replaced by 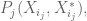 that is, if we require that the equation holds not only for one variable polynomials, but also for two-variable polynomials with arguments
that is, if we require that the equation holds not only for one variable polynomials, but also for two-variable polynomials with arguments 
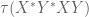 after normalization.)
after normalization.)
as a newcomer in probability theory (coming from functional analysis), I enjoy reading your book Topics in RMT very much.
However, I was a bit confused while doing Exercise 2.5.16.
I was able to verify the free independence (according to Definition 2.5.18.) of
I was surprised as I thought that the non-commutativity of the underlying group is essential. Moreover, it turns out that (according to Def. 2.5.18.) the shift operator
This latter example also shows that Exercise 2.5.15. can not be done with the current definition of free independence, because
I guess, all of these problems can be solved if in the definition of free independence (Def. 2.5.18.) all the expressions
(And in Exercise 2.5.15. we should then consider
21 February, 2018 at 8:09 am
Terence Tao
Thanks for this. There was an existing erratum to Exercise 2.5.15 adding the hypothesis of self-adjointness, but I have added an erratum for Exercise 2.5.16 as well. (The definition of free independence is standard, so it would be difficult to fix the exercises by changing the definition.)
19 December, 2018 at 2:49 am
Danny Wood
Minor typo in Lemma 1.1.3, parts iii and iv. In part iii the text
“which hold with uniformly overwhelming probability, the”
should be
“which hold with uniformly overwhelming probability, then”
similarly for part iv
[Correction added, thanks – T.]
4 December, 2019 at 10:32 pm
Topics in Random Matrix Theory | DigiBooks
[…] or learn it on-line for free right here:Download link(1.5MB, […]
31 March, 2020 at 7:55 am
Giovanni Barbarino
Sorry to disturb, but I need a clarification.
We are working with ESDs on the space of probability measures P on R or C. Now, i’m already not sure that P is \sigma-compact, but anyway I’m sure that it is not locally compact, and the errata
<>
affects them all. So, are we allowed to work on these spaces?
The results still hold?
Is there a remark in the book I’m missing?
31 March, 2020 at 7:56 am
Giovanni Barbarino
The errata is
Page 32: In Definition 1.1.29, Remark 1.1.30, and Exercise 1.1.25, “\sigma-compact” should be “\sigma-compact and locally compact”
31 March, 2020 at 8:10 am
Giovanni Barbarino
I just noticed that I assumed the Lévy–Prokhorov metric on the space of probability measures. What metric are you using?
31 March, 2020 at 12:03 pm
Terence Tao
I am using the vague topology, which is metrisable. Admittedly, or
or 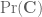 is still not quite compact (or sigma compact or locally compact) with this topology, but one can embed them as measurable subsets of the compact spaces
is still not quite compact (or sigma compact or locally compact) with this topology, but one can embed them as measurable subsets of the compact spaces 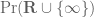 or
or  (using the one-point compactifications of
(using the one-point compactifications of  ), which suffices for the purpose of making all the definitions sensible. I’ll add an erratum to this effect.
), which suffices for the purpose of making all the definitions sensible. I’ll add an erratum to this effect.
22 May, 2020 at 1:47 am
Anonymous
The spaces of probability measures on R and C are already vaguely compact (by Banach Alaoglu).
22 May, 2020 at 2:01 pm
Terence Tao
Only the space of subprobability measures (measures of total mass less than or equal to 1) are compact. For probability measures there is a “loss of tightness” problem, for instance the Dirac probability measures on the integers have no subsequences that converges vaguely to another probability measure (instead they converge vaguely to the zero measure).
on the integers have no subsequences that converges vaguely to another probability measure (instead they converge vaguely to the zero measure).
9 April, 2021 at 11:23 am
Euiwoong Lee
Hi, thank you for the great book. One question: the first paragraph of 2.7.5. (pg 220) says that converges to the distribution
converges to the distribution  as
as 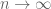 , but your previous paper and Edelman’s original paper seem to say that
, but your previous paper and Edelman’s original paper seem to say that 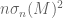 (the square of the first quantity) converges to
(the square of the first quantity) converges to  . Is this a typo or could you let me know where I misunderstood? Thanks.
. Is this a typo or could you let me know where I misunderstood? Thanks.
[This is a typo, now added to the errata – T.]
10 June, 2021 at 11:51 am
Juan Galvis
In Prop. 2.5.7, when I rewrote the problematic part of as a contour integral integral, I obtained that
as a contour integral integral, I obtained that 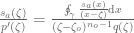 , where
, where 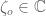 is such that
is such that  ,
, 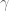 is a path which encloses
is a path which encloses  and so that
and so that 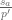 is analytic on it and on its interior (except at
is analytic on it and on its interior (except at  , of course),
, of course), 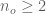 is the multiplicity of
is the multiplicity of  (w.r.t
(w.r.t  ) and
) and  is a non-vanishing polynomial on a small enough neighborhood of
is a non-vanishing polynomial on a small enough neighborhood of  enclosed by
enclosed by 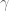 . However, in order to use Riemann’s theorem, for instance, to conclude, it seems to fail for such a
. However, in order to use Riemann’s theorem, for instance, to conclude, it seems to fail for such a  , at least, most likely, I am missing something about
, at least, most likely, I am missing something about  .
.
[Try using contour integrals of instead. -T]
instead. -T]
26 June, 2021 at 9:19 am
Anonymous
Indeed, it works. Many thanks. On the other hand, in Exercise 2.5.9, aren’t imaginary and real parts always self-adjoint?
[Yes, but the adjective is needed here because boundedness has only been defined thus far for self-adjoint elements -T.]
21 February, 2022 at 12:16 pm
John Lentfer
On page 45, in the last paragraph, should “But from (1.57), one can find…” be replaced by “But from (1.58), one can find…”?
[Correction added, thanks – T.]
9 October, 2022 at 3:09 pm
Zetai
In errata: “Page 53: In Exercise 1.3.22 (vi), (vii)”, I assume it should be “(vii), (viii)”?
Best
[Corrected, thanks – T.]
21 January, 2023 at 4:27 pm
Nicholas Christoffersen
Hi Dr. Tao,
Minor typo on pp. 267, display math right after *Hermite polynomial*. Should be $\frac{d^n}{dx^n}$ rather than $\frac{d}{dx^2}$.
Best
[Erratum added, thanks – T.]
7 April, 2023 at 12:09 pm
Noah Singer
Hi Dr. Tao,
I think there is a typo deriving the the “Gaussian-type bound” from the th moment method (eq. 2.8, p. 60 in the PDF version) – we want to set $\lambda$ as a multiple of
th moment method (eq. 2.8, p. 60 in the PDF version) – we want to set $\lambda$ as a multiple of  , not
, not  .
.
[Erratum added, thanks – T.]
4 October, 2023 at 2:24 pm
Calum Shearer
Hi Dr. Tao,
there is a typo in the errata – Correction for Proposition 2.1.19 on page 78 pertaining to the lack of absolute value signs is actually for Proposition 2.1.9 on page 68.
[Corrected, thanks -T.]
4 February, 2024 at 10:30 am
Anonymous
Hi Professor,
Is it possible that for the Gaussian type bound on the line right after equation 2.8 on page 60 that the denominator for the upper bound on lambda should be $K$ rather than $\sqrt{K}$.
[Corrected, thanks – T.]
20 March, 2024 at 6:57 am
Calum Shearer
Hi Professor Tao,
I think I spotted a couple of potential typos in section 2.7 of the draft version and corresponding blog post:
In the large paragraph in the middle of page 215, section 2.7.2, when looking at the equation for sparse
for sparse  : I think that if we have
: I think that if we have  fixed the entropy cost should just be
fixed the entropy cost should just be  , not
, not  to choose the columns that are the support of
to choose the columns that are the support of  . Apologies if this is not the case.
. Apologies if this is not the case.
For the incompressible case at the bottom of the same page, you say that if then at least
then at least  of the rows
of the rows 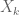 are in the span of the other
are in the span of the other 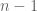 rows. I think that here and for the remainder of the argument we should consider the columns
rows. I think that here and for the remainder of the argument we should consider the columns  instead, as non-zero coordinates of
instead, as non-zero coordinates of  give a linear dependence relation involving the associated columns of
give a linear dependence relation involving the associated columns of  .
.
Minor typo in final paragraph of page 216: “eigenvalues ” should be “singular values
” should be “singular values  “
“
[Errata added, thanks – T.]