Millions long for immortality who do not know what to do with themselves on a rainy Sunday afternoon. (Susan Ertz, “Anger in the Sky”)
There is a particularly dangerous occupational hazard in this subject: one can become focused, to the exclusion of other mathematical activity (and in extreme cases, on non-mathematical activity also), on a single really difficult problem in a field (or on some grand unifying theory) before one is really ready (both in terms of mathematical preparation, and also in terms of one’s career) to devote so much of one’s research time to such a project. This is doubly true if one has not yet learnt the limitations of one’s tools or acquired a healthy scepticism of one’s own work, as this can lead to the humiliating spectacle of proudly announcing a major breakthrough on a well known problem, only to withdraw the preprint shortly afterwards after serious flaws (often arising from pushing a method well beyond its known limits, and encounting obstructions beyond those limits that were known to the experts) are pointed out in the manuscript.
When one begins to neglect other tasks (such as writing and publishing one’s “lesser” results), hoping to use the eventual “big payoff” of solving a major problem or establishing a revolutionary new theory to compensate for lack of progress in all other areas of one’s career, then this is a strong warning sign that one should rebalance one’s priorities. While it is true that several major problems have been solved, and several important theories introduced, by precisely such an obsessive approach, this has only worked out well when the mathematician involved
- had a proven track record of reliably producing significant papers in the area already; and
- had a secure career (e.g. a tenured position).
If you do not yet have both (1) and (2), and if your ideas on how to solve a big problem still have a significant speculative component (or if your grand theory does not yet have a definite and striking application), I would strongly advocate a more balanced, patient, and flexible approach instead: one can certainly keep the big problems and theories in mind, and tinker with them occasionally, but spend most of your time on more feasible “low-hanging fruit”, which will build up your experience, mathematical power, and credibility for when you are ready to tackle the more ambitious projects.
See also “Don’t base career decisions on glamour or fame” and “Use the wastebasket“. Henry Cohn also has some related advice for amateur mathematicians. This MathOverflow answer by Minhyong Kim also makes the point that one should accrue some definite mathematical results (preferably as published papers) before one can afford spending this “reputational capital” on philosophising on some “big picture” vision of mathematics.
— Addendum: on publishing proofs of famous open problems —
If you do believe that you have managed to solve a major problem, I would advise you to be extraordinarily sceptical of your own work, and to exercise the utmost care and caution before releasing it to anyone; there have been too many examples in the past of mathematicians whose reputation has been damaged by claiming a proof of a well-known result to much fanfare, only to find serious errors in the proof shortly thereafter. I recommend asking yourself the following questions regarding the paper:
- What is the key new idea or insight? How does it differ from what has been tried before? Is this idea emphasised in the introduction to the paper? (As a colleague of mine is fond of saying: “Where’s the beef?”.)
- How does the arguments in this paper relate to earlier partial results or attempts on the problem? Are there clear analogues between the steps here and steps in earlier papers? Does the new work shed some light as to why previous approaches did not fully succeed? Is this discussed in the paper?
- What is the simplest, shortest, or clearest new application of that idea? A related question: what is the first non-trivial new statement made in the paper, that was not able to have been shown before by earlier methods? Is this proof-of-concept given in the paper, or does it jump straight to the big conjecture with all its additional (and potentially error-prone) complications? In the event that there is a fatal error in the full proof, is there a good chance that a deep and non-trivial new partial result can at least be salvaged?
- Any major problem comes with known counterexamples, obstructions, or philosophical objections to various classes of attack strategies (e.g. strategy X does not work because it does not distinguish between problem Y, which is the big conjecture, and problem Z, for which counterexamples are known). Do you know why your argument does not encounter these obstructions? Is this stated in the paper? Do you know any specific limitations of the argument? Are these stated in the paper also?
- What was the high-level strategy you employed to attack the problem? Was it guided by some heuristic, philosophy, or intuition? If so, what is it? Is it stated in the paper? If the strategy was “continue blindly transforming the problem repeatedly until a miracle occurs”, this is a particularly bad sign. Can you state, in high-level terms (i.e. rising above all the technical details and computations), why the argument works?
- Does the proof come with key milestones – such as a key proposition used in the proof which is already of independent interest, or a major reduction of the unsolved problem to one which looks significantly easier? Are these milestones clearly identified in the paper?
- How robust is the argument – could a single sign error or illegal use of a lemma or formula destroy the entire argument? Good indicators of robustness include: alternate proofs (or heuristics, or supporting examples) of key steps, or analogies between key parts of the argument in this paper and in other papers in the literature.
- How critically have you checked the paper and reworked the exposition? Have you tried to deliberately disprove or hunt for errors in the paper? One expects a certain amount of checking to have been done when a major paper is released; if this is not done, and errors are quickly found after the paper is made public, this can potentially be quite embarrassing. Note that there is usually no rush when solving a major problem that has already withstood all attempts at solution for many years; taking the few extra days to go through the paper one last time can save oneself a lot of trouble.
- How much space in the paper is devoted to routine and standard theory and computations that already appears in previous literature, and how much is devoted to the new and exciting stuff which does not have any ready counterpart in previous literature? How soon in the paper does the new stuff appear? Are both parts of the paper being given appropriate amounts of detail?
Also, to reduce any potential negative reception to such a paper (especially if – as is all too likely – significant errors are detected in it) – any bragging or otherwise self-promoting text with little informative mathematical content should be kept to a minimum in the title, abstract, and introduction of the paper. For instance:
- Example of a bad title: “A proof of the Poincaré conjecture”.
- Example of a good title: “The entropy formula for the Ricci flow and its geometric applications“.
More generally, given any major open problem, the importance of the problem and its standard history will be a given to any informed reader, and should only be given a perfunctory treatment in the paper, except for those portions of the history of the problem which are of relevance to the proof. Pointing out that countless great mathematicians had tried to solve the problem and failed before you came along is in particularly bad taste and should be avoided completely.
It should also be noted that due to the sheer volume of failed attempts at solving these problems, most professional mathematicians will refuse to read any further attempts unless there is substantial auxiliary evidence that there is a non-zero chance of correctness (e.g. a previous track record of recognised mathematical achievement in the area). See for instance my editorial policy on papers involving a famous problem, or Oded Goldreich’s page on solving famous problems.
See also Scott Aaronson’s “Ten signs a claimed mathematical proof is wrong” and Dick Lipton’s “On Mathematical Diseases“.

54 comments
Comments feed for this article
19 June, 2007 at 9:16 pm
Does one have to be a genius to do math(s)? « Quomodocumque
[…] of their claims.) The pressure to try to behave in this impossible manner can cause some to become overly obsessed with “big problems” or “big theories”, others to lose any healthy scepticism in their own work or in their tools, and yet others still to […]
24 December, 2011 at 8:02 pm
John
I have always “intuitively” known to follow this excellent advice.
I use this kind of advice to know when to “give up” (temporarily) on a given approach to a particular problem and move on to other things. It is a non-obvious battle deciding whether one is wasting time repeating the same attack or being impatient by not pursuing a given approach long enough. Furthermore, an outside objective observer cannot always tell – unless they are experienced in one’s particular area of math. Same applies to any field.
28 January, 2008 at 2:07 am
Jian
Professor Terence Tao,
I am about your age, I am moved by your humility and sincerity evident in your posts given your own unusual status in the mathematical world. It has been years since I studied math and physics yet returned to my original passion art. Reading your posts made it clear that it was right that I studied math and physics and also right that I didn’t make them my profession since I don’t have the personality and working habits of a practicing mathematician as he should today in the west. Young mathematicians and students should be much benefitted upon hearing your advices.
I also feel particularly satisfied that you are Chinese and Cantonese speaking by origin (so am I).
Hug you!
17 May, 2008 at 8:59 pm
Advice to the Bright and Young « Essays by Danielle Fong
[…] this is shared by many fields), focusing prematurely on a single big problem or theory. His advice? Don’t. Try instead to be patient, and flexible. Work hard. And above all, enjoy […]
14 June, 2008 at 11:32 am
这等牛人也在wordpress上写blog! « Just For Fun
[…] of their claims.) The pressure to try to behave in this impossible manner can cause some to become overly obsessed with “big problems” or “big theories”, others to lose any healthy scepticism in their own work or in their tools, and yet others still to […]
9 May, 2009 at 2:20 pm
How to Choose a Research Topic « Successful Researcher
[…] this post of Terence Tao […]
17 April, 2011 at 12:09 pm
porton
(Not important what multifuncoids are for the general idea of this question.)
What you would advise: First to write and publish an article about finitary multifuncoids (for which I have a clear idea of their definition) or to attempt to figure an elegant set of axioms of infinitary multifuncoids, where figuring additional axioms is a trouble?
Hm, if I will first deal with finitary case I will get two articles and a citation.
I’m declined to first fully research the simpler finitary case and only then to really start the advanced infinitary case. But indeed would anyone advise me first to think hard about the right definitions even in infinitary case, before I start writing of the finitary case?
25 August, 2011 at 9:15 am
The Collatz conjecture, Littlewood-Offord theory, and powers of 2 and 3 « What’s new
[…] can lead to what Richard Lipton calls “mathematical diseases” (and what I termed an unhealthy amount of obsession on a single famous problem). (See also this xkcd comic regarding the Collatz conjecture.) As such, most practicing […]
3 October, 2011 at 4:37 pm
Larry Freeman
Thank you very much for this well-written essay. I am guilty of the very thing that you warn against (I find myself working exclusively on impossible math problems: collatz conjecture, twin primes, Legendre conjecture) and I agree with each of your points.
The only thing that keeps me chasing these unbelievably difficult problems is the humility I feel when I realize:
(1) I’ve made no progress at all
(2) Any sign of progress is more often than not a sign of a mistake in my assumptions.
(3) I am learning number theory and enjoying it.
I am too old to make real progress in mathematics (I’m 40+) but working on the famous unsolved problems gives me a great respect for the brilliant mathematicians who have made progress in the past and helps me to acknowledge my own limitations.
Regards,
-Larry
19 May, 2021 at 7:19 am
Lidia López
Excuse my question, but how do you know by your age that you can’t do a great progress in your field? I’m a physics student and I am always a bit concerned about that question of time. I’m worried about my age (24) and if I could make a difference in my 30’s.
Thank you very much for your comment anyway, it’s really inspiring.
Regards,
Lidia.
27 May, 2022 at 5:38 am
Ludwig
@Lidia López
I guess, Larry’s alluding to G.H.Hardy who claimed mathematics was a young man’s game.
24 December, 2011 at 8:09 pm
John
I meant to add: one of the great things about math, and one of the reasons I chose this field, is that one can do great math into old age, unlike fields like sports or ballet, where one has a very limited time that one can do those activities, because one’s body ages.
Thus, in math, one can always keep building and expanding on what one already has done and learned and inserting new research that comes along into one’s work.
I actually formally entered the math field relatively “late” (graduate school, after a period of work in my undergraduate major). I entered math because I needed to solve some extremely difficult applied math problems first before returning to work in my undergraduate major. I intended my foray into math to be just “temporary”, because I (in my naivete) expected to “quickly” solve the major applied math problems, say, in 4-5 years, and then “pop out” of math, and then pop back into work, applying all these wonderful results that I had proved for my math PhD. It’s been 23 years since I “entered math”, and I still have not popped out again, because the problem are just so overwhelmingly difficult, far more than in any other field.
24 December, 2011 at 8:27 pm
Anonymous
@John, would you be kind enough to share the applied math problem that got you sucked into math in the first place? I am at the verge of leaving math and I feel a sense of relief after having solved several of the open problems in my field; one of them is still pending but I believe the ideas are in place. So I would like to put my experience in perspective of others.
25 December, 2011 at 1:22 pm
John
Yes, Anonymous. Ever since 7th grade, when I openly declared that I wanted to become an “organic synthesist” when I grew up, my dream was to become a mad scientist! Since then, I’ve learned of a new hope for a path to that dream: nanotechnology. And, my years in chemical engineering lab at school, at work in a chemical lab, tutoring others in math applied to science (linear optimization, statistics, probability), and my lab courses in biotechnology all point to one burning conclusion: the technical problems of moving atoms around in nanotechnology to where you want them to be won’t be solved until we have complete solutions and understanding of the nonlinear partial differential equations (e.g. Schrodinger) that govern those atoms. I am convinced now more than ever before in my life that this is true, as a result of my experiences and interations.
26 June, 2014 at 10:11 pm
Arno Nymaus
What has lead Kenneth Arrow to prove his impossibility theorem? He designed some criteria, which for him were absolutely neccessary, and looked if something fulfils them. In this case, the answer was “no”, but I think that in the case of general ethics, maybe you would come up with something like utilitarianism. There you have a decision framework. Of course, I seriously do in no way intend to say that some certain things are morally wrong. Words can also be actions, which change mental representations (sometimes in a very indirect way).
26 June, 2014 at 10:15 pm
Arno Nymaus
*instead of “morally wrong” I should have written “based on the wrong moral framework”.
26 June, 2014 at 10:16 pm
Arno Nymaus
this is due to a symmetry argument.
9 December, 2012 at 2:25 am
[Skills] Làm việc chăm chỉ – GS Terrence Tao | Nguyen Hoai Tuong
[…] kết quả (nghĩa là làm phải có kết quả cụ thể), luôn nghĩ về phía trước, đừng chỉ nghĩ về một “vấn đề lớn”. Sẽ có những lúc mệt mỏi, mất động lực, nhưng bạn phải buộc mình phải […]
29 March, 2013 at 1:40 am
Nico Benschop
Dear John,
I like your text on not overly spend energy on a known stigmatic problem.
In fact, as an EE with some math experience I just stumbled in my (industrial) research over two of them. The clue of method employed to appraoch them both (Fermat and Goldbach) is to take, next to Gauss’ residue arithmetic, also the finite carry seriously, which (since Hensel’s p-adic number theory of 1913, with infinite carry extension) was neglected in mathematics. That is why I think a computer engineer can make a difference ;-)
During my research on digital IC design methods (Philips Research Labs, Eindhoven, Netherlands), mainly using finite semigroups to study the structure of Finite State Machines, I stumbled (1995) over a peculiar
property of the cubic roots of 1 mod p^k (prime p, any k>2). Namely they satisfy FLT for residues:
x^p + y^p = z^p (mod p^k).
This lead to an elementary proof of FLT by extending residue arithmetic with a finite carry (unlike Hensel’s infinite p-adic carry). This was published November 2005 in ACTA MATHEMATICA UNIVERSITATIS COMENIANAE :
http://pc2.iam.fmph.uniba.sk/amuc/_vol74n2.html ( p169 – 184 )
This residue & carry method soon (1996) led to an elementary proof of Goldbach’s Conjecture (GC), via a Goldbach result for residues (GR) with squarefree modulus m_k = \product { first k primes } :
Each even residue is the sum of two units (mod m_k).
This GC proof however, despite many submissions, I was unable to publish, although no rejection came forward with an error in the approach. Lately I was advised to obtain endorsement by a known mathematician in the field of number theory. I understand that the stigma of this problem is very great.
For this reason I’d much appreciate anyone’s opinion on this elementary proof of GC, and the approach taken. See homepage.
Best regards, dr. Nico Benschop ( nfbenschop-at-onsbrabantnet.nl )
1 April, 2013 at 1:14 am
Nico Benschop
GC paper at http://home.claranet.nl/goldbach2.pdf
13 April, 2013 at 12:33 pm
porton
Since the time of my first year in a university I thought about such things as continuity and connectedness. Despite of not finishing study in the university, I’ve become an amateur mathematician and have written a research monograph in a general topology topic. This monograph contains virtually all my discoveries in mathematics. But now when my monograph is already finished (and I have submitted it to a publisher) I don’t know how to continue my math research. I have no single idea neither how to solve any of my many conjectures, nor how to advance my conceptual theory development.
Would you recommend me to study (since I have forgotten my study in university) some other math theory and do research in an other topic? I have no good idea how to choose my new research topic.
3 June, 2013 at 7:03 am
Bisogna essere un genio per fare matematica? - Maddmaths
[…] sforzo di provare a comportarsi in questo modo impossibile può portare alcune persone a diventare troppo ossessionate con i "grandi problemi" e le "grandi teorie", altri a perdere quel sano scetticismo nel proprio lavoro o nei loro strumenti, e altri ancora a […]
4 July, 2013 at 9:35 pm
Fan
Prof. Tao,
What do you think of Yitang Zhang, who seems to be a counterexample to both (1) and (2) you mentioned above.
(1) AFAIK, his only paper before is an unfortunately unsuccessful proof of the Jacobi conjecture (also a notorious big problem).
(2) By the time his bounded prime gap paper was published, he was still a lecturer.
4 July, 2013 at 10:53 pm
Terence Tao
I can’t speak for Zhang, and do not know if he is satisfied with the way his career has turned out. All I can say is that I am very happy for him and for mathematics that he was able to prove his very nice theorem about bounded gaps between primes, but that I would still not advise my students to take this route; life is complicated, and being able to solve a mathematical problem is not the only goal one should take into consideration when trying to plan for the future.
31 July, 2017 at 7:21 pm
a
but have any of your students been successful future researchers?
1 August, 2017 at 7:56 am
Terence Tao
Yes, in fact several of them have continued in academia and are doing quite well.
6 August, 2017 at 4:42 pm
kingrat
you need more mathematical grand children (https://www.genealogy.math.ndsu.nodak.edu/id.php?id=43967) or else it IS LIKELY people might second guess your advising approach. But this will take time.
9 October, 2013 at 1:28 pm
math monster | Turing Machine
[…] Don’t prematurely obsess on a single “big problem” or “big theory” […]
24 October, 2013 at 9:43 am
Terry Tao: On Hard Work | Fahad's Academy
[…] Of course, to work hard, it really helps if you enjoy your work. It is also important to direct your effort in a fruitful direction rather than a fruitless one; in particular, spend some time thinking ahead, and don’t obsess on a single “big problem” or “big theory”. […]
30 November, 2013 at 10:54 am
Crowd-sourcing shrinking the prime gap | Later On
[…] actively discourages young mathematicians from heading down such a path, whichhe has called “a particularly dangerous occupational hazard” that has seldom worked well, except for […]
16 July, 2014 at 3:56 pm
Number Theory is the Cocaine of Mathematics | fractalcows
[…] table on Christmas day, and this rushed, unedited transcription of thought to paper led to assumptions and oversights that I could not justify when I revisited my […]
31 July, 2014 at 8:33 am
Together and Alone, Closing the Prime Gap | For a better Vietnam
[…] actively discourages young mathematicians from heading down such a path, which he has called “a particularly dangerous occupational hazard” that has seldom worked well, except for […]
2 June, 2015 at 7:26 am
leading authorities weigh in on P vs NP proofs | Turing Machine
[…] jokingly sometimes as a “disease” or “virus” (RJlipton, Gowers, Tao, etc) and this is partly in reference to all the bogus proof attempts. the $1M claymath prize […]
14 August, 2015 at 10:05 pm
Career advice - THE MATHS PACK
[…] Don’t prematurely obsess on a single “big problem” or “big theory”. […]
2 October, 2015 at 3:23 pm
Right To Learn, Part 2 | Minds on Fire
[…] of their claims.) The pressure to try to behave in this impossible manner can cause some to become overly obsessed with “big problems” or “big theories”, others to lose any healthy scepticism in their own work or in their tools, and yet others still to […]
2 December, 2015 at 10:58 am
Kirill Khvenkin
I think the issue is more complicated than quest for immortality. On one hand, it is not interesting to tackle marginal problems – that is why they are marginal. But there are also severe economic pressures – you are more likely to get a job/tenure if you solve something interesting. The problem is going to get worse as traditional source of income – teaching classes is going to dwindle down and be replaced by video teaching. Maybe we are getting back to the times of Gauss when only a few really strong mathematicians are going be left and there is no room for the rest.
3 December, 2016 at 6:34 am
A.T. Murray
It took me thirteen years to solve AI in theory, and another twenty years to demonstrate the solution in AI Mind software.
3 December, 2016 at 8:18 am
Sam Penrose
The Cohn link is broken; perhaps http://math.mit.edu/~cohn/Thoughts/advice.html ?
[Corrected, thanks – T.]
31 July, 2017 at 12:48 pm
Mirzakhani math superwoman 1977-2017 | Turing Machine
[…] for me, a great analogy is underwater cave exploration. there are very large/ complex caves, and very hard or even verging on dangerous to explore, with unknown extent; the solitary diver must carry his own equipment/ provisions, and one can get disoriented and lost very easily, where “lost” is sometimes equivalent to “dead”. that may sound overly melodramatic, but it is quite true that there are deep, decades- or even centuries-long open math problems (btw “deep” thanks for that, Riemann!) that mathematicians have spent almost entire lifetimes studying without finishing/ completing, although maybe making some incremental advances, but even those can be questionable. so for some its a lot like some giving up their lives to map a very complex terrain that will (hopefully) eventually be finished by those who follow in their lines. and other elite mathematicians such as Tao have warned of a kind of “danger” (aka “risk”) of working on very hard problems without anything to show for it, and the importance of avoiding the temptation of aiming for revolutionary work. […]
14 July, 2019 at 1:22 am
Anonymous
It is interesting to observe that the two biggest scientific revolutions were creates by young (still unknown) students outside of academy:
1. Newton’s “Annus mirabilis” year (1665-1666) at his home.
2. Einstein’s “Annus mirabilis” year (1905) while working at the patent office.
15 July, 2019 at 6:47 am
Andrew Krause
Note that in both cases, these two had substantial training at excellent Universities, and hence had a substantial exposure both to research results and methodologies, and many opportunities to learn from easier problems. Far more great results have been produced by hard work and perseverance over decades than by lone genius, and I think it is this fact which Terence Tao is trying to emphasize – the modern problems of mathematics and physics will require not just sheer intellectual effort, but also some familiarity with the countless avenues which have thus far been unsuccessful in answering them. For this reason, cutting one’s teeth on easier problems is invaluable simply for just building an intuition for problem-solving beyond what is done at the textbook/undergraduate level.
15 July, 2019 at 10:20 pm
Anonymous
Free sharing of ideas in a group of scientists (working as a ‘team” – like in polymath projects) could make the scientific progress MUCH faster.
The problem is that academic researchers are somewhat reluctant to share really brilliant ideas among the group members – preferring to develop it alone and get full academic credit for it.
It seems that the academic system should encourage scientists to share freely more brilliant ideas and make more polymath-like research projects by giving more academic credit to scientists working as a team on such projects.
15 July, 2019 at 7:20 am
L
The question of who builds culture and who follows will forever remain.
15 July, 2019 at 7:28 am
L
Rather ‘The question of who builds culture and who preserves still remains’.
27 October, 2019 at 6:24 am
estudiante de matématica
Dear Prof. Tao (or anyone else who might be reading this),
I have read about many conjectures in number theory, and for many of them, the numerical evidence is enormous. Yet, we can’t even prove weak versions of them.
This state of affairs is profoundly frustrating to my mind; I find it very distressing that we cannot be sure that these statements are true in the infinite.
Thus, I thought, I’d take fate into my own hands, and I experimented a little. Yet my efforts produced only one inequality, and presumably it is already known. (Using a simple sieve-theoretic argument, I was able to prove that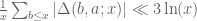 .)
.)
My (provocative) question would be: If you say that a “normal mortal” like myself would not have any chance resolving some important problem, would you not be implying that other people are somehow inherently smarter? And that they are allowed spending their time in the heavenly palace of mathematical thought, whereas all others have to confine themselves to the dark and misty forests of mundane day-to-day work?
Now I myself would have every intention of resolving some of the mysteries surrounding the prime numbers, but, especially after reading this article, I am afraid that the old bit of humanistic wisdom that says that everyone who tries really hard at something will necessarily succeed might be wrong. Indeed, there might have been loads of mathematicians who unsuccessfully tried to prove all the large conjectures in number theory. Many of them even might have been brilliant minds. And yet, most of them failed and all we have is the prime number theorem and some other results that are not even asymptotically optimal (let alone the error term).
Perhaps the reason why so many people (including myself) give it a shot is that we are forced to rely on other mathematicians, who, presumably, are much smarter and much more gifted than ourselves, yet even they fail to produce the results that we long for. Thus, we are on our own.
I’d be interested in any thoughts.
27 October, 2019 at 6:25 am
estudiante de matématica
Actually, you may replace the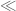 sign by $\le$; the bound is effective.
sign by $\le$; the bound is effective.
27 October, 2019 at 2:28 pm
Anonymous
Even the great mathematician Ramanujan made a false claim in a letter to Hardy to have an approximation to with bounded error term.
with bounded error term.
28 October, 2019 at 10:29 am
matemático joven o estudiante de matemática
As the thoughts expressed in the above post might indicate, I am uncertain as to whether that is supposed to make me happy or sad. After all, Ramanujan was a human like myself. And if he, being a genius, makes a mistake, what is that supposed to say about myself? Perhaps I would be happier if number theory was in a better state than it is, because it would mean that at least, members of my species are somehow able to do number theory. But we are talking about something that frankly seems too hard for us. That is not a reason for joy.
28 June, 2020 at 3:58 pm
Anonymous
I’d like to reflect on how true this post resonates with me at the moment. I’m currently having trouble finding an advisor and have as a result been bouncing around between prospective. A month or so back, I realized that a tool from one field can be potentially used in different field. I contacted a friend in the later field and we were both excited as graduate students but unfortunately we realize now that we have no idea what to do with this tool and what significance it has outside poising some wishful questions. I suppose now that this is just an opportunity to learn more about these fields, reach out and the tool itself while still carrying on with our respective lives and studies.
29 June, 2020 at 12:24 am
YahyaAA1
Keep exploring! The joy is in the chase, not in the capture (which merely brings paltry rewards like fame, food, money and glory!).
10 June, 2021 at 10:30 am
Is this correct?
Click to access 2106.04644.pdf
5 May, 2022 at 5:42 pm
A Method to Not Prove the Collatz Conjecture - good fibrations
[…] table on Christmas day, and this rushed, unedited transcription of thought to paper led to assumptions and oversights that I could not justify when I revisited my […]
9 July, 2022 at 6:15 am
Anonymous
It’s a very nice essay. And I appreciate your ability and interest in communicating with the hoi polloi.
We get a lot of them mooning around reddit and stack exchange. A turn-off to me is when they want to focus on big sexy problems but don’t find any joy, value in the conventional course of study, and are not doing well in it (high A work).
I believe there is a huge amount of valuable training (both the content and the problem solving experience) in the regular curriculum. If you’re not alive to that, you’re not observant.
15 January, 2024 at 5:55 pm
Kalit Gautam
Extremely beautifully explained Professor Tao !