In this lecture – the final one on general measure-preserving dynamics – we put together the results from the past few lectures to establish the Furstenberg-Zimmer structure theorem for measure-preserving systems, and then use this to finish the proof of the Furstenberg recurrence theorem.
— The Furstenberg-Zimmer structure theorem —
Let be a measure-preserving system, and let
be a factor. In Theorem 2 of the previous lecture, we showed that if X was not a weakly mixing extension of Y, then we could find a non-trivial compact extension Z of Y (thus
is a non-trivial superspace of
). Combining this with Zorn’s lemma (and starting with the trivial factor Y = pt), one obtains
Theorem 1. (Furstenberg-Zimmer structure theorem) Let
be a measure-preserving system. Then there exists an ordinal
and a factor
for every
with the following properties:
is a point.
- For every successor ordinal
,
is a compact extension of
.
- For every limit ordinal
,
is the inverse limit of the
for the
, in the sense that
is the closure of
.
- X is a weakly mixing extension of
.
This theorem should be compared with Furstenberg’s structure theorem for distal systems in topological dynamics (Theorem 2 from Lecture 7). Indeed, in analogy to that theorem, the factors are known as distal measure-preserving systems. The result was proven independently by Furstenberg and by Zimmer.
Exercise 1. Deduce Theorem 1 from Theorem 2 of the previous lecture.
Remark 1. Since the Hilbert spaces are increasing inside the separable Hilbert space
, it is not hard to see that the ordinal
must be at most countable. Conversely, a result of Beleznay and Foreman shows that every countable ordinal can appear as the minimal length of a Furstenberg tower of a given system. Thus, in some sense, the complexity of a system can be as great as any countable ordinal. This is because the structure theorem roots out every last trace of structure from the system, so much so that every remaining function orthogonal to the final factor
is weakly mixing. But in many applications one does not need so much weak mixing; for instance to establish k-fold recurrence for a function f, it would be enough to obtain weak mixing control on just a few combinations of f (such as
), as we already saw in the proof of Roth’s theorem in Lecture 12. In fact, it is not hard to show that to prove Furstenberg’s recurrence theorem for a fixed k, one only needs to analyse the first k-2 steps of the Furstenberg tower. As one consequence of this, it is possible to avoid the use of Zorn’s lemma (and the axiom of choice) in the proof of the recurrence theorem.
Remark 2. Analogues of the structure theorem exist for other actions, such as the action of on a measure space (which can equivalently be viewed as the action of d commuting shifts
). There is a new feature in this case, though: instead of having a tower of purely compact extensions, followed by one weakly mixing extension at the end, one instead has a tower of hybrid extensions (known as primitive extensions), each one of which is compact along one subgroup of
and weakly mixing along a complementary subgroup. See for instance Furstenberg’s book for details.
— The Furstenberg recurrence theorem —
The Furstenberg recurrence theorem asserts that every measure-preserving system has the uniform multiple recurrence (UMR) property, thus
(1)
whenever and
is non-negative with positive mean. The UMR property is trivially true for a point, and we have already shown that UMR is preserved by compact extensions (Theorem 1 of Lecture 13) and by weakly mixing extensions (Theorem 1 of Lecture 14). The former result lets us climb the successor ordinal steps of the tower in Theorem 1, while the latter lets us jump from the final distal system
to X. But to clinch the proof of the recurrence theorem, we also need to deal with the limit ordinals. More precisely, we need to prove
Theorem 2. (Limits of chains) Let
be a totally ordered family of factors of a measure-preserving system X (thus
is increasing with
, and let Y be the inverse limit of the
. If each of the
obeys the UMR, then Y does also.
With this theorem, the Furstenberg recurrence theorem (Theorem 1 from Lecture 11) follows from the previous theorems and transfinite induction.
The main difficulty in establishing Theorem 2 is that while each obeys the UMR separately, we do not know that this property holds uniformly in
. The main new observation needed to establish the theorem is that there is another way to leverage the UMR from a factor to an extension… if the support of the function f is sufficiently “dense”. We motivate this by first considering the unconditional case.
Proposition 1. (UMR for densely supported functions) Let
be a measure-preserving system, let
be an integer, and let
be a non-negative function whose support
has measure greater than
. Then (1) holds.
Proof. By monotone convergence, we can find such that
for all x outside of a set E of measure at most
. For any n, this implies that
for all x outside of the set
, which has measure at most
. In particular we see that
(2)
for all n, and the claim follows.
As with the other components of the proof of the recurrence theorem, we will need to upgrade the above proposition to a “relative” version:
Proposition 2. (UMR for relatively densely supported functions) Let
be an extension of a factor
with the UMR, let
be an integer, and let
be a non-negative function whose support
is such that the set
has positive measure in Y. Then (1) holds.
Proof. By monotone convergence again, we can find such that the set
is such that the set
has positive measure. Since Y has the UMR, this implies that (1) holds for
. In other words, there exists
such that
(3)
for all n in a set of positive lower density.
Now we turn to f. We have the pointwise lower bound , and so
. (4)
We have the crude lower bound
; (5)
inserting this into (4) and taking conditional expectations, we conclude
(6)
a.e. On the other hand, we have
. (7)
By definition of F, we thus see that if y lies in , then
. (8)
Integrating this and using (3), we obtain
(9)
for all n in a set of positive lower density, and (1) follows.
Proof of Theorem 2. Let be non-negative with positive mean
; we may normalise f to be bounded by 1. Since Y is the inverse limit of the
, we see that the orthogonal projections
converge in
norm to
. Thus, for any
, we can find
such that
. (10)
Now has the same mean c as f, and is also bounded by 1. Thus the set
must have measure at least c/2 in
. Now if
, then we have the pointwise bound
; (11)
squaring this and taking conditional expectations we obtain
, (12)
and so by (10) and Markov’s inequality we see that on a set of positive measure. The claim now follows from Proposition 2.
The proof of the Furstenberg recurrence theorem (and thus Szemerédi’s theorem) is finally complete.
Remark 3. The same type of argument yields many further recurrence theorems, and thus (by the correspondence principle) many combinatorial results also. For instance, in the original paper of Furstenberg it was noted that the above arguments allow one to strengthen (1) to
, (13)
which allows one to conclude that in a set A of positive upper density, the set of n for which has positive upper density is syndetic for every k. One can also extend the argument to higher dimensions, and to polynomial recurrence without too many changes in the structure of the proof. But some more serious modifications to the argument are needed for other recurrence results involving IP systems or Hales-Jewett type results; see Lecture 10 for more discussion.
[Update, Mar 6: Statement of Proposition 1 corrected.]
o

17 comments
Comments feed for this article
6 March, 2008 at 7:14 am
Lior
In the statement of Prop 1,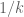 should be
should be  .
.
6 March, 2008 at 8:51 am
Terence Tao
Dear Lior: thanks for the correction!
7 January, 2009 at 10:10 pm
陶哲轩遍历论:第十五讲 « Liu Xiaochuan’s Weblog
[…] (注:遍历论为陶哲轩教授于今年年初的一门课程,我尝试将所有习题做出来,这是第十五讲的唯一一个习题,就是Zorn引理的使用。这里是本讲的链接。) […]
7 January, 2009 at 10:51 pm
Nate Chandler
Just a small correction: In the second paragraph, you wrote “In Theorem 2 of the previous lecture, we showed that X was not a weakly mixing extension of Y, then we could find a non-trivial compact extension Z of Y”. I think you meant “In Theorem 2 of the previous lecture, we showed that if X was not a weakly mixing extension of Y, then we could find a non-trivial compact extension Z of Y”.
8 January, 2009 at 5:51 am
liuxiaochuan
Dear Professor:
In the left hand side of (12), if the expectation is taken with respect to , then
, then 
8 January, 2009 at 9:15 am
Terence Tao
Thanks for the corrections!
27 February, 2010 at 5:34 am
ERT8: Weak Mixing Systems « Disquisitiones Mathematicae
[…] denote this by and is called a factor of . Theorem 1 (Furstenberg structural theorem) Given a mps , there exists an ordinal and a family of factors of , for every , such […]
1 May, 2011 at 3:34 pm
ERT16: Compact extensions « Disquisitiones Mathematicae
[…] when looked through the spectral lenses. It is a matter of fact that this dichotomy turns Furstenberg-Zimmer structural theorem direct, as we’ll prove in […]
3 June, 2011 at 7:55 pm
The Furstenberg multiple recurrence theorem and finite extensions « What’s new
[…] as a consequence of the Furstenberg-Zimmer structure theorem for measure-preserving systems. See these lecture notes for further […]
20 June, 2014 at 9:11 pm
An abstract ergodic theorem, and the Mackey-Zimmer theorem | What's new
[…] measure-preserving systems (as well as subsequent refinements of this theory by Host and Kra); see this previous blog post for some relevant discussion. One can obtain similar descriptions of non-ergodic extensions via the […]
9 April, 2017 at 8:00 pm
yaoxiao
Dear professor Tao, on a set of
on a set of  , did you here mean that out a set of … Thanks!
, did you here mean that out a set of … Thanks!
by (10) and markov inequality,
[Corrected, thanks – T.]
14 March, 2019 at 12:36 pm
Maths student
Dear Prof. Tao,
I’d really appreciate an answer to this question, and I hope that the question is sufficiently non-stupid. I’m not yet done with the proof of the Furstenberg recurrence theorem, but I noticed that in some way it was a bit similar to the proof of von Neumann’s theorem, that is to say, the first proof that was given in your book. Namely, we decompose a space into two types of elements which behave contrary to each other.
Hence, I have been asking myself whether it might be possible to generalise the Furstenberg recurrence to a Hilbert space setting, where the Integral might be replaced by some sort of scalar products against Dirac measures. (A more plausible, yet less far-reaching generalisation might be given by replacing the shift map of a dynamical system by an operator on a suitable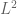 space, perhaps a space given by Bochner integrable functions.)
space, perhaps a space given by Bochner integrable functions.)
18 March, 2019 at 9:04 am
Terence Tao
The Furstenberg recurrence theorem requires the ability to take higher order correlations of
of  different functions with
different functions with  potentially larger than 2; a Hilbert space structure only gives
potentially larger than 2; a Hilbert space structure only gives 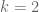 correlations and so it does not seem possible to even phrase the Furstenberg recurrence theorem in purely Hilbert space-theoretic terms, let alone prove it. (On the other hand, higher order Hilbert spaces can be used to at least describe the closely related concept of a Gowers-Host-Kra seminorm; see https://terrytao.wordpress.com/2010/05/19/higher-order-hilbert-spaces/ ).
correlations and so it does not seem possible to even phrase the Furstenberg recurrence theorem in purely Hilbert space-theoretic terms, let alone prove it. (On the other hand, higher order Hilbert spaces can be used to at least describe the closely related concept of a Gowers-Host-Kra seminorm; see https://terrytao.wordpress.com/2010/05/19/higher-order-hilbert-spaces/ ).
One natural abstract framework to describe these recurrence theorems is that of commutative tracial von Neumann algebras. One can then try to extend these theorems to the noncommutative case, but unfortunately the theorems largely break down in that case: https://terrytao.wordpress.com/2009/12/29/nonconventional-ergodic-averages-and-multiple-recurrence-for-von-neumann-dynamical-systems/
18 March, 2019 at 11:14 am
Maths student
Thanks a lot for your reply. I had questioned myself about whether there is a space that admits “pair”ings of any order, and whether such a concept would (at least given a higher cardinality) be a generalisation of some additional spaces (which would have to be found). Perhaps an appropriate generalisation would require the given forms to satisfy some consistency conditions. These are just random ideas; when I have time, I’ll give it more thought.
18 March, 2019 at 11:45 am
Maths student
In particular, the negative examples Prof. Tao gave jointly with Austin and Eisner prove that one would have to choose one’s category in a way that excludes the non-commutative systems Prof. Tao referred to.
4 December, 2022 at 11:54 pm
YV
Hi, thank you for this proof!
I have one question.
Can you elaborate on why the ordinal \alpha you mentioned in the structure theorem must be at most countable?
Thanks in advanced
5 December, 2022 at 1:58 pm
Terence Tao
If there is an increasing set of strictly increasing Hilbert subspaces
of strictly increasing Hilbert subspaces indexed by an uncountable ordinal
indexed by an uncountable ordinal  then the Hilbert space
then the Hilbert space  has an uncountable orthonormal basis (formed by choosing an orthonormal basis for each
has an uncountable orthonormal basis (formed by choosing an orthonormal basis for each  , which is non-trivial for successor ordinals
, which is non-trivial for successor ordinals 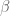 ). So if
). So if  is separable it can only admit a countable tower of such spaces.
is separable it can only admit a countable tower of such spaces.
of
inside a separable Hilbert space then
then