is the fundamental equation of motion for (non-relativistic) quantum mechanics, modeling both one-particle systems and -particle systems for
. Remarkably, despite being a linear equation, solutions
to this equation can be governed by a non-linear equation in the large particle limit
. In particular, when modeling a Bose-Einstein condensate with a suitably scaled interaction potential
in the large particle limit, the solution can be governed by the cubic nonlinear Schrödinger equation
I recently attended a talk by Natasa Pavlovic on the rigorous derivation of this type of limiting behaviour, which was initiated by the pioneering work of Hepp and Spohn, and has now attracted a vast recent literature. The rigorous details here are rather sophisticated; but the heuristic explanation of the phenomenon is fairly simple, and actually rather pretty in my opinion, involving the foundational quantum mechanics of -particle systems. I am recording this heuristic derivation here, partly for my own benefit, but perhaps it will be of interest to some readers.
This discussion will be purely formal, in the sense that (important) analytic issues such as differentiability, existence and uniqueness, etc. will be largely ignored.
— 1. A quick review of classical mechanics —
The phenomena discussed here are purely quantum mechanical in nature, but to motivate the quantum mechanical discussion, it is helpful to first quickly review the more familiar (and more conceptually intuitive) classical situation.
Classical mechanics can be formulated in a number of essentially equivalent ways: Newtonian, Hamiltonian, and Lagrangian. The formalism of Hamiltonian mechanics for a given physical system can be summarised briefly as follows:
- The physical system has a phase space
of states
(which is often parameterised by position variables
and momentum variables
). Mathematically, it has the structure of a symplectic manifold, with some symplectic form
(which would be
if one had position and momentum coordinates available).
- The complete state of the system at any given time
is given (in the case of pure states) by a point
in the phase space
.
- Every physical observable (e.g., energy, momentum, position, etc.)
is associated to a function (also called
) mapping the phase space
to the range of the observable (e.g. for real observables,
would be a function from
to
). If one measures the observable
at time
, one will obtain the measurement
.
- There is a special observable, the Hamiltonian
, which governs the evolution of the state
through time, via Hamilton’s equations of motion. If one has position and momentum coordinates
, these equations are given by the formulae
more abstractly, just from the symplectic form
on the phase space, the equations of motion can be written as
where
is the symplectic gradient of
.
Hamilton’s equation of motion can also be expressed in a dual form in terms of observables , as Poisson’s equation of motion
for any observable , where
is the Poisson bracket. One can express Poisson’s equation more abstractly as
In the above formalism, we are assuming that the system is in a pure state at each time , which means that it only occupies a single point
in phase space. One can also consider mixed states in which the state of the system at a time
is not fully known, but is instead given by a probability distribution
on phase space. The act of measuring an observable
at a time
will thus no longer be deterministic, but will itself be a random variable, whose expectation
is given by
The equation of motion of a mixed state is given by the advection equation
using the same vector field that appears in (2); this equation can also be derived from (3), (4), and a duality argument.
Pure states can be viewed as the special case of mixed states in which the probability distribution is a Dirac mass
. (We ignore for now the formal issues of how to perform operations such as derivatives on Dirac masses; this can be accomplished using the theory of distributions (or, equivalently, by working in the dual setting of observables) but this is not our concern here.) One can thus think of mixed states as continuous averages of pure states, or equivalently the space of mixed states is the convex hull of the space of pure states.
Suppose one had a -particle system, in which the joint phase space
is the product of the two one-particle phase spaces. A pure joint state is then a point
in
, where
represents the state of the first particle, and
is the state of the second particle. If the joint Hamiltonian
split as
then the equations of motion for the first and second particles would be completely decoupled, with no interactions between the two particles. However, in practice, the joint Hamiltonian contains coupling terms between that prevents one from totally decoupling the system; for instance, one may have
where ,
are written using position coordinates
and momentum coordinates
,
are constants (representing mass), and
is some interaction potential that depends on the spatial separation
between the two particles.
In a similar spirit, a mixed joint state is a joint probability distribution on the product state space. To recover the (mixed) state of an individual particle, one must consider a marginal distribution such as
(for the first particle) or
(for the second particle). Similarly for -particle systems: if the joint distribution of
distinct particles is given by
, then the distribution of the first particle (say) is given by
the distribution of the first two particles is given by
and so forth.
A typical Hamiltonian in this case may take the form
which is a combination of single-particle Hamiltonians and interaction perturbations. If the momenta
and masses
are normalised to be of size
, and the potential
has an average value (i.e. an
norm) of
also, then the former sum has size
and the latter sum has size
, so the latter will dominate. In order to balance the two components and get a more interesting limiting dynamics when
, we shall therefore insert a normalising factor of
on the right-hand side, giving a Hamiltonian
Now imagine a system of indistinguishable particles. By this, we mean that all the state spaces
are identical, and all observables (including the Hamiltonian) are symmetric functions of the product space
(i.e. invariant under the action of the symmetric group
). In such a case, one may as well average over this group (since this does not affect any physical observable), and assume that all mixed states
are also symmetric. (One cost of doing this, though, is one has to largely give up pure states
, since such states will not be symmetric except in the very exceptional case
.)
A typical example of a symmetric Hamiltonian is
where is even (thus all particles have the same individual Hamiltonian, and interact with the other particles using the same interaction potential). In many physical systems, it is natural to consider only short-range interaction potentials, in which the interaction between
and
is localised to the region
for some small
. We model this by considering Hamiltonians of the form
where is the ambient dimension of each particle (thus in physical models,
would usually be
); the factor of
is a normalisation factor designed to keep the
norm of the interaction potential of size
. It turns out that an interesting limit occurs when
goes to zero as
goes to infinity by some power law
; imagine for instance
particles of “radius”
bouncing around in a box, which is a basic model for classical gases.
An important example of a symmetric mixed state is a factored state
where is a single-particle probability density function; thus
is the tensor product of
copies of
. If there are no interaction terms in the Hamiltonian, then Hamiltonian’s equation of motion will preserve the property of being a factored state (with
evolving according to the one-particle equation); but with interactions, the factored nature may be lost over time.
— 2. A quick review of quantum mechanics —
Now we turn to quantum mechanics. This theory is fundamentally rather different in nature than classical mechanics (in the sense that the basic objects, such as states and observables, are a different type of mathematical object than in the classical case), but shares many features in common also, particularly those relating to the Hamiltonian and other observables. (This relationship is made more precise via the correspondence principle, and more precise still using semi-classical analysis.)
The formalism of quantum mechanics for a given physical system can be summarised briefly as follows:
- The physical system has a phase space
of states
(which is often parameterised as a complex-valued function of the position space). Mathematically, it has the structure of a complex Hilbert space, which is traditionally manipulated using bra-ket notation.
- The complete state of the system at any given time
is given (in the case of pure states) by a unit vector
in the phase space
.
- Every physical observable
is associated to a linear operator on
; real-valued observables are associated to self-adjoint linear operators. If one measures the observable
at time
, one will obtain the random variable whose expectation
is given by
. (The full distribution of
is given by the spectral measure of
relative to
.)
- There is a special observable, the Hamiltonian
, which governs the evolution of the state
through time, via Schrödinger’s equations of motion
Schrödinger’s equation of motion can also be expressed in a dual form in terms of observables , as Heisenberg’s equation of motion
where is the commutator or Lie bracket (compare with (3)).
The states are pure states, analogous to the pure states
in Hamiltonian mechanics. One also has mixed states
in quantum mechanics. Whereas in classical mechanics, a mixed state
is a probability distribution (a non-negative function of total mass
), in quantum mechanics a mixed state is a non-negative (i.e. positive semi-definite) operator
on
of total trace
. If one measures an observable
at a mixed state
, one obtains a random variable with expectation
. From (6) and duality, one can infer that the correct equation of motion for mixed states must be given by
One can view pure states as the special case of mixed states which are rank one projections,
Morally speaking, the space of mixed states is the convex hull of the space of pure states (just as in the classical case), though things are a little trickier than this when the phase space is infinite dimensional, due to the presence of continuous spectrum in the spectral theorem.
Pure states suffer from a phase ambiguity: a phase rotation of a pure state
leads to the same mixed state, and the two states cannot be distinguished by any physical observable.
In a single particle system, modeling a (scalar) quantum particle in a -dimensional position space
, one can identify the Hilbert space
with
, and describe the pure state
as a wave function
, which is normalised as
as has to be a unit vector. (If the quantum particle has additional features such as spin, then one needs a fancier wave function, but let’s ignore this for now.) A mixed state is then a function
which is Hermitian (i.e.
) and positive definite, with unit trace
; a pure state
corresponds to the mixed state
.
A typical Hamiltonian in this setting is given by the operator
where is a constant,
is the momentum operator
, and
is the gradient in the
variable (so
, where
is the Laplacian; note that
is skew-adjoint and should thus be thought of as being imaginary rather than real), and
is some potential. Physically, this depicts a particle of mass
in a potential well given by the potential
.
Now suppose one has an -particle system of scalar particles. A pure state of such a system can then be given by an
-particle wave function
, normalised so that
and a mixed state is a Hermitian positive semi-definite function with trace
with a pure state being identified with the mixed state
In classical mechanics, the state of a single particle was the marginal distribution of the joint state. In quantum mechanics, the state of a single particle is instead obtained as the partial trace of the joint state. For instance, the state of the first particle is given as
the state of the first two particles is given as
and so forth. (These formulae can be justified by considering observables of the joint state that only affect, say, the first two position coordinates and using duality.)
A typical Hamiltonian in this setting is given by the operator
where we normalise just as in the classical case, and .
An interesting feature of quantum mechanics – not present in the classical world – is that even if the -particle system is in a pure state, individual particles may be in a mixed state: the partial trace of a pure state need not remain pure. Because of this, when considering a subsystem of a larger system, one cannot always assume that the subsystem is in a pure state, but must work instead with mixed states throughout, unless there is some reason (e.g. a lack of coupling) to assume that pure states are somehow preserved.
Now consider a system of indistinguishable quantum particles. As in the classical case, this means that all observables (including the Hamiltonian) for the joint system are invariant with respect to the action of the symmetric group
. Because of this, one may as well assume that the (mixed) state of the joint system is also symmetric with respect to this action. In the special case when the particles are bosons, one can also assume that pure states
are also symmetric with respect to this action (in contrast to fermions, where the action on pure states is anti-symmetric). A typical Hamiltonian in this setting is given by the operator
for some even potential ; if one wants to model short-range interactions, one might instead pick the variant
for some . This is a typical model for an
-particle Bose-Einstein condensate. (Longer-range models can lead to more non-local variants of NLS for the limiting equation, such as the Hartree equation.)
— 3. NLS —
Suppose we have a Bose-Einstein condensate given by a (symmetric) mixed state
evolving according to the equation of motion (7) using the Hamiltonian (8). One can take a partial trace of the equation of motion (7) to obtain an equation for the state of the first particle (note from symmetry that all the other particles will have the same state function). If one does take this trace, one soon finds that the equation of motion becomes
where is the partial trace to the
particles. Using symmetry, we see that all the summands in the
summation are identical, so we can simplify this as
This does not completely describe the dynamics of , as one also needs an equation for
. But one can repeat the same argument to get an equation for
involving
, and so forth, leading to a system of equations known as the BBGKY hierarchy. But for simplicity we shall just look at the first equation in this hierarchy.
Let us now formally take two limits in the above equation, sending the number of particles to infinity and the interaction scale
to zero. The effect of sending
to infinity should simply be to eliminate the
factor. The effect of sending
to zero should be to send
to the Dirac mass
, where
is the total mass of
. Formally performing these two limits, one is led to the equation
One can perform a similar formal limiting procedure for the other equations in the BBGKY hierarchy, obtaining a system of equations known as the Gross-Pitaevskii hierarchy.
We next make an important simplifying assumption, which is that in the limit any two particles in this system become decoupled, which means that the two-particle mixed state factors as the tensor product of two one-particle states:
One can view this as a mean field approximation, modeling the interaction of one particle with all the other particles by the mean field
.
Making this assumption, the previous equation simplifies to
If we assume furthermore that is a pure state, thus
then (up to the phase ambiguity mentioned earlier), obeys the Gross-Pitaevskii equation
which (up to some factors of and
, which can be renormalised away) is essentially (1).
An alternate derivation of (1), using a slight variant of the above mean field approximation, comes from studying the Hamiltonian (8). Let us make the (very strong) assumption that at some fixed time , one is in a completely factored pure state
where is a one-particle wave function, in particular obeying the normalisation
(This is an unrealistically strong version of the mean field approximation. In practice, one only needs the two-particle partial traces to be completely factored for the discussion below.) The expected value of the Hamiltonian,
can then be simplified as
Again sending , this formally becomes
which in the limit is asymptotically
Up to some normalisations, this is the Hamiltonian for the NLS equation (1).
There has been much progress recently in making the above derivations precise, by Erdös-Schlein-Yau, Klainerman-Machedon, Kirkpatrick-Schlein-Staffilani, Chen-Pavlovic, and others. A key step is to show that the Gross-Pitaevskii hierarchy necessarily preserves the property of being a completely factored state. This requires a uniqueness theory for this hierarchy, which is surprisingly delicate, due to the fact that it is a system of infinitely many coupled equations over an unbounded number of variables.
[Update, Dec 8: Interestingly, the above heuristic derivation only works when the interaction scale is much larger than
. For
, the coupling constant
acquires a nonlinear correction, becoming essentially the scattering length of the potential rather than its mean. See comments below.]

14 comments
Comments feed for this article
26 November, 2009 at 10:25 pm
Anonymous
Professor Tao:
In the third paragraph, do you mean to say that the discussion will be purely informal?
26 November, 2009 at 11:39 pm
Anonymous
Mathematicians tend to use the word “formal” to describe an argument in which symbolic manipulations may not be justified rigorously. (You just cross your fingers and hope for the best.)
27 November, 2009 at 2:46 am
Mio
Dear Prof. Tao, looks like there’s a typo in (7), A should be H instead. Also, the ket above (6) is missing a \psi inside. Thanks for the post.
[Corrected, thanks – T.]
28 November, 2009 at 2:28 pm
M.S.
Really beautiful and clear, as your other post!
It made me enjoy my long train trip today, thanks.
I saw a typo immediately before the introduction of the interaction potential sum normalization, I think it should be:
If the momenta $p_j$ and masses $m_j$ are normalised to be of size
[Corrected, thanks – T.]
29 November, 2009 at 3:53 pm
CJ
Prof. Tao–There seems to be a missing equation in your definition of Hamilton’s equations on a sympletic manifold, right after “the equations of motion can be written as”.
29 November, 2009 at 3:58 pm
CJ
Prof. Tao–Actually, it looks like all the numbered equations are having difficulties being displayed. (At least I don’t see them running firefox on Ubuntu.)
[Hmm, a strange glitch – I think the equations are restored now. -T]
30 November, 2009 at 7:41 am
liuyao
minor typo: , the prime on x, not on
, the prime on x, not on 
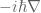 , though the minus sign is immaterial when you square it, and is more of a convention.
, though the minus sign is immaterial when you square it, and is more of a convention.
Momentum is usually identified with
Great post, by the way!
[Corrected, thanks – T.]
1 December, 2009 at 1:40 am
A semana nos arXivs… « Ars Physica
[…] From Bose-Einstein condensates to the nonlinear Schrodinger equation […]
2 December, 2009 at 2:29 pm
John Sidles
Please let me echo the above comments in saying that this is a wonderfully interesting and enjoyable post!
I would like to offer three comments on how engineering students might read (and mis-read) this post, recornizing that increasing numbers of engineering students are seeking to upgrade their mathematical understanding.
None of the following remarks should be construed as being in any respect critical of Prof. Tao’s fine essay. Rather, they should be read as fan mail—-and as an expression of thanks—from the engineering community to the mathematical community.
One of Bjarne Stroustrup’s maxims is “Whenever something can be done in two ways, someone will be confused.” And when it comes to quantum mechanics—with its plethora of invariances and conventions–few people are more easily confused than literal-minded engineering students!
Engineering students can become confused in ways that might not occur to mathematicians, as follows:
(1) When discussing dynamical state-spaces endowed with a metric and/or symplectic structure, is it better to give equations in terms of vectors, or in terms of forms? Mathematicians are happy either way, but they tend to choose vector frameworks (as Tao’s essay does), perhaps for the reason that vectors are easier to sketch than forms.
However, if we have in mind (sooner or later) to pullback dynamical equations onto lower-dimension, noneuclidean manifolds (as engineers ubiquitously do), then it is convenient to express dynamical equations (and complex structures, etc.) in terms of forms rather than vectors … and it helps engineering students to be reminded that forms pullback naturally and vectors don’t.
This boils down to assuring students that symplectic gradients can be defined to map functions to vectors, or alternatively map functions to forms, with equal validity (given a symplectic and/or metric structure that establishes a natural isomorphism).
(2) On the arxiv server there is a (unpublished, but very clear) essay by Prof. Tao titled Perelman’s proof of the Poincare conjecture: a nonlinear PDE perspective (arXiv.org:math/0610903). In particular, footnote three of this article is in itself a short yet powerfully thought-provoking essay to the effect that “a PDE flow is in many ways ‘dumber’ than a combinatorial algorithm than a combinatorial algorithm” and yet “if the flow is sufficiently geometrical in nature then the flows acquire a number of deep and delicate additional properties”.
In quantum mechanics as in topology, there is steadily increasing use of flow/PDE algorithms in conjunction with combinatorical/algebraic algorithms; an essay on this general topic would be *very* welcome (IMHO) to many students/researchers in quantum mechanics (in engineering and otherwise).
(3) Quantum mechanics has a reputation for being mysterious, and in particular, there is a widespread impression that its basic postulates are inviolate. But as is often the case with no-go arguments, a loophole exists that Prof. Tao’s present essay illustrates beautifully.
That loophole is that (in Prof. Tao’s words) “despite [quantum dynamics] being a linear equation, solutions can be governed by a non-linear equation”. Thus we are free to invent nonlinear versions of quantum mechanics, without fear of experimental contradiction, provided that we can derive the nonlinear dynamics from linear quantum mechanics.
This principle applies broadly in quantum mechanics and many other physical theories; for example there is a recent article by Stephen Adler and Angelo Bassi titled Is Quantum Theory Exact? that can be read as an another example of this same general principle.
Here too an essay on “Mathematical methods for circumventing no-go arguments in physical theories” would be very interesting—and very stimulating too!—to many students.
That’s all! And thanks also, to everyone who contributes what is becoming (IMHO) the present-day “Golden Era of Mathematical Blogging”. :)
8 December, 2009 at 10:29 am
Bob Jerrard
nice post. just a few days ago I saw a talk by Laszlo Erdos on some of his work (with Schlein and Yau and others) on these problems, and he emphasized that the correct value of the coupling constant is not the total mass of the interaction potential
is not the total mass of the interaction potential  , but rather is
, but rather is 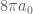 , where
, where 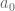 is the scattering length, defined as follows: consider a solution
is the scattering length, defined as follows: consider a solution  of the equation
of the equation 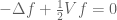 in
in 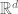 , such that
, such that  at
at 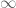 . Then if the potential
. Then if the potential  is sufficiently short-range, it is a fact that
is sufficiently short-range, it is a fact that 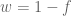 is asymptotic to
is asymptotic to  for some
for some  (for example this is clear if
(for example this is clear if  is compactly supported), and the constant
is compactly supported), and the constant 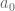 is defined to be the scattering length.
is defined to be the scattering length.
In order to see the scattering length appear in the Gross-Pitaevsky equation, one needs to modify the product state ansatz you have given above. The modified ansatz has the form
writing it for wave functions rather than density matrices, and so takes into account short-range correlations between particles. If I understand correctly, the definitions of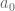 and
and 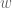 imply that
imply that
and it is via this fact that the above modified ansatz gives rise to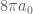 in the GP equation.
in the GP equation.
The justification of the limit thus requires establishing some information about short-range repulsive interactions between particles.
8 December, 2009 at 12:15 pm
Terence Tao
That’s a very interesting subtlety! I think it shows up for some ranges of r and N and not others, in particular if the range r of the potential is significantly longer than the mean spacing of the particles then the naive approximation should work, I think (this is for instance the case in the Chen-Pavlovic work, where the potential is rather long range and the nonlinear correction does not appear).
It is good to have examples of why one should not always trust naive limiting arguments, though…
8 December, 2009 at 6:44 pm
H.S.
Thank you for this wonderful post. I just have a couple of questions:
1) For classical interacting system, what is the “interesting limit” you mentioned in the post? Could you please explain more about that limit? For instance is there a nonlinear equation in the limit? The power law of r and N is kind of mysterious to me. What’s the value of the exponent there explicitly?
2) In quantum case, has the Mean field approximation that the two-particle mixed state can factorize in the limit been rigorously justified? [In classical case at positive temperature, there’re “propagation of chaos” type results, which can justify mean field approximation].
3) I feel like, usually, mean field approximation is valid only for long range interactions. But here we are concerned about short range interactions. Well, this is not actually a question, maybe my feeling is just incorrect.
Thank you again!
8 December, 2009 at 7:07 pm
Terence Tao
(1) I don’t have a formal derivation, but it seems to me that the limiting dynamics of the classical model should be governed by the one-particle advection equation but with an effective Hamiltonian containing a potential term proportional to the spatial density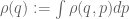 . There is undoubtedly a name for this type of nonlinear kinetic equation but it escapes me at the moment. This type of limit should obtain whenever r is much smaller than 1 but much larger than 1/N; for r=1/N I suppose one should have a correction in analogy with the quantum case as pointed out by Bob Jerrard above.
. There is undoubtedly a name for this type of nonlinear kinetic equation but it escapes me at the moment. This type of limit should obtain whenever r is much smaller than 1 but much larger than 1/N; for r=1/N I suppose one should have a correction in analogy with the quantum case as pointed out by Bob Jerrard above.
(2) As far as I am aware, most of the rigorous results require the initial state to already be factored or close to factored, and the conclusion is that this near-factored property is more or less preserved (with dynamics given by the effective equation). There are certainly efforts to generalise to broader classes of data, though.
(3) There is a parallel set of results for long-range interactions, in which the nonlinearity becomes nonlocal (of Hartree type, generally).
26 September, 2014 at 4:10 am
My great WordPress blog – Econlinks
[…] Tao makes a nice and concise exposition of some of the most beautiful parts at the intersection of Mathematics and Theoretical Physics (oh, nostalgia…), including quick reviews of classical and quantum […]