Thus far, we have only focused on measure and integration theory in the context of Euclidean spaces . Now, we will work in a more abstract and general setting, in which the Euclidean space
is replaced by a more general space
.
It turns out that in order to properly define measure and integration on a general space , it is not enough to just specify the set
. One also needs to specify two additional pieces of data:
- A collection
of subsets of
that one is allowed to measure; and
- The measure
one assigns to each measurable set
.
For instance, Lebesgue measure theory covers the case when is a Euclidean space
,
is the collection
of all Lebesgue measurable subsets of
, and
is the Lebesgue measure
of
.
The collection has to obey a number of axioms (e.g. being closed with respect to countable unions) that make it a
-algebra, which is a stronger variant of the more well-known concept of a boolean algebra. Similarly, the measure
has to obey a number of axioms (most notably, a countable additivity axiom) in order to obtain a measure and integration theory comparable to the Lebesgue theory on Euclidean spaces. When all these axioms are satisfied, the triple
is known as a measure space. These play much the same role in abstract measure theory that metric spaces or topological spaces play in abstract point-set topology, or that vector spaces play in abstract linear algebra.
On any measure space, one can set up the unsigned and absolutely convergent integrals in almost exactly the same way as was done in the previous notes for the Lebesgue integral on Euclidean spaces, although the approximation theorems are largely unavailable at this level of generality due to the lack of such concepts as “elementary set” or “continuous function” for an abstract measure space. On the other hand, one does have the fundamental convergence theorems for the subject, namely Fatou’s lemma, the monotone convergence theorem and the dominated convergence theorem, and we present these results here.
One question that will not be addressed much in this current set of notes is how one actually constructs interesting examples of measures. We will discuss this issue more in later notes (although one of the most powerful tools for such constructions, namely the Riesz representation theorem, will not be covered until 245B).
— 1. Boolean algebras —
We begin by recalling the concept of a Boolean algebra.
Definition 1 (Boolean algebras) Let
be a set. A (concrete) Boolean algebra on
is a collection
of
which obeys the following properties:
- (Empty set)
.
- (Complement) If
, then the complement
also lies in
.
- (Finite unions) If
, then
.
We sometimes say that
is
-measurable, or measurable with respect to
, if
.
Given two Boolean algebras
on
, we say that
is finer than, a sub-algebra of, or a refinement of
, or that
is coarser than or a coarsening of
, if
.
We have chosen a “minimalist” definition of a Boolean algebra, in which one is only assumed to be closed under two of the basic Boolean operations, namely complement and finite union. However, by using the laws of Boolean algebra (such as de Morgan’s laws), it is easy to see that a Boolean algebra is also closed under other Boolean algebra operations such as intersection , set differerence
, and symmetric difference
. So one could have placed these additional closure properties inside the definition of a Boolean algebra without any loss of generality. However, when we are verifying that a given collection
of sets is indeed a Boolean algebra, it is convenient to have as minimal a set of axioms as possible. (This point is discussed further in this Math Overflow comment of mine.)
Remark 1 One can also consider abstract Boolean algebras
, which do not necessarily live in an ambient domain
, but for which one has a collection of abstract Boolean operations such as meet
and join
instead of the concrete operations of intersection
and union
. We will not take this abstract perspective here, but see this blog post of mine for some further discussion of the relationship between concrete and abstract Boolean algebras, which is codified by Stone’s theorem.
Example 1 (Trivial and discrete algebra) Given any set
, the coarsest Boolean algebra is the trivial algebra
, in which the only measurable sets are the empty set and the whole set. The finest Boolean algebra is the discrete algebra
, in which every set is measurable. All other Boolean algebras are intermediate between these two extremes: finer than the trivial algebra, but coarser than the discrete one.
Exercise 1 (Elementary algebra) Let
be the collection of those sets
that are either elementary sets, or co-elementary sets (i.e. the complement of an elementary set). Show that
is a Boolean algebra. We will call this algebra the elementary Boolean algebra of
.
Example 2 (Jordan algebra) Let
be the collection of subsets of
that are either Jordan measurable or co-Jordan measurable (i.e. the complement of a Jordan measurable set). Then
is a Boolean algebra that is finer than the elementary algebra. We refer to this algebra as the Jordan algebra on
(but caution that there is a completely different concept of a Jordan algebra in mathematics.)
Example 3 (Lebesgue algebra) Let
be the collection of Lebesgue measurable subsets of
. Then
is a Boolean algebra that is finer than the Jordan algebra; we refer to this as the Lebesgue algebra on
.
Example 4 (Null algebra) Let
be the collection of subsets of
that are either Lebesgue null sets or Lebesgue co-null sets (the complement of null sets). Then
is a Boolean algebra that is coarser than the Lebesgue algebra; we refer to it as the null algebra on
.
Exercise 2 (Restriction) Let
be a Boolean algebra on a set
, and let
be a subset of
(not necessarily
-measurable). Show that the restriction
of
to
is a Boolean algebra on
. If
is
-measurable, show that
Example 5 (Atomic algebra) Let
be partitioned into a union
of disjoint sets
, which we refer to as atoms. Then this partition generates a Boolean algebra
, defined as the collection of all the sets
of the form
for some
, i.e.
is the collection of all sets that can be represented as the union of one or more atoms. This is easily verified to be a Boolean algebra, and we refer to it as the atomic algebra with atoms
. The trivial algebra corresponds to the trivial partition
into a single atom; at the other extreme, the discrete algebra corresponds to the discrete partition
into singleton atoms. More generally, note that finer (resp. coarser) partitions lead to finer (resp. coarser) atomic algebra. In this definition, we permit some of the atoms in the partition to be empty; but it is clear that empty atoms have no impact on the final atomic algebra, and so without loss of generality one can delete all empty atoms and assume that all atoms are non-empty if one wishes.
Example 6 (Dyadic algebras) Let
be an integer. The dyadic algebra
at scale
in
is defined to be the atomic algebra generated by the half-open dyadic cubes
of length
(see Exercise 14 of the prologue). These are Boolean algebras which are increasing in
:
. Draw a diagram to indicate how these algebras sit in relation to the elementary, Jordan, and Lebesgue, null, discrete, and trivial algebras.
Remark 2 The dyadic algebras are analogous to the finite resolution one has on modern computer monitors, which subdivide space into square pixels. A low resolution monitor (in which each pixel has a large size) can only resolve a very small set of “blocky” images, as opposed to the larger class of images that can be resolved by a finer resolution monitor.
Exercise 3 Show that the non-empty atoms of an atomic algebra are determined up to relabeling. More precisely, show that if
are two partitions of
into non-empty atoms
,
, then
if and only if exists a bijection
such that
for all
.
While many Boolean algebras are atomic, many are not, as the following two exercises indicate.
Exercise 4 Show that every finite Boolean algebra is an atomic algebra. (A Boolean algebra
is finite if its cardinality is finite, i.e. there are only finitely many measurable sets.) Conclude that every finite Boolean algebra has a cardinality of the form
for some natural number
. From this exercise and Exercise 3 we see that there is a one-to-one correspondence between finite Boolean algebras on
and finite partitions of
into non-empty sets (up to relabeling).
Exercise 5 Show that the elementary, Jordan, Lebesgue, and null algebras are not atomic algebras. (Hint: argue by contradiction. If these algebras were atomic, what must the atoms be?)
Now we describe some further ways to generate Boolean algebras.
Exercise 6 (Intersection of algebras) Let
be a family of Boolean algebras on a set
, indexed by a (possibly infinite or uncountable) label set
. Show that the intersection
of these algebras is still a Boolean algebra, and is the finest Boolean algebra that is coarser than all of the
. (If
is empty, we adopt the convention that
is the discrete algebra.)
Definition 2 (Generation of algebras) Let
be any family of sets in
. We define
to be the intersection of all the Boolean algebras that contain
, which is again a Boolean algebra by Exercise 6. Equivalently,
is the coarsest Boolean algebra that contains
. We say that
is the Boolean algebra generated by
.
Example 7
is a Boolean algebra if and only if
; thus each Boolean algebra is generated by itself.
Exercise 7 Show that the elementary algebra
is generated by the collection of boxes in
.
Exercise 8 Let
be a natural number. Show that if
is a finite collection of
sets, then
is a finite Boolean algebra of cardinality at most
(in particular, finite sets generate finite algebras). Give an example to show that this bound is best possible. (Hint: for the latter, it may be convenient to use a discrete ambient space such as the discrete cube
.)
The Boolean algebra can be described explicitly in terms of
as follows:
Exercise 9 (Recursive description of a generated Boolean algebra) Let
be a collection of sets in a set
. Define the sets
recursively as follows:
.
- For each
, we define
to be the collection of all sets that either the union of a finite number of sets in
(including the empty union
), or the complement of such a union.
Show that
.
— 2. -algebras and measurable spaces —
In order to obtain a measure and integration theory that can cope well with limits, the finite union axiom of a Boolean algebra is insufficient, and must be improved to a countable union axiom:
Definition 3 (Sigma algebras) Let
be a set. A
-algebra on
is a collection
of
which obeys the following properties:
- (Empty set)
.
- (Complement) If
, then the complement
also lies in
.
- (Countable unions) If
, then
.
We refer to the pair
of a set
together with a
-algebra on that set as a measurable space.
Remark 3 The prefix
usually denotes “countable union”. See also the concepts of a
-compact topological space, or a
-finite measure space, or
set for other instances of this prefix.
From de Morgan’s law (which is just as valid for infinite unions and intersections as it is for finite ones), we see that -algebras are closed under countable intersections as well as countable unions.
By padding a finite union into a countable union by using the empty set, we see that every -algebra is automatically a Boolean algebra. Thus, we automatically inherit the notion of being measurable with respect to a
-algebra, or of one
-algebra being coarser or finer than another.
Exercise 10 Show that all atomic algebras are
-algebras. In particular, the discrete algebra and trivial algebra are
-algebras, as are the finite algebras and the dyadic algebras on Euclidean spaces.
Exercise 11 Show that the Lebesgue and null algebras are
-algebras, but the elementary and Jordan algebras are not.
Exercise 12 Show that any restriction
of a
-algebra
to a subspace
of
(as defined in Exercise 2) is again a
-algebra on the subspace
.
There is an exact analogue of Exercise 6:
Exercise 13 (Intersection of
-algebras) Show that the intersection
of an arbitrary (and possibly infinite or uncountable) number of
-algebras
is again a
-algebra, and is the finest
-algebra that is coarser than all of the
.
Similarly, we have a notion of generation:
Definition 4 (Generation of
-algebras) Let
be any family of sets in
. We define
to be the intersection of all the
-algebras that contain
, which is again a
-algebra by Exercise 13. Equivalently,
is the coarsest
-algebra that contains
. We say that
is the
-algebra generated by
.
Since every -algebra is a Boolean algebra, we have the trivial inclusion
However, equality need not hold; it only holds if and only if is a
-algebra. For instance, if
is the collection of all boxes in
, then
is the elementary algebra (Exercise 7), but
cannot equal this algebra, as it is not a
-algebra.
Remark 4 From the definitions, it is clear that we have the following principle, somewhat analogous to the principle of mathematical induction: if
is a family of sets in
, and
is a property of sets
which obeys the following axioms:
is true.
is true for all
.
- If
is true for some
, then
is true also.
- If
are such that
is true for all
, then
is true also.
Then one can conclude that
is true for all
. Indeed, the set of all
for which
holds is a
-algebra that contains
, whence the claim. This principle is particularly useful for establishing properties of Borel measurable sets (see below).
We now turn to an important example of a -algebra:
Definition 5 (Borel
-algebra) Let
be a metric space, or more generally a topological space. The Borel
-algebra
of
is defined to be the
-algebra generated by the open subsets of
. Elements of
will be called Borel measurable.
Thus, for instance, the Borel -algebra contains the open sets, the closed sets (which are complements of open sets), the countable unions of closed sets (i.e.
sets), the countable intersections of open sets (i.e.
sets), the countable intersections of
sets, and so forth.
In , every open set is Lebesgue measurable, and so we see that the Borel
-algebra is coarser than the Lebesgue
-algebra. We will shortly see, though, that the two
-algebras are not equal.
We defined the Borel -algebra to be generated by the open sets. However, they are also generated by several other sets:
Exercise 14 Show that the Borel
-algebra
of a Euclidean set is generated by any of the following collections of sets:
- The open subsets of
.
- The closed subsets of
.
- The compact subsets of
.
- The open balls of
.
- The boxes in
.
- The elementary sets in
.
(Hint: To show that two families
of sets generate the same
-algebra, it suffices to show that every
-algebra that contains
, contains
also, and conversely.)
There is an analogue of Exercise 9, which illustrates the extent to which a generated -algebra is “larger” than the analogous generated Boolean algebra:
Exercise 15 (Recursive description of a generated
-algebra) (This exercise requires familiarity with the theory of ordinals, which is reviewed here. Recall that we are assuming the axiom of choice throughout this course.) Let
be a collection of sets in a set
, and let
be the first uncountable ordinal. Define the sets
for every countable ordinal
via transfinite induction as follows:
.
- For each countable successor ordinal
, we define
to be the collection of all sets that either the union of an at most countable number of sets in
(including the empty union
), or the complement of such a union.
- For each countable limit ordinal
, we define
.
Show that
.
Remark 5 The first uncountable ordinal
will make several further cameo appearances throughout this course, for instance by generating counterexamples to various plausible statements in point-set topology. In the case when
is the collection of open sets in a topological space, so that
, then the sets
are essentially the Borel hierarchy (which starts at the open and closed sets, then moves on to the
and
sets, and so forth); these play an important role in descriptive set theory.
Exercise 16 (This exercise requires familiarity with the theory of cardinals.) Let
be an infinite family of subsets of
of cardinality
(thus
is an infinite cardinal). Show that
has cardinality at most
. (Hint: use Exercise 15.) In particular, show that the Borel
-algebra
has cardinality at most
.
Conclude that there exist Jordan measurable (and hence Lebesgue measurable) subsets of
which are not Borel measurable. (Hint: How many subsets of the Cantor set are there?) Use this to place the Borel
-algebra on the diagram that you drew for Exercise 6.
Remark 6 Despite this demonstration that not all Lebesgue measurable subsets are Borel measurable, it is remarkably difficult (though not impossible) to exhibit a specific set that is not Borel measurable. Indeed, a large majority of the explicitly constructible sets that one actually encounters in practice tend to be Borel measurable, and one can view the property of Borel measurability intuitively as a kind of “constructibility” property. (Indeed, as a very crude first approximation, one can view the Borel measurable sets as those sets of “countable descriptive complexity”; in contrast, sets of finite descriptive complexity tend to be Jordan measurable (assuming they are bounded, of course).
Exercise 17 Let
be Borel measurable subsets of
respectively. Show that
is a Borel measurable subset of
. (Hint: first establish this in the case when
is a box, by using Remark 4. To obtain the general case, apply Remark 4 yet again.)
The above exercise has a partial converse:
Exercise 18 Let
be a Borel measurable subset of
.
- Show that for any
, the slice
is a Borel measurable subset of
. Similarly, show that for every
, the slice
is a Borel measurable subset of
.
- Give a counterexample to show that this claim is not true if “Borel” is replaced with “Lebesgue” throughout. (Hint: the Cartesian product of any set with a point is a null set, even if the first set was not measurable.)
Exercise 19 Show that the Lebesgue
-algebra on
is generated by the union of the Borel
-algebra and the null
-algebra.
— 3. Countably additive measures and measure spaces —
Having set out the concept of a -algebra a measurable space, we now endow these structures with a measure.
We begin with the finitely additive theory, although this theory is too weak for our purposes and will soon be supplanted by the countably additive theory.
Definition 6 (Finitely additive measure) Let
be a Boolean algebra on a space
. An (unsigned) finitely additive measure
on
is a map
that obeys the following axioms:
- (Empty set)
.
- (Finite additivity) Whenever
are disjoint, then
.
Remark 7 The empty set axiom is needed in order to rule out the degenerate situation in which every set (including the empty set) has infinite measure.
Example 8 Lebesgue measure
is a finitely additive measure on the Lebesgue
-algebra, and hence on all sub-algebras (such as the null algebra, the Jordan algebra, or the elementary algebra). In particular, Jordan measure and elementary measure are finitely additive (adopting the convention that co-Jordan measurable sets have infinite Jordan measure, and co-elementary sets have infinite elementary measure).
On the other hand, as we saw in previous notes, Lebesgue outer measure is not finitely additive on the discrete algebra, and Jordan outer measure is not finitely additive on the Lebesgue algebra.
Example 9 (Dirac measure) Let
and
be an arbitrary Boolean algebra on
. Then the Dirac measure
at
, defined by setting
, is finitely additive.
Example 10 (Zero measure) The zero measure
is a finitely additive measure on any Boolean algebra.
Example 11 (Linear combinations of measures) If
is a Boolean algebra on
, and
are finitely additive measures on
, then
is also a finitely additive measure, as is
for any
. Thus, for instance, the sum of Lebesgue measure and a Dirac measure is also a finitely additive measure on the Lebesgue algebra (or on any of its sub-algebras).
Example 12 (Restriction of a measure) If
is a Boolean algebra on
,
is a finitely additive measure, and
is a
-measurable subset of
, then the restriction
of
to
, defined by setting
whenever
(i.e. if
and
), is also a finitely additive meaure.
Example 13 (Counting measure) If
is a Boolean algebra on
, then the function
defined by setting
to be the cardinality of
if
is finite, and
if
is infinite, is a finitely additive measure, known as counting measure.
As with our definition of Boolean algebras and -algebras, we adopted a “minimalist” definition so that the axioms are easy to verify. But they imply several further useful properties:
Exercise 20 Let
be a finitely additive measure on a Boolean
-algebra
. Establish the following facts:
- (Monotonicity) If
are
-measurable and
, then
.
- (Finite additivity) If
is a natural number, and
are
-measurable and disjoint, then
.
- (Finite sub-additivity) If
is a natural number, and
are
-measurable, then
.
- (Inclusion-exclusion for two sets) If
are
-measurable, then
.
(Caution: remember that the cancellation law
does not hold in
if
is infinite, and so the use of cancellation (or subtraction) should be avoided if possible.)
One can characterise measures completely for any finite algebra:
Exercise 21 Let
be a finite Boolean algebra, generated by a finite family
of non-empty atoms. Show that for every finitely additive measure
on
there exists
such that
Equivalently, if
is a point in
for each
, then
Furthermore, show that the
are uniquely determined by
.
This is about the limit of what one can say about finitely additive measures at this level of generality. We now specialise to the countably additive measures on -algebras.
Definition 7 (Countably additive measure) Let
be a measurable space. An (unsigned) countably additive measure
on
, or measure for short, is a map
that obeys the following axioms:
- (Empty set)
.
- (Countable additivity) Whenever
are a countable sequence of disjoint measurable sets, then
.
A triplet
, where
is a measurable space and
is a countably additive measure, is known as a measure space.
Note the distinction between a measure space and a measurable space. The latter has the capability to be equipped with a measure, but the former is actually equipped with a measure.
Example 14 Lebesgue measure is a countably additive measure on the Lebesgue
-algebra, and hence on every sub-
-algebra (such as the Borel
-algebra).
Example 15 The Dirac measures from Exercise 9 are countably additive, as is counting measure.
Example 16 Any restriction of a countably additive measure to a measurable subspace is again countably additive.
Exercise 22 (Countable combinations of measures) Let
be a measurable space.
- If
is a countably additive measure on
, and
, then
is also countably additive.
- If
are a sequence of countably additive measures on
, then the sum
is also a countably additive measure.
Note that countable additivity measures are necessarily finitely additive (by padding out a finite union into a countable union using the empty set), and so countably additive measures inherit all the properties of finitely additive properties, such as monotonicity and finite subadditivity. But one also has additional properties:
Exercise 23 Let
be a measure space.
- (Countable subadditivity) If
are
-measurable, then
.
- (Upwards monotone convergence) If
are
-measurable, then
- (Downwards monotone convergence) If
are
-measurable, and
for at least one
, then
Show that the downward monotone convergence claim can fail if the hypothesis that
for at least one
is dropped. (Hint: copy the argument used for Exercise 10 in Notes 1.)
Exercise 24 (Dominated convergence for sets) Let
be a measure space. Let
be a sequence of
-measurable sets that converge to another set
, in the sense that
converges pointwise to
.
- Show that
is also
-measurable.
- If there exists a
-measurable set
of finite measure (i.e.
) that contains all of the
, show that
. (Hint: Apply downward monotonicity to the sets
.)
- Show that the previous part of this exercise can fail if the hypothesis that all the
are contained in a set of finite measure is omitted.
Exercise 25 Let
be an at most countable set with the discrete
-algebra. Show that every measure
on this measurable space can be uniquely represented in the form
for some
, thus
for all
. (This claim fails in the uncountable case, although showing this is slightly tricky.)
A null set of a measure space is defined to be a
-measurable set of measure zero. A sub-null set is any subset of a null set. A measure space is said to be complete if every sub-null set is a null set. Thus, for instance, the Lebesgue measure space
is complete, but the Borel measure space
is not (as can be seen from the solution to Exercise 16).
Completion is a convenient property to have in some cases, particularly when dealing with properties that hold almost everywhere. Fortunately, it is fairly easy to modify any measure space to be complete:
Exercise 26 (Completion) Let
be a measure space. Show that there exists a unique refinement
, known as the completion of
, which is the coarsest refinement of
that is complete. Furthermore, show that
consists precisely of those sets that differ from a
-measurable set by a
-subnull set.
Exercise 27 Show that the Lebesgue measure space
is the completion of the Borel measure space
.
— 4. Measurable functions, and integration on a measure space —
Now we are ready to define integration on measure spaces. We first need the notion of a measurable function, which is analogous to that of a continuous function in topology. Recall that a function between two topological spaces
is continuous if the inverse image
of any open set is open. In a similar spirit, we have
Definition 8 Let
be a measurable space, and let
or
be an unsigned or complex-valued function. We say that
is measurable if
is
-measurable for every open subset
of
or
.
From Lemma 7 of Notes 2, we see that this generalises the notion of a Lebesgue measurable function.
Exercise 28 Let
be a measurable space.
- Show that a function
is measurable if and only if the level sets
are
-measurable.
- Show that an indicator function
of a set
is measurable if and only if
itself is
-measurable.
- Show that a function
or
is measurable if and only if
is
-measurable for every Borel-measurable subset
of
or
.
- Show that a function
is measurable if and only if its real and imaginary parts are measurable.
- Show that a function
is measurable if and only if the magnitudes
,
of its positive and negative parts are measurable.
- If
are a sequence of measurable functions that converge pointwise to a limit
, then show that
is also measurable. Obtain the same claim if
is replaced by
.
- If
is measurable and
is continuous, show that
is measurable. Obtain the same claim if
is replaced by
.
- Show that the sum or product of two measurable functions in
or
is still measurable.
Remark 8 One can also view measurable functions in a more category theoretic fashion. Define measurable morphism or measurable map
from one measurable space
to another
to be a function
with the property that
is
-measurable for every
-measurable set
. Then a measurable function
or
is the same thing as a measurable morphism from
to
or
, where the latter is equipped with the Borel
-algebra. Also, one
-algebra
on a space
is coarser than another
precisely when the identity map
is a measurable morphism from
to
. The main purpose of adopting this viewpoint is that it is obvious that the composition of measurable morphisms is again a measurable morphism. This is important in those fields of mathematics, such as ergodic theory, in which one frequently wishes to compose measurable transformations (and in particular, to compose a transformation
with itself repeatedly); but it will not play a major role in this course.
Measurable functions are particularly easy to describe on atomic spaces:
Exercise 29 Let
be a measurable space that is atomic, thus
for some partition
of
into disjoint non-empty atoms. Show that a function
or
is measurable if and only if it is constant on each atom, or equivalently if one has a representation of the form
for some constants
in
or in
as appropriate. Furthermore, the
are uniquely determined by
.
Exercise 30 (Egorov’s theorem) Let
be a finite measure space (so
), and let
be a sequence of measurable functions that converge pointwise almost everywhere to a limit
, and let
. Show that there exists a measurable set
of measure at most
such that
converges uniformly to
outside of
. Give an example to show that the claim can fail when the measure
is not finite.
In Notes 2 we defined first an simple integral, then an unsigned integral, and then finally an absolutely convergent integral. We perform the same three stages here. We begin with the simple integral in the case when the -algebra is finite:
Definition 9 (Simple integral) Let
be a measure space with
finite. By Exercise 4,
is partitioned into a finite number of atoms
. If
is measurable, then by Exercise 29 it has a unique representation of the form
for some
. We then define the simple integral
of
by the formula
Note that, thanks to Exercise 3, the precise decomposition into atoms does not affect the definition of the simple integral.
One could also define a simple integral for absolutely convergent complex-valued functions on a measurable space with a finite -algebra, but we will not need to do so here.
With this definition, it is clear that one has the monotonicity property
whenever are unsigned measurable, as well as the linearity properties
and
for unsigned measurable and
. We also make the following important technical observation:
Exercise 31 (Simple integral unaffected by refinements) Let
be a measure space, and let
be a refinement of
, which means that
contains
and
agrees with
on
. Suppose that both
are finite, and let
be measurable. Show that
This allows one to extend the simple integral to simple functions:
Definition 10 (Integral of simple functions) An (unsigned) simple function
on a measurable space
is a measurable function that takes on finitely many values
. Note that such a function is then automatically measurable with respect to at least one finite sub-
-algebra
of
, namely the
-algebra
generated by the preimages
of
. We then define the simple integral
by the formula
where
is the restriction of
to
.
Note that there could be multiple finite -algebras with respect to which
is measurable, but Exercise 31 guarantees that all such extensions will give the same simple integral. Indeed, if
were measurable with respect to two separate finite sub-
-algebras
and
of
, then it would also be measurable with respect to their common refinement
, which is also finite (by Exercise 8), and then by Exercise 31,
and
are both equal to
, and hence equal to each other.
From this we can deduce the following properties of the simple integral. As with the Lebesgue theory, we say that a property of an element
of a measure space
holds
-almost everywhere if it holds outside of a sub-null set.
Exercise 32 (Basic properties of the simple integral) Let
be a measure space, and let
be simple functions.
- (Monotonicity) If
pointwise, then
.
- (Compatibility with measure) For every
-measurable set
, we have
.
- (Homogeneity) For every
, one has
.
- (Finite additivity)
.
- (Insensitivity to refinement) If
is a refinement of
(as defined in Exercise 31), then
.
- (Almost everywhere equivalence) If
for
-almost every
, then
.
- (Finiteness)
if and only if
is finite almost everywhere, and is supported on a set of finite measure.
- (Vanishing)
if and only if
is zero almost everywhere.
Exercise 33 (Inclusion-exclusion principle) Let
be a measure space, and let
be
-measurable sets of finite measure. Show that
(Hint: Compute
in two different ways.)
Remark 9 The simple integral could also be defined on finitely additive measure spaces, rather than countably additive ones, and all the above properties would still apply. However, on a finitely additive measure space one would have difficulty extending the integral beyond simple functions, as we will now do.
From the simple integral, we can now define the unsigned integral, similarly to what was done for the unsigned Lebesgue integral in Notes 2:
Definition 11 Let
be a measure space, and let
be measurable. Then we define the unsigned integral
of
by the formula
Clearly, this definition generalises the corresponding definition in Definition 10 of Notes 2. Indeed, if is Lebesgue measurable, then
.
We record some easy properties of this integral:
Exercise 34 (Easy properties of the unsigned integral) Let
be a measure space, and let
be measurable.
- (Almost everywhere equivalence) If

-almost everywhere, then
- (Monotonicity) If

-almost everywhere, then
.
- (Homogeneity) We have
for every
.
- (Superadditivity) We have
.
- (Compatibility with the simple integral) If
is simple, then
.
- (Markov’s inequality) For any
, one has
In particular, if
, then the sets
have finite measure for each
.
- (Finiteness) If
, then
is finite for
-almost every
.
- (Vanishing) If
, then
is zero for
-almost every
.
- (Horizontal truncation) We have
.
- (Vertical truncation) If
is an increasing sequence of
-measurable sets, then
- (Restriction) If
is a measurable subset of
, then
, where
is the restriction of
to
, and the restriction
was defined in Example 12. We will often abbreviate
(by slight abuse of notation) as
.
As before, one of the key properties of this integral is its additivity:
Theorem 12 Let
be a measure space, and let
be measurable. Then
Proof: In view of super-additivity, it suffices to establish the sub-additivity property
We establish this in stages. We first deal with the case when is a finite measure (which means that
) and
are bounded. Pick an
, and let
be
rounded down to the nearest integer multiple of
, and
be
rounded up to the nearest integer multiple. Clearly, we have the pointwise bounds
and
Since is bounded,
and
are simple. Similarly define
. We then have the pointwise bound
hence by Exercise 34 and the properties of the simple integral,
From (1) we conclude that
Letting and using the assumption that
is finite, we obtain the claim.
Now we continue to assume that is a finite measure, but now do not assume that
are bounded. Then for any natural number
, we can use the previous case to deduce that
Since , we conclude that
Taking limits as using horizontal truncation, we obtain the claim.
Finally, we no longer assume that is of finite measure, and also do not require
to be bounded. If either
or
is infinite, then by monotonicity,
is infinite as well, and the claim follows; so we may assume that
and
are both finite. By Markov’s inequality, we conclude that for each natural number
, the set
has finite measure. These sets are increasing in
, and
are supported on
, and so by vertical truncation
From the previous case, we have
Letting and using vertical truncation we obtain the claim.
Exercise 35 (Linearity in
) Let
be a measure space, and let
be measurable.
- Show that
for every
.
- If
are a sequence of measures on
, show that
Exercise 36 (Change of variables formula) Let
be a measure space, and let
be a measurable morphism (as defined in Remark 8) from
to another measurable space
. Define the pushforward
of
by
by the formula
.
- Show that
is a measure on
, so that
is a measure space.
- If
is measurable, show that
.
(Hint: the quickest proof here is via the monotone convergence theorem below, but it is also possible to prove the exercise without this theorem.)
Exercise 37 Let
be an invertible linear transformation, and let
be Lebesgue measure on
. Show that
, where the pushforward
of
was defined in Exercise 36.
Exercise 38 (Sums as integrals) Let
be an arbitrary set (with the discrete
-algebra), let
be counting measure (see Exercise 13), and let
be an arbitrary unsigned function. Show that
is measurable with
Once one has the unsigned integral, one can define the absolutely convergent integral exactly as in the Lebesgue case:
Definition 13 (Absolutely convergent integral) Let
be a measure space. A measurable function
is said to be absolutely integrable if the unsigned integral
is finite, and use
,
, or
to denote the space of absolutely integrable functions. If
is real-valued and absolutely integrable, we define the integral
by the formula
where
,
are the magnitudes of the positive and negative components of
. If
is complex-valued and absolutely integrable, we define the integral
by the formula
where the two integrals on the right are interpreted as real-valued integrals. It is easy to see that the unsigned, real-valued, and complex-valued integrals defined in this manner are compatible on their common domains of definition.
Clearly, this definition generalises the corresponding definition in Definition 13 of Notes 2.
We record some of the key facts about the absolutely convergent integral:
Exercise 39 Let
be a measure space.
- Show that
is a complex vector space.
- Show that the integration map
is a complex-linear map from
to
.
- Establish the triangle inequality
and the homogeneity property
for all
and
.
- Show that if
are such that
for
-almost every
, then
.
- If
, and
is a refinement of
, then
, and
. (Hint: it is easy to get one inequality. To get the other inequality, first work in the case when
is both bounded and has finite measure support (i.e. is both vertically and horizontally truncated).)
- Show that if
, then
if and only if
is zero
-almost everywhere.
- If
is
-measurable and
, then
and
. As before, by abuse of notation we write
for
.
— 5. The convergence theorems —
Let be a measure space, and let
be a sequence of measurable functions. Suppose that as
,
converges pointwise either everywhere, or
-almost everywhere, to a measurable limit
. A basic question in the subject is to determine the conditions under which such pointwise convergence would imply convergence of the integral:
To put it another way: when can we ensure that one can interchange integrals and limits,
There are certainly some cases in which one can safely do this:
Exercise 40 (Uniform convergence on a finite measure space) Suppose that
is a finite measure space (so
), and
(resp.
) are a sequence of unsigned measurable functions (resp. absolutely integrable functions) that converge uniformly to a limit
. Show that
converges to
.
However, there are also cases in which one cannot interchange limits and integrals, even when the are unsigned. We give the three classic examples, all of “moving bump” type, though the way in which the bump moves varies from example to example:
Example 17 (Escape to horizontal infinity) Let
be the real line with Lebesgue measure, and let
. Then
converges pointwise to
, but
does not converge to
. Somehow, all the mass in the
has escaped by moving off to infinity in a horizontal direction, leaving none behind for the pointwise limit
.
Example 18 (Escape to width infinity) Let
be the real line with Lebesgue measure, and let
. Then
now converges uniformly
, but
still does not converge to
. Exercise 40 would prevent this from happening if all the
were supported in a single set of finite measure, but the increasingly wide nature of the support of the
prevents this from happening.
Example 19 (Escape to vertical infinity) Let
be the unit interval
with Lebesgue measure (restricted from
), and let
. Now, we have finite measure, and
converges pointwise to
, but no uniform convergence. And again,
is not converging to
. This time, the mass has escaped vertically, through the increasingly large values of
.
Remark 10 From the perspective of time-frequency analysis (or perhaps more accurately, space-frequency analysis), these three escapes are analogous (though not quite identical) to escape to spatial infinity, escape to zero frequency, and escape to infinite frequency respectively, thus describing the three different ways in which phase space fails to be compact (if one excises the zero frequency as being singular).
However, once one shuts down these avenues of escape to infinity, it turns out that one can recover convergence of the integral. There are two major ways to accomplish this. One is to enforce monotonicity, which prevents each from abandoning the location where the mass of the preceding
was concentrated and which thus shuts down the above three escape scenarios. More precisely, we have the monotone convergence theorem:
Theorem 14 (Monotone convergence theorem) Let
be a measure space, and let
be a monotone non-decreasing sequence of unsigned measurable functions on
. Then we have
Note that in the special case when each is an indicator function
, this theorem collapses to the upwards monotone convergence property (Exercise 23.2). Conversely, the upwards monotone convergence property will play a key role in the proof of this theorem.
Proof: Write , then
is measurable. Since the
are non-decreasing to
, we see from monotonicity that
are non-decreasing and bounded above by
, which gives the bound
It remains to establish the reverse inequality
By definition, it suffices to show that
whenever is a simple function that is bounded pointwise by
. By horizontal truncation we may assume without loss of generality that
also is finite everywhere, then we can write
for some and some disjoint
-measurable sets
, thus
Let be arbitrary. Then we have
for all . Thus, if we define the sets
then the increase to
and are measurable. By upwards monotonicity of measure, we conclude that
On the other hand, observe the pointwise bound
for any ; integrating this, we obtain
Taking limits as , we obtain
sending we then obtain the claim.
Remark 11 It is easy to see that the result still holds if the monotonicity
only holds almost everywhere rather than everywhere.
This has a number of important corollaries. Firstly, we can generalise (part of) Tonelli’s theorem for exchanging sums (see Theorem 2 of Notes 1):
Corollary 15 (Tonelli’s theorem for sums and integrals) Let
be a measure space, and let
be a sequence of unsigned measurable functions. Then one has
Proof: Apply the monotone convergence theorem to the partial sums .
Exercise 41 Give an example to show that this corollary can fail if the
are assumed to be absolutely integrable rather than unsigned measurable, even if the sum
is absolutely convergent for each
. (Hint: think about the three escapes to infinity.)
Exercise 42 (Borel-Cantelli lemma) Let
be a measure space, and let
be a sequence of
-measurable sets such that
. Show that almost every
is contained in at most finitely many of the
(i.e.
is finite for almost every
). (Hint: Apply Tonelli’s theorem to the indicator functions
.)
Exercise 43
- Give an alternate proof of the Borel-Cantelli lemma (Exercise 42) that does not go through any of the convergence theorems, but instead exploits the more basic properties of measure from Exercise 23.
- Give a counterexample that shows that the Borel-Cantelli lemma can fail if the condition
is relaxed to
.
Secondly, when one does not have monotonicity, one can at least obtain an important inequality, known as Fatou’s lemma:
Corollary 16 (Fatou’s lemma) Let
be a measure space, and let
be a sequence of unsigned measurable functions. Then
Proof: Write for each
. Then the
are measurable and non-decreasing, and hence by the monotone convergence theorem
By definition of lim inf, we have . By monotonicity, we have
for all
, and thus
Hence we have
The claim then follows by another appeal to the definition of lim inf.
Remark 12 Informally, Fatou’s lemma tells us that when taking the pointwise limit of unsigned functions
, that mass
can be destroyed in the limit (as was the case in the three key moving bump examples), but it cannot be created in the limit. Of course the unsigned hypothesis is necessary here (consider for instance multiplying any of the moving bump examples by
). While this lemma was stated only for pointwise limits, the same general principle (that mass can be destroyed, but not created, by the process of taking limits) tends to hold for other “weak” notions of convergence. We will see some instances of this in 245B.
Finally, we give the other major way to shut down loss of mass via escape to infinity, which is to dominate all of the functions involved by an absolutely convergent one. This result is known as the dominated convergence theorem:
Theorem 17 (Dominated convergence theorem) Let
be a measure space, and let
be a sequence of measurable functions that converge pointwise
-almost everywhere to a measurable limit
. Suppose that there is an unsigned absolutely integrable function
such that
are pointwise
-almost everywhere bounded by
for each
. Then we have
From the moving bump examples we see that this statement fails if there is no absolutely integrable dominating function . The reader is encouraged to see why, in each of the moving bump examples, no such dominating function exists, without appealing to the above theorem. Note also that when each of the
is an indicator function
, the dominated convergence theorem collapses to Exercise 24.
Proof: By modifying on a null set, we may assume without loss of generality that the
converge to
pointwise everywhere rather than
-almost everywhere, and similarly we can assume that
are bounded by
pointwise everywhere rather than
-almost everywhere.
By taking real and imaginary parts we may assume without loss of generality that are real, thus
pointwise. Of course, this implies that
pointwise also.
If we apply Fatou’s lemma to the unsigned functions , we see that
which on subtracting the finite quantity gives
Similarly, if we apply that lemma to the unsigned functions , we obtain
negating this inequality and then cancelling again we conclude that
The claim then follows by combining these inequalities.
Remark 13 We deduced the dominated convergence theorem from Fatou’s lemma, and Fatou’s lemma from the monotone convergence theorem. However, one can obtain these theorems in a different order, depending on one’s taste, as they are so closely related. For instance, in Stein-Shakarchi, the logic is somewhat different; one first obtains the slightly simpler bounded convergence theorem, which is the dominated convergence theorem under the assumption that the functions are uniformly bounded and all supported on a single set of finite measure, and then uses that to deduce Fatou’s lemma, which in turn is used to deduce the monotone convergence theorem; and then the horizontal and vertical truncation properties are used to extend the bounded convergence theorem to the dominated convergence theorem. It is instructive to view a couple different derivations of these key theorems to get more of an intuitive understanding as to how they work.
Exercise 44 Under the hypotheses of the dominated convergence theorem, establish also that
as
.
Exercise 45 (Almost dominated convergence) Let
be a measure space, and let
be a sequence of measurable functions that converge pointwise
-almost everywhere to a measurable limit
. Suppose that there is an unsigned absolutely integrable functions
such that the
are pointwise
-almost everywhere bounded by
, and that
as
. Show that
Exercise 46 (Defect version of Fatou’s lemma) Let
be a measure space, and let
be a sequence of unsigned absolutely integrable functions that converges pointwise to an absolutely integrable limit
. Show that
as
. (Hint: Apply the dominated convergence theorem to
.) Informally, this tells us that the gap between the left and right hand sides of Fatou’s lemma can be measured by the quantity
.
Exercise 47 Let
be a measure space, and let
be measurable. Show that the function
defined by the formula
is a measure. (We will study such measures in greater detail in 245B.)
The monotone convergence theorem is, in some sense, a defining property of the unsigned integral, as the following exercise illustrates.
Exercise 48 (Characterisation of the unsigned integral) Let
be a measurable space.
be a map from the space
of unsigned measurable functions
to
that obeys the following axioms:
- (Homogeneity) For every
and
, one has
.
- (Finite additivity) For every
, one has
.
- (Monotone convergence) If
are a non-decreasing sequence of unsigned measurable functions, then
.
Then there exists a unique measure
on
such that
for all
. Furthermore,
is given by the formula
for all
-measurable sets
.
Exercise 49 Let
be a finite measure space (i.e.
), and let
be a bounded function. Suppose that
is complete, which means that every sub-null set is a null set. Suppose that the upper integral
and lower integral
agree. Show that
is measurable. (This is a converse to Exercise 11 of Notes 2.)
We will continue to see the monotone convergence theorem, Fatou’s lemma, and the dominated convergence theorem make an appearance throughout the rest of this course sequence.
— 6. Probability spaces (optional) —
We now pause to isolate a special type of measure space, namely an probability space. As the name suggests, these spaces are of fundamental importance in the foundations of probability, although it should be emphasised that probability theory should not be viewed as the study of probability spaces, as these are merely models for the true objects of study of that theory, namely the behaviour of random events and random variables. (See this post for further discussion of this point.) This course will not be focused on applications to probability theory, but other courses (such as the Math 275 sequence at UCLA) will certainly be taking several results from measure theory (e.g. the Borel-Cantelli lemma, Exercise 42) and transferring them to a probabilistic context in order to apply them to problems of interest in probability theory.
Definition 18 (Probability space) A probability space is a measure space
of total measure
:
. The measure
is known as a probability measure.
Note the change of notation: whereas measure spaces are traditionally denoted by symbols such as , probability spaces are traditionally denoted by symbols such as
. Of course, such notational changes have no impact on the underlying mathematical formalism, but they reflect the different cultures of measure theory and probability theory. In particular, the various components
,
,
carry the following interpretations in probability theory, that are absent in other applications of measure theory:
- The space
is known as the sample space, and is interpreted as the set of all possible states
that a random system could be in.
- The
-algebra
is known as the event space, and is interpreted as the set of all possible events
that one can measure.
- The measure
of an event is known as the probability of that event.
The various axioms of a probability space then formalise the foundational axioms of probability, as set out by Kolmogorov.
Example 20 (Normalised measure) Given any measure space
with
, the space
is a probability space. For instance, if
is a non-empty finite set with the discrete
-algebra
and the counting measure
, then the normalised counting measure
is a probability measure (known as the (discrete) uniform probability measure on
), and
is a probability space. In probability theory, this probability spaces models the act of drawing an element of the discrete set
uniformly at random.
Similarly, if
is a Lebesgue measurable set of positive finite Lebesgue measure,
, then
is a probability space. The probability measure
is known as the (continuous) uniform probability measure on
. In probability theory, this probability spaces models the act of drawing an element of the continuous set
uniformly at random.
Example 21 (Discrete and continuous probability measures) If
is a (possibly infinite) non-empty set with the discrete
-algebra
, and if
are a collection of real numbers in
with
, then the probability measure
defined by
, or in other words
is indeed a probability measure, and
is a probability space. The function
is known as the (discrete) probability distribution of the state variable
.
Similarly, if
is a Lebesgue measurable subset of
of positive (and possibly infinite) measure, and
is a Lebesgue measurable function on
(where of course we restrict the Lebesgue measure space on
to
in the usual fashion) with
, then
is a probability space, where
is the measure
The function
is known as the (continuous) probability density of the state variable
. (This density is not quite unique, since one can modify it on a set of probability zero, but it is well-defined up to this ambiguity. We will return to this point in 245B.)
Exercise 50 (No translation-invariant random integer) Show that there is no probability measure
on the integers
with the discrete
-algebra
with the translation-invariance property
for every event
and every integer
.
Exercise 51 (No translation-invariant random real) Show that there is no probability measure
on the reals
with the Lebesgue
-algebra
with the translation-invariance property
for every event
and every real
.
Many concepts in measure theory are of importance in probability theory, although the terminology is changed to reflect the different perspective on the subject. For instance, the notion of a property holding almost everywhere is now replaced with that of a property holding almost surely. A measurable function is now referred to as a random variable and is often denoted by symbols such as , and the integral of that function on the probability space (if the random variable is unsigned or absolutely convergent) is known as the expectation of that random variable, and is denoted
. Thus, for instance, the Borel-Cantelli lemma (Exercise 42) now reads as follows: given any sequence
of events such that
, it is almost surely true that at most finitely many of these events hold.
In later notes, when we develop the machinery of product measures and other tools to construct measures, we will see some more interesting examples of probability spaces, which would correspond in probability theory to random processes that are generated by an infinite number of independent random sources.
The following exercise will be moved to a more suitable location in the published version of the notes, but is here currently so as not to disrupt the exercise numbering.
Exercise 52 (Approximation by an algebra) Let
be a Boolean algebra on
, and let
be a measure on
.
- If
, show that for every
and
there exists
such that
.
- More generally, if
for some
with
for all
,
has finite measure, and
, show that there exists
such that
.

120 comments
Comments feed for this article
25 July, 2013 at 4:21 am
Luqing Ye
A remark to Theorem 17 (Dominated convergence theorem):
I proved the dominated convergence theorem using Egorove’s theorem together with Exercise 40 (Uniform convergence on a finite measure space) when I was walking outside home.
I don’t use Fatou’s lemma…..BTW,I think Fatou’s lemma is a naive and easy stuff,so I will be comfortable that I don’t use this lemma….
25 July, 2013 at 9:16 pm
Luqing Ye
Dear Prof.Tao,
In the proof of Theorem 17 (Dominated convergence theorem),I think the last inequality
should be
25 July, 2013 at 9:25 pm
Luqing Ye
I am wrong again……Maybe next time I shouldn’t put any comment until I think 10 times.
26 July, 2013 at 6:50 am
A proof of Fatou’s lemma « Asymptote
[…] In this post I give a proof of Fatou’s lemma which is the Corollary 16 of Terence Tao’s post 245A, Notes 3: Integration on abstract measure spaces, and the convergence theorems. […]
28 July, 2013 at 7:03 am
Luqing Ye
Dear Prof.Tao,
Could you please give me some hints on how the condition “Suppose that is complete, which means that every sub-null set is a null set.” is used in Exercise 49?
is complete, which means that every sub-null set is a null set.” is used in Exercise 49?
I have a bit doubt on my ability to give a correct proof because I proved Exercise 49 without using this condition……
28 July, 2013 at 8:38 am
Terence Tao
If is an indicator function of a sub-null set, what are the upper and lower integrals of
is an indicator function of a sub-null set, what are the upper and lower integrals of  ?
?
28 July, 2013 at 8:38 pm
Luqing Ye
If is an indicator function of an unmeasurable sub-null set,it seems that the upper and lower integrals of
is an indicator function of an unmeasurable sub-null set,it seems that the upper and lower integrals of  does not exist.
does not exist.
Dear Prof.Tao,
Thank you for your hint.Now I understand that I made a skip in my proof,I thought that according to Littlewood’s principle,I can ignore the subnull set and null set but actually I should not because if I ignore the unmeasurable subnull set,then I will get an unmeasurable monster.
The reason that I proved this exercise wrongly is that I used wrong intuition.I carry my intuition in Lebesgue measure into this general measure space setting,which result in my fault.More precisely,it seems that Littlewood’s three principle should only work in complete measure space,otherwise I will get a monster……
4 July, 2016 at 6:15 pm
Sunting
i think the important aspect is that if X is not complete, then if fn(measurable) converges to f, a.e., we could not say that f is measurable. if it is complete, then f is measurable.if f is an indicator function of subnull set, then upper and lower integrals both are zero, so they agree, but it seems that in this case f is not measurable.
1 September, 2014 at 4:41 pm
Anonymous
Are Borel sigma algebra![{\mathcal B}[{\bf C}]](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+B%7D%5B%7B%5Cbf+C%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) and
and ![{\mathcal B}[{\bf R}^2]](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+B%7D%5B%7B%5Cbf+R%7D%5E2%5D&bg=ffffff&fg=545454&s=0&c=20201002) the same? In Folland’s Real Analysis, the author uses
the same? In Folland’s Real Analysis, the author uses ![{\mathcal B}[{\bf C}]={\mathcal B}[{\bf R}^2]](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+B%7D%5B%7B%5Cbf+C%7D%5D%3D%7B%5Cmathcal+B%7D%5B%7B%5Cbf+R%7D%5E2%5D&bg=ffffff&fg=545454&s=0&c=20201002) to show that a complex function is measurable iff both the real and imaginary parts are measurable.
to show that a complex function is measurable iff both the real and imaginary parts are measurable.
1 September, 2014 at 5:13 pm
Terence Tao
1 September, 2014 at 5:36 pm
Anonymous
When you say “identifying”, do you mean “homeomorphism”? In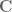 one has multiplication for
one has multiplication for 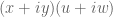 . But in
. But in 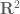 , one only has inner product
, one only has inner product 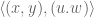 , which is not the same as the previous one. Is it because one discards such structures and considers “topology” only that one can “identify” these two Borel sigma algebra. As I understand from your comment, should one view “=” in the identity above as “homromorphism” (or some sort of “isomorphism”)?
, which is not the same as the previous one. Is it because one discards such structures and considers “topology” only that one can “identify” these two Borel sigma algebra. As I understand from your comment, should one view “=” in the identity above as “homromorphism” (or some sort of “isomorphism”)?
1 September, 2014 at 6:51 pm
Terence Tao
The standard identification between
between 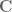 and
and 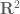 is an isomorphism of sets (otherwise known as a bijection), and is furthermore an isomorphism of topological spaces (otherwise known as a homeomorphism). As you noted, though, it is not an isomorphism of rings or of inner product spaces. (It is an isomorphism of (additive) groups, but this is not particularly relevant for the current discussion.)
is an isomorphism of sets (otherwise known as a bijection), and is furthermore an isomorphism of topological spaces (otherwise known as a homeomorphism). As you noted, though, it is not an isomorphism of rings or of inner product spaces. (It is an isomorphism of (additive) groups, but this is not particularly relevant for the current discussion.)
19 September, 2014 at 12:56 pm
Anonymous
I don’t follow the “without loss of generality” part of the proof of MCT. Suppose is not finite every where, say,
is not finite every where, say, 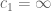 and
and 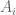 is not of measure zero. How to go on in this situation? How does “vertical truncation” help here (I don’t know what is “truncated” here…)?
is not of measure zero. How to go on in this situation? How does “vertical truncation” help here (I don’t know what is “truncated” here…)?
19 September, 2014 at 2:20 pm
Terence Tao
If g attains infinite values, replace g with (this is the “vertical truncation” of g at height N) and then let
(this is the “vertical truncation” of g at height N) and then let  .
.
24 May, 2015 at 7:20 am
Alex
Do you have any additional hint on how to prove the dominated convergence theorem for sets? Following the given hint, one takes
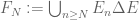

 ?
?
and by monotone convergence for sets
How can I prove that
Thank you!
[You don’t need to prove to finish the problem. One just needs an appropriate inequality relating
to finish the problem. One just needs an appropriate inequality relating  with
with  and
and  . -T.]
. -T.]
29 September, 2015 at 9:54 pm
275A, Notes 0: Foundations of probability theory | What's new
[…] begin with the notion of a measurable space. (See also this previous blog post, which covers similar material from the perspective of a real analysis graduate class rather than a […]
2 October, 2015 at 10:11 pm
TECNOLOGÍA » 275A, Notes 0: Foundations of probability theory
[…] begin with the notion of a measurable space. (See also this previous blog post, which covers similar material from the perspective of a real analysis graduate class rather than a […]
3 October, 2015 at 2:58 pm
275A, Notes 1: Integration and expectation | What's new
[…] of the details of this construction will be left to exercises. See also Chapter 1 of Durrett, or these previous blog notes, for a more detailed […]
16 December, 2015 at 4:22 pm
Anonymous
In the proof of MCT, why we need the there? What could fail if we just define
there? What could fail if we just define
the sets
16 December, 2015 at 4:26 pm
Anonymous
I meant
16 December, 2015 at 4:37 pm
Terence Tao
In this case, the need not increase to
need not increase to 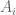 . (For instance, one could have
. (For instance, one could have  on
on 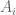 .)
.)
17 December, 2015 at 10:55 am
Anonymous
The reader is encouraged to see why, in each of the moving bump examples, no such dominating function exists, without appealing to the above theorem (DCT)
To dominate
17 December, 2015 at 12:47 pm
Terence Tao
Graph the functions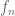 , and compare against the graph of
, and compare against the graph of 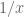 .
.
1 August, 2016 at 7:02 am
Joe Li
Small typo in Exercise 31.![f: {\mathcal B} \rightarrow [0,+\infty]](https://s0.wp.com/latex.php?latex=f%3A+%7B%5Cmathcal+B%7D+%5Crightarrow+%5B0%2C%2B%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) should be
should be ![f: X \rightarrow [0,+\infty]](https://s0.wp.com/latex.php?latex=f%3A+X+%5Crightarrow+%5B0%2C%2B%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
[Corrected, thanks – T.]
22 November, 2016 at 7:25 am
coupon_clipper
Sorry for the simple question, but can you give a hint for Exercise 34 part 10 (vertical truncation)? I feel like none of the old tricks from Lebesgue integration work here, and we don’t even know if the union of the have finite measure. Every time I try to write out a proof, I end up trying to switch limits around, which is what I’m trying to prove I can do.
have finite measure. Every time I try to write out a proof, I end up trying to switch limits around, which is what I’m trying to prove I can do.
[First try the case when is a simple function, or even an indicator function. -T.]
is a simple function, or even an indicator function. -T.]
23 November, 2016 at 2:43 pm
Coupon_clipper
Thanks Terry. Got it now. Have a great Thanksgiving!
12 March, 2017 at 11:08 pm
Ian
Concerning exercise 18, part 1: Is this statement true? How can one prove that if E has measurable projection, then its complement does too? (since projection does not commute with taking complements)
[Exercise 18 concerns slices, not projections. -T]
16 January, 2019 at 10:57 am
245A: Problem solving strategies | What's new
[…] the generating sets; in some cases one can also take balls, cubes, or rectangles); see Remark 4 of Notes 3. One can relax the set of properties required, for instance countable intersections is […]
21 June, 2020 at 12:37 am
Ruijun Lin
I want to ask a question on Exercise 26 about completion. Do we need to just to prove the existence first then find the structure of the completed space? Or first construct one then show it satisfies all the conditions?
[Either approach can work, although the latter is easier in this case -T.]
28 June, 2020 at 4:31 am
Ruijun Lin
Thanks Prof. Tao
28 June, 2020 at 4:41 am
Ruijun Lin
Dear Prof. Tao,
I tried hard but cannot figure out the complete proof of the Exercise 36 about the change of variables formula about the pushforward measure without the monotone convergence theorem. The question (i) is simple and I made it.For (ii) I only know how to show the conclusion holds for simple functions. But for general unsigned functions I failed to work it out. Can you give a proof or offer just some hints for the general case without the monotone convergence theorem?
Thank you very much.
28 June, 2020 at 6:58 am
Ruijun Lin
Yes, I’m very eager to know the proof of this problem without the monotone convergence theorem to maintain the fluency of the book.
29 June, 2020 at 10:35 pm
Leo Sera
Hi Ruijun. Looks like someone asked the same question you did here and it already has an answer. https://math.stackexchange.com/questions/3738431/proof-of-the-change-of-variables-formula-without-using-the-monotone-convergence/3738505#3738505
30 June, 2020 at 1:07 am
Ruijun Lin
(Laughter) The question there is also asked by me.
30 June, 2020 at 1:09 am
Ruijun Lin
Maybe there is an answer and I will check it.
30 June, 2020 at 3:21 am
Ruijun Lin
His answer is wrong, I think.
30 June, 2020 at 7:42 pm
Leo Sera
Oh! I just read it I didn’t see the error but looks like it has a couple of edits. Maybe the error you caught has been fixed.
4 January, 2021 at 12:46 pm
Anonymous
If one wants to develop an integration theory for functions defined on manifolds, does one need to (eventually) use coordinate charts? Or does the nature of “abstract” measure spaces allow one to define Lebesgue integrals in an intrinsic way?
4 January, 2021 at 7:31 pm
Terence Tao
There is no canonical measure that one can intrinsically assign to an smooth abstract manifold (pushing forward Lebesgue measure from a coordinate chart is a chart-dependent construction). But if one has an additional structure, such as a Riemannian metric, a symplectic form, Kahler measure, a transitive group action by an amenable group, or an immersion into Euclidean space, one can often create such a canonical measure (Riemannian volume measure, Liouville measure, Haar measure, induced Lebesgue measure, etc.).
16 March, 2022 at 7:06 am
Anonymous
In the case of the counting measure, one has in Exercise 38 the integral is actually a sum. Does one has a simple formula for when
when  is the Dirac delta measure, say
is the Dirac delta measure, say 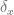 for some fixed
for some fixed 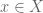 ?
?
16 March, 2022 at 9:57 am
Terence Tao
Yes, this is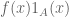 .
.
22 May, 2022 at 10:08 am
Anonymous
Dear Professor Tao: sets has most
sets has most 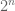 atoms, first showing by induction that
atoms, first showing by induction that  sets partition the space into at most
sets partition the space into at most 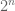 disjoint regions?
disjoint regions?
For exercise 8, is it ideal to prove it by showing that the Boolean algebra generated by
[Sure, that works – T.]
6 June, 2022 at 7:39 am
YiLi
Dear Professor Tao: For exercise 35 change of variable formula, I was confused with the version of change of variable formula in the context of calculus, where needs the transformation being at least $C^1$ diffeomorphism? why only needs morphism not isomorphism here?
11 June, 2022 at 3:21 pm
Terence Tao
The measure-theory perspective allows one to split the change of variables formula into two parts and clarifies exactly where a hypothesis of diffeomorphism is helpful. The first, which is purely measure-theoretic and requires no assumption of diffeomorphism, is Exercise 35 here. The second, which is not part of this notes, is that the pushforward of Lebesgue measure under a
under a  diffeomorphism
diffeomorphism  is given by
is given by 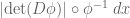 . Thus one can push forward a measure (or pull back an integral) by arbitrary measurable maps, but one is not guaranteed to have a nice formula for this change of variables unless one has a diffeomorphism structure (or other nice property of the map).
. Thus one can push forward a measure (or pull back an integral) by arbitrary measurable maps, but one is not guaranteed to have a nice formula for this change of variables unless one has a diffeomorphism structure (or other nice property of the map).
12 June, 2022 at 5:27 am
YiLi
I got it thank you, the pull back measure has some set theory beneficial, for example in the construction of the measure preserving map in the Ergodic Theory.
6 February, 2023 at 3:33 pm
Anonymous
Dear professor Tao:
For exercise $23$, What would be an example of such a sequence of sets if the hypothesis that ${\mu(E_n)<\infty}$ for at least one $n$ is dropped? I find it hard to utilize the middle third Cantor set example in this case.
[Hint: experiment with half-infinite intervals in the real line. -T]
12 February, 2023 at 4:10 pm
sam
Dear professor Tao: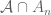 is an algebra on
is an algebra on  for each n, and then
for each n, and then  , in order to use part (1) on the finite measure space
, in order to use part (1) on the finite measure space  . (Here the intersection of an algebra with a set is the collection of the intersection of that set with the members of the algebra). Is this the way the solution is intended? What else can one approaches the problem?
. (Here the intersection of an algebra with a set is the collection of the intersection of that set with the members of the algebra). Is this the way the solution is intended? What else can one approaches the problem?
For part (2) of exercise 28(in the textbook), I think one first needs to show that
23 February, 2023 at 4:44 pm
Anonymous
Dear professor Tao: with
with  in exercise 21 of note 1?
in exercise 21 of note 1?
For exercise 37, can we prove it by simply replace
[Yes – T.]
27 February, 2023 at 3:07 pm
Anonymous
Dear professor Tao: of Exercise $ latex 39$, it looks like the fact that the integral of
of Exercise $ latex 39$, it looks like the fact that the integral of  being insensitive to refinement follows from the same property of the real-valued
being insensitive to refinement follows from the same property of the real-valued  , which follows from that of the unsigned
, which follows from that of the unsigned  , which then follows from that of the simple $f$. Why then do we need to approximate $f$ as the hint suggested?
, which then follows from that of the simple $f$. Why then do we need to approximate $f$ as the hint suggested?
For
[This also works – T.]