A few days ago, I found myself needing to use the Fredholm alternative in functional analysis:
Theorem 1 (Fredholm alternative) Let
be a Banach space, let
be a compact operator, and let
be non-zero. Then exactly one of the following statements hold:
- (Eigenvalue) There is a non-trivial solution
to the equation
.
- (Bounded resolvent) The operator
has a bounded inverse
on
.
Among other things, the Fredholm alternative can be used to establish the spectral theorem for compact operators. A hypothesis such as compactness is necessary; the shift operator on
, for instance, has no eigenfunctions, but
is not invertible for any unit complex number
. The claim is also false when
; consider for instance the multiplication operator
on
, which is compact and has no eigenvalue at zero, but is not invertible.
It had been a while since I had studied the spectral theory of compact operators, and I found that I could not immediately reconstruct a proof of the Fredholm alternative from first principles. So I set myself the exercise of doing so. I thought that I had managed to establish the alternative in all cases, but as pointed out in comments, my argument is restricted to the case where the compact operator is approximable, which means that it is the limit of finite rank operators in the uniform topology. Many Banach spaces (and in particular, all Hilbert spaces) have the approximation property that implies (by a result of Grothendieck) that all compact operators on that space are almost finite rank. For instance, if
is a Hilbert space, then any compact operator is approximable, because any compact set can be approximated by a finite-dimensional subspace, and in a Hilbert space, the orthogonal projection operator to a subspace is always a contraction. (In more general Banach spaces, finite-dimensional subspaces are still complemented, but the operator norm of the projection can be large.) Unfortunately, there are examples of Banach spaces for which the approximation property fails; the first such examples were discovered by Enflo, and a subsequent paper of by Alexander demonstrated the existence of compact operators in certain Banach spaces that are not approximable.
I also found out that this argument was essentially also discovered independently by by MacCluer-Hull and by Uuye. Nevertheless, I am recording this argument here, together with two more traditional proofs of the Fredholm alternative (based on the Riesz lemma and a continuity argument respectively).
— 1. First proof (approximable case only) —
In the finite-dimensional case, the Fredholm alternative is an immediate consequence of the rank-nullity theorem, and the finite rank case can be easily deduced from the finite dimensional case by some routine algebraic manipulation. The main difficulty in proving the alternative is to be able to take limits and deduce the approximable case from the finite rank case. The key idea of the proof is to use compactness to establish a lower bound on that is stable enough to allow one to take such limits. There is an additional subtlety (pointed out in comments) that when
is not a Hilbert space, it is not necessarily the case that
can be approximated by finite rank operators; but a modification of the argument still suffices in this case.
Fix a non-zero . It is clear that
cannot have both an eigenvalue and bounded resolvent at
, so now suppose that
has no eigenvalue at
, thus
is injective. We claim that this implies a lower bound:
Lemma 2 (Lower bound) Let
be non-zero, and suppose that
be a compact operator that has no eigenvalue at
. Then there exists
such that
for all
.
Proof: By homogeneity, it suffices to establish the claim for unit vectors . Suppose this is not the case; then we can find a sequence of unit vectors
such that
converges strongly to zero. Since
has norm bounded away from zero (here we use the non-zero nature of
), we conclude in particular that
has norm bounded away from zero for sufficiently large
. By compactness of
, we may (after passing to a subsequence) assume that the
converge strongly to a limit
, which is thus also non-zero.
On the other hand, applying the bounded operator to the strong convergence
(and using the fact that
commutes with
) we see that
converges strongly to
. Since
converges strongly to
, we conclude that
, and thus we have an eigenvalue of
at
, contradiction.
Remark 1 Note that this argument is ineffective in that it provides no explicit value of
(and thus no explicit upper bound for the operator norm of the resolvent
). This is not surprising, given that the fact that
has no eigenvalue at
is an open condition rather than a closed one, and so one does not expect bounds that utilise this condition to be uniform. (Indeed, the resolvent needs to blow up as one approaches the spectrum of
.)
From the lower bound, we see that to prove the bounded invertibility of , it will suffice to establish surjectivity. (Of course, we could have also obtained this reduction by using the open mapping theorem.) In other words, we need to establish that the range
of
is all of
.
Let us first deal with the easy case when has finite rank, so that
is some finite-dimension
. This implies that the kernel
has codimension
, and we may thus split
for some
-dimensional space
. The operator
is a non-zero multiple of the identity on
, and so
already contains
. On the other hand, the operator
maps the
-dimensional space
to the
-dimensional space
injectively (since
avoids
and
is injective), and thus also surjectively (by the rank-nullity theorem). Thus
contains
, and thus (by the short exact sequence
)
is in fact all of
, as desired.
Finally, we deal with the case when is approximable. The lower bound in Lemma 2 is stable, and will extend to the finite rank operators
for
large enough (after reducing
slightly). By the preceding discussion for the finite rank case, we see that
is all of
. Using Lemma 2 for
, and the convergence of
to
in the operator norm topology, we conclude that
is dense in
. On the other hand, we observe that the space
is necessarily closed, for if
converges to a limit
, then (by Lemma 2 and the assumption that
is Banach)
will also converge to some limit
, and so
. As
is now both dense and closed, it must be all of
, and the claim follows.
— 2. Second proof —
We now give the standard proof of the Fredholm alternative based on the Riesz lemma:
Lemma 3 (Riesz lemma) If
is a proper closed subspace of a Banach space
, and
, then there exists a unit vector
whose distance
to
is at least
.
Proof: By the Hahn-Banach theorem, one can find a non-trivial linear functional on
which vanishes on
. By definition of the operator norm
of
, one can find a unit vector
such that
. The claim follows.
The strategy here is not to use finite rank approximations (as they are no longer available), but instead to try to contradict the compactness of by exhibiting a bounded set whose image under
is not totally bounded.
Let be a compact operator on a Banach space, and let
be a non-zero complex number such that
has no eigenvalue at
. As in the first proof, we have the lower bound from Lemma 2, and we know that
is a closed subspace of
; in particular, the map
is a Banach space isomorphism from
to
. Our objective is again to show that
is all of
.
Suppose for contradiction that is a proper closed subspace of
. Applying the Banach space isomorphism
repeatedly, we conclude that for every natural number
, the space
is a proper closed subspace of
. From the Riesz lemma, we may thus find unit vectors
in
for
whose distance to
is at least
(say).
Now suppose that . By construction,
all lie in
, and thus
. Since
lies at a distance at least
from
, we conclude the separation proeprty
But this implies that the sequence is not totally bounded, contradicting the compactness of
.
— 3. Third proof —
Now we give another textbook proof of the Fredholm alternative, based on Fredholm index theory. The basic idea is to observe that the Fredholm alternative is easy when is large enough (and specifically, when
), as one can then invert
using Neumann series. One can then attempt to continously pertrb
from large values to small values, using stability results (such as Lemma 2) to ensure that invertibility does not suddenly get destroyed during this process. Unfortunately, there is an obstruction to this strategy, which is that during the perturbation process,
may pass through an eigenvalue of
. To get around this, we will need to abandon the hypothesis that
has no eigenvalue at
, and work in the more general setting in which
is allowed to be non-trivial. This leads to a lengthier proof, but one which lays the foundation for much of Fredholm theory (which is more powerful than the Fredholm alternative alone).
Fortunately, we still have analogues of much of the above theory in this setting:
Proposition 4 Let
be non-zero, and let
be a compact operator on a Banach space
. Then the following statements hold;
- (Finite multiplicity)
is finite-dimensional.
- (Lower bound) There exists
such that
for all
.
- (Closure)
is a closed subspace of
.
- (Finite comultiplicity)
has finite codimension in
.
Proof: We begin with finite multiplicity. Suppose for contradiction that was infinite dimensional, then it must contain an infinite nested sequence
of finite-dimensional (and thus closed) subspaces. Applying the Riesz lemma, we may find for each
, a unit vector
of distance at least
from
. Since
, we see that the sequence
is then
-separated and thus not totally bounded, contradicting the compactness of
.
The lower bound follows from the argument used to prove Lemma 2 after quotienting out the finite-dimensional space , and the closure assertion follows from the lower bound (again after quotienting out the kernel) as before.
Finally, we establish finite comultiplicity. Suppose for contradiction that the closed subspace had infinite codimension, then by properties of
already established, we see that
is closed and has infinite codimension in
for each
. One can then argue as in the second proof to contradict total boundedness as before.
Remark 2 The above arguments also work if
is replaced by an invertible linear operator on
, or more generally by a Fredholm operator.
We can now define the index to be the dimension of the kernel of
, minus the codimension of the range. To establish the Fredholm alternative, it suffices to show that
for all
, as this implies surjectivity of
whenever there is no eigenvalue. Note that Note that when
is sufficiently large, and in particular when
, then
is invertible by Neumann series and so one already has index zero in this case. To finish the proof, it suffices by the discrete nature of the index function (which takes values in the integers) to establish continuity of the index:
Lemma 5 (Continuity of index) Let
be a compact operator on a Banach space. Then the function
is continuous from
to
.
Proof: Let be non-zero. Our task is to show that
for all sufficiently close to
.
In the model case when is invertible (and thus has index zero), the claim is easy, because
can be inverted by Neumann series for
close enough to
, giving rise to the invertibility of
.
Now we handle the general case. As every finite dimensional space is complemented, we can split for some closed subspace
of
, and similarly split
for some finite-dimensional subspace
of
with dimension
.
From the lower bound we see that is a Banach space isomorphism from
to
. For
close to
, we thus see that
is close to
, in the sense that one can map the latter space to the former by a small perturbation of the identity (in the operator norm). Since
complements
, it also complements
for
sufficiently close to
. (To see this, observe that the composition of the obvious maps
is a small perturbation of the identity map and is thus invertible for close to
.)
Let be the projection onto
with kernel
. Then
maps the finite-dimensional space
to the finite-dimensional space
. By the rank-nullity theorem, this map has index equal to
. Gluing this with the Banach space isomorphism
, we see that
also has index
, as desired.
Remark 3 Again, this result extends to more general Fredholm operators, with the result being that the index of a Fredholm operator is stable with respect to continuous deformations in the operator norm topology.

36 comments
Comments feed for this article
10 April, 2011 at 2:57 pm
Y
With the same assumption, can theorem 1 be restated as “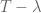 is either ‘1-1 and onto’ or ‘neither 1-1 nor onto'”?
is either ‘1-1 and onto’ or ‘neither 1-1 nor onto'”?
10 April, 2011 at 5:00 pm
ARS
The hypothesis of compactness is necessary. I think you mean to say: Some condition is necessary. There is a theory of Fredholm operators, which does not assume they come from compact perturbations of he idendity. The above theorem then says: $\lambda I-T$ is Fredholm whenever $T$ compact and $\lambda \neq 0$.
10 April, 2011 at 9:08 pm
Anonymous
Why is a compact operator on a Banach Space limit of finite rank operators?
10 April, 2011 at 10:30 pm
Yemon Choi
To elaborate on Anonymous’ hint/suggestion: there are Banach spaces which support compact operators that are not limits (in the operator norm) of sequences of finite rank operators. The norm closure of the ideal of finite rank operators is the so-called algebra of approximable operators; every approximable operator is compact, but the converse does not always hold. It does work for operators on $L^p$-spaces, though, since these have the approximation property.
10 April, 2011 at 11:58 pm
Doormat
AFAIK, the question of approximating a compact operator by finite ranks is not quite equivalent to the approximation property; the first example (which can be taken to be a subspace of \ell_p) of a Banach space X which admits a compact, non-approximable, operator is given in:
Alexander, Freda E.
Compact and finite rank operators on subspaces of lp.
Bull. London Math. Soc. 6 (1974), 341–342.
http://www.ams.org/mathscinet-getitem?mr=0355661
11 April, 2011 at 12:58 am
Yemon Choi
I knew I should just have waited for you to comment instead ;) Yes, I see that I gave a misleading impression; I knew that if X has the AP then A(X)=K(X) and so just gave that as a sufficient condition.
11 April, 2011 at 8:58 am
Terence Tao
Oops, that was a silly mistake to make. (I carelessly thought that since every compact set is approximable by a finite-dimensional set, and every finite-dimensional space is complemented, that every compact operator is approximated by a finite rank one; but the projection to the finite-dimensional space can have large operator norm if one is not in a nice ambient space such as a Hilbert space.) I’ve reworked the text, with my proof (which I also found was discovered by MacCluer-Hull and Uuye) restricted to the approximable setting, and with the two standard proofs of the alternative given for comparison.
11 April, 2011 at 11:13 am
Doormat
Well, it is a question which defeated Banach ;-> (I think it’s asked in his book if every Banach space has the approximation property, which as Yemon and I discussed above is almost, but not quite, the same as asking if every compact operator can be approximated by finite-ranks. It took Enflo until 1973 to find a counter-example. It’s still, IMHO, a poorly understood phenomena in Banach space theory– it’s also rather a recherche area…)
11 April, 2011 at 6:30 pm
Neo
Why the term alternative? Is it just because there are two alternatives in the theorem and exactly one should be true?
13 April, 2011 at 12:07 pm
Terence Tao
Yes, I believe this is the origin of the term. (I suppose that the result could also have been called the “Fredholm dichotomy”, but the existing name is too entrenched in the literature to try changing it now.)
12 April, 2011 at 8:52 am
jesús
What about if the operator under consideration is only closed? There is an analogous for Fredholm alternative theorem?
13 April, 2011 at 10:34 am
Anonymous
Dear Prof. Tao,
is the Laplacian a compact operator on , say K is a bounded domain in
, say K is a bounded domain in  or equal to
or equal to  ?
?
thanks
13 April, 2011 at 12:06 pm
Terence Tao
No; it is not even bounded or everywhere defined from to
to  , let alone continuous. However, resolvents such as
, let alone continuous. However, resolvents such as 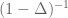 are bounded and compact on
are bounded and compact on  (this is a variant of the Rellich compactness theorem), and this can be used to start building a spectral theory for the Laplacian on bounded domains (and in particular, to show that the spectrum consists only of eigenvalues).
(this is a variant of the Rellich compactness theorem), and this can be used to start building a spectral theory for the Laplacian on bounded domains (and in particular, to show that the spectrum consists only of eigenvalues).
13 April, 2011 at 5:27 pm
Anonymous
Prof.Tao, I am a little bit confused. why is not everywhere defined? can not we apply Laplacian to any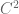 function? isn’t it true that a linear continuous operator also bounded?
function? isn’t it true that a linear continuous operator also bounded?
13 April, 2011 at 9:30 pm
Terence Tao
The Laplacian of a C^2 function will merely be in C^0, not in C^2, and so the Laplacian is not a bounded operator from C^2 to itself.
13 April, 2011 at 10:29 pm
Donald
I see. Thanks for the explanation Prof. Tao.
17 April, 2011 at 9:52 am
Orr
Thanks for the post. 3 lines above the end of the proof of lemma 5, you must have meant dim(W), not dim(V). [Corrected, thanks – T.]
19 April, 2011 at 9:32 am
timur
Following up on the question of Donald, why do we prefer Holder spaces over C^k with integer k? I read in a book that C^k are somehow not the right spaces for elliptic differential equations, but I cannot come up with any tangible argument.
19 April, 2011 at 9:58 am
Terence Tao
Holder spaces are more stable with respect to fractional and singular integrals, and do not “lose” any regularity when inverting elliptic operators. For instance, if lies in
lies in  for some
for some 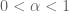 , then
, then  will lie in
will lie in  ; of course, the converse implication is trivial. In contrast, if
; of course, the converse implication is trivial. In contrast, if  lies in
lies in  , then it is not necessarily the case that
, then it is not necessarily the case that  lies in
lies in  (basically because the Riesz transforms
(basically because the Riesz transforms  are not bounded on
are not bounded on 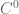 ).
).
Ultimately this is because the fractional Holder spaces have a nice Littlewood-Paley representation as Besov spaces (interactions between different frequency scales can be represented by a convergent geometric series), while the classical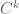 spaces do not (the interactions between frequency scales can be logarithmically divergent). (There are stable substitutes for the
spaces do not (the interactions between frequency scales can be logarithmically divergent). (There are stable substitutes for the 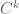 spaces available, such as Zygmund space or VMO (vanishing mean oscillation), but these are not particularly convenient to use for elliptic regularity theory, except perhaps as endpoints to interpolate from, as they do not behave so well with respect to pointwise multiplication.)
spaces available, such as Zygmund space or VMO (vanishing mean oscillation), but these are not particularly convenient to use for elliptic regularity theory, except perhaps as endpoints to interpolate from, as they do not behave so well with respect to pointwise multiplication.)
22 April, 2011 at 5:34 am
A proof of the Fredholm alternative « IMAGINATION of MATH
[…] we deal with the case when is approximable. The lower bound in Lemma 2 is stable, and will extend to the finite rank operators for large enough (after reducing […]
23 April, 2011 at 9:24 am
Fourth Linkfest
[…] Terence Tao: A proof of the Fredholm alternative […]
3 May, 2011 at 12:24 pm
Anonymous
Dear Prof. Tao,
Thanks for the nice post!
I have a (most probably trivial) question for the second proof. If we assume that is a proper subspace of
is a proper subspace of  , how to derive
, how to derive
 ? For instance, for the orthogonal projection
? For instance, for the orthogonal projection  , we always have
, we always have 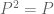 . Of course, this example is not suitable here since
. Of course, this example is not suitable here since  is not injective. But it shows some flavor of my question.
is not injective. But it shows some flavor of my question.
3 May, 2011 at 12:26 pm
Anonymous
I mean that how to show that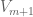 is also a proper subspace of
is also a proper subspace of  ?
?
3 May, 2011 at 12:51 pm
Terence Tao
By induction on m, using the fact that the map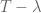 is injective.
is injective.
5 May, 2011 at 7:53 am
ugroh
Riesz Lemma
Terence, I worked through your great post because of my lecture and I got finally a problem with the proof of the Riesz lemma. I guess you proof is as following: is a closed subspace of
is a closed subspace of  , thus
, thus  is a normed vector space. Take
is a normed vector space. Take 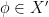 of norm one and
of norm one and  of norm one with
of norm one with  . Then
. Then  for all
for all  and all
and all  . But why can you choose a
. But why can you choose a  of norm one? The canonical map from
of norm one? The canonical map from  to
to  is open but in general not closed, nor is the boundary of the unit ball of
is open but in general not closed, nor is the boundary of the unit ball of  maped onto the boundary of the unit ball of
maped onto the boundary of the unit ball of  ? Or do I miss something?
? Or do I miss something?
Thanks Ulrich
5 May, 2011 at 9:42 am
Terence Tao
Dear Ulrich,
One does not have to explicitly work in the quotient space. First, one uses the Hahn-Banach theorem to find a non-trivial bounded linear functional that vanishes on M. This functional need not have norm 1 (in
that vanishes on M. This functional need not have norm 1 (in 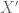 , not in
, not in  ) initially, but it can be normalised as such by multiplying by a constant. By the definition of the X’ norm, this implies that there exists a unit vector
) initially, but it can be normalised as such by multiplying by a constant. By the definition of the X’ norm, this implies that there exists a unit vector 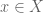 such that
such that  . Since
. Since  , this already forces
, this already forces 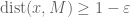 .
.
5 May, 2011 at 11:14 pm
Anonymous
Dear Prof. Tao, dear Prof. Ulrich
A well-known proof without Hahn-Banach: take any v in X, outside of
Y and let d>0 be its distance to Y. Take now a vector y in Y such that the
norm of v-y is smaller than 1+d\varepsilon. Dividing v-y by its norm
gives a suitable vector x (direct verification).
5 May, 2011 at 11:29 pm
Anonymous
Sorry, it’s me again. I’d like to add that, for class purposes, you can even act this out: hold a pen slanted over a desk. Take a point P on the desk very close to the tip of the orthogonal projection of the pen. Points directly between P and the tip
of the pen have their distances to the desk very close to their distances to P.
5 May, 2011 at 1:26 pm
Effective limiting absorption principles, and applications « What’s new
[…] at zero, then an argument (based on (a variant of) the Fredholm alternative, which as discussed in this recent blog post gives ineffective bounds) gives a bound of the […]
6 May, 2011 at 1:41 am
ugroh
Dear Terence, thanks for the remark. It opened the eyes.
@anonymous: This way of proving the lemma is known and will be used usual. The Hahn-Banch-argument was new to me (and because I will not teach the HB-Thorem unfortunately not applicable).
Ulrich
7 March, 2012 at 10:18 pm
The asymptotic distribution of a single eigenvalue gap of a Wigner matrix « What’s new
[…] (and specifically, the operator norm, Hilbert-Schmidt norm, and nuclear norm). Amusingly, the Fredholm alternative makes a key appearance, as I end up having to invert a compact perturbation of the identity at one […]
4 January, 2015 at 3:44 am
ahmed
I need to prove the A* Ax = A* b by use Fredholm Alternative Theorem
17 October, 2016 at 12:55 pm
Anonymous
In the first alternative of Theorem 1, do we have the extra property that the eigen-space (the null space of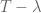 ) is of finite dimension?
) is of finite dimension?
17 October, 2016 at 1:11 pm
Terence Tao
Yes, because the unit ball in an infinite-dimensional normed vector space cannot be precompact (basically thanks to iterating the Riesz lemma).
17 October, 2016 at 1:27 pm
Anonymous
I’ve seen a version of the Fredholm alternative in the setting of Hilbert space that says the following:
If is a compact operator on the Hilbert space
is a compact operator on the Hilbert space  then
then
(1) is of finite dimension,
is of finite dimension, is closed,
is closed, ,
, iff
iff  ,
, .
.
(2)
(3)
(4)
(5)
Is it equivalent to Theorem 1 in the setting of Hilbert space (or can one deduce completely from Theorem 1)?
Does the version about give any more information than Theorem 1?
17 October, 2016 at 1:39 pm
Terence Tao
The version stated here only directly gives (4), and the Riesz lemma only directly gives (1), but these are the man ingredients in the proof of the remaining components (2), (3), (5) of the Fredholm alternative in the Hilbert space case (combined with some fairly standard tools such as the Riesz representation theorem for Hilbert spaces, and understanding how concepts such as null space, range, and adjoint change when passing to finite codimension closed subspaces). I would imagine that any functional analysis text that covers Fredholm theory would work out these derivations in detail.