This is one of the continuations of the online reading seminar of Zhang’s paper for the polymath8 project. (There are two other continuations; this previous post, which deals with the combinatorial aspects of the second part of Zhang’s paper, and a post to come that covers the Type III sums.) The main purpose of this post is to present (and hopefully, to improve upon) the treatment of two of the three key estimates in Zhang’s paper, namely the Type I and Type II estimates.
The main estimate was already stated as Theorem 16 in the previous post, but we quickly recall the relevant definitions here. As in other posts, we always take to be a parameter going off to infinity, with the usual asymptotic notation
associated to this parameter.
Definition 1 (Coefficient sequences) A coefficient sequence is a finitely supported sequence
that obeys the bounds
for all
, where
is the divisor function.
- (i) If
is a coefficient sequence and
is a primitive residue class, the (signed) discrepancy
of
in the sequence is defined to be the quantity
- (ii) A coefficient sequence
is said to be at scale
for some
if it is supported on an interval of the form
.
- (iii) A coefficient sequence
at scale
is said to obey the Siegel-Walfisz theorem if one has
for any
, any fixed
, and any primitive residue class
.
- (iv) A coefficient sequence
at scale
is said to be smooth if it takes the form
for some smooth function
supported on
obeying the derivative bounds
for all fixed
(note that the implied constant in the
notation may depend on
).
In Lemma 8 of this previous post we established a collection of “crude estimates” which assert, roughly speaking, that for the purposes of averaged estimates one may ignore the factor in (1) and pretend that
was in fact
. We shall rely frequently on these “crude estimates” without further citation to that precise lemma.
For any , let
denote the square-free numbers whose prime factors lie in
.
Definition 2 (Singleton congruence class system) Let
. A singleton congruence class system on
is a collection
of primitive residue classes
for each
, obeying the Chinese remainder theorem property
whenever
are coprime. We say that such a system
has controlled multiplicity if the
for any fixed
and any congruence class
with
.
The main result of this post is then the following:
Theorem 3 (Type I/II estimate) Let
be fixed quantities such that
and let
be coefficient sequences at scales
respectively with
with
obeying a Siegel-Walfisz theorem. Then for any
and any singleton congruence class system
with controlled multiplicity we have
The proof of this theorem relies on five basic tools:
- (i) the Bombieri-Vinogradov theorem;
- (ii) completion of sums;
- (iii) the Weil conjectures;
- (iv) factorisation of smooth moduli
; and
- (v) the Cauchy-Schwarz and triangle inequalities (Weyl differencing and the dispersion method).
For the purposes of numerics, it is the interplay between (ii), (iii), and (v) that drives the final conditions (7), (8). The Weil conjectures are the primary source of power savings ( for some fixed
) in the argument, but they need to overcome power losses coming from completion of sums, and also each use of Cauchy-Schwarz tends to halve any power savings present in one’s estimates. Naively, one could thus expect to get better estimates by relying more on the Weil conjectures, and less on completion of sums and on Cauchy-Schwarz.
— 1. The Bombieri-Vinogradov theorem —
One of the basic distribution results in this area of analytic number theory is the Bombieri-Vinogradov theorem. As first observed by Motohashi, this theorem in fact controls the distribution of a general class of Dirichlet convolutions in congruence classes. We will use the following formulation of this theorem, essentially Theorem 0 of Bombieri-Friedlander-Iwaniec;
Theorem 4 (Bombieri-Vinogradov theorem) Let
be such that
and
for some fixed
. Let
be coefficient sequences at scale
respectively. Suppose also that
obeys a Siegel-Walfisz theorem.
- (i) (First Bombieri-Vinogradov inequality) We have
for some sufficiently slowly decaying
and any fixed
.
- (ii) (Second Bombieri-Vinogradov inequality) we have
for some sufficiently slowly decaying
and any fixed
.
For sake of completeness we now recall the proof of this theorem, following the presentation in Bombieri-Friedlander-Iwaniec. (This is standard material, and experts may immediately skip to the next section.) We first need the large sieve inequality for Dirichlet characters:
Lemma 5 (Large sieve inequality) For any sequence
supported on
and any
one has
where the
summation is over primitive Dirichlet characters of conductor
.
Proof: By enlarging we may assume that
.
We use the method. By duality, the desired estimate is equivalent to
which is in turn equivalent to
We bound by a Schwartz function
whose Fourier transform is supported on
; this is possible for a fixed
when
. The left-hand side then expands as
The inner sum is when
, and zero otherwise thanks to Fourier analysis (specifically, the Poisson summation formula combined with the support of the Fourier transform of
and the fact that
is periodic of period
with mean zero). The claim follows.
Now we prove part (i) of Theorem 4. By an overspill argument (cf. Lemma 7 of this previous post) it suffices to show that
for any fixed .
Let . By multiplicative Fourier analysis we may write the left-hand side of (11) as
where the inner sum ranges over non-principal Dirichlet characters of modulus
, not necessarily primitive. Any such character can be written as
where
with
, and
is a primitive Dirichlet character of conductor
. The above sum can then be rewritten as
where the summation ranges over primitive characters modulo
. Since
, we may bound this by
which on performing the summation is bounded by
and then by dyadic decomposition this is bounded by
Let us first consider the contribution of the small moduli, specifically when for some fixed
. From the Siegel-Walfisz theorem (3) we have
for any fixed , and then by crude estimates (see Lemma 8 of this previous post) we see that this contribution is acceptable for (11). Thus we may restrict attention to those moduli with
for any fixed
. On the other hand, from Lemma 5 we have
for any . From crude estimates we have
Since
the claim follows.
Now we prove (ii). We now set for some fixed
. By overspill as before, it suffices to show that
By multiplicative Fourier analysis we have
so by splitting into primitive characters as before we may bound the left-hand side of (12) by
Arguing as before, the case is acceptable, so we assume
. From crude estimates we have
and
From Lemma 5 and Cauchy-Schwarz we can thus bound
by
as is comparable to
, this simplifies to
which is acceptable from the hypotheses on if
is chosen large enough depending on
. This concludes the proof of Theorem 4.
We remark that an inspection of the proof reveals that the or
factors in the threshold
for
may be replaced by
provided that
is sufficiently large depending on
. However, this refinement of the Bombieri-Vinogradov inequality does not lead to any improvement in the final numerology for our purposes.
— 2. Completion of sums —
At several stages in the argument we will need to consider sums of the form
for some smooth coefficient sequence , sone congruence classes
depending on a further parameter
, and further coefficients
. The completion of sums technique replaces the
term here with an exponential phase, leaving one with consideration of exponential sums such as
for various , where
for
(or
) is the standard character on
. More precisely, we have
Lemma 6 (Completion of sums) Let
be a smooth coefficient sequence at some scale
. Let
be a finite set of indices, and for each
let
be a complex number and
be a congruence class for some
. we have
for any fixed
.
Specialising to the case and
, we conclude in particular that
whenever is periodic of degree
.
Proof: We rearrange the left-hand side as
Using the Fourier expansion
and rearranging, the left-hand side then becomes
The term of this is the first term on the right-hand side of (13). The terms coming from integers
with
can be bounded by the second term in (13), bounding
crudely by
by crude estimates and also using conjugation symmetry when
is negative. So it will suffice to show that
(say) when . Writing
as in the definition of a smooth coefficient sequence, and applying Poisson summation, the left-hand side is
where is the Fourier transform of
. But from the smoothness (4) of
and integration by parts one has the bounds
for any fixed , and from the hypothesis
we obtain the claim by taking
large enough depending on
.
We remark that in the absence of cancellation in the exponential sum , the first error term in (13) could be as large as
which is about times as large as the main term in (13). In practice we will apply this lemma with
for some fixed
, in which case completion of sums will cost a factor of
or so in the bounds. However, it is still often desirable to pay this cost in order to exploit cancellation bounds for exponential sum, in particular those coming from the Weil conjectures as described below.
In our applications, the modulus will split into a product of two factors
or three factors
. The following simple lemma lets us then split exponential phases of the form
:
Lemma 7 Suppose that
for some coprime
, and let
be the intersection of the congruence classes
and
. Then for any integer
,
Similarly, if
for coprime
and
is the intersection of
,
, and
, then
Here and in the sequel we are using the convention that means
for
coprime to
, where
is the reciprocal of
modulo
.
Proof: We just prove the first identity, as the second is similar. Let be an integer such that
, and similarly let
be an integer such that
. Then
is equal to
mod
and
mod
, and thus equal to
mod
. Thus
and the claim follows by factoring the exponential.
— 3. The Weil conjectures —
For the purposes of this post, the Weil conjectures (as proven in full generality by Deligne) can be viewed as a black box device to obtain “square root cancellation” for various exponential sums of the form
where is a finite abelian group (i.e. a finite product of cyclic groups) with some additive character
and some rational function
, basically by obtaining the analogue of the Riemann Hypothesis for a certain zeta function associated to an algebraic variety related to the function
. (This is by no means the full strength of the Weil conjectures; amongst other things, one can also twist such sums by multiplicative characters, and also work with more complicated schemes than classical algebraic varieties, though the exponential sum estimates are more difficult to state succinctly as a consequence.) A basic instance of this is Weil’s classical bound on the Kloosterman sum
defined whenever are integers with
positive.
Theorem 8 (Weil bound) For any
one has
where
is the greatest common divisor of
.
Proof: (Sketch only; see e.g. Iwaniec-Kowalski for a full proof.) For simplicity we only address the case of square-free , which is the case needed in our application. By the Chinese remainder theorem we may reduce to the case when
is a prime
, then we may also reduce to the case when
are coprime to
. It then suffices to show that
whenever is an additive character and
is the hyperbola
An important trick is then to generalise from to finite dimensional extensions
of
, and then consider the Kloosterman sums
associated to these extensions, where is the field trace. For non-principal
, it is possible to show the explicit formula
for some complex numbers (depending of course on
); this is part of the general theory of
-functions associated to algebraic varieties, but can also be established by elementary means (e.g. by establishing a linear recurrence for the
). For the principal character
, of course, one has
Next, one observes the basic identity
as can be seen by computing the kernel and range of the linear map on
(this identity is also related to Hilbert’s Theorem 90). From this we have a combinatorial interpretation of the quantity
namely as the number of points on the curve
One can show (e.g. using Stepanov’s method, cf. this previous post) that the number of this points on this curve is equal to , leading to the identity
Studying the asymptotics as , one is led to the conclusion that
(this trick to “magically” delete the
error is a canonical example of the tensor power trick), and the bound (16) then follows from the
case of (17).
In practice, we shall estimate crudely by the divisor bound
(where
denotes a quantity that goes to zero as
), and the factor
will also be small in applications, so that we do indeed see the square root savings over the trivial bound
. For the Type I/II sums, the classical Weil bound is sufficient; but for the Type III sums that we will cover in a subsequent post, the full force of Deligne’s results are needed.
An important remark is that when , we can apply the change of variables
and convert the Kloosterman sum
into a Ramanujan sum
which enjoys even better cancellation than square root cancellation; in particular it is not difficult to establish the bound
using the Chinese remainder theorem to reduce to the case when is a power of a prime, and then using the divisor bound.
For the Type I and Type II sums we need a more complicated variant of this bound (Lemma 11 of Zhang’s paper):
Lemma 9 Let
be square-free natural numbers, let
and let
be integers. Then the double Kloosterman sum
obeys the bound
for some
with
for
. In particular, from Theorem 8, we have
while in the
case we have from (18) that
Here
denotes a quantity that goes to zero as
.
Proof: As are coprime, we may refactor
as
for some ,
and
, with
and
for , which in particular implies that
as claimed. Using the Chinese remainder theorem, we may now factor
as the product of the sums
and
Bounding the first sum trivially by and shifting the third sum by
we obtain the claim (note that
).
The treatment of the terms in the above analysis are crude, but in applications
is often trivial anyway, so it is not essential to obtain the sharpest estimates here.
We can combine this with the method of completion of sums:
Corollary 10 Let
be square-free natural numbers with
, let
be integers, and let
be a smooth coefficient sequence at a scale
. Then
Proof: Write . By (14) (and overspill) we may bound the left-hand side by
where we suppress the conditions from the
summation for brevity. The first term is
by Lemma 9, which is acceptable. Another application of Lemma 9 gives
From the divisor bound one has
for any , so from this and Cauchy-Schwarz the net contribution of the second term is
which is acceptable.
— 4. Factoring a smooth number —
We will need to take advantage of the smooth nature of the variable to factor it into two smaller pieces. We need an elementary lemma:
Lemma 11 Let
be a quantity of size
, and set
(say). Let
be fixed. Then, for all but
exceptions, all integers
have the property that
in particular,
Proof: Suppose that (19) failed, thus
In particular, we see that has at least
prime factors, which implies in particular that
On the other hand, we have the standard bound
and the claim now follows from Markov’s inequality.
Corollary 12 (Good factorisation) Let
, and let
be quantities such that
Let
be fixed. Then for all but
exceptions, all
have a factorisation
where
are coprime with
Furthermore
has no prime factors less than
, thus
where
.
The fact that has no tiny (i.e. less than
) prime factors will imply that any two such
will typically be coprime to each other with high probability (at least
for any fixed
), which is a key technical fact which we will need to exploit later. (The
-trick achieves a qualitatively similar effect, but would only give such a claim with probability
or maybe
for some small
if one really optimised it, which is insufficient for the applications at hand.)
Proof: By Lemma 11 we may restrict attention to those for which
Now is the product of distinct primes of size at most
, with
. Applying the greedy algorithm, one can then find a factor
of
with
If one then multiplies by all primes of size less than
that divide
to create
, then sets
, the claim follows.
— 5. The dispersion method —
We begin the proof of Theorem 3. The reader may wish to track the exponents involved in the model regime
We can restrict to the range
for some sufficiently slowly decaying , since otherwise we may use the Bombieri-Vinogradov theorem (Theorem 4). Thus we need to show that
be an exponent to be optimised later (in many cases, such as (20), it can be set very close to zero). By Corollary 12, outside of a small number of exceptions, we may factor where
with
,
is coprime to
, and
and
Let us first dispose of the set of exceptional values of
for which the above factorisation is unavailable. From Corollary 12 we have
On the other hand, we have the crude estimate
which when combined with crude estimates leads to the crude upper bound
Applying Cauchy-Schwarz we conclude that
and so gives a negligible contribution to (21) (increasing
as necessary).
For the non-exceptional , we arbitrarily select a factorisation
of the above form, and apply a dyadic decomposition. We conclude that it suffices to show that
for any fixed , where
obey the size conditions
Fix . We replace
by
, and abbreviate
and
by
and
respectively, thus our task is to show that
We now split the discrepancy
as the sum of the subdiscrepancies
and
Of the two, the first discrepancy is significantly more difficult to handle. By the triangle inequality, it will suffice to show that
We begin with (26), which is easier. For each fixed , it will suffice to show that
as the claim then follows by dividing by and summing using standard estimates (see Lemma 8 of this previous post). But this claim follows from the Bombieri-Vinogradov theorem (Theorem 4), after restricting
to the integers coprime to
(which does not affect the property of being a coefficient sequence supported at a certain scale, nor does it affect the Siegel-Walfisz theorem).
Now we establish (25). Here we will not take advantage of the summation, and use crude estimates to reduce to showing that
for each individual with
, which we now fix. Actually, we will prove the more general statement
whenever are good singleton congruence class systems. Let us see how (28) implies (27). Observe that if
is any integer, then
and
are also good singleton congruence class systems, where
consists of the primes
with
not divisible by
(thus
lies in
when
is coprime to
). By (28) we thus have
If we average over the interval
for some sufficiently small fixed
, we observe that
and similarly (using the crude divisor bound)
(The condition is redundant, but we include it for emphasis.) We conclude from the triangle inequality and the bounds on
(if
is small enough) that
On the other hand, from crude estimates one has
and the claim (27) then follows from Cauchy-Schwarz (noting from the Chinese remainder theorem that the two constraints are equivalent to the single constraint
).
It remains to prove (28). We will use the dispersion method (or Cauchy-Schwarz), playing the two congruence conditions and
against each other. We first get rid of the absolute values in (28) by introducing an additional bounded coefficient. More precisely, to prove (28) it suffices to show that
for any bounded real coefficients . We expand out the Dirichlet convolution
then relabel as
to rearrange the left-hand side as
We can write for some smooth non-negative coefficient sequence
at scale
. From crude bounds one has
so by the Cauchy-Schwarz inequality it suffices to show that
for any fixed . (As a sanity check, note that we are still only asking for a
savings over the trivial bound.) Expanding out the square, it suffices to show that
where is subject to the same constraints as
(thus
and
for
), and
is some quantity that is independent of the choice of congruence classes
,
, since by replacing the
with
or vice versa as necessary one can express (29) as a linear combination
of terms
of the form in (29) in such a way that all the
terms cancel out (
).
At this stage we need to deal with a technical problem that may share a common factor; fortunately, this event turns out to be negligible (but only thanks to the controlled multiplicity hypothesis (6)). More precisely, we split (30) into the coprime case
We first show (32). The basic point here is that because we have previously restricted to have no prime factor smaller than
, we can gain a factor of
in (32), which is strong enough to overcome logarithmic losses
but not losses
coming from the divisor bound. To avoid using the divisor bound we will need the controlled multiplicity hypothesis (6) (and this is the only place in the argument where this hypothesis is actually used).
We turn to the details. The quantities must all lie in
. We may split
and
where
are coprime. By the Chinese remainder theorem, the constraints
and
then imply that
so by the triangle inequality and interchange of summation we can bound the left-hand side by
(with understood to lie in
and be at most
) which we can write as
where
and
are the multiplicity functions associated to the congruence class systems and
.
By the elementary bound and symmetry we may thus bound the left-hand side of (32) by
plus a symmetric term which is treated similarly and will be ignored.
We rearrange the constraints
as a combination of the constraints
and
For a given choice of obeying the former set of constraints, the
obeying the second set of constraints lie in a single congruence class mod
by the Chinese remainder theorem. From the controlled multiplicity hypothesis (6) one thus has
and so the left-hand side of (32) has been bounded by
We first dispose of the error term. From the divisor bound we have
. For a given choice of
, the
sum then can be bounded by
, leading to a total contribution of
We would like to bound this by . This is possible if we have
and
for some fixed . But the former bound is immediate from (23), (10), (22), while from (9), (24), (23) we see that the latter bound will follow if we have
for some fixed . We file away this necessary condition for now and move on, though we note that these conditions are weaker than (22) except in the “Type II” case when
are close to
.
Having disposed of the error term, the remaining contribution to the left-hand side of (32) that we need to control is
Summing in using crude bounds, this is bounded by
and then by summing in this is in turn bounded by
The term sums to
, which is
thanks to (23), (22). The main term is then
Now we finally use the fact that has no small factors less than
to bound the summation here by
and since grows faster than any power of
we see that this error term is also acceptable for (32). This concludes the proof of (32) (contingent of course on the lower bounds (22), (34) on
that we will deal with later).
It remains to verify (31). Observe that must be coprime to
and
coprime to
, with
, to have a non-zero contribution to the sum. We then rearrange the left-hand side as
note that these inverses in the various rings ,
,
are well-defined thanks to the coprimality hypotheses.
We may write for some
. By the triangle inequality, and relabeling
as
, it thus suffices to show that for any particular
for some independent of the
and
.
We remark that at this stage we are only needing to gain a factor of over the trivial bound. However, we will now perform the expensive step of completion of sums (Lemma 6), which replaces the
factor by an exponential phase at the cost of requiring now a significantly larger gain over the trivial bound. Applying Lemma 6 and Lemma 7, we can write the left-hand side of (36) as the sum of the main term
an error term
is an arbitrary small fixed quantity, and
is the phase
(here we use the bounded nature of the ); and another error term that can easily be shown to be
for any fixed
. The term
is independent of the
and
, so it will suffice to show that
for a sufficiently small fixed , and we have dropped all hypotheses on
other than magnitude, and we abbreviate
as
. As noted after Lemma 6, we are no longer asking for just a
savings over the trivial bound; we must instead gain a factor of
to overcome the summation in
.
Although this is not strictly necessary for our analysis, let is confirm that is actually non-trivial in the sense that
Indeed, from (23) and (9) one has
and hence from (24)
and (40) then follows from (37). Note though in the model case (20) with that
is close to
(for any
between
and
).
We now split into two cases, one which works when are not too close to
, and one which works when
are close to
.
Theorem 13 (Type I case) If the inequalities
hold for some fixed
, then (39) holds for a sufficiently small fixed
.
The condition (42) represents a border between this case and the Type II case.
Theorem 14 (Type II case) If the inequality
holds, then (39) holds for a sufficiently small fixed
.
Both of these theorems are established by using Cauchy-Schwarz to eliminate the absolute values and factors in (39) until one is left with an expression only involving the phase
which can then be estimated using the Weil conjectures with a power saving to counteract the loss of
, however the use of Cauchy-Schwarz is slightly different in the two cases. In practice, the condition (43) is too strong to be satisfied by value of
given in Theorem 3, so we will only use Theorem 14 in the case that (42) fails, since in that case we may make
small enough for (43) to hold.
Assuming these theorems, let us now conclude the proof of Theorem 3. First suppose we are in the “Type I” regime when (42) holds for some fixed . Then by (9) we have
which means that the condition (34) is now weaker than (22) and may be omitted. By (7) we can simultaneously obey (22), (34), (41) by setting sufficiently close to zero, and the claim now follows from Theorem 13.
Now suppose instead that we are in the “Type II” regime where (42) fails for some small , so that by (9) we have
From this we see that we may replace by
in (10) and in all of the above analysis. If we set
then the conditions (22), (34) are obeyed. Theorem 14 will then give us what we want provided that
which is satisfied for small enough thanks to (8).
In the next two sections we establish Theorem 13 and Theorem 14.
— 6. The Type I sum —
We now prove Theorem 13. It suffices to show that
for any bounded real coefficients (which are vaguely related to the previous coefficients
, but this is not important for us here). We rearrange the left-hand side as
From the divisor bound we have
and we may write for some smooth coefficient sequence at scale
, so by Cauchy-Schwarz it suffices to show that
(note now we have to gain more than over the trivial bound, rather than just
). We rearrange this as
so by the triangle inequality it suffices to show that
for some fixed . We discard the
summation and reduce to showing that
for any .
To prove (44), we isolate the diagonal case and the non-diagonal case
. For the diagonal case, we make the crude bound
The contribution of the diagonal case can now be bounded by
Writing we have
, and one can estimate this by
which by the divisor bound is of the form
For this to be acceptable we need a bound of the form
which, by (37) is equivalent to
but this follows from (24), (42) for small enough.
Now we treat the non-diagonal case . The key estimate here is
for all non-diagonal . In the model case (20) with
, the two terms on the right-hand side are approximately
and
, which give the desired power saving compared to the trivial bound of
since
(and in (20),
is small, so just about any power saving suffices). As the model case indicates, the first term in (45) is the dominant one in practice.
Assume for the moment that the estimate (45) holds; then the non-diagonal contribution to (44) is
so to conclude (44) we need to show that
and
Using (37), (9) we can rewrite these criteria as
and
respectively. Applying (24), (23), it suffices to verify that
and
but these follow from (10) and (41) (the latter inequality holds with considerable room to spare).
It remains to show (45) in the non-diagonal case . From (38) we may of course assume that
and the left-hand side of (45) expands as
The first two phases
can be combined as
where and
is the residue class
and the inverses are with respect to modulus
in the first summand and
in the second summand. For future reference we note that
Similarly, the two phases
can combine as
where and
is the residue class
although the precise value of will not be important for us. The left-hand side of (45) is thus
and hence Corollary 10 and the coprimality of is bounded by
Note that
which is controlled by the first term on the right-hand side of (45). So it remains to show that
We crudely bound by
and
by
. (This is inefficient, but this term is not dominant in the analysis in any case.) By (46) we may bound
by
, and the claim follows.
— 7. The Type II sum —
We now prove Theorem 14. As before, it suffices to show that
for any bounded real coefficients . We rearrange the left-hand side slightly differently from the previous section:
From crude bounds we have
so by Cauchy-Schwarz it suffices to show that
Expanding and using the triangle inequality as in the previous section, we reduce to showing that
This is basically the same situation as in the previous section except that we have decoupled the variables from each other.
As before, we isolate a diagonal case , and now consider the contribution of this case. Arguing as in the previous section, the contribution of this case to (47) can be bounded by
which by the divisor bound is of the form
which will be acceptable if
By (37) this is equivalent to
but this is automatic from (23) and (22).
For the off-diagonal case, we use the following variant
of (45), valid for all non-diagonal . The bound here is weaker than in (45), but in the model case (20) the right-hand side terms are approximately
and
respectively, which still represents a power saving over the trivial bound of approximately
as long as
. While this does not cover all the range
that the Type I analysis does, it crucially is able to cover the case when
is very close to zero, which the Type I analysis does not cover due to the condition (42). The Type I/II border is not the critical border for optimising the exponents, so it is not a priority for us to improve bounds in the Type II analysis such as (48).
We assume (48) for now and finish the proof of Theorem 14 by numerical computations similar to that in the previous section. The non-diagonal contribution to (47) is now estimated by
so to conclude (47) we need to show that
and
Using (37), (9) we can rewrite these criteria as
and
respectively. Applying (24), (23), it suffices to verify that
and
but these follow from (10) and (43).
It remains to prove (48). This is very similar to the treatment of (45). From (38) we may assume
and the left-hand side of (48) expands as
If we set
then as before we can rewrite this sum as
where
(with the inverses with respect to the moduli in the first, second, and third summands respectively), and the value of
is unimportant for us. We have an analogue of (46), namely
We apply Corollary 10 as before, although things are not quite as favorable because need not be coprime in this case. This bounds the left-hand side of (48) by
We have
which is controlled by the first term on the right-hand side of (48). So it remains to show that
We crudely bound by
and
by
; also
and from (49) one has . The claim follows.

75 comments
Comments feed for this article
12 June, 2013 at 1:06 pm
mttpd
Shouldn’t that be “n” instead of “x” in the RHS of (1)?
// Argument of the log function.
12 June, 2013 at 1:10 pm
mttpd
Ah, no, just looked at the previous post (“As in previous posts, we let {x} be an asymptotic parameter tending to infinity”). NVM :-)
12 June, 2013 at 4:04 pm
Terence Tao
Some recording of parameters in the critical case: assuming
(following https://terrytao.wordpress.com/2013/06/10/a-combinatorial-subset-sum-problem-associated-with-bounded-prime-gaps/#comment-234015 ) we have
and the most critical case of the Type I/II analysis occurs when
Here one uses the Type I analysis and the non-diagonal case dominates, with the first term on the RHS of (43) giving the main contribution.
Due to the use of completion of sums, (45) has to gain a factor of over the trivial bound, which it barely does; one is summing a Kloosterman-type sum of period
over the trivial bound, which it barely does; one is summing a Kloosterman-type sum of period 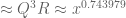 over an interval of scale
over an interval of scale  , and the square root cancellation basically estimates this sum by
, and the square root cancellation basically estimates this sum by  giving the desired savings of
giving the desired savings of 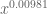 . In principle short Kloosterman sums might improve this (ideally we should get
. In principle short Kloosterman sums might improve this (ideally we should get 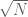 bounds and not
bounds and not  ), but N is already quite close to the square root of
), but N is already quite close to the square root of  so it doesn’t look so promising (unless the Chinese remainder theorem can somehow save us…). We also have all the averaging in
so it doesn’t look so promising (unless the Chinese remainder theorem can somehow save us…). We also have all the averaging in  that is just being discarded at present, and possibly one could take more advantage of these parameters, but it’s not clear to me how to do so (incidentally
that is just being discarded at present, and possibly one could take more advantage of these parameters, but it’s not clear to me how to do so (incidentally  is of size
is of size  ).
).
Random thought: is there a Burgess type squaring trick for short Kloosterman sums?
12 June, 2013 at 4:22 pm
Terence Tao
Another observation is that all the moduli involved (e.g. ) are very smooth. For instance, since
) are very smooth. For instance, since  , we know that
, we know that  all have at least 262 prime factors, all of which are quite small. So even though the progression
all have at least 262 prime factors, all of which are quite small. So even though the progression 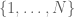 is quite short relative to the big modulus
is quite short relative to the big modulus  , it is quite long compared to each of the prime divisors of this modulus. But I don’t know of a way to exploit this; Bourgain and Chang have some clever tricks to stretch the Burgess bound for character sums to product spaces in a way that squeezes out additional gains (see http://math.ucr.edu/~mcc/paper/138%20BurgessJB.pdf ) but I have no idea if these ideas also work for Kloosterman sums.
, it is quite long compared to each of the prime divisors of this modulus. But I don’t know of a way to exploit this; Bourgain and Chang have some clever tricks to stretch the Burgess bound for character sums to product spaces in a way that squeezes out additional gains (see http://math.ucr.edu/~mcc/paper/138%20BurgessJB.pdf ) but I have no idea if these ideas also work for Kloosterman sums.
12 June, 2013 at 4:23 pm
v08ltu
Maybe something like Theorem 3 of FI, note that they use Holder with 4 in the exponent, but you can take this larger and gain more in some interval lengths (they remark this after Theorem 4, and do so in their Estimates on characters sums, for a related matter).
But the problem I had with such ideas, is that the sums are not all that “short” when I tried to apply these.
12 June, 2013 at 5:14 pm
v08ltu
Luo has a paper on incomplete Burgess estimates for Hyper-Kloosterman sums: http://www.sciencedirect.com/science/article/pii/S0022314X9892340X
12 June, 2013 at 5:32 pm
v08ltu
Shparlinski improves upon Luo, and mentions some related work. http://www.sciencedirect.com/science/article/pii/S0022314X06003027
12 June, 2013 at 5:38 pm
v08ltu
Also a 2010 paper of Karatsuba (posthumously): http://link.springer.com/article/10.1134%2FS0001434610090075
12 June, 2013 at 5:53 pm
v08ltu
It seems that Karatsuba (and Korolev) only save logs, and for quite short sums.
The most relevant I can find to our situation is Theorem 1 of this paper by Ping Xi: http://arxiv.org/pdf/1111.5459
The interval has to be as least in length for the result to be nontrivial (he demands the modulus be prime, but that might be technical).
in length for the result to be nontrivial (he demands the modulus be prime, but that might be technical).
His bound is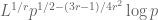 for any
for any  where the interval is length
where the interval is length  .
.
13 June, 2013 at 5:31 pm
v08ltu
This preprint of Ping Xi is not easy to figure out, but it seems that at (6) on pg5 he uses Proposition 1 (from a different preprint) rather than Lemmas 2 and 3 as stated. So the main tool is actually a mean-value result of http://arxiv.org/abs/1111.5455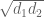 with
with  (r=2 case in above formula), which is a win in our target region I think.
(r=2 case in above formula), which is a win in our target region I think.
The Theorem 8 there is stated on pg18, but any proof exposition is deemed superfluous (“follow the arguments in this paper”). It also might be nontrivial to pass from prime moduli to composite, as FI note that much of the mess of their Section 1 is to extend as thus. However, if it all works out, it should beat
12 June, 2013 at 5:17 pm
v08ltu
A recent preprint of Browning and Haynes does not mention anything other than the Weil bound, and the Hooley conjecture, though the point is slightly different. http://arxiv.org/pdf/1204.6374
12 June, 2013 at 10:16 pm
Gaston Rachlou
A clash in terminology is always a bad thing in mathematics. This post contains two different uses of the adjective “smooth” (for coefficient sequences and for numbers). I think this is a good opportunity to definitely chose the adjective “friable” for numbers with small prime factors. See : https://blogs.ethz.ch/kowalski/2008/12/08/more-mathematical-terminology-friable/
12 June, 2013 at 10:49 pm
Terence Tao
I certainly see where you’re coming from, but in this particular case I think that the two notions of smooth are not in conflict, and in fact if one adopts an “adelic” perspective then there is actually a conceptual overlap between the two notions. A coefficient sequence is smooth if its spectrum avoids large frequencies (as measured in the Archimedean sense); and a number is smooth if its spectrum avoids large primes.
12 June, 2013 at 11:14 pm
Gaston Rachlou
If you vindicate an ambiguous use of “smooth” by an ambiguous use of “spectrum”, you’re likely to win any such debate:-)
By the way, congratulations for your blog in general and this “bounded gaps” series in particular!
13 June, 2013 at 9:48 am
Terence Tao
A fair point, but it’s worth mentioning that (as observed by Gelfand), these two notions of spectrum also have a lot of conceptual overlap: each frequency in the spectrum of a function corresponds to a prime ideal in the associated convolution algebra (of functions formed by convolving
corresponds to a prime ideal in the associated convolution algebra (of functions formed by convolving  with other functions), whereas each prime in the spectrum of an integer
with other functions), whereas each prime in the spectrum of an integer  corresponds to a prime ideal in the associated cyclic group
corresponds to a prime ideal in the associated cyclic group  . Thus in both cases the spectrum is the spectrum of a commutative ring that is naturally associated to the object.
. Thus in both cases the spectrum is the spectrum of a commutative ring that is naturally associated to the object.
13 June, 2013 at 12:23 pm
Gaston Rachlou
Interesting! I am just still a bit puzzled as I tend to think about the set of prime divisors of more as the support of
more as the support of  than as its spectrum. But, after all, this could be consistent with your identification of
than as its spectrum. But, after all, this could be consistent with your identification of  with the self-dual group
with the self-dual group  .
.
So, you almost convinced me:-( Nevertheless, I still prefer “friable”, which has a more direct, almost visual, explanation.
13 June, 2013 at 11:58 am
Eytan Paldi
This post should be added to the list of the polymath posts.
[Done, thanks – T.]
14 June, 2013 at 6:28 am
CraigH
Another followup question: MPZ[ ] is a statement about the absolute deviation of
] is a statement about the absolute deviation of 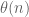 . What other number-theoretic functions can we make a similar statement about?
. What other number-theoretic functions can we make a similar statement about? for
for  prime 1 mod 4 (and 0 elsewhere)? If so, we could try to tailor admissible sets with
prime 1 mod 4 (and 0 elsewhere)? If so, we could try to tailor admissible sets with 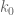 elements such that the first
elements such that the first 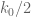 of them are 1 mod 4, and the rest are 3 mod 4, and that would effectively divide the width by two.
of them are 1 mod 4, and the rest are 3 mod 4, and that would effectively divide the width by two.
For example, could we take
14 June, 2013 at 8:47 am
Estimation of the Type III sums | What's new
[…] post, which deals with the combinatorial aspects of the second part of Zhang’s paper, and this previous post, that covers the Type I and Type II sums.) The main purpose of this post is to present (and […]
18 June, 2013 at 6:19 pm
A truncated elementary Selberg sieve of Pintz | What's new
[…] in the proof of . Indeed, if one inspects the proof of this proposition (described in these three previous posts), one sees that the key property of needed is not so much the smoothness, but a weaker […]
19 June, 2013 at 7:06 pm
Terence Tao
I am thinking that if we exploit the smoothness of the moduli, we can get (in some cases) better bounds from the incomplete Kloosterman-type sums by using Weyl differencing rather than by using completion of sums, in the spirit of what Zhang did for the Type III sums.
Let me illustrate this with the model problem of getting a non-trivial bound
for an incomplete Kloosterman sum over some squarefree modulus , with
, with 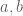 coprime to
coprime to  . The usual completion of sums method, combined with the Weil bound on Kloosterman sums, gives a non-trivial estimate of
. The usual completion of sums method, combined with the Weil bound on Kloosterman sums, gives a non-trivial estimate of  for
for 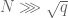 , but does not give any non-trivial bound for
, but does not give any non-trivial bound for  . But if we have a good factorisation
. But if we have a good factorisation  with
with  in the right places, we can do better through Weyl differencing. Namely, suppose
in the right places, we can do better through Weyl differencing. Namely, suppose 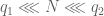 , then by shifting
, then by shifting  by
by 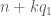 where
where  and
and  , we can basically write the sum we want as
, we can basically write the sum we want as
so after Cauchy-Schwarz and throwing away the diagonal term (acceptable as long as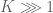 ) it suffices to show that
) it suffices to show that
We can simplify the phase as
which collapses to a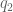 phase:
phase:
NOW if we do completion of sums, the inner sum
should be bounded by (possibly times a factor of
(possibly times a factor of  , but this is negligible after averaging),. and so we get a non-trivial bound whenever we have a factorisation
, but this is negligible after averaging),. and so we get a non-trivial bound whenever we have a factorisation  with
with
which (if is smooth) lets one get non-trivial bound for
is smooth) lets one get non-trivial bound for  almost as small as
almost as small as 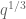 rather than
rather than 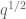 .
.
Now, this sort of gain isn’t quite the type of gain we need to improve the Type I sums at the critical numerology; instead of trying to improve the trivial bound for very short Kloosterman sums (length less than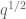 ), our problem is closer to that of improving the completion of sums bound for moderate length Kloosterman sums (length greater than
), our problem is closer to that of improving the completion of sums bound for moderate length Kloosterman sums (length greater than 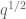 ). But it may be that one can flip one to the other via a Fourier transform. (Admittedly Kloosterman sums don’t Fourier transform as nicely as character sums, which I am more used to, so I may be a bit naive here, but still I think there is hope.)
). But it may be that one can flip one to the other via a Fourier transform. (Admittedly Kloosterman sums don’t Fourier transform as nicely as character sums, which I am more used to, so I may be a bit naive here, but still I think there is hope.)
More generally, I think one of the lessons of the Zhang analysis is that we really should be exploiting the smooth nature of our moduli whenever we can. Because of this the apparently “simpler” case of prime moduli may actually be a bit misleading; problems (such as estimating short Kloosterman sums) which are difficult for prime moduli may actually be a lot easier for smooth moduli due to the very flexible Weyl differencing technique that is available in this case.
20 June, 2013 at 11:16 am
Terence Tao
OK, the Fourier analysis wasn’t actually so bad. The new model problem is to obtain a bound on moderately long Kloosterman sums of the form
for some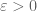 , where
, where  is squarefree and smooth,
is squarefree and smooth,  is coprime to
is coprime to  ,
,  is a smooth cutoff to an interval of length N, and
is a smooth cutoff to an interval of length N, and  is a bit larger than
is a bit larger than 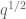 (the method described below gives a non-trivial bound basically for
(the method described below gives a non-trivial bound basically for  between
between 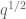 and
and 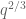 ). Note that completion of sums, together with the Weil bound on completed Kloosterman sums, only gives the bound of
). Note that completion of sums, together with the Weil bound on completed Kloosterman sums, only gives the bound of 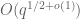 , so we are beating the methods used by Zhang, in a regime of interest. (But, as per Corollary 10 above, we will eventually also need to stick in an additional phase
, so we are beating the methods used by Zhang, in a regime of interest. (But, as per Corollary 10 above, we will eventually also need to stick in an additional phase  into the analysis.)
into the analysis.)
Anyway, by completion of sums or Poisson summation the LHS can be written as
where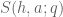 is the completed Kloosterman sum
is the completed Kloosterman sum
and is the Fourier transform
is the Fourier transform
Our objective is thus to show
which is a power saving over the Weil bound and standard bounds on (which has amplitude about
(which has amplitude about  and is concentrated on about
and is concentrated on about 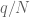 frequencies).
frequencies).
We factor where
where  are to be determined later.
are to be determined later.
We now perform Weyl differencing, replacing by
by  for
for  , where
, where 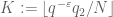 . We assume that
. We assume that 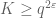 , so that
, so that
Up to acceptable errors (exploiting the smooth nature of at scale
at scale 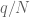 ), the LHS of (**) can then be rewritten as
), the LHS of (**) can then be rewritten as
From Lemma 7 we may factorise
By the Weyl bound, , so we may bound the previous expression by
, so we may bound the previous expression by
We can restrict to the range
to the range 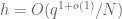 since
since  is negligible outside of this range. By Cauchy-Schwarz, it then suffices to show
is negligible outside of this range. By Cauchy-Schwarz, it then suffices to show
Note that this goal represents a saving of over the Weil bound and standard bounds on
over the Weil bound and standard bounds on  . Expanding out the square and removing the diagonal
. Expanding out the square and removing the diagonal  (which is acceptable since
(which is acceptable since 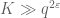 ), we reduce to showing that
), we reduce to showing that
on the average for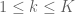 . Writing
. Writing 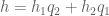 for
for 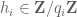 , the left-hand side becomes
, the left-hand side becomes
After some Fourier manipulation to evaluate the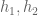 sums, we may write this as
sums, we may write this as
From Weil, the inner sum is (I think) bounded by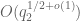 (possibly times a factor of
(possibly times a factor of  which is negligible after averaging in
which is negligible after averaging in  ), and if we assume
), and if we assume  , then we get a net bound of
, then we get a net bound of 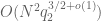 , which gives the desired power saving in the regime
, which gives the desired power saving in the regime
which in the smooth case allows one to take nearly as large as
nearly as large as  by choosing
by choosing  close to
close to  respectively.
respectively.
In principle the same sort of argument should work to get an improvement to Corollary 10 above, which in turn should lead to improvements in the Type I analysis. I haven’t checked the numerology and details yet though.
20 June, 2013 at 12:43 pm
Terence Tao
Just to get started on the numerology in the critical case: it’s looking like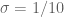 is going to be the key threshold, which upon setting
is going to be the key threshold, which upon setting  gives
gives  . We then have
. We then have  and
and 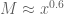 , and
, and 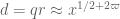 .
. 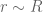 is taken close to
is taken close to  , so
, so  , then
, then  . In the Type I analysis,
. In the Type I analysis,  and
and 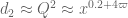 . The key sum that needs estimating is
. The key sum that needs estimating is 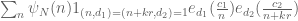 , where
, where 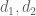 are coprime. The trivial bound is
are coprime. The trivial bound is  and the Weil + completion of sums bound is
and the Weil + completion of sums bound is  (plus an extra term which is lower order), a saving of
(plus an extra term which is lower order), a saving of 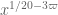 , which matches the loss
, which matches the loss  coming from completion of sums compounded by Cauchy-Schwarz when
coming from completion of sums compounded by Cauchy-Schwarz when 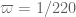 . So any improvement of the Weil + completion of sums bound here will lead to an improvement in the Type I analysis.
. So any improvement of the Weil + completion of sums bound here will lead to an improvement in the Type I analysis.
We have .
.  is less than
is less than  , so I am optimistic that the methods from the previous comment will lead to some gain here. Still have to check the gory details, though…
, so I am optimistic that the methods from the previous comment will lead to some gain here. Still have to check the gory details, though…
20 June, 2013 at 2:22 pm
Terence Tao
I realised that with regards to the exponential sum
we already have a convenient factorisation of the modulus available so we don’t even need any smoothness hypothesis to improve upon Corollary 10 of the post (= Lemma 11 of Zhang) in the regime of interest – Weyl differencing (conjugated by a Fourier transform) already basically improves the
of the modulus available so we don’t even need any smoothness hypothesis to improve upon Corollary 10 of the post (= Lemma 11 of Zhang) in the regime of interest – Weyl differencing (conjugated by a Fourier transform) already basically improves the 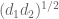 main term in Corollary 10 to
main term in Corollary 10 to  in the range
in the range  , which is the range of interest here. This should propagate to a new value of
, which is the range of interest here. This should propagate to a new value of  , but I’ll do that in the next comment. For now, the details of the above claimed bound.
, but I’ll do that in the next comment. For now, the details of the above claimed bound.
I’ll need first a Weyl-type bound on completed exponential sums, namely that
except in the degenerate case , in which case one only gets the trivial bound of
, in which case one only gets the trivial bound of  . I’m pretty sure this claim follows from the Riemann hypothesis for curves (plus some ad hoc computations in partially degenerate cases), so I’ll just take it for granted. By the Chinese remainder theorem it implies that
. I’m pretty sure this claim follows from the Riemann hypothesis for curves (plus some ad hoc computations in partially degenerate cases), so I’ll just take it for granted. By the Chinese remainder theorem it implies that
Now we return to estimation of the sum , assuming that
, assuming that 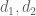 are squarefree and coprime, and that
are squarefree and coprime, and that
 . We follow the previous strategy of Weyl differencing conjugated by the Fourier transform. First, the Fourier transform lets us write
. We follow the previous strategy of Weyl differencing conjugated by the Fourier transform. First, the Fourier transform lets us write  as
as
where is the complete Kloosterman-type sum
is the complete Kloosterman-type sum
where for brevity we adopt the convention that vanishes when the denominator
vanishes when the denominator  is not coprime to the modulus
is not coprime to the modulus  , and similarly for
, and similarly for  .
.
Next, we perform Weyl shifting, replacing by
by  for
for  and
and 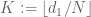 . The previous expression is then equal to
. The previous expression is then equal to
The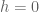 term contributes
term contributes  exactly as in the main post and we now delete this term.
exactly as in the main post and we now delete this term.
Now from the Chinese remainder theorem we have the twisted multiplicativity law
Here are the usual completed Kloosterman sums. Using the Weil bound on the
are the usual completed Kloosterman sums. Using the Weil bound on the  factor, we can bound the previous expression in magnitude by
factor, we can bound the previous expression in magnitude by
From the rapid decay of we may localise
we may localise 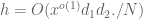 . We have
. We have
so by Cauchy-Schwarz we may bound the previous expression by
Expanding out, we encounter a diagonal term which, if one applies the Weil bound on Kloosterman sums together with the decay bounds on
which, if one applies the Weil bound on Kloosterman sums together with the decay bounds on  , eventually gives a bound of
, eventually gives a bound of  (gaining
(gaining 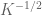 over the “trivial” bound, which is typical for a diagonal contribution in Weyl differencing). Now we restrict to the off-diagonal terms
over the “trivial” bound, which is typical for a diagonal contribution in Weyl differencing). Now we restrict to the off-diagonal terms 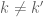 . Performing the
. Performing the  summation first using Fourier analysis, one eventually arrives at
summation first using Fourier analysis, one eventually arrives at
By (1), the innermost summation (over ) is
) is 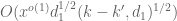 . Inserting this bound and performing all the summations, one eventually arrives at
. Inserting this bound and performing all the summations, one eventually arrives at  . Thus one has shown the following improvement to Corollary 10:
. Thus one has shown the following improvement to Corollary 10:
when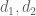 are squarefree coprime and
are squarefree coprime and  .
.
It is possible that one could improve upon this bound by using smoothness and working with a different factorisation than the factorisation that is naturally provided in Corollary 10, but this would be a bit messier and I will avoid doing that for now.
that is naturally provided in Corollary 10, but this would be a bit messier and I will avoid doing that for now.
20 June, 2013 at 4:13 pm
Terence Tao
Incidentally, I now have a reference for the Weil type bound for exponentials of rational functions that I needed: Perelmuter (1969), http://www.ams.org/mathscinet-getitem?mr=241424 . (This type of estimate can also be proven by Stepanov’s method: see Cochrane-Pinner (2006), http://www.ams.org/mathscinet-getitem?mr=2195926 .
22 June, 2013 at 12:20 am
v08ltu
I am confused when you say “Next, we perform Weyl shifting, replacing h by h+kd_2” as the next display seems (twice) to shift h by . One of these is corrected(?) a few lines later, but not the other?
. One of these is corrected(?) a few lines later, but not the other?
22 June, 2013 at 1:00 am
v08ltu
Just thinking aloud, if one possessed say higher-dim Deligne at hand, would Holder win more than Cauchy with this shift? This is often feasible in Burgess analysis.(however, Ping Xi seemed to max out at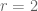
22 June, 2013 at 3:22 am
v08ltu
I am not so sure that this divisibility is something like a red hering, for now. If you plain had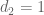 you would still win via the Weyl shift in this
you would still win via the Weyl shift in this 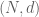 range, according in your notes as somewhat like to the method of FI (they only fail to achieve much enough gain in Type III methinks? ). Though of course the divisibility and Zhang shift should be induced for greater gains if possible. But really here, you “just” worked a short Kloosterman bound, if I am correct, with the
range, according in your notes as somewhat like to the method of FI (they only fail to achieve much enough gain in Type III methinks? ). Though of course the divisibility and Zhang shift should be induced for greater gains if possible. But really here, you “just” worked a short Kloosterman bound, if I am correct, with the 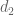 divisor effect largely negligent.
divisor effect largely negligent.
22 June, 2013 at 6:49 am
Terence Tao
Sorry about that, the shift should be by kd_2 throughout, I edited the comment accordingly.
I’m almost done with a post detailing these bounds a bit more carefully (in particular the refinement to Zhang Lemma 11 in the comments below did not quite treat some lower order terms properly, though fortunately this did not affect the dominant terms and ultimately did not affect numerology). The case of short character sums is slightly simpler than that of short Kloosterman sums so I am giving that example instead in the post.
numerology). The case of short character sums is slightly simpler than that of short Kloosterman sums so I am giving that example instead in the post.
Certainly there is scope to play with these methods further and get even better bounds, e.g. by combining carefully chosen Weyl differencing with a Burgess argument.
20 June, 2013 at 3:26 pm
Terence Tao
Now it’s time to trace this improvement of Corollary 10 back through the rest of the argument. Let me first note that the new bound of was only proven in the range
was only proven in the range  , but trivially holds outside this range also: when
, but trivially holds outside this range also: when  then
then  and one can use the existing Corollary 10, while for
and one can use the existing Corollary 10, while for 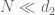 one has
one has 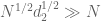 and one can use the trivial bound of
and one can use the trivial bound of  . So the new bound in fact holds universally in
. So the new bound in fact holds universally in  .
.
In the post, if we estimate the left-hand side of (45) using the new version of Corollary 10, we obtain an upper bound of
which by using the bounds given near the end of Section 7 come out to
giving an improvement to (45). The off-diagonal contribution to (44) is then
so we win when
and
Using (37), (9) these become
which from (24), (23), (10) reduces to
which we rearrange as
The third condition is implied by the second and may be dropped. These conditions replace (41) in Theorem 13 and are superior basically because they allow to be as large as 1/6 now instead of 1/8.
to be as large as 1/6 now instead of 1/8.
Following the arguments back to Theorem 3, we now see that we may replace (7) by the two essentially weaker conditions
and
From the Type II analysis we have an additional constraint
which could probably be improved with the new version of Corollary 10, but we won't do so here.
On the other hand, the Type III analysis currently works when
and we also need the combinatorial constraint
Playing (5′) off of (1′) and (2′) gives the constraints
(6′) is implied by (7′) and so may be dropped. Playing (4′) off of (1′), (2′) gives the additional constraints
and
(3′), (7′) and (8′) are implied by (9′) and may be dropped. So I claim that![MPZ'[\varpi,\delta]](https://s0.wp.com/latex.php?latex=MPZ%27%5B%5Cvarpi%2C%5Cdelta%5D&bg=ffffff&fg=545454&s=0&c=20201002) holds whenever
holds whenever
But of course I should double-check all the computations here, there is plenty of scope for numerical error.
20 June, 2013 at 3:31 pm
Terence Tao
Actually, one should be able to do better than this, because I was using the older Type III estimate, not the newer Type III estimate that also takes advantage of averaging. Recalculating…
averaging. Recalculating…
20 June, 2013 at 3:47 pm
Terence Tao
Recomputing the previous calculation with the improved Type III analysis. As stated in
this improvement replaces the condition
by the combination of
and
So now we need to play (1”), (2”) off of (1′), (2′) to replace (8′), (9′) with the new constraints
The constraint (4'') implies (3''), (5''), (6''), (3') (barely!), and (7'), so I now claim (somewhat nervously) that![MPZ'[\varpi,\delta]](https://s0.wp.com/latex.php?latex=MPZ%27%5B%5Cvarpi%2C%5Cdelta%5D&bg=ffffff&fg=545454&s=0&c=20201002) holds whenever
holds whenever
This is extremely tentative though; it is quite likely that there is at least one typo in the above (but hopefully the typos only affect secondary constraints and not the primary one). I will have to think about how to write things up so that it is easier to chase through the numerology. (I guess I will have to write up another blog post to try to describe the latest version of the argument.)
20 June, 2013 at 3:52 pm
David Roberts
So what k_0 do we get from these two new bounds on \varpi?
20 June, 2013 at 4:30 pm
Terence Tao
Have to run, but I can do a quick projection: was previously close to 1/348, but with the latest bound (if it holds up) it will become close to 1/148 (since we now know that delta is essentially negligible), a multiplicative gain of 2.35. Ever since the Bessel function technology was introduced,
was previously close to 1/348, but with the latest bound (if it holds up) it will become close to 1/148 (since we now know that delta is essentially negligible), a multiplicative gain of 2.35. Ever since the Bessel function technology was introduced, 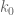 scales like
scales like 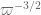 , so it should improve by about
, so it should improve by about  , so from 5,452 to about 1,512. For this range of
, so from 5,452 to about 1,512. For this range of 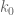 we now have tables in place for the best known H for such a k_0; specifically,
we now have tables in place for the best known H for such a k_0; specifically,  gives
gives 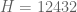 , see http://www.opertech.com/primes/webdata/k1000-1999/k1500-1599/ . But this is all just a rough calculation…
, see http://www.opertech.com/primes/webdata/k1000-1999/k1500-1599/ . But this is all just a rough calculation…
21 June, 2013 at 5:31 am
v08ltu
I have rederived (mostly independently) 1′ and 3”, and 5” using 2” (which I never checked) from your “new bound” (which I have yet to check yet). I haven’t digested the post enough to figure out the -numerology.
-numerology.
21 June, 2013 at 6:25 am
v08ltu
I’ve lost the net thread of the arguments, but I do think that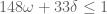 is correct arithmetic. What exactly is the purpose of this
is correct arithmetic. What exactly is the purpose of this  (besides to set it equal to 0)?
(besides to set it equal to 0)?
21 June, 2013 at 6:43 am
v08ltu
If it all works, with
with  .
.
21 June, 2013 at 6:45 am
v08ltu
21 June, 2013 at 7:24 am
Terence Tao
Combining this with the newly set up systematic tables at http://www.opertech.com/primes/webdata/ and http://math.mit.edu/~drew/records2.txt , this gives H = 12,042.
Double-checked your computation using Maple (taking advantage of Gergely and Eytan’s exact formulae for Bessel integrals). It checks out: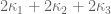 has to be bounded by
has to be bounded by  , but is instead about
, but is instead about  . As usual,
. As usual, 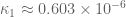 dominates, with
dominates, with  well behind and
well behind and  again negligible.
again negligible.
varpi := 1/148 - 5.9/400000;
k0 := 1470;
deltap := 1/245;
A := 2100;
delta := (1 - 148 * varpi) / 33;
theta := deltap / (1/4 + varpi);
thetat := (deltap - delta + varpi) / (1/4 + varpi);
deltat := delta / (1/4 + varpi);
j := BesselJZeros(k0-2,1);
eps := 1 - j^2 / (k0 * (k0-1) * (1+4*varpi));
kappa1 := int( (1-t)^((k0-1)/2)/t, t = theta..1, numeric);
kappa2 := (k0-1) * int( (1-t)^(k0-1)/t, t=theta..1, numeric);
e := exp( A + (k0-1) * int( exp(-A*t)/t, t=deltat..theta, numeric ) );
# using Gergely's exact expression for denominator
gd := (j^2/2) * BesselJ(k0-3,j)^2;
# using Eytan's exact expression for numerator
tn := sqrt(thetat)*j;
gn := (tn^2/2) * (BesselJ(k0-2,tn)^2 - BesselJ(k0-3,tn)*BesselJ(k0-1,tn));
kappa3 := (gn/gd) * e;
eps2 := 2*(kappa1+kappa2+kappa3);
# we win if eps2 < eps
21 June, 2013 at 7:58 am
v08ltu
If I use these better bounds on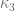 , I think I get
, I think I get  for
for  . This is best possible, even if the
. This is best possible, even if the  did not exist.
did not exist.
21 June, 2013 at 8:12 am
Terence Tao
Unfortunately Maple is not confirming these numbers.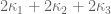 has to not exceed
has to not exceed 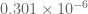 . We have
. We have  and
and  which is fine, but I’m getting
which is fine, but I’m getting 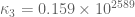 which is not fine. The exponential factor
which is not fine. The exponential factor  is coming out as
is coming out as 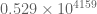 , while the Bessel numerator is
, while the Bessel numerator is  and the denominator is
and the denominator is  . Could there be a typo in your choice of parameters? For instance A does not appear to be optimal here (I accidentally entered in A=2400 and got a better bound on the exponential factor).
. Could there be a typo in your choice of parameters? For instance A does not appear to be optimal here (I accidentally entered in A=2400 and got a better bound on the exponential factor).
21 June, 2013 at 8:16 am
v08ltu
It seems to me that the numer/denom of the Bessel-integral quotient is so small that the parameter ends up being pointless. You can take
parameter ends up being pointless. You can take  if you want, I think. Although a diversion,
if you want, I think. Although a diversion, 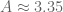 or about seems to minimize
or about seems to minimize 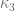 .
.
21 June, 2013 at 8:19 am
v08ltu
OK, I found my typo, e(-A*t/t) instead of e(-A*t)/t… Sorry
21 June, 2013 at 7:01 am
Terence Tao
Great, thanks!
where . In (7.1), (7.2) of Zhang,
. In (7.1), (7.2) of Zhang,  is set to be
is set to be  (i.e. infinitesimal) in the Type I case and equal to
(i.e. infinitesimal) in the Type I case and equal to  in the Type II case (actually
in the Type II case (actually  would have worked here). So, yes,
would have worked here). So, yes,  can be ignored for the Type I analysis (although it plays a more non-trivial, but still minor, role in the Type II analysis).
can be ignored for the Type I analysis (although it plays a more non-trivial, but still minor, role in the Type II analysis).
21 June, 2013 at 8:22 am
v08ltu
OK, try this again…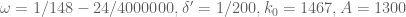
21 June, 2013 at 8:28 am
Terence Tao
This one I can confirm :-).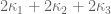 has to be at most
has to be at most  , but is
, but is  , with the overly sensitive
, with the overly sensitive 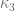 now being
now being  . From tables,
. From tables, 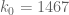 gives
gives 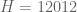 .
.
22 June, 2013 at 12:36 am
Anonymous
I am a physisist, but I am interested in your project. Since \kappa_i (i=1,2,3) is very small, can you rescale these quantities with some characterstic quantity, such that the rescaled \kappa_{i} is not small, and the corresponding round-off error can be much reduced?
22 June, 2013 at 8:03 am
Terence Tao
Unfortunately, the quantities are dimensionless and cannot be rescaled. (Actually for number theory there is not much dimensional analysis available in general, because the fundamental domain of study is the integers (or natural numbers), which do not have any natural scaling (or, if you wish, it has a natural unit, namely 1).)
quantities are dimensionless and cannot be rescaled. (Actually for number theory there is not much dimensional analysis available in general, because the fundamental domain of study is the integers (or natural numbers), which do not have any natural scaling (or, if you wish, it has a natural unit, namely 1).)
23 June, 2013 at 3:27 am
Tom
Gentlemen, H = 12012 and still falling. How low you can go with these methods?
23 June, 2013 at 9:47 am
Aubrey de Grey
Let’s at least hope they get to 11832, which in an almost completely meaningless sense would be half way from Zhang to the actual twin primes conjecture!
23 June, 2013 at 12:25 pm
Tom
2^26 = 67108864, 2^13 = 8192, 2^1 = 2.
23 June, 2013 at 3:07 pm
Aubrey de Grey
Not sure why there is no “Reply” link at the bottom of Tom’s reply to mine, but: Tom, if your comment is meant to imply that my mention of 11832 as the symbolic half-way mark was incorrect, please note that 13+13-26 is 0, not 1. 11832 is simply sqrt(2*70000000).
22 June, 2013 at 7:39 am
Bounding short exponential sums on smooth moduli via Weyl differencing | What's new
[…] Proof: See Lemma 7 of this previous post. […]
23 June, 2013 at 9:14 pm
The distribution of primes in densely divisible moduli | What's new
[…] for instead of . Inserting Theorem 4 into the Pintz sieve from this previous post gives for (see this blog comment), which when inserted in turn into newly set up tables of narrow prime tuples gives infinitely many […]
23 June, 2013 at 10:20 pm
Terence Tao
In order to try to stop the discussion from fragmenting too much, I’m rolling both this Type I/II thread and the Type III thread into a single new thread at
which has the latest version of both arguments that incorporate all of the recent improvements to Zhang’s argument, in particular the use of the q-analogue of the van der Corput lemma to improve the exponential sums in the Type I/II analysis, and the use of alpha-averaging to improve the Type III analysis.
25 June, 2013 at 10:42 am
Pace Nielsen
General question to anyone interested.
In Lemma 6, how much can one weaken the assumption that is smooth? In particular, for what types of convolutions
is smooth? In particular, for what types of convolutions  of functions
of functions 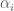 coming from the Heath-Brown identity does Lemma 6 not apply?
coming from the Heath-Brown identity does Lemma 6 not apply?
25 June, 2013 at 12:20 pm
Terence Tao
This is a good question! I think there are partial analogues of Lemma 6 in some cases but the bounds are weaker.
Roughly speaking, when dealing with a sum such as where
where  is periodic of some period
is periodic of some period  , one should think of
, one should think of  as having a Fourier expansion roughly of the form
as having a Fourier expansion roughly of the form
Here I am deliberately being vague as to what summation over means. If one uses a sharp cutoff
means. If one uses a sharp cutoff  then one gets a Dirichlet kernel at scale
then one gets a Dirichlet kernel at scale  rather than a smooth compactly supported cutoff
rather than a smooth compactly supported cutoff  ; if one inserts a Fejer weight one gets a Fejer kernel, and similarly for de Vallee-Poussin kernels, etc. To get a compactly supported kernel
; if one inserts a Fejer weight one gets a Fejer kernel, and similarly for de Vallee-Poussin kernels, etc. To get a compactly supported kernel  one needs a weight which is not completely localised in the range
one needs a weight which is not completely localised in the range  , but is instead rapidly decreasing outside of this range.
, but is instead rapidly decreasing outside of this range.
If one pretends that (*) is a rigorous formula then one easily gets Lemma 6 as a consequence (and the real proof of Lemma 6 basically proceeds through a rigorous analogue of (*)).
Anyway, now suppose we replace by
by  where
where 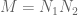 and
and  is some coefficient sequence at scale
is some coefficient sequence at scale  . The same heuristic that gives (*) also gives
. The same heuristic that gives (*) also gives
and hence
at least if we restrict to those integers coprime to
to those integers coprime to  for simplicity. If
for simplicity. If  , then the set of fractions
, then the set of fractions 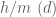 in
in  with
with 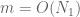 and
and  has multiplicity
has multiplicity  (from the divisor bound) and is thus spread out over a set of cardinality
(from the divisor bound) and is thus spread out over a set of cardinality 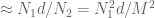 . So one can get a partial analogue of Lemma 6 in this case, in which one sums over
. So one can get a partial analogue of Lemma 6 in this case, in which one sums over  times as many frequencies
times as many frequencies  , but divides by an additional
, but divides by an additional  , for a net “loss” of
, for a net “loss” of  over Lemma 6 applied to
over Lemma 6 applied to  (or one can think of this assertion as an averaged version of Lemma 6 applied to
(or one can think of this assertion as an averaged version of Lemma 6 applied to  , in which case one is no longer losing anything and is in fact gaining (in principle, at least) because of the additional frequency averaging).
, in which case one is no longer losing anything and is in fact gaining (in principle, at least) because of the additional frequency averaging).
Incidentally this sort of “averaged completion of sums” shows up in the Type III analysis, and is the main source of our current improvement over Zhang’s Type III bound.
28 June, 2013 at 11:53 pm
சொல்வனம் » பகா எண் இடைவெளிகளின் எல்லைகள் – யீடாங் சாங், இருளைப் பிளந்த மின்னல் கீற்று
[…] https://terrytao.wordpress.com/2013/06/12/estimation-of-the-type-i-and-type-ii-sums/#comment-235545 […]
29 June, 2013 at 5:22 am
Gergely Harcos
A comment and some typos:
1. Before Lemma 7 it should be emphasized that an expression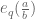 always means
always means  . This is because it is customary to use the notation
. This is because it is customary to use the notation 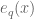 for any
for any  , in which case division is meant in the ordinary sense. For example, without this warning,
, in which case division is meant in the ordinary sense. For example, without this warning,  in Lemma 7 could be mistaken for
in Lemma 7 could be mistaken for 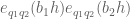 .
.
2. In the proof of Lemma 7, “ mod
mod  ” should be “
” should be “ mod
mod 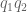 “, and
“, and  should be
should be 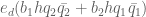 .
.
3. In the second display below (14),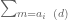 should be
should be  . In the next display, the factor
. In the next display, the factor 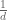 is missing.
is missing.
4. In the fifth display below (14),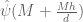 should be
should be 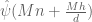 .
.
5. In (29), should be
should be  .
.
6. In the fourth display below (34),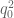 should be
should be 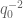 .
.
[Corrected, thanks – T.]
30 June, 2013 at 12:39 pm
Bounded gaps between primes (Polymath8) – a progress report | What's new
[…] sketch of Zhang’s argument for establishing Type I estimates (details may be found at these two posts). It is based on previous arguments of Bombieri, Friedlander, and Iwaniec, relying on […]
30 June, 2013 at 12:52 pm
Gergely Harcos
Your new blog entry tells me you arrived safely. Welcome! Two small comments and some typos:
1. In the proof of Lemma 5, I would emphasize for the sake of the reader that the vanishing of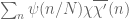
 as a linear combination of
as a linear combination of  with
with  , and then applying Poisson summation for each subsum
, and then applying Poisson summation for each subsum  .
.
follows by representing the nontrivial character
2. The inequality (16) and the preceding text might give the impression that it covers Theorem 8 for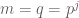 and
and  . This is only true for
. This is only true for  , since otherwise summing over
, since otherwise summing over  is different from summing over
is different from summing over 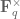 . So I would add that for
. So I would add that for 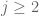 there is an elementary treatment that goes back to Salié.
there is an elementary treatment that goes back to Salié.
3. In Theorem 4,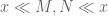 should be
should be  .
.
4. In the last display of the proof of Lemma 5,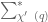 should be
should be 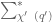 , and
, and  should be
should be 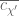 .
.
5. In (12) and the next display, should be
should be 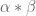 .
.
6. In the second display below (12), and
and 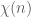 should be
should be  and
and 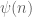 .
.
7. In the proof of Theorem 8,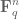 should be
should be  : 3 occurrences.
: 3 occurrences.
8. In the last display of the proof of Theorem 8,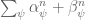 should be
should be  .
.
9. In the first display of the proof of Lemma 9, should be
should be  .
.
10. In the sixth display of the proof of Lemma 9, should be
should be  .
.
11. In the proof of Corollary 10, the conditions are missing under the three sums
are missing under the three sums  .
.
12. In the second display of the proof of Corollary 10, the factor should be omitted.
should be omitted.
[Corrected, thanks – T.]
1 July, 2013 at 11:59 am
Gergely Harcos
It seems that #6 has not been implemented. Note that “second display below (12)” really means “7 lines below (12)”. Also, in the last display of the proof of Theorem 8, I would put into parentheses for clarity.
into parentheses for clarity.
[Corrected, thanks – T.]
1 July, 2013 at 8:14 pm
Pace Nielsen
Just a few more typos:
1. The on the RHS of (6) should be
on the RHS of (6) should be  .
.
2. On the line below (10), the should be
should be  .
.
3. In Lemma 5, “whee” should be “where”.
4. Gergely’s point #6 above.
5. Three displays later, both of the should be in the subscripts. (One already is.)
should be in the subscripts. (One already is.)
6. In (14), both in the first and third lines, should be
should be 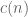 .
.
7. In the second line of the proof of Theorem 8, “needed our application” is missing the word “in”.
8. I believe that the second to last display of Lemma 9 is missing a factor of . This factor thus also seems to be missing from the first term in the bound of Corollary 10 (since it is missing in the third to last, and then last, displayed equations of the proof). I don’t know how much further this missing factor propagates.
. This factor thus also seems to be missing from the first term in the bound of Corollary 10 (since it is missing in the third to last, and then last, displayed equations of the proof). I don’t know how much further this missing factor propagates.
9. It might be helpful to define in the statement of Corollary 10 (rather than in the first line of the proof), so that in the display the summation can be over
in the statement of Corollary 10 (rather than in the first line of the proof), so that in the display the summation can be over 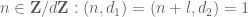 .
.
10. In the sentence before Section 5, the last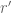 should just be
should just be  .
.
————–
I’ll try to finish reading the second half of the post tomorrow.
My impression of how the third display after (22) is established, is first to break the sum into a dyadic decompositions, then use Corollary 12, and the comes (mostly) from the number of terms in the dyadic breakdown.
comes (mostly) from the number of terms in the dyadic breakdown.
[Thanks for the corrections! Regarding point 8, the is buried in the
is buried in the 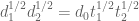 factor. Regarding point 9, the initial sum is over integers
factor. Regarding point 9, the initial sum is over integers  , but completion of sums converts this to sums over
, but completion of sums converts this to sums over  . And yes, this is how the third display after (22) is established. -T.]
. And yes, this is how the third display after (22) is established. -T.]
2 July, 2013 at 7:38 pm
Pace Nielsen
Only made it through another quarter of the post, but here are some comments.
1. In the third display after (28), on the LHS the condition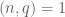 is redundant. It was actually helpful for me to have the condition there, but it also might be helpful to mention the redundance.
is redundant. It was actually helpful for me to have the condition there, but it also might be helpful to mention the redundance.
2. A few sentences before (33), it says “For fixed obeying…” and later it says “For fixed
obeying…” and later it says “For fixed  ,…”. I would recommend changing the word “fixed” to “any given” (to avoid confusion with being fixed with respect to
,…”. I would recommend changing the word “fixed” to “any given” (to avoid confusion with being fixed with respect to  ).
).
3. In the third display above (33), it took me a while to figure out how the controlled multiplicity hypothesis was being applied. I think one transforms to
to  (essentially, replacing the old singleton congruence class system with a new one where we multiply by the inverse of
(essentially, replacing the old singleton congruence class system with a new one where we multiply by the inverse of  modulo
modulo  whenever possible). If that is correct, it might be good to say a word about why this new system still has controlled multiplicity.
whenever possible). If that is correct, it might be good to say a word about why this new system still has controlled multiplicity.
4. In (34), I recommend changing to
to  (to avoid trivial technicalities later when plugging in
(to avoid trivial technicalities later when plugging in  ).
).
5. In the sentence following (39), change “As noted after Lemma 13” to “As noted after Lemma 6” (the link is to equation (13), contained in Lemma 6).
6. In the sentence after (40) which reads “Indeed, from (33) and (9) one has…”, change (33) to (23). Then in the next two displays, replace by
by  .
.
7. Directly before Theorem 13, change to
to  .
.
8. In the second paragraph after Theorem 14, there is a sentence which begins “By (7), (8) we can simultaneously…” The condition (8) is superfluous here.
9. I recommend either changing the next sentence to read: “Note that (43) is weaker than (41), so we can now suppose instead that we are in the “Type II” regime…” OR change the statement of Theorem 14 to include the assumption that (42) fails.
10. The computation following Theorem 14 shows that the in equation (6) should be
in equation (6) should be  . (This new constant matches what I saw on the wiki.)
. (This new constant matches what I saw on the wiki.)
[Corrected, thanks – T.]
3 July, 2013 at 8:41 am
Pace Nielsen
I can follow your argument involving controlled multiplicity now. Thanks for clarifying that. Here are the remainder of the comments/questions.
1. For the display following “For the diagonal case, we make the crude bound”, I believe the RHS should have an extra factor of (or just
(or just  ).
).
2. In the display which says , change
, change  to
to 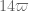 , and also change
, and also change 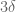 to
to  . (Fortunately, these changes do not affect any later computations.)
. (Fortunately, these changes do not affect any later computations.)
3. Two displays later, on the second line of that display where it has , the
, the  should be
should be 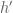 . A similar change should be made to the display following (46).
. A similar change should be made to the display following (46).
4. Three displays after (46), the are missing in the definition of
are missing in the definition of 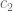 .
.
5. In Section 7, when it says “From we have” you can add “crude bounds” (or, “the divisor bound”) inbetween.
6. On the RHS of (48), there are parentheses missing ( needs to multiply both factors).
needs to multiply both factors).
7. In the fourth display above (49), on the second line the second should be
should be 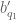 . On the third line, the second
. On the third line, the second  should be
should be 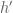 .
.
8. On the last line of the display above (49) (where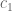 is being defined) there is a prime missing in the subscript of the
is being defined) there is a prime missing in the subscript of the 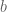 , and another prime missing from
, and another prime missing from  .
.
———
When dealing with the Type I sum, when performing the Cauchy-Schwarz the choice is made to pull out the sum on . What is the reason we don’t pull out the sum on
. What is the reason we don’t pull out the sum on 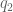 as well?
as well?
3 July, 2013 at 9:56 pm
Terence Tao
Thanks for the corrections!
Regarding Cauchy-Schwarz, there is a lot of flexibility in what we pull outside of the Cauchy-Schwarz, and what stays inside (and gets “doubled”, e.g. from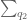 to
to 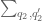 ). But one has to balance the “diagonal” terms and the “off-diagonal” terms, both to be small in order to win. If one pulls too much stuff outside the Cauchy-Schwarz then the diagonal terms get too big, but if one puts too much stuff inside then the off-diagonal terms get too big. (Some of the more recent refinements to the Type I sums have come by striking a better balance in this regard.)
). But one has to balance the “diagonal” terms and the “off-diagonal” terms, both to be small in order to win. If one pulls too much stuff outside the Cauchy-Schwarz then the diagonal terms get too big, but if one puts too much stuff inside then the off-diagonal terms get too big. (Some of the more recent refinements to the Type I sums have come by striking a better balance in this regard.)
If we pull both the sums outside then only the
sums outside then only the  summation gets doubled. But then the diagonal contribution (which becomes
summation gets doubled. But then the diagonal contribution (which becomes  instead of
instead of  ) only saves us a factor of
) only saves us a factor of 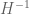 (instead of
(instead of  ) over the trivial bound, when we actually need to save
) over the trivial bound, when we actually need to save  . (The off-diagonal terms become a lot better, of course, but I don’t know how to exploit that when the diagonal terms are so bad.)
. (The off-diagonal terms become a lot better, of course, but I don’t know how to exploit that when the diagonal terms are so bad.)
4 July, 2013 at 11:48 pm
Gergely Harcos
Some typos:
1. Four displays before (49),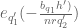 should be
should be  , and
, and  should be
should be  ; one typo in the first expression, two typos in the second one.
; one typo in the first expression, two typos in the second one.
2. In the display before (49),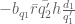 should be
should be  ; two typos here. Also, this display would look better in two lines instead of three.
; two typos here. Also, this display would look better in two lines instead of three.
[Corrected, thanks – T.]
4 July, 2013 at 11:52 pm
Gergely Harcos
Forgot one:
3. In Line 6 of Section 7, “From we have” should be “From the divisor bound we have” (with link to the divisor bound).
[Corrected, thanks – T.]
5 July, 2013 at 9:41 am
Pace Nielsen
Is there a natural multidimensional analog of the “Completion of Sums” lemma? In particular, I’m looking for simplifications for a sum of the form
5 July, 2013 at 1:27 pm
Pace Nielsen
From reading a few more comments on different threads, it appears that there is such an analog, but we run into the problem of higher dimensional Kloosterman sums.
7 July, 2013 at 11:17 pm
The distribution of primes in doubly densely divisible moduli | What's new
[…] Proof: See Lemma 7 of this previous post. […]
21 March, 2014 at 4:14 pm
Stijn Stefan Campbell Hanson
Sorry, I’ve been looking this over again and could you maybe explain a bit more why the case is acceptable in the proof of Bombieri-Vinogradov (ii)?
is acceptable in the proof of Bombieri-Vinogradov (ii)?
21 March, 2014 at 7:01 pm
Terence Tao
As I said in the post, the argument here is similar to the treatment of the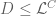 case of (i). If you could describe our own efforts to prove the estimate and where precisely you got stuck, I could be more able to try to diagnose the issue.
case of (i). If you could describe our own efforts to prove the estimate and where precisely you got stuck, I could be more able to try to diagnose the issue.
22 March, 2014 at 3:29 am
Stijn Stefan Campbell Hanson
So we have the bound on the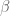 sum using Siegel-Walfisz (I think, I’m not too clear on the precise steps) but how do we combine this with the
sum using Siegel-Walfisz (I think, I’m not too clear on the precise steps) but how do we combine this with the  sum? Also would we still need to use the crude estimates, in which case which ones as it wouldn’t be the same same one, surely?
sum? Also would we still need to use the crude estimates, in which case which ones as it wouldn’t be the same same one, surely?
22 March, 2014 at 7:33 am
Terence Tao
Use Siegel-Walfisz to bound the term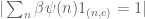 , and crude estimates to bound the sum
, and crude estimates to bound the sum  , and then continue using crude estimates to bound all of the terms that appear afterwards. Since the Siegel-Walfisz factor is going to save arbitrarily many powers of
, and then continue using crude estimates to bound all of the terms that appear afterwards. Since the Siegel-Walfisz factor is going to save arbitrarily many powers of  , it is perfectly safe to lose bounded powers of
, it is perfectly safe to lose bounded powers of  in all other estimates; thus for instance, once each term in the
in all other estimates; thus for instance, once each term in the  summation is bounded by some uniform bound
summation is bounded by some uniform bound  , the
, the  sum may then be crudely bounded by
sum may then be crudely bounded by 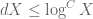 , since there are at most
, since there are at most  characters of conductor
characters of conductor  . Similarly, it is safe to discard the
. Similarly, it is safe to discard the  factor in this regime. I recommend actually inserting some estimates and seeing what you get; as I said, it doesn’t really matter if you are somewhat inefficient in your estimation because the gain of an arbitrary number of logarithms in Siegel-Walfisz will always rescue you. (See also Strategy 16 and Strategy 15 from https://terrytao.wordpress.com/2010/10/21/245a-problem-solving-strategies/ , and also my discussion of the value of attempting to partially implement a solution even when you do not yet have the full solution at https://plus.google.com/u/1/114134834346472219368/posts/Xdm8eiPLWZp .)
factor in this regime. I recommend actually inserting some estimates and seeing what you get; as I said, it doesn’t really matter if you are somewhat inefficient in your estimation because the gain of an arbitrary number of logarithms in Siegel-Walfisz will always rescue you. (See also Strategy 16 and Strategy 15 from https://terrytao.wordpress.com/2010/10/21/245a-problem-solving-strategies/ , and also my discussion of the value of attempting to partially implement a solution even when you do not yet have the full solution at https://plus.google.com/u/1/114134834346472219368/posts/Xdm8eiPLWZp .)