Let be a quasiprojective variety defined over a finite field
, thus for instance
could be an affine variety
where is
-dimensional affine space and
are a finite collection of polynomials with coefficients in
. Then one can define the set
of
-rational points, and more generally the set
of
-rational points for any
, since
can be viewed as a field extension of
. Thus for instance in the affine case (1) we have
The Weil conjectures are concerned with understanding the number
of -rational points over a variety
. The first of these conjectures was proven by Dwork, and can be phrased as follows.
Theorem 1 (Rationality of the zeta function) Let
be a quasiprojective variety defined over a finite field
, and let
be given by (2). Then there exist a finite number of algebraic integers
(known as characteristic values of
), such that
for all
.
After cancelling, we may of course assume that for any
and
, and then it is easy to see (as we will see below) that the
become uniquely determined up to permutations of the
and
. These values are known as the characteristic values of
. Since
is a rational integer (i.e. an element of
) rather than merely an algebraic integer (i.e. an element of the ring of integers
of the algebraic closure
of
), we conclude from the above-mentioned uniqueness that the set of characteristic values are invariant with respect to the Galois group
. To emphasise this Galois invariance, we will not fix a specific embedding
of the algebraic numbers into the complex field
, but work with all such embeddings simultaneously. (Thus, for instance,
contains three cube roots of
, but which of these is assigned to the complex numbers
,
,
will depend on the choice of embedding
.)
An equivalent way of phrasing Dwork’s theorem is that the (-form of the) zeta function
associated to (which is well defined as a formal power series in
, at least) is equal to a rational function of
(with the
and
being the poles and zeroes of
respectively). Here, we use the formal exponential
Equivalently, the (-form of the) zeta-function
is a meromorphic function on the complex numbers
which is also periodic with period
, and which has only finitely many poles and zeroes up to this periodicity.
Dwork’s argument relies primarily on -adic analysis – an analogue of complex analysis, but over an algebraically complete (and metrically complete) extension
of the
-adic field
, rather than over the Archimedean complex numbers
. The argument is quite effective, and in particular gives explicit upper bounds for the number
of characteristic values in terms of the complexity of the variety
; for instance, in the affine case (1) with
of degree
, Bombieri used Dwork’s methods (in combination with Deligne’s theorem below) to obtain the bound
, and a subsequent paper of Hooley established the slightly weaker bound
purely from Dwork’s methods (a similar bound had also been pointed out in unpublished work of Dwork). In particular, one has bounds that are uniform in the field
, which is an important fact for many analytic number theory applications.
These -adic arguments stand in contrast with Deligne’s resolution of the last (and deepest) of the Weil conjectures:
Theorem 2 (Riemann hypothesis) Let
be a quasiprojective variety defined over a finite field
, and let
be a characteristic value of
. Then there exists a natural number
such that
for every embedding
, where
denotes the usual absolute value on the complex numbers
. (Informally:
and all of its Galois conjugates have complex magnitude
.)
To put it another way that closely resembles the classical Riemann hypothesis, all the zeroes and poles of the -form
lie on the critical lines
for
. (See this previous blog post for further comparison of various instantiations of the Riemann hypothesis.) Whereas Dwork uses
-adic analysis, Deligne uses the essentially orthogonal technique of ell-adic cohomology to establish his theorem. However, ell-adic methods can be used (via the Grothendieck-Lefschetz trace formula) to establish rationality, and conversely, in this paper of Kedlaya p-adic methods are used to establish the Riemann hypothesis. As pointed out by Kedlaya, the ell-adic methods are tied to the intrinsic geometry of
(such as the structure of sheaves and covers over
), while the
-adic methods are more tied to the extrinsic geometry of
(how
sits inside its ambient affine or projective space).
In this post, I would like to record my notes on Dwork’s proof of Theorem 1, drawing heavily on the expositions of Serre, Hooley, Koblitz, and others.
The basic strategy is to control the rational integers both in an “Archimedean” sense (embedding the rational integers inside the complex numbers
with the usual norm
) as well as in the “
-adic” sense, with
the characteristic of
(embedding the integers now in the “complexification”
of the
-adic numbers
, which is equipped with a norm
that we will recall later). (This is in contrast to the methods of ell-adic cohomology, in which one primarily works over an
-adic field
with
.) The Archimedean control is trivial:
Proposition 3 (Archimedean control of
) With
as above, and any embedding
, we have
for all
and some
independent of
.
Proof: Since is a rational integer,
is just
. By decomposing
into affine pieces, we may assume that
is of the affine form (1), then we trivially have
, and the claim follows.
Another way of thinking about this Archimedean control is that it guarantees that the zeta function can be defined holomorphically on the open disk in
of radius
centred at the origin.
The -adic control is significantly more difficult, and is the main component of Dwork’s argument:
Proposition 4 (
-adic control of
) With
as above, and using an embedding
(defined later) with
the characteristic of
, we can find for any real
a finite number of elements
such that
for all
.
Another way of thinking about this -adic control is that it guarantees that the zeta function
can be defined meromorphically on the entire
-adic complex field
.
Proposition 4 is ostensibly much weaker than Theorem 1 because of (a) the error term of -adic magnitude at most
; (b) the fact that the number
of potential characteristic values here may go to infinity as
; and (c) the potential characteristic values
only exist inside the complexified
-adics
, rather than in the algebraic integers
. However, it turns out that by combining
-adic control on
in Proposition 4 with the trivial control on
in Proposition 3, one can obtain Theorem 1 by an elementary argument that does not use any further properties of
(other than the obvious fact that the
are rational integers), with the
in Proposition 4 chosen to exceed the
in Proposition 3. We give this argument (essentially due to Borel) below the fold.
The proof of Proposition 4 can be split into two pieces. The first piece, which can be viewed as the number-theoretic component of the proof, uses external descriptions of such as (1) to obtain the following decomposition of
:
Proposition 5 (Decomposition of
) With
and
as above, we can decompose
as a finite linear combination (over the integers) of sequences
, such that for each such sequence
, the zeta functions
are entire in
, by which we mean that
as
.
This proposition will ultimately be a consequence of the properties of the Teichmuller lifting .
The second piece, which can be viewed as the “-adic complex analytic” component of the proof, relates the
-adic entire nature of a zeta function with control on the associated sequence
, and can be interpreted (after some manipulation) as a
-adic version of the Weierstrass preparation theorem:
Proposition 6 (
-adic Weierstrass preparation theorem) Let
be a sequence in
, such that the zeta function
is entire in
. Then for any real
, there exist a finite number of elements
such that
for all
and some
.
Clearly, the combination of Proposition 5 and Proposition 6 (and the non-Archimedean nature of the norm) imply Proposition 4.
— 1. Constructing the complex -adics —
Given a field , a norm on that field is defined to be a map
obeying the following axioms for
:
- (Non-degeneracy)
if and only if
.
- (Multiplicativity)
.
- (Triangle inequality)
.
If the triangle inequality can be improved to the ultra-triangle inequality
then we say that the norm is non-Archimedean. The pair will be referred to as a normed field.
The most familiar example of a norm is the usual (Archimedean) absolute value on the complex numbers
, and thus also on its subfields
and
. For a given prime
, we also have the
-adic norm
defined initially on the rationals
by the formula
for any rational , where
is the number of times
divides an integer
(with the conventions
and
). Thus for instance
for any integer
, which is of course inverse to the Archimedean norm
. (More generally, the fundamental theorem of arithmetic can be elegantly rephrased as the identity
for all non-zero rationals
, where
ranges over all places (i.e. over all the rational primes
, together with
.) It is easy to see that
is indeed a non-Archimedean norm. A classical theorem of Ostrowski asserts that all norms on
are equivalent to either the Archimedean norm
or one of the
-adic norms
, although we will not need this result here.
A norm on a field
defines a metric
, and then one can define the metric completion
of this field in the usual manner (as equivalence classes of Cauchy sequences in
with respect to this metric). It is easy to see that the resulting completion is again a field, and that the norm
on
extends continuously to a norm on the metric completion
.
The metric closure of a non-Archimedean normed field is again a non-Archimedean normed field. Once one has metric completeness, one can form infinite series of elements of the field in the usual manner; but the non-Archimedean setting is somewhat better behaved than the Archimedean setting. In particular, it is easy to see that if
is a non-Archimedean metrically complete normed vector field, then an infinite series
is convergent if and only if it obeys the zero test
, and furthermore that convergent series are automatically unconditionally convergent. (The notion of absolute convergence is not particularly relevant in non-Archimedean fields.) Thus we can talk about a countable series
in a non-Archimedean metrically complete normed vector field being convergent without having to be concerned about the ordering of the series.
As key examples of metric completion, we recall that using the Archimedean norm , the metric completion
of the rationals is the reals
, whereas using a
-adic norm
, the metric completion
of the rationals is instead the
-adic field
.
Note that the metric notion of completeness (convergence of every Cauchy sequence) is distinct from the algebraic notion of completeness (solvability of every non-constant polynomial equation, also known as being algebraically closed). For instance, the fields and
are metrically complete, but not algebraically complete. However, the two notions of completeness are related to each other in a number of ways. Firstly, the metric completion of an algebraically complete field remains algebraically complete:
Lemma 7 Let
be a normed field which is algebraically closed. Then the metric completion
is also algebraically closed.
Proof: Let be a monic polynomial of some degree
with coefficients
in
. We need to show that
has at least one root in
. By construction of
, we can view
as the limit of polynomials
with coefficients
, where the convergence is in the sense that each coefficient
converges to
as
for
. As
is already algebraically closed, each
has
roots
(possibly with repetition). Because the
are bounded, it is easy to see from the equation
that the roots
are uniformly bounded in
. Among other things, this implies that
converges to zero as
, since
and the coefficients of
converge to zero. Writing
, we conclude that the distance between
and the zero set
goes to zero as
. From this one can easily extract a Cauchy sequence
with
, which then converges to a limit
which can be seen to be a zero of
, giving the claim.
In the other direction, in the case of the -adics at least, it is possible to extend a norm on a field to the algebraic closure of that field:
Lemma 8 For any
in the algebraic closure
of
, define the norm
of
by the formula
where
are the Galois conjugates of
in
(so in particular
). Then
becomes a non-Archimedean normed field with this norm.
The situation is much more complicated in the Archimedean case, as there is no canonical way to extend the norm in this case. For instance, if one wishes to extend the Archimedean norm from
to
, one can do so by choosing an embedding
and using the Archimedean norm on
, but this is not a Galois-invariant definition. For instance, one of the two roots of the equation
will have a larger norm than the other (one norm being the golden ratio, and the other being its reciprocal), but the choice of root that has the larger norm depends on the choice of embedding
. Note that the definition (4) fails to be a norm in the Archimedean case; for instance, in
, (4) would require
and
to have norm
, while their sum would have norm
, violating the triangle inequality.
Proof: The only difficult task to show is the ultra-triangle inequality (3). It suffices to show that for every Galois extension of
and every
, one has
We view as a finite-dimensional vector space over
of some dimension
, and identify each
with the multiplication operator
defined by
. These
can be viewed as an element of
, the space of
-linear maps from
to itself, and the determinant of
has norm
by construction. We pick some arbitrary
-basis
of
and use this to define a non-Archimedean “norm”
on
by the formula
for , and then define a “norm”
on
by
It is easy to see that the space is then a closed linear subspace of
. In particular, since
is locally compact, we see that for any compact interval
, the set
is compact. On the other hand, as all the
are invertible,
is non-zero on this compact set. Thus, for any
, there exists a constant
such that
for all . Since
, we then see from a rescaling argument that there is a constant
such that
for all . Since
, we conclude the spectral radius formula
Now we can prove the ultra-triangle inequality via the tensor power trick. If , then from (5) we have
as ; from this and the easy bounds
and binomial expansion we also conclude that
as . A second application of (5) then gives
, and the ultra-triangle inequality follows.
Combining the two lemmas, we see that if we define
to be the metric completion of the algebraic completion of the
-adic field
, then this is a non-Archimedean normed field which is both metrically complete and algebraically complete, and serves as the analogue of the complex field
. Note that
comes with an embedding
, since
may clearly be embedded into
. Also, the norm on
induced from this embedding is clearly Galois-invariant and thus independent of the choice of embedding. Finally, we remark from construction that every non-zero element of
has a norm which is a rational power
of
, so on taking limits (and using the ultra-triangle inequality) we see that the same is true for non-zero elements of
.
Remark 9 In the Archimedean case, the analogue of
is the reals
, and in this case the algebraic completion
is a finite extension of
(in fact it is just a quadratic extension) and is thus already metrically complete. However, in the
-adic case, it turns out that
is an infinite extension of
(for instance, it contains
roots of
for every
), and is no longer metrically complete, requiring the additional application of Lemma 7 to recover metric completeness.
— 2. From meromorphicity to rationality —
We now show how Proposition 3 and Proposition 4 imply Theorem 1. The basic idea is to exploit the fact that a non-zero rational integer cannot be simultaneously small in the Archimedean sense and in the
-adic sense, and in particular that we have an “uncertainty principle”
which is immediate from the fundamental theorem of arithmetic. We would like to use this uncertainty principle to eliminate the error term in Proposition 4, but run into the issue that many of the quantities involved here are not rational integers, but instead merely lie in . To get around this, we have to work with expressions that are guaranteed to be rational integers, such as polynomial combinations of the
with integer coefficients. To this end, we introduce the following classical lemma:
Lemma 10 (Rationality criterion) Let
be a sequence in a field
, with the property that there exists a natural number
such that the
determinants
vanish for all sufficiently large
. Then there exist
, not all zero, such that we have the linear recurrence
for all sufficiently large
. (Equivalently, the formal power series
is a rational function of
.)
Note that in the converse direction, row operations show that if one has the recurrence (8), then (7) vanishes.
Proof: We may assume that the determinants
are non-vanishing for infinitely many (this is a vacuous condition if
), since otherwise we can replace
by
in the hypotheses and conclusion.
Let be large enough that (7) vanishes, and suppose that the determinant (9) vanishes for this value of
. We claim that the determinant
also vanishes; induction then shows that (9) vanishes for all sufficiently large , a contradiction.
To see why (10) vanishes, we argue as follows. As (9) vanishes, there is a non-trivial linear dependence among the rows of the matrix in (9). If this dependence does not involve the first row, then it also creates a non-trivial dependence among the first
rows of the matrix (10), and we are done. Thus we may assume that the first row in (9) is a linear combination of the next
rows. As a consequence, the first row in (7) is a linear combination of the next
rows, plus a vector of the form
for some
. If
is non-zero, then the row operations and cofactor expansion show that the determinant (7) is plus or minus
times the determinant (10), giving the claim. If
is instead zero, then the first
rows of the matrix in (7) have a non-trivial linear dependence, which on deleting the first column shows that the
rows of the matrix in (10) also have a non-trivial linear dependence, giving the claim.
We thus conclude that (9) does not vanish for all sufficiently large . In particular, the matrix in (7) always has rank
. An easy induction then shows that the row span of the matrix in (7) is a hyperplane in
(spanned by either the first
rows or the last
rows), which is independent of
. Writing this hyperplane as
, we obtain the claim.
Now let be as in Proposition 3 and Proposition 4, let
be a large natural number to be chosen later, and consider the determinant (7). This is clearly a rational integer. On the one hand, from Proposition 3 we have the upper bound
for all and some
, with
independent of
. On the other hand, from Proposition 4 we can write each row in the
matrix in (7) (after applying the embedding
) as the linear combination of at most
vectors of the form
for various
, plus an error vector whose coefficients all have norm at most
(say), where
is independent of
. Taking determinants, we conclude that
for sufficiently large and some
. Inserting the two bounds (11), (12) into the uncertainty principle (6), we conclude the vanishing
for all sufficiently large . Applying Lemma 10, we conclude that there exists a natural number
and rational coefficients
, not all zero, such that
for all sufficiently large . By clearing denominators, we may assume that the
are all rational integers. By deleting zero terms, we may assume that
and
are non-zero.
We can use this recurrence to improve the conclusions of Proposition 4. Observe from that proposition, after collecting like terms and absorbing any characteristic value with
into the error term, that for any
we can find a finite number of distinct characteristic values
with
for
, as well as non-zero integers
, such that
for all . Applying (13) to eliminate the
, we conclude that
for all sufficiently large , where
is the characteristic polynomial
If one of the is not a root of
, then by applying difference operators
to eliminate all the other characteristic values, we eventually conclude that
for all sufficiently large and some
independent of
, contradicting the hypothesis
. Thus all the
are zeroes of
and in particular lie in
. If we then let
be an enumeration of the distinct zeroes of
(which are all non-zero by the non-vanishing of
), and choose
such that
for all
, we conclude that for each
, there exist integers
for
such that
for all . The coefficients
ostensibly depend on
, but a repetition of the above arguments show that they are in fact independent of
, since given two
with
, we see from the triangle inequality that
for all , and then by applying difference operators to isolate a single
, we see that
for all
. (Note that this argument also gives the uniqueness of the characteristic values that was asserted in the introduction.) As the
are independent of
, we may send
in (14), and conclude that
for all .
We are now nearly done, except that the are algebraic numbers rather than algebraic integers. However, as the
are rational integers, we have
for all
and
, and applying difference operators to (15) to isolate
we conclude that
for all
and all
. As the characteristic values are closed under the absolute Galois group of
, we conclude that all Galois conjugates of
also have
-adic norm at most one, so the minimal polynomial of
in
has coefficients that are rational and have
-adic norm at most one for every
, and are thus rational integers, so that
is an algebraic integer as required. Theorem 1 follows.
Remark 11 The argument above is has been slightly rearranged from the standard argument in the literature, in which one establishes rationality of the zeta function
directly, rather than first establishing rationality of the generating function
(which is essentially the logarithmic derivative of the zeta function). The reason I did so was to highlight the fact that transcendental operations such as exponentiation do not play a role in this portion of the argument, in contrast to Propositions 5 and 6, which crucially exploit the properties of the exponential function.
— 3. The -adic Weierstrass preparation theorem —
Now we prove Proposition 6. We begin with a theorem somewhat analogous to Rouche’s theorem in complex analysis, which approximately locates a zero of an entire function that is dominated by a monomial .
Lemma 12 (Rouche-type theorem) Let
be an entire function on
, thus
and
as
. Suppose that
for some
and
. Then there exists a root
of
(thus
) with
.
Proof: We first consider the polynomials
for some . As
is algebraically closed, there must be a factorisation
for some , thus
is plus or minus the
symmetric polynomials of the
. Since
, we conclude from the non-archimedean nature of the norm that
for at least one
. Similarly, given any
, if there are exactly
for which
, then by computing the
symmetric polynomial we conclude that
. Since
goes to zero, we conclude that for any
, the number of
for which
is bounded uniformly in
; the same argument shows that the
are uniformly bounded away from zero.
Now we run an argument somewhat similar to the proof of Lemma 7. Let be large natural numbers, and let
be such that
. We have
and hence (since )
as ; thus
On the other hand, since , and since
for all but a bounded number of
, we see from the non-archimedean nature of the norm that
for all but a bounded number of
. Since the
are also uniformly bounded away from zero, we conclude that
as . From this, we can form a Cauchy sequence
such that
and
; taking limits, we obtain
with
such that
, giving the claim.
One can refine the methods in this proof to read off the -adic magnitudes of all the zeroes of
in terms of the Newton polytope of
(yielding a
-adic analogue of Jensen’s formula from complex analysis), but we will not need to do so here.
By iteratively removing the zeroes generated by the above lemma, we have
Proposition 13 (
-adic Weierstrass preparation theorem, alternate form) Let
be an entire function on
, and let
. Then there exists a factorisation
where
and
is an entire function such that
for all
.
Proof: We can make a rational power of
, and then by rescaling we may normalise
.
Since , the function
goes to zero as
, and so there exists a natural number
such that
for all , with the convention that
, and with strict inequality if
. We now induct on
. If
then we are already done (setting
). Now suppose that
, and that the claim has already been proven for
. From the strict form of (16) with
we have
, so by Lemma 12 we can find
with
such that
. We can then factor
where
and
Since , we also have
Using (16) and the non-archimedean property, one easily verifies that
for all , with strict inequality if
. Applying the induction hypothesis to
, we obtain the claim.
Now we prove Proposition 6. Let be as in that proposition, and let
be arbitrary. By Proposition 13 we have
for some and some entire function
with for all
. Now we apply formal logarithms
to both sides. Clearly for any formal power series
that actually converges in
; comparing coefficients, we conclude that the formal identity
holds in any characteristic zero field. For similar reasons we have
for any formal power series
with
with coefficients in a characteristic zero field. We conclude that
But by working out the power series, we see that
where the coefficients obey the bounds
for some constant independent of
. The claim then follows after increasing
as necessary.
— 4. Factorising the zeta function —
Now we establish Proposition 5, which is the most “number-theoretical” component of Dwork’s argument.
First observe that by covering the quasiprojective variety into affine pieces, and using an induction on the dimension of
to take care of any double-counted terms, we may reduce to the case when
is an affine variety (1), thus
We can view as a sum
over the affine variety
. The next step is Fourier expansion in order to “complete” the sum
into exponential sums over an ambient affine space. Write
. For any
define the trace map
by the formula
This is a linear map over .
Let be a primitive
root of unity in
. Then from Fourier analysis we see that for any
, the sum
is equal to if
and equal to zero otherwise. Hence
In view of this (replacing by
, and rescaling the zeta function), it suffices to show that for any polynomial
defined over
, one can decompose the sequence
as a finite linear combination over of sequences
with
entire.
It is convenient to remove the coordinate hyperplanes. Note that splits as the space
plus some lower-dimensional spaces, where
. By an induction on dimension, it thus suffices to show that the sequence
decomposes as a finite linear combination over of sequences
with
entire.
To prove this, we will establish the following trace formula:
Theorem 14 (Trace formula) There exists a formal power series
in
variables with coefficients
in
, or more compactly
for all
and some
(where
), such that one has the trace formula
for all
, where
is the
-linear map on the (infinite-dimensional) vector space
of all formal power series
in
variables defined by
where
is the linear map
and the trace
on
is computed using the monomial basis
of
, thus if
then
one can easily verify that this sum is convergent. (We will not address the subtle issue as to whether trace is a basis-independent concept in infinite dimensions.)
Let us assume this trace formula for the moment and conclude the proof of Theorem 5. Expanding out the factor in (18) and arguing as before, it will suffice to show that the zeta function
is entire; thus if is the
coefficient of this zeta function, our task is to show that
as .
Note from the formal identity
(which is true for small complex , and is thus also true for formal power series in characteristic zero) and the Jordan normal form that
on the level of formal power series in for any finite-dimensional matrix
in characteristic zero. In particular, for any natural number
, the
coefficient of
is given by the formula
where the sum ranges over distinct elements
of
, and over permutations
of
. This is a universal polynomial identity in characteristic zero, and so we conclude that the
coefficient
of the zeta function (20) is given by the formula
where now range over distinct natural numbers, and
ranges over permutations of
; again, one can check that this sum is convergent. By the non-archimedean nature of the metric, it thus suffices to show that
as .
Now from (17) and construction of , we have
for any , and so (as
is a permutation)
But because there are only a finite number of elements of
of a given length
, we see that
grows superlinearly in
(in fact it must grow by
), and the claim follows.
It remains to establish the trace formula (18). We first write the trace in a more tractable form. For any natural number
, let
denote the group of
roots of unity.
Lemma 15 If
is a power series with
for some
and all
, then for any
we have
where we use the notation
Note that the power series for
converges at all roots of unity.
Proof: Observe that
for any . Iterating this using (19), we conclude the identity
and so to prove the lemma it suffices to do so in the case, that is to say
The right-hand side expands as
From Fourier analysis we see that equals
when
is a multiple of
and zero otherwise, so the sum simplifies to
The claim follows.
In view of this lemma, it will suffices to obtain an identity of the form
for some power series
with for some
and all
.
This will be deduced from the following basic fact in -adic analysis, namely the existence of a canonical multiplicative embedding of the algebraic closure
of
inside
.
Lemma 16 (Teichmuller lifting) Let
be the algebraic closure of
. Then there exists a map
, known as the Teichmuller lift, with the following properties:
- (Homomorphism) One has
for all
.
- (Bijection) For each
,
is a bijection (and hence group isomorphism, by (23)) between
and
. In particular,
for all
.
- (Description of trace) There exists a power series
for all
and
.
Let us see how the lemma implies an identity of the form (22). Writing
for some finite set of multi-indices and coefficients
, we have from the linearity of trace that
and hence by (24) we have
where
and . Note that the required decay of the coefficients of
follows from that of
, since the
have unit
-norm. The claim now follows from the bijective nature of the Teichmuller lift.
The only remaining task is to establish Lemma 16; here I will follow the exposition of Koblitz. We begin by constructing the Teichmuller lift for a given
. Let
be a primitive element of
, thus
(The existence of such a primitive element can be seen by counting how many elements of have order strictly less than
.) The minimal polynomial of
over
thus has degree
, that is to say it is of the form
for some . We arbitrarily lift this to the
-adic integers
as
where reduce to
modulo
. Since the minimal polynomial
is irreducible in
, the lift
is irreducible in
and hence also in
(here we use Lemma 12 to reach a contradiction if a monic factor of
has a coefficient of
-norm greater than
). Thus, if we let
be a root of
, then
and
is a degree
extension of
. In this field, we define the valuation ring
and its maximal ideal
. Then
is a field generated over
by
, which is a root of
, thus
is a degree
extension of
and may be identified with
.
We claim that the field extension is unramified in the sense that all of the non-zero elements of
have norms that are integer powers of
, and in particular that
. Suppose this were not the case, then there exists an element
of
with
. If one lets
be a linear basis of
over
, and let
be representatives of this basis in
, one can then show that
are linearly independent over
, contradicting the fact that
is a degree
extension.
Let be an element of
, then
. As discussed earlier, we can view
as an element of
. By applying (a slight variant of) Hensel’s lemma, we can find a lift
of
such that
. This gives an injective map from
to
, which on comparing cardinalities must be a bijection. Since the quotient map from
to
is a homomorphism, we see that
is a homomorphism. One can check that the maps
for different
are compatible, and glue together to form a single map
obeying the homomorphism and bijection properties.
Now we have to construct . We first give a heuristic discussion. From the construction of
, we morally have
for all
, where we are deliberately vague as to what “
” means. Since the map
should morally be periodic modulo
, we thus expect
and so one is led to the initial guess
for . To make this heuristic discussion rigorous, we have to formally define what
means as a power series in
. We write
, thus
and
so that
thus the Galois conjugates of
multiply to
, and so
. We can then define
by formal binomial expansion as
This is well-defined (over ) as a formal power series in
. However, the convergence properties are bad, because of the denominator
. Indeed, a standard computation shows that
where is the sum of the digits of the base
expansion of
, and so
The sequence does not go to infinity as
, and so the power series
does not converge for
. This is a problem, since we want to apply
to norm one quantities such as
, and furthermore we are claiming a slightly larger radius of convergence in Lemma 16, namely (almost)
.
It turns out that there is a way to tweak the series to significantly improve the
-adic convergence behaviour. Namely, we (formally) define the corrected function
where is the formal power series in two variables
defined by
one can verify that this is well-defined as a formal power series, and for fixed ,
is a formal power series in
. By telescoping series, we have
as a formal power series, whenever . In particular,
for . If we can show that
makes sense as a formal power series
with
for all
, we thus have
since are the Galois conjugates of
over
, one can verify that
are the Galois conjugates of
over
, and so
lies in
; since
has norm
, this quantity in fact lies in
. Quotienting out by the maximal ideal
, we conclude that
and (24) follows.
So we are at last reduced to showing that with
for all
. From (25) we have the identity
On the other hand, we have , and hence
for some formal power series with coefficients in
, and hence
We can expand as
, where
is a formal power series with coefficients in
and no constant term, hence
As , the
coefficient of this identity lets us express the
coefficient of
as a polynomial combination (over
) of lower degree coefficients of
(as well as coefficients of
), which by induction shows that all coefficients of
lie in
. Replacing
by
, the desired claim follows.
Remark 17 The function
can also be defined as
where
is the Artin-Hasse exponential
and
is a root of the power series
.
Remark 18 A small modification of Dwork’s argument also establishes rationality (the zeta function associated to) exponential sums such as
for some polynomial
defined over
, and some multiplicative character
.

14 comments
Comments feed for this article
13 May, 2014 at 10:11 pm
Anonymous
There is an extraneous “sup” at the start of the post.
[Corrected, thanks – T.]
14 May, 2014 at 3:04 am
KCd
In the paragraph after Theorem 2, should be
should be  . For example, if
. For example, if  then
then  and
and  with
with  converges for
converges for  , as you’d want.
, as you’d want.
[Corrected, thanks – T.]
14 May, 2014 at 10:43 am
Anonymous
“as we wil seesup below” What does that mean?
[Corrected, thanks – T.]
14 May, 2014 at 1:19 pm
Gergely Harcos
Very interesting post!
I have trouble following the argument below (14). Let us consider the polynomial . It is irreducible over
. It is irreducible over  but reducible over
but reducible over  . In fact, in
. In fact, in  , the two roots have valuations
, the two roots have valuations 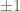 . This means that we cannot just say that
. This means that we cannot just say that  , because
, because  will depend on the embedding
will depend on the embedding  we use. Perhaps
we use. Perhaps  is meant under a suitable embedding? This should follow from the fact that if
is meant under a suitable embedding? This should follow from the fact that if  is not an algebraic integer, then
is not an algebraic integer, then  for some finite place
for some finite place  of
of  . Am I missing something?
. Am I missing something?
Further small remarks and suggestions:
1. In the display below (1), “ ” is missing from the chain of equations.
” is missing from the chain of equations.
2. “seesup” should be “see”.
3. should be
should be  .
.
4. In the proof of Proposition 3, should be
should be  .
.
5. In Proposition 6, the words “there exist” are missing.
6. The example “cube root of 2” after Lemma 8 is not the best one, as this algebraic number has the same norm in every embedding into .
.
7. In Section 2, “Proposition 4” and “Proposition 5” should really be “Proposition 3” and “Proposition 4” at several occurrences (e.g. in the beginning, or before and after (10), or after (12)).
8. Before (13), the zeros of should be labeled as
should be labeled as  , because the degree of
, because the degree of  equals
equals  .
.
[Corrected, thanks – T.]
14 May, 2014 at 4:46 pm
David Speyer
I thought I’d advertise an old blog post of mine http://sbseminar.wordpress.com/2011/12/12/rationality-of-the-zeta-function-mod-p/ where I show is given by the trace of the
is given by the trace of the  -th power of a matrix, acting on monomials in a manner similar to the infinite operator
-th power of a matrix, acting on monomials in a manner similar to the infinite operator  in this proof. My vague intuition for Dwork’s argument is that he figured out how to make this construction work to count solutions modulo any power of
in this proof. My vague intuition for Dwork’s argument is that he figured out how to make this construction work to count solutions modulo any power of  , not just the first power.
, not just the first power.
14 May, 2014 at 7:29 pm
Terence Tao
This is an interesting variant of Dwork’s argument! It’s slightly different though. In your argument, your starting point is the factorisation
for all , where
, where  is a polynomial that does not depend on k. In Dwork’s argument, the analogous factorisation is
is a polynomial that does not depend on k. In Dwork’s argument, the analogous factorisation is
in for all
for all  , where
, where  is a
is a 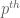 root of unity,
root of unity,  is the Teichmuller lift of x, and
is the Teichmuller lift of x, and  is a certain formal power series independent of k with coefficients in
is a certain formal power series independent of k with coefficients in  that converges at the Teichmuller lifts. In your case,
that converges at the Teichmuller lifts. In your case,  is a polynomial, which makes your matrices finite dimensional, but in Dwork’s case
is a polynomial, which makes your matrices finite dimensional, but in Dwork’s case  is transcendental, which creates the infinite-dimensional matrices.
is transcendental, which creates the infinite-dimensional matrices.
My understanding of the Teichmuller lift and associated objects (e.g. the Artin-Hasse exponential) is not firm enough to see if there is any substantial connection between the easy factorisation (1) and the harder factorisation (2). Part of the problem is that the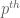 root of unity
root of unity  does not live in the p-adic field
does not live in the p-adic field  , instead being of the form
, instead being of the form  for some
for some  of norm
of norm  . The coefficients of G also live in some finite extension of
. The coefficients of G also live in some finite extension of  that I don’t understand very well. In principle one can try to reduce (2) mod p to get something more closely resembling (1), but I don’t see any precise connection. (The left-hand sides of (1), (2) are of course related through the Fourier identity
that I don’t understand very well. In principle one can try to reduce (2) mod p to get something more closely resembling (1), but I don’t see any precise connection. (The left-hand sides of (1), (2) are of course related through the Fourier identity  .)
.)
p.s. as far as I can tell, your argument does not use the smoothness or irreducibility of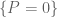 , which bothers me a little bit because I’m pretty sure one can have nontrivial even and odd cohomology in the non-smooth or reducible case.
, which bothers me a little bit because I’m pretty sure one can have nontrivial even and odd cohomology in the non-smooth or reducible case.
15 May, 2014 at 7:59 am
David Speyer
Your PS is bothering me too. The easiest way I can see that the story can be consistent is if those terms vanish modulo . That’s what happens in the simplest case: Take
. That’s what happens in the simplest case: Take  . Then the complex curve defined by
. Then the complex curve defined by  is three spheres glued into a circle, so with Betti numbers
is three spheres glued into a circle, so with Betti numbers  . The corresponding action of Frobenius is by
. The corresponding action of Frobenius is by  ,
,  and
and  ; the argument I give is computing that the second of these is
; the argument I give is computing that the second of these is  , and the reason that the third isn’t causing a problem is that it also vanishes modulo
, and the reason that the third isn’t causing a problem is that it also vanishes modulo  . A more interesting example is
. A more interesting example is  . On complex points, this is the same as the previous one (note that
. On complex points, this is the same as the previous one (note that  ) but the Frobenius action now depends on
) but the Frobenius action now depends on  . However, it still seems to be true that the action on
. However, it still seems to be true that the action on  vanishes modulo
vanishes modulo  .
.
15 May, 2014 at 9:32 pm
Will Sawin
The Lefschetz hyperplane theorem still works for the low cohomology degrees, so the issue is large degree eigenvalues. These tend to vanish modulo p – I can see an l-adic proof that they always do for smooth compact varieties using Poincare duality + the Weil conjectures, but I don’t see a similar argument for smooth hypersurface complements.
20 May, 2014 at 7:58 am
aquazorcarson
Are there bounds for S_n that use the number of defining polynomial k? Also this k seems to collide with the k for the number of characteristic values. The results of Bombieri and Hooley also remind me of work by J. Milnor that bounds the number of intersection points of two complex varieties of complementary dimension, using Morse theory.
[Notation changed, and dependence on number of defining polynomials clarified – T.]
20 May, 2014 at 5:40 pm
aquazorcarson
Thanks for the quick update. With the dependency on m, is Hooley’s bound strictly weaker than Bombieri’s?
20 May, 2014 at 7:31 pm
Terence Tao
In practice yes. Technically, the bound stated in Hooley’s paper may occasionally be stronger than that stated in Bombieri’s, if the variety is not a complete intersection, but I think that if one pushes the methods in Bombieri’s paper to the limit (beyond what is stated as the main result in his paper), it will give slightly stronger results than the corresponding limit of Hooley’s methods.
5 July, 2014 at 6:57 am
Angel Fernandez
Theorem 2 (hypothesis Riemann).
In its indication, the similarity with the classical Riemann hypothesis.
I have te inform you that it is shown by (Albana Diez) than no-trivial zeros of the zeta function are on the straight line for ( a = 1/2).
See in: Universañl Journal of Applied Mathematics Vol 1 (3);2013
title: Convergents series for Riemann hypothesis.
Regards.
Angel
20 March, 2015 at 7:05 am
A p-adic proof that pi is transcendental | Matt Baker's Math Blog
[…] following well-known characterization of rational functions, whose proof we omit (see Lemma 9 in this blog post by Terry […]
31 July, 2017 at 9:32 am
Cécile G.
Thank you for this post ! I had some trouble with two small mistakes or typos which seem to have crept into the definitions of G (for the trace formula) and F(T,Y) (for the Teichmüller lifting) :
— writing and
and  , as you do, one gets
, as you do, one gets
 and since
and since  merely is in
merely is in  , not in
, not in 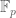 , you can’t get rid of the powers
, you can’t get rid of the powers  in order to come back to
in order to come back to  …
…
If you set instead, it arises :
instead, it arises :  , which seems to work then.
, which seems to work then.
— a may have disappeared in formula (25) :
may have disappeared in formula (25) :  works better for the next identities to hold.
works better for the next identities to hold.
[Corrected, thanks – T.]