Two of the most famous open problems in additive prime number theory are the twin prime conjecture and the binary Goldbach conjecture. They have quite similar forms:
- Twin prime conjecture The equation
has infinitely many solutions with
prime.
- Binary Goldbach conjecture The equation
has at least one solution with
prime for any given even
.
In view of this similarity, it is not surprising that the partial progress on these two conjectures have tracked each other fairly closely; the twin prime conjecture is generally considered slightly easier than the binary Goldbach conjecture, but broadly speaking any progress made on one of the conjectures has also led to a comparable amount of progress on the other. (For instance, Chen’s theorem has a version for the twin prime conjecture, and a version for the binary Goldbach conjecture.) Also, the notorious parity obstruction is present in both problems, preventing a solution to either conjecture by almost all known methods (see this previous blog post for more discussion).
In this post, I would like to note a divergence from this general principle, with regards to bounded error versions of these two conjectures:
- Twin prime with bounded error The inequalities
has infinitely many solutions with
prime for some absolute constant
.
- Binary Goldbach with bounded error The inequalities
has at least one solution with
prime for any sufficiently large
and some absolute constant
.
The first of these statements is now a well-known theorem of Zhang, and the Polymath8b project hosted on this blog has managed to lower to
unconditionally, and to
assuming the generalised Elliott-Halberstam conjecture. However, the second statement remains open; the best result that the Polymath8b project could manage in this direction is that (assuming GEH) at least one of the binary Goldbach conjecture with bounded error, or the twin prime conjecture with no error, had to be true.
All the known proofs of Zhang’s theorem proceed through sieve-theoretic means. Basically, they take as input equidistribution results that control the size of discrepancies such as
for various congruence classes and various arithmetic functions
, e.g.
(or more generaly
for various
). After taking some carefully chosen linear combinations of these discrepancies, and using the trivial positivity lower bound
one eventually obtains (for suitable ) a non-trivial lower bound of the form
where is some weight function, and
is the set of
such that there are at least two primes in the interval
. This implies at least one solution to the inequalities
with
, and Zhang’s theorem follows.
In a similar vein, one could hope to use bounds on discrepancies such as (1) (for comparable to
), together with the trivial lower bound (2), to obtain (for sufficiently large
, and suitable
) a non-trivial lower bound of the form
for some weight function , where
is the set of
such that there is at least one prime in each of the intervals
and
. This would imply the binary Goldbach conjecture with bounded error.
However, the parity obstruction blocks such a strategy from working (for much the same reason that it blocks any bound of the form in Zhang’s theorem, as discussed in the Polymath8b paper.) The reason is as follows. The sieve-theoretic arguments are linear with respect to the
summation, and as such, any such sieve-theoretic argument would automatically also work in a weighted setting in which the
summation is weighted by some non-negative weight
. More precisely, if one could control the weighted discrepancies
to essentially the same accuracy as the unweighted discrepancies (1), then thanks to the trivial weighted version
of (2), any sieve-theoretic argument that was capable of proving (3) would also be capable of proving the weighted estimate
However, (4) may be defeated by a suitable choice of weight , namely
where is the Liouville function, which counts the parity of the number of prime factors of a given number
. Since
, one can expand out
as the sum of
and a finite number of other terms, each of which consists of the product of two or more translates (or reflections) of
. But from the Möbius randomness principle (or its analogue for the Liouville function), such products of
are widely expected to be essentially orthogonal to any arithmetic function
that is arising from a single multiplicative function such as
, even on very short arithmetic progressions. As such, replacing
by
in (1) should have a negligible effect on the discrepancy. On the other hand, in order for
to be non-zero,
has to have the same sign as
and hence the opposite sign to
cannot simultaneously be prime for any
, and so
vanishes identically, contradicting (4). This indirectly rules out any modification of the Goldston-Pintz-Yildirim/Zhang method for establishing the binary Goldbach conjecture with bounded error.
The above argument is not watertight, and one could envisage some ways around this problem. One of them is that the Möbius randomness principle could simply be false, in which case the parity obstruction vanishes. A good example of this is the result of Heath-Brown that shows that if there are infinitely many Siegel zeroes (which is a strong violation of the Möbius randomness principle), then the twin prime conjecture holds. Another way around the obstruction is to start controlling the discrepancy (1) for functions that are combinations of more than one multiplicative function, e.g.
. However, controlling such functions looks to be at least as difficult as the twin prime conjecture (which is morally equivalent to obtaining non-trivial lower-bounds for
). A third option is not to use a sieve-theoretic argument, but to try a different method (e.g. the circle method). However, most other known methods also exhibit linearity in the “
” variable and I would suspect they would be vulnerable to a similar obstruction. (In any case, the circle method specifically has some other difficulties in tackling binary problems, as discussed in this previous post.)

30 comments
Comments feed for this article
10 July, 2014 at 4:57 am
Stijn Hanson
Really interesting article. What current evidence is there for the randomness of the Möbius function? I.e. is there anything which would lead us to believe that the Möbius randomness principle should fail?
10 July, 2014 at 10:45 pm
Terence Tao
We have a number of results that assert that exhibits non-trivial cancellation for many reasonable functions
exhibits non-trivial cancellation for many reasonable functions  ; see e.g. this recent paper of Liu and Sarnak for some examples. We also have smallness of the Mobius function in the Gowers uniformity norms, thanks to the work of Ben Green, Tamar Ziegler, and myself (see http://arxiv.org/abs/1009.3998 ).
; see e.g. this recent paper of Liu and Sarnak for some examples. We also have smallness of the Mobius function in the Gowers uniformity norms, thanks to the work of Ben Green, Tamar Ziegler, and myself (see http://arxiv.org/abs/1009.3998 ).
While we do not have any reason to disbelieve the Mobius pseudorandomness heuristic over the integers, the situation is more subtle over function fields, particularly in low characteristic. For instance there is an observation of Swan that shows that if is any polynomial in
is any polynomial in ![{\bf F}_2[t]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+F%7D_2%5Bt%5D&bg=ffffff&fg=545454&s=0&c=20201002) , then
, then 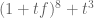 is always squarefree with an even number of irreducible factors, thus
is always squarefree with an even number of irreducible factors, thus 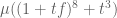 is identically
is identically  , in violation of the function field Mobius pseudorandomness heuristic. Conrad and Conrad have some further examples of this type. However, this phenomenon seems to be localised to low characteristic (and high degree) and does not seem to impact the situation over the integers.
, in violation of the function field Mobius pseudorandomness heuristic. Conrad and Conrad have some further examples of this type. However, this phenomenon seems to be localised to low characteristic (and high degree) and does not seem to impact the situation over the integers.
10 July, 2014 at 11:46 am
Eytan Paldi
the parity problem implies (as already remarked) for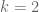 that for any admissible region
that for any admissible region  (i.e. satisfies the conditions on
(i.e. satisfies the conditions on 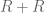 ) its M-value can’t exceed 2. This application for the Selberg variational problem is quite remarkable in the sense that it seems to be quite difficult to prove that
) its M-value can’t exceed 2. This application for the Selberg variational problem is quite remarkable in the sense that it seems to be quite difficult to prove that  for any admissible
for any admissible  by direct analytic method, and the only known proof is via the parity problem.
by direct analytic method, and the only known proof is via the parity problem.
10 July, 2014 at 12:57 pm
gowers
After such an interesting post, I hesitate to make such a trivial remark, but I may as well: there’s something odd about your last sentence (the one in brackets), which makes it seem as though there’s a couple of words accidentally missed out.
[Corrected, thanks – T.]
11 July, 2014 at 5:46 am
0_Lesh_a
And if you take information about the equations for 3,4,5,6 … and to prove that they differ in some law. Do you think it will be harder than finding a solution to the exact equation 2?
12 July, 2014 at 9:49 am
Gil Kalai
Does the parity problem also applies for the assertion that there are infinitely many solutions for p-q = T where p and q are primes and T is some fixed number other than 2?
13 July, 2014 at 9:31 pm
Terence Tao
Yes. As a general rule of thumb, whenever one is trying to find a prime pair in some graph
in some graph  over the natural numbers (or over “almost primes”), the parity problem arises as an obstruction whenever the graph
over the natural numbers (or over “almost primes”), the parity problem arises as an obstruction whenever the graph  is 2-colourable (or even “mostly 2-colourable”, in that the proportion of monochromatic edges is tiny), assuming that the 2-colouring is “non-arithmetic” in some sense (so that it does not exhibit correlation with things like the Mobius function). This is for instance the case with the graph with edges
is 2-colourable (or even “mostly 2-colourable”, in that the proportion of monochromatic edges is tiny), assuming that the 2-colouring is “non-arithmetic” in some sense (so that it does not exhibit correlation with things like the Mobius function). This is for instance the case with the graph with edges 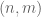 with
with 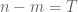 , which can be 2-coloured by a simple colouring of congruence classes, as well as the Goldbach-with-bounded error graph
, which can be 2-coloured by a simple colouring of congruence classes, as well as the Goldbach-with-bounded error graph  , which can be 2-coloured after deleting the numbers near
, which can be 2-coloured after deleting the numbers near 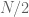 (assuming for sake of argument that there are no primes of the form
(assuming for sake of argument that there are no primes of the form 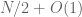 ). In contrast, the graph of edges
). In contrast, the graph of edges 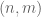 with
with 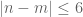 is not subject to this obstruction, even if one restricts to integers coprime to both 2 and 3, due to the presence of triangles. The situation with
is not subject to this obstruction, even if one restricts to integers coprime to both 2 and 3, due to the presence of triangles. The situation with  is more interesting; initially it appears that there are triangles, giving hope that the parity problem is not present here, but after deleting multiples of 2 and 3, all triangles are removed, and the parity problem is now evident.
is more interesting; initially it appears that there are triangles, giving hope that the parity problem is not present here, but after deleting multiples of 2 and 3, all triangles are removed, and the parity problem is now evident.
12 July, 2014 at 12:00 pm
Polymath 8 – a Success! | Combinatorics and more
[…] barrier indeed shows up causes this attempt to fail. (Update July 14:) This is further explained in this new post over Tao’s […]
17 July, 2014 at 2:29 am
Anonymous
Professor Tao.
Constant (H) in: 0 < p' – p < H
N < p' + p < N + H ; is H = 44
The solution you have in your email from last month (June)..
5 October, 2014 at 1:46 pm
sylvainjulien
You might be interested in taking a glance at my blog ideasfornumbertheory.wordpress.com that hopefully could shed a new light on these two conjectures.
4 March, 2015 at 4:30 pm
Anthony Vossman
I would think that the only way around parity obstruction would have to begin by permitting the identity elements, 0,1, to be considered “conditionally prime” within the trivial range <4, thereby generalizing the binary G conjecture to a full set Z. From there, considering that the identity elements are also perfect squares, the binary G could be restated as, "Every perfect square is the sum of a semiprime and another perfect square", thus fully relating the additive and multiplicative universes, and which would make for an easier conjecture to address. These "tough" NT problems are really only related to the fact that axiomatic systems in general, are simply constructive edifices honoring a much deeper bilateral symmetry condition that is a pre-conditional for all arithmetic axioms, terms and relations. The only way you will find 'easy' proofs for these problems is to generalize them over the entire Z. Unfortunately, the symmetric beauty of the primes is spoiled by the conventionalities required of "uniqueness". Mathematics has to realize that the human brain is a prisoner of the bilateral symmetry that defines it.
14 March, 2015 at 5:48 am
gninrepoli
Perhaps some molifer can help solve the problem, such as use in the work of Yitang Zhang:
27 March, 2015 at 6:29 am
gninrepoli
I’m not sure, but if Mobius inversion possible for the Euler function, you can use the Selberg sieve for finding suitable mollifier to smooth small arcs and possibly remove zero, which occurs in the evaluation of large arcs.
26 August, 2015 at 4:24 pm
Heath-Brown’s theorem on prime twins and Siegel zeroes | What's new
[…] can distinguish them from other twins of almost primes. The parity problem is discussed in these previous blog posts; this obstruction is ultimately powered by the Möbius pseudorandomness principle […]
1 September, 2015 at 10:29 pm
Boris Sklyar
I propose the following:
MATRIX DEFINITION” OF PRIME NUMBERS:
There are two 2-dimensional arrays:
|5 10 15 20 ..|
6i^2-1+(6i-1)(j-1)= |23 34 45 56…|
|53 70 87 104…|
|95 118 141 164…|
|149 178 207 236…|
|… … … … |
| 5 12 19 26 ..|
6i^2-1+(6i+1)(j-1)= |23 36 49 62…|
|53 72 91 110…|
|95 120 145 170…|
|149 180 211 242…|
|… … … … |
Positive integers not contained in these arrays are indexes p of all prime numbers in the sequence S1(p)=6p+5, i.e. p=0, 1, 2, 3, 4, , 6, 7, 8, 9, , 11, , 13, 14, , 16, 17, 18, , , 21, 22, , 24, , , 27, 28, 29, …
and primes are: 5, 11, 17. 23, 29, , 41, 47, 53, 59, , 71, , 83, 89, , 101, 107, 113, , , 131, 137, , 149, , , 167, 173, 179, ….
There are two 2-dimensional arrays:
|3 8 13 18 ..|
6i^2-1-2i+(6i-1)(j-1)= |19 30 41 52…|
|47 64 81 98…|
|87 110 133 156…|
|139 168 197 226…|
|… … … … |
| 7 14 21 28 ..|
6i^2-1+2i+(6i+1)(j-1)= |27 40 53 66…|
|59 78 97 116..|
|103 128 153 178…|
|159 190 221 252…|
|… … … … |
Positive integers not contained in these arrays are indexes p of all prime numbers in the sequence S2(p)=6p+7, i.e. p=0, 1, 2, , 4, 5, 6, , , 9, 10, 11, 12, , , 15 , 16, 17, , , 20, , 22, , 24, 25 , 26, , , 29, …
and primes are: 7, 13, 19. , 31, 37, 43, , , 61, 67, 73, 79, , , 97, 103, 109, , , 127, , 139, , 151, 157, 163, , , 181 ….
,
http://www.planet-source-code.com/vb/scripts/ShowCode.asp?txtCodeId=13752&lngWId=3
18 September, 2015 at 4:46 pm
The logarithmically averaged Chowla and Elliott conjectures for two-point correlations; the Erdos discrepancy problem | What's new
[…] are known to be subject to the “parity problem” (discussed numerous times previously on this blog), which roughly speaking means that they cannot be proven solely using […]
4 November, 2015 at 2:31 am
Anonymous
News:
Finally is resolved the Goldbach conjecture strong.
Applyin mathematical logis, we have the result that all:
See: http://www.hrpub.org/journals/jour_info.php?id=24 Vol 3 (3) 2015
18 November, 2015 at 9:57 am
Eulogio
I think we are in the final shown. Because, as stated in the article, with the two set![[p; p_{1}; p_{2};....] = 2N](https://s0.wp.com/latex.php?latex=%5Bp%3B+p_%7B1%7D%3B+p_%7B2%7D%3B....%5D+%3D+2N+&bg=ffffff&fg=545454&s=0&c=20201002) and
and 
We have.
If we apply the decomposition of each pair.
Being the minor of the odd not prime, then.
the minor of the odd not prime, then.
Turn:![[(2b+1) + 2] \neq (2c+1)](https://s0.wp.com/latex.php?latex=%5B%282b%2B1%29+%2B+2%5D+%5Cneq+%282c%2B1%29+&bg=ffffff&fg=545454&s=0&c=20201002)
If![[(2b+1) + 2] < (2c+1)](https://s0.wp.com/latex.php?latex=%5B%282b%2B1%29+%2B+2%5D+%3C+%282c%2B1%29+&bg=ffffff&fg=545454&s=0&c=20201002) then.
then.
And so on.
[profesor Terence Tao, would be so kind as to give his opinión on the show]
17 July, 2016 at 8:53 am
Notes on the Bombieri asymptotic sieve | What's new
[…] thus embodies the “parity problem” for the twin prime conjecture (discussed in these previous blog […]
29 November, 2017 at 4:59 pm
Pedro Caceres
(Caceres, 2017) has described the complete set of Prime numbers as:
{Primes} =
{2,3} ∪
{6kn+1 | kn≠6xy+x+y and k_n≠6xy-x-y for all x,y∈N} ∪
{6km-1 | km≠6xy-x+y for all x,y∈N}
The definition of the twin primes implies that any S2n such that S2n=kn=km will create a pair of twin primes.
The list of the first S2n is:
S2n= [1,2,3,5,7,10,12,17,…]
And the first pairs generated are:
Twin Primes from S2n = 1 =[ 5 , 7 ]
Twin Primes from S2n = 2 =[ 11 , 13 ]
Twin Primes from S2n = 3 =[ 17 , 19 ]
Twin Primes from S2n = 5 =[ 29 , 31 ]
Twin Primes from S2n = 7 =[ 41 , 43 ]
Twin Primes from S2n = 10 =[ 59 , 61 ]
Twin Primes from S2n = 12 =[ 71 , 73 ]
Twin Primes from S2n = 17 =[ 101 , 103 ]
We must add [3,5] to complete the series.
Is S2n infinite?
The members of the series S2n must verify the three primality conditions. For every s2n∈S2n there are no x, y in N that satisfy any of the following conditions:
s2n=6xy+x+y
s2n=6xy-x-y
s2n=6xy+x-y
If S2n is limited, let’s call S the last element of the set and let’s prove that S does not exist using reduction to the absurd.
If S is the last element of S2n, S is the last number that verifies that there are no (x, y) Natural numbers such that:
S=6xy+x+y
S=6xy-x-y
S=6xy+x-y
For any T>S, we will always find some values x, y Naturals that verify:
T=6xy+x+y
T=6xy-x-y
T=6xy+x-y
These conditions can also be expressed as:
(6T+1) = (6x+1)*(6y+1)
(6T+1) = (6x-1)*(6y-1)
(6T- 1) = (6x-1)*(6y+1)
Which means that all numbers of the form (6T+1) and (6T-1) with T>S are composite which is absurd as we know that all prime numbers can be expressed as (6T+1) or (6T-1) and the number of primes number is infinite.
So the numbers of Twin primes is infinite.
4 August, 2019 at 1:55 am
Samuel Bonaya Buya
In my opinion there should be a simple method of proving Goldbach Conjecture. Consider a Goldbach number 2k. The number of primes in the interval [1, 2k] is given by (1) π(2k)= 2k(1/2 – r) where r is ratio of composite odd numbers in the interval [1,2k] to the Goldbach number 2k. For 2k<=8 r =0. This means that (2) π(2k)<=k. Here k is a Goldbach integer. Some of the primes in the interval [1, 2k] are used for Goldbach partition of a Goldbach number. I takes pairs of primes for Goldbach in the interval [1,2k] for partition. The number of Goldbach partition is given by:
(3) R(2k)<= (π(2k))/2 <= k/2.
Not all the primes in the interval [1,2k] are used for Goldbach partition. Let the number used for Goldbach partition be Npg. Then for a semiprime Goldbach number:
(4) R(2k) = (Npg +1)/2
For a non semiprime Goldbach number the number of Goldbach partitions is given by:
(5) R(2k) = Npg/2.
The forms (4) and (5) are not useful for proof of the Goldbach conjecture. For proof of the conjecture write:
(6) R(2k) = k√(k^2 – m) where (7) m =( k +2k/(Npg +1))(k- 2k/(Npg+1)) for a semiprime Goldbach number or (8) m= (k+2k/Npg)(k-2k/Npg) for a non semiprime Goldbach number. Since R(2k) =4. But k>=2 and k is an integer. This implies m>=0. Now m>=0 implies R(2k)>= 1. Therefore the number of Goldbach partitions cannot be greater than 1. Thus Goldbach conjecture is proved.
I have worked on this proof and posted the same to academia.edu. Currently article is going through review.
21 August, 2019 at 2:02 am
Samuel Bonaya Buya
To Terence Tao,
While it is true that Goldbach conjecture is challenging to prove, there exists a hidden direct proof based on the basic properties of numbers that enable establishing the minimum number of Goldbach portions as 1. I discussed the direct proof here:
https://www.quora.com/When-does-a-proof-qualify-to-be-a-direct-proof-Could-there-be-a-direct-proof-of-Goldbach-conjecture/answer/Samuel-Bonaya-Buya-1?ch=8&share=5331393c&srid=3jnd2
22 September, 2019 at 3:30 pm
Buzzman
There seems to be a slow progress in this direction. I’m suggesting a way to approach this problem. Let , where
, where  for sufficiently large
for sufficiently large 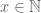 . For the integer pairs
. For the integer pairs 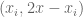 satisfying the binary GC for any sufficiently large
satisfying the binary GC for any sufficiently large  such that
such that
it is required that if
if 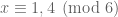 or
or  if
if  , whereas
, whereas 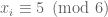 and
and  and vice versa if
and vice versa if  . Let
. Let  if
if  is prime and
is prime and  otherwise. Then we have the possible cases as
otherwise. Then we have the possible cases as
Case I: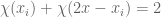 ,
,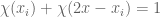 ,
, .
.
Case II:
Case III:
Let denote the number of pairs
denote the number of pairs 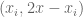 satisfying Case III. Obviously, the binary GC fails if the cardinality of Case I is zero, in which case
satisfying Case III. Obviously, the binary GC fails if the cardinality of Case I is zero, in which case  . As usual, let
. As usual, let  denote the number of primes in arithmetic progression $x_i \equiv a\pmod{q}$ below
denote the number of primes in arithmetic progression $x_i \equiv a\pmod{q}$ below 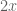 . Also let
. Also let  be the number of terms from
be the number of terms from 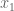 to
to  , where
, where 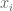 depends on the least residue class
depends on the least residue class 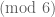 of
of  . Suppose
. Suppose  , where
, where  is the set of primes. Then for any sufficiently large
is the set of primes. Then for any sufficiently large  , the binary GC holds if
, the binary GC holds if
where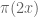 is the number of primes not exceeding
is the number of primes not exceeding 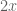 . This assumes that the primes are equally distributed between the least residue classes
. This assumes that the primes are equally distributed between the least residue classes 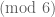 . Similarly,
. Similarly,
for . These suggest that while the primes thin out as
. These suggest that while the primes thin out as 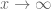 , the size of
, the size of  tends to grow larger such that there is an increasing likelihood for at least one pair of primes, not necessarily distinct, to equal
tends to grow larger such that there is an increasing likelihood for at least one pair of primes, not necessarily distinct, to equal 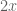 . In this setting, the crux of the matter is thus to establish the growth of
. In this setting, the crux of the matter is thus to establish the growth of  as
as 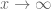 .
.
22 September, 2019 at 3:59 pm
Buzzman
Oops, should be defined above as
should be defined above as 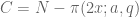 as the number of composites in the progression
as the number of composites in the progression  depending on
depending on  .
.
19 November, 2020 at 6:43 am
Aumeunier
hello
Eq={q premier |q≤√2n}
Er={q ∈ Eq | (2n)mod(q)}
∃q ∈ Eq and ∉ Er such as 2n-q=p Prime number ∀ 2n ∈ N
you will not find a counterexample because
4 very small page the most important and at the end
Click to access conjecture%20de%20Goldbach_en.pdf
by these times of confinement a small re-creation
and it’s not very, very serious, it’s just math.
cdl remy
19 November, 2020 at 7:44 am
Anonymous
A natural generalization of the problem is to find the slowest growth rate of a positive function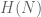 such that for sufficiently large $N$, the interval
such that for sufficiently large $N$, the interval ![[N, N+H(N)]](https://s0.wp.com/latex.php?latex=%5BN%2C+N%2BH%28N%29%5D&bg=ffffff&fg=545454&s=0&c=20201002) should contain at least one integer which is a sum of two primes.
should contain at least one integer which is a sum of two primes.
22 February, 2022 at 8:16 am
sacirisi
Goldbach’s conjecture satisfied with the strategy that the young Gauss invented to add the numbers from 1 to 100.
https://www.reddit.com/user/Proud-Yogurtcloset71/comments/syr9di/goldbachs_conjecture_satisfied_with_the_strategy/
Thanks to an intuition and a strategy, Gauss showed that the same odd number, 101, is the sum of the even numbers with the odd
11 November, 2022 at 9:34 am
phamminhduc2710
Professor Terence Tao, can you take a look for me?
https://www.researchgate.net/publication/365265295_THE-GOLDBACH-CONJECTURE
25 November, 2022 at 4:44 am
phamminhduc2710
New approach to the Goldbach conjecture
https://www.researchgate.net/publication/365703468_Goldbach
23 January, 2024 at 3:46 am
Anonymous
Aldo Pappalepore: Dear Professor Tao, I would be very grateful for your opinion on this study of the Goldbach and Hardy-Littlewood conjectures: https://alpalerweb.altervista.org/Hardy_Littlewood_and_Goldbach_conjectures.pdf