The twin prime conjecture is one of the oldest unsolved problems in analytic number theory. There are several reasons why this conjecture remains out of reach of current techniques, but the most important obstacle is the parity problem which prevents purely sieve-theoretic methods (or many other popular methods in analytic number theory, such as the circle method) from detecting pairs of prime twins in a way that can distinguish them from other twins of almost primes. The parity problem is discussed in these previous blog posts; this obstruction is ultimately powered by the Möbius pseudorandomness principle that asserts that the Möbius function is asymptotically orthogonal to all “structured” functions (and in particular, to the weight functions constructed from sieve theory methods).
However, there is an intriguing “alternate universe” in which the Möbius function is strongly correlated with some structured functions, and specifically with some Dirichlet characters, leading to the existence of the infamous “Siegel zero“. In this scenario, the parity problem obstruction disappears, and it becomes possible, in principle, to attack problems such as the twin prime conjecture. In particular, we have the following result of Heath-Brown:
Theorem 1 At least one of the following two statements are true:
- (Twin prime conjecture) There are infinitely many primes
such that
is also prime.
- (No Siegel zeroes) There exists a constant
such that for every real Dirichlet character
of conductor
, the associated Dirichlet
-function
has no zeroes in the interval
.
Informally, this result asserts that if one had an infinite sequence of Siegel zeroes, one could use this to generate infinitely many twin primes. See this survey of Friedlander and Iwaniec for more on this “illusory” or “ghostly” parallel universe in analytic number theory that should not actually exist, but is surprisingly self-consistent and to date proven to be impossible to banish from the realm of possibility.
The strategy of Heath-Brown’s proof is fairly straightforward to describe. The usual starting point is to try to lower bound , where
is the von Mangoldt function. Actually, in this post we will work with the slight variant
If there is a Siegel zero with
close to
and
a Dirichlet character of conductor
, then multiplicative number theory methods can be used to show that the Möbius function
“pretends” to be like the character
in the sense that
for “most” primes
near
(e.g. in the range
for some small
and large
). Traditionally, one uses complex-analytic methods to demonstrate this, but one can also use elementary multiplicative number theory methods to establish these results (qualitatively at least), as will be shown below the fold.
The fact that pretends to be like
can be used to construct a tractable approximation (after inserting the sieve weight
) in the range
(where
for some large
) for the second von Mangoldt function
, namely the function
One expects to be a good approximant to
if
is of size
and has no prime factors less than
for some large constant
. The Selberg sieve
will be mostly supported on numbers with no prime factor less than
. As such, one can hope to approximate (1) by the expression
Actually one does not need the full strength of the Weil bound here; any power savings over the trivial bound of will do. In particular, it will suffice to use the weaker, but easier to prove, bounds of Kloosterman:
Lemma 2 (Kloosterman bound) One haswhenever
and
are coprime to
, where the
is with respect to the limit
(and is uniform in
).
Proof: Observe from change of variables that the Kloosterman sum is unchanged if one replaces
with
for
. For fixed
, the number of such pairs
is at least
, thanks to the divisor bound. Thus it will suffice to establish the fourth moment bound
We will also need another easy case of the Weil bound to handle some other portions of (2):
Lemma 3 (Easy Weil bound) Letbe a primitive real Dirichlet character of conductor
, and let
. Then
Proof: As is the conductor of a primitive real Dirichlet character,
is equal to
times a squarefree odd number for some
. By the Chinese remainder theorem, it thus suffices to establish the claim when
is an odd prime. We may assume that
is not divisible by this prime
, as the claim is trivial otherwise. If
vanishes then
does not vanish, and the claim follows from the mean zero nature of
; similarly if
vanishes. Hence we may assume that
do not vanish, and then we can normalise them to equal
. By completing the square it now suffices to show that
While the basic strategy of Heath-Brown’s argument is relatively straightforward, implementing it requires a large amount of computation to control both main terms and error terms. I experimented for a while with rearranging the argument to try to reduce the amount of computation; I did not fully succeed in arriving at a satisfactorily minimal amount of superfluous calculation, but I was able to at least reduce this amount a bit, mostly by replacing a combinatorial sieve with a Selberg-type sieve (which was not needed to be positive, so I dispensed with the squaring aspect of the Selberg sieve to simplify the calculations a little further; also for minor reasons it was convenient to retain a tiny portion of the combinatorial sieve to eliminate extremely small primes). Also some modest reductions in complexity can be obtained by using the second von Mangoldt function in place of
. These exercises were primarily for my own benefit, but I am placing them here in case they are of interest to some other readers.
— 1. Consequences of a Siegel zero —
It is convenient to phrase Heath-Brown’s theorem in the following equivalent form:
Theorem 4 Suppose one has a sequenceof real Dirichlet characters of conductor
going to infinity, and a sequence of real zeroes
with
as
. Then there are infinitely many prime twins.
Henceforth, we omit the dependence on from all of our quantities (unless they are explicitly declared to be “fixed”), and the asymptotic notation
,
,
, etc. will always be understood to be with respect to the
parameter, e.g.
means that
for some fixed
. (In the language of this previous blog post, we are thus implicitly using “cheap nonstandard analysis”, although we will not explicitly use nonstandard analysis notation (other than the asymptotic notation mentioned above) further in this post. With this convention, we now have a single (but not fixed) Dirichlet character
of some conductor
with a Siegel zero
. Standard arguments (see also Lemma 59 of this blog post) then give
We now use this Siegel zero to show that pretends to be like
for primes that are comparable (in log-scale) to
:
Lemma 5 For any fixed, we have
For more precise estimates on the error, see the paper of Heath-Brown (particularly Lemma 3).
Proof: It suffices to show, for sufficiently large fixed , that
We begin by considering the sum (which we will eventually take to be a power of
); we will exploit the fact that this sum is very stable for
comparable to
in log-scale. By the Dirichlet hyperbola method, we can write this as
— 2. Main argument —
We let be a large absolute constant (
will do) and set
to be the primorial of
. Set
for some large fixed
(large compared to
or
). Let
be a smooth non-negative function supported on
and equal to
at
. Set
We split as
is non-negative, and supported on those products
of primes with
and
, times a square. Convolving (11) by
and using the identity
, we have
We begin with (13). Let be a small fixed quantity to be chosen later. Observe that if
is non-zero, then
must have a factor on which
is non-zero, which implies that
is either divisible by a prime
with
, or by the square of a prime. If the former case occurs, then either
or
is divisible by
; since
, this implies that either
is divisible by a prime
with
, or that
is divisible by a prime less than
. To summarise, at least one of the following three statements must hold:
-
is divisible by a prime
.
-
is divisible by the square
of a prime
.
-
is divisible by a prime
with
.
It thus suffices to establish the estimates
We begin with (15). Observe that if divides
then either
divides
or
divides
. In particular the number of
with
is
. The summand
is
by the divisor bound, so the left-hand side of (15) is bounded by
Next we turn to (14). We can very crudely bound
We use a modification of the argument used to prove Proposition 4.2 of this Polymath8b paper. By Fourier inversion, we may write
We factor where
are primes, and then write
where
and
is the largest index for which
. Clearly
and
with
, and the least prime factor
of
is such that
We write , where
denotes the number of prime factors of
counting multiplicity. We can thus bound the left-hand side of (19) by
For future reference we observe that the above arguments also establish the bound
Finally, we turn to (16). Using (17) again, it suffices to show that
It remains to prove (12), which we write as
Now we prove (23), which is where we need nontrivial bounds on Kloosterman sums. Expanding out and using the triangle inequality, it suffices (for
large enough) to show that
Fix . If
for an odd
, then we can uniquely factor
such that
,
, and
. It thus suffices to show that
We first dispose of the case when is large in the sense that
. Making the change of variables
, we may rewrite the left-hand side as
It remains to control the contribution of the case to (25). By the triangle inequality, it suffices to show that
We rearrange the left-hand side as
Suppose first that is of the form
for some integer
. Then the phase
is periodic with period
and has mean zero here (since
). From this, we can estimate the inner sum by
; since
is restricted to be of size
, this contribution is certainly acceptable. Thus we may assume that
is not of the form
. A similar argument works when
(say), so we may assume that
, so that
.
By (26), this forces the denominator of in lowest form to be
. By Lemma 2, we thus have
Finally, we prove (22), which is a routine sieve-theoretic calculation. We rewrite the left-hand side as
Recalling that

76 comments
Comments feed for this article
26 August, 2015 at 10:59 pm
Anonymous
Is there any known probabilistic argument for the existence/ nonexistence of Siegel zeros?
27 August, 2015 at 8:08 am
Terence Tao
Probabilistic arguments (in particular, the Mobius pseudorandomness principle, discussed in this previous post) suggest that the generalised Riemann Hypothesis (GRH) is true, which can be viewed as the polar opposite of having a Siegel zero (certainly the two statements are incompatible). As such, the Siegel zero problem is really quite tantalising; it is the strongest surviving alternative to the conjectural picture we have about the distribution of the primes, and eliminating it would be viewed as a significant advance towards the GRH (although there would still be a lot further to go to finish that off entirely). (Historically, there were GRH alternatives that were even stronger than the Siegel zero, such as the “tenth discriminant”, but these at least have been eliminated, though not without quite a bit of effort.)
4 September, 2015 at 4:31 am
Sergei
It is an interesting idea to use an unsquared Selberg sieve.
In fact, on the generalized Elliott-Halberstam conjecture
an unsquared Selberg sieve weight does correlate with the Möbius function,
and this can be used to deduce the twin prime conjecture from
the generalized Elliott-Halberstam conjecture.
The idea is to use the unsquared sieve weight
where is the indicator function of
is the indicator function of  and
and 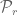 is the set of squarefree integers
is the set of squarefree integers prime factors.
prime factors.
which have exactly
Now assume the generalized Elliott-Halberstam conjecture, and let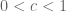 be a real number to be chosen later.
be a real number to be chosen later. to be
to be  when
when  is positive, and
is positive, and  otherwise.
otherwise.
Define the function
Take
Consider the weighted expression
where
Using Theorems 3.5, 3.6 of Polymath8b, it can be shown that
for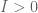 fixed if
fixed if  is close enough to
is close enough to  .
. or
or 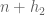 has a small prime factor give negligible contribution).
has a small prime factor give negligible contribution).
(note that integers for which
According to Chapter 16 of Friedlander-Iwaniec, if there are no pairs prime,
prime, 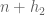 prime, then
prime, then
has a completely determined distribution function, so we can compute that
where as
as  .
.
Choosing close enough to
close enough to  ,
, and hence
and hence
we get
has a nonzero distribution function, and again by Chapter 16 of Friedlander-Iwaniec
it follows that
has a nonzero distribution function.
4 September, 2015 at 7:22 am
Terence Tao
I think that if you do the calculations carefully (in particular paying attention to the main terms that are not directly treatable by GEH, coming from convolutions in which one factor is supported very close to the origin or which otherwise fails to obey a Siegel-Walfisz condition), you will find that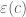 converges to I, not to 0, as
converges to I, not to 0, as 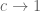 .
.
For the twin prime problem, even with GEH, one has the parity problem scenario in which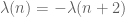 for all (or almost all)
for all (or almost all)  for which
for which 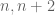 are almost prime (here
are almost prime (here  is the Liouville function, not the sieve weight). In this scenario there are essentially no twin primes (since for such primes
is the Liouville function, not the sieve weight). In this scenario there are essentially no twin primes (since for such primes  one has
one has  ), and your weight
), and your weight 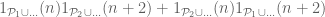 is essentially equal to 1. This scenario is consistent with GEH (assuming Mobius pseudorandomness) and with all other known inputs available to sieve theory, including those in Friedlander-Iwaniec. From the work of Bomberi we know that (on EH) this scenario is essentially the only scenario in which we have essentially no twin primes.
is essentially equal to 1. This scenario is consistent with GEH (assuming Mobius pseudorandomness) and with all other known inputs available to sieve theory, including those in Friedlander-Iwaniec. From the work of Bomberi we know that (on EH) this scenario is essentially the only scenario in which we have essentially no twin primes.
Personally, I advise against spending too much time on trying to attack the twin prime conjecture under hypotheses such as GEH unless you can pinpoint the precise input you are using (or hope to use) which breaks the parity barrier by being incompatible (at least from a heuristic, moral, or conjectural standpoint) with the scenario. (For instance, in the current blog post it is Lemma 3 which is providing the incompatibility, because the Siegel zero forces
scenario. (For instance, in the current blog post it is Lemma 3 which is providing the incompatibility, because the Siegel zero forces  to behave like
to behave like 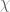 on almost primes, and Lemma 3 (plus some sieve theory) precludes the
on almost primes, and Lemma 3 (plus some sieve theory) precludes the  scenario on such almost primes.)
scenario on such almost primes.)
4 September, 2015 at 10:42 pm
Sergei
Yes, the weight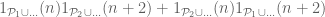 is essentially equal to
is essentially equal to  in this unique scenario, but in this scenario the unsquared weight
in this unique scenario, but in this scenario the unsquared weight  is essentially equal to
is essentially equal to  on the primes
on the primes  for which
for which  . It is different from the weight in the squared Selberg sieve, which is NOT essentially equal to
. It is different from the weight in the squared Selberg sieve, which is NOT essentially equal to  in this case?
in this case?
4 September, 2015 at 11:05 pm
Terence Tao
Actually, I don’t think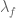 is all that small on those primes
is all that small on those primes  for which
for which 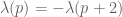 (note that
(note that 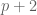 will likely have some prime factors less than
will likely have some prime factors less than  ; this is a subtlety that also shows up in Bombieri’s analysis… one can insert a further sieve to eliminate extremely small prime factors, but not factors of size near
; this is a subtlety that also shows up in Bombieri’s analysis… one can insert a further sieve to eliminate extremely small prime factors, but not factors of size near  unless one damps the function
unless one damps the function  to a higher order near
to a higher order near 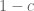 ). Indeed, Mobius pseudorandomness heuristics predict that
). Indeed, Mobius pseudorandomness heuristics predict that  will be asymptotically orthogonal to
will be asymptotically orthogonal to 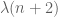 (whether one restricts
(whether one restricts  to be prime or not) and so the value of
to be prime or not) and so the value of 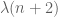 should have essentially no influence on the behaviour of
should have essentially no influence on the behaviour of  .
.
To repeat my previous comment, the parity problem is not an obstacle to be taken lightly. If you haven’t identified a precise input in your argument which is explicitly getting around the parity barrier (basically, one needs to somehow control a sum of an expression that has a nontrivial correlation with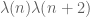 , which none of the standard sieve weights do even when weighted by
, which none of the standard sieve weights do even when weighted by 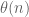 or
or 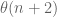 ), the chances are overwhelmingly likely that there is going to be an error in your analysis.
), the chances are overwhelmingly likely that there is going to be an error in your analysis.
5 September, 2015 at 10:59 pm
Sergei
I absolutely agree that the parity barrier is a very serious problem. It is not entirely clear where is the moral difference between the 2-dimensional weights
where
and
where
I don’t quite see how could be large when
could be large when 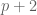 has one (say) prime factor less than
has one (say) prime factor less than  . But it is clear that
. But it is clear that  could be large when
could be large when 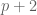 has one prime factor less than
has one prime factor less than  .
.
6 September, 2015 at 10:02 am
Terence Tao
Note that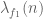 factors as
factors as 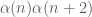 , where
, where  . Next, since
. Next, since
we can write
which on replacing by
by  is essentially (assuming
is essentially (assuming  squarefree and close to
squarefree and close to  for simplicity)
for simplicity)
If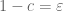 , the latter term is roughly speaking like
, the latter term is roughly speaking like 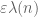 restricted to those numbers that are
restricted to those numbers that are  -rough (have no prime factors much smaller than
-rough (have no prime factors much smaller than  ). This latter set of numbers is larger than the set of primes by a factor of about
). This latter set of numbers is larger than the set of primes by a factor of about 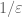 . So, while
. So, while  is of size about 1 on primes, it is also of size about
is of size about 1 on primes, it is also of size about  on a set of size about
on a set of size about 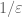 larger than the primes, and the net contribution of this set is of equal strength (in an L^1 sense) to the contribution on primes. (It may be small in an
larger than the primes, and the net contribution of this set is of equal strength (in an L^1 sense) to the contribution on primes. (It may be small in an 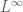 sense, but it is the
sense, but it is the  size which is the most relevant for these computations.) For instance, it is an instructive exercise to compute
size which is the most relevant for these computations.) For instance, it is an instructive exercise to compute  and find out that this is rather small (as is predicted from the Mobius pseudorandomness principle –
and find out that this is rather small (as is predicted from the Mobius pseudorandomness principle –  has to give an equal weight to numbers with an odd number of prime factors, and numbers with an even number of prime factors), even though the contribution coming from the primes (or even from all of the numbers with all prime factors larger than
has to give an equal weight to numbers with an odd number of prime factors, and numbers with an even number of prime factors), even though the contribution coming from the primes (or even from all of the numbers with all prime factors larger than  ) is quite large.
) is quite large.
Returning to , we now see that
, we now see that  can be somewhat large (of size about
can be somewhat large (of size about  ) when the smallest prime factor of
) when the smallest prime factor of 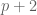 is comparable to
is comparable to  , and the contribution of this case to the
, and the contribution of this case to the 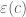 in your original argument is of about the same size as the contribution of the case when
in your original argument is of about the same size as the contribution of the case when 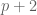 is prime, which I believe will ultimately lead to
is prime, which I believe will ultimately lead to 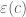 converging to I rather than to 0 as I said in my first comment (this is the only possible limiting value for
converging to I rather than to 0 as I said in my first comment (this is the only possible limiting value for 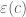 which is compatible with the Mobius pseudorandomness principle). In any event, it’s probably a good idea for you to work out the computation of
which is compatible with the Mobius pseudorandomness principle). In any event, it’s probably a good idea for you to work out the computation of 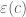 in full detail.
in full detail.
—
By the way, here is a more explicit way to think about the parity obstruction for twin primes which may help you appreciate why the inputs you are using are not strong enough to give the conclusion you wish to obtain. Sieve theory relies on inputs that can take the form of upper or lower bounds on sums of arithmetic functions, e.g.
or
or
(for some main terms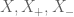 and error magnitude
and error magnitude  , and various arithmetic functions
, and various arithmetic functions  , which may for instance be the restriction of some other arithmetic function, e.g.
, which may for instance be the restriction of some other arithmetic function, e.g.  or
or 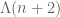 , to a residue class
, to a residue class  ) or on averaged bounds such as Elliott-Halberstam type bounds
) or on averaged bounds such as Elliott-Halberstam type bounds
Sieve theory also takes as input pointwise inequalities
between arithmetic functions (e.g. the trivial bounds ).
).
The whole game of sieve theory is to try to cleverly take linear combinations of these inputs, weighted by suitable sieves, to ultimately deduce something like
or perhaps
where the main term is significantly larger than the error term
is significantly larger than the error term  .
.
Call an estimate parity-insensitive if it is conjectured that the estimate is essentially unchanged after weighting the natural numbers by the weight
by the weight 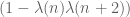 . For instance, Elliott-Halberstam type bounds on
. For instance, Elliott-Halberstam type bounds on  are conjectured (by the Mobius pseudorandomness heuristic) to also hold for the weighted sum
are conjectured (by the Mobius pseudorandomness heuristic) to also hold for the weighted sum  ; similarly if
; similarly if  is replaced by
is replaced by 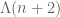 . Clearly any pointwise bound is also parity-insensitive since the weight
. Clearly any pointwise bound is also parity-insensitive since the weight 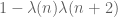 is non-negative. In fact all of the standard inputs to sieve theory (including GEH) are conjectured to be parity-insensitive. On the other hand, bounds such as (1) or (2) are parity-sensitive (and the bounds you claim would also be parity sensitive if
is non-negative. In fact all of the standard inputs to sieve theory (including GEH) are conjectured to be parity-insensitive. On the other hand, bounds such as (1) or (2) are parity-sensitive (and the bounds you claim would also be parity sensitive if 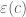 converged to any value other than I), because the weight
converged to any value other than I), because the weight 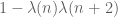 vanishes on twin primes. It is also clear that taking linear combinations of parity-insensitive inequalities weighted by sieve weights can only ever yield more parity-insensitive inequalities, no matter how cleverly one chooses the sieve weights and the linear combinations. As such, it is not possible to produce twin primes by sieve theoretic arguments, unless one uses an input that is parity sensitive, or if one is operating under a hypothesis (such as a Siegel zero hypothesis) that is incompatible with the Mobius pseudorandomness heuristic. If you are unable to identify the precise parity sensitive input or pseudorandomness-violating hypothesis in your argument, this is a very strong signal that your argument is not correct.
vanishes on twin primes. It is also clear that taking linear combinations of parity-insensitive inequalities weighted by sieve weights can only ever yield more parity-insensitive inequalities, no matter how cleverly one chooses the sieve weights and the linear combinations. As such, it is not possible to produce twin primes by sieve theoretic arguments, unless one uses an input that is parity sensitive, or if one is operating under a hypothesis (such as a Siegel zero hypothesis) that is incompatible with the Mobius pseudorandomness heuristic. If you are unable to identify the precise parity sensitive input or pseudorandomness-violating hypothesis in your argument, this is a very strong signal that your argument is not correct.
6 September, 2015 at 11:10 pm
Sergei
Thanks for this! Very enlightening.
7 September, 2015 at 5:15 am
Sergei
Is it right that it is unclear what happens with the asymptotic for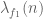 in the intermediate regime
in the intermediate regime  for various
for various  going to
going to  as
as  ?
?
7 September, 2015 at 8:19 am
Terence Tao
Depends on what you are trying to compute. A plain sum such as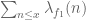 should still be computable because the constant function
should still be computable because the constant function  is extremely well distributed in arithmetic progressions. However a sum such as
is extremely well distributed in arithmetic progressions. However a sum such as 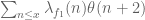 becomes very tricky, it involves understanding the distribution of
becomes very tricky, it involves understanding the distribution of 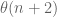 in arithmetic progressions of spacing up to
in arithmetic progressions of spacing up to  and it is known that the Elliott-Halberstam conjecture breaks down for
and it is known that the Elliott-Halberstam conjecture breaks down for  sufficiently close to 1, see the work of Friedlander and Granville. It may still be possible to use a strong version of pseudorandomness hypotheses though (e.g. Montgomery’s conjecture on the error term in the prime number theorem in arithmetic progressions) to predict what happens. Of course in the limit
sufficiently close to 1, see the work of Friedlander and Granville. It may still be possible to use a strong version of pseudorandomness hypotheses though (e.g. Montgomery’s conjecture on the error term in the prime number theorem in arithmetic progressions) to predict what happens. Of course in the limit 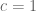 ,
,  is essentially the von Mangoldt function, which is sensitive to
is essentially the von Mangoldt function, which is sensitive to 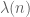 in contrast to the
in contrast to the 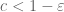 cases, so there must be some transition behaviour at some point.
cases, so there must be some transition behaviour at some point.
27 August, 2015 at 8:08 am
Will
Yes, the heuristic that the primes are distributed randomly (e.g. the Cramer model) suggests that the error term for the prime number theorem in arithmetic progressions is , which implies no Siegel zeros.
, which implies no Siegel zeros.
27 August, 2015 at 10:24 am
David Speyer
Minor suggestion: Friedlander and Iwaniec is available freely and legally online http://www.ams.org/notices/200907/rtx090700817p.pdf , but your link requires MathSciNet access. You might want to switch to the free one.
[Link changed, thanks – T.]
27 August, 2015 at 11:13 am
David Speyer
By the way, I’d enjoy a blogpost laying out what the alternative “ghostly” world looks like. I’ve picked it up in bits and pieces from your posts on the parity problem and other sources, but it would be interesting to see it all in one place, laid out as a consistent alternative.
28 August, 2015 at 8:51 am
meditationatae
I find it very stimulating that you write about this “unlikely” “alternate universe”. I can recognize terminology (e.g. “damping” ) used in sieve theory, that is also common in electronic filter terminology (signal processing). Is this semblance of an analogy between filters and sieves worthy of some consideration by students or non-specialists of analytic number theory?
31 August, 2015 at 3:05 am
Anonymous
It is interesting to observe that the (hypothetical) asymptotic orthogonality of the Mobius function to all “structured” functions does not contradict the fact that
to all “structured” functions does not contradict the fact that  has bounded algorithmic complexity.
has bounded algorithmic complexity.
31 August, 2015 at 5:27 am
meditationatae
It was my first encounter with Heath-Brown’s theorem. I’d like to know if there are heuristics or other things that give hope to analytic number theorists concerning which of (a) Twin Prime Conjecture, or (b) “No Siegel zeros”, “should” be the least difficult to prove?
26 March, 2023 at 5:26 am
TK
Rather than focusing only on Siegel zeros, i think it would be interesting to investigate the consequences of the existence of any infinite sequence of non-real zeros whose real parts converge to 1. Such zeros actually seem to exist. Kindly see:
https://figshare.com/articles/preprint/Untitled_Item/14776146
26 March, 2023 at 8:06 am
Anonymous
same nonsense as before (same issues – forgetting dependencies)
26 March, 2023 at 10:21 am
TK
Saying words like “nonsense” doesn’t make your comment any stronger or sensible. What exactly are the dependencies are you talking about ? Be explicitly clear.
26 March, 2023 at 10:47 am
Walfisz
@Anonymous, you’re probably referring to the implicit constant in (4) being dependent on epsilon, so that it may tend to infinity as epsilon tends to 0. However, that only becomes relevant if the author does let epsilon tend to 0.
Haven’t carefully checked other details, but the issue, if there is one, is definitely not on the the dependencies.
In short, you’re the one saying nonsense here.
27 March, 2023 at 10:32 am
Anonymous
the flaw has been detailed on MJR (when you truncate a convergent Dirichlet series at some fixed $x$ the remainder depends on both $s$ and $x$ and while it is true that for $s$ FIXED, the remainder goes to 0 when x to infinity, it is not true that happens uniformly in s so in particular for fixed x the remainder can be quite large when Im s is much larger – an easy example is t^(1/2)/x which goes to zero for fixed t when x goes to infinity but its integral in t is bigger than 1 as long as t is larger than x – this is essentially what happens in the Dirichlet case when uniform remainders are available precisely for x >> t= Im s only
29 March, 2023 at 9:52 pm
TK
Okay thanks, but the crux of the argument here, is not the estimate of the remainder term. Rather, it’s the summation in (1), which, if Theta_{\chi} <1, creates a generalised Dirichlet eta function in the integrand.
In the calculations, we can actually work with the exact definition of E(x) = E(x, s, \overline{\chi}).
29 March, 2023 at 11:28 pm
TK
**Definitions.** Let: be the Mobius function,
be the Mobius function, 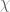 be a primitive Dirichlet character of modulus
be a primitive Dirichlet character of modulus  and
and ![\Theta_{\chi} \in [\frac{1}{2}, 1]](https://s0.wp.com/latex.php?latex=%5CTheta_%7B%5Cchi%7D+%5Cin+%5B%5Cfrac%7B1%7D%7B2%7D%2C+1%5D&bg=ffffff&fg=545454&s=0&c=20201002) be the supremum of the real parts of the zeros of
be the supremum of the real parts of the zeros of  . Define
. Define 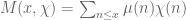 and
and  . Let
. Let 
**Theorem 1.** *One has for every
for every 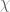 .*
.*
**PROOF.** Suppose that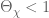 for some
for some 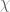 , and let
, and let 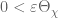 , it follows by Perron’s formula (Theorem 5.2 of
, it follows by Perron’s formula (Theorem 5.2 of
Montgomery-Vaughan (M.V.)) that
$
latex \displaystyle $/p>
Multiplying both sides of (1) by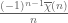 and summing from
and summing from 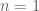 to
to 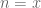 gives
gives
$ latex \displaystyle $
Since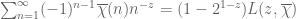 for $\Re(z) >0$, note that at
for $\Re(z) >0$, note that at 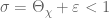 , we have
, we have
$ we have
we have 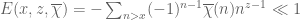 uniformly for
uniformly for 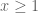 . Inserting (3) into the right-hand side of (2) gives
. Inserting (3) into the right-hand side of (2) gives
latex \displaystyle $
where for
$
latex \displaystyle
$/p>
Let if
if  , and
, and  if
if  . Let
. Let  be a zero of
be a zero of  of order
of order  , where
, where  . Similarly, the integrand of the second integral has: simple poles at
. Similarly, the integrand of the second integral has: simple poles at 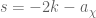 with residue
with residue  , poles of order
, poles of order  at
at  with residue
with residue 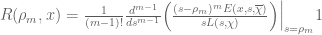 . Let
. Let  be a non-integer, so that
be a non-integer, so that  . For
. For  and
and  , note that
, note that  [M.V., pp. 330 and 334] and
[M.V., pp. 330 and 334] and 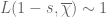 hence
hence 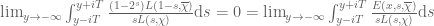 . Thus by shifting the line of integration in (4) to
. Thus by shifting the line of integration in (4) to  and applying the residue theorem, we obtain
and applying the residue theorem, we obtain
$
latex \displaystyle
f(x)&=\sum_{k=b_{\chi}}^{\infty} (g(k) + h(k)) + \sum_{|\Im(\rho_m)| \leq T} R(\rho_{m}, x) + \frac{E(x, 0, \overline{\chi})}{L(0,\chi)} + O(x^{1+\varepsilon}/T) \tag{5} \\
&= -\sum_{k=b_\chi}^{\infty}\Bigg( \frac{(1-2^{-2k-a_{\chi}})L(2k+1+a_{\chi}, \overline{\chi})}{2k+a_{\chi}} + \frac{E(x, -2k-a_{\chi})}{2k+a_{\chi}} \Bigg) + \sum_{|\Im(\rho_m)| \leq T} R(\rho_{m}, x) + O\Big(1 + \frac{x^{1+\varepsilon}}{T} \Big). \tag{6}
>$
Since $\latex R(\rho_m, x) x}\frac{(-1)^{n-1}\overline{\chi}(n)}{n^{2k+a_{\chi}+1}} \ll \sum_{n > x} n^{-2} \ll x^{-1}$ for every non-negative integer . Hence the summands of the first sum are
. Hence the summands of the first sum are  for any fixed large enough
for any fixed large enough  and all
and all 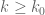 , thus the sum diverges as claimed. But we now have a contradiction, since
, thus the sum diverges as claimed. But we now have a contradiction, since  .
.
30 March, 2023 at 12:21 am
TK
Apparently, therearesomeLaTex typos in the previous comment. So, you may see the actual paper:
https://figshare.com/articles/preprint/Untitled_Item/14776146
30 April, 2023 at 2:19 am
Anonymous
@TK, it really seems you’ve actually disproved the RH. Have you submitted this anywhere yet?
30 April, 2023 at 10:19 am
Anonymous
Tk talking to TK – the wonders of sock pupetry
30 April, 2023 at 1:26 pm
Anonymous
TK haters, you should be ashamed of yourselves for hating on someone with such talent and passion as TK.
1 May, 2023 at 3:42 am
TK
@Anonymous: I submitted the paper to the Annals of Mathematics, but they’re yet to acknowledge receipt of the submission. However, I should mention that all the journals I submitted to before the Annals, returned the paper without any review comments. Some of the editors said that before submitting, I should discuss my work with some “experts”. But when I contact the “experts”, most of them suggest I send the work to some journal since it’s their job to review. I have therefore decided to post the work here, since the main result of the paper could be of relevance to this particular post.
1 May, 2023 at 11:28 am
Anonymous
Fun discussion between TK & David Farmer about this paper on MathOverflow:
https://mathoverflow.net/questions/445426/reference-request-for-pi-sum-im-rho-leq-t-n-rho-t-lambdan-o
Not sure it’s the David Farmer from AIM, though, given the ridiculously flawed comments he is posting.
1 May, 2023 at 3:56 pm
Anonymous
As usual, when someone took the time to show your errors, you reply with insults and nitpicking without actually thinking through what they say so do not be surprised that the number of people willing to engage is growing smaller and smaller;
1 May, 2023 at 10:36 pm
TK
Which insults?? Didn’t I objectively reply in the MO post with factual mathematical comments which you have obviously chosen to ignore to suit your narrative?
The claim that David Farmer made in the now deleted MO post, is that for![\gamma \in [T, 2T], f(T, \rho)=\sum_{n \leq \log T} (-1)^{n-1} n^{\rho-1}](https://s0.wp.com/latex.php?latex=%5Cgamma+%5Cin+%5BT%2C+2T%5D%2C+f%28T%2C+%5Crho%29%3D%5Csum_%7Bn+%5Cleq+%5Clog+T%7D+%28-1%29%5E%7Bn-1%7D+n%5E%7B%5Crho-1%7D&bg=ffffff&fg=545454&s=0&c=20201002) doesn’t converge as
doesn’t converge as  , but tbis is not rrue at all. Inded, here is an elementary argument why
, but tbis is not rrue at all. Inded, here is an elementary argument why 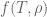 converges (to
converges (to 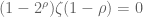 ) as
) as  tends to infinity.
tends to infinity.
Let and
and  . Then $ latex a_n$ decreases monotonically to 0 as
. Then $ latex a_n$ decreases monotonically to 0 as  tends to infinity, and
tends to infinity, and
$ latex |\sum_{n \leq log T} b_n| \leq 1$
for all . Thus by mimicking the proof of the Dirichlet convergence test:
. Thus by mimicking the proof of the Dirichlet convergence test:
https://en.m.wikipedia.org/wiki/Dirichlet%27s_test
one deduces that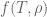 indeed converges (to
indeed converges (to  ) as
) as  tends to infinity. In particular, notice that this argument is independent of how large
tends to infinity. In particular, notice that this argument is independent of how large  is.
is.
1 May, 2023 at 10:55 pm
Walfisz
@Anonymous, please don’t impose your fallacious claims on TK. It’s a fact that converges as
converges as  , even if
, even if  .
.
2 May, 2023 at 2:05 pm
Anonymous
when the experts point out to you why you are wrong, it is a good idea to at least consider they may have a point; after all you have been provably shown to be wrong by the same experts you have been disparaging for 100 times or more and the same thing is here, confusion between uniform and nonuniform bounds; nothing to do with analytic number theory, just basic analysis
2 May, 2023 at 2:29 pm
TK
@David Farmer (commenting as “anonymous”, please vomment with your real name like I’m doing, as you informed me via email that you’re the most recent poster. Firstly, let it be known the public that you claimed via email yesterday that if the function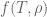 (which we can simply write as
(which we can simply write as  since
since 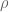 is a function of
is a function of  via
via 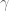 ) converges to 0 as
) converges to 0 as  tends to
tends to 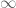 , then
, then  can be close to
can be close to  for infinitely many
for infinitely many  . You and I both know that you uttered this statement, and I had to endure the trouble of explaining to you why it’s elementarily wrong even by the standards of first year undergrad calculus. It’s quite funny that you’re here now calling yourself an “expert”, despite claims such as this. This is the very reason why it’s difficult for you to understand why
. You and I both know that you uttered this statement, and I had to endure the trouble of explaining to you why it’s elementarily wrong even by the standards of first year undergrad calculus. It’s quite funny that you’re here now calling yourself an “expert”, despite claims such as this. This is the very reason why it’s difficult for you to understand why 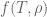 converges as
converges as  tends to
tends to 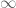 . Next time, please comment with yout real name, David Farmer.
. Next time, please comment with yout real name, David Farmer.
2 May, 2023 at 2:56 pm
John
For the benefit of some of us who didn’t see the now deleted MathOverflow post, can the constrictive critics please kindly point to us what exactly are you claiming to be the flaw? Surely, does converge independently of the magnitude of $|\rho|$ as
does converge independently of the magnitude of $|\rho|$ as  since
since 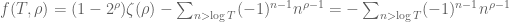 for all $T$.
for all $T$.
2 May, 2023 at 5:35 pm
Alvarez
@Anonymous, which uniform/non uniform bounds are you talking about? I seem not to see any issue with uniformity.
3 May, 2023 at 4:58 am
Anonymous
The paper got debunked for (it’s number 100 or so after all and pretty much every time we heard the same combination of insults and assured statements that now this time is surely, utterly and of course 100% right) and no number of sock puppets make it correct. The MO thread (put as usual under false pretenses) and comments clearly showed it; talking from thin air about arbitrary stuff doesn’t change it.
3 May, 2023 at 6:23 am
John
@Anonymous, seems you have no valid mathematic criticism against the paper, except trash-talking against it and referring to previous versions. You have been asked to pinpoint the exact flaw in the current two page version, but you’re still beating around the bush. Not to mention how your tone sounds extremely bitter, lol.
3 May, 2023 at 6:38 am
Alvarez
@Anonymous, it’s funny that you keep referring to the now non-existent MO post that some of is didn’t come across. We’re asking you again for the second time: what exactly are you claiming to be the flaw? Otherwise stop speaking nonsense against someone who is working hard to actually make a meaningful contribution to mathematics.
4 May, 2023 at 7:44 am
TK
The “issue” that was raised in the MathOverflow post is that, if , then
, then 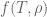 may not converge to
may not converge to  as
as  . However, this is not true.
. However, this is not true.
Indeed, fix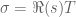 . Therefore, taking
. Therefore, taking 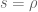 where
where  yields
yields 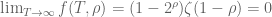 even if
even if  , as claimed. For the sake of completeness, I have added these details into the paper.
, as claimed. For the sake of completeness, I have added these details into the paper.
4 May, 2023 at 8:58 am
TK
There are some LaTex typos in the above comment as I’m not used to MathJax. But you can see the revised version of Figshare in which I added the said details for explaining why .
.
4 May, 2023 at 8:57 am
Anonymous
Good you put in details as they easily show how absurd your claim is since you take the limit of T to infinity and then claim that |\rho| >T; again same same (uniform vs pointwise), so nothing new; all debunked for the 100th time – looking forward to next try, though hopefully not too soon as it gets boring seeing same mistakes over and over
4 May, 2023 at 9:32 am
Peter
@Anonymous, why is it absurd that ? By the way, your choice of words should be more respectful. Your points do not become any stronger by trash-talking against the other person.
? By the way, your choice of words should be more respectful. Your points do not become any stronger by trash-talking against the other person.
4 May, 2023 at 7:07 pm
Alvarez
@Anonymous, it’s so annoying how you’re so arrogant and disrespectful, yet completely ignorant. And, how did your flawed comment get 10 upvotes almost instantly? Using a VPN to upvote your nonsense?
4 May, 2023 at 11:29 am
Walfisz
@Anonymous, don’t be too desperate to debunk a paper without carefully reading and understanding what is written. Equation (10) is clearly uniform in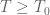 . The author then later takes
. The author then later takes  because that’s what’s relevant for the rest of the argument.
because that’s what’s relevant for the rest of the argument.
5 May, 2023 at 4:54 pm
Anonymous
Actually, there is a paper by Littlewood and Hardy whose methods can be easily adapted to show the divergence (when $T \to \infty$) of the sum $f(\rho(T), T)$ when $\rho(T) =\sigma +it, \sigma \le 1/2$ and $t$ around $T$ as D. Farmer mentioned on MO; the careless notation which doesn’t make it clear that the $\rho$ in your sum depends on $T$ (at least if you want to take $T \to \infty$ and $|\rho| >T$) obscures this
6 May, 2023 at 12:12 am
John
@Anonymous, actually, one can easily adapt the methods of the proof of Theorem 2.5 of Titchamarsh’s “The Theory of the Riemann zeta functio n”, to prove that if![I\Im(s)| \in [T, 2T]](https://s0.wp.com/latex.php?latex=I%5CIm%28s%29%7C+%5Cin+%5BT%2C+2T%5D&bg=ffffff&fg=545454&s=0&c=20201002) , then
, then  converges to
converges to 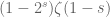 as
as  .
.
15 May, 2023 at 6:37 am
TK
The more proper way to say it, is
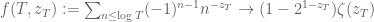 as
as  . I find that the quantitative version of Perron’s formula (Theorem 5.2 of Montgomery-Vaughan), provides a more straightforward approach to prove this.
. I find that the quantitative version of Perron’s formula (Theorem 5.2 of Montgomery-Vaughan), provides a more straightforward approach to prove this. and note that
and note that  for $\Re(s)>0$. Thus by the quantitative version of Perron’s formula, we have
for $\Re(s)>0$. Thus by the quantitative version of Perron’s formula, we have
Indeed, define
Notice that the above integrand has a meromorphic continuation to the entire complex plane, with only a simple pole at
Hence from the above two displayed equations with
15 May, 2023 at 6:41 am
TK
For the sake of completeness, i have included the above argument in the paper, as a separate Lemma:
https://figshare.com/articles/preprint/Untitled_Item/14776146
1 September, 2015 at 5:02 pm
John Mangual
The points on the hyperbola look equidistributed to me. How is this connected to Möbius pseudorandomness?
look equidistributed to me. How is this connected to Möbius pseudorandomness?

5 September, 2015 at 7:39 am
Anonymous
Are there some general rules to design a sieve (which motivate the design of the multidimensional Selberg sieve and its variants)?
8 September, 2015 at 2:33 am
Boris Sklyar
“MATRIX DEFINITION” OF PRIME NUMBERS:
There are two 2-dimensional arrays:
……………………………|5 10 15 20 ..|
6i^2-1+(6i-1)(j-1)=…..|23 34 45 56…|
……………………………|53 70 87 104…|
…………………………..|95 118 141 164…|
…………………………..|149 178 207 236…|
…………………………..|… … … … |
…………………………….| 5 12 19 26 ..|
6i^2-1+(6i+1)(j-1) =….|23 36 49 62…|
…………………………….|53 72 91 110…|
……………………………..|95 120 145 170…|
……………………………..|149 180 211 242…|
……………………………|… … … … |
Positive integers not contained in these arrays are indexes p of all prime numbers in the sequence S1(p)=6p+5, i.e. p=0, 1, 2, 3, 4, , 6, 7, 8, 9, , 11, , 13, 14, , 16, 17, 18, , , 21, 22, , 24, , , 27, 28, 29, …
and primes are: 5, 11, 17. 23, 29, , 41, 47, 53, 59, , 71, , 83, 89, , 101, 107, 113, , , 131, 137, , 149, , , 167, 173, 179, ….
There are two 2-dimensional arrays:
………………………………. |3 8 13 18 ..|
6i^2-1-2i+(6i-1)(j-1)=….. |19 30 41 52…|
…………………………………|47 64 81 98…|
…………………………………|87 110 133 156…|
…………………………………|139 168 197 226…|
…………………………………|… … … … |
……………………………….. | 7 14 21 28 ..|
6i^2-1+2i+(6i+1)(j-1)=…..|27 40 53 66…|
………………………………….|59 78 97 116..|
………………………………….|103 128 153 178..|
………………………………….|159 190 221 252..|
………………………………….|… … … … … |
Positive integers not contained in these arrays are indexes p of all prime numbers in the sequence S2(p)=6p+7, i.e. p=0, 1, 2, , 4, 5, 6, , , 9, 10, 11, 12, , , 15 , 16, 17, , , 20, , 22, , 24, 25 , 26, , , 29, …
and primes are: 7, 13, 19. , 31, 37, 43, , , 61, 67, 73, 79, , , 97, 103, 109, , , 127, , 139, , 151, 157, 163, , , 181 ….
,
http://ijmcr.in/index.php/current-issue/86-title-matrix-sieve-new-algorithm-for-finding-prime-numbers
http://www.planet-source-code.com/vb/scripts/ShowCode.asp?txtCodeId=13752&lngWId=3
9 September, 2015 at 8:38 am
Anonymous
(twin prime conjecture).
all twins prime it is the form.
Always that: .
.
9 September, 2015 at 12:24 pm
Boris Sklyar
Twin primes conjecture.
N1, N2 – primes, N2-N1=2;
N1 always belongs to the sequence S1(p)=6p+5; p = 0, 1, 2, …
N2 always belongs to the sequence S2(q)=6q+7; q = 0, 1, 2, …
When p=q; N1, N2 — are twin primes.
Twin primes condition:
Odd positive integers N1 =6p+5 and N2=6p+7 are twin primes if and only if
no one of four diophantine equations has solution;
6x^2-1 + (6x -1)y=p
6x^2-1 + (6x +1)y=p
6x^2-1 – 2x+(6x -1)y=p
6x^2-1 +2x +(6x+1)y=p
x =1,2,3,..
y=0,1,2….
0 0 Rate This
12 April, 2016 at 7:53 am
Anonymous
At the start of the proof if Lemma 5, it says for each fixed natural number n. Should the n be a k?
Also, in the paragraph that starts with: We begin with (13), there is an inequality with \chi(p) between two powers of x. I believe it should be p, as that is what is used in later lines.
[Corrected, thanks – T.]
28 July, 2017 at 8:29 pm
primenumbers
We will go on to show that the distribution of prime numbers may be best visualized in two-dimensional space.
28 July, 2017 at 8:35 pm
primenumbers
We advance our analysis with the extension of division to the divisor 3in the simplifiedprime number analysis introduced earlier.
10 May, 2019 at 8:37 am
The alternative hypothesis for unitary matrices | What's new
[…] which differs from (13) for any . (This fact was implicitly observed recently by Baluyot, in the original context of the zeta function.) Thus a verification of the pair correlation conjecture (17) for even a single with would rule out the alternative hypothesis. Unfortunately, such a verification appears to be on comparable difficulty with (an averaged version of) the Hardy-Littlewood conjecture, with power saving error term. (This is consistent with the fact that Siegel zeroes can cause distortions in the Hardy-Littlewood conjecture, as (implicitly) discussed in this previous blog post.) […]
28 May, 2020 at 1:43 pm
ES
The function introduced in (11) is remarked to be supported on integers whose prime factors satisfy
introduced in (11) is remarked to be supported on integers whose prime factors satisfy 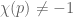 . But if
. But if 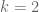 and
and  and
and 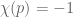 then
then  . Or is the support claim only valid when
. Or is the support claim only valid when 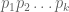 square-free ?
square-free ?
[Corrected, thanks – T.]
1 June, 2020 at 9:24 am
ES
Equation (19) needs .
.
[Added, thanks – T.]
24 June, 2020 at 11:26 am
ES
It looks like in the equation after “Standard sieve theory then gives” should contain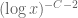 instead of
instead of  as the length of the interval is
as the length of the interval is  and the sieve is of dimension
and the sieve is of dimension 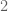 . I haven’t checked if this matters for later estimates.
. I haven’t checked if this matters for later estimates.
[Corrected, thanks – T.]
27 June, 2020 at 5:10 am
ES
Could I please ask any minor hint about the application of summation by parts in the last step of the proof of (24)?
30 June, 2020 at 12:30 pm
Terence Tao
We are trying to sum where
where  is the
is the  -periodic function
-periodic function ![a(k) := \chi(W[e,m]k/m_1 + a/m_1) \chi(W[e,m]k/m_2 + (a+2)/m_2)](https://s0.wp.com/latex.php?latex=a%28k%29+%3A%3D+%5Cchi%28W%5Be%2Cm%5Dk%2Fm_1+%2B+a%2Fm_1%29+%5Cchi%28W%5Be%2Cm%5Dk%2Fm_2+%2B+%28a%2B2%29%2Fm_2%29&bg=ffffff&fg=545454&s=0&c=20201002) and
and 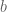 is the slowly varying function
is the slowly varying function 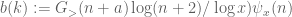 with
with ![n = W[e,m]k+a](https://s0.wp.com/latex.php?latex=n+%3D+W%5Be%2Cm%5Dk%2Ba&bg=ffffff&fg=545454&s=0&c=20201002) . The function
. The function 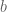 is supported on an interval of length
is supported on an interval of length ![O( x/[e,m] )](https://s0.wp.com/latex.php?latex=O%28+x%2F%5Be%2Cm%5D+%29&bg=ffffff&fg=545454&s=0&c=20201002) (we omit the bounded
(we omit the bounded  factor here) and has total variation
factor here) and has total variation 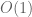 , hence by summation by parts this sum is bounded by
, hence by summation by parts this sum is bounded by 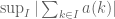 where
where 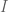 ranges over intervals of length
ranges over intervals of length ![O(x/[e,m])](https://s0.wp.com/latex.php?latex=O%28x%2F%5Be%2Cm%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . Splitting
. Splitting 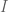 into intervals of length
into intervals of length  plus a remainder and using the bound from Lemma 3, this is
plus a remainder and using the bound from Lemma 3, this is ![O( x^{o(1)} x/q[e,m] + q )](https://s0.wp.com/latex.php?latex=O%28+x%5E%7Bo%281%29%7D+x%2Fq%5Be%2Cm%5D+%2B+q+%29&bg=ffffff&fg=545454&s=0&c=20201002) and the latter term is negligible if
and the latter term is negligible if  is large enough.
is large enough.
10 July, 2020 at 12:13 pm
ES
Many thanks!
10 July, 2020 at 12:12 pm
ES
A harmless typo: the first display after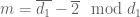 is missing
is missing  .
.
[Corrected, thanks -T.]
15 July, 2020 at 3:17 pm
ES
There is something strange in the second application of Poisson’s summation formula just before the start of the proof of (22). To use the Kloosterman bound I am guessing the text suggestion is to partition in congruence classes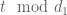 and for each such
and for each such  we have a sum of (something which is essentially)
we have a sum of (something which is essentially)  over all integers
over all integers  which is estimated with Poisson. Because of the presence of
which is estimated with Poisson. Because of the presence of  within
within 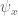 I think there is a problem in getting the error term claimed though. We are counting integers
I think there is a problem in getting the error term claimed though. We are counting integers 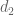 of size
of size  in a progression modulo
in a progression modulo  and in the cases where
and in the cases where  one cannot hope to get good errors by Poisson (or otherwise?). Perhaps I am missing something?
one cannot hope to get good errors by Poisson (or otherwise?). Perhaps I am missing something?
17 July, 2020 at 6:16 pm
Terence Tao
One should perform an inverse Fourier expansion of into characters a linear combination of characters
into characters a linear combination of characters  and then apply the Poisson summation formula in
and then apply the Poisson summation formula in 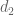 to the resulting sums to express things in terms of Fourier integrals such as
to the resulting sums to express things in terms of Fourier integrals such as  . The
. The  cutoff is fairly harmless, it is the
cutoff is fairly harmless, it is the  cutoff that provides the main contribution of
cutoff that provides the main contribution of  , but only when
, but only when  is close to an integer, which basically only happens for a single choice of
is close to an integer, which basically only happens for a single choice of  .
.
20 July, 2020 at 6:48 am
ES
Thank you very much for all the time and explanations so far! One last question: when the proof of (22) starts there is another Poisson summation happening. But the main term coming from the central coefficient doesn’t seem to take into account that![[d,e]](https://s0.wp.com/latex.php?latex=%5Bd%2Ce%5D&bg=ffffff&fg=545454&s=0&c=20201002) divides
divides  . In my calculations it looks like one should have
. In my calculations it looks like one should have ![2^{\omega[d,e]}/[d,e]](https://s0.wp.com/latex.php?latex=2%5E%7B%5Comega%5Bd%2Ce%5D%7D%2F%5Bd%2Ce%5D&bg=ffffff&fg=545454&s=0&c=20201002) instead of
instead of ![1/[d,e]](https://s0.wp.com/latex.php?latex=1%2F%5Bd%2Ce%5D&bg=ffffff&fg=545454&s=0&c=20201002) . I may be missing something though. But if that is correct then the main term should behave as
. I may be missing something though. But if that is correct then the main term should behave as  instead of
instead of 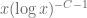 . Again, I am sorry if this is not accurate!
. Again, I am sorry if this is not accurate!
20 July, 2020 at 6:42 pm
Terence Tao
There were some summations in missing in these displays that have now been corrected. The prime factorization of
missing in these displays that have now been corrected. The prime factorization of ![[d,e]](https://s0.wp.com/latex.php?latex=%5Bd%2Ce%5D&bg=ffffff&fg=545454&s=0&c=20201002) does not affect this summation as it is coprime to
does not affect this summation as it is coprime to  .
.
20 July, 2020 at 10:10 pm
ES
Thank you for the summations! But I was alluding to the fact that the condition![[d,e] \mid n(n+2)](https://s0.wp.com/latex.php?latex=%5Bd%2Ce%5D+%5Cmid+n%28n%2B2%29&bg=ffffff&fg=545454&s=0&c=20201002) should give rise to a missing term
should give rise to a missing term ![2^{\omega([d,e])}](https://s0.wp.com/latex.php?latex=2%5E%7B%5Comega%28%5Bd%2Ce%5D%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) on the right-hand side of the first equation after “From Poisson summation one then has”.
on the right-hand side of the first equation after “From Poisson summation one then has”.
21 July, 2020 at 9:43 am
Terence Tao
Ah, I see the issue now. The main term is indeed one power of smaller than claimed (which in retrospect was clear from probabilistic heuristics such as the Cramer model), and all the error bounds have to be improved by a factor of
smaller than claimed (which in retrospect was clear from probabilistic heuristics such as the Cramer model), and all the error bounds have to be improved by a factor of  accordingly. In fact now that I see it I had wasted a factor of
accordingly. In fact now that I see it I had wasted a factor of  anyway in the proof of (19) so the two errors ended up cancelinc each other out. The post has now been updated with the correct powers of $\log x$ and other appropriate changes.
anyway in the proof of (19) so the two errors ended up cancelinc each other out. The post has now been updated with the correct powers of $\log x$ and other appropriate changes.
15 September, 2021 at 11:10 am
The Hardy–Littlewood–Chowla conjecture in the presence of a Siegel zero | What's new
[…] primes in the indicated range ; this bound is non-trivial for as large as . (See Section 1 of this blog post for some variants of this argument, which were inspired by work of Heath-Brown.) There is also a […]
14 September, 2023 at 7:59 am
Anonymous
Dear prof. Tao,
If we replaced Lambda_2 simply with von Mangoldt function, the argument obviously wouldn’t work anymore, but I have a trouble detecting what part of the proof should crumble. Apparently, in the section concerning the decomposition into G the precise shape of these functions does not have any particular significance provided that the supports are sufficiently restricted. May you give me some hint?
Best regards!
14 September, 2023 at 2:39 pm
Terence Tao
In the very last line of the argument, it is needed that the second derivative of is positive.
is positive.
15 September, 2023 at 2:10 am
Anonymous
Oh, I see! Thanks a lot.