Many problems and results in analytic prime number theory can be formulated in the following general form: given a collection of (affine-)linear forms , none of which is a multiple of any other, find a number
such that a certain property
of the linear forms
are true. For instance:
- For the twin prime conjecture, one can use the linear forms
,
, and the property
in question is the assertion that
and
are both prime.
- For the even Goldbach conjecture, the claim is similar but one uses the linear forms
,
for some even integer
.
- For Chen’s theorem, we use the same linear forms
as in the previous two cases, but now
is the assertion that
is prime and
is an almost prime (in the sense that there are at most two prime factors).
- In the recent results establishing bounded gaps between primes, we use the linear forms
for some admissible tuple
, and take
to be the assertion that at least two of
are prime.
For these sorts of results, one can try a sieve-theoretic approach, which can broadly be formulated as follows:
- First, one chooses a carefully selected sieve weight
, which could for instance be a non-negative function having a divisor sum form
for some coefficients
, where
is a natural scale parameter. The precise choice of sieve weight is often quite a delicate matter, but will not be discussed here. (In some cases, one may work with multiple sieve weights
.)
- Next, one uses tools from analytic number theory (such as the Bombieri-Vinogradov theorem) to obtain upper and lower bounds for sums such as
or
or more generally of the form
whereis some “arithmetic” function involving the prime factorisation of
(we will be a bit vague about what this means precisely, but a typical choice of
might be a Dirichlet convolution
of two other arithmetic functions
).
- Using some combinatorial arguments, one manipulates these upper and lower bounds, together with the non-negative nature of
, to conclude the existence of an
in the support of
(or of at least one of the sieve weights
being considered) for which
holds
For instance, in the recent results on bounded gaps between primes, one selects a sieve weight for which one has upper bounds on
and lower bounds on
so that one can show that the expression
is strictly positive, which implies the existence of an in the support of
such that at least two of
are prime. As another example, to prove Chen’s theorem to find
such that
is prime and
is almost prime, one uses a variety of sieve weights to produce a lower bound for
and an upper bound for
and
where is some parameter between
and
, and “rough” means that all prime factors are at least
. One can observe that if
, then there must be at least one
for which
is prime and
is almost prime, since for any rough number
, the quantity
is only positive when is an almost prime (if
has three or more factors, then either it has at least two factors less than
, or it is of the form
for some
). The upper and lower bounds on
are ultimately produced via asymptotics for expressions of the form (1), (2), (3) for various divisor sums
and various arithmetic functions
.
Unfortunately, there is an obstruction to sieve-theoretic techniques working for certain types of properties , which Zeb Brady and I recently formalised at an AIM workshop this week. To state the result, we recall the Liouville function
, defined by setting
whenever
is the product of exactly
primes (counting multiplicity). Define a sign pattern to be an element
of the discrete cube
. Given a property
of
natural numbers
, we say that a sign pattern
is forbidden by
if there does not exist any natural numbers
obeying
for which
Example 1 Let
be the property that at least two of
are prime. Then the sign patterns
,
,
,
are forbidden, because prime numbers have a Liouville function of
, so that
can only occur when at least two of
are equal to
.
Example 2 Let
be the property that
is prime and
is almost prime. Then the only forbidden sign patterns are
and
.
Example 3 Let
be the property that
and
are both prime. Then
are all forbidden sign patterns.
We then have a parity obstruction as soon as has “too many” forbidden sign patterns, in the following (slightly informal) sense:
Claim 1 (Parity obstruction) Suppose
is such that that the convex hull of the forbidden sign patterns of
contains the origin. Then one cannot use the above sieve-theoretic approach to establish the existence of an
such that
holds.
Thus for instance, the property in Example 3 is subject to the parity obstruction since is a convex combination of
and
, whereas the properties in Examples 1, 2 are not. One can also check that the property “at least
of the
numbers
is prime” is subject to the parity obstruction as soon as
. Thus, the largest number of elements of a
-tuple that one can force to be prime by purely sieve-theoretic methods is
, rounded up.
This claim is not precisely a theorem, because it presumes a certain “Liouville pseudorandomness conjecture” (a very close cousin of the more well known “Möbius pseudorandomness conjecture”) which is a bit difficult to formalise precisely. However, this conjecture is widely believed by analytic number theorists, see e.g. this blog post for a discussion. (Note though that there are scenarios, most notably the “Siegel zero” scenario, in which there is a severe breakdown of this pseudorandomness conjecture, and the parity obstruction then disappears. A typical instance of this is Heath-Brown’s proof of the twin prime conjecture (which would ordinarily be subject to the parity obstruction) under the hypothesis of a Siegel zero.) The obstruction also does not prevent the establishment of an such that
holds by introducing additional sieve axioms beyond upper and lower bounds on quantities such as (1), (2), (3). The proof of the Friedlander-Iwaniec theorem is a good example of this latter scenario.
Now we give a (slightly nonrigorous) proof of the claim.
Proof: (Nonrigorous) Suppose that the convex hull of the forbidden sign patterns contain the origin. Then we can find non-negative numbers for sign patterns
, which sum to
, are non-zero only for forbidden sign patterns, and which have mean zero in the sense that
for all . By Fourier expansion (or Lagrange interpolation), one can then write
as a polynomial
where is a polynomial in
variables that is a linear combination of monomials
with
and
(thus
has no constant or linear terms, and no monomials with repeated terms). The point is that the mean zero condition allows one to eliminate the linear terms. If we now consider the weight function
then is non-negative, is supported solely on
for which
is a forbidden pattern, and is equal to
plus a linear combination of monomials
with
.
The Liouville pseudorandomness principle then predicts that sums of the form
and
or more generally
should be asymptotically negligible; intuitively, the point here is that the prime factorisation of should not influence the Liouville function of
, even on the short arithmetic progressions that the divisor sum
is built out of, and so any monomial
occurring in
should exhibit strong cancellation for any of the above sums. If one accepts this principle, then all the expressions (1), (2), (3) should be essentially unchanged when
is replaced by
.
Suppose now for sake of contradiction that one could use sieve-theoretic methods to locate an in the support of some sieve weight
obeying
. Then, by reweighting all sieve weights by the additional multiplicative factor of
, the same arguments should also be able to locate
in the support of
for which
holds. But
is only supported on those
whose Liouville sign pattern is forbidden, a contradiction.
Claim 1 is sharp in the following sense: if the convex hull of the forbidden sign patterns of do not contain the origin, then by the Hahn-Banach theorem (in the hyperplane separation form), there exist real coefficients
such that
for all forbidden sign patterns and some
. On the other hand, from Liouville pseudorandomness one expects that
is negligible (as compared against for any reasonable sieve weight
. We conclude that for some
in the support of
, that
and hence is not a forbidden sign pattern. This does not actually imply that
holds, but it does not prevent
from holding purely from parity considerations. Thus, we do not expect a parity obstruction of the type in Claim 1 to hold when the convex hull of forbidden sign patterns does not contain the origin.
Example 4 Let
be a graph on
vertices
, and let
be the property that one can find an edge
of
with
both prime. We claim that this property is subject to the parity problem precisely when
is two-colourable. Indeed, if
is two-colourable, then we can colour
into two colours (say, red and green) such that all edges in
connect a red vertex to a green vertex. If we then consider the two sign patterns in which all the red vertices have one sign and the green vertices have the opposite sign, these are two forbidden sign patterns which contain the origin in the convex hull, and so the parity problem applies. Conversely, suppose that
is not two-colourable, then it contains an odd cycle. Any forbidden sign pattern then must contain more
s on this odd cycle than
s (since otherwise two of the
s are adjacent on this cycle by the pigeonhole principle, and this is not forbidden), and so by convexity any tuple in the convex hull of this sign pattern has a positive sum on this odd cycle. Hence the origin is not in the convex hull, and the parity obstruction does not apply. (See also this previous post for a similar obstruction ultimately coming from two-colourability).
Example 5 An example of a parity-obstructed property (supplied by Zeb Brady) that does not come from two-colourability: we let
be the property that
are prime for some collection
of pair sets that cover
. For instance, this property holds if
are both prime, or if
are all prime, but not if
are the only primes. An example of a forbidden sign pattern is the pattern where
are given the sign
, and the other three pairs are given
. Averaging over permutations of
we see that zero lies in the convex hull, and so this example is blocked by parity. However, there is no sign pattern such that it and its negation are both forbidden, which is another formulation of two-colourability.
Of course, the absence of a parity obstruction does not automatically mean that the desired claim is true. For instance, given an admissible -tuple
, parity obstructions do not prevent one from establishing the existence of infinitely many
such that at least three of
are prime, however we are not yet able to actually establish this, even assuming strong sieve-theoretic hypotheses such as the generalised Elliott-Halberstam hypothesis. (However, the argument giving (4) does easily give the far weaker claim that there exist infinitely many
such that at least three of
have a Liouville function of
.)
Remark 1 Another way to get past the parity problem in some cases is to take advantage of linear forms that are constant multiples of each other (which correlates the Liouville functions to each other). For instance, on GEH we can find two
numbers (products of exactly three primes) that differ by exactly
; a direct sieve approach using the linear forms
fails due to the parity obstruction, but instead one can first find
such that two of
are prime, and then among the pairs of linear forms
,
,
one can find a pair of
numbers that differ by exactly
. See this paper of Goldston, Graham, Pintz, and Yildirim for more examples of this type.
I thank John Friedlander and Sid Graham for helpful discussions and encouragement.

12 comments
Comments feed for this article
22 November, 2014 at 3:19 am
Anonymous
typo: near the beginning of the blog, missing “can” in “…which broadly be formulated as follows…”
[Corrected, thanks – T.]
22 November, 2014 at 5:00 am
Anonymous
Dear Pro.Terry,may I ask you a question burdened of psychology. I think I miss all mathematician’s life that they contributed 1 or 2 breakthough tools to human.They spended 20 years or over only discovering a huge tool before they die.If a tool that costs much time like ,that,so the rest of 6 best proble ms of Clay maybe cost nearly 1000 years.So, could you arrange of the difficult level of 6 that problems.I imagine someone like superman can solve them only within 30 year.Maybe I am crazy,but I always wait this become true.
years..Sould you arrange the order of difficult level of
23 November, 2014 at 9:46 am
arch1
In the paragraph following Claim 1, in the sentence “One can also check that the property ‘at least {j} of the {k} numbers {l_1,\dots,l_k}’ are subject to the parity obstruction…,” the quoted property seems incomplete (e.g. it lacks a verb).
[Corrected, thanks – T.]
25 November, 2014 at 12:58 pm
arch1
In the proof of Claim 1, should the monomials instead be
instead be  ?
?
25 November, 2014 at 1:05 pm
arch1
Never mind:-)
26 November, 2014 at 10:33 pm
arch1
1) Where do you make use of the zero-mean property of the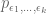 ?
?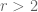 instead be
instead be  (or if not what happened to Q’s quadratic terms)?
(or if not what happened to Q’s quadratic terms)?
2) In the 3rd line after the definition of w(n), should
[Post edited to clarify (1) and correct (2) -T.]
17 March, 2015 at 10:16 pm
An averaged form of Chowla’s conjecture | What's new
[…] is a variant of the twin prime conjecture (though possibly a tiny bit easier to prove), and is subject to the notorious parity barrier (as discussed in this previous post). […]
18 March, 2015 at 8:26 am
Kurt Lovelace
Reblogged this on Inbetween Math and Poetry.
26 August, 2015 at 4:24 pm
Heath-Brown’s theorem on prime twins and Siegel zeroes | What's new
[…] them from other twins of almost primes. The parity problem is discussed in these previous blog posts; this obstruction is ultimately powered by the Möbius pseudorandomness principle that asserts […]
18 September, 2015 at 4:46 pm
The logarithmically averaged Chowla and Elliott conjectures for two-point correlations; the Erdos discrepancy problem | What's new
[…] as (2) or (3) are known to be subject to the “parity problem” (discussed numerous times previously on this blog), which roughly speaking means that they cannot be proven solely using […]
19 December, 2018 at 10:01 am
Lev
Is it possible to somehow break parity phenomenon for certain prime pairs (differing by 60, say) by a cooperation of Remark 1 and Bombieri sieve?
As far as I know, we are able to produce pairs of E_3-numbers which differs by 60, but 60 is the lowest such a positive integer right now, isn’t it?
Best regards!
19 December, 2018 at 2:06 pm
Terence Tao
Not with current methods. The trick of using reducible linear forms can only generate almost primes that contain very small prime factors such as 2,3,5, and these are a zero density subset of the almost primes and so cannot be picked up by sieves such as the Bombieri sieve (indeed one of the very first things such sieves do is throw out all numbers that are divisible by very small primes).
Basically, numbers which are divisible by very small primes are totally unhelpful for finding primes, but they are can technically still be (say)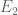 or
or  numbers, which is why the Remark 1 loophole around the parity problem can be used for problems involving such classes of numbers, but not for the primes themselves.
numbers, which is why the Remark 1 loophole around the parity problem can be used for problems involving such classes of numbers, but not for the primes themselves.