We will shortly turn to the complex-analytic approach to multiplicative number theory, which relies on the basic properties of complex analytic functions. In this supplement to the main notes, we quickly review the portions of complex analysis that we will be using in this course. We will not attempt a comprehensive review of this subject; for instance, we will completely neglect the conformal geometry or Riemann surface aspect of complex analysis, and we will also avoid using the various boundary convergence theorems for Taylor series or Dirichlet series (the latter type of result is traditionally utilised in multiplicative number theory, but I personally find them a little unintuitive to use, and will instead rely on a slightly different set of complex-analytic tools). We will also focus on the “local” structure of complex analytic functions, in particular adopting the philosophy that such functions behave locally like complex polynomials; the classical “global” theory of entire functions, while traditionally used in the theory of the Riemann zeta function, will be downplayed in these notes. On the other hand, we will play up the relationship between complex analysis and Fourier analysis, as we will incline to using the latter tool over the former in some of the subsequent material. (In the traditional approach to the subject, the Mellin transform is used in place of the Fourier transform, but we will not emphasise the role of the Mellin transform here.)
We begin by recalling the notion of a holomorphic function, which will later be shown to be essentially synonymous with that of a complex analytic function.
Definition 1 (Holomorphic function) Let
be an open subset of
, and let
be a function. If
, we say that
is complex differentiable at
if the limit
exists, in which case we refer to
as the (complex) derivative of
at
. If
is differentiable at every point
of
, and the derivative
is continuous, we say that
is holomorphic on
.
Exercise 2 Show that a function
is holomorphic if and only if the two-variable function
is continuously differentiable on
and obeys the Cauchy-Riemann equation
Basic examples of holomorphic functions include complex polynomials
as well as the complex exponential function
which are holomorphic on the entire complex plane (i.e., they are entire functions). The sum or product of two holomorphic functions is again holomorphic; the quotient of two holomorphic functions is holomorphic so long as the denominator is non-zero. Finally, the composition of two holomorphic functions is holomorphic wherever the composition is defined.
- (i) Establish Euler’s formula
for all
. (Hint: it is a bit tricky to do this starting from the trigonometric definitions of sine and cosine; I recommend either using the Taylor series formulations of these functions instead, or alternatively relying on the ordinary differential equations obeyed by sine and cosine.)
- (ii) Show that every non-zero complex number
has a complex logarithm
such that
, and that this logarithm is unique up to integer multiples of
.
- (iii) Show that there exists a unique principal branch
of the complex logarithm in the region
, defined by requiring
to be a logarithm of
with imaginary part between
and
. Show that this principal branch is holomorphic with derivative
.
In real analysis, we have the fundamental theorem of calculus, which asserts that
whenever is a real interval and
is a continuously differentiable function. The complex analogue of this fact is that
whenever is a holomorphic function, and
is a contour in
, by which we mean a piecewise continuously differentiable function, and the contour integral
for a continuous function
is defined via change of variables as
The complex fundamental theorem of calculus (2) follows easily from the real fundamental theorem and the chain rule.
In real analysis, we have the rather trivial fact that the integral of a continuous function on a closed contour is always zero:
In complex analysis, the analogous fact is significantly more powerful, and is known as Cauchy’s theorem:
Theorem 4 (Cauchy’s theorem) Let
be a holomorphic function in a simply connected open set
, and let
be a closed contour in
(thus
). Then
.
Exercise 5 Use Stokes’ theorem to give a proof of Cauchy’s theorem.
A useful reformulation of Cauchy’s theorem is that of contour shifting: if is a holomorphic function on a open set
, and
are two contours in an open set
with
and
, such that
can be continuously deformed into
, then
. A basic application of contour shifting is the Cauchy integral formula:
Theorem 6 (Cauchy integral formula) Let
be a holomorphic function in a simply connected open set
, and let
be a closed contour which is simple (thus
does not traverse any point more than once, with the exception of the endpoint
that is traversed twice), and which encloses a bounded region
in the anticlockwise direction. Then for any
, one has
Proof: Let be a sufficiently small quantity. By contour shifting, one can replace the contour
by the sum (concatenation) of three contours: a contour
from
to
, a contour
traversing the circle
once anticlockwise, and the reversal
of the contour
that goes from
to
. The contributions of the contours
cancel each other, thus
By a change of variables, the right-hand side can be expanded as
Sending , we obtain the claim.
The Cauchy integral formula has many consequences. Specialising to the case when traverses a circle
around
, we conclude the mean value property
whenever is holomorphic in a neighbourhood of the disk
. In a similar spirit, we have the maximum principle for holomorphic functions:
Lemma 7 (Maximum principle) Let
be a simply connected open set, and let
be a simple closed contour in
enclosing a bounded region
anti-clockwise. Let
be a holomorphic function. If we have the bound
for all
on the contour
, then we also have the bound
for all
.
Proof: We use an argument of Landau. Fix . From the Cauchy integral formula and the triangle inequality we have the bound
for some constant depending on
and
. This ostensibly looks like a weaker bound than what we want, but we can miraculously make the constant
disappear by the “tensor power trick“. Namely, observe that if
is a holomorphic function bounded in magnitude by
on
, and
is a natural number, then
is a holomorphic function bounded in magnitude by
on
. Applying the preceding argument with
replaced by
we conclude that
and hence
Sending , we obtain the claim.
Another basic application of the integral formula is
Corollary 8 Every holomorphic function
is complex analytic, thus it has a convergent Taylor series around every point
in the domain. In particular, holomorphic functions are smooth, and the derivative of a holomorphic function is again holomorphic.
Conversely, it is easy to see that complex analytic functions are holomorphic. Thus, the terms “complex analytic” and “holomorphic” are synonymous, at least when working on open domains. (On a non-open set , saying that
is analytic on
is equivalent to asserting that
extends to a holomorphic function of an open neighbourhood of
.) This is in marked contrast to real analysis, in which a function can be continuously differentiable, or even smooth, without being real analytic.
Proof: By translation, we may suppose that . Let
be a a contour traversing the circle
that is contained in the domain
, then by the Cauchy integral formula one has
for all in the disk
. As
is continuously differentiable (and hence continuous) on
, it is bounded. From the geometric series formula
and dominated convergence, we conclude that
with the right-hand side an absolutely convergent series for , and the claim follows.
Exercise 9 Establish the generalised Cauchy integral formulae
for any non-negative integer
, where
is the
-fold complex derivative of
.
This in turn leads to a converse to Cauchy’s theorem, known as Morera’s theorem:
Corollary 10 (Morera’s theorem) Let
be a continuous function on an open set
with the property that
for all closed contours
. Then
is holomorphic.
Proof: We can of course assume to be non-empty and connected (hence path-connected). Fix a point
, and define a “primitive”
of
by defining
, with
being any contour from
to
(this is well defined by hypothesis). By mimicking the proof of the real fundamental theorem of calculus, we see that
is holomorphic with
, and the claim now follows from Corollary 8.
An important consequence of Morera’s theorem for us is
Corollary 11 (Locally uniform limit of holomorphic functions is holomorphic) Let
be holomorphic functions on an open set
which converge locally uniformly to a function
. Then
is also holomorphic on
.
Proof: By working locally we may assume that is a ball, and in particular simply connected. By Cauchy’s theorem,
for all closed contours
in
. By local uniform convergence, this implies that
for all such contours, and the claim then follows from Morera’s theorem.
Now we study the zeroes of complex analytic functions. If a complex analytic function vanishes at a point
, but is not identically zero in a neighbourhood of that point, then by Taylor expansion we see that
factors in a sufficiently small neighbourhood of
as
for some natural number (which we call the order or multiplicity of the zero at
) and some function
that is complex analytic and non-zero near
; this generalises the factor theorem for polynomials. In particular, the zero
is isolated if
does not vanish identically near
. We conclude that if
is connected and
vanishes on a neighbourhood of some point
in
, then it must vanish on all of
(since the maximal connected neighbourhood of
in
on which
vanishes cannot have any boundary point in
). This implies unique continuation of analytic functions: if two complex analytic functions on
agree on a non-empty open set, then they agree everywhere. In particular, if a complex analytic function does not vanish everywhere, then all of its zeroes are isolated, so in particular it has only finitely many zeroes on any given compact set.
Recall that a rational function is a function which is a quotient
of two polynomials (at least outside of the set where
vanishes). Analogously, let us define a meromorphic function on an open set
to be a function
defined outside of a discrete subset
of
(the singularities of
), which is locally the quotient
of holomorphic functions, in the sense that for every
, one has
in a neighbourhood of
excluding
, with
holomorphic near
and with
non-vanishing outside of
. If
and
has a zero of equal or higher order than
at
, then the singularity is removable and one can extend the meromorphic function holomorphically across
(by the holomorphic factor theorem (4)); otherwise, the singularity is non-removable and is known as a pole, whose order is equal to the difference between the order of
and the order of
at
. (If one wished, one could extend meromorphic functions to the poles by embedding
in the Riemann sphere
and mapping each pole to
, but we will not do so here. One could also consider non-meromorphic functions with essential singularities at various points, but we will have no need to analyse such singularities in this course.) If the order of a pole or zero is one, we say that it is simple; if it is two, we say it is double; and so forth.
Exercise 12 Show that the space of meromorphic functions on a non-empty open set
, quotiented by almost everywhere equivalence, forms a field.
By quotienting two Taylor series, we see that if a meromorphic function has a pole of order
at some point
, then it has a Laurent expansion
absolutely convergent in a neighbourhood of excluding
itself, and with
non-zero. The Laurent coefficient
has a special significance, and is called the residue of the meromorphic function
at
, which we will denote as
. The importance of this coefficient comes from the following significant generalisation of the Cauchy integral formula, known as the residue theorem:
Exercise 13 (Residue theorem) Let
be a meromorphic function on a simply connected domain
, and let
be a closed contour in
enclosing a bounded region
anticlockwise, and avoiding all the singularities of
. Show that
where
is summed over all the poles of
that lie in
.
The residue theorem is particularly useful when applied to logarithmic derivatives of meromorphic functions
, because the residue is of a specific form:
Exercise 14 Let
be a meromorphic function on an open set
that does not vanish identically. Show that the only poles of
are simple poles (poles of order
), occurring at the poles and zeroes of
(after all removable singularities have been removed). Furthermore, the residue of
at a pole
is an integer, equal to the order of zero of
if
has a zero at
, or equal to negative the order of pole at
if
has a pole at
.
Remark 15 The fact that residues of logarithmic derivatives of meromorphic functions are automatically integers is a remarkable feature of the complex analytic approach to multiplicative number theory, which is difficult (though not entirely impossible) to duplicate in other approaches to the subject. Here is a sample application of this integrality, which is challenging to reproduce by non-complex-analytic means: if
is meromorphic near
, and one has the bound
as
, then
must in fact stay bounded near
, because the only integer of magnitude less than
is zero.
— 1. Local approximation of meromorphic functions —
Suppose is a non-zero rational function
, then by the fundamental theorem of algebra (see Exercise 19 below) one can write
for some non-zero constant , where
ranges over the zeroes of
(counting multiplicity) and
ranges over the zeroes of
(counting multiplicity), and assuming
avoids the zeroes of
. Taking absolute values and then logarithms, we arrive at the formula
as long as avoids the zeroes of both
and
. Alternatively, taking logarithmic derivatives, we arrive at the closely related formula
again for avoiding the zeroes of both
and
. Thus we see that the zeroes and poles of a rational function
describe the behaviour of that rational function, as well as close relatives of that function such as the log-magnitude
and log-derivative
.
In the complex approach to multiplicative number theory, it is desirable to generalise the above formulae to the case when is a meromorphic function rather than a rational one, to understand the extent to which the behaviour of a meromorphic function is controlled by its zeroes and poles. Classically, one achieves this goal by working on the entire complex plane and exploiting the tool of Weierstrass factorisation. However, for most applications in analytic number theory, one can instead work with local factorisations, which are more flexible, removing the need to consider distant poles and zeroes by trading them for a manageable boundary term. The most well known example of such a local factorisation is Jensen’s formula:
Theorem 16 (Jensen’s formula) Let
be a meromorphic function on an open neighbourhood of a disk
, with all removable singularities removed. Then, if
is neither a zero nor a pole of
, we have
where
and
range over the zeroes and poles of
respectively (counting multiplicity) in the disk
.
One should view (7) as a truncated (or localised) variant of (5). Note also that the summands are always non-positive.
Proof: By perturbing slightly if necessary, we may assume that none of the zeroes or poles of
(which form a discrete set) lie on the boundary circle
. By translating and rescaling, we may then normalise
and
, thus our task is now to show that
We may remove the poles and zeroes inside the disk by the useful device of Blaschke products. Suppose for instance that
has a zero
inside the disk. Observe that the function
has magnitude on the unit circle
, equals
at the origin, has a simple zero at
, but has no other zeroes or poles inside the disk. Thus Jensen’s formula (8) already holds if
is replaced by
. To prove (8) for
, it thus suffices to prove it for
, which effectively deletes a zero
inside the disk from
(and replaces it instead with its inversion
). Similarly we may remove all the poles inside the disk. As a meromorphic function only has finitely many poles and zeroes inside a compact set, we may thus reduce to the case when
has no poles or zeroes on or inside the disk, at which point our goal is simply to show that
Since has no zeroes or poles inside the disk, the logarithmic derivative
has no poles in the disk, and so by Cauchy’s theorem has a primitive
. By the chain rule,
has zero derivative on the disk and is thus constant, thus on taking complex logarithms (see Exercise 3) we see that
is equal to a logarithm of
up to a constant. Subtracting the constant, we thus can find a holomorphic function
that is a branch of the complex logarithm of
, thus
. In particular, the real part of
is
. The claim now follows by applying the mean value property (3) to
.
Exercise 17 (This exercise is intended for readers familiar with distribution theory, as discussed for instance in this previous blog post.) If
is holomorphic on an open set
, establish the formula
in the sense of distributions, where
and
range over the zeroes and poles of
respectively (counting multiplicity),
denotes the Dirac measure at a complex number
, and
is the distributional Laplacian
, with
denoting the real and imaginary parts of the complex variable
. In particular, we see that
is a harmonic function away from the zeroes and poles of
, and a subharmonic function away from the poles of
.
One application of Jensen’s formula is to control zeroes of a holomorphic function , given upper and lower bounds on
at various points in the complex plane. Here are some examples:
Exercise 18 Use Jensen’s formula to prove Liouville’s theorem: a bounded holomorphic function
on the entire complex plane is necessarily constant. (Hint: apply Jensen’s formula in a large disk to
for various constants
to conclude that
either vanishes entirely or has no zeroes whatsoever.)
Exercise 19 Use Jensen’s formula to prove the fundamental theorem of algebra: a complex polynomial
of degree
has exactly
complex zeroes (counting multiplicity), and can thus be factored as
for some complex numbers
with
. (Note that the fundamental theorem was invoked previously in this section, but only for motivational purposes, so the proof here is non-circular.)
Exercise 20 (Shifted Jensen’s formula) Let
be a meromorphic function on an open neighbourhood of a disk
, with all removable singularities removed. Show that
for all
in the open disk
that are not zeroes or poles of
, where
and
. (The function
appearing in the integrand is sometimes known as the Poisson kernel, particularly if one normalises so that
and
.)
Just as (7) and (10) give truncated variants of (5), we can create truncated versions of (6). The following crude truncation is adequate for our applications:
Theorem 21 (Truncated formula for log-derivative) Let
be a holomorphic function on an open neighbourhood of a disk
that is not identically zero on this disk. Suppose that one has a bound of the form
for some
and all
on the circle
. Let
be constants. Then one has the approximate formula
for all
in the disk
other than zeroes of
. Furthermore, the number of zeroes
in the above sum is
.
Proof: To abbreviate notation, we allow all implied constants in this proof to depend on .
We mimic the proof of Jensen’s formula. Firstly, we may translate and rescale so that and
, so we have
when
, and our main task is to show that
for . Note that if
then
vanishes on the unit circle and hence (by the maximum principle) vanishes identically on the disk, a contradiction, so we may assume
. From hypothesis we then have
on the unit circle, and so from Jensen’s formula (7) we see that
In particular we see that the number of zeroes with is
, as claimed.
Suppose has a zero
with
. If we factor
, where
is the Blaschke product (9), then
Observe from Taylor expansion that the distance between and
is
, and hence
for
. Thus we see from (12) that we may use Blaschke products to remove all the zeroes in the annulus
while only affecting the left-hand side of (11) by
; also, removing the Blaschke products does not affect
on the unit circle, and only affects
by
thanks to (12). Thus we may assume without loss of generality that there are no zeroes in this annulus.
Similarly, given a zero with
, we have
, so using Blaschke products to remove all of these zeroes also only affects the left-hand side of (11) by
(since the number of zeroes here is
), with
also modified by at most
. Thus we may assume in fact that
has no zeroes whatsoever within the unit disk. We may then also normalise
, then
for all
. By Jensen’s formula again, we have
and thus (by using the identity for any real
)
On the other hand, from (10) we have
which implies from (13) that and its first derivatives are
on the disk
. But recall from the proof of Jensen’s formula that
is the derivative of a logarithm
of
, whose real part is
. By the Cauchy-Riemann equations for
, we conclude that
on the disk
, as required. (One could also have proceeded here via the Borel-Carathéodory theorem.)
A variant of the above argument allows one to make precise the heuristic that holomorphic functions locally look like polynomials:
Exercise 22 (Local Weierstrass factorisation) Let the notation and hypotheses be as in Theorem 21. Then show that
for all
in the disk
, where
is a polynomial whose zeroes are precisely the zeroes of
in
(counting multiplicity) and
is a holomorphic function on
of magnitude
and first derivative
on this disk. Furthermore, show that the degree of
is
.
Remark 23 The classical theory of Beurling factorization of Hardy space functions on the disk into inner functions, outer functions, and Blaschke products can be viewed as a sort of limiting case of the above exercise when
; see for instance this text of Garnett for a treatment. However, we will not need this limiting theory in our applications.
— 2. The Fourier-Laplace and Fourier transforms —
There are a number of connections between complex analysis and Fourier analysis. The best known connection perhaps is between complex analytic functions on the unit disk and Fourier analysis on the unit circle
:
Exercise 24 (Complex analysis on disk versus Fourier analysis on circle)
- Let
be a complex analytic function on the unit disk
, and define the Fourier coefficients
for
. Show that
for all negative
, and one has the Taylor expansion
(as an absolutely convergent series) in the interior
of the disk.
- Conversely, let
be an absolutely summable sequence of complex numbers. Show that the function
is a continuous function on the unit disk
that is holomorphic on the interior of this disk, and that
for all
.
Remark 25 The relationship between the boundary behaviour of holomorphic functions
on the disk, and the integrability properties of the function
on the unit circle, is a very delicate topic, involving the theory of Hardy spaces as well as tools from harmonic analysis, and will not be discussed here; see for instance the text of Garnett for further discussion.
We will not explicitly use the above connection between complex analysis and Fourier analysis in this course (although some traces of it might be discerned in the material in the previous sections of this set of notes). Instead, we will discuss a slightly different link between the two subjects, linking complex analysis on the half-space with the Fourier-Laplace transform on the half-line. Namely, given an absolutely integrable measurable function
, the Laplace transform
is defined by the formula
Actually, for absolutely integrable there is no difficulty extending the Laplace transform to the half-space
by exactly the same formula, giving rise to the Fourier-Laplace transform. On the imaginary axis
, this becomes the Fourier transform:
where we extend by zero to the entire real line. If we also assume
to be compactly supported, then the Fourier-Laplace transform extends to the entire complex plane
.
An application of Fubini’s theorem reveals that the integral of in any closed contour in the domain of definition vanishes, so by Morera’s theorem (Corollary 10) we conclude that
is holomorphic on the right half-space
(if
is absolutely integrable on
) or on
(if
is compactly supported).
If we have a bit of smoothness on , then we can establish some asymptotics on the Fourier-Laplace transform:
Lemma 26 Let
be compactly supported and continuously twice differentiable. Then we have
for all
in the half-space
with
.
Proof: By an integration by parts, we have
since is continuous and compactly supported, and
is bounded in magnitude by
, the claim follows.
Corollary 27 Let
be compactly supported and continuously twice differentiable. Then we have
for any
. (Note from (14) that the limit exists.)
Proof: By contour shifting (using (14) to handle error terms) we see that the integral is independent of , so we may take
to be large. Applying (14) and the fundamental theorem of calculus, we see that
using the principal branch of the logarithm. The integral is
, and
converges to
as
. Taking limits as
, and then sending
to infinity, we obtain the claim.
This gives a proof of one of the basic identities in Fourier analysis, the Fourier inversion formula. Given any absolutely integrable function , let us define the Fourier transform
by the formula
(Here we use a normalisation of the Fourier transform that aligns with the traditional normalisations in complex analysis; other normalisations are used in other fields of mathematics.) We first recall some basic estimates and symmetries:
Exercise 28 (Basic estimates on Fourier transform) Let
be an integer, and let
be compactly supported and
times continuously differentiable (this is interpreted simply as continuity if
).
- (i) Establish the pointwise bounds
for all
, where
denotes the
-fold derivative of
, and with the convention that the inequality is trivially true when
and
.
- (ii) Suppose in addition that
is supported in the interval
. Show that
extends holomorphically to the entire complex plane (with the formula (15) valid now for all
), with the pointwise bounds
for all
. (There is a converse to this result known as the Paley-Wiener theorem, but we will not establish or need it here.)
Exercise 29 (Basic symmetries of the Fourier transform) Let
be absolutely integrable.
- (i) If
for some
and all
, show that
for all
.
- (ii) If
for some
and all
, show that
for all
.
- (iii) If
for some
and all
, show that
for all
.
- (iv) If
for all
, show that
for all
.
Theorem 30 (Fourier inversion formula) Let
be compactly supported and continuously twice differentiable. Then the Fourier transform
, defined by
is bounded and absolutely integrable, and one has the inversion formula
for any
. More generally, one has
for any
, where again the integrand is absolutely integrable.
Remark 31 One can certainly relax the support and smoothness hypotheses on
, particularly if one is willing to work in rougher function spaces, such as the space of tempered distributions; see e.g. these previous notes. Similarly for the other Fourier-analytic results presented below. But for the purpose of this course, it will suffice to restrict attention to fairly well behaved functions
, such as those that are compactly supported and twice continuously differentiable.
Proof: From Exercise 28 with we see that
and so is bounded and absolutely integrable as claimed.
By Exercise 29(i) we may assume without loss of generality that , thus our task is now to show that
We introduce the components of
by the formulae
for , and observe that the Fourier transform
of
is related to the Fourier-Laplace transforms of
by the formula
From Corollary 27 we have
for either choice of sign; summing, we obtain the first claim. The second claim then follows by replacing by
(or by shifting the contour).
Remark 32 In the above proof,
is split into a function
extending holomorphically and boundedly to the upper half-plane, and a function
extending holomorphically and boundedly to the lower half-plane. Such a decomposition solves a very simple example of the Riemann-Hilbert problem, but we will not discuss this problem further in this course.
The inversion formula gives an important identity, essentially due to Parseval and to Plancherel:
Corollary 33 (Parseval-Plancherel identities) Let
be compactly supported and continuously twice differentiable. Then we have
In particular
and
Proof: By the inversion formula we may write as
The claim then follows from Fubini’s theorem.
In the next set of notes, we will use a version of the above identity, which we will call a truncated Perron formula, to express smoothed summatory functions of arithmetic functions as contour integrals of the associated Dirichlet series
.
Finally, we record another important Fourier identity, the Poisson summation formula.
Theorem 34 (Poisson summation) Let
be a compactly supported, twice continuously differentiable function. Then
Proof: There are many ways to prove this identity, but given the spirit of this set of notes, it seems appropriate to give a complex analysis proof. By Exercise 29(i) we may assume without loss of generality that is supported on the positive real axis. By the dominated convergence theorem, the left-hand side of (16) may thus be written as
From the Fourier inversion formula and dominated convergence again, we may rewrite this as
summing the geometric series, this becomes
Observe that the function is meromorphic on the upper half-plane
, with poles at
for
with residue
. A routine application of the residue theorem (using Exercise 28 to handle error terms) allows us to write the previous expression as
and the claim then follows from one final application of dominated convergence.
There will be at least two key applications of the Poisson summation formula in this course. One is to establish the functional equation for the Riemann zeta function (as well as truncated versions of this equation, for instance involving the sum for some smooth cutoff
and parameters
). The other is to obtain good bounds for smooth sums
with error terms that are significantly better than what one can obtain just from the integral test (Lemma 2 from previous notes) or the fundamental theorem of calculus (Exercise 11 from the same notes):
Exercise 35 (Good error bounds on smooth sums) Let
be a compactly supported,
times continuously differentiable function for some
. Use the Poisson summation formula to show that
for all
. (This should be compared with the error term of
that one would have obtained using the methods from previous notes.) This estimate illustrates a basic principle, namely that smoother sums enjoy better asymptotics.
Exercise 36 (Fourier transform of Gaussian) Let
be the function defined by
for
. Show that
for all
. (Hint: it is not difficult to establish this claim with
replaced by some unknown positive constant
; but then one can use the Fourier inversion formula to compute
.) Conclude the functional equation
whenever
is an element of the upper half-space
, with the principal branch
of the complex square root, and
is the theta function
(Hint: use the Poisson summation formula and the symmetries of the Fourier transform.)
Exercise 37 (Mellin inversion formula) Let
be a continuous, compactly supported function. Establish the Mellin inversion formula
for all
and
, where the integral is along the straight line contour from
to
. What happens when
or
?
Remark 38 By a simple change of variables, the above formula also leads to an inversion formula for the Mellin transform
defined for compactly supported absolutely integrable
and
, but we will not use this transform or inversion formula here.
Exercise 39 (Qualitative uncertainty principle) Let
be an absolutely integrable function such that
and
are both compactly supported. Show that
is identically zero. (This is a special case of the Hardy uncertainty principle, discussed in this previous post.)
(The exercises below should be placed earlier in this set of notes, but are at the end to avoid renumbering issues.)
Exercise 40 (Borel-Carathéodory theorem) Let
be a complex analytic function in a disk
. Show that for any
, one has
and
for all
in the disk
. (Hint: there are various ways to proceed here. One is to apply Exercise 20 to
and differentiate.)
Exercise 41 (Hadamard three-lines theorem)
- (i) Let
and
be real numbers. Suppose that
is a complex analytic function in a strip
such that
and
for all
. Suppose also that one has the crude growth condition
for all
and
. Show that
for all
and
. (Hint: one can normalise
. Use the maximum principle to verify the claim in the case that
goes to zero as
. To handle the general case, mollify
by multiplying by functions such as
for suitable
.)
- (ii) Let
and
be real numbers, and let
be complex analytic function in a strip
such that
for
and
, and
for
and
. Show that
for all
and
.

24 comments
Comments feed for this article
5 December, 2014 at 10:43 am
Anonymous
I think you mean 254A in the title.
[Corrected, thanks -T.]
5 December, 2014 at 11:14 am
MrCactu5 (@MonsieurCactus)
“We will not attempt a comprehensive review of this subject; for instance, we will completely neglect the conformal geometry or Riemann surface aspect of complex analysis” ;-(
5 December, 2014 at 2:27 pm
Rogier Brussee
In cor. 34, the Plancherel formula misses a hat on g.
As always, very nice notes.
[Corrected, thanks – T.]
5 December, 2014 at 10:23 pm
jlackm
Dear Professor Tao,
can one easily use Stokes’ theorem to prove Cauchy’s integral formula without assuming continuity of the partial derivatives? A priori they aren’t even Riemann integrable, and I’ve never seen this done before. This would be very nice if it’s true.
6 December, 2014 at 7:44 am
Terence Tao
Goursat’s proof of Cauchy’s theorem (and hence the integral formula) requires only complex differentiability at each point, without continuity (although when combined with Morera’s theorem, one can recover this continuity and even obtain complex analyticity). See e.g. Stein-Shakarchi http://press.princeton.edu/chapters/s02_7563.pdf . In most applications, though, whenever one establishes differentiability of a function, one also establishes continuous differentiability without much additional effort, so this additional relaxation of hypotheses is not a significant strengthening of Cauchy’s theorem in practice.
9 December, 2014 at 12:55 am
Avi Levy
In the paragraph preceeding Exercise 12, right after the definition of a meromorphic function: “which is locally to the quotient {g/h} of holomorphic functions” (I think you’re missing a word or two).
[Corrected, thanks – T.]
17 December, 2014 at 7:37 am
peteg
In the proof of Corollary 8, what allows you to switch the sum and the integral?
17 December, 2014 at 9:56 am
Terence Tao
The dominated convergence theorem (note that is uniformly bounded on the contour
is uniformly bounded on the contour  , and
, and 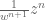 is bounded in magnitude by
is bounded in magnitude by 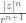 , which is absolutely convergent when summed in
, which is absolutely convergent when summed in  ). One could also use Fubini’s theorem here if desired.
). One could also use Fubini’s theorem here if desired.
27 December, 2014 at 9:00 pm
peteg
In the proof of Jensen’s formula, for the case where f has no zeros or poles in the unit disc, would a valid argument be that since log f is analytic, it satisfies the mean value property?
[Yes; this is essentially the strategy used to prove this formula in this blog post. -T.]
30 December, 2014 at 9:00 am
peteg
Can you expand on the hint for exercise 18?
3 January, 2015 at 8:54 am
Terence Tao
Suppose for instance that is not zero at the origin, but has at least one zero
is not zero at the origin, but has at least one zero 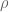 . Apply Jensen’s formula to a disk
. Apply Jensen’s formula to a disk 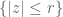 and obtain a contradiction for sufficiently large
and obtain a contradiction for sufficiently large  if
if 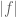 is bounded.
is bounded.
13 February, 2015 at 10:16 pm
254A, Notes 6: Large values of Dirichlet polynomials, zero density estimates, and primes in short intervals | What's new
[…] by exploiting the smooth nature of . Namely, by using the Poisson summation formula (Theorem 34 of Supplement 2), we can rewrite (2) […]
15 February, 2015 at 5:03 pm
254A, Notes 3: The large sieve and the Bombieri-Vinogradov theorem | What's new
[…] hence by Exercise 28 of Supplement 2, we have the […]
22 February, 2015 at 9:02 am
254A, Notes 7: Linnik’s theorem on primes in arithmetic progressions | What's new
[…] Jensen’s theorem (Theorem 16 of Supplement 2), we conclude that for any given non-principal and any , there are at most zeroes of (counting […]
1 March, 2015 at 1:13 pm
254A, Supplement 7: Normalised limit profiles of the log-magnitude of the Riemann zeta function (optional) | What's new
[…] A major topic of interest of analytic number theory is the asymptotic behaviour of the Riemann zeta function in the critical strip in the limit . For the purposes of this set of notes, it is a little simpler technically to work with the log-magnitude of the zeta function. (In principle, one can reconstruct a branch of , and hence itself, from using the Cauchy-Riemann equations, or tools such as the Borel-Carathéodory theorem, see Exercise 40 of Supplement 2.) […]
29 March, 2016 at 6:03 am
Terry Tao: 254A, Supplement 2: A little bit of complex and Fourier analysis | What’s new – Collected Links
[…] 254A, Supplement 2: A little bit of complex and Fourier analysis | What’s new n this supplement to the main notes, we quickly review the portions of complex analysis that we will be using in this course. We will not attempt a comprehensive review of this subject; for instance, we will completely neglect the conformal geometry or Riemann surface aspect of complex analysis, and we will also avoid using the various boundary convergence theorems for Taylor series or Dirichlet series (the latter type of result is traditionally utilised in multiplicative number theory, but I personally find them a little unintuitive to use, and will instead rely on a slightly different set of complex-analytic tools). We will also focus on the “local” structure of complex analytic functions, in particular adopting the philosophy that such functions behave locally like complex polynomials; the classical “global” theory of entire functions, while traditionally used in the theory of the Riemann zeta function, will be downplayed in these notes. On the other hand, we will play up […]
2 July, 2016 at 6:51 am
254A, Supplement 3: The Gamma function and the functional equation (optional) | What's new
[…] 34 from Supplement 2, at least in the case when is twice continuously differentiable and compactly supported), which […]
26 September, 2016 at 5:52 am
Anonymous
In the statement of Theorem 21, should the error term in the approximation formula for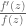 be
be  , where d is the number of zeroes of
, where d is the number of zeroes of  in the annulus
in the annulus 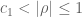 ?
?
26 September, 2016 at 9:23 am
Terence Tao
No, because the bound (12) allows one to control the combined contribution of these zeroes, as explained in the proof.
26 September, 2016 at 9:49 pm
Anonymous
Thanks! I’ve got it now.
21 January, 2017 at 3:56 pm
254A, Notes 2: Complex-analytic multiplicative number theory | What's new
[…] come from the general theory of local factorisations of meromorphic functions, as discussed in Supplement 2; the passage from (4) to (2) is accomplished by such tools as the residue theorem and the Fourier […]
5 June, 2017 at 10:04 am
Five-Value Theorem of Nevanlinna – Elmar Klausmeier's Weblog
[…] 254A, Supplement 2: A little bit of complex and Fourier analysis, proves Poisson-Jensen formula for the logarithm of a meromorphic function in relation to its zeros within a disk […]
22 June, 2019 at 8:18 am
Helene
In Ex. 35, is it enough to assume that $N \geq 1,$ instead of $N >> 1?$
[The latter case already subsumes the former. -T]
11 October, 2021 at 9:19 am
254A, Supplement 4: Probabilistic models and heuristics for the primes (optional) | What's new
[…] 22 of Notes 2) it is a routine matter (using Proposition 16 from Notes 2 and Exercise 28 of Supplement 2) to arrive at the […]