The complete homogeneous symmetric polynomial of
variables
and degree
can be defined as
thus for instance
and
One can also define all the complete homogeneous symmetric polynomials of variables simultaneously by means of the generating function
We will think of the variables as taking values in the real numbers. When one does so, one might observe that the degree two polynomial
is a positive definite quadratic form, since it has the sum of squares representation
In particular, unless
. This can be compared against the superficially similar quadratic form
where are independent randomly chosen signs. The Wigner semicircle law says that for large
, the eigenvalues of this form will be mostly distributed in the interval
using the semicircle distribution, so in particular the form is quite far from being positive definite despite the presence of the first
positive terms. Thus the positive definiteness is coming from the finer algebraic structure of
, and not just from the magnitudes of its coefficients.
One could ask whether the same positivity holds for other degrees than two. For odd degrees, the answer is clearly no, since
in that case. But one could hope for instance that
also has a sum of squares representation that demonstrates positive definiteness. This turns out to be true, but is remarkably tedious to establish directly. Nevertheless, we have a nice result of Hunter that gives positive definiteness for all even degrees . In fact, a modification of his argument gives a little bit more:
Theorem 1 Let
, let
be even, and let
be reals.
- (i) (Positive definiteness) One has
, with strict inequality unless
.
- (ii) (Schur convexity) One has
whenever
majorises
, with equality if and only if
is a permutation of
.
- (iii) (Schur-Ostrowski criterion for Schur convexity) For any
, one has
, with strict inequality unless
.
Proof: We induct on (allowing
to be arbitrary). The claim is trivially true for
, and easily verified for
, so suppose that
and the claims (i), (ii), (iii) have already been proven for
(and for arbitrary
).
If we apply the differential operator to
using the product rule, one obtains after a brief calculation
Using (1) and extracting the coefficient, we obtain the identity
The claim (iii) then follows from (i) and the induction hypothesis.
To obtain (ii), we use the more general statement (known as the Schur-Ostrowski criterion) that (ii) is implied from (iii) if we replace by an arbitrary symmetric, continuously differentiable function. To establish this criterion, we induct on
(this argument can be made independently of the existing induction on
). If
is majorised by
, it lies in the permutahedron of
. If
lies on a face of this permutahedron, then after permuting both the
and
we may assume that
is majorised by
, and
is majorised by
for some
, and the claim then follows from two applications of the induction hypothesis. If instead
lies in the interior of the permutahedron, one can follow it to the boundary by using one of the vector fields
, and the claim follows from the boundary case.
Finally, to obtain (i), we observe that majorises
, where
is the arithmetic mean of
. But
is clearly a positive multiple of
, and the claim now follows from (ii).
If the variables are restricted to be nonnegative, the same argument gives Schur convexity for odd degrees also.
The proof in Hunter of positive definiteness is arranged a little differently than the one above, but still relies ultimately on the identity (2). I wonder if there is a genuinely different way to establish positive definiteness that does not go through this identity.

18 comments
Comments feed for this article
6 August, 2017 at 6:44 pm
unowatblog
There is a typo in the definition of $h_d$: the last index is $i_d$ rather than $i_n$.
Aside, since Schur convexity seems to me a natural solution – would you consider sum of squares type identity a different solution?
7 August, 2017 at 7:43 am
Terence Tao
Thanks for the correction!
One could convert the Schur convexity proof into a (rather artificial looking) sum of squares proof, but if there was a nice looking sum of squares representation analogous to that for then I would consider that to be a different proof.
then I would consider that to be a different proof.
Here is one small observation that might help towards a different proof: if one already knows the non-negativity of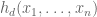 for even
for even  , then this implies the non-negativity of
, then this implies the non-negativity of  for any
for any  and even
and even  . This is because the generating function
. This is because the generating function  is equal to the generating function of
is equal to the generating function of  times
times  ; the latter has only even powers and non-negative coefficients, hence the claim. So one can “cancel” any pair
; the latter has only even powers and non-negative coefficients, hence the claim. So one can “cancel” any pair 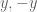 that occurs in
that occurs in 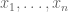 , which for instance demonstrates non-negativity of
, which for instance demonstrates non-negativity of 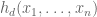 whenever the
whenever the 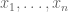 all have the same magnitude. I wasn’t able to convert this argument into a proof of the general case though.
all have the same magnitude. I wasn’t able to convert this argument into a proof of the general case though.
6 August, 2017 at 7:53 pm
andrescaicedo
At least on my screen the tag (2) is not visible. (I found it by looking at the TeX code of the displayed identity.)
[Corrected, thanks – T.]
6 August, 2017 at 11:23 pm
Orr Shalit
It might be better to start the induction with d=2 (to obtain the condition for strict inequality).
[Suggestion implemented, thanks – T.]
7 August, 2017 at 7:43 am
Anonymous
Maybe this works. Let be i.i.d exponentially distributed with parameter 1. Let
be i.i.d exponentially distributed with parameter 1. Let 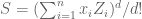 . The coefficient of a monomial
. The coefficient of a monomial 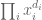 in
in  is
is  whose expected value is
whose expected value is  because the
because the 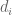 ‘th moment of
‘th moment of  is
is  . So
. So 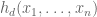 is the expected value of
is the expected value of  , clearly non-negative for even
, clearly non-negative for even  .
.
7 August, 2017 at 8:35 am
Synia
Really nice ! Another way of seeing that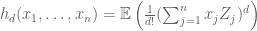 is by writing
is by writing ![h_d(x_1, \dots, x_n) = [t^d] \prod_{j = 1}^n \frac{1}{1 - x_j t} =[t^d] \prod_{j = 1}^n \mathbb{E}\left( e^{t x_j Z_j} \right)](https://s0.wp.com/latex.php?latex=h_d%28x_1%2C+%5Cdots%2C+x_n%29+%3D+%5Bt%5Ed%5D+%5Cprod_%7Bj+%3D+1%7D%5En+%5Cfrac%7B1%7D%7B1+-+x_j+t%7D+%3D%5Bt%5Ed%5D+%5Cprod_%7Bj+%3D+1%7D%5En+%5Cmathbb%7BE%7D%5Cleft%28+e%5E%7Bt+x_j+Z_j%7D+%5Cright%29&bg=ffffff&fg=545454&s=0&c=20201002)
7 August, 2017 at 9:16 am
Terence Tao
Very nice! I was hunting for a probabilistic interpretation of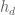 (this being another major way to prove positivity results, besides sum of squares methods and induction methods) but did not see this very neat moment interpretation. I think this is a good demonstration of the power of the probabilistic method.
(this being another major way to prove positivity results, besides sum of squares methods and induction methods) but did not see this very neat moment interpretation. I think this is a good demonstration of the power of the probabilistic method.
(It now makes me wonder more generally if Schur polynomials have a similarly nice probabilistic interpretation. Of course, one can simply plug in the probabilistic interpretation of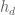 into the first Jacobi-Trudi formula, but I’m hoping for something more than this…)
into the first Jacobi-Trudi formula, but I’m hoping for something more than this…)
15 September, 2021 at 7:10 am
Aditya Guha Roy
In fact Hunter’s result says that I strongly believe that this probabilistic argument can be amplified to deduce Hunter’s original inequality too.
I strongly believe that this probabilistic argument can be amplified to deduce Hunter’s original inequality too.
8 August, 2017 at 4:54 am
David Speyer
Very nice indeed!
I would say that this is morally a “sum of squares” argument; you have expressed $h_d$ as an integral of a $d$-th power. I imagine that, by replacing the integral by a suitable average over finitely many values, you could obtain a literal sum of squares expression.
8 August, 2017 at 7:46 am
Terence Tao
True; indeed it looks like all one needs to do is to replace the exponential random variable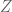 by a discrete random variable which matches moments with the continuous one up to
by a discrete random variable which matches moments with the continuous one up to  order and one would get a discrete representation. (The existence of such a discrete random variable follows from Caratheodory’s theorem.)
order and one would get a discrete representation. (The existence of such a discrete random variable follows from Caratheodory’s theorem.)
8 August, 2017 at 6:10 am
Arash B
“To establish this criterion, we again induct on $d$ “; Isn’t it induction on $n$?
[Corrected, thanks – T.]
8 August, 2017 at 3:58 pm
David Speyer
You might already know this, but there is a positivity property for Schur polynomials: If is a partition with all even parts, then
is a partition with all even parts, then 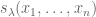 is nonnegative for any real inputs. (And, I think, positive unless the inputs are all zero, but I’m not sure.)
is nonnegative for any real inputs. (And, I think, positive unless the inputs are all zero, but I’m not sure.)
By symmetry and continuity, it is enough to show that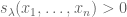 when
when 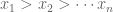 . We recall the ratio of alternants formula:
. We recall the ratio of alternants formula: 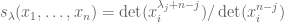 . So it is enough to show that
. So it is enough to show that  when
when 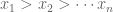 and all the
and all the 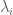 are even. By continuity, it is enough to show that
are even. By continuity, it is enough to show that  under these conditions.
under these conditions.
Suppose to the contrary that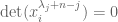 . Then there is a linear relation
. Then there is a linear relation  . In other words, the polynomial
. In other words, the polynomial 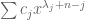 has
has  distinct real roots. But the condition that the parts of
distinct real roots. But the condition that the parts of  are even means that that the exponents
are even means that that the exponents  alternate in parity, which means Descartes’ Rule of Signs will permit only
alternate in parity, which means Descartes’ Rule of Signs will permit only 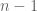 real roots, a contradiction.
real roots, a contradiction. 
If we wanted to show strict positivity, we’d need to show that only divided
only divided  once; we’ve shown strict positivity off the locus where two of the
once; we’ve shown strict positivity off the locus where two of the 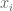 are equal already.
are equal already.
I believe this was an exercise in Barvinok’s convexity textbook, but I don’t have it at hand to check.
9 August, 2017 at 6:24 am
Synia
This gives an alternative proof for the positivity of since
since  .
.
9 August, 2017 at 12:24 pm
Terence Tao
Nice! (I knew one could use the rule of signs to prove that the Schur polynomials were positive when the inputs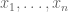 were positive, but this was already obvious from the Young tableau expansion.)
were positive, but this was already obvious from the Young tableau expansion.)
Unfortunately most Schor polynomials can vanish outside of the origin; indeed, by testing a Schur polynomial on a basis vector
on a basis vector  using the Young tableau expansion, one gets zero unless
using the Young tableau expansion, one gets zero unless  has only one non-zero part. So the only strictly positive definite Schur polynomials are the
has only one non-zero part. So the only strictly positive definite Schur polynomials are the  . (Apoorva Khare and I have an upcoming paper where we had a theorem that worked for all strictly positive definite Schur polynomials, so it was a bit disappointing to realise how few of them there were.)
. (Apoorva Khare and I have an upcoming paper where we had a theorem that worked for all strictly positive definite Schur polynomials, so it was a bit disappointing to realise how few of them there were.)
10 August, 2017 at 7:34 am
David Speyer
Oh wow, I should have noticed that about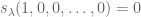 . Huh, I wonder what the real points where
. Huh, I wonder what the real points where  vanishes, when all parts of
vanishes, when all parts of  are even, look like.
are even, look like.
21 August, 2017 at 8:34 pm
Anonymous
Theorem 1(i) is easy if all the reals have the same sign. Otherwise, without loss of generality,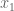 is positive and
is positive and 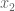 is negative. The identity
is negative. The identity
shows that is a convex combination of
is a convex combination of 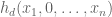 and
and 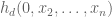 . These are each strictly positive for even
. These are each strictly positive for even  by induction on the number of non-zero components.
by induction on the number of non-zero components.
23 August, 2017 at 1:14 pm
Anonymous
Here is a proof of strict positivity, using log-convexity.
 , which I don’t see a way to get just using moment generating functions.
, which I don’t see a way to get just using moment generating functions.
This approach gives Hunter’s bound
Define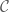 to be the set of exponential generating functions of log-convex sequences.
to be the set of exponential generating functions of log-convex sequences. is closed under products.
is closed under products.
The Davenport-Pólya theorem says that
I will use the following lemma. If then the even coefficients of
then the even coefficients of 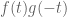 are non-negative.
are non-negative. is
is  .
. is log-convex, which implies it is convex.
is log-convex, which implies it is convex.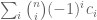 is non-negative if
is non-negative if  is even and
is even and  is convex. QED.
is convex. QED.
Proof: the coefficient of
The sequence
But a sum of the form
Assume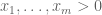 and
and 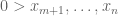 . By abuse of notation, write
. By abuse of notation, write 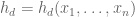 , and
, and 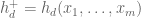 , and
, and  . We have the identity
. We have the identity  Note
Note 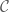 contains all functions of the form
contains all functions of the form  for
for  , and so contains
, and so contains 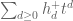 and
and 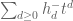 by the formula (1) in the main post. By the lemma above,
by the formula (1) in the main post. By the lemma above, 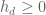 for even
for even  .
.
To get a bound in terms of , note that
, note that  is
is for
for  :
: are
are which is log-convex.
which is log-convex.


 .
.
in
the first few coefficients of
[A000266](https://oeis.org/A000266), and they tend quickly to
By the same argument as before, the even coefficients of
are non-negative. Multiplying by
gives the bound
23 August, 2017 at 3:00 pm
Anonymous
Sorry, I realised that proof doesn’t work – convexity by itself isn’t strong enough to guarantee those even coefficients are non-negative in general.