Previous set of notes: 246B Notes 4. Next set of notes: Notes 2.
The fundamental object of study in real differential geometry are the real manifolds: Hausdorff topological spaces that locally look like open subsets of a Euclidean space
, and which can be equipped with an atlas
of coordinate charts
from open subsets
covering
to open subsets
in
, which are homeomorphisms; in particular, the transition maps
defined by
are all continuous. (It is also common to impose the requirement that the manifold
be second countable, though this will not be important for the current discussion.) A smooth real manifold is a real manifold in which the transition maps are all smooth.
In a similar fashion, the fundamental object of study in complex differential geometry are the complex manifolds, in which the model space is rather than
, and the transition maps
are required to be holomorphic (and not merely smooth or continuous). In the real case, the one-dimensional manifolds (curves) are quite simple to understand, particularly if one requires the manifold to be connected; for instance, all compact connected one-dimensional real manifolds are homeomorphic to the unit circle (why?). However, in the complex case, the connected one-dimensional manifolds – the ones that look locally like subsets of
– are much richer, and are known as Riemann surfaces. For sake of completeness we give the (somewhat lengthy) formal definition:
Definition 1 (Riemann surface) If
is a Hausdorff connected topological space, a (one-dimensional complex) atlas is a collection
of homeomorphisms from open subsets
of
that cover
to open subsets
of the complex numbers
, such that the transition maps
defined by
are all holomorphic. Here
is an arbitrary index set. Two atlases
,
on
are said to be equivalent if their union is also an atlas, thus the transition maps
and their inverses are all holomorphic. A Riemann surface is a Hausdorff connected topological space
equipped with an equivalence class of one-dimensional complex atlases.
A mapfrom one Riemann surface
to another
is holomorphic if the maps
are holomorphic for any charts
,
of an atlas of
and
respectively; it is not hard to see that this definition does not depend on the choice of atlas. It is also clear that the composition of two holomorphic maps is holomorphic (and in fact the class of Riemann surfaces with their holomorphic maps forms a category).
Here are some basic examples of Riemann surfaces.
Example 2 (Quotients of
) The complex numbers
clearly form a Riemann surface (using the identity map
as the single chart for an atlas). Of course, maps
that are holomorphic in the usual sense will also be holomorphic in the sense of the above definition, and vice versa, so the notion of holomorphicity for Riemann surfaces is compatible with that of holomorphicity for complex maps. More generally, given any discrete additive subgroup
of
, the quotient
is a Riemann surface. There are an infinite number of possible atlases to use here; one such is to pick a sufficiently small neighbourhood
of the origin in
and take the atlas
where
and
for all
. In particular, given any non-real complex number
, the complex torus
formed by quotienting
by the lattice
is a Riemann surface.
Example 3 Any open connected subset
of
is a Riemann surface. By the Riemann mapping theorem, all simply connected open
, other than
itself, are isomorphic (as Riemann surfaces) to the unit disk (or, equivalently, to the upper half-plane).
Example 4 (Riemann sphere) The Riemann sphere
, as a topological manifold, is the one-point compactification of
. Topologically, this is a sphere and is in particular connected. One can cover the Riemann sphere by the two open sets
and
, and give these two open sets the charts
and
defined by
for
,
for
, and
. This is a complex atlas since the
is holomorphic on
.
An alternate way of viewing the Riemann sphere is as the projective line. Topologically, this is the punctured complex plane
quotiented out by non-zero complex dilations, thus elements of this space are equivalence classes
with the usual quotient topology. One can cover this space by two open sets
and
and give these two open sets the charts
and
defined by
for
,
. This is a complex atlas, basically because
for
and
is holomorphic on
.
Exercise 5 Verify that the Riemann sphere is isomorphic (as a Riemann surface) to the projective line.
Example 6 (Smooth algebraic plane curves) Let
be a complex polynomial in three variables which is homogeneous of some degree
, thus
Define the complex projective plane
to be the punctured space
quotiented out by non-zero complex dilations, with the usual quotient topology. (There is another important topology to place here of fundamental importance in algebraic geometry, namely the Zariski topology, but we will ignore this topology here.) This is a compact space, whose elements are equivalence classes
. Inside this plane we can define the (projective, degree
) algebraic curve
this is well defined thanks to (1). It is easy to verify that
is a closed subset of
and hence compact; it is non-empty thanks to the fundamental theorem of algebra.
Suppose thatis irreducible, which means that it is not the product of polynomials of smaller degree. As we shall show in the appendix, this makes the algebraic curve connected. (Actually, algebraic curves remain connected even in the reducible case, thanks to Bezout’s theorem, but we will not prove that theorem here.) We will in fact make the stronger nonsingularity hypothesis: there is no triple
such that the four numbers
simultaneously vanish for
. (This looks like four constraints, but is in fact essentially just three, due to the Euler identity
that arises from differentiating (1) in
. The fact that nonsingularity implies irreducibility is another consequence of Bezout’s theorem, which is not proven here.) For instance, the polynomial
is irreducible but singular (there is a “cusp” singularity at
). With this hypothesis, we call the curve
smooth.
Now supposeis a point in
; without loss of generality we may take
non-zero, and then we can normalise
. Now one can think of
as an inhomogeneous polynomial in just two variables
, and by nondegeneracy we see that the gradient
is non-zero whenever
. By the (complexified) implicit function theorem, this ensures that the affine algebraic curve
is a Riemann surface in a neighbourhood of
; we leave this as an exercise. This can be used to give a coordinate chart for
in a neighbourhood of
when
. Similarly when
is non-zero. This can be shown to give an atlas on
, which (assuming the connectedness claim that we will prove later) gives
the structure of a Riemann surface.
Exercise 7 State and prove a complex version of the implicit function theorem that justifies the above claim that the charts in the above example form an atlas, and an algebraic curve associated to a non-singular polynomial is a Riemann surface.
- (i) Show that all (irreducible plane projective) algebraic curves of degree
are isomorphic to the Riemann sphere. (Hint: reduce to an explicit linear polynomial such as
.)
- (ii) Show that all (irreducible plane projective) algebraic curves of degree
are isomorphic to the Riemann sphere. (Hint: to reduce computation, first use some linear algebra to reduce the homogeneous quadratic polynomial to a standard form, such as
or
.)
Exercise 9 If
are complex numbers, show that the projective cubic curve
is nonsingular if and only if the discriminant
is non-zero. (When this occurs, the curve is called an elliptic curve (in Weierstrass form), which is a fundamentally important example of a Riemann surface in many areas of mathematics, and number theory in particular. One can also define the discriminant for polynomials of higher degree, but we will not do so here.)
A recurring theme in mathematics is that an object is often best studied by understanding spaces of “good” functions on
. In complex analysis, there are two basic types of good functions:
Definition 10 Let
be a Riemann surface. A holomorphic function on
is a holomorphic map from
to
; the space of all such functions will be denoted
. A meromorphic function on
is a holomorphic map from
to the Riemann sphere
, that is not identically equal to
; the space of all such functions will be denoted
.
One can also define holomorphicity and meromorphicity in terms of charts: a function is holomorphic if and only if, for any chart
, the map
is holomorphic in the usual complex analysis sense; similarly, a function
is meromorphic if and only if the preimage
is discrete (otherwise, by analytic continuation and the connectedness of
,
will be identically equal to
) and for any chart
, the map
becomes a meromorphic function in the usual complex analysis sense, after removing the discrete set of complex numbers where this map is infinite. One consequence of this alternate definition is that the space
of holomorphic functions is a commutative complex algebra (a complex vector space closed under pointwise multiplication), while the space
of meromorphic functions is a complex field (a commutative complex algebra where every non-zero element has an inverse). Another consequence is that one can define the notion of a zero of given order
, or a pole of order
, for a holomorphic or meromorphic function, by composing with a chart map and using the usual complex analysis notions there, noting (from the holomorphicity of transition maps and their inverses) that this does not depend on the choice of chart. (However, one cannot similarly define the residue of a meromorphic function on
this way, as the residue turns out to be chart-dependent thanks to the chain rule. Residues should instead be applied to meromorphic
-forms, a concept we will introduce later.) A third consequence is analytic continuation: if two holomorphic or meromorphic functions on
agree on a non-empty open set, then they agree everywhere.
On the complex numbers , there are of course many holomorphic functions and meromorphic functions; for instance any power series with an infinite radius of convergence will give a holomorphic function, and the quotient of any two such functions (with non-zero denominator) will give a meromorphic function. Furthermore, we have extremely wide latitude in how to specify the zeroes of the holomorphic function, or the zeroes and poles of the meromorphic function, thanks to tools such as the Weierstrass factorisation theorem or the Mittag-Leffler theorem (covered in previous quarters).
It turns out, however, that the situation changes dramatically when the Riemann surface is compact, with the holomorphic and meromorphic functions becoming much more rigid. First of all, compactness eliminates all holomorphic functions except for the constants:
Lemma 11 Let
be a holomorphic function on a compact Riemann surface
. Then
is constant.
This result should be seen as a close sibling of Liouville’s theorem that all bounded entire functions are constant. (Indeed, in the case of a complex torus, this lemma is a corollary of Liouville’s theorem.)
Proof: As is continuous and
is compact,
must attain a maximum at some point
. Working in a chart around
and applying the maximum principle, we conclude that
is constant in a neighbourhood of
, and hence is constant everywhere by analytic continuation.
This dramatically cuts down the number of possible meromorphic functions – indeed, for an abstract Riemann surface, it is not immediately obvious that there are any non-constant meromorphic functions at all! As the poles are isolated and the surface is compact, a meromorphic function can only have finitely many poles, and if one prescribes the location of the poles and the maximum order at each pole, then we shall see that the space of meromorphic functions is now finite dimensional. The precise dimensions of these spaces are in fact rather interesting, and obey a basic duality law known as the Riemann-Roch theorem. We will give a mostly self-contained proof of the Riemann-Roch theorem in these notes, omitting only some facts about genus and Euler characteristic, as well as construction of certain meromorphic -forms (also known as Abelian differentials).
A more detailed study of Riemann surface (and more generally, complex manifolds) can be found for instance in Griffiths and Harris’s “Principles of Algebraic Geometry“.
— 1. Divisors —
To discuss the zeroes and poles of meromorphic functions, it is convenient to introduce an abstraction of the concept of “a collection of zeroes and poles”, known as a divisor.
Definition 12 (Divisor) Let
be a compact Riemann surface. A divisor on
is a formal integer linear combination
, where
ranges over a finite collection of points in
, and
are integers, with the obvious additive group structure; equivalently, the space
of divisors is the free abelian group with generators
with
(where we make the usual convention
). The number
is the degree of the divisor; we call each
the order of the divisor
at
, with the convention that the order is zero for points not appearing in the sum. A divisor is non-negative (or effective) if all the
are non-negative, and we partially order the divisors by writing
if
is non-negative. This makes
a lattice, so we can define the maximum
or minimum
of two divisors. Given a non-zero meromorphic function
, the principal divisor
associated to
is the divisor
, where
ranges over the zeroes and poles of
, and
is the order of zero (or negative the order of pole) at
. (Note that as zeroes and poles are isolated, and
is compact, the number of zeroes and poles is automatically finite.)
Informally, one should think of as the abstraction of a zero of order
at
, or a pole of order
if
is negative.
Example 13 Consider a rational function
for some non-zero complex number
and some complex numbers
. This is a meromorphic function on
, and
is also meromorphic, so
extends to a meromorphic function on the Riemann sphere
. It has zeroes at
and poles at
, and also has a zero of order
(or a pole of order
) at
, as can be seen by inspection of
near the origin (or the growth of
near infinity), and thus
In particular,
has degree zero.
Exercise 14 Show that all meromorphic functions on the Riemann sphere come from rational functions as in the above example. Conclude in particular that every principal divisor on the Riemann sphere has degree zero. Give an alternate proof of this latter fact using the residue theorem. (We will generalise this fact to other Riemann surfaces shortly; see Proposition 24.)
It is easy to see (by working in a coordinate chart around ) that if
are non-zero meromorphic functions, that one has the valuation axioms
for any (adopting the convention the zero function has order
everywhere); thus we have
again adopting the convention that is larger than every divisor. In particular, the space
of principal divisors of
is a subgroup of
. We call two divisors linearly equivalent if they differ by a principal divisor; this is clearly an equivalence relation.
The properties (2) have the following consequence. Given a divisor , let
be the space of all meromorphic functions
such that
(including, by convention, the zero function
); thus, if
, then
consists of functions that have at worst a pole of order
at
(or a zero of order
or greater, if
is negative). For instance,
is the space of meromorphic functions that have at most a double pole at
, a single pole at
, and at least a simple zero at
, if
are distinct points in
. From (2) (and the fact that non-zero constant functions have principal divisor zero) we see that each
is a vector space. We clearly have the nesting properties
if
, and also if
then
.
Remark 15 In the language of vector bundles, one can identify a divisor
with a certain holomorphic line bundle on
, and
can be identified with the space of sections of this bundle. This is arguably the more natural way to think about divisors; however, we will not adopt this language here.
If and
, then
is holomorphic on
and hence (by Lemma 11) constant. We can thus easily compute
for zero or negative divisors:
Corollary 16 Let
be a compact Riemann surface. Then
consists only of the constant functions, and
consists only of
if
. In particular,
has dimension
when
and
when
.
Exercise 17 If
and
are principal divisors with
, show that
is a constant multiple of
with
.
Exercise 18 Let
be a divisor. Show that
if and only if
is linearly equivalent to an effective divisor.
The situation for (i.e.,
has positive order at at least one point) is more interesting. We first have a simple observation from linear algebra:
Lemma 19 Let
be a compact Riemann surface,
be a divisor, and
be a point. Then
has codimension at most
in
.
Proof: Let be a chart that maps
to the origin, and suppose that
already had order
at
(so that
had order
). Then functions
, when composed with the inverse
of the chart function have Laurent expansion
for some complex coefficients (which will depend on the choice of chart). The map
is clearly a linear map from
to
, whose kernel is
, and the claim follows.
As a corollary of this lemma and Corollary 16, we see that the spaces are all finite dimensional, with the dimension
increasing by zero or one each time one adds an additional pole to
.
Here is another simple linear algebra relation between the dimensions of the spaces :
Lemma 20 Let
be a compact Riemann surface, and let
be divisors. Then
Proof: From linear algebra we have
Since and
, the claim follows.
If is a divisor and
is a principal divisor, then (2) gives an isomorphism between
and
, by mapping
to
. In particular, the dimensions
and
of the linearly equivalent divisors
are the same. If we define a divisor class to be a coset
of the principal divisors in
(that is to say, an equivalence class for linear equivalence), then we conclude that the dimension
depends only on the divisor class
of
. The space
of divisor classes is an abelian group, which is known as the divisor class group. (For nonsingular algebraic curves, this group also coincides with the Picard group, though the situation is more subtle if one allows singularities.)
It is now easy to understand the spaces for the Riemann sphere:
Exercise 21 Show that two divisors on the Riemann sphere are equivalent if and only if they have the same degree, so that the degree map gives an isomorphism between the divisor class group of the Riemann sphere and the integers. If
is a divisor on the Riemann sphere, show that
is equal to
. (Hint: first show that for any integer
, that
is the space of polynomials of degree at most
.)
From the above exercise we observe in particular that
whenever has degree
; as we will see later, this is a special case of the Riemann-Roch theorem.
— 2. Meromorphic -forms —
To proceed further, we will introduce the concept of a meromorphic -form on a compact Riemann surface
. To motivate this concept, observe that one can think of a meromorphic function
on
as a collection of meromorphic functions
on open subsets of the complex plane, where
ranges over a suitable atlas of
. These meromorphic functions
are compatible with each other in the following sense: if
and
are charts, then we have
for all (this condition is vacuous if
do not overlap). As already noted, one can define such concepts as the order of
at a pole
by declaring it to be the order of
at
for any chart
that contains
in its domain, and the compatibility condition (4) ensures that this definition is well defined.
On the other hand, several other basic notions in complex analysis do not seem to be well defined for such meromorphic functions. Consider for instance the question of how to define the residue of at a pole
. The natural thing to do is to again pick a chart
around
and use the residue of
; however one can check that this is not independent of the choice of chart in general, as from (4) one will find that the residues of
and
are related to each other, but not equal. Similarly, one encounters a difficulty integrating
on a contour
in
, even if the contour is short enough to fit into the domain
of a single chart
and also avoids all the poles of
; the natural thing to do is to compute
, but again this will depend on the choice of chart (substituting (4) will reveal that
is not equal to
in general due to an additional Jacobian factor). Finally, one encounters a difficulty trying to differentiate a meromorphic function
; on each chart
one would like to just differentiate
, but the resulting derivatives
do not obey the compatibility condition (4), but instead (by the chain rule) obey the slightly different condition
The solution to all of these issues is to introduce a new type of object on , the meromorphic
-forms.
Definition 22 A meromorphic
-form
on
is a collection of expressions
for each coordinate chart
of
, with
meromorphic on
, which obey the compatibility condition
for any pair
,
of charts and any
. If all the
are holomorphic, we say that
is holomorphic also. The space of meromorphic
-forms will be denoted
.
As with meromorphic functions, we can define the orderof
at a point
to be the order of
at
for some chart
that contains
in its domain; from (5) we see that this is well defined. Similarly we may define the divisor
of
. The divisor of a non-zero meromorphic
-form is called a canonical divisor. (We will show later that at least one non-zero meromorphic
-form is available, so that canonical divisors exist.)
Letbe a meromorphic
-form. Given a contour
that lies in the domain
of a single chart
and avoids the poles of
, we can define the integral
to be equal to
. One checks from (5) and the change of variables formula that this definition is independent of the choice of chart. One then defines
for longer contours by partitioning into short contours; again, one can check that this definition is independent of the choice of partition.
The residue ofat
can be defined as the residue of
at
for a chart
that contains
in its domain, or equivalently (by the residue theorem)
where
is a sufficiently small contour winding around
once anticlockwise (note that we have a consistent orientation on
since invertible holomorphic maps are orientation preserving).
Meromorphic -forms are also known as Abelian differentials, while holomorphic
-forms are Abelian differentials of the first kind. (Abelian differentials of the second kind are meromorphic
-forms in which all residues vanish, while Abelian differentials of the third kind are meromorphic
-forms in which all poles are simple.) To specify a meromorphic form
, it suffices to prescribe
for all
in a single atlas of
; as long as (5) is obeyed within this atlas, it is easy to see that
can then be defined uniquely using (5) for all other coordinate charts.
Formally speaking, one can “derive” the condition (5) by applying the change of variables to
to obtain
. But we will take (5) as a definition of a
-form, rather than deriving it from any other concept.
There are two basic ways to create meromorphic -forms. One is to start with a meromorphic function
and form its differential
, which when evaluated any chart
of
is given by the formula
the compatibility condition (5) is then clear from the chain rule. Another way is to start with an existing meromorphic -form
and multiply it by a meromorphic function
to give a new meromorphic
-form
, which when evaluated at a given chart
of
is given by
again, it is clear that the compatibility condition (5) holds. Conversely, given two meromorphic -forms
, with
not identically zero, one can form the ratio
to be the unique meromorphic function
such that
; it is easy to see that
exists and is unique. These properties are compatible with taking divisors, thus
and
.
Of course, one can also add two meromorphic -forms to obtain another meromorphic
-form. Thus
is in fact a one-dimensional vector space over the field
(here we assume that non-zero meromorphic
-forms exist, a claim which we will return to later). In particular, the canonical divisor is unique up to linear equivalence.
Later on we will discuss a further way to create a meromorphic -form, by taking the gradient of a harmonic function with specific types of singularities.
Example 23 The coordinate function
can be viewed as a meromorphic function on the Riemann sphere
(it has a simple zero at
and a simple pole at
). Its derivative
then has a double pole at infinity (note that in the reciprocal coordinate
,
transforms to
), so
. Any other meromorphic
-form is of the form
, where
is a meromorphic function (that is to say, a rational function). In particular, since meromorphic functions have divisor of degree
, all meromorphic
-forms on the Riemann sphere have a divisor of degree
; indeed, the canonical divisors here are precisely the divisors of degree
.
We now give a key application of meromorphic -forms to the divisors of meromorphic functions:
Proposition 24 Let
be a compact Riemann surface.
- (i) For any meromorphic
-form
, the sum of all the residues of
vanishes.
- (ii) Every principal divisor
has degree zero.
Proof: We begin with (i). By evaluating at coordinate charts, the counterclockwise integral of around any small loop
that avoids any pole is zero; thus
is closed outside of these poles, and hence by Stokes’ theorem we conclude that the integral of
around the sum of small counterclockwise loops around every pole is zero. On the other hand, by the residue theorem applied in each chart, this integral is equal to
times the sum of the residues, and the claim follows.
To prove (ii), apply (i) to the meromorphic -form
(cf. the usual proof of the argument principle).
Exercise 25 Let
be a compact Riemann surface, and let
be a divisor on
.
- (i) If
, show that
.
- (ii) If
, show that
is equal to
or
, with the latter occurring if and only if
is principal. Furthermore, any non-zero element of
has divisor
.
- (iii) If
, establish the bound
.
We have already discussed how algebraic curves give good examples of Riemann surfaces. In the converse direction, it is common for Riemann surfaces to map into algebraic curves, as hinted by the following exercise:
Exercise 26 Let
be a compact Riemann surface, and let
be two non-constant meromorphic functions on
. Show that there exists a non-zero polynomial
of two variables with complex coefficients such that
. (Hint: look at the monomials
for
for some large
, and show that they lie in
for a suitable divisor
. Then use part (iii) of the previous exercise and linear algebra.) Show furthermore that one can take
to be irreducible. (This type of argument ultimately leads to Chow’s theorem that projective complex manifolds are necessarily algebraic.)
— 3. The case of a complex torus —
For the special case when the Riemann surface being studied is a complex torus , one can obtain more precise information on the dimensions
by explicit computations. First observe we have a natural holomorphic
-form on
, namely the form
, defined in any small coordinate chart
on a small disk
in
(with
) by
, and then defined for any other coordinate chart by compatibility. This form has no poles and zeroes, and so
is a canonical divisor. Using this
-form, we have a bijection between meromorphic functions and meromorphic
-forms on
which maps
to
; in contrast to the situation with other Riemann surfaces with non-zero canonical divisor, this bijection does not affect the divisor. In particular, canonical divisors are principal and vice versa. Using this bijection, we can think of the differential
of a meromorphic function as another meromorphic function, which we call the derivative
, as per the familiar formula
. Of course, with respect to the above coordinate charts, this derivative corresponds to the usual complex derivative.
We also have a fundamental meromorphic function on , or equivalently a
-periodic function on
, namely the Weierstrass
-function
It is easy to see that the sum converges outside of , and that this is a meromorphic
-periodic function on
that has a double pole at every point in
; this descends to a meromorphic function on
with divisor at least
. By translation we can then create a meromorphic function
with divisor at least
for any
.
Using this function and some manipulations, we can compute for most divisors
:
Lemma 27 Let
be a complex torus, and let
be a divisor.
- (i) If
, then
.
- (ii) If
, then
is equal to
or
. If
for some distinct
, then
. Also,
.
- (iii) If
, then
.
Proof: Part (i) and the first claim of part (ii) follows from Exercise 25. To prove the second claim of part (ii), it suffices by Exercise 25 to show that there is no meromorphic function with divisor , that is to say a simple pole at
and a simple zero at
. But this follows from Proposition 24(i) (and identifying meromorphic functions with meromorphic
-forms) since the residue at
is non-zero and there is no other residue to cancel it. The third claim comes from Exercise 25 and the observation that
is principal if and only if
is.
Call a divisor good if
. We need to show that all divisors of positive degree are good. First we check that
is good for a point
. By Proposition 24(i) we see that the only meromorphic functions in
are constant, hence
, and so
is good.
The Weierstrass -function
at
gives a an element of
which is non-constant (it has a double pole at
), so by Lemma 19 we have
, and so
is good. Taking a derivative of
to obtain a meromorphic function with a triple pole at
, we obtain a further element of
that is not in
, and so
, and so
is good. Continuing to differentiate in this fashion we see that
is good for any natural number
.
Next, for any distinct pairs of points , we write
for some complex number
, and define the meromorphic function
where is some contour from
to
. (As
locally has an antiderivative at every point, this definition does not depend on the choice of
, though it is a little sensitive to the choice of
.) One can check that this function is meromorphic with simple poles at
and
, which shows that
. From Lemma 19 and the fact that
is good, we conclude that
is good.
Observe from Lemma 19 and Lemma 20 we see that if is a divisor and
are distinct points such that
are good, then
is also good. We have just shown that all effective divisors of degree
and
are good; by induction one can now show that all effective divisors of positive degree are good.
Call a degree one divisor very good if
is good for every
. We have shown that
is very good for all
. We now claim that if
is very good then so is
is very good. First note that
and
cannot both be principal, since their difference
is not principal. Thus by Exercise 25, at least one of
or
vanishes, and hence
by Lemma 19. On the other hand, as
is very good,
is good, and so
. By Lemma 19 we conclude that
is good.
For any , we know that
and
are good, hence by Lemma 19 the intermediate divisor
must also be good. Iterating this argument we see that
is good for every
, thus
is very good. Iterating this we see that all degree one divisors are very good, giving (iii).
An alternate way to show that is good was shown to me by Redmond McNamara as follows. By subtracting a constant from
one can find a meromorphic function
with a double pole at
and at least a single zero at
. If it is exactly a single zero, multiplying by
will create a function with precisely a simple pole at
and at most a double pole at
; subtracting a multiple of
if necessary will then give the required non-trivial element of
. If
has a double zero at
instead, multiply
by
and subtract multiples of
and
to obtain the same result. Note that
cannot have more than a double zero because of Proposition 24(ii).
As a corollary of the above proposition we obtain the complex torus case of the Riemann-Roch theorem:
valid for any divisor (regardless of degree); compare with (3). The one remaining point is to work out which degree zero divisors are principal. It turns out that there is an additional constraint beyond degree zero:
Exercise 28 Suppose that
is a principal divisor on a complex torus
(we allow repetition). Show that
using the group law on
. (Hint: if
is a meromorphic function with zeroes at
and poles at
, integrate
around a parallelogram fundamental domain of
(translating if necessary so that the boundary of the parallelogram avoids the zeroes and poles).)
In fact, this is the only condition:
Proposition 29 A degree zero divisor
is principal if and only if
.
Proof: By the above exercise it suffices to establish the “if” direction. We may of course assume . By Lemma 27, the space
is one-dimensional, thus there exists a non-zero meromorphic function
with poles at
, zeroes at
, and no further poles (counting multiplicity). By Proposition 24(ii)
must have one further zero, and by the above exercise this zero must be
. The claim follows.
One can explicitly write down a formula for these meromorphic functions using theta functions, but we will not do so here.
The above proposition links the group law on a complex torus with the group law on divisors. This is part of a more general relation involving the Jacobian variety of a curve and the Abel-Jacobi theorem, but we will not discuss this further in this course.
Exercise 30 Let
be a complex torus. Show that the Weierstrass function
obeys the differential equation
for some complex numbers
depending on
. Also show that the map
for
(with
mapping to
) is a holomorphic invertible map from
to the algebraic curve
which is non-singular and irreducible. (Thus, every complex torus is isomorphic to an elliptic curve. The converse is also true, but will not be established here.)
Exercise 31 Let
be a complex torus, and let
be a function. Show that
is holomorphic if and only if it takes the form
for all
, and some complex numbers
, with
lying in the set
. Furthermore, show that
is either equal to the integers, or to a lattice of the form
for some quadratic algebraic integer
(thus
obeys an equation
for some integers
). In the latter case, the complex torus is said to have complex multiplication.
— 4. The Riemann Roch theorem —
We now leave the example of the complex torus and return to more general compact Riemann surfaces . We would like to generalise the identity (7) (or (3)) to this setting. As a first step we establish
Proposition 32 (Baby Riemann Roch theorem) Let
be a canonical divisor in a compact Riemann surface
, and let
be an effective divisor. Then
Proof: Write where
ranges over some finite set
of points in
, and
are positive integers. As
is a canonical divisor, we can find a meromorphic
-form
, not identically zero, with divisor
. If
, then
is a holomorphic
-form. The proof relies on using linear algebra to combine the following three observations that tie together
,
, and
:
- If
and
, then
. This follows from Proposition 24(i) and the fact that the only possible poles of
are in
.
- If
and
, then we have the stronger assertion that
for each individual
. This follows because the divisor of
is at least
, and so
has no pole at
. Furthermore this is a local statement: it holds even if
is only defined on a small neighborhood of
, rather than on all of
. Finally, the claim is sharp: if
then one can find
and some
defined locally near
in
for which
- For
,
, and
is holomorphic at
, then
, since
is also holomorphic at
. Again, this is a local statement, and holds even if
is only defined in a neighbourhood of
.
Let us now see how these facts combine to give the proposition. Around each let us form a chart
that maps
to
. Then for any
,
has a pole of order at most
at the origin, and can thus be written as
for near
, where
are complex numbers and
is holomorphic at the origin. We call the expression
the principal part of
(uniformised by
) at
. If we let
denote the collection of tuples
with
complex, then
is a complex vector space of dimension
. Inside this space we have the subspace
of tuples that can actually arise as the principal parts of a meromorphic function
in
. Observe that if two functions
have the same principal parts, then their difference
is holomorphic and hence constant by Lemma 11. Thus, the space
has dimension exactly
.
As is a canonical divisor, we have a meromorphic
-form
with divisor
. If
, then
is a holomorphic
-form. If
is a tuple in
, we can define a pairing
by the formula
This is a bilinear pairing from to
. If
, then all the components of
are principal parts of some
, and by Observation 3 one can then write
as
, which then vanishes by Observation 1. Thus
whenever
and
. As row rank equals column rank, we conclude that there is a subspace
of
of dimension at least
such that whenever
and
. But then if
,
must vanish to order at least
at each
, hence
, which is equivalent to
and hence to
; this is Observation 2. One concludes that
and the claim follows by rearranging.
One can amplify this proposition if one is in possession of the following three non-trivial claims.
- There is at least one non-zero meromorphic
-form; in particular, canonical divisors exist.
- Every canonical divisor has degree
, where
is the (topological) genus of
.
- The space of holomorphic
-forms has dimension
. Equivalently, for any canonical divisor
,
. (In algebraic geometry language, this asserts that for compact Riemann surfaces, the topological genus is equal to the geometric genus.)
Example 33 The Riemann sphere
has genus
. All meromorphic
-forms, such as
, have degree
and so cannot be holomorphic, so there are no holomorphic
-forms. Meanwhile, a complex torus
has genus
. All meromorphic
-forms, such as
, have degree
. In particular, a holomorphic
-form is
times a holomorphic function, so by Lemma 11 the space of holomorphic
-forms is one-dimensional.
Assuming these claims, the above proposition gives, for any canonical divisor , that
when is effective and (replacing
by
)
when is effective. Since the second right-hand side is the negative of the first, we conclude that
whenever and
are both effective. In fact we have the more general
Theorem 34 (Riemann-Roch theorem) Let
be a compact Riemann surface of genus
, let
be a canonical divisor, and let
be any divisor. Then
This of course generalises (3) on the Riemann sphere (which has genus zero) and (7) on a complex torus (which has genus one).
It remains to establish the above three claims, and to obtain the Riemann-Roch theorem in full generality. I have not been able to locate particularly simple proofs of these steps that do not require significant machinery outside of complex analysis, so will only sketch some arguments justifying each of these.
To create meromorphic -forms one can take gradients of harmonic functions, in the spirit of the proof of the uniformization theorem that was (mostly) given in these 246A lecture notes. A function
is said to be harmonic if, for every coordinate chart
,
is harmonic; as the property of being harmonic on open subsets of the complex plane is unaffected by conformal transformations, this definition does not depend on the choice of atlas that the charts are drawn from. If
is harmonic, one can form a holomorphic
-form
on
by defining
for each chart and
.
For instance, on , the harmonic function
gives rise to the holomorphic
-form
.
Exercise 35 Show that this definition indeed defines a holomorphic
-form (thus the
are all holomorphic and obey the compatibiltiy condition (5). (The computations are slightly less tedious if one uses Wirtinger derivatives.)
Unfortunately, for compact Riemann surfaces , the same maximum principle argument used to prove Lemma 11 shows that there are no non-constant globally harmonic functions on
, so we cannot use this construction directly to produce non-trivial holomorphic or meromorphic
-forms on
. However, one can produce harmonic functions with logarithmic singularities, a prototypical example of which is the function
on the Riemann sphere, which is harmonic except at
and
. More generally, one has
Proposition 36 (Existence of dipole Green’s function) Let
be a Riemann surface, and let
be distinct points in
. Then there exists a harmonic function
on
with the property that for any chart
that maps
to
,
is equal to
plus a bounded function near
, and for any chart
that maps
to
,
is equal to
plus a bounded function near
.
This proposition is essentially Proposition 65 of these 246A notes and can be proven using (a somewhat technical modification of) Perron’s method of subharmonic functions; we will not do so here. One can combine this proposition with the preceding construction to obtain a non-constant meromorphic -form:
Exercise 37 Using the above proposition, show that if
is a compact Riemann surface and
are distinct points in
, then there is a meromorphic
-form
on
with poles only at
, with a residue of
at
and a residue of
at
.
Using this, conclude the Riemann existence theorem: for any compact Riemann surfaceand distinct points
in
, there exists a meromorphic function on
that takes different values at
and
and is in particular non-constant. (In other words, the meromorphic functions separate points.)
To prove the full Riemann-Roch theorem we will also need a variant of this exercise, not proven here:
Proposition 38 If
is a compact Riemann surface,
is a point in
, and
, then there exists a meromorphic
-form
on
with a pole of order
at
and no other poles.
The -forms
constructed by this proposition can be viewed as generalisations of the Weierstrass functions
(and their derivatives) to other Riemann surfaces, much as the
-form
constructed in Exercise 37 are generalisations of first integrals of these functions. (Indeed, one can think of
as a sort of “derivative” of
, formed as
approaches
and taking a suitable renormalised limit; more generally, one can furthermore of
as a suitably renormalised limit of
as
approaches
.) Note from Proposition 24 that the
constructed by the above proposition automatically have vanishing residue at
(in classical language, these are Abelian differentials of the third kind, while the
are Abelian differentials of the second kind).
The first claim is now settled by Exercise 37, so we now turn to the second. We first need some general facts about non-constant holomorphic maps from one compact Riemann surface
to another
. If
is a point in
, and
is its image in
, then we define (by abuse of notation)
to be the order of vanishing of the function
for any coordinate chart
in some neighbourhood
of
in
; it is not hard to see that this is independent of the choice of chart. Usually, this order will equal
, but there will be a finite number of places
where it exceeds
, which we call critical points or ramification points (in terms of coordinate charts, this is where the derivative of
vanishes). The values
are known as critical values or branch points. Let
denote the set of all branch points; this is a finite subset of
, and the preimage
is a finite subset of
.
If one deletes the branch points from
and the preimage
from
, the resulting map can be seen to be a covering map (this follows from Rouche’s theorem applied in local coordinate charts). In particular, since the base
is connected, there is a natural number
(the degree of
) such that the map is a
-fold cover; in particular, for all
, the preimage set
has cardinality
. Even if
lies in
, by using coordinate charts near each preimage
of
in
and using Rouche’s theorem, we see that we always have
Informally: the number of preimages of in
, counting multiplicity, is always equal to
.
Exercise 39 Let
be a holomorphic map between a compact Riemann surface
and a Riemann surface
. Show that
is either surjective or constant.
Next, suppose we have a meromorphic -form
on
, thus for every coordinate chart
one has a local coordinate representation
of
obeying the compatibility condition (5). Then we can define the pullback
to be the meromorphic
-form on
, defined on every coordinate chart
of
by the formula
for any coordinate chart of
and any
. One can check that this gives a well-defined
-form, as the above expression is independent of the choice of chart
, and also obeys the compatibility condition (5). An inspection of the above formula also shows that for
and
, the order of
at
is related to the order of
at
by the chain rule type formula
Now we assert some facts from algebraic topology. To any surface one can assign an integer
known as the Euler characteristic of
; informally, it is the constant that
is equal to for any triangulation (or cellular complex) of
. In the case of a compact surface of genus
, this Euler characteristic is equal to
. For instance, the Riemann sphere
has genus
and Euler characteristic
, while a complex torus
has genus
and Euler characteristic
. We now have
Theorem 40 (Riemann-Hurwitz formula) Let
be a non-constant holomorphic map between compact Riemann surfaces
of degree
, and let
be the branch points of this map. Then we have
Furthermore, for any meromorphic
-form
on
, we have
Proof: We begin with the first claim. The space is a
-fold cover of
. Any triangulation of the latter can then be pulled back to a triangulation of the former with
times as many vertices, edges, and faces. As a consequence we have
On the other hand, every time one removes a point from a surface, the Euler characteristic drops by one (we remove one vertex without deleting any edges or faces). Thus
and
Combining these identities with (8), we obtain the first claim.
Next, if we sum (9) over all in the preimage of
using (8) we have
and then if one sums over all , one obtain the second claim.
Now we can prove that every canonical divisor on a compact Riemann surface has degree
, which is equal to
. From Example 23 we see that this claim is true for the Riemann sphere
. For any other surface
, we use Exercise 37 to produce a non-constant holomorphic map
from
to the Riemann sphere, and let
be any meromorphic
-form on the Riemann sphere (e.g. one could take
). Then
, hence by both equations in the Riemann-Hurwitz formula we have
, and so the canonical divisor
has degree
. Since all canonical divisors are equivalent, the claim follows.
Exercise 41 Let
and
be compact Riemann surfaces, with
having higher genus than
. Show that there does not exist any non-constant holomorphic map from
to
.
Now we discuss the third claim. It is relatively easy to show that the dimension of the space of holomorphic -forms is upper bounded by
. Indeed, we may assume without loss of generality that there exists at least one non-zero holomorphic
-form, giving an effective canonical divisor
, which we have just shown to have degree
. From Proposition 32 applied to
we then have
and hence , giving the claimed upper bound.
The lower bound is harder. Basically, it asserts that the pairing in Proposition 32, when quotiented down to a pairing between
and
, is non-degenerate. This is a special case of an algebraic geometry fact known as Serre duality, which we will not prove here. It can also be proven from Hodge theory, using the fact that the first de Rham cohomology has dimension
; we do not pursue this approach here, but see for instance Griffiths-Harris. Alternatively, one can try to explicitly construct
linearly holomorphic
-forms on the Riemann surface
. We will not do this in general, but show how to do this in the case of a smooth algebraic curve
of degree
. The genus of such a curve turns out to be given by the genus-degree formula
One can sketch a proof of this using the Riemann-Hurwitz formula. For simplicity of notation let us assume that the polynomial is in “general position” in a number of senses that we will not specify precisely. We can form a holomorphic map
by mapping to
. Generically, this will be a non-constant map of degree
. The critical points will be those points
such that
vanishes. As
is irreducible of degree
, and
is irreducible of degree
, then Bezout’s theorem will tell us that (generically) there will be
critical points
, each of multiplicity one (so
at each such point
). Applying the Riemann-Hurwitz formula, one concludes that
since and
, this gives the genus-degree formula.
To construct linearly independent holomorphic
-forms on
one can argue as follows. The cases
follow from Exercise 8, can be worked out by hand, so suppose
. On the projective line
, the meromorphic function
has a simple pole at
, while its differential
has a double pole at
(and no zeroes). Pulling back by
, we see that the meromorphic
-form
on
has double poles at each of the
preimages of
(making the genericity hypothesis they are distinct and non-degenerate), and also acquire a simple zero at each of the
zeroes of
. This implies that for any polynomial
of degree at most
, the
-form
is well-defined and holomorphic on the projective curve ) (we have killed all the poles and removed the simple zeroes, while possibly creating new zeroes where
vanishes). The space of such polynomials has dimension
, giving the claim.
It remains to remove the condition that and
be effective to obtain the Riemann-Roch theorem in full generality. We first prove a weaker version known as Riemann’s inequality:
Proposition 42 (Riemann’s inequality) Let
be a compact Riemann surface of genus
, and let
be a divisor. Then
.
Proof: Let be a canonical divisor. Choose a non-zero effective divisor
such that
. We will show that
since from Lemma 19 we have , and
, Riemann’s inequality will follow after a brief calculation.
Dividing through by a meromorphic -form of divisor
, we see that
is the dimension of the space
of meromorphic
-forms with divisor at least
. If
with
,
is the space of meromorphic
-forms
that have poles of order at most
at each
, and no other poles.
As in the proof of Proposition 32, let be the space of tuples
with
complex; this has dimension
, and there is a linear map
that takes a meromorphic
-form
in
to the tuple of its principal parts at points in
. The image is constrained by Proposition 24(i), which forces the residues
to sum to zero. On the other hand, by taking linear combinations of the meromorphic
-forms from Exercise 37 and Propsosition 38, we see conversely that any tuple in
whose residues sum to zero lies in the image of
. Thus the image of
has dimension
. On the other hand, the kernel of
is simply the space of holomorphic
-forms, which has dimension
. The claim follows.
Now we prove the Riemann-Roch theorem. We split into cases, depending on the dimensions of and
.
First suppose that and
are both positive dimensional. By Exercise 18,
is linearly equivalent to an effective divisor, hence by Proposition 32 we have
and similarly (replacing by
and the claim then follows by using .
Now suppose that and
are both trivial. Riemann’s inequality then gives
which (again using ) gives
, and the claim again follows.
Now suppose that is trivial but
is positive dimensional. From Exercise 18 and Proposition 32 as before we have
while from Riemann’s inequality and the triviality of we have
giving the claim. The final case when is trivial and
is positive dimensional then follows by swapping
with
.
Exercise 43 Let
be a compact Riemann surface of genus one, and let
be a point on
. Show that for any points
on
, there is a unique point
on
such that
is a principal divisor. Furthermore show that this defines an abelian group law on
. What is this group law in the case that
is an elliptic curve?
Exercise 44 Let
be a compact Riemann surface, and suppose that there exists a meromorphic function
on
with one simple pole and no other poles. Show that
is an isomorphism between
and the Riemann sphere. Conclude in particular that the Riemann sphere is the only genus zero compact Riemann surface (up to isomorphism, of course).
Exercise 45 Let
be a compact Riemann surface of genus
, and let
be a divisor of degree
. Show that
when
is a canonical divisor, and
otherwise.
Exercise 46 (Gap theorems) Let
be a compact Riemann surface of genus
.
- (i) (Weierstrass gap theorem) If
is a point in
, show that there are precisely
positive integers
with the property that there does not exist a meromorphic function on
with a pole of order
at
, and no other poles. Show in addition that all of these integers are less than or equal to
.
- (ii) (Noether gap theorem) If
are a sequence of distinct points in
, show that there are precisely
positive integers
with the property that there does not exist a meromorphic function with a simple pole at
, at most a simple pole at
, and no other poles. Show in addition that all of these integers are less than or equal to
.
— 5. Appendix: connectedness of irreducible algebraic curves —
In this section we prove
Theorem 47 Let
be an irreducible homogeneous polynomial of degree
. Then
is connected.
We begin with the affine version of this theorem:
Proposition 48 Let
be an irreducible polynomial of degree
. Then the affine curve
is connected.
We observe that this theorem fails if one replaces the complex numbers by the real ones; for instance, the quadratic polynomial is irreducible, but the hyperbola it defines in
is disconnected. Thus we will need properties of the complex numbers that are not true for the reals. We will rely in particular on the fundamental theorem of algebra, the removability of bounded singularities, the generalised Liouville theorem that entire functions of polynomial growth are polynomial, and the fact that the complex numbers remain connected even after removing finitely many points.
We now prove the proposition. We will use the classical approach of thinking of as a branched
-fold cover over the complex numbers, possibly after some preparatory change of variables; the main difficulty is then to work around the ramification points of this cover. We turn to the details. Let
be an irreducible polynomial of degree
, then we can write it as
where for ,
lies in the space
of polynoimals of one variable of degree at most
. In particular
is a constant. It could happen that this constant vanishes (e.g., consider the example
and
); but in that case we will make a change of variables and consider instead the polynomial
for a complex parameter
. Now the analogue of
is a non-trivial polynomial function of
(because one of the
must have degree exactly
), and so this quantity will be non-zero for some
(in fact for all but at most
values of
).
Henceforth we assume we have placed into a form where
is non-zero. Then, for each
, the function
is a polynomial of one variable of degree exactly
, so it has
roots (counting multiplicity) by the fundamental theorem of algebra. Let us call these set of roots
, thus
and
From Rouché’s theorem we know that the zero set varies continuously in in the following sense: for any
and
, each point of
will stay within
of some point in
if
is sufficiently close to
. (In other words,
is continuous with respect to Hausdorff distance.) We also see that the elements in
grow at most polynomially in
. For some values of
, some of these roots in
may be repeated. For instance, if
, then
, which has a double root at
if
or
. However, if this occurs for some
, the the degree
polynomial
and the degree
have a common root
. This only occurs when the resultant
of
and
vanishes. (One can also use the discriminant of
here in place of the resultant; the two are constant multiples of each other.) From the definition of the resultant we see that
is a polynomial in
, and furthermore we have a Bezout identity
where are polynomials of degree at most
and
in
respectively, with coefficients that are polynomials in
. The resultant cannot vanish identically, as this would mean that
divides
viewed as polynomials in
, which contradicts unique factorisation and the irreducibility of
since
cannot divide the lower degree polynomials
or
. Thus the resultant can only vanish for a finite number of
, and so for all but finitely many
the roots of
are distinct, thus
has cardinality exactly
and
is non-vanishing at each element of
.
From this and the inverse function theorem we see that for outside of a finite number of points (known as ramification points), the set
varies holomorphically with
. Locally, one can thus describe
as a family
of holomorphic functions, although the order in which one labels these points is arbitrary, as one varies
around one of the ramification points, theis ordering may be permuted (consider for instance the case
as
goes around the origin, in which we can write
for various branches of the square root function).
Now suppose that is disconnected, so it splits into two non-empty clopen subsets
. At each non-ramified point
, the set
meets some subset of
. In local coordinates, the
are distinct and vary continuously with
, the number of points in which
meets
is locally constant; since
with finitely many points removed is connected, this number is then globally constant, thus there is
such that
has cardinality precisely
. This lets us factor
, where
is the degree
polynomial
and is the degree
polynomial
The coefficients of these polynomials are functions of that vary holomorphically with
outside of the ramification points; they also stay bounded as one approaches these points and grow at most polynomially. Hence (by the generalised Liouville theorem) they depend polynomially on
, thus
and
are in fact a polynomial jointly in
. But this contradicts the irreducibility of
, unless
or
. We conclude that
is connected after deleting its ramification points. But from the continuous dependence of
on
, the ramification points adhere to the rest of
(the zeroes of
are stable under small perturbations, even at points of ramification), so that
is connected, proving the proposition.
Now we prove the theorem. The case can be done by hand, so assume
. Let
be an irreducible homogeneous polynomial of degree
. Then
is an irreducible polynomial of degree
(it cannot be less than
, as this will make
contain a power of
which makes it reducible since
). As a consequence, we see from the proposition that the affine part
is connected; similarly if we replace the condition
with
and
. As these three pieces of
cover the whole zero locus, it will suffice to show that they intersect each other; for instance, it will suffice to show that the zero set of
is not completely contained in any line. But this is clear from the proof of the proposition, which shows that (after a linear transformation) almost every vertical line meets this zero set in
points.

65 comments
Comments feed for this article
28 March, 2018 at 3:45 pm
Victor Wang
Here is an elementary approach to removing the effectiveness assumption on D, K-D.
Let lowercase l(D) := dim L(D). We assume g = l(K) (and perhaps also deg(K) = 2g-2), in addition to the following two results:
– l(D) >= 1 + deg(D) – g (Riemann’s inequality, for arbitrary divisors D); and the more important
– l(D) <= 1 + deg(D) – g + l(K-D) (for D effective; I think this is your "Baby Riemann Roch theorem" above).
To proceed, observe that l(D) is nonzero if and only if D is linearly equivalent to some effective divisor. Now break into three cases:
(1) If l(D), l(K-D) are both nonzero, just apply the second inequality once to an eff. representative of D, and once to an eff. representative of K-D (noting that deg(K) = 2g-2, proven e.g. by taking D = 0 and D = K in the second inequality, or indirectly through Riemann-Hurwitz).
(2) Similarly, Riemann's inequality addresses the case of l(D) = l(K-D) = 0. Indeed, the vanishing of l's implies deg(D) <= g-1 and deg(K-D) <= g-1; but deg(K) = 2g-2, so in fact deg(D) = deg(K-D) = g-1. This is consistent (!) with the Riemann-Roch theorem, which resolves this case seemingly without any work.
(3) Finally, it's enough to address l(D) nonzero but l(K-D) = 0 (note that deg(K) = 2g-2 shows the symmetry of RR with D, K-D flipped), in which case Riemann's inequality and the second inequality actually do match up.
The best elementary resource I know is the sequence of exercises in Appendix A. The Riemann-Roch Theorem, Hodge Theorem, and … of Arbarello, E., Cornalba, M., Griffiths, P., Harris, J.D., "Geometry of Algebraic Curves" Volume I (available on Springer), starting p. 50.
I wasn't able to make everything rigorous the last time I worked through it (esp. in the first few exercises), but overall it felt convincing and enlightening. See in particular Exercise 13 for Riemann's inequality, and the key exercises 7, 8, and 10 earlier for understanding the genus and l(K), even allowing nodal singularities. (Unfortunately, there are several typos in this sequence of exercises, e.g. off-by-one errors.)
If memory serves, the idea in the "… case of a smooth algebraic curve of degree… killed all the poles and removed the simple zeroes, while possibly creating new zeroes… space of such polynomials has dimension" part of the blog post above is enough for Exercises 8 and 13 (the latter being Riemann's inequality). Exercise 7 is the Plucker formula allowing nodal singularities in genus computation, and Exercise 10 is a baby "Hodge theorem" proving, in particular, l(K) = g for the g used in the Riemann-Hurwitz formula.
28 March, 2018 at 6:45 pm
Terence Tao
Thanks for this! So basically the missing ingredient is Riemann’s inequality, I will look into proofs of this inequality and see if I can find anything that is suitable for this class, probably starting with the reference you provided.
28 March, 2018 at 8:57 pm
Victor Wang
Great! Actually, now that I look more carefully, Lecture 6 (9/21) of Akhil’s notes http://www.math.harvard.edu/~amathew/287y.pdf (from a course by Harris) seems to cover most of the details of the argument for Riemann’s lemma, first doing it for smooth case and then with singularities. (I didn’t think to mention these notes earlier since the finishing argument still mentioned “Jacobi inversion”, which we wanted to avoid.)
Also, I misspoke when I said there are several “off-by-one” errors: I didn’t realize that ACGH was using the notation “r(D), dimension of a linear system |D|”, which is 1 less than l(D).
28 March, 2018 at 9:22 pm
Terence Tao
Actually, I managed to derive Riemann’s inequality from the existence of Abelian differentials of the second and third kinds with prescribed principal parts (subject of course to the constraint that the residues sum to zero), which was a fact that I was basically assuming for the discussion anyways, and which also fits nicely with the complex torus discussion where the Weierstrass function is used to generate the required differentials. (Perhaps this is close in fact to Riemann’s original proof, though I think he didn’t quite use Perron’s method to construct the differentials.) So I have updated the notes accordingly.
29 March, 2018 at 9:58 pm
Victor Wang
Oh, I see. I like this perspective, where the principal parts of 1-forms play a “uniform” organizational role (minimizing the need for “genus-dependent” computation). I’m far from an expert, but I don’t know if there’s a simple algebraic way to construct those distinguished differentials in the algebraic setting without assuming Riemann-Roch. I guess it should be possible at least for hyperelliptic curves (including elliptic curves, as you mentioned).
Anyways, here are some minor typos/suggestions in the notes:
– In the first line of the paragraph defining the divisor class group, “(f) is an effective divisor” should be “(f) is a principal divisor”.
– I guess the definition of linearly equivalent should precede Exercise 18 (l(D) > 0 iff…); alternatively, Exercise 18 could be moved either after the definition of linearly equivalent, or even later (e.g. close to Exercise 25).
– Following the proof of Riemann’s inequality, in the first case of the end of the RR proof, the second display l(K-D) – l(K-D) should be l(K-D) – l(D).
[Corrected, thanks – T.]
28 March, 2018 at 4:11 pm
Fred Lunnon
following Thm 32: “holomorhpic” -> “holomorphic” .
following Ex. 35, Prop. 40: “Rouche’s” -> “Rouch\’e’s” .
[Corrected, thanks – T.]
28 March, 2018 at 6:13 pm
pallav123goyal
There’s a typo in Example 2, I guess you mean instead of
instead of  .
.
[Corrected, thanks – T.]
29 March, 2018 at 12:19 am
Anonymous
In the RHS of (6), it seems clearer to have the summands inside parentheses.
[Corrected, thanks – T.]
29 March, 2018 at 2:10 am
Konrad Burnik
Dear professor Tao, I think the statement “all compact connected one-dimensional real manifolds are homeomorphic to the unit circle” should be “all compact connected one-dimensional real manifolds are homeomorphic to the unit circle or to the segment [0,1]”.
29 March, 2018 at 2:30 am
Konrad Burnik
sorry, my last comment it’s true only for compact connected one-dimensional real manifolds with boundary
29 March, 2018 at 3:40 am
Anonymous
It seems that the beginning sentence of proposition 37 is not part of it (it appears also just before the proposition.)
[Corrected, thanks – T.]
29 March, 2018 at 12:54 pm
David Roberts
In Example 3, aren’t the Riemann surfaces isomorphic to the disc the *bounded* simply connected open subsets of the plane?
[Corrected, thanks – T.]
30 March, 2018 at 12:53 pm
christopherlloydsimon
It suffices to ask that they are open, simply connected and different from the whole complex plane.
For instance the upper half plane is biholomorphic to the disc via (z+i)/(z-i).
31 March, 2018 at 11:05 pm
Born
I’m seeing
“Note from Proposition 24 that the *Formula does not parse* constructed by the above proposition automatically have vanishing residue at {P} (in classical language, these are Abelian differentials of the third kind, while the {\omega_{(P)-(Q)}} are Abelian differentials of the second kind).”
[Corrected, thanks – T.]
1 April, 2018 at 6:45 am
John Mangual
I always wondered what was meant by “divisor”. Let’s try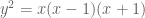 . Then the divisor of
. Then the divisor of  . This this just a way of generalizing partial fractions? This curve doesn’t look very toric to me. Maybe try: $
. This this just a way of generalizing partial fractions? This curve doesn’t look very toric to me. Maybe try: $ $
$ surface in a flat
surface in a flat  4-space. So now I can try to integrate something:
4-space. So now I can try to integrate something: $
$ . Then we could compute the pairing
. Then we could compute the pairing  ?
?
This could also be an
$
and I’ll use a circle of radius 2,
We haven’t even found the number yet. Or explored its properties.
The word “good” in math is like the word “here” or “there”. It doesn’t mean anything by itself, and tells is to read around for a way of telling apart “good” and “bad”.
1 April, 2018 at 9:45 am
Terence Tao
Divisors in algebraic geometry are abstractions of the elementary arithmetic notion of a divisor, in much the same fashion that ideals in commutative algebra are abstractions of numbers. Note for instance that if are non-zero polynomials, then
are non-zero polynomials, then  divides
divides 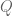 in the ring of polynomials if and only if the divisor
in the ring of polynomials if and only if the divisor  is less than or equal to the divisor
is less than or equal to the divisor  . Algebraic geometry divisors are also closely tied to divisor ideals in commutative algebra; see for instance the answer to this MathOverflow question.
. Algebraic geometry divisors are also closely tied to divisor ideals in commutative algebra; see for instance the answer to this MathOverflow question.
The complex curve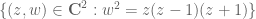 (or more precisely, its projective version
(or more precisely, its projective version ![\{ [z,w,u] \in {\bf CP}^2: w^2 u = z(z-u)(z+u) \}](https://s0.wp.com/latex.php?latex=%5C%7B+%5Bz%2Cw%2Cu%5D+%5Cin+%7B%5Cbf+CP%7D%5E2%3A+w%5E2+u+%3D+z%28z-u%29%28z%2Bu%29+%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) ) is topologically equivalent to a torus. The real slice
) is topologically equivalent to a torus. The real slice  (or more precisely, its projective version
(or more precisely, its projective version ![\{ [x,y,t] \in {\bf RP}^2: y^2 t = x(x-t)(x+t) \}](https://s0.wp.com/latex.php?latex=%5C%7B+%5Bx%2Cy%2Ct%5D+%5Cin+%7B%5Cbf+RP%7D%5E2%3A+y%5E2+t+%3D+x%28x-t%29%28x%2Bt%29+%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) ) is a slice of this torus. More generally, real elliptic curves are to tori as conic sections are to cones. See for instance this note of Arapura on how to visualise elliptic curves as tori.
) is a slice of this torus. More generally, real elliptic curves are to tori as conic sections are to cones. See for instance this note of Arapura on how to visualise elliptic curves as tori.
Let me use for the complex coordinates of
for the complex coordinates of  rather than
rather than  . The divisor of
. The divisor of  in the Riemann sphere is
in the Riemann sphere is  , but the divisor of
, but the divisor of  in the curve
in the curve  , or more precisely (and projectively) the divisor of
, or more precisely (and projectively) the divisor of 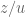 in
in ![X({\bf C}) = \{ [z,w,u]: w^2 u = z(z-u)(z+u)\}](https://s0.wp.com/latex.php?latex=X%28%7B%5Cbf+C%7D%29+%3D+%5C%7B+%5Bz%2Cw%2Cu%5D%3A+w%5E2+u+%3D+z%28z-u%29%28z%2Bu%29%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) , is
, is ![2 \cdot ([0,0,1]) - 2 \cdot ([0,1,0])](https://s0.wp.com/latex.php?latex=2+%5Ccdot+%28%5B0%2C0%2C1%5D%29+-+2+%5Ccdot+%28%5B0%2C1%2C0%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) , as
, as 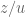 has a double zero at
has a double zero at ![[0,0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) (using
(using 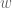 as the smooth coordinate and setting
as the smooth coordinate and setting  , so that
, so that 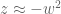 ) and a double pole at
) and a double pole at ![[0,1,0]](https://s0.wp.com/latex.php?latex=%5B0%2C1%2C0%5D&bg=ffffff&fg=545454&s=0&c=20201002) (using
(using  as the smooth coordinate and setting
as the smooth coordinate and setting 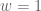 , so that
, so that  ).
).
The fact that “good” does not have a precise pre-assigned meaning in mathematics makes it useful as a nonce, as is done in these notes to denote a concept that is desirable to establish, but will not be needed outside of a single proof.
4 April, 2018 at 10:37 am
Anonymous
You forgot to say that manifolds are second countable.
4 April, 2018 at 11:53 am
Terence Tao
In the context of Riemann surfaces, I generally prefer to omit this condition, as it makes Rado’s theorem easier to state. Of course, once one has that theorem, the question of whether to impose second countability on Riemann surfaces becomes moot. (But I’ve added a parenthetical remark on how in other areas of mathematics it can be convenient to impose the second countability hypothesis.)
4 April, 2018 at 12:53 pm
M. Klazar
In Definition 1 (map f from M to M’) there should be, I think,
phi_{alpha}(U_{alpha}cap…) in place of
V_{alpha}cap(phi)_{\alpha}(…).
[Corrected, thanks – T.]
5 April, 2018 at 1:39 am
j.c.
There’s a typo before Lemma 19. “(i.e. D contains at least one pole)” should be something like “ has at least one pole.”
has at least one pole.”
[Corrected, thanks – T.]
5 April, 2018 at 11:33 am
j.c.
Perhaps in the correction you meant to say that D has positive order at at least one point?
[Corrected, thanks – T.]
7 April, 2018 at 9:15 am
Aula
In Example 2, it would be clearer to change “any discrete subgroup” to “any discrete additive subgroup” since it is also possible to take quotients of by discrete multiplicative subgroups for which the given additive atlas construction won’t work.
by discrete multiplicative subgroups for which the given additive atlas construction won’t work.
In the last sentence above Remark 15, I think should be
should be  instead.
instead.
[Corrected, thanks – T.]
8 April, 2018 at 10:51 pm
Anonymous
I believe there is a typo after Definition 10. The charts should map into $C$ not $X$.
[Corrected, thanks – T.]
9 April, 2018 at 7:49 am
Alstav Trivas Sava
Dear Prof Tao,
I would firstly like to apologize for posting this question at the wrong place, but I had to do so because I wasn’t sure if you’re busy schedule would allow you to answer the questions posted on the ‘Career Advice’ and related sections of your blog.
Sir, I am a high school student, and I aspire to become a mathematician. I wanted to know if research Mathematics is just as intuitive as high school level mathematics? Of course, the ability to develop an intuition for a certain concept depends on the person who is trying to do so. But is it always possible to develop an intuition at all?
And secondly, I wanted to know what is more important for mathematicians with respect to solving unsolved problems:
1) Finding one of the possible solutions, or
2) Finding an “elegant” solution.
(Here by elegant, I mean a solution which gives you such a deep insight into the problem, that the problem seems to be trivial, and intuitively true.)
Thanks a lot, Professor. You’re an inspiration and a source of enlightenment to many!
Yours truly,
Vatsal Srivastava.
10 April, 2018 at 7:08 am
dopemathblog
In reference to Ex 21: How is L(m* (\infity)) be the space of polynomials of degree at most m when m is negative? Are we thinking of rational functions as polynomials of negative degree? Or do polynomials have their usual definition- limited to positive, finite degree?
10 April, 2018 at 8:23 am
Terence Tao
By convention, the zero polynomial has degree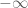 , all other constant polynomials have degree 0, and the remaining polynomials have positive degree. Other rational functions are not considered to be polynomials.
, all other constant polynomials have degree 0, and the remaining polynomials have positive degree. Other rational functions are not considered to be polynomials.
10 April, 2018 at 4:26 pm
dopemathblog
I see now…. The only possible principal divisors (f) such that (f) + m*(\infinity) is effective are the divisors f for which f has no poles (i.e n=0 in the expansion of f given in Ex 13) Therefore, f = a(z- z1)…(z-zS) ) (f) = (1)z1 + …+(1)zS + -S*(\infity). So that (f) + m*(\infity) effective only when -S \geq – m => S \leq m. Thus f is a (pole-free) meromorphic function having total degree \leq m. []
10 April, 2018 at 4:42 pm
Dan Asimov
In Exercise 44, part i), “pole of order n at X” should apparently read “pole of order n at P”.
[Corrected, thanks – T.]
11 April, 2018 at 10:59 pm
Anonymous
In Definition 22 of a meromorphic 1 form, in the second paragraph regarding order of poles, it should state that $\phi$ is a chart whose domain contains $P$, not $U.$
[Corrected, thanks – T.]
12 April, 2018 at 8:28 pm
Anonymous
For exercise 28, the point [1,0,0] lies on the elliptic curve but is clearly not attained from the mapping (hence contradicting surjectivity). I assume there should be some reordering of the variables.
13 April, 2018 at 7:11 am
Terence Tao
Oops, you are right,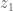 and
and  needed to be interchanged.
needed to be interchanged.
12 April, 2018 at 9:17 pm
Pallav Goyal
In the sentence between Remark 15 and Corollary 16, you probably mean rather than
rather than  .
.
14 April, 2018 at 4:44 am
John Mangual
Can we find examples where ? I have been looking at Riemann surfaces $y^m = (x-a_1)(x-a_2)(x-a_3)(x – a_4)$ possibly with
? I have been looking at Riemann surfaces $y^m = (x-a_1)(x-a_2)(x-a_3)(x – a_4)$ possibly with  . These examples I found in a paper of Curtis McMullen called “Braid Groups and Hodge Theory” seem to be related to the braid group.
. These examples I found in a paper of Curtis McMullen called “Braid Groups and Hodge Theory” seem to be related to the braid group.
Then maybe we could choose a divisor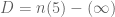 . I still have to check your theorems to make sure that we don’t already have
. I still have to check your theorems to make sure that we don’t already have  in those cases.
in those cases.
I can prove these are Riemann surfaces by using the projection map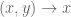 but this is only well-defined if we don’t cross certain line segments at the real axis. So I have a chart made of
but this is only well-defined if we don’t cross certain line segments at the real axis. So I have a chart made of 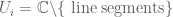 . Unfortunately, computers aren’t nuanced enough to remember which sheet of the branch cover we are using and the sign jumps as I cross around the real axis. E.g.
. Unfortunately, computers aren’t nuanced enough to remember which sheet of the branch cover we are using and the sign jumps as I cross around the real axis. E.g.  this is already a problem.
this is already a problem.
The idea is we have a wealth of examples of Holomorphic vector bundles. Which is crucial.
15 April, 2018 at 6:52 pm
Anonymous
In exercise 41, what conditions should be placed on ? If
? If  is the Riemann sphere, then it seems that any point
is the Riemann sphere, then it seems that any point  would have the property that
would have the property that  is principal.
is principal.
15 April, 2018 at 10:07 pm
Terence Tao
Oops! The key assumption that the surface has genus 1 was omitted.
[Edit: I now realise that this exercise requires an additional assertion, namely that quasiconformal maps are absolutely continuous along lines, which is now included in the notes. -T.]
15 April, 2018 at 8:49 pm
Lexing Ying
Right after equation (6), should the divisor of the Weierstrass {p}-function be two poles plus two zeros? Thanks!
[Corrected, thanks – T.]
16 April, 2018 at 9:32 am
Maths student
Dear Prof. Tao,
As promised, I’m now reading the notes and will post any typos as I read along.
I’ve also noticed that each manifold is automatically (indeed locally Hausdorff implies
(indeed locally Hausdorff implies  , but not Hausdorff, as can be seen by the line with doubled origin), so that one could require
, but not Hausdorff, as can be seen by the line with doubled origin), so that one could require  instead of Hausdorff.
instead of Hausdorff.
17 April, 2018 at 5:56 am
Maths student
I was trying to prove that in fact, a compact, connected Hausdorff manifold was in fact diffeomorphic to a circle (I could handle the homeomorphic part, by using the argument that one may choose finitely many charts, eliminate superfluous charts, prove that the set of those elements not covered by any chart is a connected interval, and then define the homeomorphism using a closed, continuous, bijective loop). It seems as though we might use some convolution with some smooth kernel; monotonicity at the points where the loop was smooth before is preserved since the convolution of two positive functions is positive, and the remainder we do by continuity. (Note: Zero at an isolated point does not harm strict monotonicity.)
The definition of holomorphic atlases of course works in greater generality.
I read in the elementary book of M. Artin that there are a limited number of discrete groups in the plane. In fact, one can restrict to lattices in 0-d, 1-d and 2-d.
In example 2, the “plus” notation is bold and seems to indicate the standard action of on
on  . The example seems to show that there are plenty holomorphic structures on a topological torus.
. The example seems to show that there are plenty holomorphic structures on a topological torus.
17 April, 2018 at 11:24 am
Maths student
In example 6, nonsingular curves are weirdly defined. There is a reference to “three numbers”, but only “two” or “four” gives a reasonable interpretation. (Neither seems enough to deduce that the gradient does not vanish in the case of interest, and they are further equivalent.) In order to get the gradient nonzero in the subsequent section, one needs that![[z_1, z_2, 1]](https://s0.wp.com/latex.php?latex=%5Bz_1%2C+z_2%2C+1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is contained in the set of zeroes, I suppose?
is contained in the set of zeroes, I suppose?
[Corrected, thanks – T.]
18 April, 2018 at 12:45 pm
Maths student
Dear Prof. Tao, in example 13, it seems as though the extension of any meromorphic functions that have their singularities contained in a bounded set is meromorphic on , for the simple reason that
, for the simple reason that  is then a point isolated away from the other singularities. The argument given (theone about
is then a point isolated away from the other singularities. The argument given (theone about 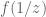 seems to indicate that
seems to indicate that  is a rational function in all charts of the atlas that we had constructed.
is a rational function in all charts of the atlas that we had constructed.
But very fun lecture notes!
18 April, 2018 at 3:51 pm
Terence Tao
Meromorphicity requires more than just having isolated singularities; these isolated singularities also need to be poles rather than essential singularities. For instance, the exponential function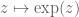 is entire on the complex plane, but does not extend meromorphically to the Riemann sphere (using the chart variable
is entire on the complex plane, but does not extend meromorphically to the Riemann sphere (using the chart variable 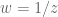 to analyse the behaviour near infinity, we obtain an essential singularity
to analyse the behaviour near infinity, we obtain an essential singularity 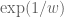 at the origin).
at the origin).
19 April, 2018 at 12:18 am
Maths student
How could I miss this? Of course!
19 April, 2018 at 12:29 am
Maths student
Here’s a real typo: In the displaystyle equation before example 23 (in FF Strg+F gets you to the centered point) is not actually a function on
is not actually a function on  .
.
[Corrected, thanks – T.]
15 May, 2018 at 5:40 pm
Scott Lawrence
In Exercise 17, perhaps it should say that $f$ and $g$ are both defined on a compact Riemann surface?
15 May, 2018 at 6:16 pm
Scott Lawrence
Ah, this is implicit in the definition of divisor, of course. Apologies.
16 January, 2019 at 6:38 am
Martin Stoller
Thank You very much for these great notes, Prof. Tao, I learned a lot from them.
Some remarks:
In the proof of Riemann’s inequality, I think the intermediate claim that the dimension of L(K+D’) equals deg(D’) + g -1 should be replaced by the weaker claim that dim(L(K+D’)) is at least deg(D’) + g -1 (which is enough to prove the Proposition), because the kernel of the map T considered later only *contains* the space of holomorphic one forms, so has dimension at least g.
Just before Exercise 25, I think “meromorphic function” should be replaced by “meromorphic 1-form”.
In Lemma 27, part (ii), a minus sign is miss-typed. It should be dim(L(D)) = dim(L(-D)).
[Corrected, thanks – T.]
16 January, 2019 at 10:03 am
Martin Stoller
Never mind about the first comment on Riemann’s inequality. No changes have to be made there. Apologies.
4 August, 2019 at 1:16 pm
Dan Asimov
In Example 2, line -3, it appears the U should be U_α.
4 August, 2019 at 1:18 pm
Dan Asimov
I withdraw my comment.
14 August, 2019 at 10:17 pm
John Baez
A typo: “triangulartion”.
[Corrected, thanks – T.]
25 August, 2019 at 8:15 am
matemático joven
One may also prove Liouville’s theorem from Lemma 11: If is entire, then the Riemann theorem on removable singularities implies that it extends to a holomorphic function on the compact Riemann surface
is entire, then the Riemann theorem on removable singularities implies that it extends to a holomorphic function on the compact Riemann surface 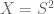 .
.
12 August, 2020 at 3:02 pm
Thomas
« … Stokes’ theorem we conclude that the integral of {\gamma} around the sum of … » I guess you meant the integral of {\omega} there.
(btw if anyone has trouble understanding this affirmation, it is detailed there https://math.stackexchange.com/a/446273/23001)
[Corrected, thanks – T.]
18 December, 2020 at 7:48 am
Max
I appreciate that you took extra care in making the distinction between functions on the Riemann surface and their coordinate representations in a specific chart in defining meromorphic forms. It is distressingly common in books on Riemann surfaces to have something like , where
, where 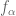 is a function on an open set
is a function on an open set 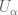 , and
, and  is a chart map, and then launching into computations as if
is a chart map, and then launching into computations as if 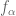 were a function defined on an open set in
were a function defined on an open set in  . Why do you think this is so common, when it presents so much difficulties to the beginner?
. Why do you think this is so common, when it presents so much difficulties to the beginner?
2 February, 2021 at 7:03 pm
246B, Notes 3: Elliptic functions and modular forms | What's new
[…] law governing meromorphic functions on other compact Riemann surfaces (and is discussed further in these 246C notes). So far we have focused on studying a single torus . However, another important mathematical […]
27 February, 2021 at 9:40 am
246B, Notes 4: The Riemann zeta function and the prime number theorem | What's new
[…] Previous set of notes: Notes 3. Next set of notes: 246C Notes 1. […]
27 February, 2021 at 9:48 am
246C notes 2: Circle packings, conformal maps, and quasiconformal maps | What's new
[…] set of notes: Notes 1. Next set of notes: Notes 3. We now leave the topic of Riemann surfaces, and turn now to the […]
19 February, 2022 at 12:58 am
Georges Elencwajg
Dear Terence,
thank you for this splendid synthesis in your inimitable style.
An infinitesimal nitpick: in Definition 2, line -4 the two equalities do not make sense because you cannot add alpha, an equivalence class of complex numbers, to a genuine complex number z (belonging to the open subset U of the complex plane).
11 March, 2022 at 9:30 am
Anonymous
In section 2, “Formula does not parse” in the last sentence of:
On the other hand, several other basic notions in complex analysis do not seem to be well defined for such meromorphic functions. Consider for instance the question of how to define the residue of {f} at a pole {P}. The natural thing to do is to again pick a chart {\phi_\alpha} around {P} and use the residue of {f_\alpha}; however one can check that this is not independent of the choice of chart in general, as from (4) one will find that the residues of {f_\beta} and {f_\alph} are related to each other, but not equal.
[Corrected, thanks – T.]
11 March, 2022 at 12:49 pm
Anonymous
Are there simple examples showing integration of a 1-form coincides (does it?) with the complex integral
coincides (does it?) with the complex integral 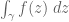 introduced in 246A?
introduced in 246A?
11 March, 2022 at 12:56 pm
Anonymous
Formally, it seems that one can simply let to connect these two notions.
to connect these two notions.
You also mentioned “line integrals” are integral of forms in the set of 246A notes (Remark 19): https://terrytao.wordpress.com/2016/09/27/246a-notes-2-complex-integration/
I am wondering if that has anything to do with the integral here.
11 March, 2022 at 2:37 pm
Terence Tao
Yes, contour integrals can be viewed as an integral of a (complex) 1-form on the complex plane, at least when the contour is piecewise smooth. Contour integrals are also a special case of line integrals (writing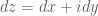 ).
).
17 February, 2023 at 11:55 am
Thomas
After equation (6), you say *this descends to a meromorphic function on … with divisor …* and mention a divisor which has degree 2 (just after you proved it should have degree 0, which is confusing).
I suppose the Weierstrass function must have zeroes somewhere…
[Typos corrected – T.]
17 April, 2023 at 8:09 pm
Facts about divisors on a compact Riemann surface – Mathematics – Forum
[…] am trying to prove the following question from here without relying on the Riemann-Roch […]
17 April, 2023 at 11:43 pm
Question about divisors on a compact Riemann surface – Mathematics – Forum
[…] am trying to prove the following question from here without relying on the Riemann-Roch […]
18 April, 2023 at 1:01 am
Sam
Dear Professor Tao,
Beginning on line 3 of lemma 27, you wrote that “…that is to say a simple pole at {P} and a simple zero at {Q}. But this follows from Proposition 24(i) (and identifying meromorphic functions with meromorphic {1}-forms) since the residue at {P} is non-zero.” Do you mean to write “a simple zero at {P} and a simple pole at {Q}” and “the residue at {Q} is non-zero” for the divisor D = (P) – (Q)? I would be thankful if you could point out if I am confusing myself. Thank you
[This was a typo, now corrected, thanks – T.]