The primary objective of this lecture and the next few will be to give a proof of the Furstenberg recurrence theorem (Theorem 2 from the previous lecture). Along the way we will develop a structural theory for measure-preserving systems.
The basic strategy of Furstenberg’s proof is to first prove the recurrence theorems for very simple systems – either those with “almost periodic” (or compact) dynamics or with “weakly mixing” dynamics. These cases are quite easy, but don’t manage to cover all the cases. To go further, we need to consider various combinations of these systems. For instance, by viewing a general system as an extension of the maximal compact factor, we will be able to prove Roth’s theorem (which is equivalent to the k=3 form of the Furstenberg recurrence theorem). To handle the general case, we need to consider compact extensions of compact factors, compact extensions of compact extensions of compact factors, etc., as well as weakly mixing extensions of all the previously mentioned factors.
In this lecture, we will consider those measure-preserving systems which are compact or almost periodic. These systems are analogous to the equicontinuous or isometric systems in topological dynamics discussed in Lecture 6, and as with those systems, we will be able to characterise such systems (or more precisely, the ergodic ones) algebraically as Kronecker systems, though this is not strictly necessary for the proof of the recurrence theorem.
— Almost periodic functions —
We begin with a basic definition.
Definition 1. Let
be a measure-preserving system. A function
is almost periodic if the orbit closure
is compact in
.
Example 1. If f is periodic (i.e. for some
) then it is clearly almost periodic. In particular, any shift-invariant function (such as a constant function) is almost periodic.
Example 2. In the circle shift system , every function
is almost periodic, because the orbit closure lies inside the set
, which is the continuous image of a circle
and therefore compact.
Exercise 1. Let be a measure-preserving system, and let
. Show that f is almost periodic in the ergodic theory sense (i.e. Definition 1 above) if and only if it is almost periodic in the topological dynamical systems sense (see Lecture 3), i.e. if the sets
are syndetic for every
. (Hint: if f is almost periodic in the ergodic theory sense, show that the orbit closure is an isometric system and thus a Kronecker system, at which point Theorem 2 from Lecture 3 can be applied. For the converse implication, use the Heine-Borel theorem and the isometric nature of T on
.)
Exercise 2. Let be a measure-preserving system. Show that the space of almost periodic functions in
is a closed shift-invariant subspace which is also closed under the pointwise operations
and
. Similarly, show that the space of almost periodic functions in
is a closed subspace which is also an algebra (closed under products) as well as closed under
and
.
Exercise 3. Show that in any Bernoulli system , the only almost periodic functions are the constants. (Hint: first show that if
has mean zero, then
, by first considering elementary functions.
Let us now recall the Furstenberg recurrence theorem, which we now phrase in terms of functions rather than sets:
Theorem 1. (Furstenberg recurrence theorem) Let
be a measure-preserving system, let
, and let
be a non-negative function with
. Then we have
.
Exercise 4. Show that Theorem 1 is equivalent to Theorem 2 from the previous lecture.
We can now quickly establish this theorem in the almost periodic case:
Proposition 1. Theorem 1 is true whenever f is almost periodic.
Proof. Without loss of generality we may assume that f is bounded a.e. by 1. Let be chosen later. Recall from Exercise 1 that
lies within
of f in the
topology for a syndetic set of n. For all such n, one also has
for all j, since T acts isometrically. By the triangle inequality, we conclude that
lies within
of f in
for
. On the other hand, from Hölder’s inequality we see that on the unit ball of
with the
topology, pointwise multiplication is Lipschitz. Applying this fact repeatedly, we conclude that for n in this syndetic set,
lies within
in
of
. In particular,
. (1)
On the other hand, since , we must have
. Choosing
sufficiently small, we thus see that the left-hand side of (1) is uniformly bounded away from zero in a syndetic set, and the conclusion of Theorem 1 follows.
Remark 1. Because f lives in a Kronecker system, one can also obtain the above result using various multiple recurrence theorems from topological dynamics, such as Proposition 3 from Lecture 6 or the Birkhoff multiple recurrence theorem from Lecture 4 (though to get the full strength of the results, one needs to use either syndetic van der Waerden theorem, see Exercise 15.3 from Lecture 5, or the Varnavides averaging trick from the previous lecture). We leave the details to the reader.
— Kronecker systems and Haar measure —
We have seen how nice almost periodic functions are. Motivated by this, we define
Definition 2. A measure-preserving system
is said to be compact if every function in
is almost periodic.
Thus, for instance, by Example 2, the circle shift system is compact, but from Exercise 3, no non-trivial Bernoulli system is compact. From Proposition 1 we know that the Furstenberg recurrence theorem is true for compact systems.
One source of compact systems comes from Kronecker systems, as introduced in Lecture 6. As such systems are topological rather than measure-theoretic, we will need to endow them with a canonical measure – Haar measure – first.
Let G be a compact metrisable topological group (not necessarily abelian). Without an ambient measure, we cannot yet define the convolution of two continuous functions
. However, we can define the convolution
of a finite Borel measure
on G and a continuous function
to be the function
(2)
which (by the uniform continuity of f) is easily seen to be another continuous function. We similarly define
(2′)
Also, one can define the convolution of two finite Borel measures to be the finite Borel measure defined as
(3)
for all Borel sets E. For instance, the convolution of two Dirac masses is another Dirac mass
. Fubini’s theorem tells us that the convolution of two finite measures is another finite measure. Convolution is also bilinear and associative (thus
,
,
, and
for measures
and continuous f); in particular, left-convolution and right-convolution commute. Also observe that the convolution of two Borel probability measures is again a Borel probability measure. Convolution also has a powerful smoothing effect that can upgrade weak convergence to strong convergence. Specifically, if
converges in the vague sense to
, and f is continuous, then an easy application of compactness of the underlying group G reveals that
converges in the uniform sense to
.
Let us say that a number c is a left-mean (resp. right-mean) of a continuous function if there exists a probability measure
such that
(resp.
) is equal to a constant c. For compact metrisable groups G, this mean is well defined:
Lemma 1. (Existence and uniqueness of mean) Let G be a compact metrisable topological group, and let
. Then there exists a unique constant c which is both a left-mean and right-mean of f.
Proof. Without loss of generality we can take f to be real-valued. Let us first show that there exists a left-mean. Define the oscillation of a real-valued continuous function to be the difference between its maximum and minimum. By the vague sequential compactness of probability measures (Lemma 1 from Lecture 7), one can find a probability measure which minimises the oscillation of
. If this oscillation is zero, we are done. If the oscillation is non-zero, then (using the compactness of the group and the transitivity of the group action) it is not hard to find a finite number of left rotations of
whose average has strictly smaller oscillation than that of
(basically by rotating the places where
is near its maximum to cover where it is near its mimum). Thus we have a finitely supported probability
with
having smaller oscillation than
, a contradiction. We thus see that a left-mean exists. Similarly, a right-mean exists. But since left-convolution commutes with right-convolution, we see that all left-means are equal to all right-means, and the claim follows.
The map from a continuous function to its mean is a bounded non-negative linear functional on C(G) which preserves constants, and thus by the Riesz representation theorem is given by a unique probability measure
; since left- and right-convolution commute, we see that this measure is both left- and right- invariant. Conversely, given any such measure
we easily see (again using the commutativity of left-and right-convolution) that
. We have thus shown
Corollary 1. (Existence and uniqueness of Haar measure) If G is a compact metrisable topological group, then there exists a unique Borel probability measure
on G which is both left and right invariant.
In particular, every topological Kronecker system can be canonically converted into a measure-preserving system, which is then compact by the same argument used to establish Example 2. (Actually this observation works for non-abelian Kronecker systems as well as abelian ones.)
Remark 2. One can also build left- and right- Haar measures for locally compact groups; these measures are locally finite Radon measures rather than Borel probability measures, and are unique up to constants; however it is no longer the case that such measures are necessarily equal to each other except in special cases, such as when the group is abelian or compact. These measures play an important role in the harmonic analysis and representation theory of such groups, but we will not discuss these topics further here.
— Classification of compact systems —
We have just seen that every Kronecker system is a compact system. The converse is not quite true; consider for instance the disjoint union of two Kronecker systems from different groups (with the probability measure being split, say, 50-50, between the two components). The situation is similar to that in Lecture 6, in which every Kronecker system was equicontinuous and isometric, but the converse only held under the additional assumption of minimality. There is a similar situation here, but first we need to define the notion of equivalence of two measure-preserving systems.
Define an abstract measure-preserving system to be an abstract separable
-algebra
(which, by Stone’s theorem, can be viewed as consisting of subsets of some ambient space X, though for our purposes it is better here to stay in the abstract world), together with an abstract probability measure
and an abstract invertible shift
which preserves the measure
(but does not necessarily come from an invertible map
on some ambient space). (An abstract measure space
is sometimes also known as a measure algebra.) There is an obvious notion of a morphism
between abstract measure-preserving systems, in which
(note the contravariance) is a
-algebra homomorphism with
and
. This makes the class of abstract measure-preserving systems into a category. In particular we have a notion of two abstract measure-preserving systems being isomorphic.
Example 3. Let be a skew shift
and let
be the underlying circle shift
. These systems are of course non-isomorphic, although there is a factor map
which is a morphism. If however we consider the
-algebra
(which are the Cartesian products of horizontal Borel sets with the vertical circle
), we see that
induces an isomorphism between the abstract measure-preserving systems
and
.
Given a concrete measure-preserving system , we can define its abstraction
, where
is the equivalence relation of almost everywhere equivalence modulo
. In category theoretic language, abstraction is a covariant functor from the category of concrete measure-preserving systems to the category of abstract measure-preserving systems. We say that two concrete measure-preserving systems are equivalent if their abstractions are isomorphic. Thus for instance, in Example 3 above,
and
are equivalent; there is no concrete isomorphism between these two systems, but once one abstracts away the underlying sets X and Y, we can recover an equivalence. As another example, we see that if we add or remove a null set to a measure-preserving system, we obtain an abstractly equivalent measure-preserving system.
Remark 3. Up to null sets, we can also identify an abstract measure-preserving system with its abelian von Neumann algebra
(which acts on the Hilbert space
by pointwise multiplication), together with an automorphism T of that algebra; conversely, one can recover the algebra
as the idempotents
of the von Neumann algebra, and the measure
of a set being the trace of the idempotent
. A significant portion of ergodic theory can in fact be rephrased in terms of von Neumann algebras (which, in particular, naturally suggests a non-commutative generalisation of the subject), although we will not adopt this perspective here.
Many results and notions about concrete measure-preserving systems can be rephrased to not require knowledge of the underlying space X (and to be stable under modification by null sets), and so can be converted to statements about abstract measure-preserving systems; for instance, the Furstenberg recurrence theorem is of this form once one replaces “non-empty” with “positive measure” (see Exercise 1 from Lecture 10). The notion of ergodicity is also of this form. In particular, such results and notions automatically become preserved under equivalence. In view of this, the following classification result is of interest:
Theorem 2. (Classification of ergodic compact systems) Every ergodic compact system is equivalent to an (abelian) Kronecker system.
To prove this theorem, it is convenient to use a harmonic analysis approach. Define an eigenfunction of a measure-preserving system to be a bounded measurable function f, not a.e. zero, such that
a.e..
Let denote the
-algebra generated by all the eigenfunctions. Note that this contains
, which is the
-algebra generated by the eigenfunctions with eigenvalue 1. We have the following fundamental result:
Proposition 2. (Description of the almost periodic functions) Let
be an ergodic measure-preserving system, and let
. Then f is almost periodic if and only if it lies in
, i.e. if it is
-measurable (note that
contains all null sets of
).
Remark 4. One can view as the maximal compact factor of
, in much the same way that
is the maximal factor on which the system is essentially trivial (every function is essentially invariant).
Proof. It is clear that every eigenfunction is almost periodic. From repeated application of Exercise 2 we conclude that the indicator of any set in is also almost periodic, and thus (by more applications of Exercise 2) every function in
is almost periodic.
Conversely, suppose is almost periodic. Then the orbit closure
of f is an isometric system; the orbit of f is clearly dense in
, and thus by isometry the orbit of every other point is also dense. Thus
is minimal, and therefore Kronecker by Proposition 1 from Lecture 6; thus we have an isomorphism
from a group rotation
to
. By rotating if necessary we may assume that
.
By Corollary 1, K comes with an invariant probability measure . The theory of Fourier analysis on compact abelian groups then says that
is spanned by an (orthonormal) basis of characters
. In particular, the Dirac mass at 0 (the group identity of K) can be expressed as the weak limit of finite linear combinations of such characters.
Now we need to move this information back to X. For this we use the operator defined by
; one checks from Minkowski’s integral inequality that this is a bounded linear map. Because
is a morphism, and each character is an eigenfunction of the group rotation
, one easily checks that the image
of a character
is an eigenfunction. Since the image of the Dirac mass is (formally) just f, we thus conclude that f is the weak limit of finite linear combinations of characters. (One can in fact use compactness and continuity to make this a strong limit, but this is not necessary here.) In particular, f is equivalent a.e. to a
-measurable function, as desired.
Exercise 5. (Spectral description of Kronecker factor) Show that the product of two eigenfunctions is again an eigenfunction. Using this and Proposition 2, conclude that is in fact equal to
, the closed subspace of the Hilbert space
generated by the eigenfunctions of the shift operator T.
Exercise 6. Let be a measure-preserving system, and let
. We say that f is quasiperiodic if the orbit
lies in a finite-dimensional space. Show that a function is quasiperiodic if and only if it is a finite linear combination of eigenfunctions. Deduce that a function is almost periodic if and only if it is the limit in
of quasiperiodic functions.
Exercise 7. The purpose of this exercise is to show how abstract measure-preserving systems, and the morphisms between them, can be satisfactorily modeled by concrete systems and morphisms.
- Let
be an abstract measure-preserving system. Show that there exists a concrete regular measure-preserving system
which is equivalent to
(thus after omitting X’ and quotienting out both
-algebras by null sets, the two resulting abstract measure-preserving systems are isomorphic); the notion of regularity was defined in Definition 2 of Lecture 9. Hint: take a countable shift-invariant family of sets that generate
(thus T acts on this space by permutation), and use this to create a
-algebra morphism from
to
, the product
-algebra of some boolean space
, endowed with a permutation action T’.
- Let
be an abstract morphism. Show that there exist regular measure-preserving systems
and
equivalent to
and
, together with a concrete morphism
, such that obvious commuting square connecting the abstract
-algebras
quotiented out by null sets does indeed commute.
Remark 6. Exercise 7 (and various related results) show that the distinction between concrete and abstract measure-preserving systems are very minor in practice. There are however other areas of mathematics in which taking an abstract or “point-less” approach by deleting (or at least downplaying) the underlying space can lead to non-trivial generalisations or refinements of the original concrete concept, for instance when moving from varieties to schemes.
Proof of Theorem 2. Note that if f is an eigenfunction then T|f|=|f|, and so (if the system is ergodic) |f| is a.e. constant (which implies also that the eigenvalue lies on the unit circle). In particular, any eigenfunction is invertible. The quotient of two eigenfunctions of the same eigenvalue is then T-invariant and thus constant a.e. by ergodicity, which shows that all eigenspaces have geometric multiplicity 1 modulo null sets. As T is unitary, any eigenfunctions of different eigenvalues are orthogonal to each other; as is separable, we conclude that the number of eigenfunctions (up to constants and a.e. equivalence) is at most countable.
Let be a collection of representative eigenfunctions for some at most countable index set A with eigenvalues
; we can normalise
a.e.. By modifying each eigenfunction on a set of measure zero (cf. Exercise 7 of Lecture 8) we can assume that
and
everywhere rather than just almost everywhere. Then the map
is a morphism from
to the torus
with the product
-algebra
, the push-forward measure
, and the shift
, where
. From Proposition 2 we see that every measurable set in
differs by a null set from a set in the pullback
-algebra
. From this it is not hard to see that
is equivalent to the system
.
Now, is a compact metrisable space. The orbit closure K of
inside this space is thus also compact metrisable. The support of
is shift-invariant and thus K-invariant; but from the ergodicity of
we conclude that the support must in fact be a single translate of K. In particular,
is just a translate of Haar measure on K. From this one easily concludes that
is equivalent to the Kronecker system
with the Borel
-algebra and Haar measure, and the claim follows.
Exercise 8. Let be a compact system which is not necessarily ergodic, and let
be the ergodic decomposition of
relative to the projection
given by Proposition 4 of Lecture 9. Show that
is a compact ergodic system for
-almost every y. From this and Theorem 2, we conclude that every compact system can be disintegrated into ergodic Kronecker systems (cf. the discussion after Proposition 2 of Lecture 6).
Remark 7. We comment here on finitary versions of the above concepts. Consider the cyclic group system with the discrete
-algebra and uniform probability measure. Strictly speaking, every function on this system is periodic with period N and thus almost periodic, and so this is a compact system. But suppose we consider N as a large parameter going to infinity (in which case one can view these systems, together with some function
on these systems, “converging” to some infinite system with some limit function f, as in the derivation of Theorem 3 from Theorem 2 in the previous lecture). Then we would be interested in uniform control on the almost periodicity of the function or the compactness of the system, i.e. quantitative bounds involving expressions such as O(1) which are bounded uniformly in N. With such a perspective, the analogue of a quasiperiodic function (see Exercise 6) is a function
which is a linear combination of at most O(1) characters (i.e. its Fourier transform is non-zero at only O(1) frequencies), whilst an almost periodic function f is one which is approximable in
by quasiperiodic functions, thus for every
one can find a function with only
frequencies which lies within
of f in
norm. Most functions on
for large N are not like this, and so the cyclic shift system is not compact in the asymptotic limit
; however if one coarsens the underlying
-algebra significantly one can recover compactness, though unfortunately one has to replace exact shift-invariance by approximate shift-invariance when one does so. For instance if one considers a
-algebra
generated by a bounded (O(1)) number of Bohr sets
, then
is no longer shift-invariant in general, but all the functions which are measurable with respect to this algebra are uniformly almost periodic in the above sense. For some further developments of these sorts of “quantitative ergodic theory” ideas, see these papers of Ben Green and myself.
[Update, Feb 12: Another exercise and remark added.]
[Update, Feb 13: Examples 1 and 2 corrected.]

23 comments
Comments feed for this article
12 February, 2008 at 7:20 pm
IU student
Dear Dr. Tao,
I am interested in knowing that for what compact systems it can be
 with
with 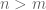
asserted that for any continuous function f, the averages
converge a.e.
12 February, 2008 at 9:11 pm
Terence Tao
Dear IU student,
For Kronecker systems, at least, one can approximate any continuous function uniformly as the finite linear combination of eigenfunctions. For the latter, convergence (in the limit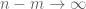 ) is easy to establish, so for general continuous functions we in fact have uniform convergence in this case.
) is easy to establish, so for general continuous functions we in fact have uniform convergence in this case.
I would imagine one has the same result for general compact systems, though one needs to now how the topology of the system interacts with the measure structure. (Note that the notion of equivalence defined above need not preserve topological concepts such as continuity. But at least one can still use the ergodic decomposition to reduce to the ergodic case.)
13 February, 2008 at 9:49 am
Emmanuel Kowalski
I think in examples 1 and 2, the adjective “almost” is missing (“every periodic function is clearly almost periodic”, and “every function is almost periodic”, respectively).
is almost periodic”, respectively).
14 February, 2008 at 9:26 am
Anonymous
Can you give some historical explanation? When was theorem 2 proved and what was reason this was studied?
14 February, 2008 at 4:48 pm
Terence Tao
Dear Emmanuel: Thanks for the corrections!
Dear Anonymous: I am not sure of the historical background of this result; the books and papers that I have read seem to attribute it either to folklore, or to be very classical. Perhaps other readers may know of a more precise origin of this classification of compact ergodic systems, though.
14 February, 2008 at 6:26 pm
Terence Tao
An update to my previous comment: I have now been informed via email (by a friend who is too shy to post directly here :-) ) that Theorem 2 was essentially established by von Neumann and Halmos. More precisely, they showed that any ergodic system in which the spectrum of the shift map is purely discrete is equivalent to a Kronecker system, and the claim then follows from Proposition 2 and Exercise 5 (which are also extremely classical).
Furthermore, the Kronecker system can also be constructed quite explicitly via Pontraygin duality: if is the group of eigenvalues (with the discrete topology) and G is the Pontryagin dual (which is thus compact abelian metrisable), then the inclusion map from
is the group of eigenvalues (with the discrete topology) and G is the Pontryagin dual (which is thus compact abelian metrisable), then the inclusion map from 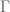 to
to 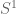 is a character of
is a character of  and thus identifiable with a point
and thus identifiable with a point  on G. Then the proof of Theorem 2 shows that an ergodic compact system is equivalent to the Kronecker system
on G. Then the proof of Theorem 2 shows that an ergodic compact system is equivalent to the Kronecker system  .
.
21 February, 2008 at 8:20 pm
254A, Lecture 12: Weakly mixing systems « What’s new
[…] Hilbert-Schmidt, randomness, Roth’s theorem, strong mixing, van der Corput, weak mixing In the previous lecture, we studied the recurrence properties of compact systems, which are systems in which all measurable […]
27 February, 2008 at 6:25 pm
254A, Lecture 13: Compact extensions « What’s new
[…] compact extensions, Hilbert modules, multiple recurrence, structure, van der Waerden’s theorem In Lecture 11, we studied compact measure-preserving systems – those systems in which every function was almost […]
3 March, 2008 at 8:49 am
254A, Lecture 14: Weakly mixing extensions « What’s new
[…] of a weakly mixing extension. Just as compact extensions are “relative” versions of compact systems, weakly mixing extensions are “relative” versions of weakly mixing systems, in which […]
16 December, 2008 at 6:18 am
liuxiaochuan
Dear Professor Tao:
The label of Examples and Exercises are confused:There are no example 3 and example 4 before example 5.
After definition 2, from”example 3″ should be “exercise 3”;
After example 5, “isomorphism between the these…”, where “the” should be deleted.
In the paragraph before Corollary 1, the first sentence, I don’t see why the mean is non-negative.
16 December, 2008 at 9:00 am
Terence Tao
Thanks for the corrections! If f is non-negative, then is non-negative for every probability measure
is non-negative for every probability measure  , and hence every left-mean of f must also be non-negative.
, and hence every left-mean of f must also be non-negative.
18 December, 2008 at 8:03 am
liuxiaochuan
Dear Professor Tao:
In the proof of theorem 2, the first sentence, why “any eigenfunction is invertible” is true?
18 December, 2008 at 10:49 am
Terence Tao
Dear liuxiaochuan,
If f is an eigenfunction, then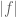 is T-invariant, hence constant; since f is non-zero, this implies that
is T-invariant, hence constant; since f is non-zero, this implies that 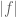 is always non-zero, hence invertible.
is always non-zero, hence invertible.
13 April, 2017 at 2:27 pm
254A, Lecture 15: The Furstenberg-Zimmer structure theorem and the Furstenberg recurrence theorem | What's new
[…] this theorem, the Furstenberg recurrence theorem (Theorem 1 from Lecture 11) follows from the previous theorems and transfinite […]
22 December, 2018 at 6:01 am
Abhishek Khetan
Dear Professor Tao,
In the proof of proposition 2 we have a compact group with Haar measure
with Haar measure  . At one point you have mentioned that since the characters of
. At one point you have mentioned that since the characters of  form an orthonormal basis of
form an orthonormal basis of 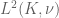 , the “Dirac mass at
, the “Dirac mass at  (the additive identity) can be expressed as a weak limit of a finite linear combinations of these characters.”
(the additive identity) can be expressed as a weak limit of a finite linear combinations of these characters.”
I am not able to follow the meaning of the statement in quotes. The Dirac mass is a probability measure while the characters are maps from to
to  .
.
Is it that we are thinking of the characters as members of and the Dirac mass also as a member of
and the Dirac mass also as a member of  (by means of the Riesz representation theorem)?
(by means of the Riesz representation theorem)?
If so, can you say why one can get the Dirac mass as a weak limit (or perhaps weak* limit?) of a linear combination of characters.
Thank you.
(I apologize if this is a stupid question. I am only starting to learn analysis.)
22 December, 2018 at 9:55 am
Terence Tao
Here I am using the Haar measure to identify locally integrable functions on
to identify locally integrable functions on  with distributions (which in particular allows one to view elements of
with distributions (which in particular allows one to view elements of  , such as linear combinations of characters, as distributions).
, such as linear combinations of characters, as distributions).
Using approximations to the identity, one can express the Dirac distribution as the weak limit of elements of (e.g., one can take
(e.g., one can take  where
where  are a shrinking set of neighbourhoods of the identity), and as the characters form a basis of
are a shrinking set of neighbourhoods of the identity), and as the characters form a basis of  , any such elements can be approximated to arbitrary accuracy by finite linear combinations of characters (in the
, any such elements can be approximated to arbitrary accuracy by finite linear combinations of characters (in the 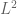 metric). Combining the two statements give the claim.
metric). Combining the two statements give the claim.
24 December, 2018 at 3:09 am
Abhishek Khetan
Dear Professor Tao,
I have a question regarding the notion of a *maximal* factor.
Suppose we have a measure preserving system where
where  is a compact metric space and
is a compact metric space and 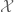 is its Borel
is its Borel  -algebra.
-algebra.
Let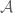 be a sub-
be a sub- -algebra of
-algebra of 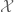 which is invariant under
which is invariant under  . Then we can find a factor
. Then we can find a factor 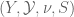 of
of  with factor map
with factor map  such that
such that 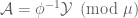 .
.
My question is: Is there a maximal such factor and is a maximal factor unique?
Admittedly, I am not very clear as to what I mean by maximality here. But at the very least, any other factor should be a factor of a maximal factor.
(I am asking this because of Remark 4 above. Also, I was reading Einsiedler and Wards Ergodic Theory with a view towards Number Theory, and Theorem 6.10 in the text uses the definite article when considering a factor of a certain sub- -algebra.)
-algebra.)
24 December, 2018 at 9:24 am
Terence Tao
I think if a maximal factor exists, then it is unique up to isomorphism by general abstract nonsense (uniqueness of universal objects in categories). If one works with abstract measurable spaces instead of concrete ones
instead of concrete ones 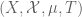 then there is a canonical choice of maximal factor, namely
then there is a canonical choice of maximal factor, namely  ; in many applications one can get by just using these abstract spaces (and the corresponding abstract notion of factor). One could then use something like the Loomis-Sikorski theorem to generate a concrete measure-preserving space that is abstractly isomorphic to this factor, but there might be some descriptive set theory or measurability issues when trying to concretely exhibit this space as a factor of the original space (typically one needs some regularity hypotheses on the spaces, e.g. that they are standard Borel spaces or at least separable, to do this). One might have a look at Glasner’s book as I have a vague memory that he may discuss these sorts of issues.
; in many applications one can get by just using these abstract spaces (and the corresponding abstract notion of factor). One could then use something like the Loomis-Sikorski theorem to generate a concrete measure-preserving space that is abstractly isomorphic to this factor, but there might be some descriptive set theory or measurability issues when trying to concretely exhibit this space as a factor of the original space (typically one needs some regularity hypotheses on the spaces, e.g. that they are standard Borel spaces or at least separable, to do this). One might have a look at Glasner’s book as I have a vague memory that he may discuss these sorts of issues.
24 December, 2018 at 7:53 pm
Abhishek Khetan
I also thought that the uniqueness of a maximal factor would follow from abstract nonsense. But the problem is that, since we are not requiring factor maps to be surjective, a maximal factor may not be an initial object.
I guess I am sweating this too much. Let me read and reflect on your suggestion about using abstract measurable spaces.
Thanks.
20 May, 2020 at 11:45 pm
Anonymous
Dear Professor Tao,
Just before Proposition 2, you have defined as the
as the  -algerba generated by the bounded measurable eigenfunctions.
-algerba generated by the bounded measurable eigenfunctions.
Suppose we define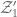 as the
as the  -algebra generated by the eigenfunctions in
-algebra generated by the eigenfunctions in  .
.
Then clearly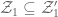 and this is in fact an equality in the ergodic case.
and this is in fact an equality in the ergodic case.
I am wondering if this is also an equality in general.
Thank you.
21 May, 2020 at 9:06 pm
Terence Tao
Yes; if is an eigenfunction then
is an eigenfunction then 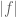 is invariant, so one can always truncate an eigenfunction
is invariant, so one can always truncate an eigenfunction  to be bounded while still generating the same measurable sets, e.g., by replacing
to be bounded while still generating the same measurable sets, e.g., by replacing  with
with  (with the convention that the latter vanishes when
(with the convention that the latter vanishes when  vanishes.
vanishes.
7 July, 2020 at 9:30 am
Math Genius: Spectral description of the Kronecker factor - TECHPRPR
[…] periodic if the closure of $set{T^nf: nin Z}$ is compact in $L^2$. It is shows in Proposition 2 of this blog post of Tao, assuming ergodicity of $T$, that$f$ is almost periodic if and only if $f$ is measurable with […]
14 March, 2022 at 9:06 am
Dante Tjowasi
Dear Professor Tao,
For Proposition 2, why does the system need to be ergodic? I tried following the proof and I can’t see where ergodicity is used.
Thank you.
[Ergodicity is indeed not needed in this proposition, but for the application to Theorem 2 we only need the ergodic case. -T]