In the next few lectures, we will be studying four major classes of function spaces. In decreasing order of generality, these classes are the topological vector spaces, the normed vector spaces, the Banach spaces, and the Hilbert spaces. In order to motivate the discussion of the more general classes of spaces, we will first focus on the most special class – that of (real and complex) Hilbert spaces. These spaces can be viewed as generalisations of (real and complex) Euclidean spaces such as and
to infinite-dimensional settings, and indeed much of one’s Euclidean geometry intuition concerning lengths, angles, orthogonality, subspaces, etc. will transfer readily to arbitrary Hilbert spaces; in contrast, this intuition is not always accurate in the more general vector spaces mentioned above. In addition to Euclidean spaces, another fundamental example of Hilbert spaces comes from the Lebesgue spaces
of a measure space
. (There are of course many other Hilbert spaces of importance in complex analysis, harmonic analysis, and PDE, such as Hardy spaces
, Sobolev spaces
, and the space
of Hilbert-Schmidt operators, but we will not discuss those spaces much in this course. Complex Hilbert spaces also play a fundamental role in the foundations of quantum mechanics, being the natural space to hold all the possible states of a quantum system (possibly after projectivising the Hilbert space), but we will not discuss this subject here.)
Hilbert spaces are the natural abstract framework in which to study two important (and closely related) concepts: orthogonality and unitarity, allowing us to generalise familiar concepts and facts from Euclidean geometry such as the Cartesian coordinate system, rotations and reflections, and the Pythagorean theorem to Hilbert spaces. (For instance, the Fourier transform is a unitary transformation and can thus be viewed as a kind of generalised rotation.) Furthermore, the Hodge duality on Euclidean spaces has a partial analogue for Hilbert spaces, namely the Riesz representation theorem for Hilbert spaces, which makes the theory of duality and adjoints for Hilbert spaces especially simple (when compared with the more subtle theory of duality for, say, Banach spaces). Much later (next quarter, in fact), we will see that this duality allows us to extend the spectral theorem for self-adjoint matrices to that of self-adjoint operators on a Hilbert space.
These notes are only the most basic introduction to the theory of Hilbert spaces. In particular, the theory of linear transformations between two Hilbert spaces, which is perhaps the most important aspect of the subject, is not covered much at all here (but I hope to discuss it further in future lectures.)
— Inner product spaces —
The Euclidean norm
(1)
in real Euclidean space can be expressed in terms of the dot product
, defined as
(2)
by the well-known formula
. (3)
In particular, we have the positivity property
(4)
with equality if and only if . One reason why it is more advantageous to work with the dot product than the norm is that while the norm function is only sublinear, the dot product is bilinear, thus
(5)
for all vectors x,y and scalars c,d, and also symmetric,
. (6)
These properties make the inner product easier to manipulate algebraically than the norm.
The above discussion was for the real vector space , but one can develop analogous statements for the complex vector space
, in which the norm
(7)
can be represented in terms of the complex inner product defined by the formula
(8)
by the analogue of (3), namely
. (9)
In particular, as before with (4), we have the positivity property
, (10)
with equality if and only if x=0. The bilinearity property (5) is modified to the sesquilinearity property
(11)
while the symmetry property (6) needs to be replaced with
(12)
in order to be compatible with sesquilinearity.
We can formalise all these properties axiomatically as follows.
Definition 1. (Inner product space) A complex inner product space
is a complex vector space V, together with an inner product
which is sesquilinear (i.e. (11) holds for all
and
) and symmetric in the sesquilinear sense (i.e. (12) holds for all
), and obeys the positivity property (10) for all
, with equality if and only if x=0. We will usually abbreviate
as V.
A real inner product space is defined similarly, but with all references to
replaced by
(and all references to complex conjugation dropped).
Example 1. with the standard dot product (2) is a real inner product space, and
with the complex inner product (8) is a complex inner product space.
Example 2. If is a measure space, then the complex
space
with the complex inner product
(13)
(which is well defined, by the Cauchy-Schwarz inequality) is easily verified to be a complex inner product space, and similarly for the real space (with the complex conjugate signs dropped, of course. Note that the finite dimensional examples
can be viewed as the special case of the
examples in which X is
with the discrete
-algebra and counting measure.
Example 3. Any subspace of a (real or complex) inner product space is again a (real or complex) inner product space, simply by restricting the inner product to the subspace.
Example 4. Also, any real inner product space V can be complexified into the complex inner product space , defined as the space of formal combinations
of vectors
(with the obvious complex vector space structure), and with inner product
.
(14)
Example 5. Fix a probability space . The space of square-integrable real-valued random variables of mean zero is an inner product space if one uses covariance as the inner product. (What goes wrong if one drops the mean zero assumption?)
Given a (real or complex) inner product space V, we can define the norm of any vector space V by the formula (9), which is well defined thanks to the positivity property; in the case of the
spaces, this norm of course corresponds to the usual
norm. We have the following basic facts:
Lemma 1. Let V be a real or complex inner product space.
- (Cauchy-Schwarz inequality) For any
, we have
.
- The function
is a norm on V. (Thus every inner product space is a normed vector space.)
Proof. We shall just verify the complex case, as the real case is similar (and slightly easier). The positivity property tells us that the quadratic form is non-negative for all complex numbers a, b. Using sesquilinearity and symmetry, we can expand this form as
. (15)
Optimising in a, b (see also my blog post on the amplification trick) we obtain the Cauchy-Schwarz inequality. To verify the norm property, the only non-trivial verification is that of the triangle inequality . But on expanding
we see that
(16)
and the claim then follows from the Cauchy-Schwarz inequality.
Observe from the Cauchy-Schwarz inequality that the inner product is continuous.
Exercise 1. Let be a linear map from one (real or complex) inner product space to another. Show that T preserves the inner product structure (i.e.
for all
) if and only if T is an isometry (i.e.
for all
). [Hint: in the real case, express
in terms of
and
. In the complex case, use
instead of
.]
Inspired by the above exercise, we say that two inner product spaces are isomorphic if there exists an invertible isometry from one space to the other; such invertible isometries are known as isomorphisms.
Exercise 2. Let V be a real or complex inner product space. If are a finite collection of vectors in V, show that the Gram matrix
is Hermitian and positive semi-definite, and is positive definite if and only if the
are linearly independent. Conversely, given a Hermitian positive semi-definite matrix
with real (resp. complex) entries, show that there exists a real (resp. complex) inner product space V and vectors
such that
for all
.
In analogy with the Euclidean case, we say that two vectors x, y in a (real or complex) vector space are orthogonal if . (With this convention, we see in particular that 0 is orthogonal to every vector, and is the only vector with this property.)
Exercise 3. (Pythagorean theorem) Let V be a real or complex inner product space. If are a finite set of pairwise orthogonal vectors, then
. In particular, we see that
whenever
is orthogonal to
.
A (possibly infinite) collection of vectors in a (real or complex) inner product space is said to be orthonormal if they are pairwise orthogonal and all of unit length.
Exercise 4. Let be an orthonormal system of vectors in a real or complex inner product space. Show that this system is (algebraically) linearly independent (thus any non-trivial finite linear combination of vectors in this system is non-zero). If x lies in the algebraic span of this system (i.e. it is a finite linear combination of vectors in the system), establish the inversion formula
(17)
(with only finitely many of the terms non-zero) and the (finite) Plancherel formula
.
(18)
Exercise 5. (Gram-Schmidt theorem) Let be a finite orthonormal system in a real or complex inner product space, and let v be a vector not in the span of
. Show that there exists a vector
with
such that
is an orthonormal system. Conclude that an n-dimensional real or complex inner product space is isomorphic to
or
respectively. Thus, any statement about inner product spaces which only involves a finite-dimensional subspace of that space can be verified just by checking it on Euclidean spaces.
Exercise 6 (Parallelogram law). For any inner product space V, establish the parallelogram law
. (19)
Show that this inequality fails for for
as soon as X contains at least two disjoint sets of non-zero finite measure. On the other hand, establish the Hanner inequalities
(20)
and
(21)
for , with the inequalities being reversed for
. (Hint: (21) can be deduced from (20) by a simple substitution. For (20), reduce to the case when f,g are non-negative, and then exploit the inequality
(22)
for all non-negative x,y, , and
, with the inequality being reversed for
, and with equality being attained when
and
.
— Hilbert spaces —
Thus far, our discussion of inner product spaces has been largely algebraic in nature; this is because we have not been able to take limits inside these spaces and do some actual analysis. This can be rectified by adding an additional axiom.
Definition 2. (Hilbert spaces) A (real or complex) Hilbert space is a (real or complex) inner product space which is complete (or equivalently, an inner product space which is also a Banach space).
Example 6. From Proposition 1 from Notes 3, (real or complex) is a Hilbert space for any measure space
. In particular,
and
are Hilbert spaces.
Exercise 7. Show that a subspace of a Hilbert space H will itself be a Hilbert space if and only if it is closed. (In particular, proper dense subspaces of Hilbert spaces are not Hilbert spaces.)
Example 7. By Example 6, the space of doubly infinite square-summable sequences is a Hilbert space. Inside this space, the space
of sequences of finite support is a proper dense subspace (e.g. by Proposition 2 of Notes 3, though this can also be seen much more directly), and so cannot be a Hilbert space.
Exercise 8. Let V be an inner product space. Show that there exists a Hilbert space which contains a dense subspace isomorphic to V; we refer to
as a completion of V. Furthermore, this space is essentially unique in the sense that if
,
are two such completions, then there exists an isomorphism from
to
which are the identity on V (if one identifies V with the dense subspaces of
and
. Because of this fact, inner product spaces are sometimes known as pre-Hilbert spaces, and can always be identified with dense subspaces of actual Hilbert spaces.
Exercise 9. Let H, H’ be two Hilbert spaces. Define the direct sum of the two spaces to be the vector space
with inner product
. Show that
is also a Hilbert space.
Example 8. If H is a complex Hilbert space, one can define the complex conjugate of that space to be the set of formal conjugates
of vectors in H, with complex vector space structure
and
, and inner product
. One easily checks that
is again a complex Hilbert space. Note the map
is not a complex linear isometry; instead, it is a complex antilinear isometry.
A key application of the completeness axiom is to be able to define the “nearest point” from a vector to a closed convex body.
Proposition 1. (Existence of minimisers) Let H be a Hilbert space, let K be a non-empty closed convex subset of H, and let x be a point in H. Then there exists a unique y in K that minimises the distance
to x. Furthermore, for any other z in K, we have
.
Proof. Observe from the parallelogram law (19) the (geometrically obvious) fact that if y and y’ are distinct and equidistant from x, then their midpoint is strictly closer to x than either of y or y’. This ensures that the distance minimiser, if it exists, is unique. Also, if y is the distance minimiser and z is in K, then
is at least as distant from x as y is for any
, by convexity; squaring this and rearranging, we conclude that
. (23)
Letting we obtain the final claim in the proposition.
It remains to show existence. Write . It is clear that D is finite and non-negative. If the infimum is attained then we would be done. We cannot conclude immediately that this is the case, but we can certainly find a sequence
such that
. On the other hand, the midpoints
lie in K by convexity and so
. Using the parallelogram law (19) we deduce that
as
and so
is Cauchy; by completeness, it converges to a limit y, which lies in K since K is closed. From the triangle inequality we see that
, and thus
, and so y is a distance minimiser.
Exercise 10. Show by constructing counterexamples that the existence of the distance minimiser y can fail if either the closure or convexity hypothesis on K is dropped, or if H is merely an inner product space rather than a Hilbert space. (Hint: for the last case, let H be the inner product space , and let K be the subspace of continuous functions supported on
.) On the other hand, show that existence (but not uniqueness) can be recovered if K is assumed to be compact rather than convex.
Exercise 11. Using the Hanner inequalities (Exercise 6), show that Proposition 1 also holds for the spaces as long as
. (The specific feature of the
spaces that is allowing this is known as uniform convexity.) Give counterexamples to show that the propsition can fail for
and for
.
This proposition has some importance in calculus of variations, but we will not pursue those applications here.
Since every subspace is necessarily convex, we have a corollary:
Exercise 12. (Orthogonal projections) Let V be a closed subspace of a Hilbert space H. Then for every there exists a unique decomposition
, where
and
is orthogonal to every element of V. Furthermore,
is the closest element of V to x.
Let be the map
, where
is given by the above exercise; we refer to
as the orthogonal projection from H onto V. It is not hard to see that
is linear, and from the Pythagorean theorem we see that
is a contraction (thus
for all
). In particular,
is continuous.
Exercise 13. (Orthogonal complement) Given a subspace V of a Hilbert space H, define the orthogonal complement of V to be the set of all vectors in H that are orthogonal to every element of V. Establish the following claims:
is a closed subspace of H, and that
is the closure of V.
is the trivial subspace {0} if and only if V is dense.
- If V is closed, then H is isomorphic to the direct sum of V and
.
- If V, W are two closed subspaces of H, then
and
.
Every vector in a Hilbert space gives rise to a continuous linear functional
, defined by the formula
(the continuity follows from the Cauchy-Schwarz inequality). The Riesz representation theorem for Hilbert spaces gives a converse:
Theorem 1. (Riesz representation theorem for Hilbert spaces) Let H be a complex Hilbert space, and let
be a continuous linear functional on H. Then there exists a unique v in H such that
. A similar claim holds for real Hilbert spaces (replacing
by
throughout).
Proof. We just show the claim for complex Hilbert spaces, as the claim for real Hilbert spaces is very similar. First, we show uniqueness: if , then
, and in particular
, and so v=v’.
Now we show existence. We may assume that is not identically zero, since the claim is obvious otherwise. Observe that the kernel
is then a proper subspace of H, which is closed since
is continuous. By Exercise 13, the orthogonal complement
must contain at least one non-trivial vector w, which we can normalise to have unit magnitude. Since w doesn’t lie in V,
is non-zero. Now observe that for any x in H,
lies in the kernel of
, i.e. it lies in V. Taking inner products with w, we conclude that
(24)
and thus
(25)
Thus we have , and the claim follows.
Remark 1. This result gives an alternate proof of the p=2 case of Theorem 1 from Notes 3, and by modifying Remark 10 from Notes 3, can be used to give an alternate proof of the Lebesgue-Radon-Nikodym theorem (this proof is due to von Neumann).
Remark 2. In the next set of notes, when we define the notion of a dual space, we can reinterpret the Riesz representation theorem as providing a canonical isomorphism .
Exercise 14. Using Exercise 11, give an alterate proof of the case of Theorem 1 from Notes 3.
One important consequence of the Riesz representation theorem is the existence of adjoints:
Exercise 15. Let be a continuous linear transformation. Show that that there exists a unique continuous linear transformation
with the property that
for all
and
. The transformation
is called the (Hilbert space) adjoint of T; it is of course compatible with the notion of an adjoint matrix from linear algebra.
Exercise 16. Let be a continuous linear transformation.
- Show that
.
- Show that T is an isometry if and only if
.
- Show that T is an isomorphism if and only if
and
.
- If
is another continuous linear transformation, show that
.
Remark 3. An isomorphism of Hilbert spaces is also known as a unitary transformation. (For real Hilbert spaces, the term orthogonal transformation is sometimes used instead.) Note that unitary and orthogonal matrices generate unitary and orthogonal transformations on
and
respectively.
Exercise 17. Show that the projection map from a Hilbert space to a closed subspace is the adjoint of the inclusion map
.
— Orthonormal bases —
In the section on inner product spaces, we studied finite linear combinations of orthonormal systems. Now that we have completeness, we turn to infinite linear combinations.
We begin with countable linear combinations:
Exercise 18. Suppose that is a countable orthonormal system in a complex Hilbert space H, and
is a sequence of complex numbers. (As usual, similar statements will hold here for real Hilbert spaces and real numbers.)
- Show that the series
is conditionally convergent in H if and only if
is square-summable.
- If
is square-summable, show that
is unconditionally convergent in H, i.e. every permutation of the
sums to the same value.
- Show that the map
is an isometry from the Hilbert space
to H. The image V of this isometry is the smallest closed subspace of H that contains
, and which we shall therefore call the (Hilbert space) span of
.
- Take adjoints of 3. and conclude that for any
, we have
and
. Conclude in particular the Bessel inequality
.
Remark 4. Note the contrast here between conditional and unconditional summability (which needs only square-summability of the coefficients ) and absolute summability (which requires the stronger condition that the
are absolutely summable). In particular there exist non-absolutely summable series that are still unconditionally summable, in contrast to the situation for scalars, in which one has the Riemann rearrangement theorem.
Now we can handle arbitrary orthonormal systems . If
is square-summable, then at most countably many of the
are non-zero (by Exercise 3 of Notes 3). Using parts 1,2 of Exercise 18, we can then form the sum
in an unambiguous manner. It is not hard to use Exercise 18 to then conclude that this gives an isometric embedding of
into H. The image of this isometry is the smallest closed subspace of H that contains the orthonormal system, which we call the (Hilbert space) span of that system. (It is the closure of the algebraic span of the system.)
Exercise 19. Let be an orthonormal system in H. Show that the following statements are equivalent:
- The Hilbert space span of
is all of H.
- The algebraic span of
(i.e. the finite linear combinations of the
) is dense in H.
- One has the Parseval identity
for all
.
- One has the inversion formula
for all
(in particular, the coefficients
are square summable).
- The only vector that is orthogonal to all the
is the zero vector.
- There is an isomorphism from
to H that maps
to
for all
(where
is the Kronecker delta at
).
A system obeying any (and hence all) of the properties in Exercise 19 is known as an orthonormal basis of the Hilbert space H. All Hilbert spaces have such a basis:
Proposition 2. Every Hilbert space has at least one orthonormal basis.
Proof. We use the standard Zorn’s lemma argument. Every Hilbert space has at least one orthonormal system, namely the empty system. We order the orthonormal systems by inclusion, and observe that the union of any totally ordered set of orthonormal systems is again an orthonormal system. By Zorn’s lemma, there must exist a maximal orthonormal system . There cannot be any unit vector orthogonal to all the elements of this system, since otherwise one could add that vector to the system and contradict orthogonality. Applying Exercise 19 in the contrapositive, we obtain an orthonormal basis as claimed.
Exercise 19.5. Show that every vector space V has at least one algebraic (or Hamel) basis, i.e. a set of basis vectors such that every vector in V can be expressed uniquely as a finite linear combination of basis vectors.
Corollary 1. Every Hilbert space is isomorphic to
for some set A.
Exercise 20. Let A, B be sets. Show that and
are isomorphic iff A and B have the same cardinality. (Hint: the case when A or B is finite is easy, so suppose A and B are both infinite. If
and
are isomorphic, show that B can be covered by a family of at most countable sets indexed by A, and vice versa. Then apply the Schroder-Bernstein theorem.
We can now classify Hilbert spaces up to isomorphism by a single cardinal, the dimension of that space:
Exercise 21. Show that all orthonormal bases of a given Hilbert space H have the same cardinality. This cardinality is called the (Hilbert space) dimension of the Hilbert space.
Exercise 22. Show that a Hilbert space is separable (i.e. has a countable dense subset) if and only if its dimension is at most countable. Conclude in particular that up to isomorphism, there is exactly one separable infinite-dimensional Hilbert space.
Exercise 23. Let H, H’ be two complex Hilbert spaces. Show that there exists another Hilbert space , together with a map
with the following properties:
- The map
is bilinear, thus
and
for all
;
- We have
for all
.
- The (algebraic) span of
is dense in
.
Furthermore, show that and
are unique up to isomorphism in the sense that if
and
are another pair of objects obeying the above properties, then there exists an isomorphism
such that
for all
. (Hint: to prove existence, create orthonormal bases for H and H’ and take formal tensor products of these bases.) The space
is called the (Hilbert space) tensor product of H and H’, and
is the tensor product of x and x’.
Exercise 24. Let and
be measure spaces. Show that
is the tensor product of
and
, if one defines the tensor product
of
and
as
.
We do not yet have enough theory in other areas to give the really useful applications of Hilbert space theory yet, but let us just illustrate a simple one, namely the development of Fourier series on the unit circle . We can give this space the usual Lebesgue measure (identifying the unit circle with [0,1), if one wishes), giving rise to the complex Hilbert space
. On this space we can form the characters
for all integer n; one easily verifies that
is an orthonormal system. We claim that it is in fact an orthonormal basis. By Exercise 19, it suffices to show that the algebraic span of the
, i.e. the space of trigonometric polynomials, is dense in
. But from an explicit computation (e.g. using Fejér kernels) one can show that the indicator function of any interval can be approximated to arbitrary accuracy in
norm by trigonometric polynomials, and is thus in the closure of the trigonometric polynomials. By linearity, the same is then true of an indicator function of a finite union of intervals; since Lebesgue measurable sets in
can be approximated to arbitrary accuracy by finite unions of intervals, the same is true for indicators of measurable sets. By linearity, the same is true for simple functions, and by density (Proposition 2 of Notes 3) the same is true for arbitrary
functions, and the claim follows.
The Fourier transform of a function
is defined as
. (26)
From Exercise 19, we obtain the Parseval identity
(in particular, and the inversion formula
where the right-hand side is unconditionally convergent. Indeed, the Fourier transform is a unitary transformation between
and
. (These facts are collectively referred to as Plancherel’s theorem for the unit circle.) We will develop Fourier analysis on other spaces than the unit circle later in this course (or next quarter).
Remark 5. Of course, much of the theory here generalises the corresponding theory in finite-dimensional linear algebra; we will continue this theme much later in the course when we turn to the spectral theorem. However, not every aspect of finite-dimensional linear algebra will carry over so easily. For instance, it turns out to be quite difficult to take the determinant or trace of a linear transformation from a Hilbert space to itself in general (unless the transformation is particularly well behaved, e.g. of trace class). The Jordan normal form also does not translate to the infinite-dimensional setting, leading to the notorious invariant subspace problem in the subject. It is also worth cautioning that while the theory of orthonormal bases in finite-dimensional Euclidean spaces generalises very nicely to the Hilbert space setting, the more general theory of bases in finite dimensions becomes much more subtle in infinite dimensional Hilbert spaces, unless the basis is “almost orthonormal” in some sense (e.g. if it forms a frame).
[Update, Jan 21: notation for Hilbert space adjoint changed from to
, for reasons that will become clearer in the next notes.]
[Update, Jan 22: Exercise 19.5 added.]

65 comments
Comments feed for this article
17 January, 2009 at 2:17 pm
S
Title should be 245B instead of 254A. [Corrected, thanks – T.]
17 January, 2009 at 2:26 pm
Américo Tavares
Typo: formula (5) does not parse [I have IE] [Fixed, thanks – T.]
17 January, 2009 at 3:26 pm
S
Typo in the correction: 245B instead of 254B. [Ack – fixed, this time for real hopefully – T.]
18 January, 2009 at 2:24 pm
Anonymous
Hello Professor Tao,
Do you have any recommendations on further books to continue studying Hilbert spaces, especially into modern areas of research?
18 January, 2009 at 10:44 pm
Anonymous
Does anyone know why lectures 3 and 5 did not show up in my google reader?? All other lectures for 245B have so far as well as other recent posts.
19 January, 2009 at 12:56 am
liuxiaochuan
Dear Anonymous:
The same situation happens to my google reader and it is not the first time, I have no idea why this is happening.
21 January, 2009 at 2:13 am
Ulrich
Dear Prof. Tao, do you know whether the minimiser theorem (proposition 1), as you called it, characterizes convex, closed sets in a Hilbert space?
Thanks for an answer
Ulrich
21 January, 2009 at 6:30 am
Mark Meckes
While the standard, optimization-based proof of Cauchy-Schwarz has its nice points, there’s another approach (used for example in Axler’s rather audaciously named linear algebra text) which seems less mysterious to me. Assuming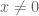 , you can write
, you can write 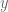 as a scalar multiple of
as a scalar multiple of  plus some vector orthogonal to
plus some vector orthogonal to  . Once you’ve worked out what those two summands are, plugging this representation of
. Once you’ve worked out what those two summands are, plugging this representation of 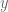 into the inner product and using orthogonality and positivity yields Cauchy-Schwarz immediately.
into the inner product and using orthogonality and positivity yields Cauchy-Schwarz immediately.
What I like about this approach in part is that it immediately introduces the idea of orthogonal projection in a geometric way.
21 January, 2009 at 7:29 am
Terence Tao
Dear Ulrich,
Well, if you require all the conclusions of the proposition (existence and uniqueness of the minimiser, together with the obtuse angle condition), then the answer seems to be yes: if K is not closed, then picking x to be an adherent point will give a counterexample, and if K is not convex, then picking x to lie outside of K in an interval whose endpoints a, b lie in K will give another counterexample (as it is not possible for a, b to both lie in the half-space without x lying in this space also, which is not possible unless x=y, which forces x to lie in K, a contradiction).
without x lying in this space also, which is not possible unless x=y, which forces x to lie in K, a contradiction).
I don’t know what happens though if one starts dropping assumptions. The obtuse angle condition implies uniqueness; but if one drops both the obtuse angle condition and uniqueness, then any compact set K will have minimisers.
21 January, 2009 at 9:46 am
Ulrich Groh
Dear Professor Tao, thank you for the fast answer. As I see, my question was not precise enough. Is the following true: Let H be a Hilbert space and K a closed subset of H with the following property: For every x in H there exist an unique z in K which minimizes the distance of x to the set K. Then K is convex. Maybe I overlooked something and the answer is trivial …
Thanks.
Ulrich
21 January, 2009 at 10:25 am
Dussau
Dear Ulrich,
As prof. Tao said if K in not convex then there exists x in H which does not admit only one extremiser. And you can see that this fact is equivalent with the property that you evoke.
22 January, 2009 at 8:13 am
Eric
If we drop the obtuse angle condition, I don’t see why uniqueness alone should imply convexity. I can’t come up with a counterexample, but the proof above certainly breaks down.
22 January, 2009 at 9:50 am
Terence Tao
Hmm, an interesting problem. I think I can prove the converse in the case when K is finite-dimensional (say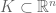 ) and bounded, by an induction on dimension, though it was trickier than I anticipated. First observe that K must be closed (otherwise any limit point outside K will contradict existence of the minimiser), hence compact. This, together with uniqueness, can be used to show that the function
) and bounded, by an induction on dimension, though it was trickier than I anticipated. First observe that K must be closed (otherwise any limit point outside K will contradict existence of the minimiser), hence compact. This, together with uniqueness, can be used to show that the function  from a point to its unique minimiser must be continuous (for if
from a point to its unique minimiser must be continuous (for if  and the sequence
and the sequence  did not converge to f(x), then some subsequence would converge to an alternate minimiser). So now we have a continuous retraction from
did not converge to f(x), then some subsequence would converge to an alternate minimiser). So now we have a continuous retraction from  to K.
to K.
It is not hard to show (by looking at how nearby balls of the same radius intersect each other) that if one has unique minimisers depending continuously on the initial point x, then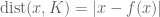 cannot have a local maximum outside of K. From this we see that the complement of the compact set K contains no bounded connected components, and is therefore connected.
cannot have a local maximum outside of K. From this we see that the complement of the compact set K contains no bounded connected components, and is therefore connected.
Now look at the convex hull of K, and let
of K, and let  be a tangent hyperplane for
be a tangent hyperplane for  . We claim that
. We claim that  has the unique minimiser property inside
has the unique minimiser property inside  ; indeed, if x lies in
; indeed, if x lies in 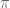 and does not have unique minimisers to
and does not have unique minimisers to  , then by moving x in the normal direction to
, then by moving x in the normal direction to 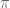 away from K and using compactness of K one eventually contradicts unique minimisation for K. By induction hypothesis, this implies
away from K and using compactness of K one eventually contradicts unique minimisation for K. By induction hypothesis, this implies  is convex and thus equal to
is convex and thus equal to 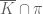 . Taking unions over all
. Taking unions over all 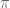 , we conclude that K contains the entire boundary of its convex hull; since the complement of K has only one connected component, we conclude
, we conclude that K contains the entire boundary of its convex hull; since the complement of K has only one connected component, we conclude  , which gives convexity.
, which gives convexity.
It may be that this argument extends to the case of compact K in infinite dimensions, but I do not know what to predict in the non-compact or unbounded case.
22 January, 2009 at 6:27 pm
liuxiaochuan
Dear Professor Tao:
About (22), since the left-hand side is symmetric and the right-hand side is seemingly not, I am thinking if the nonnegative x, y should be asked to satisfy x>y.
Xiaochuan
22 January, 2009 at 6:39 pm
Terence Tao
Hmm, you’re right. I’ve adjusted the hint somewhat to deal with this.
23 January, 2009 at 10:27 pm
Dmitriy
Concerning Ulrich’s question: As far as I know this is an open question in the Hilbert space theory (at least it was about 3 years ago when I heard about it)
The sets with this property are called Chebyshev sets.
I just googled it a little and it seems that this problem (whether the class of Chebyshev sets in an infinite-dimensional Hilbert space coincides with the class of convex sets) is still unsolved.
24 January, 2009 at 12:42 am
Ulrich
Prof. Tao, Dmitriy, thank you for the effort and the interesting remark.
24 January, 2009 at 7:11 pm
Anonymous
Dear Prof Tao,
I’m reading Hahn-Banach Thm, and I’m thinking is it because in the case of Hilbert Space the Thm is trivial, so we want to have this Thm in Banach Space? And we also want to bound the functional with some Norm?
Paul
24 January, 2009 at 7:12 pm
Anonymous
Actually, it’s much more general, it’s just a vector space.
26 January, 2009 at 9:35 am
245B, Notes 6: Duality and the Hahn-Banach theorem « What’s new
[…] other topological space).) In other cases, most notably with Hilbert spaces as discussed in Notes 5, the dual object is identical to X […]
10 February, 2009 at 2:31 am
Anonymous
Dear Terry,
Does the set of all inner products of a vector space have some (algebraic, analytic, geometric) structure or interpretation?
Best, Billy Blanc.
16 February, 2009 at 7:28 am
实分析0-10 « Liu Xiaochuan’s Weblog
[…] 第五节更是老朋友了,Hilbert空间。本节中除了一般书籍中常见的知识之外,有一个Hanner不等式(习题6)我从来没有见过,该不等式加强了平行四边形法则。另一个值得注意的地方是,Riesz表示定理竟然可以跟Lebesgue-Radon-Nikodym定理互推。在正交基的存在定理中,传说中的选择公理又来了。 […]
14 March, 2009 at 9:19 pm
gokhan
Dear Prof. Tao,
if we have two seperable Hilbert spaces H, H’, can we say that their tensor product is isometrically isomorphic to the space of Hilbert Schmidt operators from H to H’ with Hilbert Schmidt inner product?
if we have tensor product of H by itself 3 times ,i.e, , is it isometrically isomorphic to the followings:
, is it isometrically isomorphic to the followings:
1)Hilbert Schmidt operators from H to
 to H
to H
2)Hilbert Schmidt operators from
thanks,
14 March, 2009 at 9:31 pm
Terence Tao
Dear gokhan,
For real Hilbert spaces, this is correct. For complex Hilbert spaces, there is a small subtlety: the space of Hilbert-Schmidt operators from H to H’ is naturally isomorphic to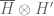 (or
(or 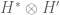 ) rather than
) rather than  . (Of course, if one picks an orthonormal basis, then one can produce an isomorphism between H and
. (Of course, if one picks an orthonormal basis, then one can produce an isomorphism between H and 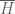 , and thus between
, and thus between  and
and 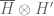 , but this isomorphism depends on the choice of basis and is thus not natural (in the category-theoretic sense).)
, but this isomorphism depends on the choice of basis and is thus not natural (in the category-theoretic sense).)
(In the above discussion, one has to of course use the Hilbert space tensor product, which is slightly different from the vector space tensor product.)
6 April, 2009 at 2:59 pm
254C, Notes 2: The Fourier transform « What’s new
[…] of at the corresponding frequency. Applying the general theory of orthonormal bases (see Notes 5), we obtain the following consequences: Corollary 5 (Plancherel theorem for compact abelian […]
22 April, 2009 at 12:33 pm
Anonymous
Dear Professor Tao,
I encountered an example of a continuous probability measure on a unit sphere of a separable Hilbert space such that the scalar product of two independent copies from this measure is discrete. It sounds counterintuitive, so I was wondering if there is a simple way to see the existence of such measure, or if this contradicts anything you know?
Thank you.
19 May, 2010 at 3:54 pm
Higher order Hilbert spaces « What’s new
[…] is extremely standard, and can be found in any graduate real analysis course (I myself covered it here.) But what is perhaps less well known (except inside the fields of additive combinatorics and […]
11 June, 2010 at 11:26 pm
Kestutis Cesnavicius
Several typos:
1. In display (15) |b| should be squared.
2. In (21) a closing parenthesis is missing.
3. In Exercise 9 in the definition of the inner product on the direct sum x’ and y should be switched on the RHS.
[Corrected, thanks – T.]
26 June, 2010 at 9:28 am
The uncertainty principle « What’s new
[…] Hilbert space duality An element in a Hilbert space can either be thought of in physical space as a vector in that space, or in momentum space as a covector on that space. The fundamental connection between the two is given by the Riesz representation theorem for Hilbert spaces. […]
27 August, 2010 at 8:19 am
QTheorist
There is one thing I cannot figure out how to do about Hilbert space.
Consider an Hilbert space with a countably infinite basis. How can I by taking a limit of some sort, go to an Hilbert space with a continuous (not countable) basis ?
In other words, consider the following basis vector in the first Hilbert space (……0 0 0 1 0 0 ….) that is with a 1 somewhere. How can I go to the obvious basis vector for the continuous hilbert space, which is a Dirac delta function at some point x by taking a limit of some sort from the first to the second ??
27 August, 2010 at 9:11 am
Terence Tao
One has to be a little careful with the notion of a basis when one works in the uncountable setting. For instance, when working with the Hilbert space![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) of square-integrable functions on the unit interval, the Dirac masses
of square-integrable functions on the unit interval, the Dirac masses 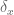 for
for ![x \in [0,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) are technically not a basis for this space, as they do not even lie in the Hilbert space to begin with. Also, while it may appear at first glance that the space of functions on [0,1] has an uncountable number of degrees of freedom, the requirement that the function be measurable (and, a fortiori, square-integrable) is actually quite a strong constraint (particularly when combined with the convention of identifying any two functions that agree almost everywhere), and reduces the number of degrees of freedom to only countably many. This for instance can be seen by using the Fourier transform and Plancherel’s theorem to identify
are technically not a basis for this space, as they do not even lie in the Hilbert space to begin with. Also, while it may appear at first glance that the space of functions on [0,1] has an uncountable number of degrees of freedom, the requirement that the function be measurable (and, a fortiori, square-integrable) is actually quite a strong constraint (particularly when combined with the convention of identifying any two functions that agree almost everywhere), and reduces the number of degrees of freedom to only countably many. This for instance can be seen by using the Fourier transform and Plancherel’s theorem to identify ![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) with
with  .
.
31 August, 2010 at 2:32 am
QTheorist
I am sorry I probably was not clear enough. I am a physicist and used to work with Hilbert spaces more or less as vector spaces for my wave functions. For example if I work with spin-1/2 with two levels I use a wave function which is a vector of functions (F1 F2) and operators acting on it are just 2*2 matrices. The simplest basis for the vectors in this space are (1 0) and (0 1) which is indeed what we use as this basis refers to some bare states of the system we know (like up spin and down spin).
Now when we deal with continuous degrees of freedom such as position and momentum, my vector of functions (my wave function) is an infinite length vector and operators are infinite matrices. But most importantly, this objects are continuous now. So the most convenient basis we use is the Dirac delta function, which even though it does not lies in the Hilbert space is very convenient for representation of the states. Indeed if I want to represent my wave function in the position basis, momentum states are plane waves, which physicists like for their simple properties. Same thing for position states in the momentum basis. The dirac delta function, which we thus use a for the basis “state” has the usual propoerties we expect for a basis (closure relation, orthogonality)…
I remarked that even though I seems perfectly natural to use this as basis, there is no evident way of going to the basis I used for the discrete case to the continuous case, by taking for example a limit of some sort that would bring the number of degrees of freedom to infinity and reduce the “distance” between them so as to make the result continuous. How do I get from e.g (1 0) to delta(x) by some limit ?
This question is very important for new treatments of paths integrals where one knows the discrete limit, the continuous limit, but going from one to the other by taking an obvious limit is mathematically tricky.
31 August, 2010 at 9:26 am
Terence Tao
One way to represent a “continuous” Hilbert space as a limit of “discrete” ones is by letting the finest scale one permits to go to zero. For instance, inside the Hilbert space![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) of square-integrable functions on [0,1], consider the subspace
of square-integrable functions on [0,1], consider the subspace ![L^2[0,1]_n](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D_n&bg=ffffff&fg=545454&s=0&c=20201002) of functions in
of functions in ![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) which are constant on the dyadic intervals
which are constant on the dyadic intervals 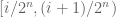 for
for  . This is a finite-dimensional Hilbert space, with an (un-normalised) orthogonal basis given by the
. This is a finite-dimensional Hilbert space, with an (un-normalised) orthogonal basis given by the 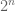 functions
functions 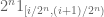 for
for  , which are approximations to the Dirac delta functions. Letting n go to infinity, the subspaces
, which are approximations to the Dirac delta functions. Letting n go to infinity, the subspaces ![L^2[0,1]_n](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D_n&bg=ffffff&fg=545454&s=0&c=20201002) increase and have
increase and have ![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) as their direct limit (because the Hilbert space closure of
as their direct limit (because the Hilbert space closure of ![\bigcup_{n=1}^\infty L^2[0,1]_n](https://s0.wp.com/latex.php?latex=%5Cbigcup_%7Bn%3D1%7D%5E%5Cinfty+L%5E2%5B0%2C1%5D_n&bg=ffffff&fg=545454&s=0&c=20201002) is
is ![L^2[0,1]](https://s0.wp.com/latex.php?latex=L%5E2%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) ), while the approximate delta functions converge (in the sense of distributions) to Dirac delta functions.
), while the approximate delta functions converge (in the sense of distributions) to Dirac delta functions.
1 September, 2010 at 12:51 am
QTheorist
This is a very nice idea indeed ! with
with 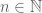 , which would be the case for a quantum system evolving on an infinite lattice for example. But then if I want to go from this lattice to a continuous space, that is ending up with
, which would be the case for a quantum system evolving on an infinite lattice for example. But then if I want to go from this lattice to a continuous space, that is ending up with  varying continuously with some parameter
varying continuously with some parameter 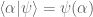 how can I get this from
how can I get this from  ? I cannot see how I can use the trick you presented before as I would need to start with an infinity of intervals ?
? I cannot see how I can use the trick you presented before as I would need to start with an infinity of intervals ?
But I noticed that it does not allow the case of infinite vectors with discrete levels. Indeed I can consider a wave function of the type
1 September, 2010 at 11:11 am
Terence Tao
Well, one can truncate in space (to finitise the largest scale) simultaneously with discretising (to finitise the smallest scake). For instance one can approximate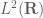 by the finite-dimensional subspace
by the finite-dimensional subspace  of functions that are piecewise constant on dyadic intervals of length
of functions that are piecewise constant on dyadic intervals of length 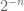 , while being supported on the interval
, while being supported on the interval ![[-2^{n}, 2^n]](https://s0.wp.com/latex.php?latex=%5B-2%5E%7Bn%7D%2C+2%5En%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
2 September, 2010 at 5:38 am
QTheorist
Thank you that makes perfect sense, I shall try to put this idea in practice shortly !
31 August, 2010 at 8:51 am
Hilbert spaces from the mathematician’s perspective « Polariton
[…] 245B Notes 5: Hlibert spaces […]
18 March, 2011 at 4:04 pm
Anonymous
In exercise 12, what if one drops the assumption that the subspace is “closed”? The decomposition still exists?(Though not unique?)
18 March, 2011 at 5:20 pm
Terence Tao
This is a good exercise to test your intuition, and I won’t spoil it. (However, I will say that a good example of a non-closed subspace is a dense subspace.)
18 March, 2011 at 7:37 pm
Anonymous
When we define the complex inner product space, why use instead of
instead of  . I remember you mentioned in the linear algebra course that things like
. I remember you mentioned in the linear algebra course that things like 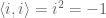 may happen and thus lose the positivity property if one only uses symmetry property.(Isn’t is? ) Is there any other reason for this?
may happen and thus lose the positivity property if one only uses symmetry property.(Isn’t is? ) Is there any other reason for this?
22 April, 2011 at 8:51 am
Anonymous
Dear Prof. Tao,
In proposition 2, you prove that ” Every Hilbert space has at least one orthonormal basis.” Since you use Zorn’s lemma here, as you said before, the proof is non-constructive. I was wondering that whether one can prove this proposition in some special cases by construction.
22 April, 2011 at 11:22 am
timur
I am not sure I understand your question completely but if it helps, you can construct explicit orthogonal bases for many situations; for example, the trigonometric polynomials are an orthogonal basis for L^2 on the circle, or sine functions with integer frequencies are an orthogonal basis for L^2 on (0,pi) etc.
7 December, 2013 at 4:06 pm
Ultraproducts as a Bridge Between Discrete and Continuous Analysis | What's new
[…] proof of the existence of orthogonal projections in Hilbert spaces (see e.g. Proposition 1 of this previous blog post), so on some level the two proofs of the regularity lemma are essentially equivalent. However, the […]
20 June, 2014 at 9:11 pm
An abstract ergodic theorem, and the Mackey-Zimmer theorem | What's new
[…] closed, convex, and non-empty in a Hilbert space, it is a classical fact (see e.g. Proposition 1 of this previous post) that it has a unique element of minimal norm. It is clearly -invariant, since if then the […]
25 December, 2015 at 10:05 am
Anonymous
What do you mean mathematically by “Optimising in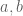 ” in the proof of Lemma 1?
” in the proof of Lemma 1?
25 December, 2015 at 10:46 am
Terence Tao
This means selecting the values of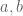 that give the strongest bound on
that give the strongest bound on  from the non-negativity of (15). In this case, one can select (assuming that
from the non-negativity of (15). In this case, one can select (assuming that  are non-zero, as the inequality is obvious otherwise)
are non-zero, as the inequality is obvious otherwise)  and
and  to conclude that
to conclude that  , which on further optimising by choosing
, which on further optimising by choosing 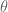 to be the phase of
to be the phase of  gives the Cauchy-Schwarz inequality.
gives the Cauchy-Schwarz inequality.
25 December, 2015 at 3:15 pm
Anonymous
The method you describe (letting ), looks quite different from the one you give in
), looks quite different from the one you give in
While the later one is quite easy to remember and recover, the one you gave (which appears in lots of textbooks also) in the comment looks a little bit “ad hoc“. Are they essential the same?
29 January, 2023 at 6:57 am
Vi
Can you please clarify how you selected those values that turned out to give the tightest bound? The selection seems quite mysterious. What am I missing>
25 December, 2015 at 11:25 am
Anonymous
In Exercise 6, “as soon as X contains at least two disjoint sets of non-empty finite measure”? What is “non-empty finite measure”?
[This was a typo; it should be “non-zero finite measure”. -T.]
6 March, 2016 at 1:33 pm
Anonymous
In Example 8, how should one understand the difference between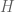 and
and 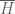 ? For instance if
? For instance if  , then isn’t is true that
, then isn’t is true that  ?
?
7 March, 2016 at 12:26 pm
Terence Tao
25 November, 2016 at 9:46 am
Anonymous
In the infinite dimensional case, do you have an example that a Hamel basis is also an orthonormal basis for a Hilbert space?
Are non-separable Hilbert spaces very rare? (Just like non-Lebesgue measurable sets?) I really can’t find an easy example. Do you have any “handy” example for a non-separable Hilbert space?
25 November, 2016 at 1:32 pm
Terence Tao
An infinite orthonormal basis, such as , cannot be a Hamel basis, since (for instance)
, cannot be a Hamel basis, since (for instance)  will converge to an element not in the algebraic span of that basis. (Similarly for uncountable orthonormal bases.)
will converge to an element not in the algebraic span of that basis. (Similarly for uncountable orthonormal bases.)
For an example of a non-separable Hilbert space, take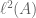 for any uncountable
for any uncountable  . But it is true that most Hilbert spaces one encounters in analysis and PDE (outside of functional analysis, nonstandard analysis, and other branches of analysis dealing with extremely large spaces) are indeed separable.
. But it is true that most Hilbert spaces one encounters in analysis and PDE (outside of functional analysis, nonstandard analysis, and other branches of analysis dealing with extremely large spaces) are indeed separable.
25 April, 2017 at 1:56 pm
Anonymous
In Exercise 18.(4), what does “Take adjoints of (2).” mean?
[This should have been “Take adjoints of (3)”, i.e., to take adjoints of the linear map used in part (3). -T.]
28 April, 2017 at 7:43 am
Anonymous
By the existence of orthonormal basis of a Hilbert space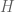 , any
, any 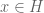 can be written as
can be written as 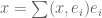 and thus for any continuous linear functional
and thus for any continuous linear functional  on
on 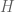 , we have
, we have
If one sets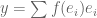 , then the Riesz representation is done.
, then the Riesz representation is done.
This works perfectly well in the finite dimensional case. Would we have any trouble in the infinite case? (or even worse, the nonseparable case?)
[Yes, this will work in general, even in nonseparable Hilbert spaces, after one uses the Bessel inequality or Plancherel identity to help ensure convergence of all the relevant sums. -T]
31 December, 2021 at 10:56 pm
Aditya Guha Roy
A particular consequence of Exercise 6 is that every finite dimensional inner product space over is a Hilbert space. Isn’t the following a more direct proof of it:
is a Hilbert space. Isn’t the following a more direct proof of it:
We would do induction on the dimension. over
over  , of dimension
, of dimension  and let the claim be true for all dimensions
and let the claim be true for all dimensions  .
.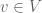 be a unit vector; set
be a unit vector; set 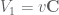 (the space spanned by
(the space spanned by  ) and
) and  to be the orthogonal complement of
to be the orthogonal complement of  in
in  (i.e.,
(i.e.,  ).
). is the direct sum of
is the direct sum of  and $V_2$. and
and $V_2$. and  is a
is a  dimensional vector space.
dimensional vector space.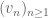 in
in  , we can write
, we can write 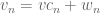 for
for  and
and  , and the Cauchy condition of
, and the Cauchy condition of 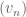 implies that the sequences
implies that the sequences  and
and 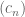 are also Cauchy, whence they converge (thanks to the induction hypothesis), thus $(v_n)$ must also converge to an element of
are also Cauchy, whence they converge (thanks to the induction hypothesis), thus $(v_n)$ must also converge to an element of  , which proves the claim.
, which proves the claim. 
For the case of dimension = 1, it is trivial.
Take any finite dimensional inner product space
Let
Then
Now take any Cauchy sequence
Is this appropriate?
1 January, 2022 at 7:25 am
Aditya Guha Roy
I think this proof would also allow us to show that the direct sum of two Hilbert spaces is also a Hilbert space.
2 January, 2022 at 9:30 am
Aditya Guha Roy
Here is a more detailed discussion on the direct sum of Hilbert spaces being a Hilbert space.
https://proofwiki.org/wiki/Hilbert_Space_Direct_Sum_is_Hilbert_Space
17 January, 2022 at 7:21 am
Anonymous
In the case of![L^2([0,1])](https://s0.wp.com/latex.php?latex=L%5E2%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) , if one consider an orthonormal basis
, if one consider an orthonormal basis  , then
, then  for all
for all  implies that
implies that  a.e..
a.e..
Do we have such an analog if we lose orthogonality? For instance, consider the separable space![L^1([0,1])](https://s0.wp.com/latex.php?latex=L%5E1%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . Let
. Let  be a sequence of continuous functions on
be a sequence of continuous functions on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) so that it is dense in
so that it is dense in ![L^1([0,1])](https://s0.wp.com/latex.php?latex=L%5E1%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . If
. If  for all
for all  , can we say
, can we say  a.e.?
a.e.?
20 January, 2022 at 5:23 pm
Terence Tao
If the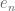 span a dense subspace of
span a dense subspace of ![C([0,1])](https://s0.wp.com/latex.php?latex=C%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) then this follows from the Riesz representation theorem. Not sure if density in
then this follows from the Riesz representation theorem. Not sure if density in  is sufficient (the natural space to use here is something like a dual or predual to
is sufficient (the natural space to use here is something like a dual or predual to  ).
).
18 September, 2022 at 5:27 am
Aditya Guha Roy
Some nitpicking: in Exercise 12 the conclusion assumes we are not treating the zero vector orthogonal to every vector; I think then in the statement you should mention that is a “proper” subspace of
is a “proper” subspace of 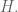
[I believe Exercise 12 is correct as stated, with the conventions on orthogonality as stated – T.]
Well I see a proof using Proposition 1 as follows: there is a unique
there is a unique 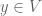 such that
such that 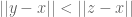 for all
for all 
 for all
for all  playing around with this (plugging appropriate transformations of
playing around with this (plugging appropriate transformations of  such as
such as 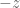 and
and  ) gives us
) gives us  for all
for all  take
take  and
and  we are done.
we are done.
since subspaces are convex sets, closed subspaces are closed convex subsets. Thanks to Proposition 1, for any given
We also have
Thanks,
Adi
1 February, 2023 at 4:55 am
Anonymous
Inspired by Example 2, is it true that every (complex) Hilbert space can be represented as an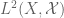 space for some measure space
space for some measure space 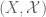 ?
?
10 February, 2023 at 6:03 pm
Anonymous
I just realized that this stupid question is answered completely by Corollary 1.
1 February, 2023 at 5:19 am
Anonymous
In the proof of Cauchy-Schwarz in Lemma 1, if one works with the real case, does one have a real version of the amplification trick?
1 February, 2023 at 9:44 am
Anonymous
You can just set the complex part to be zero.