This week I was in my home town of Adelaide, Australia, for the 2009 annual meeting of the Australian Mathematical Society. This was a fairly large meeting (almost 500 participants). One of the highlights of such a large meeting is the ability to listen to plenary lectures in fields adjacent to one’s own, in which speakers can give high-level overviews of a subject without getting too bogged down in the technical details. From the talks here I learned a number of basic things which were well known to experts in that field, but which I had not fully appreciated, and so I wanted to share them here.
The first instance of this was from a plenary lecture by Danny Calegari entitled “faces of the stable commutator length (scl) ball”. One thing I learned from this talk is that in homotopy theory, there is a very close relationship between topological spaces (such as manifolds) on one hand, and groups (and generalisations of groups) on the other, so that homotopy-theoretic questions about the former can often be converted to purely algebraic questions about the latter, and vice versa; indeed, it seems that homotopy theorists almost think of topological spaces and groups as being essentially the same concept, despite looking very different at first glance. To get from a space to a group, one looks at homotopy groups
of that space, and in particular the fundamental group
; conversely, to get from a group
back to a topological space one can use the Eilenberg-Maclane spaces
associated to that group (and more generally, a Postnikov tower associated to a sequence of such groups, together with additional data). In Danny’s talk, he gave the following specific example: the problem of finding the least complicated embedded surface with prescribed (and homologically trivial) boundary in a space
, where “least complicated” is measured by genus (or more precisely, the negative component of Euler characteristic), is essentially equivalent to computing the commutator length of the element in the fundamental group
corresponding to that boundary (i.e. the least number of commutators one is required to multiply together to express the element); and the stable version of this problem (where one allows the surface to wrap around the boundary
times for some large
, and one computes the asymptotic ratio between the Euler characteristic and
) is similarly equivalent to computing the stable commutator length of that group element. (Incidentally, there is a simple combinatorial open problem regarding commutator length in the free group, which I have placed on the polymath wiki.)
This theme was reinforced by another plenary lecture by Ezra Getzler entitled “-groups”, in which he showed how sequences of groups (such as the first
homotopy groups
) can be enhanced into a more powerful structure known as an
-group, which is more complicated to define, requiring the machinery of simplicial complexes, sheaves, and nerves. Nevertheless, this gives a very topological and geometric interpretation of the concept of a group and its generalisations, which are of use in topological quantum field theory, among other things.
Mohammed Abuzaid gave a plenary lecture entitled “Functoriality in homological mirror symmetry”. One thing I learned from this talk was that the (partially conjectural) phenomenon of (homological) mirror symmetry is one of several types of duality, in which the behaviour of maps into one mathematical object (e.g. immersed or embedded curves, surfaces, etc.) are closely tied to the behaviour of maps out of a dual mathematical object
(e.g. functionals, vector fields, forms, sections, bundles, etc.). A familiar example of this is in linear algebra: by taking adjoints, a linear map into a vector space
can be related to an adjoint linear map mapping out of the dual space
. Here, the behaviour of curves in a two-dimensional symplectic manifold (or more generally, Lagrangian submanifolds in a higher-dimensional symplectic manifold), is tied to the behaviour of holomorphic sections on bundles over a dual algebraic variety, where the precise definition of “behaviour” is category-theoretic, involving some rather complicated gadgets such as the Fukaya category of a symplectic manifold. As with many other applications of category theory, it is not just the individual pairings between an object and its dual which are of interest, but also the relationships between these pairings, as formalised by various functors between categories (and natural transformations between functors). (One approach to mirror symmetry was discussed by Shing-Tung Yau at a distinguished lecture at UCLA, as transcribed in this previous post.)
There was a related theme in a talk by Dennis Gaitsgory entitled “The geometric Langlands program”. From my (very superficial) understanding of the Langlands program, the behaviour of specific maps into a reductive Lie group , such as representations in
of a fundamental group, étale fundamental group, class group, or Galois group of a global field, is conjecturally tied to specific maps out of a dual reductive Lie group
, such as irreducible automorphic representations of
, or of various structures (such as derived categories) attached to vector bundles on
. There are apparently some tentatively conjectured links (due to Witten?) between Langlands duality and mirror symmetry, but they seem at present to be fairly distinct phenomena (one is topological and geometric, the other is more algebraic and arithmetic). For abelian groups, Langlands duality is closely connected to the much more classical Pontryagin duality in Fourier analysis. (There is an analogue of Fourier analysis for nonabelian groups, namely representation theory, but the link from this to the Langlands program is somewhat murky, at least to me.)
Related also to this was a plenary talk by Akshay Venkatesh, entitled “The Cohen-Lenstra heuristics over global fields”. Here, the question concerned the conjectural behaviour of class groups of quadratic fields, and in particular to explain the numerically observed phenomenon that about of all quadratic fields
(with
prime) enjoy unique factorisation (i.e. have trivial class group). (Class groups, as I learned in these two talks, are arithmetic analogues of the (abelianised) fundamental groups in topology, with Galois groups serving as the analogue of the full fundamental group.) One thing I learned here was that there was a canonical way to randomly generate a (profinite) abelian group, by taking the product of randomly generated finite abelian
-groups for each prime
. The way to canonically randomly generate a finite abelian
-group is to take large integers
, and look at the cokernel of a random homomorphism from
to
. In the limit
(or by replacing
with the
-adics and just sending
), this stabilises and generates any given
-group
with probability
where is the group of automorphisms of
. In particular this leads to the strange identity
where ranges over all
-groups; I do not know how to prove this identity other than via the above probability computation, the proof of which I give below the fold.
Based on the heuristic that the class group should behave “randomly” subject to some “obvious” constraints, it is expected that a randomly chosen real quadratic field has unique factorisation (i.e. the class group has trivial
-group component for every
) with probability
whereas a randomly chosen imaginary quadratic field has unique factorisation with probability
The former claim is conjectural, whereas the latter claim follows from (for instance) Siegel’s theorem on the size of the class group, as discussed in this previous post. Ellenberg, Venkatesh, and Westerland have recently established some partial results towards the function field analogues of these heuristics.
— 1. -groups —
Henceforth the prime will be fixed. We will abbreviate “finite abelian
-group” as “
-group” for brevity. Thanks to the classification of finite abelian groups, the
-groups are all isomorphic to the products
of cyclic -groups.
The cokernel of a random homomorphism from to
can be written as the quotient of the
-group
by the subgroup generated by
randomly chosen elements
from that
-group. One can view this quotient as a
-fold iterative process, in which one starts with the
-group
, and then one iterates
times the process of starting with a
-group
, and quotienting out by a randomly chosen element
of that group
. From induction, one sees that at the
stage of this process (
), one ends up with a
-group isomorphic to
for some
-group
.
Let’s see how the group transforms to the next group
. We write a random element of
as
, where
and
. Observe that for any
,
is a multiple of
(but not
) with probability
. (The remaining possibility is that
is zero, but this event will have negligible probability in the limit
.) If
is indeed divisible by
but not
, and
is not too close to
, a little thought will then reveal that
. Thus the size of the
-groups
only grow as
increases. (Things go wrong when
gets close to
, e.g.
, but the total size of this event as
ranges from
to
sums to be
as
(uniformly in
), by using the tightness bounds on
mentioned below. Alternatively, one can avoid a lot of technicalities by taking the limit
before taking the limit
(instead of studying the double limit
), or equivalently by replacing the cyclic group
with the
-adics
.)
The exponentially decreasing nature of the probability in
(and in
) furthermore implies that the distribution of
forms a tight sequence in
: for every
, one has an
such that the probability that
is less than
for all choices of
. (This tightness is necessary to prove the equality in (2) rather than just an inequality (from Fatou’s lemma).) Indeed, the probability that
converges as
to the
coefficient in the generating function
In particular, this claim is true for the final cokernel . Note that this (and the geometric series formula) already yields (1) in the case of the trivial group
and the order
group
(note that
has order
and
in these respective cases). But it is not enough to deal with higher groups. For instance, up to isomorphism there are two
-groups of order
, namely
and
, whose automorphism group has order
and
respectively. Summing up the corresponding two expressions (1) one can observe that this matches the
coefficient of (3) (after some applications of the geometric series formula). Thus we see that (3) is consistent with the claim (1), but does not fully imply that claim.
To get the full asymptotic (1) we try a slightly different tack. Fix a -group
, and consider the event that the cokernel of a random map
is isomorphic to
. We assume
so large that all elements in
have order at most
. If this is the case, then there must be a surjective homomorphism
such that the range of
is equal to the kernel of
. The number of homomorphisms from
to
is
(one has to pick
generators in
). If
is large, it is easy to see that most of these homomorphisms are surjective (the proportion of such homomorphisms is
as
). On the other hand, there is some multiplicity; the range of
can emerge as the kernel of
in
different ways (since any two surjective homomorphisms
with the same kernel arise from an automorphism of
). So to prove (1), it suffices to show that for any surjective homomorphism
, the probability that the range of
equals the kernel of
is
The range of is the same thing as the subgroup of
generated by
random elements
of that group. The kernel of
has index
inside
, so the probability that all of those random elements lie in the kernel of
is
. So it suffices to prove the following claim: if
is a fixed surjective homomorphism from
to
, and
are chosen randomly from the kernel of
, then
will generate that kernel with probability
But from the classification of -groups, the kernel of
(which has bounded index inside
) is isomorphic to
where means “bounded uniformly in
“, and there are
factors here. As in the previous argument, one can now imagine starting with the group (5), and then iterating
times the operation of quotienting out by the group generated by a randomly chosen element; our task is to compute the probability that one ends up with the trivial group by applying this process.
As before, at the stage of the iteration, one ends up with a group of the form
where there are factors of
. The group
is increasing in size, so the only way in which one ends up with the trivial group is if all the
are trivial. But if
is trivial, the only way that
is trivial is if the randomly chosen element from (6) has a
component which is invertible (i.e. not a multiple of
), which occurs with probability
(assuming
is large enough). Multiplying all these probabilities together gives (4).

23 comments
Comments feed for this article
2 October, 2009 at 7:38 am
Greg Kuperberg
indeed, it seems that homotopy theorists almost think of topological spaces and groups as being essentially the same concept, despite looking very different at first glance
Well, not always. When people study spaces with a trivial or tightly controlled fundamental group, then (in interesting cases) no serious connection arises between manifolds and group theory. For instance, the study of simply-connected smooth 4-manifolds. However, when a space has a complicated fundamental group, then there is already lots to study if you simplify the space to the classifying space of its fundamental group. Indeed, many interesting spaces, for instance hyperbolic manifolds, already are classifying spaces.
In 3-manifold topology, you never step all that far away from classifying spaces of the fundamental groups that can arise. They aren’t exactly the same in all cases, but close. On the other hand, this is a phenomenon that only holds up to dimension 3.
2 October, 2009 at 7:44 am
Greg Kuperberg
Sorry, you meant your comment in the more general sense of all of the homotopy groups of a space rather than just the fundamental group; and in the weaker sense of homotopy type rather than (say) diffeomorphism type.
In this case, yes, there is a classic construction, called a Postnikov tower, that models all of the homotopy information of any cell complex in terms of homotopy groups. The motivation is fairly simple. Suppose that X and Y are two cell complexes and you are trying to compute the homotopy types of maps from X to Y. If you freeze the (n-1)-skeleton of the map, then the different things that the n-cells can do are described by homotopy groups. You can then climb up the skeleta of X by induction.
2 October, 2009 at 8:12 am
David Speyer
I think that this claim “If x is indeed divisible by p^i but not p^{i+1}, a little thought will then reveal that |G_{j+1}| = p^i |G_j|” does not quite work.
Let G_j be Z/p^2, let y generate G_j and let x be divisible by p^{n-1} but not p^n. Then G_{j+1} has order p^n, not p^{n+1} as your formula would give.
This sort of issue is negligible as n goes to infinity. I can show that there is no problem if we send n to infinity first, and then send d to infinity. (In which case, one can just think about random maps from Z_p^d to itself, where Z_p is the p-adics.) But it seems to me to be not completely obvious if d goes to infinity first.
2 October, 2009 at 3:44 pm
Terence Tao
Hmm, fair point. One can still control everything by slapping quantitative bounds on how large the G_j get most of the time (there’s a lot of exponential decay around the place that prevents the G_j from getting anywhere close to in size, and which then means that it’s only the incredibly rare large i that cause difficulty), but it begins to get a bit icky, and I suppose the simplest solution is indeed to retreat to the p-adics.
in size, and which then means that it’s only the incredibly rare large i that cause difficulty), but it begins to get a bit icky, and I suppose the simplest solution is indeed to retreat to the p-adics.
4 October, 2009 at 2:59 am
Paul Leopardi
Thanks for writing up your summaries of key points in these plenary lectures. I attended the Calegari and Venkatesh talks, but missed the Getzler, Abuzaid and Gaitsgory talks, due to a combination of illness and having to work on my MASCOS talk. You certainly got more out of these talks than I did. I’ll have a bit of work when I get back to my office in looking up all the references to Hatcher’s book – being a rank beginner in algebraic topology myself. I wonder if the rest of the plenary audiences were as on-the-ball as you were?
4 October, 2009 at 6:43 pm
Anonymous
Dear Terry,
When considering real quadratic fields of class number one, you should probably restrict to fields with
with 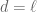 prime. (When
prime. (When  has at least three divisors, the class group always has even order.) [Corrected, thanks! Akshay mentioned this in passing during the lecture, but I forgot to mention it here. -T.]
has at least three divisors, the class group always has even order.) [Corrected, thanks! Akshay mentioned this in passing during the lecture, but I forgot to mention it here. -T.]
5 October, 2009 at 2:36 am
David Corfield
I wonder if you could tell us about your sense of the Two Cultures divide when you attend talks such as those you describe from the other side.
Recently I came across a course introduction by Noam Elkies in which he says:
“The Harvard math curriculum leans heavily towards the systematic, theory-building style; analytic number theory as usually practiced falls in the problem-solving camp. This is probably why, despite its illustrious history (Euclid, Euler, Riemann, Selberg, … ) and present-day vitality, analytic number theory has rarely been taught here. … Now we shall see that there is more to analytic number theory than a bag of unrelated ad-hoc tricks, but it is true that partisans of contravariant functors, adelic tangent sheaves, and etale cohomology will not find them in the present course. Still, even ardent structuralists can benefit from this course. … An ambitious theory-builder should regard the absence thus far of a Grand Unified Theory of analytic number theory not as an insult but as a challenge. Both machinery- and problem-motivated mathematicians should note that some of the more exciting recent work in number theory depends critically on symbiosis between the two styles of mathematics.”
5 October, 2009 at 9:43 am
Terence Tao
Actually, I found the plenary talks at this conference remarkably accessible – there was a strong emphasis on basic examples, motivation, and intuition rather than definitions and proofs. But it helped that I already had familiarity with some of the concepts being discussed (e.g. connections, simplicial homology, schemes, Lagrangian submanifolds, number fields, Picard variety, etc.).
12 October, 2009 at 12:06 am
David Corfield
I suppose what really interests me is how you see your structure/pseudorandomness dichotomy relate to work on the ‘theory-building’ side. The latter seem to be aiming for a huge web of categorified dualities, possibly to be seen as a form of space-quantity duality.
Do you see this work as an exploration of the ‘structure’ part of your dichotomy, so that pseudorandomness will escape their grasp, or is it better not to conflate your ‘structure’ and their ‘structure’?
12 October, 2009 at 8:17 am
Terence Tao
Hmm. It does seem that categorification and similar theoretical frameworks are currently better for manipulating the type of exact mathematical properties (identities, exact symmetries, etc.) that show up in structured objects than the fuzzier type of properties (correlation, approximation, independence, etc.) that show up in pseudorandom objects, but this may well be just a reflection of the state of the art than of some fundamental restriction. For instance, in my work on the Gowers uniformity norms, there are hints of some sort of “noisy additive cohomology” beginning to emerge – for instance, one may have some sort of function which is “approximately linear” in the sense that its second “derivative” is “mostly negligible”, and one wants to show that it in fact differs from a genuinely linear function by some “small” error; this strongly feels like a cohomological question, but we do not yet have the abstract theoretical machinery to place it in the classical cohomology framework (except perhaps in the ergodic theory limit of these problems, where there does seem to be a reasonable interpretation of these informal concepts). Similarly, when considering inverse theorems in additive combinatorics, a lot of what we do has the feel of “noisy group theory”, and we can already develop noisy analogues of some primitive group theory concepts (e.g. quotient groups, group extensions, the homomorphism theorems, etc.), but we are nowhere near the level of sophistication (and categorification, etc.) with noisy algebra that exact algebra enjoys right now. But perhaps that will change in the future.
14 October, 2009 at 2:34 am
David Corfield
Fascinating, thanks for this. When you finally write the book called ‘Noisy Group Theory’ it will be interesting to see in which sections the bookshops mistakenly place it.
14 October, 2009 at 2:48 pm
TooMuchCoffeeMan
At the risk of talking at cross-purposes, or being facile, there are simpler (but still quite hard and interesting, for some of us at least) versions of some of the questions Terry mentions: see
MR0928525 (89h:46072) Johnson, B. E. Approximately multiplicative maps between Banach algebras. J. London Math. Soc. (2) 37 (1988), no. 2, 294–316.
MR0864452 (87k:46105) Johnson, B. E. Approximately multiplicative functionals. J. London Math. Soc. (2) 34 (1986), no. 3, 489–510.
MR0701524 (85f:28006)
Kalton, N. J.(1-MO); Roberts, James W.(1-SC)
Uniformly exhaustive submeasures and nearly additive set functions.
Trans. Amer. Math. Soc. 278 (1983), no. 2, 803–816.
The last of these is related (I think) to certain questions about the cohomology of a certain Banach algebra, namely the l^1-completion of the polynomial algebra in countably many variables – although I have never quite wrung the full details out of the person who assured me of this. I’d be very interested to know if it fits into the circle of ideas concerning decomposition into structured and pseudorandom parts.
On reflection, all of the articles I mention are imposing quite strong global conditions on the “approximate cocycle”, and this might not be what you want – the notion of small second derivative is still quite a local condition and may not fit into the approaches I’ve referred to.
8 October, 2009 at 6:01 am
john mangual
I am not denying that measure you give on p-groups is very interesting, but why not naively pick random sequences of integers and choose your group to be
and choose your group to be  ? Is there something special about this particular measure?
? Is there something special about this particular measure?
8 October, 2009 at 7:32 am
Terence Tao
Unfortunately, there is no canonical choice of probability measure on the integers to use here (also, one needs to somehow pick the integer k), so the notion of “random sequences of integers” is not well defined.
The idea of building a random p-group by placing a large number of random relations on a large number of generators is broadly analogous to (a commutative, torsion version of) Gromov’s notion of a random group, which is of importance in geometric group theory. And, of course, there is the intriguing connection to number theory as mentioned in the post, somewhat analogous to the (still not well understood) connection between the eigenvalue spacing statistics of GUE random matrices and the spacing statistics of zeroes of the Riemann zeta function.
8 October, 2009 at 7:36 am
Thomas
Dear Terry,
Do you tend to take notes at conferences? Or do you think that this is a bad practice?
8 October, 2009 at 11:13 am
Terence Tao
I used to take notes fairly frequently when I was a graduate student, but nowadays I find it is generally more effective to try to understand the talk in real time, and try to catch up afterwards if necessary by asking questions of the speaker, and/or obtaining and reading the slides and source references. In many cases, my main objective is just to get a flavour of the subject, rather than the details, and notes are not particularly useful for that task.
The main exception is for talks which I intend to transcribe in full to this blog, such as the distinguished lecture series at UCLA, in which I do indeed take plenty of notes.
19 October, 2009 at 4:26 pm
Grothendieck’s definition of a group « What’s new
[…] a recent talk by Ezra Getzler, I learned a more sophisticated perspective on a group, somewhat analogous to Thurston’s […]
12 August, 2014 at 8:04 pm
Avila, Bhargava, Hairer, Mirzakhani | What's new
[…] a certain random -adic matrix, very much in the spirit of the Cohen-Lenstra heuristics discussed in this previous post). But what is even more impressive is that Manjul and his coauthors have been able to verify […]
26 December, 2014 at 1:31 pm
Galois Groups vs. Fundamental Groups | CL-UAT
[…] a recent blog post Terry Tao mentions in passing […]
13 April, 2017 at 5:08 pm
Counting objects up to isomorphism: groupoid cardinality | What's new
[…] groups in number theory and combinatorics, such as the class groups of random quadratic fields; see this previous blog post for more discussion. I’ve been told that this notion of cardinality up to isomorphism is also […]
14 April, 2020 at 8:56 am
Charlie O'Mara
why are the products taken over all odd primes, and don’t include p=2 when making the probability calculations? I feel like i’m missing something rather fundamental.
14 April, 2020 at 10:39 am
Terence Tao
I’m not an expert in algebraic number theory, but I think this has to do with Gauss’s genus theory which constrains the 2-torsion component of the class group for both real and imaginary quadratic fields. This paper of Gerth may be able to give more detail, but I currently do not have access to it.
14 April, 2020 at 11:34 am
Charlie O'Mara
Yes, thank you. Xuejun Guo gives a nice writeup. http://maths.nju.edu.cn/~guoxj/articles/2009Gauss.pdf