As laid out in the foundational work of Kolmogorov, a classical probability space (or probability space for short) is a triplet , where
is a set,
is a
-algebra of subsets of
, and
is a countably additive probability measure on
. Given such a space, one can form a number of interesting function spaces, including
- the (real) Hilbert space
of square-integrable functions
, modulo
-almost everywhere equivalence, and with the positive definite inner product
; and
- the unital commutative Banach algebra
of essentially bounded functions
, modulo
-almost everywhere equivalence, with
defined as the essential supremum of
.
There is also a trace on
defined by integration:
.
One can form the category of classical probability spaces, by defining a morphism
between probability spaces to be a function
which is measurable (thus
for all
) and measure-preserving (thus
for all
).
Let us now abstract the algebraic features of these spaces as follows; for want of a better name, I will refer to this abstraction as an algebraic probability space, and is very similar to the non-commutative probability spaces studied in this previous post, except that these spaces are now commutative (and real).
Definition 1 An algebraic probability space is a pair
where
is a unital commutative real algebra;
is a homomorphism such that
and
for all
;
- Every element
of
is bounded in the sense that
. (Technically, this isn’t an algebraic property, but I need it for technical reasons.)
A morphism
is a homomorphism
which is trace-preserving, in the sense that
for all
.
For want of a better name, I’ll denote the category of algebraic probability spaces as . One can view this category as the opposite category to that of (a subcategory of) the category of tracial commutative real algebras. One could emphasise this opposite nature by denoting the algebraic probability space as
rather than
; another suggestive (but slightly inaccurate) notation, inspired by the language of schemes, would be
rather than
. However, we will not adopt these conventions here, and refer to algebraic probability spaces just by the pair
.
By the previous discussion, we have a covariant functor that takes a classical probability space
to its algebraic counterpart
, with a morphism
of classical probability spaces mapping to a morphism
of the corresponding algebraic probability spaces by the formula
for . One easily verifies that this is a functor.
In this post I would like to describe a functor which partially inverts
(up to natural isomorphism), that is to say a recipe for starting with an algebraic probability space
and producing a classical probability space
. This recipe is not new – it is basically the (commutative) Gelfand-Naimark-Segal construction (discussed in this previous post) combined with the Loomis-Sikorski theorem (discussed in this previous post). However, I wanted to put the construction in a single location for sake of reference. I also wanted to make the point that
and
are not complete inverses; there is a bit of information in the algebraic probability space (e.g. topological information) which is lost when passing back to the classical probability space. In some future posts, I would like to develop some ergodic theory using the algebraic foundations of probability theory rather than the classical foundations; this turns out to be convenient in the ergodic theory arising from nonstandard analysis (such as that described in this previous post), in which the groups involved are uncountable and the underlying spaces are not standard Borel spaces.
Let us describe how to construct the functor , with details postponed to below the fold.
- Starting with an algebraic probability space
, form an inner product on
by the formula
, and also form the spectral radius
.
- The inner product is clearly positive semi-definite. Quotienting out the null vectors and taking completions, we arrive at a real Hilbert space
, to which the trace
may be extended.
- Somewhat less obviously, the spectral radius is well-defined and gives a norm on
. Taking
limits of sequences in
of bounded spectral radius gives us a subspace
of
that has the structure of a real commutative Banach algebra.
- The idempotents
of the Banach algebra
may be indexed by elements
of an abstract
-algebra
.
- The Boolean algebra homomorphisms
(or equivalently, the real algebra homomorphisms
) may be indexed by elements
of a space
.
- Let
denote the
-algebra on
generated by the basic sets
for every
.
- Let
be the
-ideal of
generated by the sets
, where
is a sequence with
.
- One verifies that
is isomorphic to
. Using this isomorphism, the trace
on
can be used to construct a countably additive measure
on
. The classical probability space
is then
, and the abstract spaces
may now be identified with their concrete counterparts
,
.
- Every algebraic probability space morphism
generates a classical probability morphism
via the formula
using a pullback operation
on the abstract
-algebras
that can be defined by density.
Remark 1 The classical probability space
constructed by the functor
has some additional structure; namely
is a
-Stone space (a Stone space with the property that the closure of any countable union of clopen sets is clopen),
is the Baire
-algebra (generated by the clopen sets), and the null sets are the meager sets. However, we will not use this additional structure here.
The partial inversion relationship between the functors and
is given by the following assertion:
- There is a natural transformation from
to the identity functor
.
More informally: if one starts with an algebraic probability space and converts it back into a classical probability space
, then there is a trace-preserving algebra homomorphism of
to
, which respects morphisms of the algebraic probability space. While this relationship is far weaker than an equivalence of categories (which would require that
and
are both natural isomorphisms), it is still good enough to allow many ergodic theory problems formulated using classical probability spaces to be reformulated instead as an equivalent problem in algebraic probability spaces.
Remark 2 The opposite composition
is a little odd: it takes an arbitrary probability space
and returns a more complicated probability space
, with
being the space of homomorphisms
. while there is “morally” an embedding of
into
using the evaluation map, this map does not exist in general because points in
may well have zero measure. However, if one takes a “pointless” approach and focuses just on the measure algebras
,
, then these algebras become naturally isomorphic after quotienting out by null sets.
Remark 3 An algebraic probability space captures a bit more structure than a classical probability space, because
may be identified with a proper subset of
that describes the “regular” functions (or random variables) of the space. For instance, starting with the unit circle
(with the usual Haar measure and the usual trace
), any unital subalgebra
of
that is dense in
will generate the same classical probability space
on applying the functor
, namely one will get the space
of homomorphisms from
to
(with the measure induced from
). Thus for instance
could be the continuous functions
, the Wiener algebra
or the full space
, but the classical space
will be unable to distinguish these spaces from each other. In particular, the functor
loses information (roughly speaking, this functor takes an algebraic probability space and completes it to a von Neumann algebra, but then forgets exactly what algebra was initially used to create this completion). In ergodic theory, this sort of “extra structure” is traditionally encoded in topological terms, by assuming that the underlying probability space
has a nice topological structure (e.g. a standard Borel space); however, with the algebraic perspective one has the freedom to have non-topological notions of extra structure, by choosing
to be something other than an algebra
of continuous functions on a topological space. I hope to discuss one such example of extra structure (coming from the Gowers-Host-Kra theory of uniformity seminorms) in a later blog post (this generalises the example of the Wiener algebra given previously, which is encoding “Fourier structure”).
A small example of how one could use the functors is as follows. Suppose one has a classical probability space
with a measure-preserving action of an uncountable group
, which is only defined (and an action) up to almost everywhere equivalence; thus for instance for any set
and any
,
and
might not be exactly equal, but only equal up to a null set. For similar reasons, an element
of the invariant factor
might not be exactly invariant with respect to
, but instead one only has
and
equal up to null sets for each
. One might like to “clean up” the action of
to make it defined everywhere, and a genuine action everywhere, but this is not immediately achievable if
is uncountable, since the union of all the null sets where something bad occurs may cease to be a null set. However, by applying the functor
, each shift
defines a morphism
on the associated algebraic probability space (i.e. the Koopman operator), and then applying
, we obtain a shift
on a new classical probability space
which now gives a genuine measure-preserving action of
, and which is equivalent to the original action from a measure algebra standpoint. The invariant factor
now consists of those sets in
which are genuinely
-invariant, not just up to null sets. (Basically, the classical probability space
contains a Boolean algebra
with the property that every measurable set
is equivalent up to null sets to precisely one set in
, allowing for a canonical “retraction” onto
that eliminates all null set issues.)
More indirectly, the functors suggest that one should be able to develop a “pointless” form of ergodic theory, in which the underlying probability spaces are given algebraically rather than classically. I hope to give some more specific examples of this in later posts.
— 1. Details —
We now flesh out the construction of that was sketched above. The arguments here are drawn from these two previous blog posts, with some minor simplifications coming from the commutativity of the algebraic probability space.
We begin with an algebraic probability space . As indicated, we then give
an inner product
on
by the formula
By construction we see that this is a positive semi-definite inner product. We let be the associated completion of
after quotienting out by null vectors, thus
is a real Hilbert space and we have an isometry
with dense image. We use
to denote the norm on
, thus
for .
From the Cauchy-Schwarz inequality, we see that
for all . In particular, since
, we have
which implies that is a non-decreasing function of
. As each
is assumed to be bounded, we thus have a well-defined spectral radius
Also, from many applications of Cauchy-Schwarz we have
for and
with
summing to a power of two; in particular
which by the binomial theorem gives
and also
thus is an algebra norm on
; a similar argument also gives the inequality.
From this, we see that for each , the multiplication operator
on
induces a self-adjoint bounded linear operator on
; of operator norm at most
; in fact, from the definition of
we see that this operator cannot have norm strictly less than
. Thus we have identified
as a commutative normed algebra with a subalgebra of the space
of bounded linear operators on
, with the operator norm.
We now define to be the space of functions
in
which are limits (in
) of sequences
in
of uniformly bounded spectral radius. The associated multiplication operators
are then uniformly bounded in operator norm, and converge in
for fixed
; thus
defines a multiplication operator
that is a self-adjoint bounded linear operator on
, which one can check to be independent of the choice of sequence. This identifies each element of
with a self-adjoint element of
; we then define the
norm of an element
to be its operator norm in
, thus this extends the spectral radius
on
. Specialising
to
we see that this identification of
with a subset of
is injective, and this gives
the structure of a commutative Banach algebra, with
being a module over
. From construction, we also see that every closed ball in
is also closed in
.
Define an idempotent element of to be an element
such that
; we let
denote an index set for the set of idempotents
. We have the following basic density result, which ensures an ample supply of idempotents:
Lemma 2 The linear space spanned by the idempotents is dense in
.
Proof: Let ; our task is to approximate
to arbitrary accuracy in
norm by a finite linear combination of idempotents.
We view as a bounded self-adjoint linear operator on
, which contains the unit vector
. By the spectral theorem, we can find a Radon probability measure
on
such that
for all , and in particular that
for any polynomial . Also we see that
where denotes the
-essential supremum. From this and a density argument, we have an
functional calculus: given any bounded Borel function
, we can find
such that
and
and such that the map is a homomorphism. In particular, if
is an indicator function, then
is an idempotent. Approximating the identity function in
by a finite combination of indicator functions, we obtain the claim.
Now, we can give the structure of an abstract Boolean algebra by defining intersection
and complement
and then defining union by de Morgan’s law . One can verify (somewhat tediously) that
obeys the axioms of an abstract Boolean algebra, and acquires an ordering
in the usual manner, with minimal element
and maximal element
. If
, then a short computation shows that
In particular, if is a decreasing sequence in
, then the
are Cauchy in
, and thus converge to another idempotent
; we write
, and observe that this is the greatest lower bound of the
. Similarly, any increasing sequence
has a least upper bound
.
Now we consider the Boolean homomorphisms from
to the two-element Boolean algebra, or equivalently the space of finitely additive Boolean measures on
. We index this space by
, thus
is the space of Boolean homomorphisms. From Lemma 2, every such Boolean homomorphism
uniquely determines a algebra homomorphism
, and conversely every homomorphism comes from exactly one such homomorphism, thus
is the space of algebra homomorphisms from
to
.
One can identify with a closed subspace of the product space
, and so by Tychonoff’s theorem
is a compact space. Every element
of the abstract Boolean algebra
induces a subset
of
defined by
The map is easily seen to be a Boolean homomorphism. Let
be the
-algebra generated by the sets
. Define a basic null set to be a subset of
of the form
with
in
such that
, and let
be the collection of countable unions of basic null sets. This is a
-ideal of
, so we may form the quotient
-algebra
. The map
can be easily verified to be a
-algebra homomorphism (not just a boolean algebra homomorphism). We claim that this homomorphism is bijective (and thus an isomorphism). Surjectivity is clear from construction. For injectivity, suppose for contradiction that there was
with
such that
was in
, that is to say that
could be covered by a countable sequence of intersections
with
and
.
By induction, we may find such that
is not covered by
for each
. If we let
, we thus see that
with each
, but
non-empty for all
. But from the ultrafilter lemma,
is non-empty for each
, and
is also closed, so we obtain a contradiction from compactness.
From the above isomorphism, we see that every element of
differs (up to an element of
) by a unique set
in
. We then define the measure
of
by the formula
One can check that this gives a countably additive probability measure. We may now associate to each finite linear combination of idempotents, an element
of
in such a way that the map
is an algebra homomorphism with
which implies that is the essential supremum of
, and
is the
norm of
. This and Lemma 2 allow us to define maps from
to
and
to
, which one easily verifies to be isomorphisms of Banach algebras and Hilbert spaces respectively.
We have now constructed the action of the functor on algebraic probability spaces. To finish the construction of
, we have to describe the classical probability morphism
associated to an algebraic probability space morphism
. The pullback map
preserves the
norm and spectral radius, and thus also extends to a Hilbert space isometry
and a Banach algebra isometry
. As a consequence, we also have a
-algebra homomorphism
. We then define
by the formula
for all and
; one verifies that this indeed defines
as an element of
(i.e.,
is a Boolean algebra homomorphism. It is then a routine but tedious matter to check that
is a classical probability morphism and that
is a functor.
Finally, the homomorphism can viewed as a morphism from the abstract probability space
to
. Given a morphism
, the pullback maps
and
are intertwined by these morphisms, so we have a natural transformation from
to the identity functor, as claimed.

14 comments
Comments feed for this article
28 June, 2014 at 10:41 pm
Will Sawin
Once you quotient out by the null sets, are these adjoint functors?
29 June, 2014 at 9:35 am
Terence Tao
There does seem to be some relationship of this form (although to state it properly, one would need an intermediate category between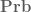 and
and 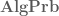 , consisting of measure algebras in which the null sets have been quotiented out). Given a classical probability space
, consisting of measure algebras in which the null sets have been quotiented out). Given a classical probability space  and an algebraic probability space
and an algebraic probability space 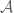 , a morphism from
, a morphism from 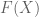 to
to 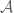 is essentially a representation of
is essentially a representation of 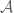 in
in 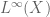 . One can then represent
. One can then represent  in
in 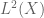 , and thence
, and thence  in
in 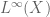 , which one can use to write
, which one can use to write  as a factor of
as a factor of  on the level of measure algebras (i.e. after quotienting by null sets). These steps are all reversible, and I’m pretty sure they’re natural. So it looks like one can identify
on the level of measure algebras (i.e. after quotienting by null sets). These steps are all reversible, and I’m pretty sure they’re natural. So it looks like one can identify 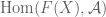 with
with  if we apply the appropriate forgetful functors for quotienting out null sets.
if we apply the appropriate forgetful functors for quotienting out null sets.
30 June, 2014 at 2:04 am
J
In Definition 1, what do you mean by a *-homomorphism? I do not see any involution… Isn’t a unital algebra morphism enough? Thanks.
[Oops, this is a leftover from a previous iteration of the post; corrected now. -T.]
30 June, 2014 at 7:40 pm
Amy Huang
Why the morphis needs to be trace-preserving?
[By definition – T.]
2 July, 2014 at 2:02 pm
vznvzn
congratulations! :idea: :!:
3 July, 2014 at 9:28 am
$3M Breakthrough Prizes now awarded in mathematics! | Turing Machine
[…] CONGRATULATIONS! :idea: :!: […]
7 July, 2014 at 8:30 pm
omar aboura
There is an extra space in “Somewh at less obviously”.
[Corrected, thanks – T.]
8 July, 2014 at 2:42 am
jb
Thank you so much for writing this. I’d heard about the random variable / probability space divide in probability theory, and I had always assumed it was parallel to the ring / variety dichotomy in algebraic geometry. So it’s nice to see it all laid out. So would you say then that working probabilists think in terms of algebraic probablility spaces rather than (usual) probability space? Or that algebraic probability spaces are the true objects of study in probability theory? Or am I missing the point?
I’m really looking forward to the follow-up posts. I’d be particularly interested to hear more about the boundedness axiom in your definition of algebraic probability space. You say you need it only for technical reasons. So is there any chance of removing it or replacing it with something more palatable from the algebraic or category theoretic perspective while maintaining the ability to ‘do probability theory’ on such a thing?
A second question: In algebraic geometry, a ring/scheme is not much more general than a nilpotent-free ring/variety. This is because all rings with nilpotents can be obtained by intersecting varieties together, as long as you do it in the algebraically natural manner, i.e. just tensor coordinate rings together and don’t follow that by modding out by nilpotents (=ignore tangency information when intersecting). Further, infinitely generated rings can be obtained as limits of finitely generated rings. So finitely generated rings without nilpotents, the objects of classical algebraic geometry, reassuringly determine the whole scheme-theoretic story as long as you take a suitably enlightened point of view. Is there any counterpart to this in the world of probability spaces? Is there some sense in which every algebraic probability space can be built out usual ones by applying some routine constructions?
8 July, 2014 at 10:39 am
Terence Tao
When working with noncommutative probability (e.g. with quantum probability, or with free probability) then one certainly takes the algebraic perspective (although often with some additional analytic axioms beyond the boundedness axiom here, e.g. that the algebra of random variables forms a von Neumann algebra). Indeed, much as in algebraic geometry, in the noncommutative setting it becomes quite unwieldy to try to work in a classical setting of spaces of points. See https://terrytao.wordpress.com/2010/02/10/245a-notes-5-free-probability/ for more discussion. [Note that in the noncommutative framework, one cannot easily reduce to the consideration of purely real (or more precisely, self-adjoint) random variables, since the space of such random variables is no longer closed under multiplication, and must instead work in a *-algebra of random variables rather than a real algebra, with a trace that is now complex-linear instead of real-linear. So the axiomatisation in the noncommutative case is a little different from the one given in this post.]
With more traditional probability, the philosophy is indeed largely to suppress the precise nature of the sample space and to work primarily with concepts flowing from the algebra of random variables, e.g. expectation, variance, correlation, and independence. See https://terrytao.wordpress.com/2010/01/01/254a-notes-0-a-review-of-probability-theory/ for more discussion. However, for some applications (particularly in ergodic theory) it has traditionally been convenient to impose some additional topological regularity hypotheses on the probability space (e.g. that it is a standard Borel space) in order to use some tools from descriptive set theory and classical analysis (e.g. Riesz representation, disintegration of measures, measurable sections). I believe though that by pursuing a primarily algebraic approach, most of these additional topological assumptions may be dropped, albeit at the cost of making the arguments look rather different (as one has to make everything that is currently based on a classical point-theoretic interpretation of the sample space “pointless” or “point-free”). I hope to give some examples of this in future posts.
As regards the second question, certainly in many applications (e.g. in the ergodic theory of actions of countable groups) one can often reduce to probability spaces which are separable (countably generated), which is perhaps analogous to the finitely generated rings in the algebraic geometry context. (Nilpotency does not arise as an issue in commutative probability (the spectral theorem eliminates the possibility of nilpotents when one commutes with one’s adjoint), though of course one could consider it in noncommutative contexts. But the dividing line between normal (commuting with one’s adjoint) and non-normal is typically more important than the dividing line between nilpotent and non-nilpotent, at least in the context of free probability which is the subfield of noncommutative probability that I am the most familiar with; I think this flows from the heavy reliance on the trace in algebraic probability theory, which does not have much of an analogue in algebraic geometry since one doesn’t do much integration on varieties from a purely algebraic viewpoint, whereas one is always taking expectations of random variables.)
15 July, 2014 at 4:22 am
Real analysis relative to a finite measure space | What's new
[…] standard Borel spaces (in fact, I will take them to be algebraic probability spaces, as defined in this previous post), in which case disintegrations are not available. However, it appears that the stochastic analysis […]
31 August, 2014 at 6:05 am
jingpyi
Reblogged this on jingpyi.
3 October, 2015 at 2:58 pm
275A, Notes 1: Integration and expectation | What's new
[…] the foundations of probability theory on the sample space models as discussed in Notes 0. (See this previous post for one such axiomatic […]
29 June, 2019 at 3:13 pm
Symmetric functions in a fractional number of variables, and the multilinear Kakeya conjecture | What's new
[…] commutative von Neumann algebra type structure (or the abstract probability structure discussed in this previous post) and then interpret it as a genuine measure space rather than as a virtual one. (This failure of […]
20 December, 2021 at 10:55 pm
Anonymous
What is the conditions on \tau_{\mu} so the one-to-one relation between the Classical and the Algebraic probability spaces holds? Could any functional other than expectation work?