In the foundations of modern probability, as laid out by Kolmogorov, the basic objects of study are constructed in the following order:
- Firstly, one selects a sample space
, whose elements
represent all the possible states that one’s stochastic system could be in.
- Then, one selects a
-algebra
of events
(modeled by subsets of
), and assigns each of these events a probability
in a countably additive manner, so that the entire sample space has probability
.
- Finally, one builds (commutative) algebras of random variables
(such as complex-valued random variables, modeled by measurable functions from
to
), and (assuming suitable integrability or moment conditions) one can assign expectations
to each such random variable.
In measure theory, the underlying measure space plays a prominent foundational role, with the measurable sets and measurable functions (the analogues of the events and the random variables) always being viewed as somehow being attached to that space. In probability theory, in contrast, it is the events and their probabilities that are viewed as being fundamental, with the sample space
being abstracted away as much as possible, and with the random variables and expectations being viewed as derived concepts. See Notes 0 for further discussion of this philosophy.
However, it is possible to take the abstraction process one step further, and view the algebra of random variables and their expectations as being the foundational concept, and ignoring both the presence of the original sample space, the algebra of events, or the probability measure.
There are two reasons for wanting to shed (or abstract away) these previously foundational structures. Firstly, it allows one to more easily take certain types of limits, such as the large limit
when considering
random matrices, because quantities built from the algebra of random variables and their expectations, such as the normalised moments of random matrices tend to be quite stable in the large
limit (as we have seen in previous notes), even as the sample space and event space varies with
. (This theme of using abstraction to facilitate the taking of the large
limit also shows up in the application of ergodic theory to combinatorics via the correspondence principle; see this previous blog post for further discussion.)
Secondly, this abstract formalism allows one to generalise the classical, commutative theory of probability to the more general theory of non-commutative probability theory, which does not have a classical underlying sample space or event space, but is instead built upon a (possibly) non-commutative algebra of random variables (or “observables”) and their expectations (or “traces”). This more general formalism not only encompasses classical probability, but also spectral theory (with matrices or operators taking the role of random variables, and the trace taking the role of expectation), random matrix theory (which can be viewed as a natural blend of classical probability and spectral theory), and quantum mechanics (with physical observables taking the role of random variables, and their expected value on a given quantum state being the expectation). It is also part of a more general “non-commutative way of thinking” (of which non-commutative geometry is the most prominent example), in which a space is understood primarily in terms of the ring or algebra of functions (or function-like objects, such as sections of bundles) placed on top of that space, and then the space itself is largely abstracted away in order to allow the algebraic structures to become less commutative. In short, the idea is to make algebra the foundation of the theory, as opposed to other possible choices of foundations such as sets, measures, categories, etc..
[Note that this foundational preference is to some extent a metamathematical one rather than a mathematical one; in many cases it is possible to rewrite the theory in a mathematically equivalent form so that some other mathematical structure becomes designated as the foundational one, much as probability theory can be equivalently formulated as the measure theory of probability measures. However, this does not negate the fact that a different choice of foundations can lead to a different way of thinking about the subject, and thus to ask a different set of questions and to discover a different set of proofs and solutions. Thus it is often of value to understand multiple foundational perspectives at once, to get a truly stereoscopic view of the subject.]
It turns out that non-commutative probability can be modeled using operator algebras such as -algebras, von Neumann algebras, or algebras of bounded operators on a Hilbert space, with the latter being accomplished via the Gelfand-Naimark-Segal construction. We will discuss some of these models here, but just as probability theory seeks to abstract away its measure-theoretic models, the philosophy of non-commutative probability is also to downplay these operator algebraic models once some foundational issues are settled.
When one generalises the set of structures in one’s theory, for instance from the commutative setting to the non-commutative setting, the notion of what it means for a structure to be “universal”, “free”, or “independent” can change. The most familiar example of this comes from group theory. If one restricts attention to the category of abelian groups, then the “freest” object one can generate from two generators is the free abelian group of commutative words
with
, which is isomorphic to the group
. If however one generalises to the non-commutative setting of arbitrary groups, then the “freest” object that can now be generated from two generators
is the free group
of non-commutative words
with
, which is a significantly larger extension of the free abelian group
.
Similarly, when generalising classical probability theory to non-commutative probability theory, the notion of what it means for two or more random variables to be independent changes. In the classical (commutative) setting, two (bounded, real-valued) random variables are independent if one has
whenever are well-behaved functions (such as polynomials) such that
,
both vanish. In the non-commutative setting, one can generalise the above definition to two commuting bounded self-adjoint variables; this concept is useful for instance in quantum probability, which is an abstraction of the theory of observables in quantum mechanics. But for two (bounded, self-adjoint) non-commutative random variables
, the notion of classical independence no longer applies. As a substitute, one can instead consider the notion of being freely independent (or free for short), which means that
whenever are well-behaved functions such that all of
vanish.
The concept of free independence was introduced by Voiculescu, and its study is now known as the subject of free probability. We will not attempt a systematic survey of this subject here; for this, we refer the reader to the surveys of Speicher and of Biane. Instead, we shall just discuss a small number of topics in this area to give the flavour of the subject only.
The significance of free probability to random matrix theory lies in the fundamental observation that random matrices which are independent in the classical sense, also tend to be independent in the free probability sense, in the large limit
. (This is only possible because of the highly non-commutative nature of these matrices; as we shall see, it is not possible for non-trivial commuting independent random variables to be freely independent.) Because of this, many tedious computations in random matrix theory, particularly those of an algebraic or enumerative combinatorial nature, can be done more quickly and systematically by using the framework of free probability, which by design is optimised for algebraic tasks rather than analytical ones.
Much as free groups are in some sense “maximally non-commutative”, freely independent random variables are about as far from being commuting as possible. For instance, if are freely independent and of expectation zero, then
vanishes, but
instead factors as
. As a consequence, the behaviour of freely independent random variables can be quite different from the behaviour of their classically independent commuting counterparts. Nevertheless there is a remarkably strong analogy between the two types of independence, in that results which are true in the classically independent case often have an interesting analogue in the freely independent setting. For instance, the central limit theorem (Notes 2) for averages of classically independent random variables, which roughly speaking asserts that such averages become gaussian in the large
limit, has an analogue for averages of freely independent variables, the free central limit theorem, which roughly speaking asserts that such averages become semicircular in the large
limit. One can then use this theorem to provide yet another proof of Wigner’s semicircle law (Notes 4).
Another important (and closely related) analogy is that while the distribution of sums of independent commutative random variables can be quickly computed via the characteristic function (i.e. the Fourier transform of the distribution), the distribution of sums of freely independent non-commutative random variables can be quickly computed using the Stieltjes transform instead (or with closely related objects, such as the -transform of Voiculescu). This is strongly reminiscent of the appearance of the Stieltjes transform in random matrix theory, and indeed we will see many parallels between the use of the Stieltjes transform here and in Notes 4.
As mentioned earlier, free probability is an excellent tool for computing various expressions of interest in random matrix theory, such as asymptotic values of normalised moments in the large limit
. Nevertheless, as it only covers the asymptotic regime in which
is sent to infinity while holding all other parameters fixed, there are some aspects of random matrix theory to which the tools of free probability are not sufficient by themselves to resolve (although it can be possible to combine free probability theory with other tools to then answer these questions). For instance, questions regarding the rate of convergence of normalised moments as
are not directly answered by free probability, though if free probability is combined with tools such as concentration of measure (Notes 1) then such rate information can often be recovered. For similar reasons, free probability lets one understand the behaviour of
moments as
for fixed
, but has more difficulty dealing with the situation in which
is allowed to grow slowly in
(e.g.
). Because of this, free probability methods are effective at controlling the bulk of the spectrum of a random matrix, but have more difficulty with the edges of that spectrum (as well as with related concepts such as the operator norm, Notes 3) as well as with fine-scale structure of the spectrum. Finally, free probability methods are most effective when dealing with matrices that are Hermitian with bounded operator norm, largely because the spectral theory of bounded self-adjoint operators in the infinite-dimensional setting of the large
limit is non-pathological. (This is ultimately due to the stable nature of eigenvalues in the self-adjoint setting; see this previous blog post for discussion.) For non-self-adjoint operators, free probability needs to be augmented with additional tools, most notably by bounds on least singular values, in order to recover the required stability for the various spectral data of random matrices to behave continuously with respect to the large
limit. We will discuss this latter point in a later set of notes.
— 1. Abstract probability theory —
We will now slowly build up the foundations of non-commutative probability theory, which seeks to capture the abstract algebra of random variables and their expectations. The impatient reader who wants to move directly on to free probability theory may largely jump straight to the final definition at the end of this section, but it can be instructive to work with these foundations for a while to gain some intuition on how to handle non-commutative probability spaces.
To motivate the formalism of abstract (non-commutative) probability theory, let us first discuss the three key examples of non-commutative probability spaces, and then abstract away all features that are not shared in common by all three examples.
Example 1: Random scalar variables. We begin with classical probability theory – the study of scalar random variables. In order to use the powerful tools of complex analysis (such as the Stieltjes transform), it is very convenient to allow our random variables to be complex valued. In order to meaningfully take expectations, we would like to require all our random variables to also be absolutely integrable. But this requirement is not sufficient by itself to get good algebraic structure, because the product of two absolutely integrable random variables need not be absolutely integrable. As we want to have as much algebraic structure as possible, we will therefore restrict attention further, to the collection of random variables with all moments finite. This class is closed under multiplication, and all elements in this class have a finite trace (or expectation). One can of course restrict further, to the space
of (essentially) bounded variables, but by doing so one loses important examples of random variables, most notably gaussians, so we will work instead with the space
. (This will cost us some analytic structure – in particular,
will not be a Banach space, in contrast to
– but as our focus is on the algebraic structure, this will be an acceptable price to pay.)
The space of complex-valued random variables with all moments finite now becomes an algebra over the complex numbers
; i.e. it is a vector space over
that is also equipped with a bilinear multiplication operation
that obeys the associative and distributive laws. It is also commutative, but we will suppress this property, as it is not shared by the other two examples we will be discussing. The deterministic scalar
then plays the role of the multiplicative unit in this algebra.
In addition to the usual algebraic operations, one can also take the complex conjugate or adjoint of a complex-valued random variable
. This operation
interacts well with the other algebraic operations: it is in fact an anti-automorphism on
, which means that it preserves addition
, reverses multiplication
, is anti-homogeneous (
for
), and it is invertible. In fact, it is its own inverse (
), and is thus an involution.
This package of properties can be summarised succinctly by stating that the space of bounded complex-valued random variables is a (unital)
-algebra.
The expectation operator can now be viewed as a map
. It obeys some obvious properties, such as being linear (i.e.
is a linear functional on
). In fact it is
-linear, which means that it is linear and also that
for all
. We also clearly have
. We will remark on some additional properties of expectation later.
Example 2: Deterministic matrix variables. A second key example is that of (finite-dimensional) spectral theory – the theory of complex-valued matrices
. (One can also consider infinite-dimensional spectral theory, of course, but for simplicity we only consider the finite-dimensional case in order to avoid having to deal with technicalities such as unbounded operators.) Like the space
considered in the previous example,
is a
-algebra, where the multiplication operation is of course given by matrix multiplication, the identity is the matrix identity
, and the involution
is given by the matrix adjoint operation. On the other hand, as is well-known, this
-algebra is not commutative (for
).
The analogue of the expectation operation here is the normalised trace . Thus
is a *-linear functional on
that maps
to
. The analogy between expectation and normalised trace is particularly evident when comparing the moment method for scalar random variables (based on computation of the moments
) with the moment method in spectral theory (based on a computation of the moments
).
Example 3: Random matrix variables. Random matrix theory combines classical probability theory with finite-dimensional spectral theory, with the random variables of interest now being the random matrices , all of whose entries have all moments finite. It is not hard to see that this is also a
-algebra with identity
, which again will be non-commutative for
. The normalised trace
here is given by
thus one takes both the normalised matrix trace and the probabilistic expectation, in order to arrive at a deterministic scalar (i.e. a complex number). As before, we see that is a
-linear functional that maps
to
. As we saw in Notes 3, the moment method for random matrices is based on a computation of the moments
.
Let us now simultaneously abstract the above three examples, but reserving the right to impose some additional axioms as needed:
Definition 1 (Non-commutative probability space, preliminary definition) A non-commutative probability space (or more accurately, a potentially non-commutative probability space)
will consist of a (potentially non-commutative)
-algebra
of (potentially non-commutative) random variables (or observables) with identity
, together with a trace
, which is a
-linear functional that maps
to
. This trace will be required to obey a number of additional axioms which we will specify later in this set of notes.
This definition is not yet complete, because we have not fully decided on what axioms to enforce for these spaces, but for now let us just say that the three examples ,
,
given above will obey these axioms and serve as model examples of non-commutative probability spaces. We mention that the requirement
can be viewed as an abstraction of Kolmogorov’s axiom that the sample space has probability
.
To motivate the remaining axioms, let us try seeing how some basic concepts from the model examples carry over to the abstract setting.
Firstly, we recall that every scalar random variable has a probability distribution
, which is a probability measure on the complex plane
; if
is self-adjoint (i.e. real valued), so that
, then this distribution is supported on the real line
. The condition that
lie in
ensures that this measure is rapidly decreasing, in the sense that
for all
. The measure
is related to the moments
by the formula
for . In fact, one has the more general formula
Similarly, every deterministic matrix has a empirical spectral distribution
, which is a probability measure on the complex plane
. Again, if
is self-adjoint, then distribution is supported on the real line
. This measure is related to the moments
by the same formula (1) as in the case of scalar random variables. Because
is finite, this measure is finitely supported (and in particular is rapidly decreasing). As for (2), the spectral theorem tells us that this formula holds when
is normal (i.e.
), and in particular if
is self-adjoint (of course, in this case (2) collapses to (1)), but is not true in general. Note that this subtlety does not appear in the case of scalar random variables because in this commutative setting, all elements are automatically normal.
Finally, for random matrices , we can form the expected empirical spectral distribution
, which is again a rapidly decreasing probability measure on
, which is supported on
if
is self-adjoint. This measure is again related to the moments
by the formula (1), and also by (2) if
is normal.
Now let us see whether we can set up such a spectral measure for an element
in an abstract non-commutative probability space
. From the above examples, it is natural to try to define this measure through the formula (1), or equivalently (by linearity) through the formula
whenever is a polynomial with complex coefficients (note that one can define
without difficulty as
is a
-algebra). In the normal case, one may hope to work with the more general formula
whenever is a polynomial of two complex variables (note that
can be defined unambiguously precisely when
is normal).
It is tempting to apply the Riesz representation theorem to (3) to define the desired measure , perhaps after first using the Weierstrass approximation theorem to pass from polynomials to continuous functions. However, there are multiple technical issues with this idea:
- In order for the polynomials to be dense in the continuous functions in the uniform topology on the support of
, one needs the intended support
of
to be on the real line
, or else one needs to work with the formula (4) rather than (3). Also, one also needs the intended support
to be bounded for the Weierstrass approximation theorem to apply directly.
- In order for the Riesz representation theorem to apply, the functional
(or
) needs to be continuous in the uniform topology, thus one must be able to obtain a bound of the form
for some (preferably compact) set
. (To get a probability measure, one in fact needs to have
.)
- In order to get a probability measure rather than a signed measure, one also needs some non-negativity:
needs to be non-negative whenever
for
in the intended support
.
To resolve the non-negativity issue, we impose an additional axiom on the non-commutative probability space :
- (Non-negativity) For any
, we have
. (Note that
is self-adjoint and so its trace
is necessarily a real number.)
In the language of von Neumann algebras, this axiom (together with the normalisation ) is essentially asserting that
is a state. Note that this axiom is obeyed by all three model examples, and is also consistent with (4). It is the noncommutative analogue of the Kolmogorov axiom that all events have non-negative probability.
With this axiom, we can now define an positive semi-definite inner product on
by the formula
This obeys the usual axioms of an inner product, except that it is only positive semi-definite rather than positive definite. One can impose positive definiteness by adding an axiom that the trace is faithful, which means that
if and only if
. However, we will not need the faithfulness axiom here.
Without faithfulness, is a semi-definite inner product space with semi-norm
In particular, we have the Cauchy-Schwarz inequality
This leads to an important monotonicity:
Exercise 2 (Monotonicity) Let
be a self-adjoint element of a non-commutative probability space
. Show that we have the monotonicity relationships
for any
.
As a consequence, we can define the spectral radius of a self-adjoint element
by the formula
in which case we obtain the inequality
for any . We then say that a self-adjoint element is bounded if its spectral radius is finite.
Example 3 In the case of random variables, the spectral radius is the essential supremum
, while for deterministic matrices, the spectral radius is the operator norm
. For random matrices, the spectral radius is the essential supremum
of the operator norm.
Guided by the model examples, we expect that a bounded self-adjoint element should have a spectral measure
supported on the interval
. But how to show this? It turns out that one can proceed by tapping the power of complex analysis, and introducing the Stieltjes transform
for complex numbers . Now, this transform need not be defined for all
at present, because we do not know that
is invertible in
. However, we can avoid this problem by working formally. Indeed, we have the formal Neumann series expansion
which leads to the formal Laurent series expansion
If is bounded self-adjoint, then from (6) we see that this formal series actually converges in the region
. We will thus define the Stieltjes transform
on the region
by this series expansion (8), and then extend to as much of the complex plane as we can by analytic continuation. (There could in principle be some topological obstructions to this continuation, but we will soon see that the only place where singularities can occur is on the real interval
, and so no topological obstructions will appear. One can also work with the original definition (7) of the Stieltjes transform, but this requires imposing some additional analytic axioms on the non-commutative probability space, such as requiring that
be a
-algebra or a von Neumann algebra, and I wish to avoid discussing these topics here as they are not the main focus of free probability theory.)
We now push the domain of definition of into the disk
. We need some preliminary lemmas.
Exercise 4 Let
be bounded self-adjoint. For any real number
, show that
. (Hint: use (5), (6)).
Now let be a large positive real number. The idea is to rewrite the (formal) Stieltjes transform
using the formal identity
and take Neumann series again to arrive at the formal expansion
From the previous two exercises we see that
and so the above Laurent series converges for .
Exercise 6 Give a rigorous proof that the two series (8), (10) agree for
large enough.
We have thus extended analytically to the region
. Letting
, we obtain an extension of
to the upper half-plane
. A similar argument (shifting by
instead of
) gives an extension to the lower half-plane, thus defining
analytically everywhere except on the interval
.
On the other hand, it is not possible to analytically extend to the region
for any
. Indeed, if this were the case, then from the Cauchy integral formula (applied at infinity), we would have the identity
for any , which when combined with (5) implies that
for all such
, which is absurd. Thus the spectral radius
can also be interpreted as the radius of the smallest ball centred at the origin outside of which the Stieltjes transform can be analytically continued.
Now that we have the Stieltjes transform everywhere outside of , we can use it to derive an important bound (which will soon be superceded by (3), but will play a key role in the proof of that stronger statement):
Proposition 7 (Boundedness) Let
be bounded self-adjoint, and let
be a polynomial. Then
Proof: (Sketch) We can of course assume that is non-constant, as the claim is obvious otherwise. From Exercise 5 (replacing
with
, where
is the polynomial whose coefficients are the complex conjugate of that of
) we may reduce to the case when
has real coefficients, so that
is self-adjoint. Since
is bounded, it is not difficult (using (5), (6)) to show that
is bounded also (Exercise!).
As is bounded self-adjoint, it has a Stieltjes transform defined outside of
, which for large
is given by the formula
By the previous discussion, to establish the proposition it will suffice to show that the Stieltjes transform can be continued to the domain
For this, we observe the partial fractions decomposition
of into linear combinations of
, at least when the roots of
are simple. Thus, formally, at least, we have the identity
One can verify this identity is consistent with (11) for sufficiently large. (Exercise! Hint: First do the case when
is a scalar, then expand in Taylor series and compare coefficients, then use the agreement of the Taylor series to do the general case.)
If is in the domain
, then all the roots
of
lie outside the interval
. So we can use the above formula as a definition of
, at least for those
for which the roots of
are simple; but there are only finitely many exceptional
(arising from zeroes of
) and one can check (Exercise! Hint: use the analytic nature of
and the residue theoremto rewrite parts of
as a contour integral.) that the singularities here are removable. It is easy to see (Exercise!) that
is holomorphic outside of these removable singularities, and the claim follows.
Exercise 8 Fill in the steps marked (Exercise!) in the above proof.
From Proposition 7 and the Weierstrass approximation theorem, we see that the linear functional can be uniquely extended to a bounded linear functional on
, with an operator norm
. Applying the Riesz representation theorem, we thus can find a unique Radon measure (or equivalently, Borel measure)
on
of total variation
obeying the identity (3) for all
. In particular, setting
see that
has total mass
; since it also has total variation
, it must be a probability measure. We have thus shown the fundamental
Theorem 9 (Spectral theorem for bounded self-adjoint elements) Let
be a bounded self-adjoint element of a non-commutative probability space
. Then there exists a unique Borel probability measure
on
(known as the spectral measure of
) such that (3) holds for all polynomials
.
Remark 10 If one assumes some completeness properties of the non-commutative probability space, such as that
is a
-algebra or a von Neumann algebra, one can use this theorem to meaningfully define
for other functions
than polynomials; specifically, one can do this for continuous functions
if
is a
-algebra, and for
functions
if
is a von Neumann algebra. Thus for instance we can start define absolute values
, or square roots
, etc.. Such an assignment
is known as a functional calculus; it can be used for instance to go back and make rigorous sense of the formula (7). A functional calculus is a very convenient tool to have in operator algebra theory, and for that reason one often completes a non-commutative probability space into a
-algebra or von Neumann algebra, much as how it is often convenient to complete the rationals and work instead with the reals. However, we will proceed here instead by working with a (possibly incomplete) non-commutative probability space, and working primarily with formal expressions (e.g. formal power series in
) without trying to evaluate such expressions in some completed space. We can get away with this because we will be working exclusively in situations in which the spectrum of a random variable can be reconstructed exactly from its moments (which is in particular true in the case of bounded random variables). For unbounded random variables, one must usually instead use the full power of functional analysis, and work with the spectral theory of unbounded operators on Hilbert spaces.
Exercise 11 Let
be a bounded self-adjoint element of a non-commutative probability space, and let
as the spectral measure of
. Establish the formula
for all
. Conclude that the support of the spectral measure
must contain at least one of the two points
.
Exercise 12 Let
be a bounded self-adjoint element of a non-commutative probability space with faithful trace. Show that
if and only if
.
Remark 13 It is possible to also obtain a spectral theorem for bounded normal elements along the lines of the above theorem (with
now supported in a disk rather than in an interval, and with (3) replaced by (4)), but this is somewhat more complicated to show (basically, one needs to extend the self-adjoint spectral theorem to a pair of commuting self-adjoint elements, which is a little tricky to show by complex-analytic methods, as one has to use several complex variables).
The spectral theorem more or less completely describes the behaviour of a single (bounded self-adjoint) element in a non-commutative probability space. As remarked above, it can also be extended to study multiple commuting self-adjoint elements. However, when one deals with multiple non-commuting elements, the spectral theorem becomes inadequate (and indeed, it appears that in general there is no usable substitute for this theorem). However, we can begin making a little bit of headway if we assume as a final (optional) axiom a very weak form of commutativity in the trace:
- (Trace) For any two elements
, we have
.
Note that this axiom is obeyed by all three of our model examples. From this axiom, we can cyclically permute products in a trace, e.g. . However, we cannot take non-cyclic permutations; for instance,
and
are distinct in general. This axiom is a trivial consequence of the commutative nature of the complex numbers in the classical setting, but can play a more non-trivial role in the non-commutative setting. It is however possible to develop a large part of free probability without this axiom, if one is willing instead to work in the category of von Neumann algebras. Thus, we shall leave it as an optional axiom:
Definition 14 (Non-commutative probability space, final definition) A non-commutative probability space
consists of a
-algebra
with identity
, together with a
-linear functional
, that maps
to
and obeys the non-negativity axiom. If
obeys the trace axiom, we say that the non-commutative probability space is tracial. If
obeys the faithfulness axiom, we say that the non-commutative probability space is faithful.
From this new axiom and the Cauchy-Schwarz inequality we can now get control on products of several non-commuting elements:
Exercise 15 Let
be bounded self-adjoint elements of a tracial non-commutative probability space
. Show that
for any non-negative integers
. (Hint: Induct on
, and use Cauchy-Schwarz to split up the product as evenly as possible, using cyclic permutations to reduce the complexity of the resulting expressions.)
Exercise 16 Let
be those elements
in a tracial non-commutative probability space
whose real and imaginary parts
,
are bounded and self-adjoint; we refer to such elements simply as bounded elements. Show that this is a sub-*-algebra of
.
This allows one to perform the following Gelfand-Naimark-Segal (GNS) construction. Recall that has a positive semi-definite inner product
. We can perform the Hilbert space completion of this inner product space (quotienting out by the elements of zero norm), leading to a complex Hilbert space
into which
can be mapped as a dense subspace by an isometry
. (This isometry is injective when
is faithful, but will have a non-trivial kernel otherwise.) The space
acts on itself by multiplication, and thus also acts on the dense subspace
of
. We would like to extend this action to all of
, but this requires an additional estimate:
Lemma 17 Let
be a tracial non-commutative probability space. If
with
self-adjoint, then
Proof: Squaring and cyclically permuting, it will suffice to show that
Let be arbitrary. By Weierstrass approximation, we can find a polynomial
with real coefficients such that
on the interval
. By Proposition 7, we can thus write
where
is self-adjoint with
. Multiplying on the left by
and on the right by
and taking traces, we obtain
By non-negativity, . By Exercise 15, we have
. Sending
we obtain the claim.
As a consequence, we see that the self-adjoint elements of
act in a bounded manner on all of
, and so on taking real and imaginary parts, we see that the same is true for the non-self-adjoint elements too. Thus we can associate to each
a bounded linear transformation
on the Hilbert space
.
Exercise 18 (Gelfand-Naimark theorem) Show that the map
is a
-isomorphism from
to a
-subalgebra of
, and that one has the representation
for any
, where
is the unit vector
.
Remark 19 The Gelfand-Naimark theorem required the tracial hypothesis only to deal with the error
in the proof of Lemma 17. One can also establish this theorem without this hypothesis, by assuming instead that the non-commutative space is a
-algebra; this provides a continuous functional calculus, so that we can replace
in the proof of Lemma 17 by a continuous function and dispense with
altogether. This formulation of the Gelfand-Naimark theorem is the one which is usually seen in the literature.
The Gelfand-Naimark theorem identifies with a
-subalgebra of
. The closure of this
-subalgebra in the weak operator topology is then a von Neumann algebra, which we denote as
. As a consequence, we see that non-commutative probability spaces are closely related to von Neumann algebras (equipped with a tracial state
). However, we refrain from identifying the former completely with the latter, in order to allow ourselves the freedom to work with such spaces as
, which is almost but not quite a von Neumann algebra. Instead, we use the following looser (and more algebraic) definition in Definition 14.
— 2. Limits of non-commutative random variables —
One benefit of working in an abstract setting is that it becomes easier to take certain types of limits. For instance, it is intuitively obvious that the cyclic groups are “converging” in some sense to the integer group
. This convergence can be formalised by selecting a distinguished generator
of all groups involved (
in the case of
, and
in the case of the integers
), and noting that the set of relations involving this generator in
(i.e. the relations
when
is divisible by
) converge in a pointwise sense to the set of relations involving this generator in
(i.e. the empty set). Here, to see the convergence, we viewed a group abstractly via the relations between its generators, rather than on a concrete realisation of a group as (say) residue classes modulo
. (For more discussion of this notion of convergence for finitely generated groups, see this earlier blog post.)
We can similarly define convergence of random variables in non-commutative probability spaces as follows.
Definition 20 (Convergence) Let
be a sequence of non-commutative probability spaces, and let
be an additional non-commutative space. For each
, let
be a sequence of random variables in
, and let
be a sequence of random variables in
. We say that
converges in the sense of moments to
if we have
as
for any sequence
. We say that
converge in the sense of
-moments to
if
converges in the sense of moments to
.
If
(viewed as a constant
-tuple in
) converges in the sense of moments (resp.
-moments) to
, we say that
and
have matching joint moments (resp. matching joint
-moments).
Example 21 If
converge in the sense of moments to
then we have for instance that
as
for each
, while if they converge in the stronger sense of
-moments then we obtain more limits, such as
Note however that no uniformity in
is assumed for this convergence; in particular, if
varies in
(e.g. if
), there is now no guarantee that one still has convergence.
Remark 22 When the underlying objects
and
are self-adjoint, then there is no distinction between convergence in moments and convergence in
-moments. However, for non-self-adjoint variables, the latter type of convergence is far stronger, and the former type is usually too weak to be of much use, even in the commutative setting. For instance, let
be a classical random variable drawn uniformly at random from the unit circle
. Then the constant sequence
has all the same moments as the zero random variable
, and thus converges in the sense of moments to zero, but does not converge in the
-moment sense to zero.
It is also clear that if we require that
be generated by
in the
-algebraic sense (i.e. every element of
is a polynomial combination of
and their adjoints) then a limit in the sense of
-moments, if it exists, is unique up to matching joint
-moments.
For a sequence of a single, uniformly bounded, self-adjoint element, convergence in moments is equivalent to convergence in distribution:
Exercise 23 Let
be a sequence of self-adjoint elements in non-commutative probability spaces
with
uniformly bounded, and let
be another bounded self-adjoint element in a non-commutative probability space
. Show that
converges in moments to
if and only if the spectral measure
converges in the vague topology to
.
Thus, for instance, one can rephrase the Wigner semi-circular law (in the convergence in expectation formulation) as the assertion that a sequence of Wigner random matrices with (say) subgaussian entries of mean zero and variance one, when viewed as elements of the non-commutative probability space
, will converge to any bounded self-adjoint element
of a non-commutative probability space with spectral measure given by the semi-circular distribution
. Such elements are known as semi-circular elements. Here are some easy examples of semi-circular elements:
- A classical real random variable
drawn using the probability measure
.
- The identity function
in the Lebesgue space
, endowed with the trace
.
- The function
in the Lebesgue space
.
Here is a more interesting example of a semi-circular element:
Exercise 24 Let
be the non-commutative space consisting of bounded operators
on the natural numbers with trace
, where
is the standard basis of
. Let
be the right shift on
. Show that
is a semicircular operator. (Hint: one way to proceed here is to use Fourier analysis to identify
with the space of odd functions
on
, with
being the operator that maps
to
; show that
is then the operation of multiplication by
.) One can also interpret
as a creation operator in a exercise when
is odd. Note that this provides a (very) slightly different proof of the semi-circular law from that given from the moment method in Notes 4.
Because we are working in such an abstract setting with so few axioms, limits exist in abundance:
Exercise 25 For each
, let
be bounded self-adjoint elements of a tracial non-commutative space
. Suppose that the spectral radii
are uniformly bounded in
. Show that there exists a subsequence
and bounded self-adjoint elements
of a tracial non-commutative space
such that
converge in moments to
as
. (Hint: use the Bolzano-Weierstrass theorem and the Arzelá-Ascoli diagonalisation trick to obtain a subsequence in which each of the joint moments of
converge as
. Use these moments to build a noncommutative probability space.)
— 3. Free independence —
We now come to the fundamental concept in free probability theory, namely that of free independence.
Definition 26 (Free independence) A collection
of random variables in a non-commutative probability space
is freely independent (or free for short) if one has
whenever
are polynomials and
are indices with no two adjacent
equal.
A sequence
of random variables in a non-commutative probability space
is asymptotically freely independent (or asymptotically free for short) if one has
as
whenever
are polynomials and
are indices with no two adjacent
equal.
Remark 27 The above example describes freeness of collections of random variables
. One can more generally define freeness of collections of subalgebras of
, which in some sense is the more natural concept from a category-theoretic perspective, but we will not need this concept here. (See e.g. this survey of Biane for more discussion.)
Thus, for instance, if are freely independent, then
will vanish for any polynomials
for which
all vanish. This is in contrast to classical independence of classical (commutative) random variables, which would only assert that
whenever
both vanish.
To contrast free independence with classical independence, suppose that . If
were freely independent, then
. If instead
were commuting and classically independent, then we would instead have
, which would almost certainly be non-zero.
For a trivial example of free independence, and
automatically are freely independent if at least one of
is constant (i.e. a multiple of the identity
). In the commutative setting, this is basically the only way one can have free independence:
Exercise 28 Suppose that
are freely independent self-adjoint elements of a faithful non-commutative probability space which also commute. Show that at least one of
is equal to a scalar. (Hint: First normalise
to have trace zero, and consider
.)
A less trivial example of free independence comes from the free group, which provides a clue as to the original motivation of this concept:
Exercise 29 Let
be the free group on two generators
. Let
be the non-commutative probability space of bounded linear operators on the Hilbert space
, with trace
, where
is the Kronecker delta function at the identity. Let
be the shift operators
for
and
. Show that
are freely independent.
For classically independent commuting random variables , knowledge of the individual moments
,
gave complete information on the joint moments:
. The same fact is true for freely independent random variables, though the situation is more complicated. We begin with a simple case: computing
in terms of the moments of
. From free independence we have
Expanding this using linear nature of trace, one soon sees that
So far, this is just as with the classically independent case. Next, we consider a slightly more complicated moment, . If we split
, we can write this as
In the classically independent case, we can conclude the latter term would vanish. We cannot immediately say that in the freely independent case, because only one of the factors has mean zero. But from (12) we know that . Because of this, we can expand
and now free independence does ensure that this term vanishes, and so
So again we have not yet deviated from the classically independent case. But now let us look at . We split the second
into
and
. Using (12) to control the former term, we have
From (13) we have , so we have
Now we split into
and
. Free independence eliminates all terms except
which simplifies to
which differs from the classical independence prediction of .
This process can be continued:
Exercise 30 Let
be freely independent. Show that any joint moment of
can be expressed as a polynomial combination of the individual moments
of the
. (Hint: induct on the complexity of the moment.)
The product measure construction allows us to generate classically independent random variables at will (after extending the underlying sample space): see Exercise 18 of Notes 0. There is an analogous construction, called the amalgamated free product, that allows one to generate families of freely independent random variables, each of which has a specified distribution. Let us give an illustrative special case of this construction:
Lemma 31 (Free products) For each
, let
be a non-commutative probability space. Then there exists a non-commutative probability space
which contain embedded copies of each of the
, such that whenever
for
, then
are freely independent.
Proof: (Sketch) Recall that each can be given an inner product
. One can then orthogonally decompose each space
into the constants
, plus the trace zero elements
.
We now form the Fock space to be the inner product space formed by the direct sum of tensor products
where , and
are such that no adjacent pair
of the
are equal. Each element
then acts on this Fock space by defining
when , and
when . One can thus map
into the space
of linear maps from
to itself. The latter can be given the structure of a non-commutative space by defining the trace
of an element
by the formula
, where
is the vacuum state of
, being the unit of the
tensor product. One can verify (Exercise!) that
embeds into
and that elements from different
are freely independent.
Exercise 32 Complete the proof of Lemma 31. (Hint: you may find it helpful to first do Exercise 29, as the construction here is in an abstraction of the one in that exercise.)
Finally, we illustrate the fundamental connection between free probability and random matrices observed by Voiculescu, namely that (classically) independent families of random matrices are asymptotically free. The intuition here is that while a large random matrix will certainly correlate with itself (so that, for instance,
will be large), once one interposes an independent random matrix
of trace zero, the correlation is largely destroyed (thus, for instance,
will usually be quite small).
We give a typical instance of this phenomenon here:
Proposition 33 (Asymptotic freeness of Wigner matrices) Let
be a collection of independent
Wigner matrices, where the coefficients all have uniformly bounded
moments for each
. Then the random variables
are asymptotically free.
Proof: (Sketch) Let us abbreviate as
(suppressing the
dependence). It suffices to show that the traces
for each fixed choice of natural numbers , where no two adjacent
are equal.
Recall from Notes 3 that is (up to errors of
) equal to a normalised count of paths of length
in which each edge is traversed exactly twice, with the edges forming a tree. After normalisation, this count is equal to
when
is odd, and equal to the Catalan number
when
is even.
One can perform a similar computation to compute . Up to errors of
, this is a normalised count of coloured paths of length
, where the first
edges are coloured with colour
, the next
with colour
, etc. Furthermore, each edge is traversed exactly twice (with the two traversals of each edge being assigned the same colour), and the edges form a tree. As a consequence, there must exist a
for which the block of
edges of colour
form their own sub-tree, which contributes a factor of
or
to the final trace. Because of this, when one instead computes the normalised expression
, all contributions that are not
cancel themselves out, and the claim follows.
Exercise 34 Expand the above sketch into a full proof of the above theorem.
Remark 35 This is by no means the only way in which random matrices can become asymptotically free. For instance, if instead one considers random matrices of the form
, where
are deterministic Hermitian matrices with uniformly bounded eigenvalues, and the
are iid unitary matrices drawn using Haar measure on the unitary group
, one can also show that the
are asymptotically free; again, see the paper of Voiculescu for details.
— 4. Free convolution —
When one is summing two classically independent (real-valued) random variables and
, the distribution
of the sum
is the convolution
of the distributions
and
. This convolution can be computed by means of the characteristic function
by means of the simple formula
As we saw in Notes 2, this can be used in particular to establish a short proof of the central limit theorem.
There is an analogous theory when summing two freely independent (self-adjoint) non-commutative random variables and
; the distribution
turns out to be a certain combination
, known as the free convolution of
and
. To compute this free convolution, one does not use the characteristic function; instead, the correct tool is the Stieltjes transform
which has already been discussed earlier.
Here’s how to use this transform to compute free convolutions. If one wishes, one can that is bounded so that all series involved converge for
large enough, though actually the entire argument here can be performed at a purely algebraic level, using formal power series, and so the boundedness hypothesis here is not actually necessary.
The trick (which we already saw in Notes 4) is not to view as a function of
, but rather to view
as a function of
. Given that one asymptotically has
for
, we expect to be able to perform this inversion for
large and
close to zero; and in any event one can easily invert (8) on the level of formal power series.
With this inversion, we thus have
for some of trace zero. Now we do some (formal) algebraic sleight of hand. We rearrange the above identity as
Similarly we have
and so
We can combine the second two terms via the identity
Meanwhile
and so
We can rearrange this a little bit as
We expand out as (formal) Neumann series:
This expands out to equal plus a whole string of alternating products of
and
.
Now we use the hypothesis that and
are free. This easily implies that
and
are also free. But they also have trace zero, thus by the definition of free independence, all alternating products of
and
have zero trace. (In the case when there are an odd number of terms in the product, one can obtain this zero trace property using the cyclic property of trace and induction.) We conclude that
and so
Comparing this against (15) for we conclude that
Thus, if we define the -transform
of
to be (formally) given by the formula
then we have the addition formula
Since one can recover the Stieltjes transform (and hence the
-transform
) from the spectral measure
and vice versa, this formula (in principle, at least) lets one compute the spectral measure
of
from the spectral measures
, thus allowing one to define free convolution.
For comparison, we have the (formal) addition formula
for classically independent real random variables . The following exercises carry this analogy a bit further.
Exercise 36 Let
be a classical real random variable. Working formally, show that
where the cumulants
can be reconstructed from the moments
by the recursive formula
for
. (Hint: start with the identity
.) Thus for instance
is the expectation,
is the variance, and the third and fourth cumulants are given by the formula
Establish the additional formula
where
ranges over all partitions of
into non-empty cells
.
Exercise 37 Let
be a non-commutative random variable. Working formally, show that
where the free cumulants
can be reconstructed from the moments
by the recursive formula
for
. (Hint: start with the identity
.) Thus for instance
is the expectation,
is the variance, and the third and fourth free cumulants are given by the formulae
Establish the additional formula
where
ranges over all partitions of
into non-empty cells
which are non-crossing, which means that if
lie in
, then it cannot be the case that
lie in one cell
while
lie in a distinct cell
.
Remark 38 These computations illustrate a more general principle in free probability, in that the combinatorics of free probability tend to be the “non-crossing” analogue of the combinatorics of classical probability; compare with Remark 7 of Notes 3.
Remark 39 The
-transform allows for efficient computation of the spectral behaviour of sums
of free random variables. There is an analogous transform, the
-transform, for computing the spectral behaviour (or more precisely, the joint moments) of products
of free random variables; see for instance these notes of Speicher.
The -transform clarifies the privileged role of the semi-circular elements:
Exercise 40 Let
be a semi-circular element. Show that
for any
. In particular, the free convolution of
and
is
.
Exercise 41 From the above exercise, we see that the effect of adding a free copy of
to a non-commutative random variable
is to shift the
-transform by
. Explain how this is compatible with the Dyson Brownian motion computations in Notes 4.
It also gives a free analogue of the central limit theorem:
Exercise 42 (Free central limit theorem) Let
be a self-adjoint random variable with mean zero and variance one (i.e.
and
), and let
be free copies of
. Let
. Show that the coefficients of the formal power series
converge to that of the identity function
. Conclude that
converges in the sense of moments to a semi-circular element
.
The free central limit theorem implies the Wigner semi-circular law, at least for the GUE ensemble and in the sense of expectation. Indeed, if is an
GUE matrix, then the matrices
are a.s. uniformly bounded (by the Bai-Yin theorem, Notes 3), and so (after passing to a subsequence, if necessary), they converge in the sense of moments to some limit
.
On the other hand, if is an independent copy of
, then
from the properties of gaussians. Taking limits, we conclude that
, where (by Proposition 33)
is a free copy of
. Comparing this with the free central limit theorem (or just the additivity property of
-transforms we see that
must have the semi-circular distribution. Thus the semi-circular distribution is the only possible limit point of the
, and the Wigner semi-circular law then holds (in expectation, and for GUE). Using concentration of measure, we can upgrade the convergence in expectation to a.s. convergence; using the Lindeberg replacement trick one can replace GUE with arbitrary Wigner matrices with (say) bounded coefficients; and then by using the truncation trick one can remove the boundedness hypothesis. (These latter few steps were also discussed in Notes 4.)

54 comments
Comments feed for this article
11 February, 2010 at 5:08 am
Johan
In example 1 I believe there are a few places where has become
has become 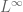 because of typos.
because of typos.
Specifically, I believe the range of the multiplication operation should be , that this should also be both the domain and the range of the involution operation and that the expectation operator is a linear operator on
, that this should also be both the domain and the range of the involution operation and that the expectation operator is a linear operator on 
[Corrected, thanks – T.]
12 February, 2010 at 6:18 pm
George Lowther
I don’t know if I’m misunderstanding something here, but in Exercise 1 I don’t see any reason why the sequence should be non-decreasing. If X was a centered Gaussian, or any other symmetric RV, then it will be zero for odd k and positive and non-decreasing for even k.
12 February, 2010 at 7:08 pm
Terence Tao
Ah, right, the monotonicity is only partial for the odd moments (the odd moments are bounded by the next even moment, but not vice versa). I’ve changed the text accordingly.
13 February, 2010 at 6:53 am
George Lowther
Also, I think you should have exponent of k+1 rather than k in the denominator in expressions (8),(10),(11) for s_X.
[Corrected, thanks – T.]
13 February, 2010 at 12:18 am
Greg Kuperberg
In the non-commutative setting, the correct notion is now of two (bounded, self-adjoint) non-commutative random variables {X, Y} being freely independent (or free for short)
I would say a correct, not the correct. If you accept von Neumann algebras and C*-algebras, but instead retain ordinary commutative independence, then the theory is standard quantum probability. In the context of empirical science, standard quantum probability is more often correct than classical probability (which it generalizes), and it is far more often correct than free probability (whose relevance to physics is credible but speculative).
However, we will proceed here instead by working with a (possibly incomplete) non-commutative probability space, and working primarily with formal expressions (e.g. formal power series in z) without trying to evaluate such expressions in some completed space.
This amounts to reducing all probability to a theory of moments. This has led to all sorts of confusion in parts of the literature in quantum probability. Everyone understands that a classical distribution has more information in it than just its moments; thus axioms based only on moments aren’t very good axioms. The same thing happens in non-commutative probability of course. The only reason that this simplification is somewhat accountable in free probability is that typical limit laws (like the Wigner semicircle) are bounded. Of course this is not true in standard quantum probability, which again is non-commutative but with a commutative independence law. (It’s also not a full excuse to just look at moments, although you seem to acknowledge that completions could be important later.)
So I would put a stronger disclaimer here.
13 February, 2010 at 8:46 am
Terence Tao
Fair enough; I’ve amended the text accordingly.
Quantum observables, while not exactly commutative in general, are still often approximately commutative, thanks to the correspondence principle, which is why classical independence is still a useful concept; in contrast, a pair of random matrices tends to be “maximally non-commutative”, making free probability the more relevant concept. So in some sense they represent the two opposite extremes of non-commutative probability.
It’s also true that the moment-centric viewpoint of free probability, which makes computations purely algebraic in nature rather than analytic, breaks down for unbounded variables, which of course occur all the time in quantum mechanics. I mention this restriction to bounded variables in the introduction.
13 February, 2010 at 11:09 am
Greg Kuperberg
Quantum observables, while not exactly commutative in general, are still often approximately commutative, thanks to the correspondence principle, which is why classical independence is still a useful concept
I have really learned something from this remark: Although I always knew that commutative independence (as opposed to free independence) is still important in quantum probability, I didn’t consider that you would want a dynamical reason to justify it. That said, I only half agree with you. One reason that commutative independence is still relevant in physics is indeed that we live in a semiclassical regime of the laws of physics. (So when you say “often”, it is in the same sense that if we were fish, we would think that 3-dimensional regions are “often” filled with water.)
But two other reasons that commutative independence are relevant in quantum probability are (1) finite communication speed, and (2) weak coupling. These two reasons, and not the semiclassical limit, are why quantum computation is premised on standard quantum probability rather than (say) free probability. One of the things that I did not realize, and which is definitely useful to say, is that in the human realm (again, if we were fish…), is that neither finite communication speed nor weak coupling are directly the point. If the price of groceries in Atlanta is statistically independent from the distribution of potholes in Seattle, it isn’t because of a bound on the speed of light or sound, nor a bound the strength of the electromagnetic field. Instead, there is an emergent statistical weak coupling, which is related to the emergent classical/semiclassical regime that we live in.
Actually, I guess there are also examples of emergent weak coupling in quantum physics. They are associated with classical limits, but that is not strictly necessary.
As you imply, free probability could be a relevant model when quantum random variables are as interdependent as possible. The nuclear physics motivation of random matrix theory reflects this. Voiculescu also told me that free probability models large N gauge theory, presumably for similar reasons.
13 February, 2010 at 7:01 am
Anonymous
Dear Prof. Tao,
How do we define infinite products?
is the limit of partial products?
the limit of partial products?
Thanks
16 February, 2010 at 6:00 am
Anonymous
Yes
29 June, 2014 at 12:17 am
Labair Abdelkader
See here http://en.wikipedia.org/wiki/Infinite_product
16 February, 2010 at 2:35 pm
Jérôme Chauvet
Dear Pr. Tao,
In section: 3. Free Independence (in the text right after Remark5), I see you wrote “vanish” twice instead of once.
Regards,
[Corrected, thanks – T.]
17 February, 2010 at 5:25 am
Jérôme Chauvet
Dear Pr. Tao,
There is an important loss, in section 3 again (at least with Explorer). In the definition box #7 of free independence, the right hand side term in the limit, i.e., the limit condition on tau for a sequence of variables to be asymptotically free, is out of the box, so one cannot read it at all.
Best,
[Corrected, thanks – T.]
26 February, 2010 at 9:59 pm
mmailliw/william
In the proof of Theorem 2, you decompose 1/(P(w) – z) as the sum of
(P'(zeta))^(-1)/(w – zeta), summing over the values of zeta for which P(zeta) = z.
After integrating, you then conclude that ‘formally’,
s_(P(X))(z) = Sigma[1/(P'(zeta)) s_X(z)], summing over zeta with P(zeta) = z.
However, I’m wondering whether the s_X(z) should actually be an s_X(zeta). After all, we know that zeta lies outside the interval [-rho(X), rho(X)], so s_X is defined on zeta, but we don’t seem to have this same guarantee for z!
(In other words, should the formal formula really be
s_(P(X))(z) = Sigma[1/(P'(zeta)) s_X(zeta)]?)
[Corrected, thanks – T.]
8 March, 2010 at 7:19 am
Brian Davies
The heavy emphasis on the use of the trace in these notes reminds me of the theory of Hilbert algebras in Jacques Dixmier’s very old Operator Algebra book Chapter 1 section 5 and in his C*-algebra book Chapter 13. Algebras with traces are very special and have a correspondingly nice mathematical theory.
In quantum statistical mechanics it has been found that the non-commutative algebras involved do not have natural traces (except in the case of infinite temperature) and the corresponding theory involves Type 3 von Neumann algebras. The trace condition is replaced by a KMS condition, but it seems hard to define this in your purely algebraic context.
8 March, 2010 at 2:28 pm
Sungjin Kim
In exercise 2, it seems that (5) and (6) give only = ?
8 March, 2010 at 2:33 pm
Sungjin Kim
In exercise 2, it seems (5) and (6) give only $\leq$, and it is enough for the rest of argument. How is it possible to obtain $\geq$ ?
p.s. $\leq$ and $\geq$ has been disappeared in previous comment because of HTML..
10 March, 2010 at 5:37 pm
Terence Tao
From (5), we have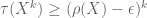 whenever k is even and sufficiently large depending on
whenever k is even and sufficiently large depending on  . This is enough to obtain the lower bound (though, as you say, it is not strictly necessary to have this bound for the application at hand).
. This is enough to obtain the lower bound (though, as you say, it is not strictly necessary to have this bound for the application at hand).
14 March, 2010 at 11:33 am
254A, Notes 8: The circular law « What’s new
[…] failure of the moment method also shows that methods of free probability (Notes 5) do not work directly. For instance, observe that for fixed , and (in the noncommutative […]
31 March, 2010 at 3:32 pm
wang
Maybe the title “245A, Notes 5: Free probability” should be “254A …”. When I search your
245A notes in google (terrytao 245a), I get here :-)
[Corrected, thanks – T.]
2 June, 2010 at 5:33 pm
Aaron F.
Maybe it’s just my browser (Firefox 3.0.19), but some of the displayed equations seem to be missing! I’ve noticed gaps in the following places:
“The measure {\mu_X} is related to the moments {\tau(X^k) = \mathop{\mathbb E} X^k} by the formula…”
“it is natural to try to define this measure through the formula (1), or equivalently (by linearity) through the formula…”
“In fact, one has the more general formula…”
“In the normal case, one may hope to work with the more general formula…”
“we can define the spectral radius {\rho(X)} of a self-adjoint element {X} by the formula…”
“in which case we obtain the inequality…”
[Fixed, thanks – T.]
p.s. Even with missing equations, these notes are wonderful. :)
30 July, 2010 at 10:37 pm
Anonymous
It could be my browser, but I think there is a missing “1/2” in
is a semi-definite inner product space with semi-norm
[]:=(_{L^2(\tau)})^{1/2}=[]
[Corrected, thanks – T.]
2 August, 2010 at 7:14 pm
Anonymous
It seems like the last modification change some latex code, because the numered equation are missing and the equations are not centered.
[Fixed, thanks – T.]
4 August, 2010 at 10:04 pm
Anonymous
I have notice some typos (if I’m not misunderstanding something).
In the definition of spectral radius the exponent is 1/(2K) [instead 1/2k].
In Exercise 6 the formula must say \mu_X(x) [instead \mu_X(z)].
I think that the right side of the equation that follows “cyclic property of trace and induction.) We conclude that” must be 1. The next equation shouldn’t be \tau(…)=s?
In the last formula of exercise 20, you use \kappa instead C (but using C we have two letters C, for free cumulants and for cells).
In remark 8, I think there is a missing link in “these notes of Speicher”.
[Corrected, thanks – T.]
Nice notes, I learned a lot. Thanks!
10 August, 2010 at 6:13 pm
Anonymous
In the last formula of exercise 20, kappa is used for free cumulants, while the right letter is C.
Thanks a lot.
[Corrected, thanks – T.]
30 November, 2010 at 8:29 pm
Free Probability | Honglang Wang's Blog
[…] link about the survey of free probability. I hope it will be useful for you. Terry Tao also have a post about […]
3 March, 2011 at 10:11 am
FP Recent Follows « YW's E-Profile
[…] https://terrytao.wordpress.com/2010/02/10/245a-notes-5-free-probability/ […]
19 June, 2011 at 1:11 pm
Jérôme Chauvet
Dear Pr. Tao,
What if one is considering a setting {A,B}, with A and B being 2 (real-valued) sqaure matrices that do not commute with each other + a composition law on this set + a recursion that chooses at random for each step the multiplication order according to a Bernouilli law as follows:
u(n+1) = ABu(0) or u(n+1) = BAu(0)
I guess one instance of the recursion up to p (amongst 2^p of them) would look like:
u(n+p) = ABBABAAB….BAu(0)
And it would be akin to some sort of chaotic matrix K such that:
u(n+p) = K u(0) where X=ABBABAAB….BA
Though being not properly a random matrix (I mean matrices for which coefficients are gaussian variables…)
The question is: Would the probability measure of this system attainable by the theory you are presenting here?
Thanks a lot :)
20 June, 2011 at 10:38 am
Terence Tao
Random products of fixed matrices are well studied, being related to random walks on groups and expander graphs, but the regime studied (long products of small matrices) is different from the one where free probability is useful (short products of large matrices) and other tools are used instead (entropy, representation theory, spectral gaps, etc.).
27 March, 2012 at 7:00 am
Anonymous
Prof Tao,
Scalar (commutative) random variables should be a special case of non-commutative random variables, so I think that in this special case the two kinds of convolutions should be the same? But then we would have two central limit theorem with two different limit distribution?
27 March, 2012 at 7:15 am
Anonymous
Also, if A is a symmetric matrix, with entries i.i.d. Gaussian, the distribution of it is NOT the semicircle law. Then we take sum of n copies of it and divided by square root of n, and we get the same matrix, but on the other hand it converges to semicircle law?
I guess there is something fundamental that I misunderstood.
27 March, 2012 at 8:17 am
Anonymous
Sorry I read your notes again, and found that freeness is not the same with independence even in the commuting case! Please ignore my question!
18 August, 2012 at 9:06 pm
Noncommutative probability « Annoying Precision
[…] noncommutative probability provides such an approach. Terence Tao’s notes on free probability develop a version of noncommutative probability approach geared towards applications to random […]
25 October, 2012 at 10:11 am
Walsh’s ergodic theorem, metastability, and external Cauchy convergence « What’s new
[…] any , which we will use in the sequel without further comment; see e.g. these previous blog notes for proofs. (Actually, for the purposes of proving Theorem 3, one can specialise to the case (and […]
14 February, 2014 at 6:01 am
shubhashedthikere
Prof Tao,
I needed clarification regarding Example 3: Random matrix variables. Here is the space of random matrices a tensor product of the vector space L^{\infty-}( which is infinite dimensional) and (finite dimensional) vector space M_n({\bf C})? If yes, could you please tell me how would a tensor product for an infinite dimensional vector space is defined?
If {X \in L^{\infty-} \otimes M_n({\bf C})}, is not tensor product, then, could you please explain what exactly is this space of random matrices?
14 February, 2014 at 9:27 am
Terence Tao
If is an infinite-dimensional vector space and
is an infinite-dimensional vector space and  is a finite-dimensional vector space, one can define the tensor product by selecting a basis
is a finite-dimensional vector space, one can define the tensor product by selecting a basis 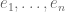 for
for  and defining
and defining  to be the set of all formal vectors of the form
to be the set of all formal vectors of the form 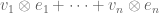 with
with 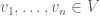 , with the vector space operations defined in the obvious manner. This defines a vector space
, with the vector space operations defined in the obvious manner. This defines a vector space  with a bilinear tensor product
with a bilinear tensor product 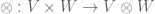 which obeys the usual tensor product axioms, and up to isomorphism this space does not depend on the choice of basis
which obeys the usual tensor product axioms, and up to isomorphism this space does not depend on the choice of basis 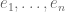 .
.
In the specific case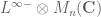 , this construction gives the space of
, this construction gives the space of  matrices whose entries are all in
matrices whose entries are all in 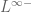 , i.e. random matrices with all moments finite.
, i.e. random matrices with all moments finite.
28 June, 2014 at 10:22 pm
Algebraic probability spaces | What's new
[…] probability space, and is very similar to the non-commutative probability spaces studied in this previous post, except that these spaces are now commutative (and […]
28 June, 2014 at 11:51 pm
Mustafa Said
Is there a version of the Erdos probabilistic method in the non-commutative setting?
16 April, 2015 at 11:09 pm
Anonymous
Could I ask for some hint to prove the first inequality in Exercise 3? My idea was to write the normal operator in terms of the bounded self-adjoint and commuting real and imaginary components. For the first two values of the exponent (1 and 2) it follows from the obvious identities (including Schwarz inequality). The case when the exponent is 3 or 4 has already some issues: some generalized (or perhaps smarter) versions of Schwarz inequality seem to be needed. I can handle the case 3 but the case 4 is even harder. Any suggestion?
17 April, 2015 at 8:02 am
Terence Tao
If is normal, then
is normal, then  .
.
28 March, 2017 at 3:12 pm
tornado92
A few typos: In Exercises 19 and 20, the final “additional formulas” seem to be swapped. Also, I think the formula for the third cumulant should actually be equal to the formula given for the third free cumulant. I guess they start differing at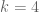 …
…
[Corrected, thanks – T.]
25 May, 2017 at 2:19 pm
Ranjan
The Expected value of f(X) not necessarily 0 for being independent with Y, please change the above notation.
31 August, 2017 at 1:03 pm
numberoftargets
It is never mentioned that expected of f(X) needs to be 0 for being independent with Y.
31 August, 2017 at 6:03 am
burakcakmakblog
Professor, In section 4 (i.e. Free convolution), how do you guarantee that we can expand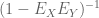 into a (formal) Neumann series? Because it requires that
into a (formal) Neumann series? Because it requires that  has the bounded eigenvalues below one.
has the bounded eigenvalues below one.
31 August, 2017 at 8:27 am
Terence Tao
A formal series does not require the partial sums to converge; in particular, a formal Neumann series such as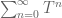 is well-defined even if
is well-defined even if  has spectral radius larger than 1.
has spectral radius larger than 1.
16 September, 2017 at 2:08 pm
Inverting the Schur complement, and large-dimensional Gelfand-Tsetlin patterns | What's new
[…] these previous notes for a discussion of free probability topics such as the […]
27 April, 2018 at 2:34 pm
tornado92
Possible typo: Example 3 states that for deterministic matrices, the spectral radius is the operator norm. This seems false–for example, what if the matrix is nilpotent? Then the spectral radius is zero, but the operator norm could easily be nonzero. I guess you need the matrix to be normal for this to work.
Another question: For bounded operators on a Hilbert space, there is already an existing notion of spectral radius, which is simply the radius of the smallest disc containing the spectrum. It turns out this is the limit of the kth root of the operator norm of the kth power, as k goes to infinity. However, in these notes, the spectral radius is defined in terms of the state. So my question is, is the spectral radius independent of the state you choose? If not, is there a state for which you recover the existing notion of spectral radius?
29 April, 2018 at 1:22 pm
Terence Tao
In these notes the spectral radius is only defined for self-adjoint elements. In the case where the noncommutative probability space is a space of bounded operators on a Hilbert space with trace given by a state, the spectral radius on this noncommutative space will always be bounded by the operator norm, and one will have equality as long as the state has a nontrivial component at the edge of the spectrum of the Hilbert space operator.
1 November, 2018 at 8:22 am
tpfly
Dear Mr. Tao,
I think I’ve found a counterexample of Exercise 28 (if I didn’t misunderstand the concept of free independence). Take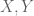 iid random variables uniformly distributed on the unit circle, with
iid random variables uniformly distributed on the unit circle, with 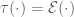 . then for any polynomial P,
. then for any polynomial P,  iff
iff 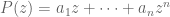 .
.
Now suppose ,
, 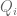 are polynomials without constant term, then we have
are polynomials without constant term, then we have
 . As defined,
. As defined,  are freely independent. But they are not scalars.
are freely independent. But they are not scalars.
Maybe in the definition of free independence we should be able to take in the polynomials?
in the polynomials?
[Oops, I meant to insert the hypothesis that are self-adjoint -T.]
are self-adjoint -T.]
4 September, 2019 at 11:30 am
Bharath Krishnan
Dear Professor Tao,
This does not directly address your post but is related to probability/measure theory. Measure theory, for continuous functions, has always been based on intuition. Currently, the most intuitive and well-known measure of functions defined in![[a,b]\cap\mathbb{R}](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%5Ccap%5Cmathbb%7BR%7D&bg=ffffff&fg=545454&s=0&c=20201002) , is the Lebesgue measure. However, when the Lebesgue measure of a function’s domain, defined on a subset of
, is the Lebesgue measure. However, when the Lebesgue measure of a function’s domain, defined on a subset of ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) is zero, the average could be outside the infimum and supremum of the function’s range. Since the average is strongly related to the measure and integration, we can say the Lebesgue measure is not intuitive enough.
is zero, the average could be outside the infimum and supremum of the function’s range. Since the average is strongly related to the measure and integration, we can say the Lebesgue measure is not intuitive enough.
If the Lebesgue measure is not intuitive enough what is an intuitive, unique average of a function on any domain.
There is a website below-showing intuitions and measures that I and other people think are alternatives to Lebesgue measure when the measure of the domain is zero.
https://math.stackexchange.com/questions/3329506/most-intuitive-average-of-p-for-all-x-in-a-cap-a-b-where-a-subseteq-m
8 December, 2019 at 3:47 pm
States on *-Algebras | Almost Sure
[…] the semi-norm defined above. Interestingly, Terry Tao uses exactly this definition of the norm in his posts on NC probability, although he does concentrate on tracial […]
26 December, 2021 at 3:48 pm
co.combinatorics - Combinatorial/diagrammatic fashions totally free significance partition polynomials Answer - Lord Web
[…] relationships“by Ebrahimi-Fard, Foissy, Kock and Patras; Ex. 37 by Terry Tao’s Notes on free chance; and P. 22 of “Enumeration geometry, tau capabilities and Heisenberg-Virasoro […]
31 December, 2021 at 5:57 pm
co.combinatorics - Combinatorics for the motion of Virasoro / Kac-Schwarz operators: partition polynomials of free chance principle Answer - Lord Web
[…] relationships“by Ebrahimi-Fard, Foissy, Kock and Patras; Ex. 37 by Terry Tao’s Notes on free chance; and P. 22 of “Enumeration geometry, tau features and Heisenberg-Virasoro algebra“by […]
8 January, 2022 at 12:19 pm
Tom Copeland
The previous two spam pingbacks from Lord Web contain corrupted copies of my MO-Q that completely algebraically characterizes the transformations between the free cumulants and moments for the single variable case, an alternative to Ex. 37 above, related to Kac-Schwarz operators. Correct version: Combinatorics for the action of Virasoro / Kac–Schwarz operators: partition polynomials of free probability theory
6 August, 2022 at 12:55 pm
What is the trace? – Alexander Van Werde
[…] probability theory is a beautiful subject but it would lead us too far to go into detail here. See this blog post by Terrence Tao or the list of literature on Roland Speicher’s blog if you wish to […]